A modified local control model for Ca²⁺ transients in cardiomyocytes: Junctional flux is accompanied by release from adjacent non-junctional RyRs

Abstract

Excitation-contraction coupling in cardiomyocytes requires Ca²⁺ influx through dihydropyridine receptors in the sarcolemma, which gates Ca²⁺ release through sarcoplasmic ryanodine receptors (RyRs). Ca²⁺ influx, release and diffusion produce a cytosolic Ca²⁺ transient. Here, we investigated the relationship between Ca²⁺ transients and the spatial arrangement of sarcolemma including the transverse tubular system (t-system). To accomplish this, we studied isolated ventricular myocytes of rabbit, which exhibit a heterogeneously distributed t-system. We developed protocols for fluorescent labeling and triggered two-dimensional confocal microscopic imaging with high spatiotemporal resolution. From sequences of microscopic images, we measured maximal upstroke velocities and onset times of local Ca²⁺ transients together with their distance from the sarcolemma. Analyses indicate that not only sarcolemmal release sites, but also those that are within 1 μm of the sarcolemma actively release Ca²⁺. Our data also suggest that release does not occur at sites further than 2.5 μm from the sarcolemma. The experimental data are in agreement with results from a mathematical model of Ca²⁺ release and diffusion. Our findings can be explained by a modified local control model, which constrains the region of regenerative activation of non-junctional RyR clusters. We believe that this model will be useful for describing excitation-contraction coupling in cardiac myocytes with a sparse t-system, which includes those from diseased heart tissue as well as atrial myocytes of some species.

1. Introduction

It is well established that the central mechanism underlying excitation-contraction coupling in heart is Ca²⁺ induced Ca²⁺ release (CICR). This was largely established by Fabiato (e.g. [1]), who inferred that an abrupt elevation of Ca²⁺ in the solution surrounding skinned cardiac cells produced a release of Ca²⁺ from the sarcoplasmic reticulum (SR) sufficient to activate contraction. Direct evidence that the Ca²⁺ current triggered contractions and presumably SR Ca²⁺ release was subsequently obtained by London and Krueger [2]. This was important since it suggested that a small transmembrane Ca²⁺ flux could trigger a much larger SR release flux, i.e. an amplification of release as Fabiato first suggested [1]. Fabiato’s work also suggested that, since Ca²⁺ itself triggers Ca²⁺ release one expects regenerative activation of all Ca²⁺ release sites in the cell.

However, Cannell et al. and Barcenas-Ruiz et al. were the first to demonstrate in isolated ventricular myocytes from rat and guinea pig, respectively, that the size of this release could be graded with the size of the Ca²⁺ current under voltage clamp [3, 4]. This created a difficulty. How could an inherently regenerative process (CICR) produce graded release? Stern proposed that one could explain graded release if it was controlled locally [5]. He proposed a “Ca²⁺ Synapse” model consisting in various arrangements of dihydropyridine receptors (DHPRs) and ryanodine receptors (RyRs). With these proposals it was possible to construct local control models that produced graded release.

Based on structural studies both Stern [6] and Franzini-Amstrong [7] subsequently proposed the existence of discrete Ca²⁺ release units or couplons for skeletal and cardiac myocytes, respectively. In cardiac myocytes couplons comprise more than one DHPR [8] in the sarcolemma, mainly in the transverse tubules (t-tubules). DHPRs are apposed to clusters of RyRs [9, 10] on the terminal cisternae of the SR. DHPRs and RyR clusters are separated by a junctional region of ~12 nm across. Sparks or local release events are evoked in the couplons [11, 12]. These are controlled locally [13] and sum to produce a macroscopic Ca²⁺ transient [14]. Moreover the recruitment of sparks and hence couplons was found to be graded with membrane voltage [13].

The existence of release events that could be controlled locally and recruited as a function of Ca²⁺ current magnitude supported Stern’s original explanation of the way that graded release could occur (4). However, during an action potential it seems that couplon recruitment is at maximum [8], which is consistent with the finding of Janczewski et al. that Ca²⁺ transients saturate under voltage clamp [15]. If this is the case it seems likely that the transient magnitude is controlled by modulating SR Ca²⁺ content and/or size of DHPR current. Other factors that could modulate the transient magnitude include the degree to which SR Ca²⁺ release is synchronized [16].

This fairly simple picture of EC coupling has been clouded by a number of studies suggesting the existence of RyR clusters that are not associated with DHPRs (e.g. [9, 17, 18]). Jorgensen originally suggested that these non-junctional RyRs are activated by a diffusional agent [19]. Such clusters are known to exist in atrial myocytes and are presumably activated by a mechanism of the type proposed by Jorgensen [20]. Spontaneous sparks produced by couplons do not necessarily activate other couplons or non-junctional RyRs regeneratively nor do spontaneous sparks produced by non-junctional RyRs evoke global Ca²⁺ release. This leads to a number of unanswered questions: For example, to what extent does the activation of non-junctional RyRs contribute to Ca²⁺ transients? What is the mechanism by which they are activated and can this activation be graded? These issues are of particular relevance to heart disease where non-junctional RyRs are produced by t-tubule loss [21].

To gain insight into these issues we acquired and analyzed two-dimensional images of the sarcolemma and Ca²⁺ transients at a high spatial and temporal resolution. The study was based on our previous work, in which we applied three-dimensional confocal microscopy to living left ventricular cardiac myocytes of adult New Zealand white rabbits to reconstruct and analyze their transverse tubular system (t-system) [22]. The image data revealed remarkable heterogeneity of t-system density in these cells. Regions with dense t-system exhibited a regular arrangement of tubules with spacing of ~2 μm in the longitudinal and ~1 μm in the transversal direction. However, in some intracellular regions t-system was absent and the distance to the closest sarcolemma was larger than in regions with a regular arrangement of the t-system. We took advantage of this spatial heterogeneity in isolated rabbit ventricular cells to investigate the relationship between Ca²⁺ release and the distance to sarcolemma. We tested the hypotheses that (1) Ca²⁺ release can occur at sites distant to the sarcolemma and (2) regions of ventricular myocytes lacking t-system do not exhibit Ca²⁺ release.

2. Material and Methods

2.1 Isolation of Rabbit Ventricular Myocytes

Ventricular myocytes were isolated from adult New Zealand White rabbits (2–2.5 kg) as previously described [22]. The animals received an intravenous injection of sodium pentobarbital (50 mg/ml) and heparin (10,000 USP/ml). The heart was quickly excised and the aorta cannulated. We used Collagenase P (Roche, Indianapolis, IN) and protease XIV (Sigma-Aldrich, St. Louis, MO) for enzymatic isolation of the cells using retrograde perfusion of the heart as described previously [23]. We stored the cells in a 1 mM Ca²⁺-HEPES-buffered saline solution at room temperature until usage. All procedures were in accordance with the NIH Guide for the Care and Use of Laboratory Animals and animal protection guidelines of the University of Utah.

2.2 Loading of Cells with Fluo-4 and Di-8-ANEPPS

Isolated cardiomyocytes were loaded with di-8-ANEPPS and fluo-4-AM (Invitrogen, Carlsbad, CA) as a marker for sarcolemma and indicator for Ca, respectively. We loaded the cells with 12.5 μM of fluo-4-AM (Invitrogen, Carlsbad, CA, USA) for 15 min at room temperature. After 10 min we added 6.25 μM of di-8-ANEPPS (Invitrogen, Carlsbad, CA, USA). After 15 min we placed the cells in an imaging chamber and let them set for 10 min. The glass slide at the bottom of the imaging chamber was coated with mouse laminin (BD Biosciences, San Jose, CA). Subsequently, the cells were constantly superfused at room temperature with a modified Tyrode solution containing (in mM): 4.4 KCl, 138 NaCl, 1 MgCl₂, 2 CaCl₂, 11 dextrose, 24 Hepes, 0.5 probenecid (pH 7.4 adjusted with NaOH).

2.3 High Speed Scanning of Living Cardiomyocytes

Cell segments were imaged within 5 h after isolation. Imaging was performed with a confocal microscope (Zeiss Live 5 Duo, Carl Zeiss, Jena, Germany) using a 63x oil immersion lens having a numerical aperture of 1.4. A schematic representation of imaging setup is presented in Fig. Supp 1. The measured point spread function (PSF) for this imaging system is shown in Fig. Supp 2. The confocal aperture was set to an Airy number of 1. Images covered an area of 1024 x 96 pixels with a spatial sampling at 0.1 μm and a temporal resolution of 3.64 ms. The dyes were excited with a 489 nm laser diode. The laser intensity was set to a small level allowing for analysis of the signals to minimize photobleaching. The fluorescent emission was separated using a dichroic beam splitter (NFT 535 nm). The emitted light was filtered using band-pass filters of 505–610 nm and 560–675 nm. Image acquisition was triggered 36.4 ms before electrical stimulation of the imaged cell using an adjacent electrode. Typically 50 images of the fluo-4 and di-8-ANEPPS associated fluorescence were acquired. Only image scans before significant contraction of the myocytes were used for subsequent analysis.

2.4 Image Segmentation from Di-8-ANEPPS Scans and Generation of Distance Maps

The outer sarcolemma of myocyte segments was manually outlined in the initial di-8-ANEPPS image. Gaussian filtering (stddev: σ_x=σ_y=0.05 μm, σ_t=3.64 ms) was applied to the image sequence. Thresholding of the filtered initial image was applied to identify the sarcolemma including t-system. The threshold t was calculated as:

$$\mathrm{t}=\mathrm{m}+2\mathrm{\sigma }$$

with the mode m and stddev σ of the intensity distribution. We calculated distance maps, which specify the distance between each pixel in the cell and its closest pixel identified as sarcolemma. All methods of image processing and analyses were implemented in Matlab (R2012b, Mathworks, Natick, MA). For a more detailed description of the image processing methods we refer to, for instance, Gonzalez and Woods [24].

2.5 Analysis of Fluo-4 Images

The fluo-4 images provide local information on the initial phase of the Ca²⁺ transient configured by several processes including diffusion of Ca²⁺ from neighboring sites, sarcolemmal fluxes and release from the SR. Analysis of fluo-4 images was limited to regions adjacent to sarcolemma and in the cell interior. Mean background signal intensity was detected in the cell exterior and removed. Gaussian filtering (stddev: σ_x=σ_y=0.1 μm, σ_t=3.64 ms) was applied to the image sequence. The images were self-ratioed using the mean fluo-4 intensity (I₀) in the cell interior before stimulation. Approximately 10 images were used to calculate I₀. A 4^th-order polynomial was fit to the filtered self-ratioed transient of each pixel. Analysis of this polynomial allowed us to estimate the maximal upstroke velocity and the time that it occurs. We defined maximal upstroke velocity as the maximal derivative of the self-ratioed local Ca²⁺ signal and present it in percent per millisecond (%/ms). We determined the maximal upstroke velocity by the maximal derivative of the 4^th-order polynomial of the Ca²⁺ signal. Using the polynomial fit, the time of maximal upstroke velocity for each pixel was determined. We used it as an indicator for the onset of the local transient. Only cells with mean onset time below 25 ms after stimulation were analyzed.

2.6 Distance-Onset Time and Distance-Maximal Upstroke Velocity Relationships

Relationships between sarcolemmal distance and onset time were described by a quadratic equation. Parameters of the relationship were determined by least square minimization:

$$\underset{\mathrm{a},\mathrm{b}}{min}\sum _{\mathrm{x}\in \mathrm{S}}{\left(\text{onset}(\mathrm{x})-(\mathrm{a}+\mathrm{b}\text{distance}(\mathrm{x}))\right)}^2$$

with the parameters a and b, and the set of pixels S. The functions onset(x) and distance(x) yield the onset time and distance to the sarcolemma for a given pixel at location x. We described the relationship between sarcolemmal distance and maximal upstroke velocity by minimization:

$$\underset{\mathrm{a},\mathrm{b}}{min}\sum _{\mathrm{x}\in \mathrm{S}}{\left(\text{upstroke}(\mathrm{x})-(\mathrm{a}+\mathrm{b}\text{distance}(\mathrm{x}))\right)}^2$$

Here, the relationship is described by a linear function. The function upstroke(x) yields the maximal upstroke velocity for a pixel at location x.

2.7 Computational Modeling of Ca²⁺ Signals and Their Imaging

Simple models of Ca²⁺ diffusion and binding to buffers were developed to simulate confocal image data. The models were implemented in CalC (version 7.2)[25] and based on previously published parameters [26–29]. The spatial domain was hexahedral and had a size of LX x 1 μm x 1 μm with a length in x-direction LX of 2, 4 and 6 μm (Fig. Supp 3A). The spatial domain was discretized with cubic elements with an edge length of 0.05 μm.

The concentration of free Ca²⁺ in the myoplasm [Ca²⁺]_MYO was described based on the 3-dimensional diffusion equation:

$$\frac{\partial {\left[{\text{Ca}}^{2+}\right]}_{\text{MYO}}}{\partial \mathrm{t}}={\mathrm{D}}_{\text{MYO}}{\nabla }^2{\left[{\text{Ca}}^{2+}\right]}_{\text{MYO}}+{\mathrm{J}}_{\text{RYR}}-{\mathrm{J}}_{\text{BUF}}-{\mathrm{J}}_{\text{FLUO}}$$

with the diffusion coefficient D_MYO, the fluxes through RyR clusters J_RYR, fluxes related to binding of free Ca²⁺ to immobile buffers J_BUF, and fluxes related to binding of free Ca²⁺ to fluo-4. Fluxes were defined as

$$\begin{array}{l}{\mathrm{J}}_{\text{RYR}}=\frac{{\mathrm{\delta }}_0{\mathrm{I}}_{\text{RYR}}}{\left(2\mathrm{F}\mathrm{\delta }\mathrm{V}\right)}\\ {\mathrm{J}}_{\text{BUF}}={\mathrm{\alpha }}_{\text{BUF}}{\left[{\text{Ca}}^{2+}\right]}_{\text{MYO}}\left({[\text{BUF}]}_{\text{TOTAL}}-[\text{BUF}-\text{Ca}]\right)-{\mathrm{\beta }}_{\text{BUF}}[\text{BUF}-\text{Ca}]\\ {\mathrm{J}}_{\text{FLUO}}={\mathrm{\alpha }}_{\text{FLUO}}{\left[{\text{Ca}}^{2+}\right]}_{\text{MYO}}\left({[\text{FLUO}]}_{\text{TOTAL}}-[\text{FLUO}-\text{Ca}]\right)-{\mathrm{\beta }}_{\text{FLUO}}[\text{FLUO}-\text{Ca}]\end{array}$$

with parameters described in Table 1, the Faraday constant F, the volume fraction δV, the concentration of Ca²⁺-bound immobile buffers [BUF-Ca], and the concentration of Ca²⁺-bound fluo-4 [FLUO-Ca]. Two different formulations of J_RYR were used: an exponential decay function (default) and a rectangular function. The function δ₀ is 1 at grid elements of the release site and 0 elsewhere. The release site was central in the spatial domain (Fig. Supp 3B). The diffusion of Ca²⁺-bound fluo-4 was described as:

$$\frac{\partial [\text{FLUO}-\text{Ca}]}{\partial \mathrm{t}}={\mathrm{D}}_{\text{FLUO}}{\nabla }^2[\text{FLUO}-\text{Ca}]+{\mathrm{J}}_{\text{FLUO}}$$

TABLE 1.

Model parameters.

Parameter	Symbol	Value
Ca2+ diffusion coefficient in myoplasm	DMYO	0.3 μm2/ms
Initial Ca2+ concentration in myoplasm	[Ca2+]	0.1 μM
Fluo-4 diffusion coefficient	DFLUO	0.09 μm2/ms
Total fluo-4 concentration	[FLUO]	50 μM
Forward rate of Ca2+ binding to fluo-4	αFLUO	0.4/(μM ms)
Backward rate of Ca2+ binding to fluo-4	βFLUO	0.16/ms
Total immobile buffer concentration	[BUF]	123 μM
Forward rate of Ca2+ binding to buffer	αBUF	0.1/(μM ms)
Backward rate of Ca2+ binding to buffer	βBUF	0.1/ms
Time range for Ca2+ release	-	5 – 10 ms
Radius of Ca2+ release site	-	0.1 μm
Release current	IRYR
- Duration		10 ms
- Exponential: Amplitude/Time constant/Offset		9.5 pA/2 ms/0.5 pA
- Rectangular: Amplitude		2 pA

Neumann boundary conditions for [Ca²⁺]_MYO and [FLUO-Ca] were assigned to all borders of the spatial domains to model an periodic arrangement of release sites in cells (Fig. Supp 3C–E).

Confocal imaging as described above for the fluo-4 signal was approximated by convolution of the distribution of calculated [FLUO-Ca] with the measured PSF. The PSF was modeled using a Gaussian function with stddev σ of 355, 230 and 720 nm in x-, y- and z-direction (Fig. Supp 2). The simulation data were resampled with a spatial discretization of 0.1 μm and temporal discretization at 277 Hz, before analyzing it using the same methods as for analysis of fluo-4 signals.

2.8 Measurements of Spontaneous Sparks in Rabbit Ventricular Myocytes

Isolated myocytes were loaded with fluo-4-AM and placed in an imaging chamber as described above. We evoked spontaneous sparks with the cells in modified Tyrode solution having a Ca²⁺ concentration of 4 mM and 1 μM isoproterenol. We recorded continuous transverse line scans with a confocal microscope (Biorad MC-1024, Bio-Rad Laboratories, Hercules, CA). We used a spatial sampling of 0.13 or 0.26 μm and a temporal resolution of 2 ms/scan line. The fluo-4 was excited with a 488 nm laser. Emitted light was filtered using a 522DF22 filter. We processed the images using ImageJ [30] and Sparkmaster [31]. The sparks were detected with a detection threshold of 3.8. We measured the maximal upstroke velocity and the full width at half-maximal amplitude (FWHM) from background corrected and self-ratioed images.

2.9 Characterization of RyR distributions in Cardiomyocytes

The sarcolemma of isolated cardiac myocytes was labeled using wheat germ agglutinin (WGA) conjugated to Alexa Fluor 555 (Molecular Probes, Eugene, OR) as described before [22]. After labeling with WGA the cells were fixed for 20 min at room temperature with 2% paraformaldehyde and washed afterwards with phosphate buffered saline (PBS) solution. Cells were attached to a chamber using polylysine and permeabilized with PBS solution containing 0.1% Triton X-100 for 15 min. Cells were incubated in Image-iT FX Signal Enhancer (Molecular Probes, Eugene, OR) for 30 min and blocked during 60 min using a PBS solution with additional 10% normal goat serum (NGS, Millipore, Billerica, MA). Afterwards the cells were incubated overnight at 4°C with the monoclonal anti-RyR2 antibody (C3-33, Pierce Biotechnology, Rockford, IL) prepared in PBS. Next day the cells were incubated for 60 min with a secondary goat anti mouse IgG (H+L) antibody attached to Alexa Fluor 488 (Molecular Probes, Eugene, OR) and stored in PBS solution. The cells were rinsed three times with PBS for 15 min per rinse between incubation steps. ProLong Gold Antifade Reagent (Molecular Probes, Eugene, OR) was added to the cells 24 h prior to image them.

Three-dimensional imaging was performed with a confocal microscope (Zeiss Live 5 Duo) equipped with an oil immersion lens (magnification: 63x, numerical aperture: 1.4). The confocal aperture was set to an Airy number of 1. The Alexa Fluor 488 was excited with a 488 nm laser line. The emitted light was band-pass filtered at 505 to 530 nm. Alexa Fluor 555 was excited with a 543 nm laser. The emitted light was long-pass filtered at 560 nm. We used a two-track protocol for spatial registration of WGA and RyR2 image stacks. Image data were filtered, deconvolved and corrected for background signals and depth dependent attenuation as previously described [32]. The sarcolemma was detected by thresholding of the WGA image stacks followed by median filtering [33]. The threshold was calculated from image statistics as described above. Two different Euclidean distance maps were calculated from the sarcolemmal segments. The first distance map (3D) was based on the three-dimensional segmentation of the WGA image stacks. The second distance map (2D) was calculated for each horizontal image individually. Only WGA segments in a horizontal image were considered for the calculation of its distance map. From both Euclidean distance maps, distances between centers of RyR clusters and the sarcolemma were determined.

2.10 Statistical Analysis

Statistical data are presented as mean±standard deviation (stddev). Statistical significance was assessed using OriginPro (9, Northampton, MA) by one-way ANOVA followed by post-hoc Tukey-Kramer (P < 0.01).

3. Results

3.1 Measurement of Two-Dimensional Ca²⁺ Transients

Our previous study on isolated rabbit ventricular cells indicated that a significant fraction of RyR clusters are not associated with the sarcolemma [33]. Those clusters that are associated with sarcolemma (including t-system) and form couplons appear to be under local control [13]. However it is unclear how those RyRs that are not associated with t-system (non-junctional RyRs) are activated and controlled during an action potential.

We simultaneously loaded cells with di-8-ANEPPS and fluo-4 to identify the location of sarcolemma and to measure Ca²⁺ transients. Fig. 1A shows di-8-ANEPPS signals from a section through a myocyte. The cells were subject to two-dimensional rapid scans prior to and during the upstroke of the transient. The scans (Fig. 1B) clearly show the development of the transient. Initially (at 7.2 ms after stimulation) local release events can be clearly distinguished and these appear to coincide with the location of sarcolemma, predominantly t-tubules. These Ca²⁺ transients are spatially inhomogeneous. Eventually fluorescence spreads from regions associated with sarcolemma to regions that are not (14.4 to 28.8 ms). From the di-8-ANEPPS image we segmented the cell interior including t-system. The t-system was subsequently identified using thresholding (Fig. 2A). Examples of fluo-4 transients from two locations are presented before and after pre-processing in Fig. 2B and C, respectively. One location is close to a t-tubule and another distant from the sarcolemma where one expects to find non-junctional RyRs. It is clear that the transient from some regions close to the sarcolemma, primarily t-tubules, rises rapidly and that those from regions distant from the sarcolemma display a slower delayed rise, but do reach a similar peak value as transients measured close to the t-tubule.

Fig. 1.

Imaging of dual-labeled isolated myocyte and image analysis. (A) Di-8-ANEPPS labeling reveals the sarcolemma including the t-system. (B) Labeling with the Ca²⁺ indicator fluo-4 produced low intensity signals in cells at rest. Scattered increases of fluo-4 intensity occurred 7.2 ms after stimulation. Fluo-4 images at 14.4, 21.6 and 28.8 ms after stimulation show progressively increasing signal intensities. Bar: 10 μm.

Fig. 2.

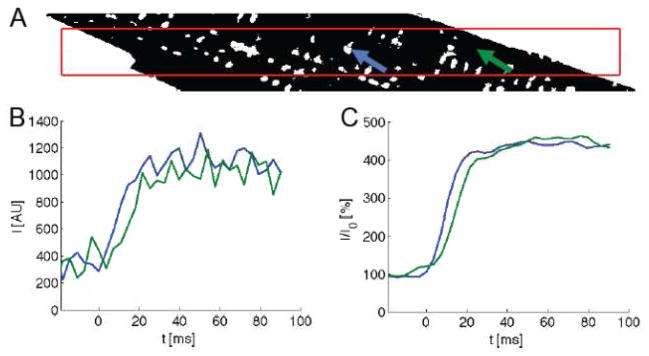
Image processing from a representative myocyte (same cell as in Fig. 1). (A) A myocyte segment was manually outlined in the di-8-ANEPPS image and then refined by thresholding. The cell interior and exterior is shown in black and white, respectively. The red box indicates the area used for later statistical analyses. (B) Fluo-4 signals at the sites marked with arrows in (A). (C) The signals after filtering and self-ratioing.

To understand the origin of these transients we constructed maps of the spatial relationships between transients and the membranes nearest to them. We used the maximal upstroke velocity for each pixel to characterize the transients. If a pixel happens to reside at the site of a couplon then the maximal upstroke velocity will provide a measure of the release of Ca²⁺ from that couplon. The same thing is true of a pixel that resides at the site of a non-junctional RyR cluster. If release is activated from that cluster then the maximal upstroke velocity will measure its release flux. Pixels residing in other locations with no release sites will reflect the diffusion of Ca²⁺ from the release sites.

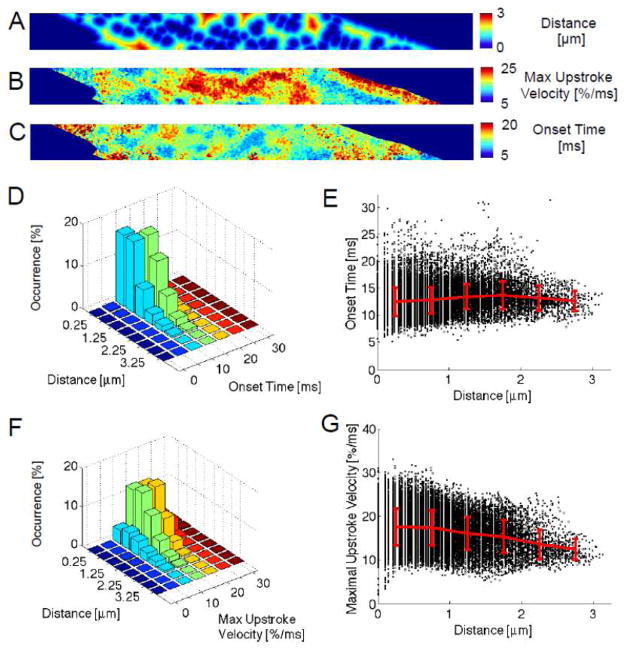
Analysis of distance maps created from the di-8-ANEPPS images revealed that in regions without t-system, the distance to the sarcolemma was up to 3 μm, although the majority of pixels were within 1 μm of the sarcolemma (Figs. 3A and Supp 4). The distribution of maximal upstroke velocities is shown in the map in Fig. 3B. Our analysis also yielded maps of the delay to the initiation of the fluo-4 signal increase (Fig. 3C). By comparing the maximal upstroke velocity maps with the distance maps one can see that regions with maximal upstroke velocity tend to coincide with regions close to the sarcolemma, whereas maximal upstroke velocities of lower magnitude are apparent in regions distant from the sarcolemma. It seems highly likely that the rapid upstroke velocities near membranes are due to Ca²⁺ from couplons associated with, for example, t-tubules. However, it is not immediately apparent from these maps whether or not the rate of rise of fluorescence in regions at varying distances from the sarcolemma are due to release from non-junctional RyR clusters or simply reflect diffusion from distant release sites that are activated. It is also clear in the map in Fig. 3C that onset times often increase with distance from the sarcolemma. This could simply reflect the time required for Ca²⁺ to diffuse from sites where active release occurs or could reflect delays in the time required to generate active triggered release from RyR clusters that are non-junctional. For further analysis, the data are presented as three-dimensional histograms and scatter plots. First we plotted the occurrence of pixels with specified Ca²⁺ transient onset times as a function of distance from the nearest sarcolemma (Figs. 3D and E). We found an increasing relationship between sarcolemmal distances and onset times with a slope of 0.66 ms/μm. At distances less than 1 μm from the sarcolemma mean onset times were smaller than at distances larger than 2 μm (P<0.001). It is apparent that extremely short onset times occur less frequently in regions farther from the sarcolemma. However, even sites in close proximity to the membrane exhibited late onset times. The relationship between sarcolemmal distances and maximal upstroke velocities in this cell was more distinct (slope: −1.73 %/ms/μm) (Figs. 3F and G). The difference between maximal upstroke velocities in a distance of 0–0.5 μm and 0.5–1 μm was not significant (P: 0.09). For both distance ranges pixels exhibited large maximal upstroke velocities (for instance, velocities >25 %/ms). Mean maximal upstroke velocities were higher in these distance ranges than at distances between 2–2.5 and 2.5–3 μm (for all comparisons P<0.001). An overview of measured distances, maximal upstroke velocities and onset times for this cell is shown in the histograms in Fig. Supp 5.

Fig. 3.

Analysis of image scans from a representative myocyte (same cell as in Fig. 1). (A) A distance map specifies the distance of each pixel to the nearest pixel classified as sarcolemma. (B) Maximal upstroke velocity in the self-ratioed fluo-4 signal of each pixel is presented as a map. (C) The map of onset times describes the time of maximal upstroke velocity in the fluo-4 signal. (D,E) Distance-onset time and (F,G) distance-maximal upstroke velocity relationships of the representative myocyte. Each point in the scatter plots in (E) and (G) corresponds to a pixel and its extracted features. These points are grouped according to distance and their mean±stddev is shown in red. Analyses involved 30151 pixels.

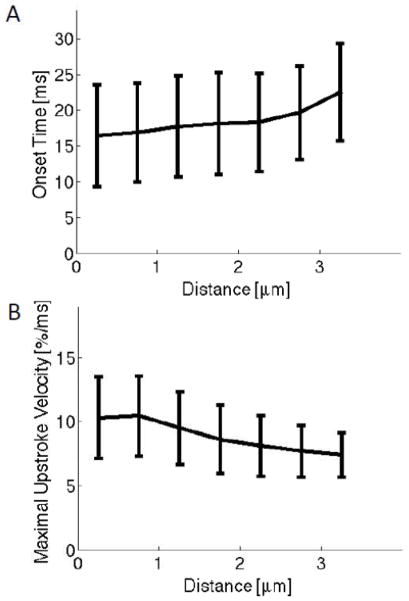
Results of analysis of 11 cells from 7 animals are summarized in Fig. 4. Onset times increased from 16.5±7.1 ms at sites with sarcolemmal distances smaller than 0.5 μm to 22.5±6.8 ms at distances ranging between 3 and 3.5 μm (Fig. 4A). Maximal upstroke velocities at sarcolemmal sites decreased from 10.4±3.2 %/ms to 7.4±1.7 %/ms at distances between 3 and 3.5 μm (Fig. 4B). We compared the maximal upstroke velocities in a distance of 0–0.5 μm and 0.5–1 μm. Differences were statistically significant (P<0.001), but the differences of mean and SD were very small (0.14 and 0.05%/ms, respectively) in these groups. Statistical data for the group of cells are presented in Table 2. Ca²⁺ transients exhibited a positive relationship between sarcolemmal distance and onset time, and a negative relationship between distance and maximal upstroke velocity. Mean onset times were smaller at sites within 1 μm of the sarcolemma than at distances larger than 2 μm (for all comparisons P<0.001). Mean maximal upstroke velocities were higher at sites within 1 μm of the sarcolemma than at distances larger than 2 μm (for all comparisons P<0.001).

Fig. 4.

Statistical analysis of group of 12 cells. (A) Onset time increased with distance from the sarcolemma. (B) Maximal upstroke velocity decreased with sarcolemmal distance. Data were grouped according to distance to the sarcolemma. Bars specify stddev.

TABLE 2.

Statistical analyses of cells presented as mean±stddev and parameters of linear fit.

Feature	Value
Sarcolemmal distance	0.89±0.14 μm
Onset time	17.25±4.99 ms
Distance-onset time (a, b)	(16.74 ms, 0.37 ms/μm2)
Maximal upstroke velocity	9.87±5.33 %/ms
Distance-maximal upstroke velocity (a, b)	(10.87 %/ms, −1.08 %/ms/μm)

3.2 Computational Modeling of Ca²⁺ Signals and Their Imaging

It is widely accepted that Ca²⁺ transients are the summation of local release events [14]. Our measurements are largely consistent with this view. However, it is clear that there are two types of local release events to be considered. The first is evoked release from couplons, which comprise both SR Ca²⁺ release and some Ca²⁺ current. The second type of local release event, if it occurs, must come from non-junctional RyR clusters, which appear to be quite numerous in rabbit. We therefore considered the hypothesis that the Ca²⁺ rise in non-junctional regions occurred because Ca²⁺ diffused from junctional regions. The alternative to this is that some or all of the Ca²⁺ appearing in non-junctional regions is produced by evoked release from some or all of the non-junctional RyRs together with any Ca²⁺ that diffuse from couplons which are activated relatively synchronously (see discussion). We therefore examined the properties of a modeled spark based on numerical solutions of 3D diffusion equations. A spark modeled using this approach does not appear as a measured spark because properties of the imaging systems are neglected. Furthermore, the labeling approach applied by us does not provide direct information on the distribution of free Ca²⁺ in the myoplasm, but on the Ca²⁺ bound to fluo-4. However, our modeling does provide a starting point for understanding how Ca²⁺ might diffuse from a source region e.g. a couplon to extra-sarcolemmal regions. Results of the modeling display the variation in Ca²⁺ signal, i.e. the self-ratioed [FLUO-Ca], as a function of time, distance to a release site and size of the spatial domain. Figs. 5A and B show the Ca²⁺ signal at different time points over a distance of 1 μm to the release site. In this simulation, the spatial domain approximating an intracellular region spanned 2 μm x 1 μm x 1 μm and the release site was central in this domain. The signal first rises from a low value of 1 at 0 ms (Fig. 5B, blue line) and at its peak exceeds 4 at 10 ms (red line). At 20 ms the spark has dissipated and the signal is significantly above background (light blue line). The spark continues to dissipate until at 30 ms the Ca²⁺ distribution is equilibrated. We convolved this signal with a suitable PSF, re-sampled the signals at a rate of 277 Hz and filtered it to obtain a more realistic view of what one might observe with a confocal microscope. The characteristics of the signal changed after this procedure; in particular the peak value is reduced (Figs. 5C and D). However, the spatial distribution and time course of the transient change little. We also performed simulations in spatial domains with increased sizes in x-direction (Fig. Supp 6). These arrangements reflect cell regions with increased distances to release sites.

Fig. 5.

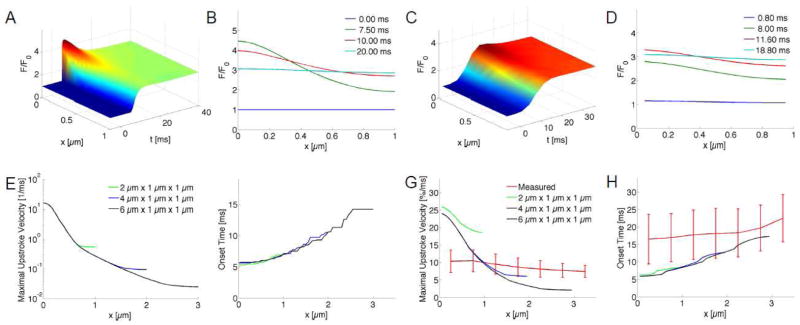
Modeling and analysis of Ca²⁺ signals. (A) [FLUO-Ca] was calculated in a three-dimensional domain with a size of 2 μm x 1 μm x 1 μm with a single central release site. Release at the site (x=0 μm) occurred at t=5 ms. The self-ratioed signal [FLUO-Ca]/ [FLUO-Ca]₀ (F/F₀) was plotted along the along the x-semiaxis. (B) The signal along the x-axis is shown at 0, 7.5, 10 and 20 ms. (C,D) The signal was sampled at 277 Hz, convolved with a PSF and filtered as for processing of measured fluo-4 images. The signal exhibits blurring and attenuated peak values versus (A). (E) The maximal upstroke velocities were calculated from simulations with different domain sizes. All models had a single central release site. Upstroke velocities were maximal at the release site and exhibit an approximately exponential attenuation with distance to the release site. (F) Activation times were minimal at the release site and delayed of up to 14.2 ms at distal sites (x=3 μm). (G) Maximal upstroke velocity of self-ratioed modeled transient from (C) overlaid with measured data (red). (H) Modeled activation times overlaid with measured data (red).

Analyses of the modeled sparks are presented in Figs. 5E–H. Using the data shown in Figs. 5A, Supp 6A and Supp 6E, the maximal upstroke velocities exceed 15/ms at the release site (Fig. 5E). Onset times have an increasing relationship with the distance to the release site (Fig. 5F). Their range is 5.1 to 14.2 ms. Using the convolved, resampled and filtered data in Fig. 5C, Supp 6C and Supp 6G, the maximal upstroke velocity is decreased to 26.0, 24.1 and 24.1 %/ms, respectively (Fig. 5G). Velocities at 1 μm are reduced to 18.5, 10.2 and 9.8 %/ms. Onset times have a range from 5.9 to 17.4 ms (Fig. 5H). The onset times exhibit a similar distribution as the onset times from the original signal before accounting for the imaging process (Fig. 5F).

We next compared our experimental data with computed onset times and maximal upstroke velocities. Both, simulated and mean experimental maximal upstroke velocities, decrease with distance to the release site and sarcolemmal distance, respectively (Fig. 5G). At the release site mean experimental maximal upstroke velocities are smaller than the computed velocities, which reflects that only a small number of pixels are associated with release sites. This is also visible in Fig. 3G showing peak upstroke velocities similar as the simulated velocities. The simulated upstroke velocities from all models decrease monotonically with increasing distance to the release site. This is inconsistent with the mean and stddev of measured upstroke velocities, which are similar within a sarcolemmal distance between 0 to 1 μm. Both, simulated and mean experimental onset times, increase with distance to the release site and sarcolemmal distance, respectively (Fig. 5H). For distances between 0 and 1 μm, the simulated onset times are similar to mean minus one stddev of the experimental onset times. The slope of simulated onset times is larger than the slope of mean experimental onset times.

In additional simulations we explored sensitivity of these findings on model parameters, in particular D_MYO, [FLUO]_TOTAL and the formulation of I_RYR (Fig. Supp 7). These simulations demonstrate that an increase of D_MYO to 0.6 μm²/ms, an increase of [FLUO]_TOTAL to 250 μM and a rectangular I_RYR of 2pA for 10 ms affect the maximal upstroke velocities. However, the distance-upstroke velocity relationship remains similarly monotonically decreasing as in simulations using the standard model parameters (Fig. 5G). The simulations revealed also sensitivity of onset time on model parameters. In particular, the rectangular I_RYR led to increases in onset time (Fig. Supp 7F) versus simulations with an exponentially decaying I_RYR (Fig. 5H).

From these results we reached the broad conclusion that at least within 1 μm of the sarcolemma non-junctional RyRs are activated. Based on our spatial analysis (Fig. 6), approximately 75% of RyR clusters are within this distance and at least one third of those are non-junctional. The reason for our conclusion is straightforward. If upstroke velocities were determined by diffusion they would fall rapidly with distance as the model suggests. However, our imaging data reveal that the upstroke velocity distributions are similar over the first micrometer, which is difficult to explain unless non-junctional RyRs are activated.

Fig. 6.

Distribution of RyR clusters and their spatial relationship to the sarcolemma in rabbit ventricular myocytes. (A) Overlay of images showing arrangement of sarcolemma including t-system and RyR clusters. WGA is shown in blue, RyRs in red. The images reveal RyR clusters in close proximity to the sarcolemma, but also clusters in distance from the sarcolemma. Scale bar: 5 μm. (B) Three-dimensional visualization of sarcolemma and RyR clusters in cell segment. Centers of RyR clusters are marked by spheres. (C) Histogram of distances between centers of RyR cluster to the closest sarcolemma. Distances of the centers were calculated from the image stacks (3D) and for each image slice (2D). Calculations in 2D overestimate the distance between sarcolemma and RyR cluster centers.

3.2 Computational Modeling and Measurement of Spontaneous Sparks in Rabbit Ventricular Myocytes

Computational modeling allowed us to characterize the spatial distribution of maximal upstroke velocities and onset times in small regions of a myocyte. Using Neumann boundary conditions the models reflect a periodic arrangement of release sites. Insights from the modeling were primarily based on the spatial distribution of maximal upstroke velocities, in particular, their decrease proximally and distally to the release site (Fig. 5E and G). The maximal upstroke velocities occurred within the first 12.2 ms after initiating release (Fig. 5F and H).

Here, we provide an evaluation of our modeling approach using measurements of spontaneous sparks in isolated cells. We modeled the spontaneous spark similarly as described above but with an enlarged spatial domain (6 μm x 6 μm x 6 μm) to account for low probability of spontaneous sparks under our experimental conditions. The maximal upstroke velocity in this simulation was 12.6 %/ms. Results from the analysis of 16 sparks measured in 8 myocytes are presented in Table Supp 1. The maximal upstroke velocity was 19.4±5.9 %/ms. Myocytes were bathed in Tyrode solution having a Ca²⁺ concentration of 4 mM and 1 μM isoproterenol to produce the spontaneous sparks. It is well established that these conditions cause increased Ca²⁺ release [34], which at least in part explains the larger maximal upstroke velocities in our experimental versus modeling data.

We used the same simulation setup to investigate the variance of maximal upstroke velocities and onset times observed in the measured transients. We calculated variances caused by Ca²⁺ releases, which are above or below the image plane (Fig. S8). The distance of sources in z-direction varied between −1 and 1 μm. The z-distance of the release site to the image plane has a strong effect on the simulated maximal upstroke velocities. Mean and stddev of the velocities decreased with increasing distance in x-direction. The measured decrease is inconsistent with the mean and stddev of measured upstroke velocities, which are similar within a sarcolemmal distance between 0 to 1 μm. In contrast the effect of z-distance on onset time was small. For all studied z-distances the mean onset times exhibited a similar relationship to the distance in x-direction. The stddev of the simulated onset times was small in comparison the measured stddev.

3.3 Characterization of RyR Distribution in Cardiomyocytes

Our prior studies on isolated ventricular myocytes of rabbit revealed non-junctional RyR clusters [33]. Here, we provide detailed quantitative information on the spatial relationship between RyR clusters and sarcolemma. We imaged segments of 10 cardiomyocytes that were labeled with antibodies for RyR2 and WGA as a marker for sarcolemma including the t-system. Visual inspection of image slices and three-dimensional reconstructions reaffirmed the occurrence of RyR clusters that are not associated with sarcolemma (Figs. 6A and B). Based on 3D distance maps calculated from the WGA images, the RyR-sarcolemma distance was 0.57±0.61 μm. Furthermore, we measured distances between the RyR clusters and sarcolemma from 2D distance maps. Using those maps the RyR-sarcolemma distance was 0.95±1.13 μm. Histograms of the distribution of RyR-sarcolemma distances for 3D and 2D distance maps are shown in Fig. 6C. The histogram comprises two populations of RyR clusters, one junctional, the other one non-junctional. Junctional RyR clusters are adjacent to sarcolemma and thus contribute to occurrence in the group with a sarcolemmal distance of 0–0.5 μm. The group-wise occurrence of non-junction RyR clusters for sarcolemmal distances larger than 0.5 μm exhibits an approximately exponential decay. Our analyses of Ca²⁺ transients are based on distance maps that are similar to 2D distance maps. Calculations based on 2D distance maps overestimate the distance between sarcolemma and RyR cluster centers by 0.37±0.72 μm.

4. Discussion

Studies of Ca²⁺ transients during excitation-contractions coupling are commonly based on fast line scanning confocal microscopy, which limits the characterization of complex three-dimensional structure-functional relationships. To mitigate this limitation, we used rapid two-dimensional scanning confocal microscopy. We undertook this study to establish the nature of the Ca²⁺ transient as it occurs in two dimensions. A similar approach was chosen by Cleeman et al. to investigate transients in rat ventricular myocytes [35]. In these cells the t-system is dense and most RyRs are junctional. The study suggested that most Ca²⁺ releases occur at t-tubules. Here, we were particularly interested in establishing whether or not non-junctional clusters of RyRs are activated during evoked Ca²⁺ transients. For several (but not all) types of heart failure it is known that t-tubules are lost and reorganized and the number of non-junctional RyRs increases [32]. It is therefore of interest to know how this affects transients. In general isolated rabbit cells exhibit relatively sparse t-tubules and numerous non-junctional RyRs. The extent to which this is an intrinsic property of these cells or is to some extent an artifact of the cell isolation procedure is unknown. In either case these cells are useful for examining the way that Ca²⁺ spreads into areas that contain non-junctional RyRs. Studies with these cells provide some insights into the consequences of t-tubular loss in heart failure.

Our results clearly indicate that Ca²⁺ transients originate in the vicinity of sarcolemmal membranes principally t-tubules. Transients in these regions arise in an, in part, synchronous manner, with some sarcolemmal regions lagging. Ca²⁺ then spreads from initially activated sarcolemmal areas to regions where only non-junctional RyRs exist. Similar results have been established in skeletal muscle [36] and it was proposed that opening of RyR3s was activated by Ca²⁺, secondarily to Ca²⁺ release through junctional RyR1s. Although it provides some precedent for our ideas the situation differs in cardiac and skeletal muscle. RyR isoforms and their affinities for Ca²⁺ differ in the two cellular types [37]. For this reason we have tried to explain the spread of Ca²⁺ across regions containing non-junctional RyRs in heart muscle as well as the synchronous origin of Ca²⁺ at junctions.

The spread of Ca²⁺ is both spatially and temporarily non-uniform. For convenience we refer to spatial non-uniformity as inhomogeneity and temporal non-uniformity as asynchrony. It is clear that all junctional RyRs are activated rapidly and do not display significant asynchrony in their activation. If we suppose that there is only one DHPR in each junction and that this DHPR is capable of triggering a spark [38] we expect that the variance in the latency of spark production would reflect the first latency distribution of a single DHPR. First latencies of a single DHPR can be described with an exponential distribution [39]. In distributions of this type the mean is equal to the stddev. The stddev will measure the extent to which first openings and hence the appearance of sparks is synchronized. However, it has been demonstrated that there is more than one DHPR per couplon [40–42]. If all N channels open independently, the first latency of N channels P_N will be determined by the first latency of all individual channels P₁ [43]:

$$\begin{array}{c}{P}_1(\mathit{latency}>t)=e^{-t/\mathrm{\tau }}\\ P_N(\mathit{all}N\mathit{latencies}>t)={[P_1(\mathit{latency}>t)]}^N=e^{-\frac{t}{\mathrm{\tau }/N}}\end{array}$$

where τ is the mean first latency time. The mean first latency for any one of the N channels to open is τ/N, which suggests that the presence of significant numbers of DHPR per couplon [40] ensures that sparks are highly synchronized. If we assume that Ca²⁺ from junctional sites, which are inhomogeneous, diffuses to non-junctional RyRs and activates them we may expect this to produce significant spatial inhomogeneity of the Ca²⁺ transient in non-junctional regions. Non-junctional RyRs nearest to junctional regions will be the first to be activated. Those non-junctional RyR clusters further from the junctions will be activated later (or not at all), which produces asynchrony. In addition if the non-junctional RyRs are not activated the local transient will display diffusional delays as Ca²⁺ spreads from regions that are activated. In cells with disease-associated depletion of the t-system this situation will be exacerbated, for instance in cells from hearts with dyssynchronous heart failure [32]. Here, we found slowed and attenuated Ca²⁺ transients. We suggested that these alterations of the Ca²⁺ transient were caused by reduced and asynchronous Ca²⁺ release. We also suggested that the reduced and asynchronous Ca²⁺ release has a profound effect on the synchrony and extent of sarcomere shortening, and subsequently on cell shortening and efficiency of cardiac pump function. We discussed the mechanism and consequences of this remodeling in more detail in our previous work [32].

Our simulations and imaging studies account for the variance of maximal upstroke velocities and onset times in the measured transients (Fig. 4). A major source for the variance is that we have only knowledge of the sarcolemma from 2D image data, but not of exact three-dimensional location of release sites (Fig. 1A versus Fig. 6B). Simulations with models having different distances between release sites suggest a further source of variance of maximal upstroke velocities (Fig. 5G). In these simulations the distance between sources along the sarcomeres was varied (Fig. Supp 3). Further computational studies suggest that Ca²⁺ sources outside of the image plane contribute to the variance of maximal upstroke velocities. Mean and stddev of maximal upstroke velocities decreased with distance in x-direction (Fig. S8C). Obviously this decrease is inconsistent with the similarity of mean and stddevs in the measured velocities within 1 μm to the sarcolemma. The simulations did not reconstruct the measured variance of onset times. Variances of onset times might reflect asynchrony due to delayed activation of non-junctional RyRs, which we did not investigate in our computational studies.

Our analyses are based on detection of the maximal upstroke velocity and the associated onset time in a large collection of pixels. To simplify the interpretation of our results we identify five types of sites associated with pixels that we characterized (Fig. 7). The sites mimic sites in cardiac ventricular myocytes (Figs. 6A and B). Some of these sites will precisely coincide with release that takes place very close to couplons (region 1 in Fig. 7A) or further away from couplons even when they are activated (region 5). Other pixels will be unrelated to release sites. These can be either near (region 2) or further away (regions 3 and 4) from the sarcolemma. We expect a RyR cluster in region 1 can trigger release from a (non-junctional) RyR cluster in region 5. However, a RyR cluster in region 1 or region 5 cannot trigger a release from a (non-junctional) RyR cluster in region 4. We note that there are many values of maximal upstroke velocity that are above and below the limit of one stddev (for example Fig. 3G) falling below and exceeding the maximal upstroke velocity observed in the model. We found that the spread of upstroke velocities measured by the stddev remains constant up to distances that are ~1 μm from the sarcolemma (Figs. 3H and 4B). Because the sarcolemma comprises couplons we conclude that release is also activated at non-junctional sites that are distant from the nearest membranes. If this was not the case we should expect the upstroke velocity to fall as described by diffusion into these regions. From distances beyond 1 μm it is difficult to decide whether release is activated in non-junctional sites. At intermediate distances (1 – 2 μm) the experimental data are in good agreement with the 4 μm x 1 μm x 1 μm model, although there are rates of rise of Ca²⁺ that are higher than those expected from diffusion (Fig. 5G). Above 2.5 μm the variance in the rate of rise of Ca²⁺ is small indicating absence of release sites. We explain the higher upstroke velocities versus the 6 μm x 1 μm x 1 μm model by superposition of Ca²⁺ diffusing from several distant release site (Fig. 5G). In summary, at these distances the rate of rise of Ca²⁺ is simply due to diffusion from activated sites or alternatively slowed release that happens to coincide with the rate of rise of Ca²⁺ due to diffusion (although the latter seems improbable). If non-junctional RyRs are activated we assume it is because release is triggered from Ca²⁺ initially released from couplons. Based on these reasons we classify measured onset times and maximal upstroke velocities dependent on the distance to release site and their location (Figs. 7B and C).

Fig. 7.

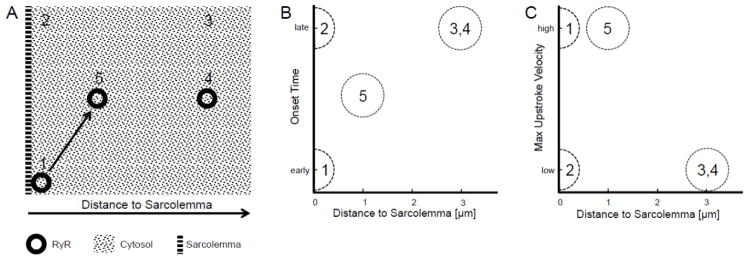
Proposed mechanisms of Ca²⁺ transients. (A) Schematic of imaged region. Five different regions are distinguished: (1) couplon with triggered activation, (2) adjacent to sarcolemma, (3) distant to sarcolemma, (4) RyR clusters not activated, and (5) RyR clusters activated through couplon or other release site. (B) Onset time is dependent on distance to early activated couplon. Only couplons are associated with an early onset time. (C) The relationship between distance and maximal upstroke velocity is dependent on the region. Only regions with couplons or indirectly activated RyR clusters exhibit a high upstroke velocity.

Neither a local control nor a common pool model can explain our data. The common pool model assumes that all Ca²⁺ that enters or leaves the cell passes through a single compartment, i.e. the cytosol, and its Ca²⁺ concentration activates RyRs [5]. Here we are dealing with a modified local control model because Ca²⁺ released from couplons passes into the cytosol to activate only adjacent non-junctional RyRs. We expected that Ca²⁺ release from either junctional or non-junctional RyRs would produce a regenerative all-or-none release of Ca²⁺ from non-junctional clusters. This is not the case. We know that the Ca²⁺ efflux from couplons consists of both Ca²⁺ current from DHPRs and sarcoplasmic release through junctional RyRs. We suggest that this efflux can activate some of the adjacent non-junctional RyRs. It appears this process eventually fails although we do not know why. A possible explanation for this is that the underlying Ca²⁺ current plus the junctional release dissipates by diffusion and processes that remove Ca²⁺ from the cytosol. In this case, release from non-junctional clusters alone would be insufficient to propagate release.

Isolated ventricular cells do show shortening and Ca²⁺ transients that are graded with membrane voltage (e.g. [44, 45]). Presumably voltage dependent recruitment of couplons can partially explain this [5]. However, if the extent of inhomogeneity of couplons changes with voltage so would the inhomogeneity of non-junctional cluster activation. This would in turn affect the rate of rise and amplitude of the Ca²⁺ transient. The greater the degree of inhomogeneity the slower the upstroke velocity and magnitude of the cellular transient.

The modified local control model offers an explanation of patterns of Ca²⁺ transients and activation of non-junctional RyR clusters in isolated rabbit ventricular myocytes. We suggest that the model applies also to cells with a sparse t-system including heart failure cells [46] and atrial cells of some species [47]. However, in cardiomyocytes with a dense t-system, for instance, from rat and mouse, the number of non-junctional RyR clusters farther from the t-tubules is small. Here, we expect that all RyR clusters are synchronously activated.

Limitations

Several limitations of experimental conditions, analysis methods and modeling approach constrain our conclusions. We discussed limitations of our imaging approach in a previous publication [22]. In short, a limitation is the spatial resolution of confocal microscopy, which leads to errors in our segmentation of t-system and local characterization of Ca²⁺ transients. The errors are characterized by the PSF of the imaging system. Our preparation of myocytes with sparse t-system might differ from those with sparse t-system in cardiac disease. Our analysis did not correct for bleaching and crosstalk of dyes. While we developed correction methods, bleaching and crosstalk were negligible for the type of analyses that we performed. A further limitation of our approach for analyses of 2D imaging data is that we moderately underestimate distances of pixels to the sarcolemma. This error is smaller than the error in similar analyses performed on conventional line scans. Our analyses are based on measures of distances, maximal upstroke velocities and activation times. We did not consider an analysis of the magnitude of the Ca²⁺ signal. In some regions of the cell those magnitudes are reached after the cell started to contract. The contraction complicates establishing relationships to distances, maximal upstroke velocities and activation times measured while the cell is static. Our computational model is simplistic in various aspects and thus cannot fully capture the three-dimensional Ca²⁺ release and diffusion process that occurs within a cell. For instance, the model neglects micro-structural heterogeneities, including mitochondria and t-system. We did not model mobile Ca²⁺ buffers beyond fluo-4 as well as removal of Ca²⁺ from the myoplasm through the sarcolemma and SR membrane. Thus, the intracellular Ca²⁺ is not decreasing to diastolic levels at the end of simulations (Fig. Supp 9). Also, similar to most previously developed models ours predicts a FWHM that is only half that observed experimentally (Table Supp 1)[48]. Nevertheless, we believe that the applied qualitative model provides important insights and supports our conclusions.

Highlights.

• We examined the relationship of Ca²⁺ transients to the sarcolemma of cardiomyocytes.

• The analyses suggest that sites within 1 μm of the sarcolemma actively release Ca²⁺.

• The data indicate absence of release at sites more than 2.5 μm from the sarcolemma.

• We explain our finding using a modified local control model.