Abstract
The brain is treated as a nested hierarchical complex system with substantial interactions across spatial scales. Local networks are pictured as embedded within global fields of synaptic action and action potentials. Global fields may act top-down on multiple networks, acting to bind remote networks. Because of scale-dependent properties, experimental electrophysiology requires both local and global models that match observational scales. Multiple local alpha rhythms are embedded in a global alpha rhythm.
Global models are outlined in which cm-scale dynamic behaviors result largely from propagation delays in cortico-cortical axons and cortical background excitation level, controlled by neuromodulators on long time scales. The idealized global models ignore the bottom-up influences of local networks on global fields so as to employ relatively simple mathematics. The resulting models are transparently related to several EEG and steady state visually evoked potentials correlated with cognitive states, including estimates of neocortical coherence structure, traveling waves, and standing waves.
The global models suggest that global oscillatory behavior of self-sustained (limit-cycle) modes lower than about 20 Hz may easily occur in neocortical/white matter systems provided: Background cortical excitability is sufficiently high; the strength of long cortico-cortical axon systems is sufficiently high; and the bottom-up influence of local networks on the global dynamic field is sufficiently weak. The global models provide "entry points" to more detailed studies of global top-down influences, including binding of weakly connected networks, modulation of gamma oscillations by theta or alpha rhythms, and the effects of white matter deficits.
Keywords: electroencephalography, global fields, axon propagation, cross-frequency interactions, white matter disease
1. Introduction
1.1 Scope and motivations for this paper
This paper addresses the following issues that cross traditional boundaries between electrophysiological studies at the disparate spatial scales of local field potentials (LFP), electrocorticography (ECoG) and electroencephalography (EEG) as indicated in table 1. The main topics are: 1) Contributions of cortico-cortical axon delays to observed spatial-temporal properties of EEG, including traveling and standing waves. 2) Data studied at the large, but distinct, scales of low and high resolution EEG. 3) Relations between anatomical and functional connectivity measured at large scales, the latter often estimated with EEG coherence. 4) The potential importance of such functional connectivity measures for clinical studies of white matter disease. 5) The effects of top-down global dynamics on local networks, including modulation of gamma oscillations by theta or alpha rhythms.
Table 1.
Estimated spatial resolution of recorded potentials or magnetic fields generated by cortical sources
| Recording Method | Typical Spatial Resolution (mm) |
|---|---|
| microelectrode of radius ξ | ≥ ξ |
| LFP | 0.1–1 |
| ECoG | 2–5 |
| intra-skull recording | 5–10 |
| untransformed EEG | 50 |
| untransformed MEG | 50 |
| high resolution EEG | 20–30 |
| high resolution MEG | unknown |
Why do we focus here on global rather than local models of neocortical dynamics? We review several neocortical global models in which predicted large-scale spatial-temporal dynamic behaviors are due largely to propagation delays in cortico-cortical axons. That is, all bottom-up influences on global dynamics based only on axon delays are neglected to first approximation as indicated by the dashed arrow in fig. 1. We do not claim that these (limiting case) idealizations of cortical-white matter systems represent genuine brains with high accuracy; rather they are proposed mainly as convenient "entry points" into more comprehensive multiscale theoretical, experimental and clinical studies. Given this focus, we do not attempt to review the large body of theoretical work based on networks operating at multiple local scales, which model various aspects of brain dynamics. Such local network models often consist of coupled differential equations, with solutions for various field variables that may be related to data recorded at matching scales. For example, intermediate (mm) scale local models appear appropriate for some comparisons to ECoG studies. This picture is consistent with the inherent spatial filtering associated with data collected at the LEP, ECoG, and EEG scales as discussed in Sec 1.6, although such local (mm scale) dynamics may be substantially modulated by global (cm scale) dynamics in some brain states.
fig. 1.
In this paper’s oversimplification only the top-down interactions of global dynamics on local networks are considered (solid arrow); bottom-up interactions (dashed arrow) associated with local networks are neglected to first approximation to create tractable and easily interpretable mathematical models.
Comprehensive reviews of local network models and their connections to genuine data at EEG and/or ECoG scales include (Uhl 1998; Friston 2005; Jirsa and McIntosh 2007; Moran et al 2013). We do not claim that the global models outlined in this paper are in any sense "better" than such local network models. Rather, we view global models as complementary to local network models, providing explicit top-down mechanisms that may modulate and/or facilitate different aspects of local network dynamics, e.g. the production or synchronization of gamma oscillations by global alpha or theta rhythms.
Human brains are highly complex systems exhibiting distinct properties observed at different spatial and temporal scales. As long emphasized by many (e.g. Freeman 1975, 1987; Ingber 1982; Nunez 1995, 2000; Jirsa and Kelso 1999; Friston 2005; Nunez and Srinivasan 2006a; Sporns 2011) multiple models are required to make contact with experimental observations of different brain variables, recorded at different spatial and temporal scales, and related to different cognitive functions or disease states. The global models of this paper make certain experimental predictions about very large scale spatial-temporal EEG properties: oscillation frequencies lower than about 20 Hz, coherence patterns, standing waves, and traveling waves. The extensive EEG literature has long demonstrated robust correlations between these slow oscillations and cognitive functions and clinical disease states. Readers may naturally question the relationships of these large scale events to the many other phenomena observed with EEG, ECoG and LFP. Our general answer is that many other phenomena, especially when recorded at the smaller scales of ECoG and LEP, cannot be modeled by purely global models; rather they require complementary models developed at multiple smaller scales matching the appropriate experimental conditions as indicated in tables 1 and 2. The scientific notion of "complementarity" was famously promoted by Niels Bohr, not only in the context of quantum systems, but for macroscopic systems belonging to the broad category that we now label "complex systems" (Heisenberg 1971).
Table 2.
Spatial scales of cortical tissue structure related to function
| Structure | Scale (mm) | # Neurons | Anatomical Description |
|---|---|---|---|
| minicolumn | 0.03 | 102 | spatial extent of inhibitory connections |
| module | 0.3 | 104 | input scale for cortico-cortical fibers |
| macrocolumn | 3.0 | 106 | intracortical spread of pyramidal cell |
| region | 50 | 108 | Brodmann area |
| Lobe | 170 | 109 | areas bordered by major cortical folds |
| hemisphere | 400 | 1010 | ½ brain |
To sum up the general approach of this paper, we employ Galilean idealizations in order to create relatively simple global models that modulate local networks and are more easily related to certain kinds of experimental data, especially several observed properties very large scale scalp potentials (EEG), e.g., coherence structures observed in several frequency bands and multiple local alpha rhythms embedded in a global alpha rhythm. This general philosophy was famously employed by Galileo, who modeled falling bodies with no air resistance even though he lacked the technology to remove the air. Similarly, we are unable to shut down brain networks in living brains such that the remaining phenomena due only to axon delays are easily observed, although some anesthesia and even waking (resting, eyes closed) alpha states may crudely approximate such simple dynamics at large scales. We promote these simple models because they facilitate a transparent conceptual framework that incorporates axon delays with broad experimental and clinical implications. The basic question of whether or not our focus on global models is scientifically useful is addressed further in the context of experimental work discussed in Sec. 3. There we show that perhaps a dozen large scale (scalp) dynamic behaviors are anticipated by axon delay mechanisms, whereas many other aspects of EEG and especially ECoG (recorded from either epidural or subdural cortex) and LFP can only be explained by local network models developed at matching scales as implied by table 2. In addition, many other phenomena are expected to depend critically on combined local and global mechanisms (Nunez 1989, 1995, 2000; Jirsa and Haken 1997; Haken 1999; Robinson et al 2004; Nunez and Srinivasan 2006a).
1.2 Complementary local and global models
We contend that descriptions of the brain at large scales should not be regarded as poorly resolved approximations of an underlying microscopic order; rather different scales offer parallel and complementary views of brain organization. This idea has long been appreciated by complex physical systems scientists (Ingber 1982; Haken 1983; Nunez 1995, 2010) and is nicely developed specifically for brain networks in a recent book (Sporns 2011). Even in relatively simple systems, multi-scale theories are typically required for experimental verification as in the prominent example of separate micro and macroscopic versions of Maxwell's equations governing electromagnetic phenomena. Much of early 20th century physics was concerned with establishing cross-scale relations between electromagnetic fields observed at different scales (Jackson 1962). The analogous developments in electrophysiology are now only in their very early stages (Freeman 1975; Ingber 1982; Nunez 1982, 1995; Nunez and Srinivasan 2006).
With this general multi-scale view in mind, we classify neocortical dynamic models as local, global, and combined local/global. The label global model applies to the work here, indicating mathematical models in which delays in the cortico-cortical axons forming most of the white matter in humans provide the underlying time scales for dynamic behaviors. Periodic boundary conditions, which force all cortical variables to be continuous functions of cortical surface coordinates, are generally essential to global theories because the cortical-white matter system of each hemisphere is topologically close to a spherical shell (Dale et al 1999; Fischl et al 1999). Homogeneous models typically predict standing and traveling waves with frequencies and damping (attenuation) depending on cortical background excitability, controlled on long time scales by neuromodulators. The models predict a human global alpha rhythm environment in which several independent local alpha processes are embedded, consistent with EEG and ECoG data. We also employ the label regional (Silberstein 1995b; Jirsa 2009) to indicate resonances due to point-to-point (inhomogeneous and anisotropic) axon delays between isolated pairs of cortical locations as developed here.
The label local model indicates mathematical treatment of cortical or thalamo-cortical interactions in which cortico-cortical axon propagation delays are neglected; that is, axon propagation speeds are assumed to be infinite as in the classic local model of Wilson and Cowan (1972, 1973). The underlying time scales in such models are often PSP rise and decay times due to membrane capacitive-resistive properties, typically resulting in coupled differential equations and often predicting self-sustained (limit cycle) oscillations in local networks. Thalamo-cortical networks are also “local” from the viewpoint of surface electrodes, which cannot distinguish purely cortical from thalamo-cortical networks. These models are also “local” in the sense of being independent of global boundary conditions. While such local models are apparently needed to model much of mm scale dynamics (e.g., gamma or local alpha) observed with ECoG, here we focus on global models that can explain several aspects of the cm scale dynamics (e.g., global alpha) observed with EEG.
We review several complementary global models of brains that may facilitate useful intuitive steps towards the development and interpretation of more comprehensive brain theory. The basic idea behind global models is simple; action potentials at each cortical location generate synaptic action at distant locations after time delays that depend on axon propagation speed and separation distance. For this reason, most models based on cortico-cortical axon delays employ a similar mathematical structure consisting of integral or integro-differential equations incorporating axon propagation speeds, cortical separation distances and anatomical connectivity functions or matrices. Here we focus on the simplest of these global models with either homogeneous or very simple heterogeneous connections, thereby allowing relatively simple analytic solutions to be obtained. Nevertheless, these models employ enough genuine physiology and anatomy to provide several qualitative and semi-quantitative connections to (cm scale) EEG, but they cannot predict smaller scale phenomena unless coupled with local theories. Some of this global work has been published earlier, but often with different emphasis and mathematical methods at various times (Nunez 1974a, 1981, 1989, 2000; Katznelson 1981; Nunez et al 2001; Nunez and Srinivasan 2006a,b) and in different publications, including several PhD dissertations (Katznelson 1982; Srinivasan 1995; Wingeier 2004) and a book now out of print (Nunez 1995).
1.3 Top-down modulation of local rhythms by global theta and alpha
Our aim here is to provide an easily accessible overview of several global models with simple analytic solutions and account for some recent experimental and theoretical developments by ourselves and others, especially involving global top-down influences on local networks, as suggested by fig. 1. We have, for example, recently employed a modified Wilson-Cowan (local) model embedded in a global alpha band environment to model global top-down modulations of locally generated gamma activity (Thorpe 2012; Srinivasan et al 2013). Low frequency global oscillations (e.g. theta or global alpha, less than 20 Hz) are predicted by such models to facilitate and/or couple (bind) high frequency oscillations (e.g. local alpha or gamma) in distinct local networks.
This general kind of theoretical approach makes contact with several recent experiments. Human ECoG studies indicate that ongoing high gamma (80–150 Hz) amplitudes are modulated by the phase of low-frequency theta (4–8 Hz) (Canolty et al 2006; He et al 2010; Voytek et al 2010) and alpha (8–12 Hz) (Osipova et al 2008; Crone et al 1998a; Voytek et al 2010) oscillations. Such cross-frequency coupling may be central to the distinct functional roles played by various brain rhythms, perhaps acting to bind remote networks to produce a unified behavior and consciousness (Izhikevich 1999; Jensen and Colgin 2007; Nunez 2010; Srinivasan et al 2013). Low-frequency oscillations may coordinate long-range communication between different brain regions (von Stein and Sarnthein 2000), whereas gamma activity appears to be more spatially restricted and reflects local cortical processing (Crone et al 1998b; Fries et al 2001; Canolty et al 2007). The top-down conceptual framework implied by these studies appears to have broad implications for future studies of healthy brains as well as white matter disease.
Coupling between discrete networks can occur at multiple scales smaller than the (approximate) 2–5 cm scale observed with EEG or the (approximate) 2–5 mm scale of ECoG as implied in tables 1 and 2. Multiple local circuits apparently support different, discrete frequencies of neocortical rhythms. Several dynamic mechanisms have been proposed to support spectral information processing. In one theoretical study (Roopun et al 2008), activity in two co-active local circuits may combine to generate a third frequency whose period originates from a sum of the original two. In an experimental LEP study of macaque visual cortex Spaak et al (2012) found a robust coupling between alpha rhythm phase in deeper layers and gamma amplitude in granular and superficial layers. Furthermore, increases in alpha amplitude occurred when gamma amplitude and burst length decreased. These findings demonstrate robust inter-laminar cross-frequency coupling, thereby supporting the view that local neuronal activity in the alpha frequency range modulates processing in cortical microcircuits in a top-down manner. Such interrelationships between discrete network rhythms provide plausible dynamic substrates for multi-scale, parallel processing of sensory information over a range of temporal and spatial scales (Wiskott and Sejnowski 2002; Smith et al 2006).
1.4 Our focus on axon propagation delays and global top-down effects
When author PLN first proposed a global traveling/standing wave model based on axon propagation delays over 40 years ago (Nunez 1972, 1974a), all existing neocortical dynamic models were strictly local. Over the same 5–10 year period several new local models were advanced, notably the works of Wilson-Cowan (1972, 1973), Freeman (1975, 1987, 1992a,b), Lopes da Silva and colleagues (van Rotterdam et al 1982), and Ingber (1982). Inclusion of cortico-cortical axon delays in combined local/global models came much later, occurring mainly (if not exclusively) over the past 15–25 years or so; a few examples are (Nunez 1989, 2000; Jirsa and Haken 1997; Jirsa et al 1999; Haken 1999; Robinson et al, 1997, 1998, 2003, 2004; Liley et al 1999, 2002, 2003; Jirsa and Kelso 2000; Wright et al 2001; Bojak et al 2004; Jirsa 2004, 2009; Breakspear et al 2006; Ingber and Nunez 2010; Freyer et al 2011; Pinotsis et al 2013). We have previously discussed several of these (mostly) complementary studies, including their relationships to pure global models (Nunez 2000; Nunez and Srinivasan 2006a).
One can conjecture several reasons for the 15–20 year gap between sophisticated local model development and the later inclusion of axon propagation delays to produce combined local/global models. The most obvious and defensible reasons involve the mathematical complexity of combined local/global models. Another reason appears to have been a relative disinterest in cortico-cortical connections by early neuroscientists, although important exceptions are noted, namely Krieg (1963, 1973), Braitenberg (1978), and Braitenberg and Schuz (1991). In reply to questions about cortico-cortical axons by author PLN in 1978, one prominent neuroanatomist responded that he was a "cortical anatomist" and cared little about lower brain structures. The estimate that more than 95% of human white matter consists of cortico-cortical axons with only a few per cent thalamo-cortical was not widely appreciated in the 1970s (Nunez 1981, 1995); it may not be fully appreciated even today. Regardless of this history, many of today's neuroscientists are focused on brain connections, including cortico-cortical axons largely responsible for "small world" dynamic behavior (Friston 2005; Jirsa and McIntosh 2007; Sporns 2011; Seung 2012). This increased interest in connectivity provides one motivation for this (partly) review paper. Another motivation stems from more recent experimental results that can be interpreted in the context of these global models. These data include evidence for global alpha band dynamics with multiple embedded local alpha networks in both spontaneous EEG and steady state visually evoked potentials (SSVEP), the latter demonstrating local processes influenced by global resonances with implications for binding of local networks. The relatively recent association of a broad range of psychiatric and neurodevelopmental disorders with white matter deficits that may disrupt network timing (Hao et al 2006; Fields 2008) provides still another motivation for this paper.
1.5 Brains as complex systems with state-dependent functional connections
Human brains are typically viewed as the preeminent complex systems with cognition believed to emerge from dynamic interactions within and between brain sub-systems (Ingber 1982, 1995; Freeman 1992a,b; Ingber and Nunez 1995; Friston et al 1995; Haken 1996, 1999; Mountcastle 1998; Tononi and Edelman 1998; Edelman and Tononi 2000; Buzsaki 2006; Sporns 2011; Bassett and Gazzaniga 2011). How can we reconcile high brain complexity with the simple traveling and standing waves predicted by the global models of this paper? One answer is to avoid taking oversimplified model details too seriously. Rather, we emphasize the more general point that global dynamic behavior can provide important top-down influences on local dynamics in many physical and biological systems (Haken 1983; Jirsa and Haken 1997; Nunez 1995, 2010; Ingber and Nunez 2010), for example production of local vortices and tornadoes by global weather patterns in the atmosphere's spherical shell. In physical systems, global boundary conditions can facilitate spatial coherence even when the temporal behavior of individual oscillatory modes becomes chaotic (Bishop et al 1983; Tabor 1989). In neocortex analogous global spatial structure could substantially influence embedded networks.
Standing waves of global fields can naturally exhibit multiple synchronized regions with zero phase lag without need for direct interconnections (Nunez 1995, 2010; Nunez and Srinivasan 2006a,b). More generally, we suggest that such top-down influences directly address the binding problem of brain science (Habeck and Srinivasan 2000; Nunez et al 2001, 2013; Nunez 2010; Nunez and Srinivasan 2007, 2010; Srinivasan et al 2013). That is, how is the unity of conscious perception generated by the brain's distributed local networks (Gazzaniga 2011)? An implied conjecture is that diseases like schizophrenia, autism, and Parkinson's may be manifestations of faulty binding of local networks, an idea with support from known neurotransmitter actions and EEG studies (Silberstein 1995b; Brock et al 2002; Murias et al 2007; Boersma et al 2013).
The global models of this paper imply close relationships of EEG/SSVEP functional connectivity measures like narrow band (e.g. 1 Hz) alpha and theta coherence to cortico-cortical axon propagation delays; such relations may have important implications for the diagnosis and treatment of several brain diseases. Myelin controls action potential speed, and the synchrony of impulse traffic between distant cortical regions may be critical for optimal mental performance and learning (Fields 2008). A broad range of psychiatric disorders, including schizophrenia, chronic depression, bipolar disorder, obsessive-compulsive disorder and posttraumatic stress disorder, has recently been associated with white matter defects, as have neurodevelopmental cognitive and emotional disorders including autism, dyslexia and attention-deficit hyperactivity disorder. The evidence for white matter involvement consists of gene expression studies, several different kinds of brain imaging methods and histological analysis of post mortem tissue (Fields 2008). Given these close relationships between white matter myelination and brain diseases, the theoretical global dynamic behaviors developed here imply specific connections between brain disease and global EEG, thereby potentially impacting future clinical study designs.
Here we cite two salient anatomical and physiological features that contribute to brain complexity and, by implication, the conditions apparently required for healthy cognition. These features give rise to multi-scale spatial-temporal patterns of brain activity, revealed with imaging techniques like EEG, which are strongly correlated with mental states. One such salient feature is anatomical and physiological nested hierarchy as indicated in table 2. Cortical anatomy and physiology consist of neurons within minicolumns within modules within macrocolumns (Szentagothai 1978; Ingber 1982; Nunez 1995; Mountcastle 1998; Feinberg 2009, 2012; Fingelkurts et al 2013). Emergence and complexity generally occur in hierarchically nested physical and biological systems where each higher level of complexity displays novel emergent features based on the levels below it, their interactions, and their interactions with higher levels. Such systems may follow general principles that underlie many complex systems, including anthropology, artificial intelligence, chemistry, economics, meteorology, molecular biology, neuroscience, physics, psychology, and sociology (Ingber 1985; Haken 1983; Scott 1995; Gell-Mann and Lloyd 1996; Nunez and Srinivasan 2007; Edelman and Tononi 2000; Sporns 2011; Bassett and Gazzaniga 2011).
Another salient feature of many complex systems is non-local interactions in which dynamic activity at one location influences distant locations without affecting intermediate regions, as enabled in human brains by long (up to 15–20 cm) cortico-cortical fibers (Krieg 1963, 1973; Braitenberg 1978; Braitenberg and Schuz 1991; Nunez 1995, 2010, 2011) and in human social systems by modern long distant communications facilitating small world behavior (Watts 1999; Bassett and Bullmore 2009). For example, the high density of short-range (mm scale) intra-cortical connections coupled with an admixture of cortico-cortical axons favors small world behavior. Small worlds often promote high complexity; they also appear to be abundant in brain structural networks, across systems, scales and species (Sporns 2011; Bassett and Gazzaniga 2011).
1.6 Multiscale dynamics and corresponding observational scales
Each of the following techniques-- raw EEG, high resolution EEG, ECoG (either cortical or dura surface recordings), LFP (local field potentials, typically intra-cortical), MEG (magnetoencephalography), fMRI (functional magnetic resonance imaging), and PET (positron emission topography) image brain activity over a limited range of spatial-temporal scales. Given the acknowledged complexity of brains, these methods provide complementary measures of multi-scale dynamic behavior in neocortex; such data call for distinct neural models at matching scales. In particular, experimental electrophysiology spans about five orders of magnitude of spatial scale as indicated in table 1. The fractal-like morphology of neocortical columns at multiple scales implies that recorded dynamics are scale-sensitive, depending on the size and location of intracranial electrodes and the spatial filtering of scalp potentials (Abeles 1983; Nunez 1995, 2010, 2012; von Stein and Sarnthein 2000; Nunez and Srinivasan 2006a,b; Srinivasan et al 2007; Otto et al 2012).
Even scalp-recorded EEG can exhibit distinct dynamics at different spatial scales, notably unprocessed potentials (roughly 5–10 cm) and high resolution EEG (surface Laplacians and dura images, roughly 2–3 cm) as indicated in table 1. For example, the raw potential and dura image maps of a time slice of alpha rhythm are shown in fig. 2 (Wingeier 2004; Nunez 2010); these two disparate maps provide complementary, not competing, measures of neocortical dynamics, a point not always appreciated by EEG scientists (Nunez and Srinivasan 2006a). The potential map indicates that anterior and posterior regions are roughly 180 degrees out of phase (e.g. a simple anterior-posterior standing wave), whereas the corresponding high resolution (dura image) estimate reveals multiple alternating in and out-of-phase regions. Remote regions with the same shading exhibit zero phase lag with no apparent need for direct connections between them. The high resolution estimate may reveal some combination of embedded multiple network and correlated higher mode standing wave activity, perhaps suggesting that local networks evolve in a manner that is "dynamically compatible" (in some poorly understood sense) with global boundary conditions (Nunez 2010).
fig. 2.
A time slice of alpha rhythm topography recorded with 131 channels at the time of peak potential in a posterior-midline electrode is shown (Wingeier 2004). Light and dark areas are approximately 180 deg out of phase. (a) Average referenced potential. (b) High resolution (spatially high pass filtered) estimate of the same raw data based on the Melbourne dura image algorithm (using a 4-sphere head model, Nunez et al 1994; Silberstein 1995a). The New Orleans spline Laplacian (independent of head model) yields nearly identical estimates of dura potential with dense electrode arrays. Areas with similar shading are roughly in phase, demonstrating so-called “zero phase lag” dynamics. The correlation coefficient based on point to point comparison of the 2 independent high resolution estimates is ~ 0.95 (Nunez et al 1994; Nunez and Srinivasan 2006a).
Power spectra and coherence patterns over the scalp are generally quite scale-dependent, exhibiting large differences when time series analysis is applied to both raw potentials and the corresponding Laplacian or dura images estimated from the same data sets (Pfurtscheller and Neuper 1992; Nunez 1995, 2000, 2001; Nunez et al 1997, 1999; Andrew and Pfurtscheller 1997; Srinivasan et al 1998, 2007; Nunez and Srinivasan 2006a). One robust observation of high resolution EEG is a substantial reduction in alpha rhythm power relative to other frequency bands, indicating that high-pass spatial filtering tends to suppress the long wavelength global alpha. This can occur while leaving local alpha rhythms, which may be generated in thalamo-cortical networks, in place (Wingeier et al 2001; Nunez et al 2001; Wingeier 2004; Nunez and Srinivasan 2006a,b; Nunez 2011).
Even the EEG, in which most of the short wavelength (high and intermediate spatial frequency) electrical activity has been suppressed by volume conduction, exhibits distinct multi-scale dynamics. Thus, we should be especially mindful of the inherent limitations of neural models that ignore spatial scale issues as emphasized by the works of Ingber (1982, 1995), Freeman (1992b), Sporns (2011) and others. The global models outlined here, when used in isolation, are limited to dynamics recorded at the very large (5–10 cm) scale of unprocessed scalp-recorded EEG; however, they have much broader top-down implications for local network influences as suggested by fig. 1. We can quantify issues of spatial scale in experimental electrophysiology with the following thought experiment involving a real computer algorithm that transforms MRI images of cortical hemispheres into topologically equivalent spheres (Fischl et al 1999; Dale et al 1999). This idealized picture ignores complications due to cortical folding; however, the fundamental experimental issues are unaltered by such technical details.
Let Ω represent angular surface location expressed in the usual spherical coordinates (θ,ϕ), essentially (latitude, longitude). Suppose that some dynamic variable Φ(Ω,t) like subdural potential (ECoG) is to be measured over this idealized spherical surface. We can never measure Φ(Ω,t) with arbitrary precision; that is, the measurement process allows only estimates Φ̂(Ω,t) of this variable. We can express any arbitrary surface dynamics, be they theoretical or experimental, in a series of orthogonal functions (generalized Fourier series). Given that our idealized (single hemisphere) cortical surface is a sphere, we naturally adopt the standard spherical harmonics Ylm (Ω) as basis functions as follows: :
| (1.1) |
The functions Ylm (Ω) where (l,m) are restricted to integers have following basic mathematical properties required to represent any genuine physical variable Φ(Ω,t) over the entire sphere: 1) finite everywhere on the sphere 2) continuous over the sphere such that Φ(Ω,t) satisfies periodic boundary conditions; that is, each spherical harmonic function is a single valued function of surface location Ω. The Ylm (Ω) functions are the two-dimensional spatial analogous of the sin(ωt) and cos(ωt) functions of ordinary spectral analysis. Each spatial function (or mode or pattern) Ylm (Ω) is weighted by a corresponding time-dependent function alm (t) due only to the underlying dynamics, independent of experimental conditions. At each time slice ti, is the power associated with the spatial function Ylm (Ω). Thus, any general spatial pattern may be decomposed into different components Ylm (Ω), each one weighted by the corresponding time-varying function alm(t).
The actual variable to be measured Φ(Ω,t), which we can never know exactly, is given by the same expression Eq (1.1), but with all the coefficients Klm = 1; the Klm are spatial mode (pattern) weights that account for experimental conditions. That is, the condition Klm = 1 is required in the expression for the actual variable Φ(Ω,t) since all dynamic behaviors are (by definition) included in the functions alm(t). The functions Ylm (Ω) consist of progressively higher spatial frequencies in two surface dimensions for larger indices (l,m); for example, Y00 (Ω) is constant over the entire spherical surface while Y10 (Ω) has opposite signs over the two halves. The alpha rhythm topography of fig. 2a suggests dominant contributions from Y10 (Ω) and Y20 (Ω) in each hemisphere, but the corresponding high resolution image of fig 2b reveals much more relative contributions from higher spatial frequencies (l,m). High resolution EEG essentially involves estimating the Klm to remove volume conduction effects, but this process necessarily also removes genuine contributions from large correlated source regions.
Each mode (l, m) is associated with a distinct time series alm(t), which is determined only by cortical source dynamics, independent of the measurement process. By contrast, the Klm values depend only on experimental methods (EEG, MEG, ECoG, LFP), independent of cortical dynamics. Volume conduction models estimate the Klm that relate scalp potentials Ф̂(Ω,t) to the underlying (unfolded) dural surface potential Ф(Ω,t) of the combined cortical hemispheres (Srinivasan 1995; Srinivasan et al 1998; Nunez and Srinivasan 2006a). The Klm constitute band pass spatial filters determined by the following factors: 1) the spatial extent of the sensor array (e.g. electrode or magnetic coil). 2) sensor spacing density. 3) volume conduction, including sensor separation distance from sources. 4) in the case of intracranial recordings, electrode size (Abeles 1982; Nunez 1995). The electrode size influence may be minimized by spatial smoothing over scales smaller than the electrode surface; this occurs naturally in EEG and (to a lesser extent in ECoG) by volume conduction. In intracortical recordings, the standard LFP is obtained from microelectrodes placed sufficiently far from membrane surfaces to avoid domination by individual neurons; data are also typically low-pass filtered (< 350 Hz) to remove fast activity coming from action potential sources (Legatt et al 1980; Gray et al 1995). Both procedures are expected to produce data smoothing over very small spatial scales such that LEP is independent of electrode size down to these small scales (Otto et al 2012; Nunez 2012).
Our estimates of the Klm coefficients relating EEG to ECoG recorded from the smooth dura surface (of the combined hemispheres) are based on calculations employing volume conductor head models. They have been partly verified by calculating spatial spectra (Srinivasan et al 2006) and coherence patterns (Srinivasan et al 2007; Winter et al 2007) from recorded brain "noise." That is, scalp recordings outside driving frequency bands of SSVEP and spontaneous EEG frequencies above 40 Hz were assumed to lack spatial structure so that recorded scalp potentials could be compared to scalp potentials and high resolution (Laplacian) estimates simulated by random dipole sources in head models. Due to volume conduction, the Klm values in unprocessed EEG peak at l = 1 and become negligible for l > 5–10. By contrast, with high resolution EEG (Laplacian or dura image), Klm values are small to moderate at l = 1, peak near l = 4 – 6 and remain significant beyond l ~ 20, although practical estimates of Klm for large l from EEG data (typically employing spline fits) become progressively less accurate (Nunez and Srinivasan 2006a). Average reference potentials force K00 = 0.
To sum up this section, we first note that any spherical surface dynamics may be expressed as a linear sum of temporal functions alm(t), each weighted by the corresponding experimental spatial filter term and spherical harmonic function. For other surfaces, one might choose other basis functions, but such alternate choice would not significantly change the general ideas of this discussion. The linear superposition of modes, Eq (1.1), is valid even though the underlying anatomy and source dynamics are expected to be nonlinear, inhomogeneous, and anisotropic. This general applicability may be appreciated by noting the general validity of Fourier transforms of time series, regardless of the underlying process, including chaos and other strongly nonlinear phenomena. Thus, the formalism applies to any system with spherical surface geometry, for example, weather patterns over the earth or the quantum wave function of the hydrogen atom (omitting radial functions). The following temporal Fourier transform of Eq (1.1) is equally general:
| (1.2) |
The spatial filter coefficients Klm tend to be small for small l if the electrode array diameter is small as in many ECoG experiments, essentially because low spatial frequency activity will typically appear nearly constant over an array that is small compared to dominant wavelengths. Thus, any oscillations alm(ω) corresponding to small l may be suppressed in localized ECoG or LFP recordings. Such unintended high pass spatial filtering depends partly on the effectiveness of reference electrode placement. That is, the longest possible wavelengths equal effective cortical circumference, potentially contributing signal to any body reference. In sharp contrast, the Klm coefficients of scalp recordings tend to be small for moderate or large l due to volume conduction. High resolution EEG represents an intermediate case between EEG and ECoG. Thus, we generally expect to see different spectra, observed in experiments as weighted sums of the functions alm(ω), in different kinds of recordings. This has been demonstrated in simultaneous EEG/ECoG recordings in which beta rhythms recorded from cortex were largely missing at the scalp (Pfurtscheller and Cooper 1975; Nunez 1981, 1995). In another example, comparisons of raw scalp spectra to high resolution spectra of (the same) spontaneous EEG data show a large reduction in relative alpha power in the high resolution estimates (Wingeier 2004; Nunez and Srinivasan 2006a). Correlation patterns over the scalp (e.g. covariance and coherence) are also sensitive functions of spatial scale as revealed by comparing raw scalp potential data to high resolution EEG (Nunez 1995; Nunez et al 1997, 1999; Srinivasan et al 1998, 2006; Srinivasan 1999). The theory and data cited here show conclusively that temporal filtering of EEG is a byproduct of spatial filtering as suggested by Eq (1.2).
1.7 Possible origins of neocortical oscillations
As discussed in the context of spatial scales, the distinct spatial and dynamical properties of EEG oscillations in low (less than about 20 Hz) and high (greater than about 20 Hz) frequency bands suggest the need for distinct models to explain these phenomena. Given any unknown physical or biological system that produces oscillations at some preferred (or resonant) frequency f = ω / 2π, a reasonable starting point for model development is to identify the origins of the implied underlying time delay τ, roughly estimated as the interval of substantial phase change of the oscillation, that is,
| (1.3) |
The implied physiological time scale for the (8 to 13 Hz) alpha rhythm is τ = 12 to 20 ms. More generally, the most robust human EEG rhythms recorded from the scalp (1 to 20 Hz) correspond to time delays τ = 8 to 160 ms. How does this delay range compare with mammalian physiology? Whereas early studies of membrane time constants in mammalian cortex were typically less than 10 ms, more modern studies with improved recording methods report a wider range up to about 100 ms (Koch et al 1996). While synaptic delays (PSP rise and decay times) lie in a general range (within a factor of perhaps five) that might account for dominant EEG frequencies, claims of close agreement between the details of observed EEG spectra and dynamic theories based on membrane time constants do not by themselves offer critical model validation (Nunez 2011). Model parameters can always be chosen to “match” EEG data, which, in any case, vary widely between brain states.
Models that incorporate the spatial extent of neocortex and axon transmission delays between neural populations are called global models. These predict global oscillations over the surface of the cortex that can exhibit high spatial coherence and have wave-like properties that depend primarily on the transmission delays between cortical populations; that is, on axon propagation speeds and length (Nunez and Srinivasan 2006a,b, 2010). The dominant modes of these spatially distributed oscillations are often predicted to lie below about 15–20 Hz in the theta and alpha bands. While both global and local network theories have been developed independently, their interaction across spatial and temporal scales is not well understood.
The underlying time scales in local network models are typically postsynaptic potential rise and decay times due to membrane capacitive-resistive properties (Wilson and Cowan 1972, 1973). Local theories often predict EEG signals with frequencies above 20 Hz. These results are consistent with more detailed studies of spiking neuron models (Izhikevich 2006; Izhikevich and Edelman 2008) that predict fast frequency oscillations in cortical populations unless coupled with axon delays as in a global network or field. Physiologically realistic compartment models incorporating the interactions between excitatory and inhibitory populations in cortex give rise to fast oscillations at gamma band frequencies (Bush and Sejnowski 1996; Traub et al 1997; Whittington et al 2000).
In these kinds of models, the dynamics are determined primarily by PSP delays and strengths of excitatory and inhibitory synaptic connections. More specific local models in sensory systems incorporate the essential spiking dynamics and connectivity of thalamo-cortical networks (Lumer et al 1997), also giving rise to gamma band oscillations. While physiologically detailed models are useful to compare to data obtained in animal experiments, we suggest that comparisons to EEG and ECoG require model development in macroscopic variables that describe synaptic mass action as generally accomplished by the global and local/global models cited here.
2. Global Models
2.1 Axon propagation delays and dependent variables
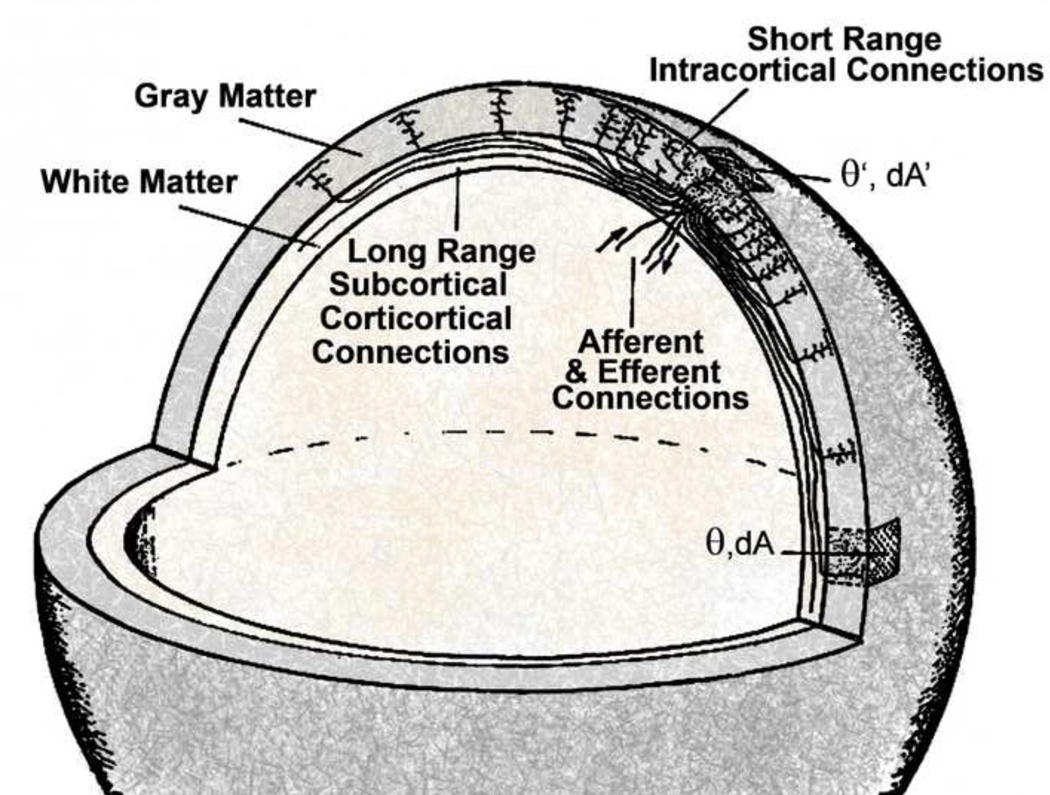
The following simplified versions of global models propose equations for the two field variables, H(r,t) and G(r,t). H(r,t) is the modulation of excitatory synaptic action density about background, expressed as a function of time t and cortical location r. If Ψe(r,t) is the number of active excitatory synapses per unit cortical tissue area at the mm to cm scale, its modulation is H(r,t) ≡ δΨe(r,t). Since axons with inhibitory synapses are believed to be almost exclusively intra-cortical and non-myelinated, corresponding axon delays are assumed here to be negligible to first approximation, and inhibitory synaptic action Ψi(r,t) then only influences cortical background excitability in this very large scale model. The variable G(r,t) is the mm to cm scale modulation of action potential density about background. The interrelations between the following limited case models are indicated in fig. 3 with appropriate section numbers shown in boxes.
fig. 3.
Relationships between the 3 global models based on assumed distributions of cortico-cortical axons given by ℜ(r, r1, v1); appropriate section numbers are listed.
All three models described in this paper are based on the following linear integral equation relating the variables H(r,t) and G(r,t); solutions require coupling to a second (generally nonlinear) equation. The excitatory synaptic action at cortical location r may be expressed in terms of an inner integral over the cortical surface and outer integral over distributed axon propagation speeds as
| (2.1) |
Equation (2.1) is based on the simple, non-controversial idea that excitatory synaptic action at cortical location r is due to local sub-cortical input H0(r,t) plus excitatory action potential density G(r,t) transported by cortico-cortical axons and integrated over the entire neocortical hemisphere. Callosal action potentials are neglected in this simple version. The inner integrals in Eq (2.1) are over cortical surface coordinates; action potentials at locations r1 produce synaptic activity at location r after a delay that is proportional to cortical separation distance and inversely proportional to axon speed ν1. Distances are defined on an idealized smooth cortical surface as in an imagined inflated cortical hemisphere (Fischl et al 1999; Dale et al 1999). All the complications of white matter (cortico-cortical) axon tracts (after cortical smoothing) are included in the kernel or distribution function ℜ(r,r1,ν1). The outer integral is over generally distributed axon propagation velocities ν1.
2.2 Homogeneous and heterogeneous cortico-cortical systems may co-exist
The earliest global models were based on translationally invariant (homogeneous) cortico-cortical distribution functions; that is, the number of axon connections between any pair of equally separated cortical locations was assumed constant, expressed mathematically as ℜ(r,r1,ν1) = ℜ(|r–r1|,ν1) . Model axon systems exhibiting assumed exponential fall-offs in connection density with cortical separation distances |r – r1| were employed mainly for mathematical convenience (Nunez 1994, 1989; 2000; Katznelson 1981, 1982; Jirsa and Haken 1997; Nunez and Srinivasan 2006a,b). The idealized models were partly justified in separate studies employing alternate homogeneous distribution functions (Nunez 1995; Haken 1999), which suggest that predicted EEG properties are relatively insensitive to the assumed exponential distribution, provided it remains homogeneous and connection density tends to fall off with separation distance.
Models that treat cortico-cortical connections as purely homogeneous are not generally expected to be physiologically realistic; rather they provide convenient analytic solutions and "entry points" to models with more realistic connections. One appropriate first step is to embed heterogeneous two-point connections into the otherwise homogeneous connectivity matrix representing ℜ(|r – r1|, ν1) as proposed by Jirsa (2009) and the alternate version developed in Sec 2.4 below. This general approach holds promise for more anatomically realistic models since arbitrary connectivity matrices can be constructed from linear sums of two-point connections. In a more physiologically realistic example Ghosh et al (2008) modeled functional connectivity using a primate connectivity matrix and individual network nodes consisting of neural oscillators embedded in the model network. A more recent study of both homogeneous and more realistic heterogeneous connections in a one-dimensional model has delineated several kinds of dynamics to be expected in each system (Pinotsis et al 2013). For example, homogenous connectivity matrices predict spatially periodic modes, while progressively more localized dynamics reflect increasing degrees of heterogeneous coupling topologies. The resulting effect on oscillatory dynamics at different scales in one and two dimensional heterogeneous systems is likely to be the subject of much further study.
The basic question of the relationships between anatomical and functional connectivity as raised by Buzsaki (2006), Sporns (2011), Pinotsis et al (2013) and many others involves a number of subtle issues including the spatial and temporal scales at which all measures are obtained. Axon connectivity may be estimated from the injection of tracers transported along cell projections in the living brains of animals (Kotter 2007). In humans, structural connectivity is accessible by postmortem examination of dissected tissue (Krieg 1963, 1973) or noninvasive brain imaging methods like DTI (diffusion tensor imaging) that provide major tract information. Human white matter consists mostly of 1010 cortico-cortical axons (Braitenberg 1978). DTI images demonstrate impressive technology, but they currently fall far short of the resolution required to view most individual axons. That is, diameter histograms of human cortico-cortical axons are peaked in the 1µm range (Tomasch 1954; Bishop and Smith 1964; Blinkov and Glezer 1968); that is, about 1000 times smaller than the 1 mm resolution of DTI. Full agreement between tract tracing and DTI is unlikely to be achieved anytime soon since both techniques probe structural connectivity at specific scales and with limited resolution. Comprehensive maps of axon connectivity at multiple mesoscopic and macroscopic scales may be some years away (Sporns 2011).
Given these limitations on anatomical connectivity estimates, journal references to "realistic connections" should perhaps be re-worded to say "more realistic connections." Any anatomical connection matrix employed by field theories must be defined at some chosen spatial scale. Thus, the coordinates (r,r1) used in ℜ(r,r1,ν1) locate patches of neocortex of a certain scale, and any associated field variable must be defined at the same scale. Our field variable, synaptic action density Ψe(r,t), is defined as the number of active excitatory synapses within patches (neural masses) at the 2–5 cm minimum scale of recordable scalp potentials. One can imagine, for example, a high degree of connection heterogeneity at mesoscopic (mm) scales perhaps superimposed on a more homogeneous connection system at the 2–5 cm scale (Braitenberg 1978; Nunez 1995, see fig. 11–14). The 2–5 cm scale connectivity may be more appropriate for models of the very large scale EEG, whereas the smaller scale ECoG may be better predicted by more heterogeneous connections as apparently implied by Pinotsis et al (2013).
The question of whether the above approximate approach to modeling scalp potentials represents a useful scientific contribution is addressed further in the experimental Sec. 3, but here we emphasize that EEG functional connectivity as measured by EEG coherence depends strongly on spatial scale, frequency band, and brain state (Nunez et al 1997, 1999, 2001; Srinivasan 1999). For example, large scale (low resolution) coherence in parts of the theta and alpha bands is easily manipulated by eyes opening or cognitive tasks (Nunez 1995; Silberstein et al 2003, 2004). High resolution EEG coherence patterns (estimated from spline-Laplacians) generally differ from low resolution patterns. Thus, the experimental data show unequivocally that fixed anatomy does not dictate functional connectivity, although the latter must be constrained by the former.
Functional connectivity may depend on temporal as well as spatial scales. In one study DTI and fMRI data were obtained from a single brain slice (Koch et al 2002). Functional connectivity on relatively long time scales (compared to EEG) was estimated from cross-correlation of BOLD signal fluctuations between voxel pairs, whereas structural connectivity was estimated from DTI. Structural and functional connectivity were generally positively correlated in the following sense. Low functional connectivity was only rarely found between structurally linked voxels; however, high functional connectivity often occurred between voxels that were not linked. The possible generalization of these data to other temporal and spatial scales is far from clear.
2.3 Quasi-linear approximations
The modulation density of action potentials G(r, t) fired in a neural mass may be plausibly related to the modulation of active excitatory synapses H(r,t) through a sigmoid function. The sigmoid function quantifies the idea that action potential density in a neural tissue mass is expected to progressively increase as a result of increased excitatory synaptic input, but at a much slower rate for high input levels. The underlying assumption is that excessive excitatory input to a cortical tissue mass will generate enhanced negative feedback in healthy brains due to inhibitory synaptic action from contiguous cortex and/or thalamus well before a large fraction of neurons in the tissue mass fire, as in epilepsy. This picture differs from the local Wilson-Cowan (1972, 1973) sigmoid functions, which are based on refractory periods limiting action potential density. By expanding an assumed sigmoid relationship between action potential density and synaptic action, a second equation in the variables is employed forming a well posed mathematical model (Jirsa and Haken 1997; Nunez 2000)
| (2.2) |
Here ρ is the number of excitatory synapses per cortico-cortical axon, β is a parameter determined by the background excitability of neocortex controlled by chemical neuromodulators on long time scales, and α is a parameter determined by the strength of inhibitory feedback. In the linear version of the global theory (α → 0), a dynamic transfer function (or its inverse, the dispersion function) is obtained. The dispersion relation is determined by the poles of the transfer function in the usual manner of linear systems analysis. A linear partial differential equation in the variable H(r,t) follows from the dispersion relation. The model cortical-white matter system then acts as a spatial-temporal filter with certain dominant frequencies.
In the linear approximation, an x% increase in excitatory synaptic action in a neural tissue mass results in a y% increase in action potentials, with the ratio y/x fixed for any constant background excitation level β. Approximate nonlinear versions of this model are based on physiological arguments, especially the postulate that instability is prevented in healthy brains by recruitment of additional inhibitory mechanisms (negative feedback) from thalamus or contiguous cortex, perhaps involving lateral inhibition. Quasi-linear analyses (α ≠ 0) may employ modifications of the dispersion relation to derive nonlinear partial differential equations subject to numerical and semi-analytic solutions, as outlined in Sec. 2.7 and appendix D (Nunez 2000).
2.4 Regional resonances: point-to-point axon connections
An extreme limiting case of inhomogeneous and anisotropic axon distributions is the case of reciprocal (point-to-point) connections between two cortical locations xa and xb (Silberstein 1995b; Jirsa 2009). From Eq (2.1) axon propagation in a one-dimensional closed loop of cortex of circumference L is expressed as
| (2.3) |
By employing the linear approximation (α → 0) in Eq (2.2) it is shown in Appendix A that the predicted oscillation frequencies ωR and damping γ are
| (2.4) |
| (2.5) |
Here the regional time delay is and ν is the (assumed) constant axon propagation speed. Unstable oscillations occur for β > 0.5 in this linear limiting case. Consider a fiber system connecting cortical locations xa and xb of length 15 cm with (typical) axon speed equal to 600 cm/sec (Nunez 1995). The delay time is τ = 25 ms and predicted resonant frequencies occur at
| (2.6) |
Local delays due to PSP rise and decay times may be simply modeled by adding such local delay to τ, thereby lowering the predicted resonance frequencies. Nonlinear effects could further reduce predicted frequencies (Nunez 2000; Nunez and Srinivasan 2006a). This same analysis could also apply to simple, point-to-point thalamo-cortical feedback loops.
2.5 Distributed axons in one dimension
In the original one-dimensional version (Nunez 1972, 1974a), axons were assumed to run only in the anterior-posterior direction of each hemisphere forming a closed loop of length L. Cortico-cortical axons may be parceled into Q homogeneous fiber systems with connection densities that fall off exponentially with separation |x – x1 | plus multiple heterogeneous systems ℝ(x, x1, ν1):
| (2.7) |
Consider the idealized case when all but one of the systems consist only of short axons with negligible delays (ν1 → ∞), and the single long range system (λ1 → λ) has a single axon speed ν. In this limiting case, the short axon systems act only to increase the background excitability of the cortex, effectively adding to the parameter β in Eq (2.2) (Nunez 1995). The linear global model then predicts frequencies and damping (Nunez 1995, 2000; Nunez and Srinivasan 2006a,b).
| (2.8) |
| (2.9) |
The fundamental mode (n = 1) is omitted from Eq (2.8) based on a separate study of the effect of finite loop circumference L (see appendix B). Note that unstable oscillations are predicted in the linear approximation Eq (2.2) when the cortical background excitability parameter β > 1. Some parameter ranges allow for linearly stable (β ≤ 1), weakly damped (γ / ω << 1) slow oscillations, especially for axon systems that fall off very slowly with distance (λL < 1 – 5); however, we believe it much more likely that brains operate normally in nonlinear states. Quasi-linear (α ≠ 0) analytic and numerical approximations suggest the production of limit cycle-like modes due mainly to inhibitory feedback in healthy brains (Nunez 2000); thus, we focus here on β ≥ 1. Similarly, the classic Wilson-Cowan (local) model, focuses on dynamics near unstable critical (spiral) points, allowing for stable limit cycle oscillations (Wilson and Cowan 1973; Srinivasan et al 2013).
Consider a somewhat arbitrary example using the following physiologically plausible parameter choices (ν,L,λ) = (700 cm/s, 60 cm, 0.15 cm−1). The predicted linear oscillation frequencies (Hz) for the modes n = 1,4 are shown in table 3 for cortical excitation level 1 ≤ β ≤ 2.7 . Nonlinear effects are expected to alter these estimates, but perhaps only moderately (Nunez 2000), as discussed in appendix D. Mode number and corresponding wavelength (cm) are shown in the first column. The fundamental mode (n = 1) produces no oscillations over this range of β as it becomes non-oscillatory for β > 0.7, a level below which it is strongly damped. Mode frequencies generally fall off slowly for increasing β at first, but drop sharply near some critical excitation level βn; still larger β results in non-oscillatory lower modes, labeled "None." In other words, each oscillatory mode frequency is generated over a preferred range of cortical excitability β, a finding with EEG connections discussed in the experimental section.
Table 3.
Modes n with corresponding wavelengths (cm) are shown in the first column. Corresponding frequencies (Hz) of linearly unstable oscillations predicted by the one-dimensional model (Sec 2.5) are shown in columns 2–8; they depend on cortical excitation level β (top row). These numerical predictions are based on the assumed cortical/white matter parameters (ν, L, λ) = (700 cm/s, 60 cm, 0.15 cm−1).
| n ↓ β → | 1.0 | 1.2 | 1.3 | 1.37 | 1.4 | 2.0 | 2.7 |
|---|---|---|---|---|---|---|---|
| 1, 60 cm | None | None | None | None | None | None | None |
| 2, 30 | 16 | 12 | 8 | 4 | None | None | None |
| 3, 15 | 31 | 28 | 27 | 26 | 26 | 10 | None |
| 4, 7.5 | 43 | 42 | 42 | 40 | 40 | 32 | 12 |
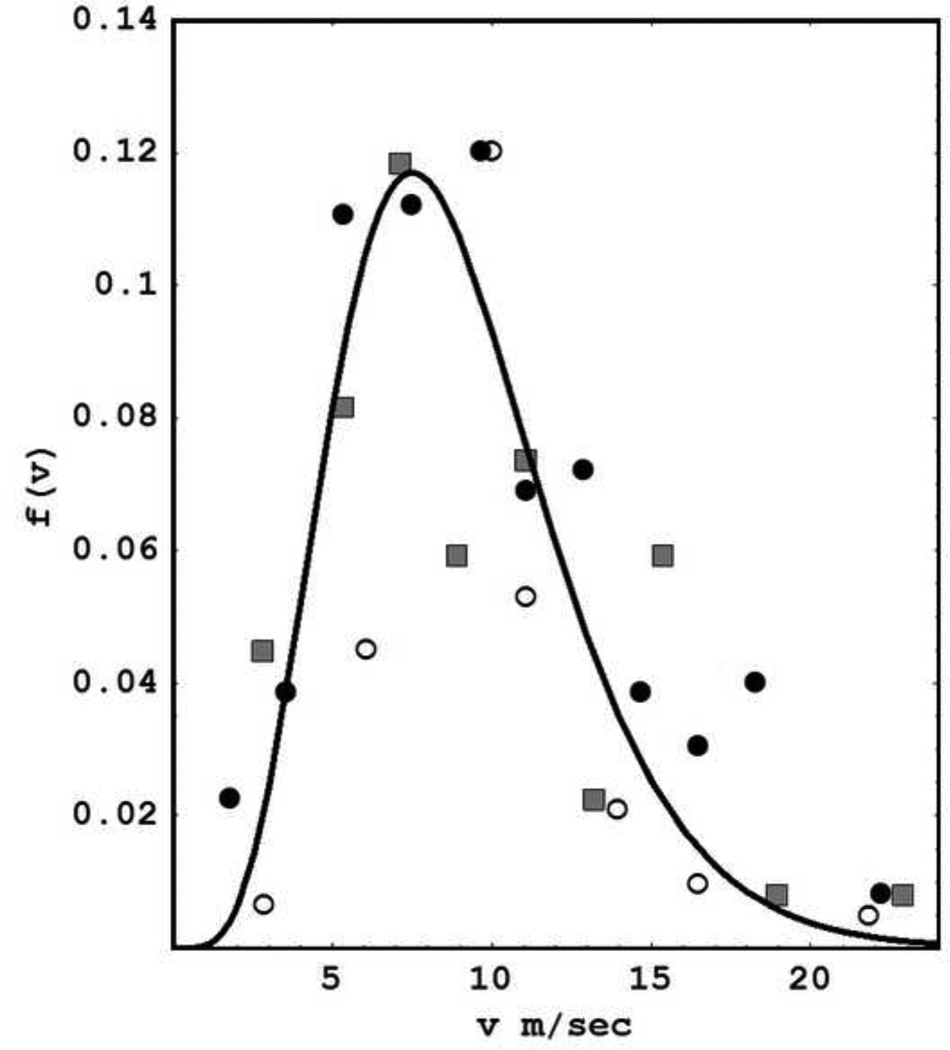
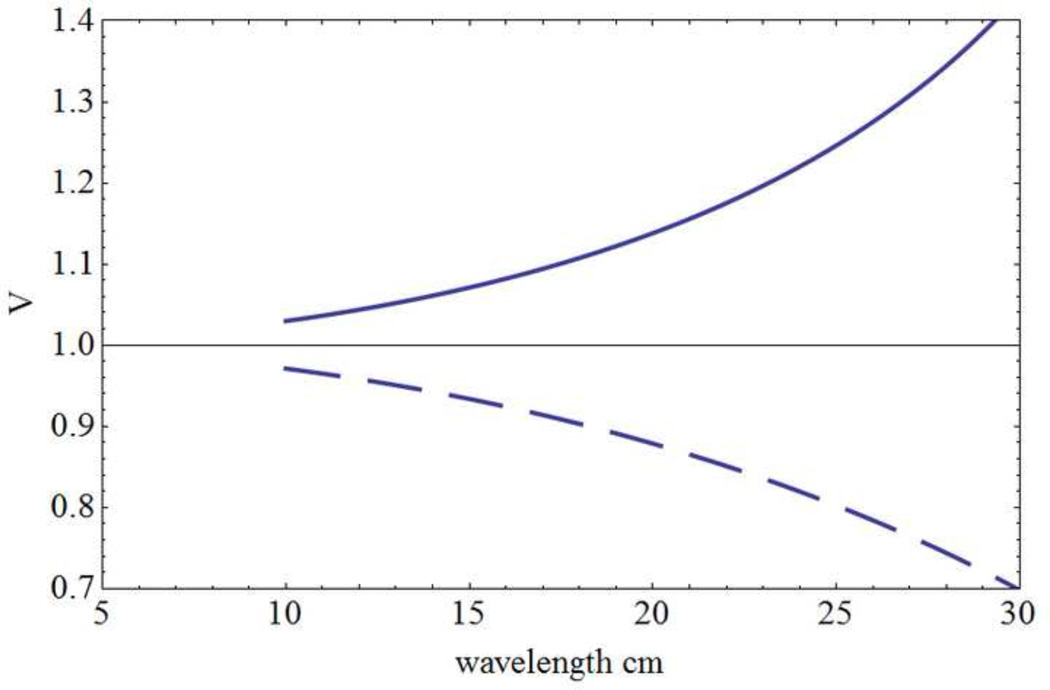
Equations (2.8) and (2.9) are based on the idealized assumption of a single axon speed, that is, f(ν1) = δ(ν1 – ν). In contrast, fig. 4 shows composite experimental estimates of human axon speeds based on three independent studies. We fitted these data to the function (solid line)
| (2.10) |
and recalculated resonance complex frequencies (poles of the dispersion relation). Predicted oscillation frequencies are essentially unchanged. The main outcome resulting from adopting this more realistic axon speed distribution is to "wash out" higher modes by increasing their relative damping. In other words, γ → γn with progressively larger values of β required to produce linear instability in the higher modes as indicated in appendix B.
fig. 4.
Distribution of axon propagation speeds in myelinated human cortico-cortical axons is estimated from 3 independent studies and normalized for plotting on the same scale; the solid line is a fit to the function f(ν1) given by Eq (2.10). Diameter histograms in humans (empty and filled circles) were transformed based on a axon speed of 5.5 m/sec per micrometer of axon diameter (Waxman and Bennett 1972). Empty circle measurements were obtained from corpus callosum (Tomasch 1954). Filled circle data were obtained from frontal lobe (Bishop and Smith 1964). Direct speed estimates (filled squares) were obtained from callosal fibers of rhesus monkey (Swadlow et al 1978). Additional data from Blinkov and Glezer (1968) were consistent with this picture, but could not be normalized to fit on the same scale so they were excluded. This plot was redrawn based on a similar plot shown in Nunez (1995).
2.6 Solutions in a spherical shell
Here we outline solutions to Eq (2.1) in the spherical shell (fig. 6), representing one idealized cortical hemisphere, that is, mentally inflated to smooth out cortical folds (Katznelson 1981, 1982; Nunez 1995). The chosen axon distribution function is
| (2.11) |
fig. 6.
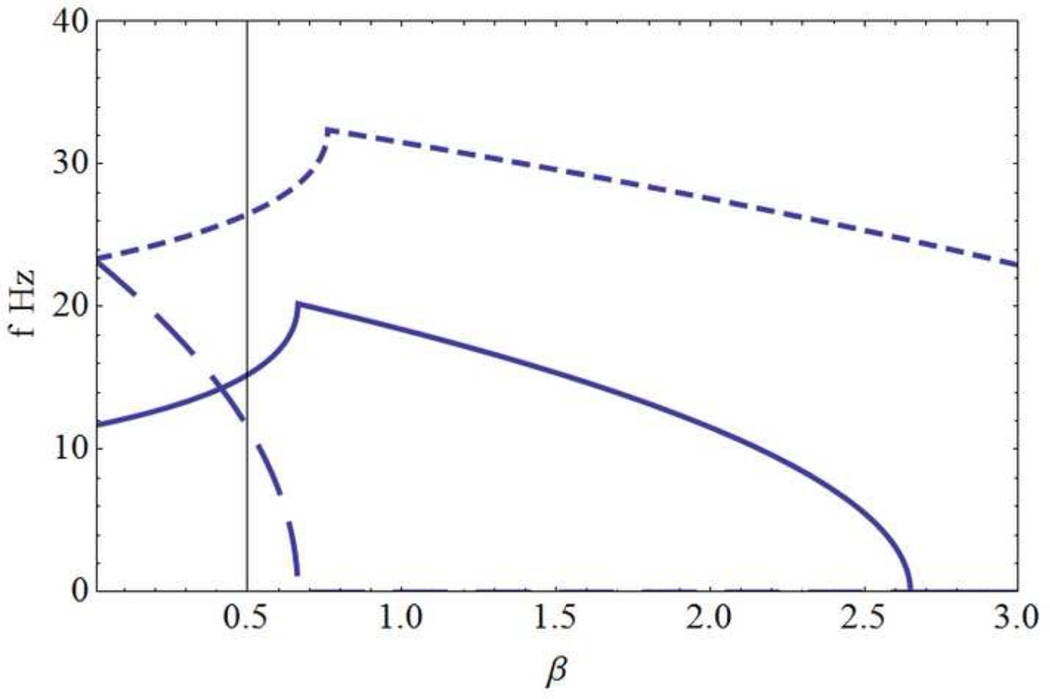
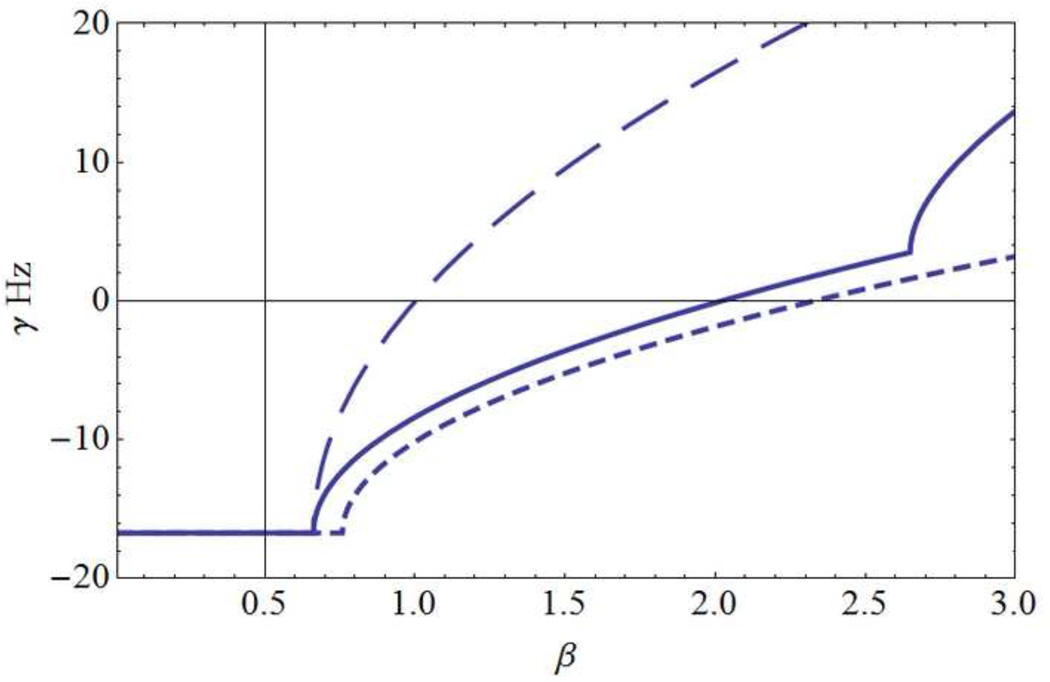
Predictions of the spherical shell model of Sec. 2.6. (a) Mode frequencies f (Hz) and (b) corresponding damping γ (Hz) for the 3 lowest modes with corresponding wavelengths dl: (long dashes, d1 = 60 cm), (solid line, d2= 30 cm ), (short dashes, d3= 15 cm). The horizontal axis is the background cortical excitation parameter β. Physiological parameters adopted here are (λ = 0.15 cm, R = 9.55 cm, ν = 7 m/sec). The first (fundamental) mode l= 1 becomes non-oscillatory for β ~ 0.7, well before it becomes weakly damped; with these parameter choices, this mode is predicted to be non-observable. The mode l=2 exhibits progressively slower oscillations over the 20 to 0 Hz range as β increases from about 0.7 to 2.6. However, this mode doesn’t become weakly damped until β gets close to 2 when oscillation frequencies are in the 10 Hz range. Still larger β values cause further frequency reduction of mode 2, which becomes unstable (γ1 > 0) for β > 2. For larger values of β higher modes oscillate with progressively lower frequencies, a process very similar to that of the one-dimensional model. Discontinuities in curve slopes occur where multiple branches of the dispersion relation intersect; higher frequency branches are omitted for plot clarity.
As in Sec 2.5 cortico-cortical axons are parceled into Q homogeneous fiber systems with connection densities that fall off exponentially with separation distance, here expressed in terms of the angle η(Ω,Ω1) between locations Ω and Ω1 in a spherical shell of radius R (fig. 5). Also included in Eq (2.11) are multiple short anisotropic and inhomogeneous systems ℝ(Ω,Ω1) for which delays are assumed negligible. We again consider the idealized case of a single long homogeneous system λ → λn with sharply peaked speeds f1(ν1) = δ(ν1–ν).
fig. 5.
Spherical shell of radius R representing an idealized neocortex-white matter system of one hemisphere as in a computer inflated model to smooth out cortical folds as in the work of Dale et al (1999) and Fischl et al (1999). Angular location in the shell is given by the spherical coordinates (θ,ϕ), essentially (latitude, longitude), represented by the solid angle Ω. A small surface area in a thin spherical shell is dA = R2 sin θdθdϕ) = R2dΩ. Standing waves in this model occur based on axon speeds in assumed long cortico-cortical axon systems. Shorter axons contribute only to background cortical excitability as discussed in Sec 2.
The factors in front of the exponential function Eq (2.11) provide the required normalization of the surface integral in terms of the number of synapses per axon ρ, that is
| (2.12) |
As shown in appendix C, the predicted synaptic action density in neocortex H(Ω,t) resulting from arbitrary synaptic input H0 (Ω,t) is given by the following sum over spatial modes, that is, the spherical harmonic functions Ylm(Ω)
| (2.13) |
The functions Sl (ω) are evaluated in appendix C. This idealized neocortex/white matter system acts as a band pass spatial-temporal filter with one (or more) discrete preferred oscillation frequency for each spatial mode l. These resonant frequencies are obtained from the poles of Eq (2.13); they are independent of the index m because the single long range axon system in this model is homogeneous and isotropic. When the poles ωpl are found, Eq (2.13) becomes
| (2.14) |
Here the sum over the index p indicates possible multiple branches of the dispersion function; that is, multiple poles for each mode l. The coefficients blm are determined by the spatial-temporal properties of cortical input, but the dominant (resonant) oscillation frequencies are given by the real parts of the complex frequencies ωpl when the imaginary parts are small or positive (minimally damped or unstable modes).
Given our basic premise that instability is prevented in healthy brains by enhanced inhibitory actions, that is α ≠ 0 in Eq (2.2), our study focuses on modes close to or above the linear instability level. Figure 6 shows plots of resonant frequencies fl (Hz) and damping γl(Hz) for l = 1,2,3,… as a function of cortical excitation β using parameters consistent with the closed cortical loop of length L in Sec 2.5. The effective sphere radius is R = L/2π = 9.6 cm. As in the one-dimensional example, linear oscillations become lower in frequency, progressively less damped, and ultimately unstable (γl > 0) as background cortical excitation β increases, but in contrast to the one-dimensional solution, different mode instabilities occur at different values of β.
2.7 Quasi-linear solutions to the one-dimensional model
The model of Sec 2.5 has been extended to include weak nonlinear effects by employing the input-output Eq (2.2) with α ≠ 0 (Nunez 2000; Nunez and Srinivasan 2006a). The procedure is to convert the basic integral equation (2.1), combined with Eq (2.2), to a nonlinear partial differential equation (PDE). Two approaches were followed to find oscillatory solutions: 1) Numerical solutions to the PDE were obtained for different parameter choices. 2) Semi-analytic methods were employed to approximate the PDE by an ordinary differential equation for each (approximately) uncoupled mode as outlined in appendix D. For weak to moderate linear instability and nonlinearity (roughly, 1 < β < 3 and α < 0.5), the net results of these studies are summarized as follows: 1) The coupling between spatial modes is very weak or zero. 2) Each spatial mode is essentially a genuine limit cycle oscillation, thus the caveat "like" in our use of "limit cycle-like oscillations" may be omitted to first approximation. 3) Each mode frequency is a reasonable approximation to its equivalent linear oscillation frequency; that is, using the same β, but with α ≠ 0) The main effect of nonlinearity is to limit the amplitude of linearly unstable oscillations to relative values approximated by Eq (3.1) below.
3. Experimental Implications for EEG
Experimental connections to EEG and steady state visually evoked potentials (SSVEP) are outlined here; most are common to both the one dimensional cortical loop (Sec 2.5) and spherical models (Sec 2.6). Some are semi-quantitative, others only qualitative. The accuracy of our quasi-linear model predictions with local networks "turned off" is expected to be quite limited, but here we address several broader issues that may survive moderate nonlinearity and bottom-up network influences, indicated by the dashed arrow in fig. 1. Any of these experimental connections can have alternate explanations, for example, from one or more of the local or local/global models cited in Sec. 1 or from other properties of neural networks. A plausible conjecture for any complex system is that observed effects can easily have multiple causes; this cautionary point is especially applicable to brains. Thus, we claim only relationships not comprehensive explanations to complex physiological processes. Many questions remain, including the effects of cortico-cortical axon inhomogeneity and nonlinear cortical tissue responses discussed in Secs 2 and 4. Nevertheless, the following wide range of EEG studies seems to paint a compelling picture when interpreted in the context of physiologically-based brain theory, even if such theory is presented in the context of greatly oversimplified quasi-linear models.
3.1 Temporal frequency range
From the plausible parameters ranges given in the one-dimensional model (Sec 2.5), ν/L ~ 7–15 Hz. In the example discussed, the lowest oscillatory mode occurs for n = 2, yielding oscillations in the general range of alpha frequencies near the instability level β = 1. Predicted modes in the spherical model (Sec 2.6) also yield alpha band frequencies for the first overtone l = 2 over a range of cortical excitation levels. These predictions involve an unknown parameter, the cortical background excitation level β, which is conjectured to be under neuromodulatory control and vary widely in different brain states. Subject to the assumption that β can be in the right range to produce oscillatory activity in at least some brain states, predicted frequencies of the lowest modes are roughly in the EEG range. We cannot claim that this very approximate agreement, by itself, verifies the models. On the other hand, if the frequency estimates were clearly off by more than a order of magnitude, we might have discarded the models. In any case, strong nonlinear effects are expected to generally alter quasi-linear frequency predictions, but perhaps only moderately, depending on the strength of nonlinearity as indicated in appendix D and (Nunez 2000).
We do not claim that axon propagation delays provide an exclusive time scale for alpha oscillations. Rather we suggest that the alpha band generally consists of both local (perhaps multiple thalamo-cortical networks in different cortical locations) and global field (or "global network") phenomena that are distinguished by different reactivity to tasks or stimuli and experimental spatial scale. For example, activation of motor cortex is associated with desynchronization of local alpha rhythms in both EEG (Pfurtscheller and Lopes da Silva 1999) and ECoG (Crone et al 1998) studies; however, this local "desynchronization" (typically meaning amplitude reduction) typically occurs with an intact global alpha (Andrew and Pfurtscheller 1997; Andrew 2000). A combination of low and high resolution EEG applied to the same scalp data allows us to view neocortical dynamics at different spatial scales (both larger than the ECoG scale); thereby distinguishing global from more local alpha rhythms in scalp data (Nunez 1989, 2000; Nunez et al 2001; Nunez and Srinivasan 2006a; Buzsaki 2006). The existence of multiple human alpha rhythms was, in fact, firmly established long ago through extensive EEG and ECoG recordings, although some modern work has apparently failed to appreciate this history. Here is EEG pioneer Grey Walter's description of observed alpha band dynamics expressed in 1964 (Basar et al 1997):
We have managed to check the alpha band rhythm with intra cerebral electrodes in the occipital-parietal cortex; in regions which are practically adjacent and almost congruent one finds a variety of alpha rhythms, some are blocked by opening and closing the eyes, some are not, some respond in some way to mental activity and some do not. What one can see on the scalp is a spatial average of and large number of components, and whether you see an alpha rhythm of a particular type or not depends on which component happens to be the most highly synchronized process over the largest superficial area; there are complex rhythms in everybody.
3.2 Amplitude versus frequency
Amplitude predictions require nonlinear models. In appendix D, a crude estimate of the relative amplitudes of oscillations in the one-dimensional model of Sec. 2.5 was derived from the quasi-linear partial differential equation (D3). For the case of weak to moderate nonlinearity, we obtained the following result, similar to that obtained in earlier studies with somewhat different methods (Nunez 2000; Nunez and Srinivasan 2006a)
| (3.1) |
In fairness, we note that local limit cycle modes may also exhibit increased local network source amplitudes as frequency decreases. We must distinguish EEG amplitudes from synaptic action amplitudes H(r,t) because EEG amplitudes depend strongly on cortical source synchrony over regions close to electrodes (Pfurtscheller and Lopes da Silva 1999; Nunez and Srinivasan 2006a). Synchrony could change with cortical excitation level independent of synaptic action (or source) amplitudes. For these reasons, we only tentatively associate larger β with larger EEG amplitudes. The linear models of Sec 2.5 and 2.6 predict lower frequencies for all modes as β increases; thus these models imply an inverse relationship between EEG amplitude and frequency, one of the most robust of all EEG properties across a broad range of cognitive states (Barlow 1993; Nunez 1995).
3.3 Tuning the brain
As the parameter β (background cortical excitability) increases, each predicted mode frequency is reduced and ultimately becomes non-oscillatory. At the same time, new high frequency modes become excited. Similar behavior has been observed in the halothane anesthesia rhythm. Deeper anesthesia, which could result in higher cortical excitability, causes lower frequencies and larger amplitudes. That is, halothane anesthesia "tunes" the brain to produce global oscillations roughly in the 4 to 16 Hz range. As the dominant mode frequency decreases, new higher frequency oscillations appear (Nunez 1974b, 1981; Nunez and Srinivasan 2006a).
Stage 1 sleep typically involves EEG transitions from alpha (8–13 Hz) to more prominent theta (4–7 Hz). Deep sleep is dominated by large amplitude delta rhythms (< 2 Hz), but various sleep stages exhibit superimposed faster oscillations in the alpha and beta bands (8–20 Hz). This observation is consistent with increased β as sleep deepens, thereby lowering at least some of the normal alpha frequencies and, at the same time, allowing new higher modes, which are strongly damped for smaller β, to reached their zero damping levels. In one study using 256 electrodes, sleep slow oscillations consisted of traveling waves that sweep the human cerebral cortex up to once per second (Massimini et al 2004). Each slow oscillation exhibited a definite site of origin and direction of propagation. Of course, observed theta and delta rhythms at the scalp could be due to combinations of global and local networks, the latter influenced by top-down global dynamics, including traveling delta sleep waves.
3.4 Effect of cortico-cortical axon propagation speeds
In global models, the faster the propagation, the faster the global mode frequencies. If all parameters except cortico-cortical propagation speed ν are fixed, brains with faster speeds should produce higher global frequencies. Axon velocity depends on axon diameter and myelination (Waxman and Bennett 1972). Maturation of neocortex during childhood and adolescence involves substantial increases in white-matter volume, including increased myelination and axon diameters (Paus et al 2001; Hagmann et al 2010). A posterior rhythm of about 4 Hz develops in babies in the first few months; it attenuates with eye closure and is believed to be the precursor of the global adult alpha rhythm (Nunez 1995). Frequency gradually increases until an adult-like 10-Hz rhythm is achieved at about age ten, consistent with global model predictions.
The suggestion that cortico-cortical axon maturation strongly influences alpha rhythms is supported by multiple studies showing progressive coherence increases across the scalp with children's increasing age (Thatcher et al 1987). In one study, alpha rhythms were recorded with 128 electrodes in children aged 6 to 11 and young adults (Srinivasan 1999). A high resolution (spline-Laplacian) algorithm was employed to obtain power and coherence estimates at a second scale smaller than the raw EEG, essentially applying a high pass spatial filter to the same data. Power and coherence characterized the spatial structures of the alpha rhythm at the two distinct spatial scales of raw EEG and Laplacian. In adults, the alpha rhythm was characterized by high coherence between distant electrodes in both measures. The children had reduced anterior power and reduced coherence of raw EEG between anterior and posterior electrodes at the peak alpha frequency (in comparison to adults). By contrast, the children's Laplacian alpha rhythm showed much higher power than adults at both anterior and posterior electrodes, but was weakly correlated across the scalp. In other words, children produced strong local alpha and, at the same time, weak global alpha compared to adults, apparently due to immature axon myelination.
The proposed relationship between cortico-cortical axon myelination, propagation speed, and EEG is also consistent with aging studies. Old age (> 60–70) is associated with a substantial decline in myelinated fibers (Meier et al 1992; Guttmann et al 1998; Walhovd et al 2005), reduction in peak alpha frequency, reduction in % of alpha epochs, increased alpha bandwidths (Chatrian and Lairy 1976, Nunez et al 1978), and reduced working memory performance (Clark et al 2004).
3.5 Effect of brain size
If all other parameters are fixed, brains with longer cortico-cortical axons are predicted to produce lower frequencies simply because of longer propagation delays. To the extent that larger brains contain longer axons of the same diameter and myelination (remembering that speed increases with diameter and myelination), we can postulate an inverse relationship between head size and peak alpha frequency. Children must be excluded from such studies because axon myelination increases propagation speed by factors of perhaps 5 to 10 (Waxman and Bennett 1972). By contrast, the brain weight of 5 year old child is about 90% of its adult weight, implying that the linear scale factor (e.g., the parameter L in Eq 2.8) is 97% of the adult value (Blinkov and Glezer 1968; Dekaban 1978). Thus, the effect of maturating myelination (increasing frequency) is expected dominate any small size effect (lowering frequency).
We are aware of three independent studies of alpha frequency versus head size in adults. Two such studies (Nunez et al 1978; Posthuma et al 2001) found the predicted negative correlation (p = 0.01 to 0.02 and p = 0.003, respectively). By contrast, Valdés-Hernández et al (2009) found only a very small negative correlation between peak alpha frequency and cortical surface area that failed the significance test (p > 0.05). This group did, however, find statistically significant relations between several aspects of white matter architecture observed with MRI and peak alpha frequency. Given that the alpha band apparently consists of both local network activity and global fields (Nunez and Srinivasan 2006a), we have suggested that future work in this direction distinguish these alpha phenomena, for example, by focusing on alpha peaks with high anterior-posterior coherence that are more likely to be globally generated (Nunez 2011).
3.6 Traveling waves
A number of human studies of scalp potentials have found traveling waves in both SSVEP (steady state visually evoked potentials) and spontaneous EEG with propagation speeds approximately in the 1 to 10 m/sec range; that is, roughly in the range of cortico-cortical axon propagation speeds. Our purpose in this section is to employ both volume conduction considerations (Sec 1.6) and global dynamic models (Secs 2.5 and 2.6) to: 1) Interpret existing studies and 2) Suggest designs for future experimental work.
In many local and global models subcortical inputs to cortex are expected to create epicenters for wave propagation away from such centers. In animal experiments cortical surface propagation speeds in the 0.1 to 0.3 m/sec have been reported for alpha band activity (Lopes da Silva and Storm van Leeuwen 1978; Wright and Sergejew 1991). These are small scale phenomena involving mm scale wavelengths much too short to be recorded on the scalp because of spatial filtering by volume conduction as in Eq (1.1). This small scale propagation may be due to intra-cortical and/or thalamic PSP delays and possibly non-myelinated intra-cortical axon delays (Nunez 1995).
In the case of much longer wavelengths (~ 5–30 cm) recorded from human scalp, the locations of cortical epicenters may be visual cortex in the case of SSVEP and possibly random locations (e.g. spatial-temporal white noise) for EEG. From an experimental viewpoint we might expect to see short periods when waves travel in some consistent direction, other periods when traveling waves combine (interfere) to produce standing waves, and many periods with mixed traveling and standing waves due to partial interference. Still other periods may be dominated by local networks that act to erase most wave activity.
Here we outline issues using the one dimensional model of Sec 2.5 as our example since most experimental studies are based on one dimensional anterior-posterior propagation. Predictions of this crude model are not expected to match experiments closely because: We anticipate substantial nonlinear behavior in actual brain waves, and we have ignored possible network influences; nevertheless, some general issues may be valid. First, we note that phase velocities are not predicted to exactly equal axon speeds ν; that is, at least two kinds of "propagation velocity," phase velocity νp and group velocity νg, typically characterize most kinds of traveling waves. This duality occurs because genuine waves typically travel in groups (or "packets") composed of multiple components with somewhat different wavelengths and phase velocities. As a result such wave packets distort and spread out (disperse) as they propagate. The phase velocity νpn (cm/sec) of each wave component n is related to its frequency fn (Hz) and wavelength dn (cm) by
| (3.2) |
Note that wavelengths are not restricted by boundary conditions for traveling waves that have not yet combined to form standing waves. Water waves provide a useful example because we can see them and, like EEG waves, they have different properties at different spatial scales. Phase velocities of small scale water waves (ripples due to surface tension) are lower than their group velocities. By contrast, phase velocities of intermediate and large scale wind-driven waves are larger than their group velocities (Nunez 2000). Thus, individual wave components can move faster or slower than the group causing distortion of the wave packet's spatial shape. We can picture this phenomenon as similar to a group of marathon runners running at almost the same speed, but some a little faster than others. The simple linear model of Sec. 2.5 predicts the following relationship between axon speed ν, phase velocity and group velocity for all modes:
| (3.3) |
Group velocity vgn is essentially the speed of the "center of mass" of a wave packet containing components with wavelengths typically distributed over a narrow range. If this range is too large, wave packet distortion may make it impossible to identify any unambiguous group velocity. After some delay from their points of origin, waves must either be attenuated or combined by interference as forced by global boundary conditions. In the latter case only discrete wavelengths remain, that is, standing waves are produced. Using the parameter choices in Sec. 2.5 for the "alpha-like" mode n = 2 with excitation level β = 1, predicted phase and group velocities are νp2= 0.7ν and νg2 = 1.4ν. With higher modes (n > 2, shorter wavelengths) the two velocities are more nearly equal as shown in fig. 7. As excitation level β increases, mode frequencies decrease and phase and group velocities become even more unequal. The wavelength range in the plot matches possible scalp estimates, limited at the short end by electrode density and volume conduction (5–10 cm) and the long end by electrode array length on the scalp (25 ~ 30 cm) .
fig. 7.
Ratios of phase velocity (dashed line) and group velocity (solid line) to axon propagation speed predicted by the one dimensional model of length L of Sec 2.5. and are plotted versus spatial wavelength for wave components traveling in a packet. Parameters are (λ = 0.15 cm, L = 60 cm, β = 1)
Estimates of EEG and SSVEP propagation speeds and other wave properties have employed several approaches: 1) Measurement of statistically significant progressive phase shifts across the scalp (Hughes et al 1995; Nunez 1995; Silberstein 1995a; Burkitt et al 2000; Nunez and Srinivasan 2006a; Klimesch et al 2007; Patten et al 2011). 2) Fourier transforms in one surface dimension using the Exp[jknx] as basis functions (Nunez 1974b; Nunez 1981; Srinivasan et al 2006a). 3) Generalized Fourier transforms in two surface dimensions using the spherical harmonics Ylm (Ω) as basis functions (Wingeier et al 2001; Wingeier 2004; Nunez and Srinivasan 2006a). 4) Other methods (Massimini et al 2004; Nunez and Srinivasan 2006a).
Experimental estimates face several challenges due to volume conduction distortion, reference electrode issues, and the unknown properties of genuine brain waves. Reference effects are expected to overestimate propagation velocities; close bipolar electrodes generally do better, but may be biased toward shorter wavelengths (Nunez 1974b; Silberstein 1995; Burkitt et al. 2000). Fourier transforms could possibly bias propagation velocities towards the slow end because the longest waves, which travel fastest for a fixed frequency band, may be poorly resolved due to limited length of the electrode array. On the other hand, phase shift estimates along linear arrays may overestimate velocities if they are biased towards longer wavelengths (Srinivasan et al 2006). We emphasize that none of these approaches is generally inaccurate; rather they tend to emphasize different wavelengths propagating inside wave packets.
Here we cite four independent studies of EEG propagation velocity, three of alpha rhythm and one of sleep delta oscillations. When phase velocities are estimated from progressive phase shifts, typically along the anterior-posterior scalp of each hemisphere, the estimates are checked for statistical significance with surrogate data or simply by scrambling electrode positions using the same phase estimates. Alternately, both phase and group velocities may be estimated with spatial-temporal Fourier transforms. Speeds are expressed here with respect to scalp, but because of cortical folding, equivalent cortical surface speeds are about twice scalp speeds. The appropriate speed comparison to global models depends on the geometry of cortico-cortical axon paths that bypass cortical folds; thus, one cannot claim agreement with theory closer than a factor of two for this reason alone.
Alpha phase velocity estimates along the scalp were obtained by Nunez (1995, 3 to 7 m/sec) and Patten et al (2011, 6.5 ± 0.9 m/sec). Note that the model of Sec 2.5 predicts that the lowest undamped mode is the first overtone (n = 2) with a wavelength of about 30 cm. From Eq (3.2), a 10 Hz alpha wave is predicted to have a phase velocity of 3 m/sec, but again such estimate can be no closer than a factor of two because of axon path uncertainty around cortical folds. Estimates of alpha wave group velocity based on whole head recordings with 131 electrodes in five subjects report scalp speeds in the 3 to 5 m/sec range (Wingeier 2004; Nunez and Srinivasan 2006a). Note that EEG group velocities can exist only if increasing temporal frequency through and above the alpha band occurs with increasing spatial frequency. Thus, any positive test for the existence of a robust positive group velocity supports the presence of traveling waves in the data.
Finally, we note that delta oscillations in sleep consist of traveling waves with propagation speeds reported to vary over the 1 to 7 m/sec range (Massimini et al 2004). We do not know how these latter methods might have weighted different wavelengths in wave packets, but generally, speed variations over time are predicted by global models to be associated with changes in wavelength distributions within wave packets. Such distributions could be determined by the spatial properties of cortical input; broad synchronous input being associated with longer wavelengths (Nunez 1995). These effects are expected before a few surviving wavelengths are later selected by boundary conditions. We note also that the model of Sec 2.5 predicts large differences between phase and group velocities for delta range oscillations, perhaps adding to "propagation speed" ambiguity.
3.7 Traveling steady state visually evoked potential (SSVEP) waves
The global models of this paper suggest that SSVEP speeds should be in the same general range as the alpha wave speed estimates, but differ somewhat due to different distributions of wavelengths in wave packets. Whereas global alpha rhythms appear to have substantial power near 30 cm wavelengths (n = 2 in the one-dimensional model), wavelength distributions of SSVEPs might have more relative power at shorter wavelengths, expected because of the relatively small size of the primary visual cortex input region (Nunez 1995, Nunez and Srinivasan 2006a,b). In this case, we might expect estimated SSVEP wave speeds to be somewhat slower than alpha wave speeds. In one study based on progressive phase shifts in bipolar recordings, scalp phase velocities of 2–6 m/sec were obtained (Silberstein 1995a; Burkitt et al 2000). In another study based on Fourier transforms, typical scalp phase velocities of 1–3 m/sec were found (Srinivasan et al 2006).
Several evoked potential studies suggest relations between cognitive functions and traveling waves; for example, some view the waves as a means of communication between distant brain areas, thereby impacting working memory, or serving other cognitive functions (Hughes et al 1995; Ding et al 2006; Klimesch et al 2007; Hanslmayr et al 2007). We offer no specific mechanisms that might link the waves to cognition; however, it seems apparent that waves and networks interact dynamically in some manner thereby altering both phenomena and perhaps facilitating binding of disparate networks (Nunez 2010) or otherwise effecting the precision of synaptic input and subsequent summation in critical target neurons (Fields 2008). If cognition is associated with networks, it follows that both network and wave (or other global synaptic field activity) will be closely associated with the integration of cognitive events, constrained by fixed anatomy and physiology, including axon connection structure, axon speeds, and global boundary conditions.
3.8 Standing EEG and SSVEP waves
Most SSVEP waves travel in the posterior to anterior direction away from primary visual cortex (Silberstein 1995a; Burkitt et al 2000; Srinivasan et al 2006), whereas alpha wave packets travel about half the time in either direction (Nunez 1995; Patten et al 2011). In Nunez (1995) waves in about 8% of all epochs traveled in each direction, a figure that depends weakly on the severity of statistical tests. What happens with the other 84% of epochs? With multiple wave packets traveling in any confined space, traveling waves must either attenuate (damp out) or combine (interfere) with other traveling waves to form standing waves. The suggested interference phenomenon for brain waves may occur when a cortical tissue mass (e.g. column) with elevated excitatory synaptic action due to one wave packet receives elevated inhibitory input from another wave packet, resulting in a partial cancellation effect as detailed in our global models.
In one SSVEP study (Silberstein 1995a; Burkitt et al 2000) two kinds of stimuli were presented: A checkerboard or uniform flicker driven at the subject's peak alpha frequency. Checkerboard patterns were found to be more likely to produce progressive phase shifts associated with posterior-to-anterior traveling waves. By contrast, the unstructured stimulus tended to produce an abrupt phase change in central regions of the array, more consistent with standing waves. A number of subjects switched their phase topography with stimulus change.
In other studies, low frequency (< 20 Hz) SSVEPs elicit resonant responses in large-scale networks whose spatial distribution depends strongly on the input temporal frequency (Silberstein 1995; Ding et al 2006; Srinivasan et al 2006). That is, the spatial patterns of SSVEP, far away from visual cortex are sensitive to small (~ 1 Hz) changes in input frequency, suggesting global rather than local (primary visual system) resonance. Most convincingly, robust frontal responses are easily recorded only for input frequencies in selective parts of the alpha band, possibly revealing standing waves with amplitude peaks near occipital and frontal cortex. Raw (unprocessed) and high resolution SSVEPs, obtained with 128 channel recordings, reveal that both large scale (10–25 cm) and smaller scale (2–5 cm) cortical spatial structures are sensitive functions of input frequency (Srinivasan et al 2006). Maximum responses in frontal cortex all occur within the alpha band at both scales, but at different alpha frequencies, providing still more evidence for simultaneous, but distinct, local and global alpha processes with resonance peaks typically separated by 1–3 Hz. The large scale responses appear to be combinations of traveling and standing waves; small scale responses may indicate local networks.
3.9 Temporal and spatial frequencies are related
In the proposed global wave framework we generally expect to observe higher temporal frequencies associated with higher spatial frequencies (shorter wavelengths) above the fundamental mode. This is a basic feature of nearly all wave phenomena, one of the defining properties, at least of linear “waves.” Without this property no robust and positive group velocity is expected in any spatial-temporal dynamic process. The specific relationship between spatial and temporal frequencies, called the dispersion relation, is a property only of the wave medium; Eq (2.8) is an example. Such relationship has been reported for EEG dynamics at three different laboratories using different estimation methods. In (Nunez 1974b) crude spatial-temporal Fourier transforms based on 8 or 16 electrodes (maximum available at the time) along the midline indicated that the lower half of the alpha band had consistently lower spatial frequencies than the upper half, consistent with the alpha wave packet conjecture.
A separate study used a one-dimensional array around the head circumference (Shaw 1991, reviewed by Nunez 1995). This array mixed activity from the two hemispheres preventing phase velocity estimates. However, it did allow scalp power estimates for long wavelengths (~ 60 cm). Recorded EEG power spectra were fitted to spatial wavelength d and frequency f according to
| (3.4) |
In both eyes closed and eyes open resting EEG, the exponent q(f) ranged from about 1.5 to 4 over the frequency range 0 < f < 30 Hz. Since q(f) > 0 for all frequencies, scalp power consistently fell off at shorter wavelengths as expected due only to volume conduction. Volume conduction is independent of EEG range frequencies (Cooper et al 1965; Nunez 1995; Winter et al 2007), yet the fall-off of power at shorter wavelengths occurred most sharply with a maximum q(f) ~ 4 near f0 ~ 10 Hz and became progressively less sharp at higher alpha and beta frequencies. The apparent explanation is that the observed scalp power fall-off at shorter wavelengths was due to a combination of volume conduction and source dynamics. That is, the underlying cortical dynamics involves peak alpha oscillations with the longest wavelengths, and higher alpha and beta temporal frequencies tend to be associated with higher spatial frequencies (shorter wavelengths), as expected with genuine wave phenomena.
This association of temporal to spatial frequencies was supported in a separate analysis (Shaw 1991). Spatially aliased power was estimated as a function of frequency by comparing power obtained with 2 and 5 cm electrode spacing. That is, two samples per wavelength are required to avoid spatial aliasing just as in the time domain. In the four subjects studied, aliased power showed a minimum at the peak alpha frequency f0 in both eyes open and eyes closed states. Aliased power increased monotonically for higher alpha and beta frequencies consistent with the existence of a dispersion relation for dynamic activity above f0.
In still another study, two dimensional spatial spectra were obtained from a 131-channel array (Wingeier et al. 2001, Wingeier 2004). Data were Fourier transformed in time and the spatial structure was fit to series of spherical harmonic functions Ylm(Ω) corresponding to progressively higher spatial frequencies as in Eq (1.1). Frequency-wavelength power structure was estimated for (1 < f < 40 Hz and l = 1,6) for EEG and SSVEP. Above the peak alpha frequency f0, greater relative power consistently occurred in low temporal and spatial frequencies (l ~ 1 – 2) and high temporal and spatial frequencies (l ~ 4 – 6), again consistent with the existence of a dispersion relation with estimated scalp group velocity of 3–5 m/sec for dynamic activity above f0.
3.10 Long range alpha coherence can be high and varies with brain state
If EEG were composed simply of linear standing waves with no active local networks, scalp topography could be similar to fig. 2a or 2b, with zero phase lag between selective regions. Coherence between cortical locations could be close to 1, determined partly by spatial-temporal cortical input properties. At the other extreme, a cortex dominated by uncorrelated local networks would exhibit scalp coherence close to zero provided reference and volume conduction distortions were removed. Here we emphasize that EEG dynamic behavior can apparently approach either of these limiting cases depending on brain state. We suggest a conceptual framework in which local networks are generally embedded in global fields (or "global networks") as indicated below.
One important application of high resolution EEG is to provide more accurate estimates of scalp coherence patterns, which provide important measures of functional segregation and integration between cortical regions; such measures vary substantially across cognitive tasks. Before the 1990s some EEG scientists and animal physiologists suspected that the observed high scalp coherence (e.g. 0.6–0.9) over large distances (> 10 to 20 cm) did not reflect cortical source coherence, but resulted only from volume conduction. This view was based partly on the fast fall off of coherence (typically over less than 1 cm) recorded from animal cortex with mm scale electrodes. But, this volume conduction interpretation ignores the fact that high human scalp coherence is mostly confined to narrow frequency bands (typically the lower range of alpha frequencies), and volume conduction is essentially independent of frequency. Furthermore, alpha coherence is easily manipulated by eye opening or cognitive tasks having no connection to volume conduction.
This misunderstanding of scalp coherence also involved a failure to appreciate that the dynamic variables that characterize complex systems are generally expected to be scale-sensitive (Nunez 1995, 2010; Nunez et al. 1997, 2001; Nunez and Srinivasan 2010; Sporns 2011). Thus, cortical coherence patterns estimated with mm scale (mesoscopic) cortical electrodes are not generally expected to mirror (macroscopic) scalp coherence between the same cortical regions as suggested in Sec 1.6. It has been shown that spline-Laplacian and dura image (two independent high resolution approaches) coherence estimates are typically conservative; that is, they tend to underestimate cortical source coherence by filtering out the very low spatial frequencies, which may only partly result from volume conduction (Srinivasan et al. 1998; Nunez and Srinivasan 2006a). Note also that large (0.5–0.9) and narrow (~ 1 Hz) alpha band coherence at 10 to 20 cm scalp separations is also easily obtained with (close) bipolar recordings that substantially minimize volume conduction effects (Nunez 1995).
The observation that the smaller local networks, global systems and intermediate scale systems exhibit distinct properties emphasizes the importance of multi-scale coherence measures. To approach this goal, combined low and high resolution EEG can provide complementary coherence estimates that are maximally sensitive to large (~ 5–10 cm) and intermediate (~ 2–3 cm) spatial scale source regions, respectively (Nunez 1995; Nunez et al 1997, 1999; Nunez and Srinivasan 2006a). Such two-scale coherence patterns then provide distinct estimates of local versus global processes (Pfurtscheller and Neuper 1992; Andrew and Pfurtscheller 1997; Srinivasan 1999; Srinivasan et al 1998, 1999, 2007; Andrew 2000; Silberstein et al 2003, 2004).
4. Conclusions
This paper reviews three idealized global models suggesting large scale oscillatory dynamic behaviors that depend on long axon propagation delays and background level of cortical excitability. Excitation level is quantified by the single nondimensional parameter β, which determines the fraction of new action potentials produced in mesoscopic (mm to cm scale) cortical tissue masses for each fractional increase in excitatory synaptic input. Cortical excitation level is believed due to neuromodulatory control on long time scales in addition to inhibitory and the excitatory synaptic action associated with the shorter axon systems; delays in the shorter axons are neglected to first approximation here. Linear and quasi-linear models are emphasized to keep the mathematics not only tractable, but easily interpretable in the context of EEG experiments. In all three linear models, this idealization leads to the prediction of damped oscillations for small β and various linear instabilities, including unstable oscillations, for large β.
We doubt that such linear processes actually occur often (if ever) in real brains. Rather, we conjecture that brains normally operate in nonlinear ranges where the linear models break down. This may occur in healthy brains if excessive active excitatory synapses in a tissue mass enlist additional inhibitory feedback, either from contiguous cortex or thalamus, thereby preventing runaway excitation associated with epilepsy. In other words, linear instabilities may result in stable "limit cycle-like" global modes similar to the simple limit cycles predicted by local models. This conjecture is based on the idea that natural selection has favored healthy brains, in this case implying that linear instability normally results in stable oscillatory modes rather than epilepsy. This view differs from many physics and engineering studies of much simpler systems that focus on weakly damped waves. The postulated enhanced inhibition was approximately quantified by the nondimensional parameter α multiplying the nonlinear term in Eq (2.2), producing quasi-linear models in which brain state is determined by both parameters α and β (Jirsa and Haken 1997; Nunez 2000). In the limiting case of weak nonlinearity with negligible mode coupling in the one-dimensional model, each spatial mode can undergo its own uncoupled oscillation; that is, the "limit cycle-like" modes become genuine limit cycles. The predicted EEG is then given by a linear sum of spatial modes, Eq (D4), as in the linear case.
None of these global models are expected to closely represent accurate anatomy, in part because they ignore specificity of cortico-cortical connections believed to form parts of functional neural networks. Rather, the models are chosen to produce simple analytic solutions that are easy to interpret and compare with experimental data, especially the large scale scalp potentials recorded in states with small to moderate (bottom-up) local network influences on the global dynamics as indicated in fig. 1 by the dashed arrow. The three global models outlined here attempt to bracket the ranges of several kinds of cortico-cortical axon distributions by examining simple limiting cases of the inhomogeneous and anisotropic systems expected in actual brains. One approach to cortico-cortical inhomogeneity is to combine the models of Sec. 2.4 and 2.5 by assuming homogeneous connections superimposed on a single point-to-point connection, similar to the study by Jirsa (2009).
The global models, viewed together, suggest that recordable global oscillatory behavior (limit-cycle like modes) in the general range of EEG frequencies (roughly 1 to 40 Hz) may occur in neocortical/white matter systems provided three conditions are met: 1) Background cortical excitability (variable) is sufficiently high. While global oscillations may be clearly evident in only a minority of brain states, the general top-down influence of global dynamics on local networks may be pervasive. 2) The strength of long cortico-cortical axon systems (fixed) is sufficiently high, as determined by axon numbers and numbers of excitatory synapses per axon. 3) The bottom-up influence of local networks on the global dynamic field (variable) is sufficiently weak, as may occur in some epileptic and anesthesia states as well as the (resting, eyes closed) alpha state. When this third condition is violated in cognitive task data, global, robust oscillations are still predicted by several local/global models cited in Sec. 1 (reviewed in Nunez, 1995, 2000; Nunez and Srinivasan 2006a; Jirsa and McIntosh 2007; Moran et al 2013). These general qualitative predictions appear to be consistent with a wide range of EEG observations as discussed in the experimental section.
In a recently studied one-dimensional global model system with more realistic heterogeneous cortico-cortical axon connections, the spatially periodic oscillatory modes associated with homogeneous axon connection systems appear to be absent (Pinotsis et al 2013), although the associated influences on oscillatory temporal dynamics are unclear. Other related issues that are likely to be studied for some time in the future include the effects of two versus one spatial cortical dimension and the spatial scale of the connection matrix. In particular, we have suggested that multiscale connection matrices may be required to model dynamic behavior recorded at multiple scales. Moreover, in theory, one can employ mm scale heterogeneous axon connection systems superimposed on 2–5 cm scale homogeneous systems to predict EEG behaviors at the large scale.
The basic question of relationships between anatomical and functional connectivity involves the spatial and temporal scales at which all measures are obtained. Axon connectivity may be estimated from the injection of tracers transported along cell projections in the living brains of animals (Kotter 2007). In humans, structural connectivity is accessible by postmortem examination of dissected tissue (Krieg 1963, 1973) or noninvasive brain imaging methods like DTI. In DTI, MRI is used to measure the preferred direction of water diffusion in each brain voxel, thereby providing estimates of major white matter tracks at the 1 mm scale. This approach is based on the idea that the direction of fastest diffusion indicates voxel fiber orientation, where here the label "fiber" indicates bundles of many parallel axons. While DTI images demonstrate impressive technology, they currently fall far short of the resolution required to view most individual axons. Diameter histograms of human cortico-cortical axons are peaked in the 1 µm range (Tomasch 1954; Bishop and Smith 1964; Blinkov and Glezer 1968); that is, about 1000 times smaller than the 1 mm resolution of DTI. Human white matter actually contains about 1010 cortico-cortical axons (Braitenberg 1978), far more than the number of tracts revealed by DTI images. Thus comprehensive maps of axon connectivity at multiple mesoscopic and macroscopic scales may be "years away" as argued by Sporns 2011.
We have further addressed the issue of heterogeneous systems by considering models containing both homogeneous and heterogeneous connection systems as given by Eqs (2.7) and (2.11). In one idealized case the heterogeneous systems are all short range (negligible axon delays) and at least one homogeneous system is long range. In this case the heterogeneous short range systems only add to the background excitability (parameter β) and the oscillatory solutions Eqs (2.8) and (2.14) remain intact (Nunez 1995; Nunez and Srinivasan 2006a). Also, the simple point-to-point heterogeneous system yields oscillatory solutions given by Eq (2.6). These models suggest that the question of oscillations in genuine heterogeneous/homogeneous systems is a quantitative one depending partly on several poorly known details of fixed anatomy including lengths and relative strengths of various kinds of axon connections. While much further work is required to access the accuracy of this approach, the experimental data outlined in Sec 3 provides reason to affirm its usefulness.
We further suggest that functional connectivity can vary substantially from that implied by fixed axon connections. Cortical dynamics revealed with EEG offers a wide range of dynamic behaviors in its power spectra and coherence structure. Long range (> 15–20 cm) coherence in narrow alpha sub-bands can be high (e.g. 0.5 to 0.9) in both raw and high resolution EEG or SSVEP and exhibits robust changes with eye opening and mental tasks (Nunez 1995; Silberstein et al 2001, 2003, 2004; Srinivasan et al 1999, Ding et al 2006). High coherence (at large scales) between the occipital cortex of one hemisphere to frontal cortex of the contralateral hemisphere can occur in the alpha band, even though direct axon connections between these regions are unlikely (Nunez 1995). The implication is that functional interactions between cortical regions can perhaps be turned on and off more quickly, partly independent of fixed connections.
One such possible mechanism of binding local networks into large-scale functional systems is "binding by resonance," a generalization of Singer's "binding by synchrony" (Singer 1993; Hoppensteadt and Izhikevich 1998; Izhikevich 1999; Roopun et al 2008; Nunez and Srinivasan 2010; Nunez 2010). The spatial-temporal resonance structure proposed here is functionally useful because it allows spatially overlapping neurons to be part of distinct functional networks, where the functional separation is due to the underlying dynamics. In other words large scale networks that operate in different frequency bands can be kept segregated from each other even when they occupy overlapping space in the brain. This is also a natural extension of Singer’s binding hypothesis, which postulates that distinct percepts must be kept segregated as distinct oscillations. This type of dynamic segregation is observed in SSVEP studies of attention where functionally distinct networks operate at different frequencies in the same tissue (Ding et al 1996; Bridwell and Srinivasan 2012).
Another point supporting the robust production of global oscillations due to axon delays is that EEG and SSVEP experiments demonstrate that the phenomena of traveling cortical waves is robust in both waking and sleeping states. In a confined system like the cortex-white matter system with a closed topology, these waves must either damp out or interfere to produce standing waves with remote regions possibly exhibiting zero phase lag in their dynamic structures in the absence of interconnections as indicated in fig 2b. Accurate measurements of wave damping have not, to our knowledge, been reported, partly because EEG typically involves a mixture of local and global dynamics and partly because of alpha band non-stationarity, but wave damping appears to be small or moderate in many studies (Nunez 2011). Finally, we have reported direct evidence for standing waves in Sec. 3. We suggest that such periodic spatial structure is associated with temporal oscillations even though many specific aspects of the quasi-linear models based mainly on homogeneous connections are probably wrong.
These issues associated with global systems of cortico-cortical axons are likely to occupy experimentalists and theoreticians well into the future as they seem central to the broader issues of top-down network binding and brain disease. Given the wide range of psychiatric and neurodevelopmental disorders now associated with white matter defects (Fields 2008), multiple measures of functional connectivity obtained with fMRI, EEG, and so forth should prove useful in clinical studies. In particular, the proposed close association of global EEG dynamics to cortico-cortical axon delays provides a theoretical basis for relating white matter defects to spatial patterns of EEG oscillations, including narrow band (~ 1 Hz) measures of multi-scale functional connectivity, e.g., coherence estimated from both low and high resolution EEG.
Highlights.
-
We propose neocortical global fields of synaptic action with embedded networks.
Bottom-up influence of networks on global fields is neglected to first approximation.
Scale-dependent properties of experimental electrophysiology physiology are outlined.
Global models are developed in which cortical dynamics are due mainly to axon delays.
Model implications for a broad range of experimental studies are considered.
Acknowledgments
This research was supported by National Institutes of Health grant 2R01MH68004
Appendix A
Regional resonances: One-dimensional theory
Consider axon propagation in a one-dimensional closed loop of cortex of circumference L
| (A1) |
If axons entering arbitrary location x originate only at location xa, and there is only a single axon speed ν, the axon distribution function may be expressed as
| (A2) |
ρ is the number of synapse per axon (assumed constant) entering the arbitrary cortical location x (in this case all axons originate at xa). Normalization requires
| (A3) |
Substitution of Eq (A2) into Eq (A1) yields
| (A4) |
The regional time delay is . Evaluate Eq (A4) at x = xb to obtain
| (A5) |
Equation (A5) yields the synaptic action at location xb due to action potentials that originate at xa. Now we consider the opposite case where action potentials originate at xb and terminate at xa. The derivation is identical with a and b interchanged; that is
| (A6) |
Thus, we now have 2 equations in the 4 unknowns H(xa,t), H(xb,t), G(xa,t), G(xb,t); 2 more are needed to find a solution. Define the temporal Fourier transform
| (A7) |
Thus, the Fourier transformed versions of Eqs (A5) and (A6) are
| (A8) |
| (A9) |
Note that τ = τa = τb is just the fixed delay between locations a and b. To obtain the required additional equations, we make the linearity assumption α → 0 in Eq (2.2)
| (A10) |
Solving, we find
| (A11) |
A similar solution may be obtained for H(xb,ω). The inverse Fourier transform of the synaptic action field H(xa, ω) is given by the following integral in the complex ω plane
| (A12) |
Regional resonances are given by the poles of the integrand in Eq (A12), that is
| (A13) |
To find the poles, let ω = ωR – jγ; this form is consistent with γ > 0 indicating instability. For Eq (A13) to be valid, the real part of the frequency must satisfy
| (A14) |
Also, for Eq (A13) to be valid, the imaginary part of the frequency must satisfy
| (A15) |
Noting that cos(nπ) = (−1)n we see that this equation can only be satisfied for even integers, n = 2,4,6,… We keep only even integers in Eq (A14) to obtain
| (A16) |
| (A17) |
| (A18) |
Appendix B
Neocortical oscillation in an idealized one-dimensional loop
The excitatory synaptic action at cortical location x may be expressed in terms of an inner integral over a closed cortical loop of length L and outer integral over distributed axon propagation speeds as
| (B1) |
In this simplest (anisotropic) one-dimensional version (Nunez 1972, 1974a), axons are assumed to run only in the anterior-posterior direction of each hemisphere. In later versions (Nunez 1995), the cortico-cortical axons are parceled into M fiber systems with connection densities that fall off exponentially with separation |x–x1|, that is
| (B2) |
where ρq is the number of synapses per q-system axon. Define the Fourier transform in an infinite neocortical-white matter medium
| (B3) |
or, alternately, in a closed neocortical loop of length L
| (B4) |
Periodic boundary conditions in the closed loop require that H(x,t) and ∂H(x,t) / ∂x be continuous functions of x, requiring all wavelengths to equal L divided by an integer; that is, only the following discrete spatial modes are allowed
| (B5) |
Such periodic boundary conditions differ by the factor 2 above from waves in media with fixed end conditions like a violin string. Consider the limiting case where all but one (λ1→λ) of the axon systems in Eq (B2) have much shorter ranges than the dominant waves, that is, kn << λq. In this case, the short axon systems add to background cortical excitability, but don’t alter the form of the dispersion function (Nunez 1995). Equations (B1), (B2), and (B4) then yield
| (B6) |
Here ρ is the number of synapse per axon, and the function X(ω) accounts for the finite length L of the cortical loop; that is, X(ω) = 1 when the Fourier transform (B3) is used to approximate the Fourier series (B4). Analytic and numerical studies (Srinivasan 1995; Nunez 1995) show that this is a reasonable approximation in cortical-white matter systems with λL ≫1 and n > 1. For example, if the longest cortico-cortical system consists of axons with characteristic fall off over 5–10 cm in a closed loop of L = 60 cm, λL = 6–12; however, the effect of finite size L tends to eliminate the fundamental mode n =1. Additional effects of finite size are considered by the spherical shell model outlined in appendix C.
One approach is to convert Eq (B6) to a plausible partial differential equation and apply boundary conditions afterwards, a procedure with precedent in studies of physical systems. This approach facilitates the development of approximate nonlinear models (Jirsa and Haken 1997; Nunez 1995, 2000; Nunez and Srinivasan 2006a). However, we focus here on linear models that provide easily interpreted analytic solutions. By expanding an assumed sigmoid relationship between action potential density and synaptic action, one may obtain the a second relation between synaptic activity and action potentials in tissue mass (Jirsa and Haken 1997)
| (B7) |
In the linear limit (α → 0), Eq (B7) may be Fourier transformed as in Eq (B3) to obtain
| (B8) |
With the approximation X(ω) = 1, Eqs (B6) and (B8) yield cortical output in terms of input, that is
| (B9) |
where the dispersion function (inverse of cortical transfer function) is
| (B10) |
With the usual methods of linear systems analysis in two independent variables, the inverse Fourier transform yields the synaptic action density
| (B11) |
Equation (B11) involves contour integrals in the complex plane. Predicted oscillation frequencies and damping are obtained from the poles of the integrand, obtained from the dispersion relation
| (B12) |
The complex frequency is given in terms of real and imaginary parts by
| (B13) |
consistent with γ > 0 predicting unstable waves in this linear approximation.
In the idealized case of a strongly peaked axon speed distribution f(ν1) = δ(ν1 – ν), Eqs (B12) and (B5) yield predicted oscillation frequencies and damping
| (B14) |
| (B15) |
Figure 4 shows composite data from three independent studies on cortico-cortical axon speeds (Nunez 1995). The solid line represents the following fit
| (B16) |
Here the numerical factor in Eq (B16) is required to force the normalization
| (B17) |
Numerical studies of Eq (B12) may be summarized as follows. The mode frequencies given by Eq (B14) are essentially unchanged by the more realistic fEx(ν1). The main effect of distributed axon speeds is to "wash out" higher modes due to increases in relative damping. When f(ν1) = δ(ν1 – ν), Eq (B15) predicts that all linear modes become unstable for β > 1. By contrast, distributed axon speeds fEx (ν1) cause γ→ γn. The minimum values of cortical excitability required for linear instability may be estimated from the relation
| (B18) |
Appendix C
Neocortical oscillations in an idealized spherical shell
In this model, the surface integral in Eq (2.1) now applies to the shell shown in fig. 4
| (C1) |
Here dΩ1 = sin θ1dθ1dϕ is an element of solid angle and the vectors r and r1 locate the spherical surface coordinates (θ,ϕ → Ω) and (θ1,ϕ → Ω1), respectively. The axon distribution function may be expressed in terms of Q homogeneous and isotropic systems with exponential fall offs in connection density plus generally inhomogeneous and anisotropic systems ℝ(θ,ϕ,θ1,ϕ, ν1)
| (C2) |
Here η(Ω,Ω1) is the angle between the surface coordinates Ω and Ω1 and R is sphere radius. Again we proceed with the idealized case where all axon systems except one λ1 → λ have negligible propagation delays; the short axon systems then only contribute by adding to background cortical excitability. We also assume a peaked axon speed distribution f1(ν1) = δ(ν1 – ν) so that axon distribution reduces to
| (C3) |
The factors in front of the exponential provide the proper normalization of the surface integral
| (C4) |
where ρ is the number of synapses per axon on the long fiber system. Define the temporal Fourier transform
| (C5) |
which is to be expressed in terms of the usual spherical harmonic functions (generalized Fourier series)
| (C6) |
These spherical harmonics are orthogonal in the Hermitian sense on the sphere such that
| (C7) |
The equivalent action potential functions Glm(ω) and G(Ω,ω) obey relations similar to Eqs (C5–C7). From the relations above, we obtain the following equation relating the spherical harmonic coefficients
| (C8) |
Here we have defined the function
| (C9) |
where the functions Pl (cos β) are the usual Legendre polynomials. From the linear approximation to Eq (2.2) (α → 0), we obtain
| (C10) |
Substitution into Eq (C8) yields the cortical synaptic output coefficients Hlm(ω) an terms of inputs H0lm(ω)
| (C11) |
Here the cortical excitability parameter for the sphere is
| (C12) |
The spatial-temporal behavior of waves in the spherical shell is obtained from the inverse Fourier transform of Eq (C5) and the series expansion Eq (C6)
| (C13) |
Preferred oscillation frequencies for each spatial mode l are obtained from the poles of the integrand in Eq (C13). These resonant frequencies are independent of the index m because the single retained axon system was assumed to be homogeneous and isotropic. These preferred frequencies are obtained from the solutions to
| (C14) |
The integrals Sl(ω) were evaluated recursively (Katznelson, 1981,1982) as follows
| (C15) |
Here we have defined , where the complex frequencies of modes l are ωl = ωRl − jγl, consistent with γl > 0 indicating mode instability. Given our basic premise that instability is prevented in healthy brains by enhanced inhibitory actions, e.g. α ≠ 0 in Eq (2.2), our numerical study of Eq (C14) focuses on modes close to instability (γl ≈ 0). The real and imaginary frequencies are related to z by
| (C16) |
Appendix D
Quasi-linear approximation to the one-dimensional loop model
Full nonlinear analyses of wave phenomena typically involve mathematics too complicated to allow analytic solutions; rough approximations or numerical solutions are often the main options. Expected nonlinear effects of general wave phenomena include coupling of different spatial modes and amplitude limits on linearly unstable oscillations. Here we assume weak to moderate nonlinearity in the model derived in appendix B to obtain an approximate analytic solution that is then checked against numerical solutions. From B6 with f(ν1) = δ(ν1 – ν), we obtain
| (D) |
The function X(ω) accounts for the finite length L of the cortical loop. Other studies indicate that X(ω) = 1 is a reasonable approximation for λL ≫ 1 and modes n > 1 (Srinivasan 1995); that is, the Fourier transform (B3) is used to approximate the Fourier series B4. One approach is to convert Eq (D1) to a partial differential equation and apply boundary conditions afterwards (Jirsa and Haken 1997; Nunez 1995, 2000; Nunez and Srinivasan 2006a). The differential equation equivalent to Eq (D1) is
| (D2) |
The proposed input-output sigmoid functional relation is approximated by
| (B7) |
yielding the nonlinear partial differential equation in the modulation of synaptic action
| (D3) |
Our numerical solutions of this equation indicate that mode coupling tends to be small for small values of α as expected. In the following semi-analytical approach we seek oscillatory solutions of the form
| (D4) |
which satisfies the required periodic boundary conditions that H and are continuous around the cortical loop provided
| (D5) |
In the linear limit α → 0, each function Wn(t) oscillates with the mode frequency ω(kn); that is, with negligible mode coupling. Consider the case of no external input H0 = 0 with an initial condition (cortical state) H(x, 0) that excites only a single mode kn. In the limit of weak nonlinearity, we neglect mode coupling to express
| (D6) |
The time average over any integer number of cycles of any oscillation frequency is
| (D7) |
where An is the amplitude of mode n. Substitute into D6 into D3 and focus on oscillations at the location with maximum amplitude, x = 0, which is any arbitrary location determined by rotation of the coordinate system. Replacing the nonlinear terms by their cycle averages yields the ordinary differential equation
| (D8) |
Compare Eq (D8) to the well known 2nd order system for a linear damped oscillator with damping γ and real oscillation frequency
| (D9) |
For β > 1 we expect amplitudes to grow until the cycle-averaged γ equals zero; that is, when the oscillation amplitude reaches
| (D10) |
We obtained numerical solutions to Eq (D8) for the uncoupled mode n = 2 and fit the asymptotic amplitude to the function A2 ∝ α−a(β –1)b for the parameter range 0.05 ≤ α ≤ 0.5, 1.1 ≤ β ≤ 1.6 obtaining a = 0.476, b = 0.501 in close agreement to Eq (D10).
If we identify the term as the coefficient of W in Eq (D8) and use Eq (D10), we obtain a new (nonlinear) estimate for the frequency of the n th mode
| (D11) |
From comparison of Eq (D11) to Eq (B14) we see that the factor 0.7 < for 1 ≤ β ≤ 1.6 is the estimated "correction" due to small nonlinear effects, which cause only minimal changes in oscillation frequencies over this range of β. This outcome was also confirmed by numerical solutions of Eq (D3).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abeles M. Local Cortical Circuits. Berlin: Springer-Verlag; 1982. [Google Scholar]
- Andrew C. Sensorimotor EEG rhythms and their connection to local/global neocortical dynamic theory. Behavioral and Brain Sciences. 2000;23:399–400. [Google Scholar]
- Andrew C, Pfurtscheller G. On the existence of different alpha band rhythms in the hand area of man. Neuroscience Letters. 1997;222:103–106. doi: 10.1016/s0304-3940(97)13358-4. [DOI] [PubMed] [Google Scholar]
- Barlow JS. Its Patterns and Origins. Cambridge, Mass: MIT Press; 1993. The Electroencephalogram. [Google Scholar]
- Basar E, Schurmann M, Basar-Eroglu C, Karakas S. Alpha oscillations in brain functioning: an integrative theory. International Journal of Psychophysiology. 1997;26:5–29. doi: 10.1016/s0167-8760(97)00753-8. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Bullmore ET. Human brain networks in health and disease. Current Opinion in Neurobiology. 2009;22:340–347. doi: 10.1097/WCO.0b013e32832d93dd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Gazzaniga MS. Understanding complexity in the human brain. Trends in Cognitive Science. 2011;15:200–209. doi: 10.1016/j.tics.2011.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop GH, Smith JM. The size of nerve fibers supplying cerebral cortex. Experimental Neurology. 1964;9:483–501. doi: 10.1016/0014-4886(64)90056-1. [DOI] [PubMed] [Google Scholar]
- Bishop AR, Fesser K, Lomdahl PS, Trullinger SE. Influence of solitons in the initial state of chaos in the driven, damped sine-Gordon system. Physica. 1983;7D:259–279. [Google Scholar]
- Blinkov SM, Glezer II. The Human Brain in Figures and Tables. New York: Plenum Press; 1968. [Google Scholar]
- Boersma M, Kemner C, Marcel A, de Reus MA, Collin G, Snijders TM, Hofman D, Buitelaar JK, Stam CJ, van den Heuvel1 MP. Disrupted functional brain networks in autistic toddlers. Brain Connectivity. 2013;3:41–49. doi: 10.1089/brain.2012.0127. [DOI] [PubMed] [Google Scholar]
- Bojak I, Liley DTJ, Cadusch PJ, Cheng K. Electrorhythmogenesis and anaesthesia in a physiological mean field theory. Neurocomputing. 2004;58–60:1197–1202. [Google Scholar]
- Braitenberg V. Cortical architectonics. General and areal. In: Brazier MAB, Petsche H, editors. Architectonics of the Cerebral Cortex. New York: Raven Press; 1978. pp. 443–465. [Google Scholar]
- Braitenberg V, Schuz A. Statistics and Geometry. New York: Springer; 1991. Anatomy of the Cortex. [Google Scholar]
- Breakspear M, Roberts JA, Terry JR, Rodrigues S, Mahant N, Robinson PA. A unifying explanation of primary generalized seizures through nonlinear brain modeling and bifurcation analysis. Cerebral Cortex. 2006;16:1296–1313. doi: 10.1093/cercor/bhj072. [DOI] [PubMed] [Google Scholar]
- Bridwell DA, Srinivasan R. Distinct attention networks for feature enhancement and suppression in vision. Psychological Science. 2012;23:1151–1158. doi: 10.1177/0956797612440099. [DOI] [PubMed] [Google Scholar]
- Brock J, Brown CC, Boucher J, Rippon G. The temporal binding deficit hypothesis of autism. Development and Psychopathology. 2002;14:209–224. doi: 10.1017/s0954579402002018. [DOI] [PubMed] [Google Scholar]
- Burkitt GR, Silberstein RB, Cadusch PJ, Wood AW. The steady-state visually evoked potential and travelling waves. Clinical Neurophysiology. 2000;111:246–258. doi: 10.1016/s1388-2457(99)00194-7. [DOI] [PubMed] [Google Scholar]
- Bush P, Sejnowski T. Inhibition synchronizes sparsely connected cortical neurons within and between columns in realistic network models. Journal of Computational Neuroscience. 1996;3:91–110. doi: 10.1007/BF00160806. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Rhythms of the Brain. New York: Oxford University Press; 2006. [Google Scholar]
- Canolty RT, Soltani M, Dalal SS, Edwards E, Dronkers N, Nagarajan SS, Kirsch HE, Barbaro NM, Knight RT. Spatiotemporal dynamics of word processing in the human brain. Frontiers in Neuroscience. 2007;1:185–196. doi: 10.3389/neuro.01.1.1.014.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatrian GE, Lairy GC. The EEG of the waking adult. Handbook of Electroencephalography and Clinical Neurophysiology. 1976;6A:275–292. [Google Scholar]
- Clark RC, Veltmeyer MD, Hamilton RJ, Simms E, Paul R, Hermens D, Gordon E. Spontaneous alpha peak frequency predicts working memory performance across the age span. International Journal of Psychophysiology. 2004;53:1–9. doi: 10.1016/j.ijpsycho.2003.12.011. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, Sieracki JM, Wilson MT, Uematsu U, Lesser RP. Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. Brain. 1998a;121:2271–2299. doi: 10.1093/brain/121.12.2271. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, Lesser RP. Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. II. Event-related synchronization in the gamma band. Brain. 1998b;121:2301–2315. doi: 10.1093/brain/121.12.2301. [DOI] [PubMed] [Google Scholar]
- Cooper R, Winter AL, Crow HJ, Walter WG. Comparison of subcortical, cortical, and scalp activity using chronically indwelling electrodes in man. Electroencephalography and Clinical Neurophysiology. 1965;18:217–228. doi: 10.1016/0013-4694(65)90088-x. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis I: Segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dekaban AS. Changes in brain weights during the span of human life: Relation of brain weights to body heights and body weights. Annals of Neurology. 1978;4:345–356. doi: 10.1002/ana.410040410. [DOI] [PubMed] [Google Scholar]
- Ding J, Sperling G, Srinivasan R. Attentional modulation of SSVEP power depends on the network tagged by the flicker frequency. Cerebral Cortex. 2006;16:1016–1029. doi: 10.1093/cercor/bhj044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman GM, Tononi G. A Universe of Consciousness. New York: Basic Books; 2000. [Google Scholar]
- Feinberg TE. From Axons to Identity. New York: Norton; 2009. [Google Scholar]
- Feinberg TE. Neuroontology, neurobiological naturalism, and consciousness: A challenge to scientific reduction and a solution (including commentaries by author PLN and others) Physics of Life Reviews. 2012;9:13–46. doi: 10.1016/j.plrev.2011.10.019. [DOI] [PubMed] [Google Scholar]
- Fields RD. White matter in learning, cognition and psychiatric disorders. Trends in Neuroscience. 2008;31:361–370. doi: 10.1016/j.tins.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fingelkurts AA, Fingelkurts AA, Neves CFH. Consciousness as a phenomenon in the operational architectonics of brain organization: Criticality and self-organization considerations. Chaos, Solitons & Fractals. 2013 in press. [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis II: Inflation, flattening, a surface-based coordinate system. NeuroImage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Freeman WJ. Mass Action in the Nervous Systems. New York: Academic Press; 1975. [Google Scholar]
- Freeman WJ. Simulation of chaotic EEG patterns with a dynamic model of the olfactory system. Biological Cybernetics. 1987;56:139–150. doi: 10.1007/BF00317988. [DOI] [PubMed] [Google Scholar]
- Freeman WJ. Predictions on neocortical dynamics derived from studies in paleocortex. In: Basar E, Bullock TH, editors. Induced Rhythms in the Brain. Berlin: Birhauser; 1992a. [Google Scholar]
- Freeman WJ. Tutorial on neurobiology--from single neurons to brain chaos. International Journal of Bifurcation and Chaos. 1992b;2:451–482. [Google Scholar]
- Freyer F, Roberts JA, Becker R, Robinson PA, Ritter P, Breakspear M. Biophysical mechanisms of multistability in resting-state cortical rhythms. The Journal of Neuroscience. 2001;31:6353–6361. doi: 10.1523/JNEUROSCI.6693-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Friston K. A theory of cortical responses. Philosophical Transactions of the Royal Society B Biological Sciences. 2005;360:815–836. doi: 10.1098/rstb.2005.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Tononi G, Sporns O, Edelman GM. Characterising the complexity of neuronal interactions. Human Brain Mapping. 1995;3:302–314. [Google Scholar]
- Gazzaniga M. Who's In Charge? New York: HarperCollins; 2011. [Google Scholar]
- Gell-Mann M, Lloyd S. Information measures, effective complexity, and total information. Complexity. 1996;2:44–52. [Google Scholar]
- Ghosh A, Rho Y, McIntosh AR, Kotter R, Jirsa VK. Cortical network dynamics with time delays reveals functional connectivity in the resting brain. Cognitive Neurodynamics. 2008;2:115–120. doi: 10.1007/s11571-008-9044-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray CM, Maldonado PE, Wilson M, McNaughton B. Tetrodes markedly improve the reliability and yield of multiple single-unit isolation from multi-unit recordings in cat striate cortex. Journal of Neuroscience Methods. 1995;63:43–54. doi: 10.1016/0165-0270(95)00085-2. [DOI] [PubMed] [Google Scholar]
- Guttmann CRG, Jolesz FA, Kikinis R, Killiany RJ, Moss MB, Sandor T, Albert MS. White matter changes with normal aging. Neurology. 1998;50:972–978. doi: 10.1212/wnl.50.4.972. [DOI] [PubMed] [Google Scholar]
- Habeck CG, Srinivasan R. Natural solutions to the problem of functional integration. Behavioral and Brain Sciences. 2000;23:402–403. [Google Scholar]
- Hagmann P, Sporns O, Madan N, Cammoun L, Pienaar R, Wedeen VJ, Meuli R, Thiran JP, Grant PE. White matter maturation reshapes structural connectivity in the late developing human brain. Proceedings of the National Academy of Sciences of the USA. 2010;107:19067–19072. doi: 10.1073/pnas.1009073107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haken H. An Introduction. 3rd edition. Berlin: Springer; 1983. Synergetics. [Google Scholar]
- Haken . Principles of Brain Functioning: A Synergetic Approach to Brain Activity, Behavior, and Cognition. Berlin: Springer; 1996. [Google Scholar]
- Haken H. What can synergetics contribute to the understanding of brain functioning? In: Uhl C, editor. Analysis of Neurophysiological Brain Functioning. Berlin: Springer-Verlag; 1999. pp. 7–40. [Google Scholar]
- Hanslmayr S, Sauseng P, Gruber W, Doppelmayr M. The P1 and travelling alpha waves: Evidence for evoked oscillations. Journal of Neurophysiology. 2007;97:1311–1318. doi: 10.1152/jn.00876.2006. [DOI] [PubMed] [Google Scholar]
- Hao Y, Liu Z, Jiang T, Gong G, Liu H, Tan L, Kuang F, Xu L, Yi Y, Zhang Z. White matter integrity of the whole brain is disrupted in first-episode schizophrenia. NeuroReport. 2006;17:23–26. doi: 10.1097/01.wnr.0000195664.15090.46. [DOI] [PubMed] [Google Scholar]
- He BJ, Zempel JM, Snyder A, Raichle ME. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010;66:353–369. doi: 10.1016/j.neuron.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heisenberg W. Physics and Beyond. New York: Harper & Row; 1971. [Google Scholar]
- Hoppensteadt FC, Izhikevich EM. Thalamo-cortical interactions modeled by weakly connected oscillators: Could brains use FM radio principles? Biosystems. 1998;48:85–92. doi: 10.1016/s0303-2647(98)00053-7. [DOI] [PubMed] [Google Scholar]
- Hughes JR, Ikram A, Fino JJ. Characteristics of traveling waves under various conditions. Electroencephalography and Clinical Neurophysiology. 1995;26:7–22. doi: 10.1177/155005949502600104. [DOI] [PubMed] [Google Scholar]
- Ingber L. Statistical mechanics of neocortical interactions. i. basic formulation. Physica D. 1982;5:83–107. [Google Scholar]
- Ingber L. Statistical mechanics of neocortical interactions: Stability and duration of the 7±2 rule of short-term-memory capacity. Physical Review A. 1985;31:1183–1186. doi: 10.1103/physreva.31.1183. [DOI] [PubMed] [Google Scholar]
- Ingber L. Statistical mechanics of multiple scales of neocortical interactions. In: Nunez PL, editor. Neocortical Dynamics and Human EEG Rhythms. New York: Oxford University Press; 1995. pp. 628–681. [Google Scholar]
- Ingber L, Nunez PL. Statistical mechanics of neocortical interactions; High resolution path-integral calculation of short-term memory. Physical Review E. 1995;51:5074–5083. doi: 10.1103/physreve.51.5074. [DOI] [PubMed] [Google Scholar]
- Ingber L, Nunez PL. Neocortical dynamics at multiple scales, EEG standing waves, statistical mechanics, and physical analogs. Mathematical Biosciences. 2010;229:160–173. doi: 10.1016/j.mbs.2010.12.003. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Weakly connected quasi-periodic oscillators, FM interactions, and multiplexing in the brain. SIAM Journal of Applied Mathematics. 1999;59:2193–2223. [Google Scholar]
- Izhikevich EM. Polychronization: computation with spikes. Neural Computation. 2006;18:245–282. doi: 10.1162/089976606775093882. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proceedings of the National Academy of Sciences USA. 2008;105:3593–3598. doi: 10.1073/pnas.0712231105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson JD. Classical Electrodynamics. New York: Wiley; 1962. [Google Scholar]
- Jensen O, Colgin L. Cross-frequency coupling between neuronal oscillations. Trends in Cognitive Science. 2007;11:267–269. doi: 10.1016/j.tics.2007.05.003. [DOI] [PubMed] [Google Scholar]
- Jirsa VK. Information processing in brain and behavior displayed in large-scale topographies such as EEG and MEG. International Journal of Bifurcation and Chaos. 2004;14:679–692. [Google Scholar]
- Jirsa VK. Neural field dynamics with local and global connectivity and time delay. Philosophical Transactions of the Royal Society. Mathematical Physics and Engineering Science. 2009;367:1131–1143. doi: 10.1098/rsta.2008.0260. [DOI] [PubMed] [Google Scholar]
- Jirsa VK, Haken H. A derivation of a macroscopic field theory of the brain from the quasi-microscopic neural dynamics. Physica D. 1997;99:503–526. [Google Scholar]
- Jirsa VK, Kelso JAS. Spatiotemporal pattern formation in continuous systems with heterogeneous connection topologies. Physical Review E. 2000;62:8462–8465. doi: 10.1103/physreve.62.8462. [DOI] [PubMed] [Google Scholar]
- Jirsa VK, McIntosh AR, editors. Handbook of Brain Connectivity. Berlin: Springer; 2007. [Google Scholar]
- Jirsa VK, Kelso JAS, Fuchs A. Traversing scales of brain and behavioral organization III Theoretical modeling. In: Uhl C, editor. Analysis of Neurophysiological Brain Functioning. Berlin: Springer-Verlag; 1999. pp. 107–125. [Google Scholar]
- Katznelson RD. Normal modes of the brain: Neuroanatomical basis and a physiological theoretical model. In: Nunez PL, editor. Electric Fields of the Brain: The Neurophysics of EEG, First Edition. New York: Oxford University Press; 1981. pp. 401–442. [Google Scholar]
- Katznelson RD. PhD Dissertation. La Jolla, CA: The University of California at San Diego; 1982. Deterministic and Stochastic Field Theoretic Models in the Neurophysics of EEG. [Google Scholar]
- Koch C, Rapp M, Segev I. A brief history of time (constants) Cerebral Cortex. 1996;6:93–101. doi: 10.1093/cercor/6.2.93. [DOI] [PubMed] [Google Scholar]
- Koch MA, Norris DG, Hund-Georgiadis M. An investigation of functional and anatomical connectivity using magnetic resonance imaging. Neuroimage. 2002;16:241–250. doi: 10.1006/nimg.2001.1052. [DOI] [PubMed] [Google Scholar]
- Kotter R. Anatomical concepts of brain connectivity. In: Jirsa VK, McIntosh AR, editors. Handbook of Brain Connectivity. Berlin: Springer; 2007. pp. 149–167. [Google Scholar]
- Krieg WJS. Connections of the Cerebral Cortex. Evanston IL: Brain Books; 1963. [Google Scholar]
- Krieg WJS. Architectonics of Human Cerebral Fiber System. Evanston IL: Brain Books; 1973. [Google Scholar]
- Legatt AD, Arezzo J, Vaughan HG. Averaged multiple unit activity as an estimate of phasic changes in local neuronal activity: effects of volume-conducted potentials. Journal of Neuroscience Methods. 1980;2:203–217. doi: 10.1016/0165-0270(80)90061-8. [DOI] [PubMed] [Google Scholar]
- Liley DTJ, Cadusch PJ, Wright JJ. A continuum theory of electro-cortical activity. Neurocomputing. 1999;26–27:795–800. [Google Scholar]
- Liley DTJ, Cadusch PJ, Dafilis MP. A spatially continuous mean field theory of electrocortical activity network. Computation in Neural Systems. 2002;13:67–113. [PubMed] [Google Scholar]
- Liley DTJ, Cadusch PJ, Gray M, Nathan PJ. Drug-induced modification of the system properties associated with spontaneous human electroncephalographic activity. Physical Review E. 2003;68:051906. doi: 10.1103/PhysRevE.68.051906. [DOI] [PubMed] [Google Scholar]
- Lopes da Silva FH, Storm van Leeuwen. The cortical alpha rhythm in dog. The depth and surface profile of phase. In: Brazier MA, Petsche M, editors. Architecture of the Cerebral Cortex. New York: Raven Press; 1978. pp. 319–333. [Google Scholar]
- Lumer ED, Edelman GM, Tononi G. Neural dynamics in a model of the thalamocortical system. I. Layers, loops and the emergence of fast synchronous rhythms. Cerebral Cortex. 1997;7:207–227. doi: 10.1093/cercor/7.3.207. [DOI] [PubMed] [Google Scholar]
- Massimini M, Huber R, Ferrarelli F, Hill S, Tononi G. The sleep slow oscillation as a traveling wave. The Journal of Neuroscience. 2004;24:6862–6870. doi: 10.1523/JNEUROSCI.1318-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier-Ruge W, Ulrich J, Bruulmann M, Meier E. Age-related white matter atrophy in the human brain. Annals of the New York Academy of Sciences. 1992;673:260–269. doi: 10.1111/j.1749-6632.1992.tb27462.x. [DOI] [PubMed] [Google Scholar]
- Moran R, Pinotsis DA, Friston K. Neural masses and fields in dynamic causal modeling. Frontiers in Computational Neuroscience. 2013;7:57. doi: 10.3389/fncom.2013.00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountcastle V. Perceptual Neuroscience: The Cerebral Cortex. Cambridge: Harvard University Press; 1998. [Google Scholar]
- Murias M, Webb SJ, Greenson J, Dawson G. Resting state cortical connectivity reflected in EEG coherence in individuals with autism. Biological Psychiatry. 2007;62:270–273. doi: 10.1016/j.biopsych.2006.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL. The brain wave equation: A model for the EEG; paper presented to the American EEG Society meeting; Houston. 1972. [Google Scholar]
- Nunez PL. The brain wave equation: A model for the EEG. Mathematical Biosciences. 1974a;21:279–297. [Google Scholar]
- Nunez PL. Wavelike properties of the alpha rhythm. IEEE Transactions on Biomedical Engineering. 1974b;21:473–482. [Google Scholar]
- Nunez PL. Electric Fields of the Brain: The Neurophysics of EEG. First Edition. New York: Oxford University Press; 1981. [Google Scholar]
- Nunez PL. Generation of human EEG by a combination of long and short range neocortical interactions. Brain Topography. 1989;1:199–215. doi: 10.1007/BF01129583. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Neocortical Dynamics and Human EEG Rhythms. New York: Oxford University Press; 1995. [Google Scholar]
- Nunez PL. Toward a large-scale quantitative description of neocortical dynamic function and EEG (target article, 18 commentaries, and response) Behavioral and Brain Sciences. 2000;23:371–437. doi: 10.1017/s0140525x00003253. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Brain, Mind, and the Structure of Reality. New York: Oxford University Press; 2010. [Google Scholar]
- Nunez PL. Implications of white matter correlates of EEG standing and traveling waves. NeuroImage. 2011;57:1293–1299. doi: 10.1016/j.neuroimage.2010.03.087. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Electric and magnetic fields produced by brain sources. In: Wolpaw JR, Wolpaw EW, editors. Brain-computer Interfaces for Communication and Control. New York: Oxford University Press; 2012. pp. 45–63. [Google Scholar]
- Nunez PL, Srinivasan R. Electric Fields of the Brain: The Neurophysics of EEG. Second Edition. New York: Oxford University Press; 2006a. [Google Scholar]
- Nunez PL, Srinivasan R. A theoretical basis for standing and traveling brain waves measured with human EEG with implications for an integrated consciousness. Clinical Neurophysiology. 2006b;117:2424–2435. doi: 10.1016/j.clinph.2006.06.754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R. Hearts don’t love and brains don’t pump: Neocortical dynamic correlates of conscious experience. Journal of Consciousness Studies. 2007;14:20–34. [Google Scholar]
- Nunez PL, Srinivasan R. Scale and frequency chauvinism in brain dynamics: Too much emphasis on gamma band oscillations. Brain Structure and Function. 2010;215:67–71. doi: 10.1007/s00429-010-0277-6. invited “Brain Mythology” contribution. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL, Reid L, Bickford RG. The relationship of head size to alpha frequency with implications to a brain wave model. Electroencephalography and Clinical Neurophysiology. 1978;44:344–352. doi: 10.1016/0013-4694(78)90309-7. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Silberstein RB, Cadusch PJ, Wijesinghe R, Westdorp AF, Srinivasan R. A theoretical and experimental study of high resolution EEG based on surface Laplacians and cortical imaging. Electroencephalography and Clinical Neurophysiology. 1994;90:40–57. doi: 10.1016/0013-4694(94)90112-0. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R, Westdorp AF, Wijesinghe RS, Tucker DM, Silberstein RB, Cadusch PJ. EEG coherency I: Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalography and Clinical Neurophysiology. 1997;103:516–527. doi: 10.1016/s0013-4694(97)00066-7. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Silberstein RB, Shi Z, Carpenter MR, Srinivasan R, Tucker DM, Doran SM, Cadusch PJ, Wijesinghe R. EEG coherence II: Experimental measures of multiple EEG coherence measures. Clinical Neurophysiology. 1999;110:469–486. doi: 10.1016/s1388-2457(98)00043-1. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Wingeier BM, Silberstein RB. Spatial-temporal structure of human alpha rhythms: Theory, microcurrent sources, multiscale measurements, and global binding of local networks. Human Brain Mapping. 2001;13:125–164. doi: 10.1002/hbm.1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R, Ingber L. Theoretical and experimental electrophysiology in human neocortex: Multiscale dynamic correlates of conscious experience. In: Pesenson M, editor. Multiscale Analysis and Nonlinear Dynamics. 2013. in press. [Google Scholar]
- Osipova D, Hermes D, Jensen O, Rustichini A. Gamma power is phase-locked to posterior alpha activity. PLoS ONE. 2008;3:1–7. doi: 10.1371/journal.pone.0003990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto K, Ludwig KA, Kipke DR. Acquiring brain signals from within the brain. In: Wolpaw JR, Wolpaw EW, editors. Brain-computer Interfaces for Communication and Control. New York: Oxford University Press; 2012. pp. 81–103. [Google Scholar]
- Patten TM, Rennie CJ, Robinson PA, Gong P. Human cortical traveling waves: dynamical properties and correlations with responses. PLOS ONE. 2011 doi: 10.1371/journal.pone.0038392. URL: http://www.plosone.org/article/info:doi/10.1371/journal.pone.0038392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus T, Collins DL, Evans AC, Leonard G, Pike B, Zijdenbos A. Maturation of white matter in the human brain: A review of magnetic resonance studies. Brain Research Bulletin. 2001;54:255–266. doi: 10.1016/s0361-9230(00)00434-2. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Cooper R. Frequency dependence of the transmission of the EEG from cortex to scalp. Electroencephalography and Clinical Neurophysiology. 1975;38:93–96. doi: 10.1016/0013-4694(75)90215-1. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C. Simultaneous EEG 10 Hz desynchronization and 40 Hz synchronization during finger movements. Neurology Report. 1992;3:1057–1060. doi: 10.1097/00001756-199212000-00006. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH. Event related EEG/MEG synchronization and desynchronization: basic principles. Electroencephalography and Clinical Neurophysiology. 1999;110:1842–1857. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- Pinotsis DA, Hansen E, Friston KJ, Jirsa VK. Anatomical connectivity and the resting state activity of large cortical networks. NeuroImage. 2013;65:127–138. doi: 10.1016/j.neuroimage.2012.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posthuma D, Neale MC, Boomsma DI, de Geus EJC. Are smarter brains running faster? Heritability of alpha peak frequency, IQ, and their interrelation. Behavior Genetics. 2001;31:567–579. doi: 10.1023/a:1013345411774. [DOI] [PubMed] [Google Scholar]
- Robinson PA, Rennie CJ, Wright JJ. Propagation and stability of waves of electrical activity in the cerebral cortex. Physical Review E. 1997;55:826–840. [Google Scholar]
- Robinson PA, Wright JJ, Rennie CJ. Synchronous oscillations in the cerebral cortex. Physical Review E. 1998;57:4578–4580. [Google Scholar]
- Robinson PA, Whitehouse RW, Rennie CJ. Nonuniform corticothalamic continuum model of electroencephalographic spectra with application to split alpha peaks. Physical Review E. 2003;68:1–10. doi: 10.1103/PhysRevE.68.021922. 021922. [DOI] [PubMed] [Google Scholar]
- Robinson PA, Rennie CJ, Rowe DL, O’Conner SC. Estimation of multiscale neurophysiologic parameters by electroencephalographic means. Human Brain Mapping. 2004;23:53–72. doi: 10.1002/hbm.20032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roopun AK, Kramer MA, Carracedo LM, Kaiser M, Davies CH, Traub RD, Kopell NJ, Whittington MA. Temporal interactions between cortical rhythms. Frontiers in Neuroscience. 2008;2:145–154. doi: 10.3389/neuro.01.034.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott A. Stairway to the Mind. New York: Springer-Verlag; 1995. [Google Scholar]
- Seung S. Connectome. Boston: Houghton Miffiln Harcourt; 2012. [Google Scholar]
- Shaw GR. PhD Dissertation. The University of Alberta; Canada: 1991. Spherical harmonic analysis of the electroencephalogram. [Google Scholar]
- Silberstein RB. Steady-state visually evoked potentials, brain resonances, and cognitive processes. In: Nunez PL, editor. Neocortical Dynamics and Human EEG Rhythms. Oxford University Press; 1995a. pp. 272–303. [Google Scholar]
- Silberstein RB. Neuromodulation of neocortical dynamics. In: Nunez PL, editor. Neocortical Dynamics and Human EEG Rhythms. Oxford University Press: 1995b. pp. 591–627. [Google Scholar]
- Silberstein RB, Nunez PL, Pipingas A, Harris P, Danieli F. Steady state visually evoked potential (SSVEP) topography in a graded working memory task. International Journal of Psychophysiology. 2001;42:219–232. doi: 10.1016/s0167-8760(01)00167-2. [DOI] [PubMed] [Google Scholar]
- Silberstein RB, Danieli F, Nunez PL. Fronto-parietal evoked potential synchronization is increased during mental rotation. NeuroReport. 2003;14:67–71. doi: 10.1097/00001756-200301200-00013. [DOI] [PubMed] [Google Scholar]
- Silberstein RB, Song J, Nunez PL, Park W. Dynamic sculpting of brain functional connectivity is correlated with performance. Brain Topography. 2004;16:249–254. doi: 10.1023/b:brat.0000032860.04812.b1. [DOI] [PubMed] [Google Scholar]
- Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annual Reviews of Physiology. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. 1993. [DOI] [PubMed] [Google Scholar]
- Smith ML, Gosselin F, Schyns PG. Perceptual moments of conscious visual experience inferred from oscillatory brain activity. Proceedings of the National Academy of Sciences USA. 2006;103:5626–5631. doi: 10.1073/pnas.0508972103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spaak E, Bonnefond M, Maier A, Leopold DA, Jensen O. Layer-specific entrainment of gamma-band neural activity by the alpha rhythm in monkey visual cortex. Current Biology. 2012;22:2313–2318. doi: 10.1016/j.cub.2012.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. Networks of the Brain. Cambridge: MIT Press; 2011. [Google Scholar]
- Srinivasan RA. PhD Dissertation. Tulane University; 1995. Theoretical and Experimental Study of Neocortical Dynamics. [Google Scholar]
- Srinivasan R. Spatial structure of the human alpha rhythm: global correlation in adults and local correlation in children. Clinical Neurophysiology. 1999;110:1351–1362. doi: 10.1016/s1388-2457(99)00080-2. [DOI] [PubMed] [Google Scholar]
- Srinivasan R, Nunez PL, Silberstein RB. Spatial filtering and neocortical dynamics: estimates of EEG coherence. IEEE Transactions on Biomedical Engineering. 1998;45:814–825. doi: 10.1109/10.686789. [DOI] [PubMed] [Google Scholar]
- Srinivasan R, Russell DP, Edelman GM, Tononi G. Frequency tagging competing stimuli in binocular rivalry reveals increased synchronization of neuromagnetic responses during conscious perception. Journal of Neuroscience. 1999;19:5435–5448. doi: 10.1523/JNEUROSCI.19-13-05435.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R, Bibi FA, Nunez PL. Steady-state visual evoked potentials: distributed local sources and wave-like dynamics are sensitive to flicker frequency. Brain Topography. 2006;18:167–187. doi: 10.1007/s10548-006-0267-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R, Winter WR, Ding J, Nunez PL. EEG and MEG coherence: Measures of functional connectivity at distinct spatial scales of neocortical dynamics. Journal of Neuroscience Methods. 2007;166:41–52. doi: 10.1016/j.jneumeth.2007.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R, Thorpe S, Nunez PL. Top-down influences on local networks: Basic theory with experimental implications. Frontiers in Computational Neuroscience. 2013 doi: 10.3389/fncom.2013.00029. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swadlow HA, Rosene DL, Waxman SG. Characteristics of interhemispheric impulse conduction velocity between prelunate gyri of the rhesus monkey. Experimental Brain Research. 1978;33:455–467. doi: 10.1007/BF00235567. [DOI] [PubMed] [Google Scholar]
- Szentagothai J. The neuron network of the cerebral cortex. A functional interpretation, Proceedings of the Royal Society of London. 1978;B201:219–248. doi: 10.1098/rspb.1978.0043. [DOI] [PubMed] [Google Scholar]
- Tabor M. Chaos and Integrability in Nonlinear Dynamics. New York: Wiley; 1989. [Google Scholar]
- Thatcher RW, Walker RA, Giudice S. Human cerebral hemispheres develop at different rates and ages. Science. 1987;236:1110–1113. doi: 10.1126/science.3576224. [DOI] [PubMed] [Google Scholar]
- Thorpe S. PhD Dissertation. University of California at Irvine; 2012. Dynamic modulation of sensory cortex by top-down spatial attention. [Google Scholar]
- Thorpe S, Nunez PL, Srinivasan R. Identification of wave-like spatial structure in the SSVEP: comparison of simultaneous EEG and MEG. Statistics in Medicine. 2007;26:3911–3926. doi: 10.1002/sim.2969. [DOI] [PubMed] [Google Scholar]
- Tomasch J. Size distribution and number of fibers in human corpus callosum. Anatomical Record. 1954;119:119–135. doi: 10.1002/ar.1091190109. [DOI] [PubMed] [Google Scholar]
- Tononi G, Edelman GM. Consciousness and complexity. Science. 1998;282:1846–1851. doi: 10.1126/science.282.5395.1846. [DOI] [PubMed] [Google Scholar]
- Traub RD, Jefferys JG, Whittington MA. Simulation of gamma rhythms in networks of interneurons and pyramidal cells. Journal of Computational Neuroscience. 1997;4:141–150. doi: 10.1023/a:1008839312043. [DOI] [PubMed] [Google Scholar]
- Uhl C, editor. Analysis of Neurophysiological Brain Functioning. Berlin: Springer-Verlag; 1999. [Google Scholar]
- Valdés-Hernández PA, Ojeda-González A, Martínez-Montes E, Lage-Castellanos A, Virués-Alba T, Valdés-Urrutia L, Valdes-Sosa PA. White matter architecture rather than cortical surface area correlates with the EEG alpha rhythm. NeuroImage. 2009;49:2328–2339. doi: 10.1016/j.neuroimage.2009.10.030. [DOI] [PubMed] [Google Scholar]
- van Rotterdam A, Lopes da Silva FH, van der Ende J, Viergever MA, Hermans AJ. A model of the spatial-temporal characteristics of the alpha rhythm. Bulletin of Mathematical Biology. 1982;44:283–305. doi: 10.1007/BF02463252. [DOI] [PubMed] [Google Scholar]
- von Stein A, Sarnthein J. Different frequencies for different scales of cortical integration: from local gamma to long range alpha/theta synchronization. International Journal of Psychophysiology. 2000;38:301–313. doi: 10.1016/s0167-8760(00)00172-0. [DOI] [PubMed] [Google Scholar]
- Voytek B, Canolty RT, Shestyuk A, Crone NE, Parvizi J, Knight RT. Shifts in gamma phase–amplitude coupling frequency from theta to alpha over posterior cortex during visual tasks. Frontiers in Human Neuroscience. 2010;4:191. doi: 10.3389/fnhum.2010.00191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walhovd KB, Fjell AM, Reinvang I, Lundervold A, Dale AM, Eilertsen DE, Quinn BT, Salat D, Makris DN, Fischl B. Effects of age on volumes of cortex, white matter and subcortical structures. Neurobiology of Aging. 2005;26:1261–1270. doi: 10.1016/j.neurobiolaging.2005.05.020. [DOI] [PubMed] [Google Scholar]
- Watts DJ. Small Worlds. Princeton: Princeton University Press; 1999. [Google Scholar]
- Waxman SG, Bennett MVL. Relative conduction velocities of small myelinated and non-myelinated fibers in central nervous system. Nature New Biology. 1972;238:217–219. doi: 10.1038/newbio238217a0. [DOI] [PubMed] [Google Scholar]
- Whittington MA, Traub RD, Kopell N, Ermentrout B, Buhl EH. Inhibition-based rhythms: experimental and mathematical observations on network dynamics. International Journal of Psychophysiology. 2000;38:315–336. doi: 10.1016/s0167-8760(00)00173-2. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysics Journal. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. doi: 10.1007/BF00288786. [DOI] [PubMed] [Google Scholar]
- Wingeier BM. Ph.D. Dissertation. Tulane University; 2004. A High Resolution Study of Coherence and Spatial Spectra in Human EEG. [Google Scholar]
- Wingeier BM, Nunez PL, Silberstein RB. Spherical harmonic decomposition applied to spatial-temporal analysis of human high-density electroencephalogram. Physical Review E. 2001;64:1–9. doi: 10.1103/PhysRevE.64.051916. 051916. [DOI] [PubMed] [Google Scholar]
- Winter WR, Nunez PL, Ding J, Srinivasan R. Comparison of the effect of volume conduction on EEG coherence with the effect of field spread on MEG Coherence. Statistics in Medicine. 2007;26:3946–3957. doi: 10.1002/sim.2978. [DOI] [PubMed] [Google Scholar]
- Wiskott L, Sejnowski TJ. Slow feature analysis: unsupervised learning of invariances. Neural Computation. 2002;14:715–770. doi: 10.1162/089976602317318938. [DOI] [PubMed] [Google Scholar]
- Wright JJ, Sergejew AA. Radial coherence, wave velocity, and damping of electro-cortical waves. Electroencephalography and Clinical Neurophysiology. 1991;79:403–412. doi: 10.1016/0013-4694(91)90205-i. [DOI] [PubMed] [Google Scholar]
- Wright JJ, Robinson PA, Rennie CJ, Gordon E, Bourke PD, Chapman CL, Hawthorn N, Lees GJ, Alexander D. Toward an integrated continuum model of cerebral dynamics: the cerebral rhythms, synchronous oscillations and cortical stability. Biosystems. 2001;63:71–88. doi: 10.1016/s0303-2647(01)00148-4. [DOI] [PubMed] [Google Scholar]