The RAND Health Insurance Experiment, Three Decades Later

Abstract

We re-present and re-examine the analysis from the famous RAND Health Insurance Experiment from the 1970s on the impact of consumer cost sharing in health insurance on medical spending. We begin by summarizing the experiment and its core findings in a manner that would be standard in the current age. We then examine potential threats to the validity of a causal interpretation of the experimental treatment effects stemming from different study participation and differential reporting of outcomes across treatment arms. Finally, we re-consider the famous RAND estimate that the elasticity of medical spending with respect to its out-of-pocket price is −0.2, emphasizing the challenges associated with summarizing the experimental treatment effects from non-linear health insurance contracts using a single price elasticity.

In the voluminous academic literature and public policy discourse on how health insurance affects medical spending, the famous RAND Health Insurance Experiment stands apart. Between 1974 and 1981, the RAND experiment provided health insurance to more than 5,800 individuals from about 2,000 households in six different locations across the United States, a sample which was designed to be representative of families with adults under the age of 62. The experiment randomly assigned the families to health insurance plans with different levels of cost sharing, ranging from full coverage (“free care”) to plans that provided almost no coverage for the first approximately $4,000 (in 2011 dollars) that were incurred during the year. The RAND investigators were pioneers in what was then relatively novel territory for the social sciences, both in the conduct and analysis of randomized experiments and in the economic analysis of moral hazard in the context of health insurance.

More than three decades later, the RAND results are still widely held to be the “gold standard” of evidence for predicting the likely impact of health insurance reforms on medical spending, as well as for designing actual insurance policies. In light of the rapid growth of health spending, and the pressure this places on public sector budgets, such estimates have enormous influence as federal and state policy-makers consider potential policy interventions to reduce public spending on health care. On cost grounds alone, we are unlikely to see something like the RAND experiment again: the overall cost of the experiment—funded by the U.S. Department of Health, Education, and Welfare (now the Department of Health and Human Services)—was roughly $295 million in 2011 dollars (Greenberg and Shroder 2004).¹

In this essay, we re-examine the core findings of the RAND health insurance experiment in light of the subsequent three decades of work on the analysis of randomized experiments and the economics of moral hazard. For our ability to do so, we owe a heavy debt of gratitude to the original RAND investigators for putting their data in the public domain and carefully documenting the design and conduct of the experiment. To our knowledge, there has not been any systematic re-examination of the original data and core findings from the RAND experiment.²

We have three main goals. First, we re-present the main findings of the RAND experiment in a manner that is more similar to the way they would be presented today, with the aim of making the core experimental results more accessible to current readers. Second, we re-examine the validity of the experimental treatment effects. All real-world experiments must address the potential issues of differential study participation and differential reporting of outcomes across experimental treatments: for example, if those who expected to be sicker were more likely to participate in the experiment when the insurance offered more generous coverage, this could bias the estimated impact of more generous coverage. Finally, we re-consider the famous RAND estimate that the elasticity of medical spending with respect to its out-of-pocket price is −0.2. We draw a contrast between how this elasticity was originally estimated and how it has been subsequently applied, and more generally we caution against trying to summarize the experimental treatment effects from non-linear health insurance contracts using a single price elasticity.

The Key Economic Object of Interest

Throughout the discussion, we focus on one of RAND’s two enduring legacies—its estimates of the impact of different health insurance contracts on medical spending—and do not examine its influential findings regarding the health impacts of greater insurance coverage. We made this choice in part because the publicly available health data are not complete (and therefore do not permit replication of the original RAND results), and in part because the original health impact estimates were already less precise than those for health spending, and our exercises below examining potential threats to validity would only add additional uncertainty.

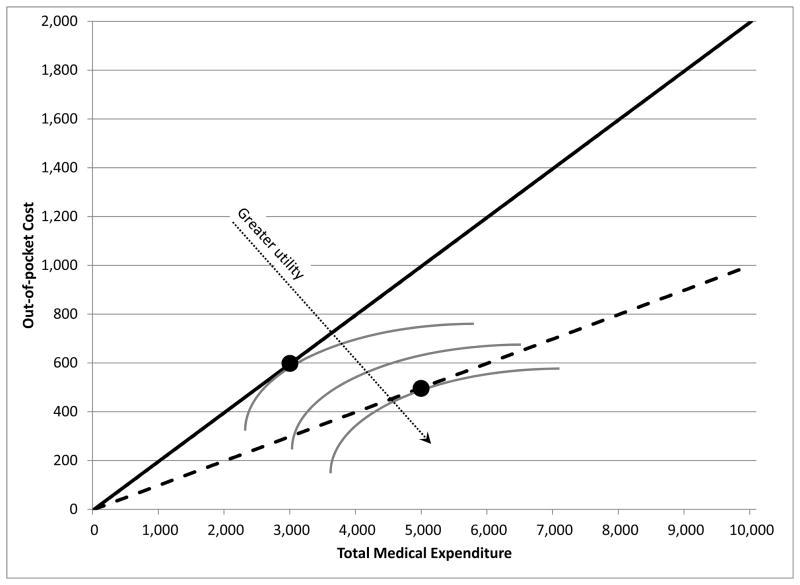
Figure 1 illustrates the key object of interest. Health care utilization is summarized on the horizontal axis by the total dollar amount spent on health care services (regardless of whether it is paid by the insurer or out of pocket). The amount of insurance coverage is represented by how this total amount translates to out-of-pocket spending on the vertical axis. The figure presents two different budget sets arising from two different hypothetical insurance contracts: the solid line represents the individual’s budget set if he has an insurance contract in which the individual pays 20 cents for any dollar of health care utilization—that is a plan with a constant 20 percent coinsurance rate—while the dashed line represents the budget set under a more generous insurance plan in which the individuals pays only 10 cents for any dollar of health care spending—that is, a 10 percent coinsurance.

Figure 1.

The Price Elasticity of Health Care Utilization

Our focus in this essay is on the effect of the health insurance coverage on health care utilization. If individuals’ utility increases in health care utilization and in income net of out-of-pocket medical spending, their optimal spending can be represented by the tangency point between their indifference curve and the budget set, as shown in Figure 1. The way the figure is drawn, individuals would increase their total health care spending from $3,000 to $5,000 in response to a 50 percent reduction in the out-of-pocket price; that is, an elasticity of −1.33. A focus of the RAND experiment was to obtain estimates of this elasticity from an experiment that randomized which budget set consumers faced. This elasticity is generally known as the “moral hazard” effect of health insurance. This term was (to our knowledge) first introduced into the modern academic literature by Arrow (1963) who defined moral hazard in health insurance as the notion that “medical insurance increases the demand for medical care”; it has since come to be used more specifically to refer to the price sensitivity of demand for health care, conditional on underlying health status (Pauly 1968; Cutler and Zeckhauser 2000).

Figure 1 abstracts, of course, from many important aspects of actual health insurance contracts and health care consumption choices that are faced in the real world and in the RAND Health Insurance Experiment. First, summarizing health care utilization by its overall dollar cost does not take into account the heterogeneity in health care needs. One common distinction is often drawn between inpatient and outpatient spending. The former is associated with hospitalizations, while the latter is associated with visits to the doctor’s office, lab tests, or procedures that do not require an over-night stay. It seems plausible that the rate at which individuals trade off health care spending and residual income could differ across such very different types of utilization and, therefore, that these different types of spending would respond very differently to a price reduction through insurance.

A second simplification is that Figure 1 considers two linear contracts, for which the concept of price, and price elasticity, is clearly defined. However, most health insurance contracts in the world, as well as those offered by the RAND experiment, are non-linear, and annual health care utilization consists of many small and uncertain episodes that accumulate. The concept of a single elasticity, or even of a single price, is therefore not as straightforward as may be suggested by Figure 1. We return to this point later in this essay.

A Brief Summary of the RAND Health Insurance Experiment

In the RAND experiment, families were assigned to plans with one of six consumer coinsurance rates (that is, the share of medical expenditures paid by the enrollee), and were covered by the assigned plan for three to five years. Four of the six plans simply set different overall coinsurance rates of 95, 50, 25, or 0 percent (the last known as “free care”). A fifth plan had a “mixed coinsurance rate” of 25 percent for most services but 50 percent for dental and outpatient mental health services, and a sixth plan had a coinsurance rate of 95 percent for outpatient services but zero percent for inpatient services (following the RAND investigators, we refer to this last plan as the “individual deductible plan”). The most common plan assignment was free care (32 percent of families), followed by the individual deductible plan (22 percent), the 95 percent coinsurance rate (19 percent), and the 25 percent coinsurance rate (11 percent). The first three columns of Table 1 show the six plans, the number of individuals and families in each, and the average share of medical expenses that they paid out-of-pocket. Newhouse et al. (1993, Chapter 2 and Appendix B) provide considerably more detail on this and all aspects of the experiment.³

Table 1.

Plan Summary Statistics and Refusal and Attrition Rates

Plan (1)	Individuals (Families) (2)	Avg. out-of- pocket sharec (3)	Share Refusing Enrollment (4)	Share Attriting (5)	Share Refusing or Attriting (6)
Free Care	1,894 (626)	0%	6%	5%	12%
25% Coinsurance	647 (224)	23%	20%	6%	26%
Mixed Coinsurancea	490 (172)	28%	19%	9%	26%
50% Coinsurance	383 (130)	44%	17%	4%	21%
Individual Deductibleb	1,276 (451)	59%	18%	13%	28%
95% Coinsurance	1,121 (382)	76%	24%	17%	37%
All Plans	5,811 (1,985)	34%	16%	10%	24%
p-value, all plans equal			< 0.0001	< 0.0001	< 0.0001
p-value, Free Care vs. 95%			< 0.0001	< 0.0001	< 0.0001
p-value, Free Care vs. 25%			0.0001	0.5590	0.0001
p-value, 25% vs. 95%			0.4100	0.0003	0.0136

Table Notes: “Coinsurance rate” refers to the share of the cost that is paid by the individual. In the 25%, mixed, 50%, and 95% coinsurance rate plans, families were assigned out-of-pocket maximums of 5%, 10%, or 15% of family income, up to a limit of $750 or $1,000. In the individual deductible plan, the out-of-pocket maximum was $150 per-person up to a maximum of $450 per family. The sample counts for the 95% coinsurance rate plans include 371 individuals who faced a 100% coinsurance rate in the first year of the experiment. Refusal and attrition rates are regression-adjusted for site and contact month fixed effects and interactions, because plan assignment was random only conditional on site and month of enrollment (see Newhouse et al. 1993, Appendix B). “Contact month” refers to the month in which the family was first contacted by the experiment and is used in lieu of month of enrollment because month of enrollment is available only for individuals who agreed to enroll. Refusal and attrition rates exclude the experiment’s Dayton site (which accounted for 1,137 enrollees) because data on Dayton refusers were lost. An individual is categorized as having attrited if he leaves the experiment at any time prior to completion.

^aThe “Mixed Coinsurance” plan had a coinsurance rate of 50% for dental and outpatient mental health services, and a coinsurance rate of 25% for all other services.

^bThe “Individual Deductible” plan had a coinsurance rate of 95% for outpatient services and 0% for inpatient services.

^cTo compute the average out-of-pocket share we compute the ratio of out-of-pocket expenses to total medical expenditure for each enrollee, and report the average ratio for each plan.

In order to limit participants’ financial exposure, families were also randomly assigned – within each of the six plans – to different out-of-pocket maximums, referred to as the “Maximum Dollar Expenditure.” The possible Maximum Dollar Expenditure limits were 5, 10, or 15 percent of family income, up to a maximum of $750 or $1,000 (roughly $3,000 or $4,000 in 2011 dollars). On average, about one-third of the individuals who were subject to a Maximum Dollar Expenditure hit it during the year, although this of course was more likely for plans with high coinsurance rate.

Families were not assigned to plans by simple random assignment. Instead, within a site and enrollment month, the RAND investigators selected their sample and assigned families to plans using the “finite selection model” (Morris, 1979; Newhouse et al., 1993, Appendix B), which seeks to a) maximize the sample variation in baseline covariates while satisfying the experiments’ budget constraint; and b) use a form of stratified random assignment to achieve better balance across a set of baseline characteristics than would likely be achieved (given the finite sample) by chance alone.

The data come from several sources. Prior to plan assignment, a screening questionnaire collected basic demographic information and some information on health, insurance status, and past health care utilization from all potential enrollees. During the three-to-five year duration of the experiment, participants signed over all payments from their previous insurance policy (if any) to the RAND experiment and filed claims with the experiment as if it was their insurer; to be reimbursed for incurred expenditures, participants had to file claims with the experimenters. These claim filings, which provide detailed data on health expenditures incurred during the experiment, make up the data on health care spending and utilization outcomes. The RAND investigators have very helpfully made all these data and detailed documentation available online, allowing us to (almost) perfectly replicate their results (see Table A1 of the online Appendix) and to conduct our own analysis of the data.⁴

Experimental Analysis

As in all modern presentations of randomized experiments, we begin by reporting estimates of experimental treatment effects. We then continue by investigating potential threats to the validity of interpreting these treatment effects as causal estimates.

Empirical Framework

In our analysis, we follow the RAND investigators and use the individual-year as the primary unit of analysis. We denote an individual by i, the plan the individual’s family was assigned to by p, the calendar year by t, and the location and start month by l and m, respectively.

The baseline regression takes the form of

$$y_{i,t}={\lambda }_p+{\tau }_t+{\alpha }_{l,m}+{\epsilon }_{i,t}$$

where an outcome y_i,t (for example, medical expenditure) is used as the dependent variable, and the explanatory variables are plan, year, and location-by-start-month fixed effects. The key coefficients of interest are the six plan fixed effects, λ_p. Because, as described earlier, there was an additional randomization of Maximum Dollar Expenditure limits, the estimated coefficients represent the average effect of each plan, averaging over the different limits that families were assigned to within the plan. Because plan assignment was only random conditional on location and start (i.e. enrollment) month, we include a full set of location by start month interactions, α_l,m. We also include year fixed effects, τ_t, to account for any underlying time trend in the cost of medical care. Because plans were assigned at the family, rather than individual level, all regression results cluster the standard errors on the family.

Treatment Effects

Table 2 reports the treatment effects of the different plans based on estimating the basic regression for various measures of health care utilization. The reported coefficients (i.e. the λ_p’s from the above regression) indicate the impact of the various plans on that measure of utilization relative to the free care plan (whose mean is given by the constant term). Column 1 reports results for a linear probability model in which the dependent variable takes the value of one when spending is positive and zero otherwise. In column 2 the dependent variable is the amount of annual medical spending (in 2011 dollars).

Table 2.

Effects on Utilization

	Total Spendinga		Inpatient Spending		Outpatient Spending
	Share with Any (1)	OLS (levels) (2)	Share with Any (3)	OLS (levels) (4)	Share with Any (5)	OLS (levels) (6)
Constant (Free Care Plan, N = 6,840)	0.931 (0.006)	2170 (78)	0.103 (0.004)	827 (60)	0.930 (0.006)	1343 (35)
25% Coins (N = 2,361)	−0.079 (0.015)	−648 (152)	−0.022 (0.009)	−229 (116)	−0.078 (0.015)	−420 (62)
Mixed Coins (N = 1,702)	−0.053 (0.015)	−377 (178)	−0.018 (0.009)	21 (141)	−0.053 (0.016)	−398 (70)
50% Coins (N = 1,401)	−0.100 (0.019)	−535 (283)	−0.031 (0.009)	4 (265)	−0.100 (0.019)	−539 (77)
Individual Deductible (N = 4,175)	−0.124 (0.012)	−473 (121)	−0.006 (0.007)	−67 (98)	−0.125 (0.012)	−406 (52)
95% Coins (N = 3,724)	−0.170 (0.015)	−845 (119)	−0.024 (0.007)	−217 (91)	−0.171 (0.016)	−629 (50)
p-value: all differences from Free Care = 0	< 0.0001	< 0.0001	0.0008	0.1540	< 0.0001	< 0.0001

Table Notes: Table reports coefficients on plan dummies; the ommitted category is the free care plan (whose mean is given by the constant term that we report in the first row). The dependent variable is given in the column headings. Standard errors, clustered on family, are in parentheses below the coefficients. Because assignment to plans was random only conditional on site and start month (Newhouse et al., 1993), all regressions include site by start month dummy variables, as well as year fixed effects. All spending variables are inflation adjusted to 2011 dollars (adjusted using the CPI-U). Site by start month and year dummy variables are demeaned so that the coefficients reflect estimates for the “average” site-month-year mix.

^aTotal spending is the sum of inpatient and outpatient spending (where outpatient spending includes dental and outpatient mental health spending).

The point estimates of both specifications indicate a consistent pattern of lower spending in higher cost-sharing plans. For example, comparing the highest cost-sharing plan (the 95 percent coinsurance plan) with the free care plan, the results indicate a 17 percentage point (18 percent) decline in the fraction of individuals with zero annual medical spending and a $845 (39 percent) decline in average annual medical spending. As the last row shows, we can reject the null hypothesis that spending in the positive cost-sharing plans is equal to that in the free care plan.

The other columns of Table 2 break out results separately for inpatient spending, which accounted for 42 percent of total spending, and outpatient spending, which accounted for the other 58 percent. Once again the patterns suggest less spending in plans with higher cost-sharing. We are able to reject the null of no differences in spending across plans for “any inpatient” and for both measures of outpatient spending. The effect of cost sharing on the level of inpatient spending is consistently small and generally insignificant, suggesting that more serious medical episodes may be less price-sensitive, which seems plausible.

Another way to approach the data is to look at the extent to which the effect of cost-sharing might vary for those with higher levels of medical spending. To explore this, we use quantile regressions to estimate the above equation, and then assess the way by which the estimated plan effects vary across the quantiles of medical spending. Detailed results for these specifications are available in Table A2 of the online Appendix available with this article at http://e-jep.org. The results are consistent with a lower percentage treatment effect for higher-spending individuals. This pattern is likely to arise from a combination of two effects. First, consistent with the results for inpatient spending, more serious and costly medical episodes may be less responsive to price. Second, individuals with high utilization typically hit the Maximum Dollar Expenditure limit early in the coverage year, and so for much of their coverage period they face a coinsurance rate of zero percent regardless of plan assignment.

Threats to Validity

The great strength of a randomized experimental approach, of course, is that a straight comparison of those receiving the treatment and those not receiving the treatment, like the regression coefficients reported in Table 2, can plausibly be interpreted as a causal effect of the treatment. However, this interpretation requires that no systematic differences exist across individuals who participate in the different plans that could be correlated with measured utilization. In this section, we consider three possible sources of systematic differences that need to be considered in any real-world experimental context: 1) non-random assignment to plans, 2) differential participation in the experiment across treatment arms, and 3) differential reporting (in this case, of medical care utilization) across treatment arms. We consider these in turn.

First, as described earlier, plans were assigned by a form of stratified random assignment. To investigate whether random assignment across plans was successfully implemented, we estimated a version of the earlier equation but, instead of using health care spending as the dependent variable, we used as outcomes various personal characteristics, such as age or education, of people assigned to different plans. In effect, such regressions show whether there is a statistically significant correlation between any particular characteristic of a person and the plan to which that person was assigned—which would be a warning sign for concern about the randomization process. We first focused on characteristics used by the investigators in the finite selection model that determined the randomization, including, for example, variables for size of family, age categories, education level, income, self-reported health status, and use of medical care in the year prior to the start of the experiment. Unsurprisingly, given that the assignment algorithm was explicitly designed to achieve balances across plan assignment on these characteristics, our statistical tests are unable to reject the null that the characteristics used in stratification are balanced across plans. (More specifically, we used joint F-test, as reported in panel A of Table A3 of the online Appendix available with this paper at http://e-jep.org.)

We next estimated these same types of regressions, but now using as the dependent variable individual characteristics not used by the original researchers in plan assignment. These include, for example, the kind of insurance (if any) the person had prior to the experiment, whether family members grew up in a city, suburb, or town, or spending on medical care and dental care prior to the experiment. Using these statistics, people’s characteristics did not appear to be randomly distributed across the plans (as shown by the joint F-test results in Panel B of Table A3 of the online Appendix). However, as we looked more closely, this result appeared to be driven only by assignment in the 50 percent coinsurance plan, which has relatively few people assigned to it. While these imbalances may have been due to sampling variation, there may also have been some problem with the assignment of families to the 50 percent plan; indeed, midway through the assignment process the RAND investigators stopped assigning families to this plan. With this (small) plan deleted, our statistical tests are unable to reject the null hypothesis that covariates that were not used in stratification are also balanced across plans. We proceed below on the assumption that the initial randomization was in fact valid—at least for all plans except for the 50 percent coinsurance plan. However, we also assess the sensitivity of the results to the inclusion of baseline covariates as controls.

To examine the second threat to validity—the concern that differential participation across plans might affect the findings—we begin with the observation that individuals assigned to more comprehensive insurance will have greater incentive to participate in the experiment. Indeed, the RAND investigators anticipated this issue, and attempted to offset these differential incentives by offering a higher lump sum payment for those randomized into less comprehensive plans. While this differential payment may make participation incentives more similar across plans, it can do so only on average. Unless the participation incentive varies with a family’s pre-experiment expectation of medical spending (and it did not), the incremental benefit from more comprehensive coverage remains greater for individuals who anticipate greater medical spending.

Thus, differential participation (or attrition) could bias the estimates of the spending response to coverage. For example, if individuals incur a fixed cost of participating in the experiment, high expected spending individuals might participate regardless of plan assignment, but lower expected spending individuals might be inclined to drop out if not randomized into a comprehensive plan, which could bias downward the estimated effect of insurance coverage on medical utilization. Alternatively, if high expected spending and low expected spending families were about equally likely to participate in the experiment when assigned to the free care plan, but high expected spending families were less likely than low expected spending families to participate when assigned to less comprehensive plans, this differential selection would bias upward the estimated effect of insurance coverage on medical utilization.

Columns 4–6 of Table 1 presented earlier suggest scope for bias from differential participation across plans. Overall, 76 percent of the individuals offered enrollment ended up completing the experiment. Completion rates were substantially and systematically higher in more comprehensive insurance plans, ranging from 88 percent in the (most comprehensive) free care plan to 63 percent in the (least comprehensive) 95 percent coinsurance plan. Most of the difference in completion rates across plans was due to differences in initial enrollment rates—that is, the share of families refusing coverage from the experiment—although subsequent attrition from the experiment also plays a non-trivial role. As shown in the bottom rows of Table 1, neither the initial refusal nor the subsequent attrition differentials can be attributed to sampling variation alone.

The differential participation by plan assignment was noted and investigated by the original RAND investigators (Newhouse et al. 1993, Chapter 2). The RAND investigators primarily investigated attrition (rather than refusal), and focused on testing particular mechanisms by which bias might have arisen. We took a more agnostic view and implemented an omnibus test for differences in available observable pre-randomization characteristics among those completing the experiment in the different plans—and we reach somewhat different conclusions. First, we divided up all the pre-randomization measures into two groups: those that directly measure prior health care utilization—which are closely related to the primary post-randomization outcomes—and all other baseline demographic information. For either set of covariates (or for both combined) we are able to reject at the 1 percent level that these pre-randomization covariates are balanced across plans for those completing the experiment (using a joint F-test; see Table A4 in the on-line Appendix for additional details). These differentials mostly reflect imbalances that arise after assignment.⁵ Of particular note, by the end of the experiment, there are imbalances across plans in participants’ average number of doctors’ visits in the year before the experiment and in the share of participants who had a medical exam in the year before the experiment.

The potential bias from differential non-response or attrition across experimental treatments is now a well-known concern for analysis of randomized social experiments. For example, Ashenfelter and Plant (1990) document the contamination to estimates arising from non-random attrition in the Negative Income Tax experiments from the 1970s, which were implemented around the same time. We discuss below possible ways of trying to account for this potential bias.

Finally, the third potential threat to validity is the extent to which participants in more comprehensive plans had differential incentives to report their medical spending. Data on medical utilization and expenditures from experimental participants were obtained from Medical Expense Report (“claims”) forms which required a provider’s signature and which the participant (or the health care provider) had to file with the experiment in order to be reimbursed for the expenditure. The incentive for filing claims was to get reimbursed, and so the filing incentive was weaker for participants enrolled in higher coinsurance rate plans (or their providers) than for those enrolled in lower coinsurance rate plans or the free care plan. For example, a participant assigned to the 95 percent coinsurance plan, who had yet to satisfy the Maximum Dollar Expenditure, would have had little to gain from filing a claim toward the end of the coverage year. This differential reporting would therefore be expected to bias the estimates in the direction of over-stating the spending response to coverage.⁶

Again, the original RAND investigators anticipated this potential problem and conducted a contemporaneous survey to try to determine the extent of the reporting bias (Rogers and Newhouse 1985). In this study of roughly one-third of all enrollees, the investigators contacted the providers for whom claims were filed by the participant or his family members, as well as a random subset of providers mentioned by other participants. From these providers, they requested all outpatient billing records for the participants and family members. For the 57 percent of providers who responded, the investigators matched the outpatient billing records to the experiments’ outpatient claims data and computed the amounts corresponding to matched and unmatched billing records. The results indicate that, on average, participants in the free care plan failed to file claims for 4 percent of their total outpatient spending, while those in the 95 percent coinsurance plan failed to file claims for 12 percent of their total outpatient spending. Under-reporting by participants in the other plans fell in between these two extremes (Rogers and Newhouse, 1985, Table 7.3). Once again, in what follows we will attempt to adjust the estimates to address the bias that may arise from this greater under-reporting of expenditures in the higher cost sharing plans.

Robustness of Treatment Effects

The potential for bias in the RAND experiment has been a source of some recent controversy: for example, Nyman (2007, 2008) raises concerns about bias stemming from differential participation across plans, and in Newhouse et al. (2008) the RAND investigators offer a rebuttal. To our knowledge, however, there has been no attempt to quantify the potential magnitude of the bias. Nor, to our knowledge, has there been a formal attempt to quantify the potential bias arising from the differential reporting documented by Rogers and Newhouse (1985).

Table 3 reports the results from such attempts. The different columns report results for different measures of spending, while the different panels show results for different pairwise plan combinations: free care vs. 95 percent coinsurance; free care vs. 25 percent coinsurance; and 25 percent vs. 95 percent coinsurance. For each, we report results from four different specifications. Row 1 of each panel replicates the baseline results from Table 2, where here we also add estimates from log specifications due to the extreme sensitivity of the levels estimates to some of our adjustments.

Table 3.

Sensitivity of Results to Additional Covariates and Bounding Exercises

	Total Spending			Inpatient Spending		Outpatient Spending
	Share with Any (1)	OLS (Levels) (2)	OLS (Logs) (3)	Share with Any (4)	OLS (Levels) (5)	Share with Any (6)	OLS (Levels) (7)	OLS (Logs) (8)
Panel A: 95% coinsurance plan vs. free care (N = 10,564)
(1) Baseline specification (from Table 2)	−0.170 (0.015)	−845 (119)	−1.381 (0.096)	−0.024 (0.007)	−217 (91)	−0.171 (0.016)	−629 (50)	−1.361 (0.093)
(2) Adjustment for underreporting	−0.100 (0.017)	−786 (123)	−1.313 (0.097)	−0.024 (0.007)	−217 (91)	−0.102 (0.018)	−582 (55)	−1.299 (0.095)
(3) Adjustment for underreporting + adding pre- randomization	−0.095 (0.016)	−728 (111)	−1.276 (0.087)	−0.023 (0.007)	−183 (85)	−0.096 (0.016)	−558 (50)	−1.261 (0.084)
(4) Lee bounds + adjustment for underreporting	−0.080 (0.018)	745 (96)	−0.672 (0.098)	0.079 (0.005)	592.1 (70.59)	−0.081 (0.018)	151 (38)	−0.751 (0.095)
Panel B: 25% coinsurance plan vs. free care (N = 9,201)
(1) Baseline specification (from Table 2)	−0.079 (0.015)	−648 (152)	−0.747 (0.095)	−0.022 (0.009)	−229 (116)	−0.078 (0.015)	−420 (62)	−0.719 (0.093)
(2) Adjustment for underreporting	−0.065 (0.016)	−645 (155)	−0.734 (0.096)	−0.022 (0.009)	−229 (116)	−0.065 (0.016)	−418 (65)	−0.706 (0.094)
(3) Adjustment for underreporting +adding pre-randomization	−0.069 (0.014)	−585 (137)	−0.748 (0.084)	−0.022 (0.008)	−181 (107)	−0.068 (0.014)	−405 (59)	−0.718 (0.082)
(4) Lee bounds + adjustment for underreporting	−0.055 (0.016)	639 (133)	−0.335 (0.096)	0.081 (0.008)	581 (99)	−0.054 (0.016)	205 (52)	−0.369 (0.093)
Panel C: 95% coinsurance plan vs. 25% coinsurance plan (N = 6,085)
(1) Baseline specification (from Table 2)	−0.091 (0.020)	−197 (160)	−0.633 (0.120)	−0.002 (0.009)	12 (122)	−0.093 (0.020)	−209 (61)	−0.641 (0.117)
(2) Adjustment for underreporting	−0.035 (0.022)	−141 (164)	−0.579 (0.122)	−0.002 (0.009)	12 (122)	−0.037 (0.022)	−164 (66)	−0.592 (0.118)
(3) Adjustment for underreporting + adding pre-randomization	−0.026 (0.019)	−143 (141)	−0.529 (0.106)	−0.001 (0.009)	−2 (108)	−0.028 (0.019)	−153 (60)	−0.543 (0.103)
(4) Lee bounds + adjustment for underreporting	−0.020 (0.022)	764 (105)	−0.248 (0.120)	0.078 (0.006)	657 (78)	−0.021 (0.023)	185 (42)	−0.313 (0.117)

Table Notes: Table reports coefficients on plan dummies; the ommitted category is the free care plan. Sample sizes given in parentheses are the number of people enrolled in the plans being compared. The dependent variable is given in the column headings. Standard errors are in parentheses below the coefficients. Standard errors are clustered on familiy. Because assignment to plans was random only conditional on site and start month (Newhouse et al., 1993), all regressions include site by start month dummy variables, as well as year fixed effects to adjust for inflation; level regressions use inflation-adjusted spending variables (in 2011 dollars, adjusted using the CPI-U). Log variables are defined as log(var + 1) to accomodate zero values. The regressions adding pre-randomization covariates as controls (row 3) include the full set of covariates shown in Table A4 of the on-line Appendix. Adjustment for underreporting and bounding procedures are explained in the main text

We begin in row 2, by trying to adjust the estimates for the differential filing of claims by plan detected by Rogers and Newhouse (1985). Specifically, we proportionally scale up outpatient spending for participants in each plan based on the plan-specific under-reporting percentages they report (Rogers and Newhouse, 1985, Table 7.3).⁷ We do not make any adjustment to inpatient spending, because there is no study on under-reporting of inpatient spending and because we think inpatient spending is less likely to be subject to reporting bias. Most inpatient episodes were costly enough that even participants in the 95 percent coinsurance plan should have had strong incentives to file claims because doing so would put them close to or over their Maximum Dollar Expenditure limit. Moreover, claims for inpatient episodes were generally filed by hospitals, which had large billing departments and systematic billing procedures and so were presumably less likely than individuals to fail to file claims. As shown in row 2, the adjustment reduces the estimated effects, but not by much.

The remaining rows try to assess the impact of differential-participation across plans on the estimates from row 2 that account for differential filing. We first consider the potential impact of observable differences across those who choose to participate in different plans. Row 3 quantifies the impact of the observable differences in participant characteristics across plans, by re-estimating the regression from row 2, but now controlling for the full set of pre-randomization covariates. These controls reduce further the estimated plan treatment effects, but again not by much. Of course, this is only reassuring in so far as we believe we have a very rich set of observables that capture much of the potential differences across participants in the different plans.

A trickier issue is how to account for potential unobservable differences across individuals who select into participation in different experimental arms. There are, broadly speaking, three main approaches to this problem. Probably the most direct way to address potential bias stemming from differential non-participation across plans would be to collect data on outcomes (in this case, health care utilization) for all individuals, including those who failed to complete the experiment. Such data would allow comparison of outcomes for individuals based on initial plan assignment, regardless of participation, and then could be used for unbiased two-stage least squares estimates of the effects of cost-sharing on utilization. Unfortunately, we know of no potential source of such data – individual-level hospital discharge records do not, to our knowledge, exist from this time period, and even if the records existed, there is no legal permission to match RAND participants (or non-participants) to administrative data.

A second approach is to make assumptions about the likely economic model of selection and use these to adjust the point estimates accordingly. Angrist et al. (2006) formalize one such approach in a very different experimental setting. Depending on the economic model, one might conclude in our context that the existing point estimates are under- or over-estimates of the true experimental treatment effects.

A final approach, which is the one we take here, is to remain agnostic about the underlying economic mechanism generating the differential selection and instead perform a statistical exercise designed to find a lower bound for the treatment effect. In other words, this approach is designed to ask the statistical question of how bad the bias from differential participation could be. Specifically, in row 4, we follow Lee’s (2009) bounding procedure by dropping the top group of spenders in the lower cost sharing plan. The fraction of people dropped is chosen so that with these individuals dropped, participation rates are equalized between the lower cost sharing plan and the higher cost sharing plan to which it is being compared. As derived by Lee (2009), these results provide worst case lower bounds for the treatment effect under the assumption that any participant who refused participation in a given plan would also have refused participation in any plan with a higher coinsurance rate. For example, since 88 percent of those assigned to the free care plan completed the experiment compared to only 63 percent of those assigned to the 95 percent coinsurance (Table 1, column 6), for this comparison we drop the highest 28% (= (88−63)/88) of spenders in the original free care sample, thus obtaining equal participation rates across the two samples.

Our primary conclusion from Table 3 is that after trying to adjust for differential selection and differential reporting by plan, the RAND data still reject the null hypothesis of no utilization response to cost sharing.⁸ In particular, when the outcome is total spending, our ability to reject the null that utilization does not respond to consumer cost sharing survives all of our adjustments in two of the three specifications, any spending and log spending.⁹

The sensitivity analysis does, however, reveal considerable uncertainty about the magnitude of the response to cost-sharing. The combination of adjusting for differential reporting and the Lee (2009) bounding exercise in row 4 opens up scope for the possibility that the treatment effects could be substantially lower than what is implied by the unadjusted point estimates. For example, focusing on column 3, our point estimate in row 1 indicates that spending under the 95 percent coinsurance plan is 75 percent lower than under the free care plan, but the adjusted lower bound estimate in row 4 suggests that spending may only be 49 percent lower.¹⁰

Table 3 also shows that we can continue to reject the null of no response of outpatient spending (for either the “any spending” specification or in the log specification), but are no longer able to reject the null of no response of inpatient utilization to higher cost sharing. The large and highly statistically significant response of inpatient spending to cost sharing was (to us) one of the more surprising results of the RAND experiment. The bounding exercise indicates that the response of inpatient spending is not robust to plausible adjustments for non-participation bias, and thus the RAND data do not necessarily reject (although they also do not confirm) the hypothesis of no price responsiveness of inpatient spending.

Finally, it is worth re-emphasizing that the results in row 4 of Table 3 represent lower bounds, rather than alternative point estimates. We interpret the exercise as indicating that the unadjusted point estimates could substantially overstate the causal effect of cost sharing on health care utilization, rather than providing alternative point estimates for this causal effect.

Estimating the Effect of Cost-Sharing on Medical Spending

The most enduring legacy of the RAND experiment is not merely the rejection of the null hypothesis that price does not affect medical utilization, but rather the use of the RAND results to forecast the spending effects of other health insurance contracts. In extrapolating the RAND results out of sample, analysts have generally relied on the RAND estimate of a price elasticity of demand for medical spending of −0.2 (for which Manning et al. 1987 is widely cited, but Keeler and Rolph 1988 is the underlying source).

This −0.2 elasticity estimate is usually treated as if it emerged directly from the randomized experiment, and often ascribed the kind of reverence that might be more appropriately reserved for universal constants like π. Despite this treatment, the famous elasticity estimate is in fact derived from a combination of experimental data and additional modeling and statistical assumptions, as any out-of-sample extrapolation of experimental treatment effects must be. And, as with any estimate, using the estimate out of sample must confront a number of statistical as well as economic issues.

Some Simple Attempts to Arrive at Estimates of the Price Elasticity

A major challenge for any researcher attempting to transform the findings from experimental treatment effects of health insurance contracts into an estimate of the price elasticity of demand for medical care is that health insurance contracts—both in the real world and in the RAND experiment—are highly-non linear, with the price faced by the consumer typically falling as total medical spending cumulates during the year. The RAND contracts, for example, required some initial positive cost-sharing, which falls to zero when the Maximum Dollar Expenditure is reached. More generally, pricing under a typical health insurance contract might begin with a consumer facing an out-of-pocket price of 100 percent of his medical expenditure until a deductible is reached, at which point the marginal price falls sharply to the coinsurance rate that is typically around 10–20 percent, and then falls to zero once an out-of-pocket limit has reached.

Due to the non-linear form of the health insurance contracts, any researcher who attempts to summarize the experiment with a single price elasticity must make several decisions. One question is how to analyze medical expenditures that occur at different times, and therefore under potentially different cost sharing rules, but which stem from the same underlying health event. Another issue is that the researcher has to make an assumption as to which price individuals respond to in making their medical spending decision. It is not obvious what single price to use. One might use the current “spot” price of care paid at the time health care services are received (on the assumption that individuals are fully myopic), the excepted end-of-year price (based on the assumption that individuals are fully forward looking and with an explicit model of expectation formation), the realized end-of-year price (on the assumption that changes in health care consumption happen at that margin), or perhaps some weighted-average of the prices paid over a year. These types of modeling challenges – which were thoroughly studied and thought through by the original RAND investigators (Keeler, Newhouse, and Phelps 1977) – are inherent to the problem of extrapolating from estimates of the spending impact of particular health insurance plans, and in this sense are not unique to the RAND experiment.

To get some sense of the challenges involved in translating the experimental treatment effects into an estimate of the price elasticity of demand, Table 4 reports a series of elasticity estimates that can be obtained from different, relatively simple and transparent ad-hoc manipulations of the basic experimental treatment effects. In Panel A of Table 4 we convert—separately for each pair of plans—the experimental treatment effects from column 2 of Table 2 to arc elasticities with respect to the coinsurance rate. (These pairwise-arc elasticities are calculated as the change in total spending as a percentage of the average spending, divided by the change in price as a percentage of the average price; in panel A we define the price as the coinsurance rate of the plan).¹¹ We obtain pairwise elasticities that are for the most part negative, ranging from about −0.1 to −0.5; the few positive estimates are associated with coinsurance rates that are similar and plans that are small.

Table 4.

Sensitivity of Elasticity Estimates to Choice of Plan Comparisons and Price Measures

Panel A: Arc Elasticities of Total Spending w.r.t Coinsurance Rate, for Different Plan Pairsa
	25% Coins	Mixed CoinsC	50% Coins	Individual DeductibleC	95% Coins
Free Care	−0.180 (0.044)	−0.091 (0.051)	−0.149 (0.080)	−0.119 (0.031)	−0.234 (0.039)
25% Coins		0.749 (0.533)	0.097 (0.281)	0.159 (0.128)	−0.097 (0.101)
Mixed Coins			−0.266 (0.422)	−0.101 (0.195)	−0.295 (0.126)
50% Coins				0.429 (1.176)	−0.286 (0.280)
Individual Deductible					−0.487 0.187

Panel B: Elasticities of Total Spending w.r.t Various Price Measures
	Coinsurance Rate		Average Out-of-Pocket Price
	Arc Elasticitya	Elasticityb	Arc Elasticitya	Elasticityb
All Plans	−0.094 (0.066)	NA	−0.144 (0.051)	NA
All Plans Except Free Care	−0.039 (0.131)	−0.523 (0.082)	−0.133 (0.097)	−0.524 (0.085)
All Plans Except Free Care and Ind. Deductible	−0.039 (0.108)	−0.537 (0.084)	−0.038 (0.108)	−0.600 (0.094)

Table Notes: Panel A reports the pairwise arc-elasticities caluclated based on Table 2, column 2. Panel B reports the sample-size weighted average of various pairwise elasticities, calculated as detailed in the column-specific notes. Standard errors are in parentheses below the coefficient values. Standard errors are clustered on family. Arc-elasticity standard errors are bootstrapped standard errors based on 500 replications, clustered on family.

^aPairwise arc-elasticities are calculated as the change in total spending as a percentage of the average, divided by the change in price as a percentage of the average price, where the price is either the coinsurance rate of the plan (in Panel A) or (in panel B) either (depending on the column) the coinsurance rate of the the average out-of-pocket price paid by people assigned to that plan (the average out-of-pocket price of each plan is shown in Table 1).

^bElasticities are calculated based on pairwise regressions of log(total spending + 1) on log(price), where price is either the coinsurance rate of the plan or the average out-of-pocket price paid by people assigned to that plan.

^cFor the mixed coinsurance plan and the individual deductible plan, we take the initial price to be the average of the two coinsurance rates, weighted by the shares of initial claims that fall into each category. For the mixed coinsurance rate plans, this gives an initial price of 32 percent. For the individual deductible plan, it gives an initial price of 58 percent.

We use Panel B of Table 4 to report weighted averages of pairwise estimates under alternative assumptions regarding 1) the definition of the price, and 2) the definition of the elasticity. In terms of the definition of the price, in computing the elasticities in Panel A we used the plan’s coinsurance rate as the price, and ignored the fact that once the Maximum Dollar Expenditure is reached the price drops to zero in all plans. In Panel B we consider both this elasticity with respect to the plan’s coinsurance rate, but also report the elasticity with respect to the average, plan-specific (but not individual-specific) out-of-pocket price. The plan’s average out of pocket price (reported in Table 1, column 3) will be lower than the plan’s coinsurance rate since it is a weighted average of the coinsurance rate and zero, which would be the “spot” price after the Maximum Dollar Expenditure is reached. For each price definition, we also consider two definitions of the elasticity; specifically, we calculate both arc-elasticities as in Panel A and more standard elasticities that are based on regression estimates of the logarithm of spending on the logarithm of price.¹² We also report results excluding the individual deductible plan, which has a different coinsurance rate for inpatient and outpatient care. Across these various simple manipulations of the experimental treatment effects in Panel B, we find price elasticities that range between −0.04 and −0.6. (This exercise does not consider the additional adjustments for differential participation and reporting discussed in Table 3).

The RAND Elasticity: A Brief Review of Where It Came From

We now review the particular assumptions made by the original RAND investigators that allowed them to arrive at their famous estimate of a price elasticity of demand for medical care of −0.2; Keeler and Rolph (1988) provide considerably more detail.

To transform the experimental treatment effects into a single estimate of the single price elasticity of demand for health care, the RAND investigators grouped individual claims into “episodes.” Each episode – once occurring – is thought of as an unbreakable and perfectly forecastable “bundle” of individual claims. The precise grouping relies on detailed clinical input, and depends on the specific diagnosis. For example, each hospitalization constitutes a separate single episode. Routine spending on diabetes care over the entire year is considered a single episode and is fully anticipated at the start of the year, while “flare-ups” are not. Each cold or accident is a separate episode, but these could run concurrently. Once claims are grouped into episodes, the RAND investigators regress average costs per episode on plan fixed effects (and various controls) and find that plan assignment has virtually no effect on costs per episode. From this they conclude that spending on the intensive margin—that is, spending conditional on an episode occurring—does not respond to price, and focus their analysis on the price responsiveness of the extensive margin only—that is, on the occurrence rate of episodes.

To investigate the price to which individuals respond, the RAND investigators looked at whether the occurrence rate of episodes differs between individuals who face similar current prices for medical care but different future prices. Specifically, they look at whether spending is higher within a plan for individuals who are closer to hitting their Maximum Dollar Expenditures, and whether it is higher among people in cost-sharing plans who have exceeded their Maximum Dollar Expenditures compared to people in the free care plan. Of course, a concern with this comparison is that families with higher underlying propensities to spend are more likely to come close to hitting their Maximum Dollar Expenditures; the RAND investigators address this via various modeling assumptions. Finding no evidence in support of higher episode rates among individuals who are closer to hitting their Maximum Dollar Expenditure limits, the RAND investigators conclude that participants’ extensive margin decisions about care utilization appear to be based entirely on the current, “spot” price of care.

Given these findings, in the final step of the analysis the RAND investigators limit the sample to individuals in periods of the year when they are sufficiently far from hitting the Maximum Dollar Expenditure (by at least $400 in current dollars) so that they can assume that the coinsurance rate (or “spot” price) is the only relevant price. They then compute the elasticity of medical spending with respect to the experimentally assigned coinsurance rate. Specifically, for each category of medical spending— hospital, acute outpatient, and so on—they compute arc-elasticities of spending in a particular category in the free care vs. 25 percent coinsurance plan and in the free care vs. 95 percent coinsurance plan. To compute these arc-elasticities, they estimate spending changes for these individuals across contracts by combining their estimates of the responsiveness of the episode rate to the coinsurance rate with data on average costs per episode (which is assumed to be unresponsive to the coinsurance rate). The enduring elasticity estimate of -0.2 comes from noting that most of these arc-elasticities—summarized in Keeler and Rolph (1988, Table 11) —are close to −0.2.

Using The RAND Elasticity: The Need to Summarize Plans with a Single Price

Application of the −0.2 estimate in a manner that is fully consistent with the way the estimate was generated is a non-trivial task. The RAND elasticity was estimated based on the assumption that in deciding whether to consume medical care, individuals fully anticipate spending within an “episode of care” but make their decision myopically—that is, only with regard to the current “spot” price of medical care--with respect to the potential for spending during the year on other episodes. Therefore a researcher who wanted to apply this estimate to forecasting the impact of an out of sample change in cost sharing would need to obtain micro data on medical claims, group these claims into “episodes” as described earlier, and calculate the “spot” price that each individual would face in each episode. Although there exist notable exceptions that do precisely this (Buchanan et al. 1991; and Keeler et al. 1996), this has not been standard practice for using the RAND estimates. Rather, many subsequent researchers have applied the RAND estimates in a much simpler fashion. In doing so, arguably the key decision a researcher faces is how to summarize the non-linear coverage with a single price. This is because the RAND elasticity is a single elasticity estimate, so it has to be applied to a single price.

Researchers have taken a variety of different approaches to summarizing the price of medical care under a non-linear insurance contract by a single number. For example, in predicting how medical spending will respond to high deductible health savings accounts, Cogan, Hubbard, and Kessler (2005) applied the −0.2 elasticity estimate to the change in the average price that was paid out of pocket, where the average was taken over claims that were made at different parts of the non-linear coverage. In extrapolating from the RAND experiment to the impact of the spread of insurance on the growth of medical spending, researchers have also used an “average price approach,” summarizing the changes in the price of medical care by changes in the overall ratio between out-of-pocket medical spending and total spending (Newhouse 1992; Cutler 1995; Finkelstein 2007). Other work on the price elasticity of demand for medical care has summarized the price associated with a non-linear coverage using the actual, realized price paid by each individual for his last claim in the coverage year (Eichner 1998; Kowalski 2010) or the expected end-of-year price (Eichner 1997).

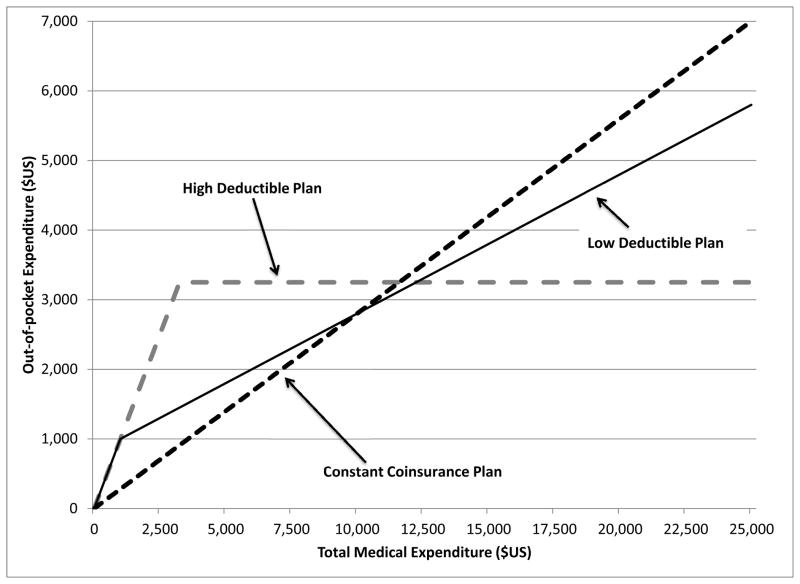
These different methods for summarizing a non-linear coverage with a single price can have an important impact on the estimated spending effects of alternative contracts. To illustrate this point, consider three “budget neutral” alternative coverage designs, depicted in Figure 2: a “high deductible” plan with a $3,250 per-family deductible and full insurance above the deductible, a “low deductible” plan with a $1,000 per-family deductible and a 20 percent coinsurance rate above the deductible, and a “no deductible” plan with a constant coinsurance rate of 28 percent. In describing these plans as “budget neutral,” we mean that we picked them so that they would all have the same predicted cost (for the insurer) when we ignore potential behavioral responses to the different contracts and apply to each of them the same distribution of annual medical expenditures from the RAND’s free care plan (in 2011 dollars). The “no deductible” plan always has the same single price: that is, the buyer always pays 28 percent of the cost of health services. However, in the two non-linear plans, the price paid by the individual will change from 100 percent of health care cost before the deductible is reached, to the coinsurance rate above that level.

Figure 2.

Non-Linear Health Insurance Coverage

As we described, in summarizing such a plan by a single number, one might look at a variety of “price” definitions, including the “spot” price paid at the time health care services are received, the realized end-of-year price, the expected end-of-year price, or at some weighted-average of the prices paid over a year. The concern is that when evaluating how changing from one insurance contract to another (or from no insurance to having insurance) would affect health care utilization, the method that is used to boil down the insurance contract into a single price (to which the −0.2 elasticity estimate is then applied) can yield very different conclusions about how the change in insurance contracts would increase the amount of health care consumed.

To illustrate the potential magnitudes at stake, consider a simple exercise in which we try to forecast the effect of reducing coverage from RAND’s 25 percent coinsurance plan to a plan with a constant coinsurance rate of 28 percent, which is one of the options depicted in Figure 2. Because the new coverage has a constant coinsurance rate, the price of medical care under this coverage is clear and well defined: it is 28 cents for every dollar of health care spending. But in order to apply the RAND estimate of −0.2, we also need to summarize RAND’s 25 percent coinsurance with a single price. Recall that the RAND plan had a Maximum Dollar Expenditure limit, so the price starts at 25 cents for every dollar, but then becomes zero once the limit is reached, so summarizing the RAND plan with a single price essentially means a choice of weights in the construction of an average price. We use three different ways to summarize the RAND 25 percent coinsurance plan with a single price: a dollar-weighted average price, a person-weighted average price, and a person-weighted average end-of-year price. Applying the distribution of spending under the free care plan, these result in three different summary prices, of 10, 17, and 13 cents for every dollar of medical spending, respectively. Applying the −0.2 estimate to changing from each of these prices to 28 cents, which is the constant price in the alternative coverage, we obtain a reduction in health care spending of 18, 9, and 14 percent, respectively. That is, in this example, the decision of how to define the price leads to differences in the predicted reduction of spending that vary by a factor of 2.

The Dangers of Summarizing Non-Linear Coverage by a Single Price

The preceding exercise illustrated how the manner by which a non-linear coverage is summarized by a single price could be important. In general, there is no “right” way to summarize a non-linear budget set with a single price. The differing implications of alternative – reasonable, yet ad hoc – “fixes” to this problem should give us pause when considering many of the subsequent applications of the RAND experimental results. It also suggests that, going forward, attempts to estimate the impact of health insurance contracts on health care spending would benefit from more attention to how the non-linearities in the health insurance contracts may impact the spending response.

Fortunately, just as there has been intellectual progress in the design and analysis of experimental treatment effects in the decades since RAND, there has similarly been progress on the analysis of the behavioral response to non-linear budget sets (for example, Hausman 1985). Much of the initial work in this area focused on analyzing the labor supply response to progressive taxation. Recently, however, researchers have begun to apply the techniques of non-linear budget set estimation to the analysis of the impact of (non-linear) health insurance contracts (Marsh 2011; Kowalski 2012), and further work in this area could be of great value.

Of course, even equipped with these techniques, current researchers must grapple with many of the same issues that the original RAND investigators faced. In particular, they must model the distribution of medical shocks throughout the year in the population under analysis, as well as the evolution of individuals’ beliefs about these shocks. Another key issue is whether individuals take into account the entire non-linear budget set induced by the health insurance contract in making their spending decision, or whether they respond only to the current “spot” price, or to something in between. Although fully forward looking rational individuals should only respond to the expected end-of-year price, if individuals are myopic, liquidity constrained, or unsure of the details of their contract, they might also respond, at least to some extent, to the “spot” price. In recent empirical work (Aron-Dine et al. 2012) we investigate this question using data on medical spending by people covered by employer-provided health insurance. We concluded that, in our specific setting, individuals do appear to take into account the non-linear budget set in making medical spending decisions, but that they are not fully forward looking, as they also take account of the spot price. In our calibration results, the predicted spending change associated with introducing a non-linear health insurance contract can vary greatly depending on what one assumes about the degree of forward looking behavior, suggesting that more evidence on this question would be useful.

More generally, any transformation of the experimental treatment effects into estimates that can be used out-of-sample will require more assumptions than required to obtain those treatment effects in the first place. More than three decades after the RAND experiment, the development and use of new approaches to doing such out-of-sample extrapolation remains an active, and interesting, area for research.

Concluding Remarks

At the time of the RAND Health Insurance Experiment, it was vigorously argued that medical care was determined by “needs,” and therefore was not sensitive to price. As Cutler and Zeckhauser (2000) wrote, the RAND experiment was instrumental in rejecting this view: “Sound methodology, supported by generous funding, carried the day. The demand elasticities in the Rand Experiment have become the standard in the literature, and essentially all economists accept that traditional health insurance leads to moderate moral hazard in demand.”

But as this core lesson of the RAND experiment has become solidified in the minds of a generation of health economics and policymakers, there has been a concomitant fading from memory of the original experimental design and analytical framework. While this may be a natural progression in the life-cycle of transformative research, it seems useful to remind a younger generation of economics of the details, and limitations, of the original work.

In this essay, we re-presented and re-examined the findings of the RAND experiment from the perspective of three subsequent decades of progress in empirical work on the design and analysis of randomized experiments, as well as on the analysis of moral hazard effects of health insurance—much of it inspired, no doubt, to a large degree by the enduring influence of the RAND results. This landmark and pioneering study was uniquely ambitious, remarkably sophisticated for its time, and entrepreneurial in the design and implementation of the then-new science of randomized experiments in the social sciences.

Our re-examination concludes that despite the potential for substantial bias in the original estimates stemming from systematically differential participation and reporting across experimental arms, one of the central contributions of the RAND experiment is robust: the rejection of the null hypothesis that health spending does not respond to the out-of-pocket price. Naturally, however, these potential biases introduce uncertainty about the magnitude of the impact of the different insurance plans on medical spending. Moreover, the translation of these experimental estimates into economic objects of interest – such as a price elasticity of demand for medical care – requires further assumptions and machinery, which go beyond the “raw” experimental results. While economic analysis has made progress in the intervening decades in developing techniques that may offer new approaches to the economic analysis of moral hazard effects of health insurance, it will always be the case that, like the famous −0.2 price elasticity of demand estimate produced by the original RAND investigators, any attempt by researchers to apply the experimental estimates out of sample will involve more assumptions – and hence scope for uncertainty – than the direct experimental estimates themselves. This point, while (we’d think) simple and uncontroversial, may have been somewhat lost in the intervening decades of use of the RAND estimates. Our hope is that this essay may help put both the famous experiment and its results back in context.