Abstract
The multiphoton fluorescence recovery after photobleaching (MP-FRAP) technique has been developed to measure the three-dimensional (3D) solute diffusion within biological systems. However, current 3D MP-FRAP models are based on isotropic diffusion and spatial domain analysis. The 3D anisotropic diffusion and frequency domain analysis for MP-FRAP measurements are rarely studied. In this study, a new technique is demonstrated for the quantitative and non-destructive determination of 3D anisotropic solute diffusion tensors within biological fibrosis tissues by multiphoton photobleaching and spatial Fourier analysis (SFA). Compared to the spatial domain analysis based MP-FRAP techniques, this SFA-based method has the capability for determining the 3D anisotropic diffusion tensors as well as the flexibility for satisfying initial and boundary conditions. First, a close-form solution of the 3D anisotropic diffusion equation is derived by solely using SFA. Next, this new method is validated by computer-simulated MP-FRAP experiments with pre-defined 3D anisotropic diffusion tensors as well as experimental diffusion measurements of FITC-Dextran (FD) molecules in aqueous glycerol solutions. Finally, this MP-FRAP technique is applied to the measurement of 3D anisotropic diffusion tensors of FD molecules within porcine tendon tissues. This study provides a new tool for complete determination of 3D anisotropic solute diffusion tensor in biological tissues.
Keywords: Multiphoton fluorescence recovery after photobleaching (MP-FRAP), Spatial Fourier analysis (SFA), Anisotropic diffusion, Diffusion tensor, Porcine tendon
INTRODUCTION
Fluorescence recovery after photobleaching (FRAP) is a versatile and widely used tool for the determination of local diffusion properties within solutions, cells, tissues, and biomaterials. Due to the high spatial resolution, FRAP offers the possibility to microscopically examine a specific region of a sample. More importantly, a variety of FRAP techniques has been developed to understand the relationship between tissue structure and solute diffusion properties by determining the diffusional anisotropy in the biological tissues. For example, the fluorescence imaging of continuous point photobleaching (FICOPP)14, elliptical surface photobleaching19, line FRAP4, 25 and spatial Fourier analysis (SFA) based FRAP22, 23, 28 techniques have been utilized to investigate the diffusional anisotropy of different solutes in varying types of tissues (e.g., the cartilaginous tissues and fibrosarcoma tumors). It was found that the structure and orientation of collagen fibers in the tissue extracellular matrix (ECM) leads to diffusion anisotropy.
The current anisotropic FRAP techniques mainly determine the solute diffusion properties in two-dimension (2D). Previous studies22, 27 have determined the three-dimensional (3D) anisotropic solute diffusion properties by dissecting and measuring samples in three orthogonal planes. However, the destructive sample preparation procedure may change the local 3D solute diffusion properties. To our knowledge, there is no FRAP method currently available for the non-destructive measurements of 3D anisotropic diffusion tensors. Therefore, the goal of this study was to develop a mathematical model and corresponding technique of 3D anisotropic FRAP method.
In the past decade, the development of multiphoton microscopy has allowed the FRAP techniques6, 15 to non-destructively measure 3D solute diffusion in biological samples. Due to the nonlinear excitation in multiphoton-based photobleaching experiments, only the fluorophore within the focal spot is photobleached and the photobleaching profile yields a well-defined 3D geometry6, 13, 16. Moreover, due to the deeper penetration of multiphoton imaging12, multiphoton fluorescence recovery after photobleaching (MP-FRAP) techniques can be applied to thick samples with large light scattering5, 26. However, current 3D MP-FRAP models and techniques focus on the isotropic diffusion measurements due to the primary application involving the study of protein mobilities within intracellular structures. Therefore, the determination of 3D anisotropic diffusion tensors in biological samples remains a significant challenge for current MP-FRAP techniques. Previous studies have demonstrated the strength of SFA-based FRAP techniques in the determination of 2D anisotropic diffusion tensors in cartilaginous tissues22, 28, 29. This approach can be extended to 3D anisotropic diffusion tensor measurements by incorporating with multiphoton microscopy. Therefore, in this study, a new 3D MP-FRAP technique with SFA was developed to non-destructively and completely determine the anisotropic solute diffusion tensors in biological tissues.
First, the new mathematical model and technique were validated by experimental diffusion measurements of FITC-Dextran (FD) molecules in aqueous glycerol solutions, as well as computer-simulated MP-FRAP experiments with pre-defined 3D anisotropic diffusion tensors (described in Supplementary Material). Then, this anisotropic MP-FRAP technique was applied to the measurement of 3D diffusion tensors of FD molecules within porcine tendon tissues.
MATERIALS AND METHODS
Solving 3D Diffusion Equation by SFA
Diffusional transport is governed by Fick's second law and the 3D governing equation is given as10:
| (1) |
where (x,y,z) are the spatial coordinates and t is the time. The function C(x, y, z, t) represents the spatial concentration distribution of the solute and D is the diffusion tensor which is assumed to be symmetric. Within the observation field of MP-FRAP experiments, it is assumed that the diffusion tensor (D) is independent of position and time. Therefore, Eq. (1) could be rewritten as:
| (2) |
where Dxx, Dyy, Dzz, Dxy, Dxz, and Dyz are the six independent components of D in the (x,y,z) coordinate system.
Given that is the Fourier transform of C(x, y, z, t), with an arbitrary initial condition and a boundary condition that C(x, y, z, t) is constant as (x,y,z) → ±∞, Eq. (2) can be solved by using 3D SFA in the frequency domain3, 24, 27, 29, 30, which are similar to the strategies used in the 2D condition:
| (3) |
where C̃(u,v,w,0) is the Fourier transform of the initial solute concentration. D(u,v,w) represents the diffusion coefficient in the Fourier space (with frequencies u, v, and w) and is defined as:
| (4) |
The function D(u,v,w) can be determined by curve-fitting the light intensity of a time series of 3D fluorescence recovery image stack in the Fourier space to Eq. (3).
Determining all Components of the Diffusion Tensor
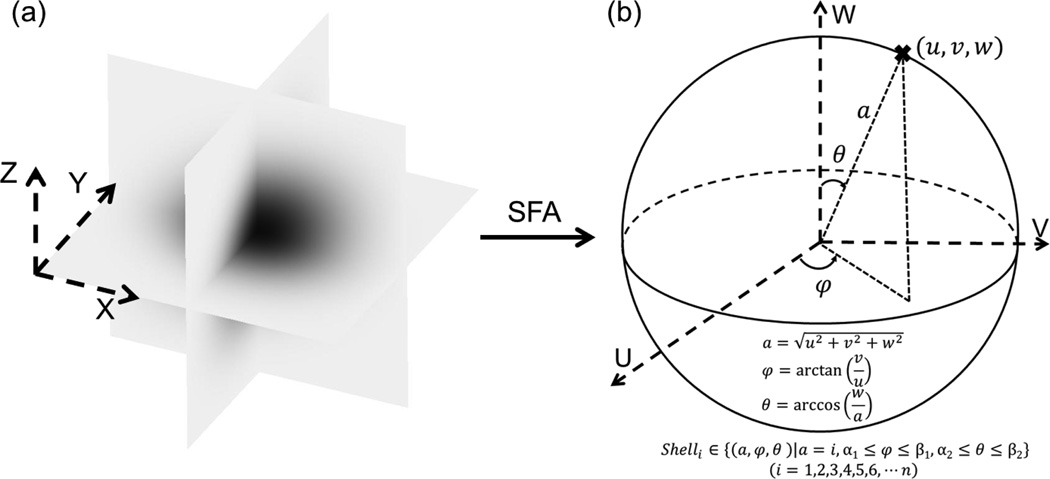
The diffusivity D(u,v,w) can be averaged over a shell of a spherical surface in the frequency domain. The geometry of a shell is defined in Fig. 1 by three parameters [i.e., radius , azimuthal angle φ = arctan(v/u), and polar angle θ = arccos−1(w/a)].
Figure 1.
An illustration of the SFA and averaging the diffusivity in the frequency domain over a shell. In the SFA, the solute concentration distribution is transformed from the spatial domain (a) to the frequency domain (b) by using the Fourier transform. In the frequency domain, the diffusivity D(u,v,w) is averaged over a shell of a spherical surface to obtain all components of the 3D diffusion tensor. The level of shell is defined by the radius a (i.e., commonly positive integers) and the range of shell is determined by azimuthal angle φ and polar angle θ.
When φ and θ range from α1 to β1 and α2 to β2, respectively, Dα1,β1,α2,β2, representing the average of D(u,v,w) over an arbitrary shell (Integral shell, Σ: u2 + v2 + w2 = a2, a is an arbitrary constant), can be given as:
| (5) |
Where
| (6) |
Based on Eqs. (5) and (6), the average of D(u,v,w) over the shell with α1 = 0, β1 = π, α2 = 0, β2 = π can be related to the components of the diffusion tensor D as:
| (7) |
Similarly, the other averages of D(u,v,w) over the different angle ranges can be calculated
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
According to Eqs. (7)–(12), all components of the diffusion tensor (i.e., Dxx, Dyy, Dzz, Dxy, Dxz, and Dyz) can be obtained and expressed as the functions of D0,π,0,π, D0,π/2,0,π, D0,π,0,π/2, D0,π/2,0,π/2, D0,π/4,0,π, and D0,π,0,3π/4:
| (13) |
Experimental MP-FRAP Apparatus and Protocol
All MP-FRAP experiments were performed on a Zeiss LSM 510 NLO confocal laser scanning microscope (Carl Zeiss Microscopy, LLC, Thornwood, NY) equipped with a Coherent Mira 900 femtosecond pulsed Ti:Sapphire laser for multiphoton excitation (Coherent, Santa Clara, CA) at room temperature (22°C). Multiphoton excitation of fluorescein isothiocyanate-dextran (FITC-Dextran, FD) (Sigma-Aldrich®, St. Louis, MO) in the specimens was accomplished by a 790nm laser. To minimize the contribution of the fluorescence emission of the background, one pre-bleaching image stack was obtained in the observation volume (e.g., 150×150×150µm3 for 40× lens or 102×102×102µm3 for 63× lens) and subsequently subtracted from the post-bleaching Z-stack image series. An imaging mode with low multiphoton laser energy (6%~30% laser energy) was applied during the recovery course. Images were collected as 64×64×64 pixel X-Y-Z-scans at an 8-bit intensity resolution using a 40×/1.2NA water immersion objective (working distance: 0.22mm) for the glycerol solution samples or a 63×/1.3NA water immersion objective (working distance: 0.17mm) for the tissue samples. The central region of the observation volume was then photobleached by a high energy multiphoton laser (85%~100% laser power) at the different Z-levels to create a cubic photobleaching block (the photobleaching time was about 2–3 seconds) with a dimension of about 18.75×18.75×18.75µm3 (40× lens) or 12.75×12.75×12.75µm3 (63× lens). For each experiment, 40 stacks of recovery images, plus 1 stack prior to photobleaching, were acquired at an approximate rate of 18 seconds/stack.
Diffusion in Glycerol/PBS Solutions
14µL of the solutions were pipetted into a small chamber obtained by attaching two layers of a 120-µm-thick double-side adhesive spacer (Secure-Seal spacers, Life Technologies, Grand Island, NY) on a microscope slide. The chamber was then sealed with a microscope coverslip. The 3D diffusion of FD500 molecules (500KDa, 4mg/mL) in the glycerol/phosphate buffered saline (PBS) solutions with five different concentrations (v/v: 75%, 80%, 85%, 90%, and 95%) were measured to test our MP-FRAP technique.
Diffusion in Porcine Tendon Tissues
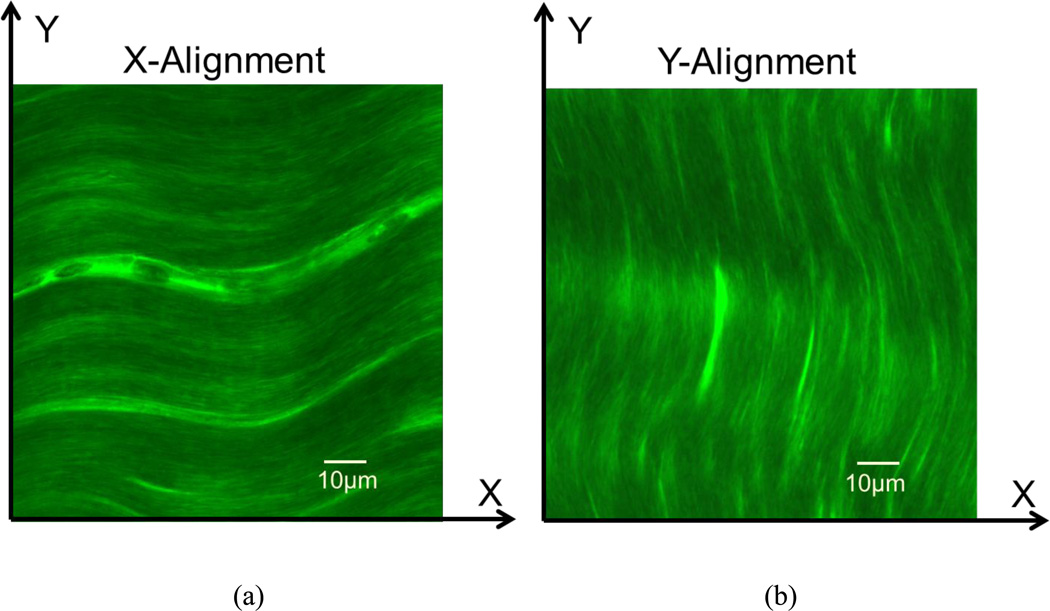
The porcine calcaneal tendon tissue samples (N=20) from adult pig legs, obtained from a local slaughterhouse, were used to test our MP-FRAP technique. The tissue segments were microtomed along the fiber direction into 150µm slices by using a microtome (SM24000, Leica Microsystems GmbH, Wetzlar, Germany) with a freezing stage (Model BFS-30, Physitemp, Clifton, NJ). Tendon tissue specimens were then immersed in PBS solution containing two types of FD molecules (FD70 and FD150, 6mg/mL) for 72 hours. Tissue swelling was prevented during the incubation by confining the specimen with two porous platens. The tissue specimen was then transferred into a small chamber, which was filled with a glycerol/PBS solution (v/v: 60%) containing FD70 or FD150 molecules (6mg/mL) to enhance the penetration depth in tissues for multiphoton microscopy9, 11. The 3D anisotropic diffusion tensors of the FD molecules (70KDa and 150KDa) in the tendon tissue slices were measured by the MP-FRAP technique. First, each specimen was measured when the fiber orientation aligned with X-axis of microscopy coordinate (X-Alignment in Fig. 2a), and then repeated, when the field of view (FOV) was rotated 90 degrees to allow the fiber direction to align with the Y-axis (Y-Alignment in Fig. 2b). Correspondingly, the six components (i.e., Dxx, Dyy, Dzz, Dxy, Dxz, and Dyz) and the traces of the 3D diffusion tensors were obtained from those MP-FRAP experiments.
Figure 2.
Two observation protocols for fluorescent solute diffusion measurements in the porcine tendon tissues. X-Y coordinates represent the microscopy coordinates fixed on the microscope sample stage. (a) In the protocol of X-Alignment, the main fiber orientation is aligned with the X-axis. (b) In the protocol of Y-Alignment, the main fiber orientation is aligned with the Y-axis.
Images and Data Processing
The Fourier transform of the image intensity (8-bit grayscale) obtained from the microscope camera obeys the same exponential decay as the solute concentration profile [see Eq. (3)] in the frequency domain3, 17. Therefore, the 3D fluorescence recovery image stacks were directly analyzed by the spatial Fourier transform to calculate the 3D diffusion tensors. For both computer simulated (see Supplementary Material) and experimental MP-FRAP tests, the image processing was completed by custom written codes in MATLAB (MATLAB 7.0, The MathWorks Inc., Natick, MA). Based on Eq. (3), the codes performed the 3D Fourier transform and nonlinear curve-fitting to yield D(u,v,w) which was the diffusion coefficient in the frequency domain. Based on Eqs. (7)–(12), D(u,v,w) was averaged on “Shell4” over different angle ranges to obtain D0,π,0,π, D0,π/2,0,π, D0,π,0,π/2, D0,π/2,0,π/2, D0,π/4,0,π, and D0,π,0,3π/4. The selection of “Shell4” was suggested by the results from the simulation experiments (see Supplementary Material). Finally, the MATLAB codes calculated all components of the diffusion tensor by using Eq. (13).
Statistical Analysis
One-way ANOVA and Tukey’s post hoc tests were performed on the diagonal components (i.e., Dxx, Dyy, and Dzz) of the diffusion tensors to examine the extent of anisotropy of solute diffusion in both the glycerol and tissue specimens. A student’s T-test was performed to compare the means of the off-diagonal components and the diagonal components of the diffusion tensors. An independent t-test was also performed on the nominal diffusivity (tr(D)/3) of diffusion tensors for the FD70 and FD150 in the porcine tendon tissue experiments to examine the size effect of solute diffusion in the tissue samples. The SPSS 16.0 software (SPSS Inc., Chicago, IL) was used for all statistical analysis and significant differences were reported at p-values < 0.05.
RESULTS
Diffusion Measurements in Glycerol/PBS Solutions
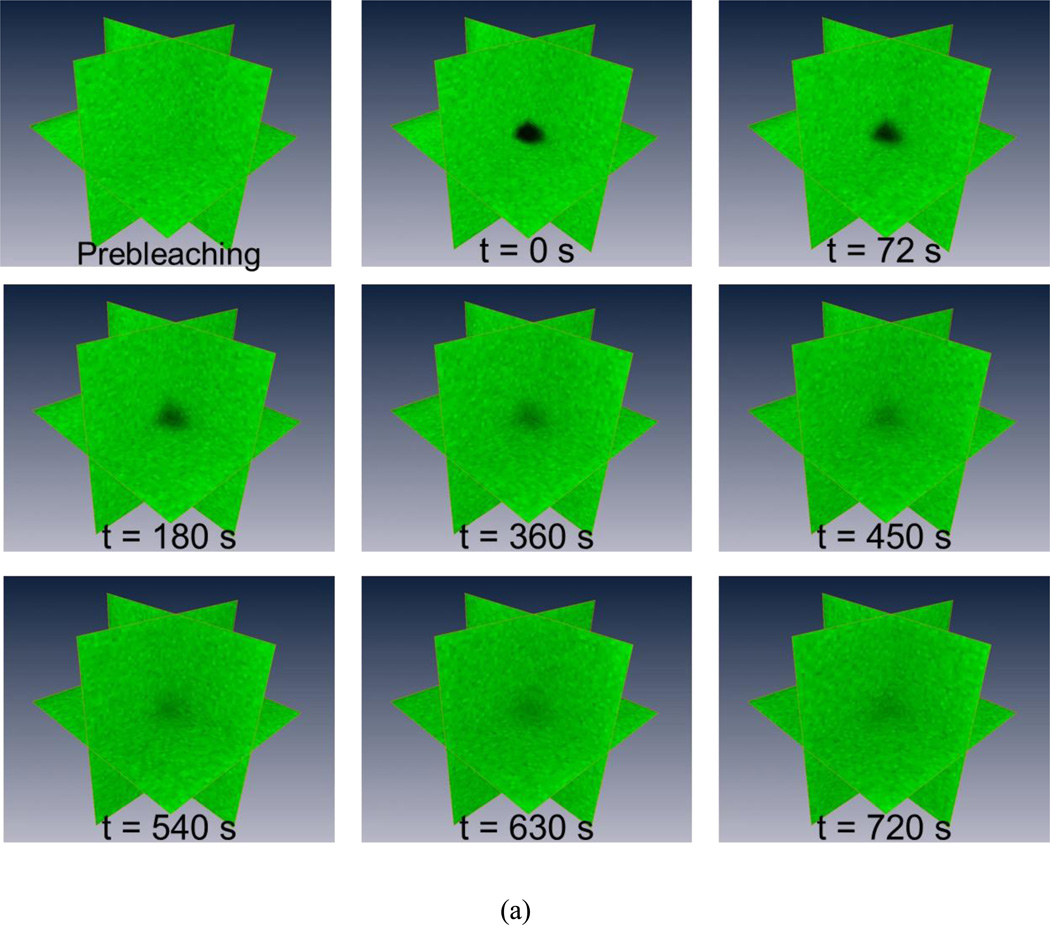
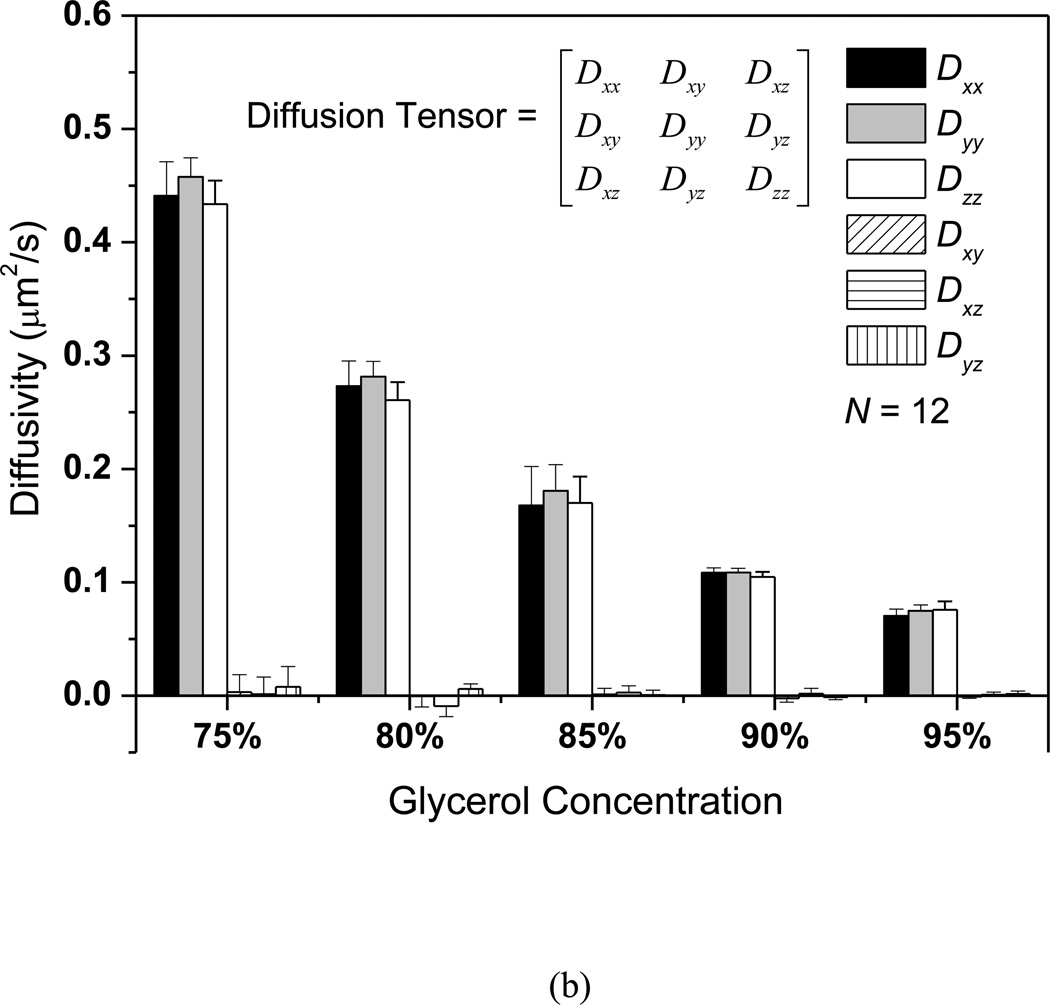
The MP-FRAP technique was applied to the measurement of the 3D diffusion properties of FD500 molecules in glycerol/PBS solutions with varying concentrations (from 75% v/v to 95% v/v). A typical MP-FRAP image stack series of FD500 in the 95% glycerol/PBS solution was shown in Fig. 3a. Three ortho-slices of the 3D fluorescent profile were displayed and the dark region represented the multiphoton laser induced photobleaching geometry. The results of the FD500 diffusion measurements were summarized in Fig. 3b. In each concentration group (N=12), there were no significant differences between the diagonal diffusion components (i.e., Dxx, Dyy, and Dzz). The mean of the off-diagonal components was significantly smaller than the mean of the diagonal components (p<0.0001) for all experimental groups. Moreover, the ratio of the off-diagonal components to the diagonal components was less than 3%. These results demonstrated that the diffusion of FD500 molecules in the glycerol/PBS solutions is isotropic. The nominal diffusivity (mean±SD) of the diffusion tensor of the FD500 molecules in each group (75%: 0.444±0.015µm2/s; 80%: 0.272±0.012µm2/s; 85%: 0.173±0.026µm2/s; 90%: 0.107±0.002µm2/s; 95%: 0.074±0.003µm2/s) were compared to examine the concentration effect on the nominal diffusivities. Significant differences (ANOVA, p < 0.0001) were found between each concentration group. The nominal diffusivities of FD500 decreased with increasing glycerol concentrations.
Figure 3.
The 3D isotropic diffusion of FD500 molecule in glycerol/PBS solutions. (a) Typical time series of 3D MP-FRAP Z-stack image of fluorescent solutes for the experimental diffusion measurements in the glycerol/PBS solutions. For each experiment, typically, 40 stacks of post-bleaching images, plus 1 stack prior to photobleaching, are acquired at an approximate rate of 18 seconds/stack. The central region of the observation volume is photobleached by the multiphoton laser and fluorescence recovers completely in the last Z-stack image series (t=720s). (b) The results of 3D diffusion tensors (mean±SD). In each concentration group, there were no significant differences between the diagonal diffusion components (i.e., Dxx, Dyy, and Dzz), while the off-diagonal diffusion components were significantly smaller than the diagonal diffusion components (p<0.0001). Additionally, the nominal diffusivities (tr(D)/3) of FD500 significantly decreased (ANOVA, p<0.0001) with the increasing glycerol concentrations.
Diffusion Measurements in Porcine Tendon Tissues
The 3D anisotropic diffusion tensors of FD70 and FD150 solutes in porcine tendon tissues with an optical clearing agent (i.e., glycerol) application were experimentally determined by the new MP-FRAP method. The images in Fig. 4a showed the typical MP-FRAP experiment process in the tissue specimen (e.g., FD70 and 60% glycerol). The collagen fiber distribution can also be observed in the ortho-slices.
Figure 4.
The 3D anisotropic diffusion of FD molecules in the porcine tendon tissues. (a) Typical time series of 3D MP-FRAP Z-stack image of fluorescent solutes for the experimental diffusion measurements in the porcine tendon tissues. For each experiment, typically, 40 stacks of post-bleaching images, plus 1 stack prior to photobleaching, are acquired at an approximate rate of 18 seconds/stack. The central region of the observation volume is photobleached by the multiphoton laser and fluorescence recovers completely in the last Z-stack image series (t=720s). (b) The results of 3D diffusion tensors (mean±SD). The diffusion of FD70 and FD150 along the major fiber orientation was significantly faster than the other two diffusions transverse to the fiber direction in both the X- and Y-Alignment observation protocols.
The six components of the 3D diffusion tensors of FD70 and FD150 in the tendon tissues were calculated by the proposed method and the results were shown in Fig. 4b. The first two groups (N=10) of diffusivities were the result of the FD70 diffusion in the tissue specimens with two different observation protocols (i.e., X-Alignment and Y-Alignment). In the X-Alignment group, the collagen fibers were largely aligned with the X-axis of microscopy coordinate. The results indicated that Dxx was significantly higher (ANOVA, p < 0.0001) than Dyy and Dzz in this group and there was no significant difference (ANOVA, p = 0.884) between Dyy and Dzz. In the Y-Alignment group, the FOV was rotated by 90 degrees and the fiber orientation was primarily aligned along the Y-axis of microscopy coordinate. The results showed that the diffusion (Dyy) along the Y-axis was significantly faster (ANOVA, p =0.0007) than the other two directions (Dxx and Dzz,) in the Y-Alignment group. The mean of the off-diagonal components was significantly smaller than the mean of the diagonal components (p<0.0001) for the two experimental groups. The ratio of the off-diagonal components to the diagonal components was less than 15%. The third and fourth groups (N=10) of diffusivities (Fig. 4b) further demonstrated that the exact same trends existed in the results of FD150 diffusion in the tissue specimens. Thus, the 3D diffusion properties of these two types of FD solutes in the tendon tissue slices were highly anisotropic and the diffusion along the fiber orientation was faster than the diffusion transverse to the fiber direction. Moreover, the FD70 (0.117±0.023µm2/s, Stokes radius: 6nm) had about 1.4 times higher (t-test, p = 0.002) nominal diffusivity than the FD150 (0.081±0.016µm2/s, Stokes radius: 8.5nm) in the tendon tissue specimens.
DISCUSSION
The MP-FRAP technique has been well-established to measure the diffusion of macromolecules within biological systems. However, current 3D MP-FRAP models are based on the isotropic diffusion assumption and spatial domain analysis. In this study, a close-form solution of the 3D anisotropic diffusion equation was first derived by solely using spatial Fourier analysis for the MP-FRAP technique. The accuracy of this new method was evaluated by using computer-simulated MP-FRAP experiments with the pre-defined 3D anisotropic diffusion tensors (see Supplementary Material) and experimental diffusion measurements of FD molecules in glycerol/PBS solutions. The new MP-FRAP technique was then implemented to determine the 3D diffusion tensors of FD molecules within porcine tendon tissues. This study provided a new tool for complete determination of 3D anisotropic solute diffusion tensor in biological tissues.
Strength of SFA-based 3D FRAP Technique
The major strengths of SFA-based FRAP techniques, compared to the conventional FRAP techniques based on spatial domain analysis, have been discussed in previous 2D studies3, 30. Our study confirmed that all these strengths persist in the new 3D MP-FRAP method. First, SFA-based FRAP techniques possesses intrinsic flexibility to accommodate complex initial conditions during the FRAP process. For instance, the photobleaching volume could be any 3D geometry and the “real” first recovery image stack right after photobleaching is not required for the calculation. Second, the anisotropic diffusion tensor can be calculated without measuring the point spread function or optical transfer function of the multiphoton microscope3, 17. Due to these features, our technique can be conveniently carried out on a commercial multiphoton laser scanning microscope (MPLSM) for 3D anisotropic diffusion measurements.
Validation of MP-FRAP Model
The accuracy and robustness of the new method was first assessed by the computer simulated MP-FRAP experiments (see Supplementary Material). As shown in Fig. S2, the new method yielded accurate values for the components of the diffusion tensors. Overall, the relative errors were less than 1.8% when the pre-defined diffusion tensors were rotated at different angles across the 3D space.
The diffusion measurements of FD500 molecules in the glycerol/PBS solutions were performed to experimentally validate the new MP-FRAP technique. Since the new technique is designed for 3D anisotropic diffusion measurements, full 3D diffusion tensors were determined in all test groups. There were no significant differences between the diagonal diffusion components of the diffusion tensor, while the off-diagonal diffusion components were very small (<3%) compared to the diagonal components. These results indicated that the diffusion of FD500 molecules in the glycerol/PBS solutions is isotropic, which is expected. The nominal diffusivities (0.44µm2/s and 0.27µm2/s) of FD500 in the two types of glycerol solutions (75% v/v and 80% v/v) were comparable to the diffusivities (0.60µm2/s and 0.36µm2/s) of the same solute in the glycerol solutions (80% w/w and 85% w/w) measured by another MP-FRAP technique15. The minor differences were probably caused by the different sample preparation procedures and observational volumes. The trend of decreasing nominal diffusivities with increasing glycerol concentrations was in agreement with the relationship between solute diffusivity and solvent viscosity, which is defined in the Stokes-Einstein equation.
3D Anisotropic Diffusion in Porcine Tendon Tissue
The goal of this study was to develop a 3D MP-FRAP technique to determine anisotropic solute diffusion tensors in biological tissues. The 3D diffusion of FD70 and FD150 molecules in porcine tendon tissues was measured to assess the capability of the new MP-FRAP technique. Generally, tendon and ligament tissues have well organized collagen fiber structures, resulting in anisotropic mechanical and transport properties14, 31. Based on the measured 3D diffusion tensors, it was found that diffusion coefficients of FD70 and FD150 were significantly higher in a direction parallel to the collagen fibers in both the X-Alignment and Y-Alignment testing protocols. Diffusional anisotropy can be represented by the ratio of diffusivity along the fiber orientation to the diffusivity perpendicular to the fiber orientation. Our results showed an average anisotropic value of 2.1 for FD70 and a value of 2.2 for FD150 in porcine tendon tissue. These results were comparable to the diffusional anisotropy measurements in porcine ligament tissues in the literature. In a previous 2D diffusion study14 using Fluorescence Imaging of Continuous Point Photobleaching (FICOPP), an anisotropic value of 2.2 was found for FD500 in porcine ligament tissue. Other 2D diffusion techniques, such as elliptical surface photobleaching19 and video-FRAP imaging technique29, have also been utilized to investigate the diffusional anisotropy of different solutes in varying types of tissues (e.g., mouse spinal cord19, porcine knee cartilage14, bovine annulus fibrosus in the IVD27, and bovine meniscus29). A brief summary of those studies was shown in Table 1. Apparently, diffusional anisotropy exists in many biological tissues with complex tissue structures. The highest diffusional anisotropy was found in the mouse spinal cord due to the highly aligned axon fibers.
Table 1.
The comparison of diffusional anisotropy of fluorescent solutes in biological tissues. (“Anisotropy” is defined as the ratio of the diffusivity parallel to the primary fiber direction to the diffusivity perpendicular to the primary fiber direction.)
| Tissue | Solute | Anisotropy | Reference |
|---|---|---|---|
| Mouse spinal cord | FD70 | 5 | 19 |
| Porcine ligament tissue | FD500 | 2.2 | 14 |
| Porcine knee cartilage (surface) | FD500 | 1.5 | 14 |
| Bovine annulus fibrosus in the IVD | Fluorescein(332Da) | 1.5 | 27 |
| Bovine meniscus | Fluorescein(332Da) | 3.6 | 29 |
| Porcine tendon tissue | FD70 | 2.1 | Present study |
| Porcine tendon tissue | FD150 | 2.2 | Present study |
Due to the strong light scattering in the tendon tissue slices, the depth of multiphoton imaging with sufficient contrast and signal to noise ratio (SNR) is limited. Therefore, an optical clearing agent (OCA), glycerol, was applied to reduce the scattering and significantly enhance the light penetration depth and SNR of deep-tissue imaging9, 11. Additionally, the use of glycerol in the testing model slowed down the diffusion of FD molecules, which allowed the multiphoton microscopy system to fully capture the 3D fluorescence recovery processes by a limited sampling rate (18 second/stack). Even though the application of glycerol might change the biochemical properties of the ECM in tendon tissues, the diffusion of FD molecules is not likely to be affected by the binding reactions due to their uncharged and biologically inert nature. The results demonstrated the effect of solute size on the diffusion properties. The ratio (1.44) of two nominal diffusivities was in agreement with the ratio (1.42) of the two Stokes radii for FD70 and FD150 molecules, which follows the Stokes-Einstein equation for solute diffusion.
The current 3D image sampling rate of multiphoton microscopy significantly limits the capability of our technique for fast diffusion measurement. In this study, reliable measurements of diffusion coefficients up to 0.5µm2/s can be achieved in tissue (see Supplementary Material). Recent studies1, 18 have shown the development of various multifocus microscopy techniques, which can significantly increase the scanning speed of fast 3D fluorescence imaging. By incorporating these techniques, the capabilities and applications of our MP-FRAP method could be significantly enhanced and broadened. In addition, photoactivatable green fluorescence protein (PA-GFP) has been widely used for living cell imaging20, 21 and diffusion measurements2, 7, 8, 15. Our 3D MP-FRAP method can be easily transformed to analyze the image data from multiphoton fluorescence redistribution after photoactivation (MP-FRAPa) experiments with the use of PA-GFP. A higher SNR can be achieved in the MP-FRAPa experiment since less laser energy is generally necessary for photoactivation compared to photobleaching, which could benefit living tissue/cell imaging by reducing the effects of photodamage. Therefore, the development of a 3D MP-FRAPa technique for the diffusion measurements of PA-GFP could be the next step of this study.
Supplementary Material
ACKNOWLEGEMENTS
This project was supported by NIH grants DE021134, DE018741, and AR055775, a NSF RII grant predoctoral fellowship (EPS-0903795) to CS, and a NSF Graduate Research Fellowship to SEC.
Footnotes
CONFLICT OF INTEREST
None of the authors of this paper have a conflict of interest that might be construed as affecting the conduct or reporting of the work presented.
REFERENCES
- 1.Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, Mizuguchi G, Soule P, Mueller F, Dugast Darzacq C, Darzacq X, Wu C, Bargmann CI, Agard DA, Dahan M, Gustafsson MG. Fast multicolor 3D imaging using aberration-corrected multifocus microscopy. Nat Methods. 2013;10:60–63. doi: 10.1038/nmeth.2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Beaudouin J, Mora-Bermudez F, Klee T, Daigle N, Ellenberg J. Dissecting the contribution of diffusion and interactions to the mobility of nuclear proteins. Biophys. J. 2006;90:1878–1894. doi: 10.1529/biophysj.105.071241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berk DA, Yuan F, Leunig M, Jain RK. Fluorescence photobleaching with spatial Fourier analysis: measurement of diffusion in light-scattering media. Biophys. J. 1993;65:2428–2436. doi: 10.1016/S0006-3495(93)81326-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Braeckmans K, Remaut K, Vandenbroucke RE, Lucas B, De Smedt SC, Demeester J. Line FRAP with the confocal laser scanning microscope for diffusion measurements in small regions of 3-D samples. Biophys. J. 2007;92:2172–2183. doi: 10.1529/biophysj.106.099838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brown EB, Boucher Y, Nasser S, Jain RK. Measurement of macromolecular diffusion coefficients in human tumors. Microvasc. Res. 2004;67:231–236. doi: 10.1016/j.mvr.2004.02.001. [DOI] [PubMed] [Google Scholar]
- 6.Brown EB, Wu ES, Zipfel W, Webb WW. Measurement of molecular diffusion in solution by multiphoton fluorescence photobleaching recovery. Biophys. J. 1999;77:2837–2849. doi: 10.1016/S0006-3495(99)77115-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Calvert PD, Peet JA, Bragin A, Schiesser WE, Pugh EN., Jr Fluorescence relaxation in 3D from diffraction-limited sources of PAGFP or sinks of EGFP created by multiphoton photoconversion. J. Microsc. 2007;225:49–71. doi: 10.1111/j.1365-2818.2007.01715.x. [DOI] [PubMed] [Google Scholar]
- 8.Calvert PD, Schiesser WE, Pugh EN., Jr Diffusion of a soluble protein, photoactivatable GFP, through a sensory cilium. J. Gen. Physiol. 2010;135:173–196. doi: 10.1085/jgp.200910322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cicchi R, Sampson D, Massi D, Pavone F. Contrast and depth enhancement in two-photon microscopy of human skin ex vivo by use of optical clearing agents. Opt. Express. 2005;13:2337–2344. doi: 10.1364/opex.13.002337. [DOI] [PubMed] [Google Scholar]
- 10.Crank J. The mathematics of diffusion. New York: Oxford University Press; 1975. p. 5. [Google Scholar]
- 11.Genina EA, Bashkatov AN, Tuchin VV. Tissue optical immersion clearing. Expert. Rev. Med. Devices. 2010;7:825–842. doi: 10.1586/erd.10.50. [DOI] [PubMed] [Google Scholar]
- 12.Helmchen F, Denk W. Deep tissue two-photon microscopy. Nat. Methods. 2005;2:932–940. doi: 10.1038/nmeth818. [DOI] [PubMed] [Google Scholar]
- 13.Kubitscheck U, Tschodrich-Rotter M, Wedekind P, Peters R. Two-photon scanning microphotolysis for three-dimensional data storage and biological transport measurements. J. Microsc. 1996;182:225–233. doi: 10.1046/j.1365-2818.1996.60424.x. [DOI] [PubMed] [Google Scholar]
- 14.Leddy HA, Haider MA, Guilak F. Diffusional anisotropy in collagenous tissues: fluorescence imaging of continuous point photobleaching. Biophys. J. 2006;91:311–316. doi: 10.1529/biophysj.105.075283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mazza D, Braeckmans K, Cella F, Testa I, Vercauteren D, Demeester J, De Smedt SS, Diaspro A. A new FRAP/FRAPa method for three-dimensional diffusion measurements based on multiphoton excitation microscopy. Biophys. J. 2008;95:3457–3469. doi: 10.1529/biophysj.108.133637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mazza D, Cella F, Vicidomini G, Krol S, Diaspro A. Role of three-dimensional bleach distribution in confocal and two-photon fluorescence recovery after photobleaching experiments. Appl. Opt. 2007;46:7401–7411. doi: 10.1364/ao.46.007401. [DOI] [PubMed] [Google Scholar]
- 17.Meyvis TK, De Smedt SC, Van Oostveldt P, Demeester J. Fluorescence recovery after photobleaching: a versatile tool for mobility and interaction measurements in pharmaceutical research. Pharm. Res. 1999;16:1153–1162. doi: 10.1023/a:1011924909138. [DOI] [PubMed] [Google Scholar]
- 18.Mondal PP, Diaspro A. Simultaneous multilayer scanning and detection for multiphoton fluorescence microscopy. Sci Rep. 2011;1:149. doi: 10.1038/srep00149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Papadopoulos MC, Kim JK, Verkman AS. Extracellular space diffusion in central nervous system: anisotropic diffusion measured by elliptical surface photobleaching. Biophys. J. 2005;89:3660–3668. doi: 10.1529/biophysj.105.068114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Patterson GH, Lippincott-Schwartz J. A photoactivatable GFP for selective photolabeling of proteins and cells. Science. 2002;297:1873–1877. doi: 10.1126/science.1074952. [DOI] [PubMed] [Google Scholar]
- 21.Schneider M, Barozzi S, Testa I, Faretta M, Diaspro A. Two-photon activation and excitation properties of PA-GFP in the 720–920-nm region. Biophys. J. 2005;89:1346–1352. doi: 10.1529/biophysj.104.054502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shi C, Kuo J, Bell PD, Yao H. Anisotropic solute diffusion tensor in porcine TMJ discs measured by FRAP with spatial Fourier analysis. Ann. Biomed. Eng. 2010;38:3398–3408. doi: 10.1007/s10439-010-0099-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shi C, Wright GJ, Ex-Lubeskie CL, Bradshaw AD, Yao H. Relationship between anisotropic diffusion properties and tissue morphology in porcine TMJ disc. Osteoarthr. Cartilage. 2013;21:625–633. doi: 10.1016/j.joca.2013.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Smith BA, Clark WR, McConnell HM. Anisotropic molecular motion on cell surfaces. Proc. Natl. Acad. Sci. USA. 1979;76:5641–5644. doi: 10.1073/pnas.76.11.5641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stylianopoulos T, Diop-Frimpong B, Munn LL, Jain RK. Diffusion anisotropy in collagen gels and tumors: the effect of fiber network orientation. Biophys. J. 2010;99:3119–3128. doi: 10.1016/j.bpj.2010.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sullivan KD, Sipprell WH, 3rd, Brown EB, Jr, Brown EB., 3rd Improved model of fluorescence recovery expands the application of multiphoton fluorescence recovery after photobleaching in vivo. Biophys. J. 2009;96:5082–5094. doi: 10.1016/j.bpj.2009.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Travascio F, Gu WY. Anisotropic diffusive transport in annulus fibrosus: experimental determination of the diffusion tensor by FRAP technique. Ann. Biomed. Eng. 2007;35:1739–1748. doi: 10.1007/s10439-007-9346-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Travascio F, Jackson AR, Brown MD, Gu WY. Relationship between solute transport properties and tissue morphology in human annulus fibrosus. J. Orthop. Res. 2009;27:1625–1630. doi: 10.1002/jor.20927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Travascio F, Zhao W, Gu WY. Characterization of anisotropic diffusion tensor of solute in tissue by video-FRAP imaging technique. Ann. Biomed. Eng. 2009;37:813–823. doi: 10.1007/s10439-009-9655-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tsay TT, Jacobson KA. Spatial Fourier analysis of video photobleaching measurements. Principles and optimization. Biophys. J. 1991;60:360–368. doi: 10.1016/S0006-3495(91)82061-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Williams LN, Elder SH, Bouvard JL, Horstemeyer MF. The anisotropic compressive mechanical properties of the rabbit patellar tendon. Biorheology. 2008;45:577–586. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.