Abstract
Acquisition of ultrasound data negatively affects image registration accuracy during image-guided therapy because of tissue compression by the probe. We present a novel compression correction method that models sub-surface tissue displacement resulting from application of a tracked probe to the tissue surface. Patient landmarks are first used to register the probe pose to pre-operative imaging. The ultrasound probe geometry is used to provide boundary conditions to a biomechanical model of the tissue. The deformation field solution of the model is inverted to non-rigidly transform the ultrasound images to an estimation of the tissue geometry before compression. Experimental results with gel phantoms indicated that the proposed method reduced the tumor margin modified Hausdorff distance (MHD) from 5.0 ± 1.6 to 1.9 ± 0.6 mm, and reduced tumor centroid alignment error from 7.6 ± 2.6 to 2.0 ± 0.9 mm. The method was applied to a clinical case and reduced the tumor margin MHD error from 5.4 ± 0.1 to 2.6 ± 0.1 mm and the centroid alignment error from 7.2 ± 0.2 to 3.5 ± 0.4 mm.
Keywords: Image-guided surgery, Tissue deformation, Finite-element model, Biomechanical model, Boundary conditions, Image registration
INTRODUCTION
Ultrasound is commonly used as an intra-operative imaging modality to monitor surgical targets such as tumors. The need to maintain acoustic coupling between the probe and tissue often results in significant compression of the target by the user. This is especially a concern when using ultrasound strain imaging, in which a certain level of pre-compression of the tissue may be necessary. However, this tissue deformation affects the geometry of the scanned objects and the resulting images. Soft tissue can undergo surface compression on the order of 1 cm during routine freehand imaging (Artignan et al. 2004; Xiao et al. 2002). This leads to incorrect estimates of the size and location of landmarks within the ultrasound images.
Compressional effects from the probe are especially apparent in image-guided procedures, which align intra-operative data with pre-operative tomographic images. In these procedures, it is important that data collected during the surgery are accurately registered to high-resolution computed tomography (CT) or magnetic resonance (MR) image volumes for optimal guidance. Typically this is done by digitizing physical landmarks on the patient with a tracked instrument, selecting the corresponding landmarks in the tomograms and computing a rigid transformation that best aligns the two coordinate spaces. Although there are a variety of methods to track and calibrate an ultrasound probe such that each image slice is recorded with a known pose in physical space (Blackall et al. 2000; Boctor et al. 2006; Hsu et al. 2008a, 2008b; Mercier et al. 2005; Muratore and Galloway 2001), the usefulness of tracked ultrasound relies on an accurate registration. Registration accuracy is compromised by non-rigid tissue deformation such as that which occurs with manipulation of the ultrasound probe. The goal of this work was to improve the usefulness of tracked ultrasound in image-guided procedures by improving this registration.
There are several approaches in the literature that have sought to address the problem of tissue deformation exerted by an ultrasound probe. One method is to create a digital representation of the surface and then use a combination of Bayesian theory and prior knowledge of the surgical scene to create a deformation that matches the observed ultrasound data (King et al. 2000), but this approach did not incorporate a physical model of tissue which could be used to provide more realistic priors. Another approach is to acquire B-mode or raw radiofrequency data from the ultrasound and use non-rigid image-based registration and positional tracking to correct for deformation (Treece et al. 2005; Xiao et al. 2002), but this approach requires a series of ultrasound images to provide sequential estimates of compression correction. There has also been work done to model tissue compression using data from a force transducer attached to the ultrasound probe along with a position sensor to drive a tissue model (Burcher et al. 2001; Sun et al. 2010). Our proposed method is similar to this method, but eliminates the need for a force measurement apparatus on the probe by using measured 3-D surface displacements, rather than force, to drive the model. Our method uses just the tracking system which is routinely used in surgical procedures such as image-guided neurosurgery. To our knowledge, there has not been an attempt to model the tissue deformation from the physical probe surface itself in the correction. This work presents a compression correction method that measures and compensates for this effect using a biomechanical tissue model with validation in simulations, phantoms and a preliminary clinical case.
METHODS
We present our compression correction method as one component in the context of a patient-specific data pipeline for image-guided therapy. Before correction, we perform several data acquisition and processing steps. The procedures described below were used in all phantom experiments and were similar for the acquisition and analysis of clinical data.
Phantom construction
Two compliant phantoms were each constructed by mixing 7% by mass polyvinyl alcohol (PVA) in water, 10% by volume glycerol and heating to 80°C to ensure saturation (Fromageau et al. 2007; Surry et al. 2004). For each phantom, a smaller amount of PVA was treated with barium sulfate powder for CT contrast and poured into a separate mold to act as the tumor target. The tumor was subjected to five freeze-thaw cycles in which it was frozen at –40°C for 12 h and then thawed for an additional 12 h, to produce a stiffer material. The tumor was then suspended in the bulk phantom mixture, and the phantom underwent one freeze-thaw cycle to produce a tissue-like phantom containing a stiff tumor. The volumes of the tumor and bulk phantom mixtures were 3.2 and 720 cm3, respectively. The stiffness properties for the bulk tissue and tumor were tested using small samples with an ElectroForce 3100 instrument (Bose, Eden Prairie, MN, USA). One of the phantoms was constructed in a small cup-like container covered in fiducial markers and was used for the baseline accuracy test described under Phantom Experiments. The second phantom was fixed to a rigid base, which contained eight evenly distributed fiducial markers used in the image-to-physical registration, and was used to test the compression correction method.
Patient model from pre-operative image volume
Computed tomography image volumes of the phantoms were acquired using a clinical CT machine. These data simulated a typical pre-operative tomogram acquisition, and were defined in the experiment as the baseline un-deformed state against which our corrected ultrasound data would be compared. All volumes were 512 × 512 × 422 with 0.6-mm isotropic voxels. The phantom structures were segmented using intensity thresholding tools within Analyze 9.0 (Mayo Clinic, Rochester, MN, USA). Isosurfaces were generated from the bulk phantom and tumor segmentations via the marching cubes algorithm, and were smoothed using a Laplacian filter. A tetrahedral mesh was generated from the segmentation surfaces using custom-built mesh generation methods (Sullivan et al. 1997). One phantom and mesh are illustrated in Figure 1.
Fig. 1.
Experimental setup with a gel phantom attached to a base with fiducial markers (a), and the digital phantom and tumor surfaces segmented from the CT image volume (b).
Intra-operative data collection
All ultrasound images were acquired with an Acuson Antares ultrasound machine (Siemens, Munich, Germany), using a VFX13-5 linear array probe with a 6 cm depth setting at 10 MHz. The ultrasound unit was also capable of producing strain images via the eSie Touch elasticity software. For the compression correction experiment, B-mode images were collected, as were strain images, and both types of images were analyzed to evaluate the effect of correction on target locations in ultrasound images having different contrast mechanisms. Ultrasound data were tracked in 3-D space by synchronizing the ultrasound video and tracking data using software based on the Visualization Toolkit on a host PC (Boisvert et al. 2008; Pace et al. 2009). The video was captured by a Matrox Morphis Dual card (Matrox Imaging, Dorval, QC, Canada), which recorded the analogue video output of the ultrasound machine in real time. A passive optical tracking rigid body (Northern Digital, Waterloo, ON, Canada) was fixed to the ultrasound probe, as illustrated in Figure 2. The pose of the rigid body was measured with a Polaris Spectra (Northern Digital, Waterloo, ON, Canada) optical tracking system. The tracked ultrasound system was calibrated using a method that relies on imaging a tracked tool in the ultra-sound plane (Muratore and Galloway 2001). Once the tracked ultrasound system was calibrated, all pixels in each image were associated with a 3-D pose.
Fig. 2.
Polaris tracking system (a) and laser range scanner with passively tracked targets (b). A passively tracked target was also used to track the ultrasound probe (c), and the laser range scanner was used to construct a digital representation of the probe surface (d).
Proposed compression error correction
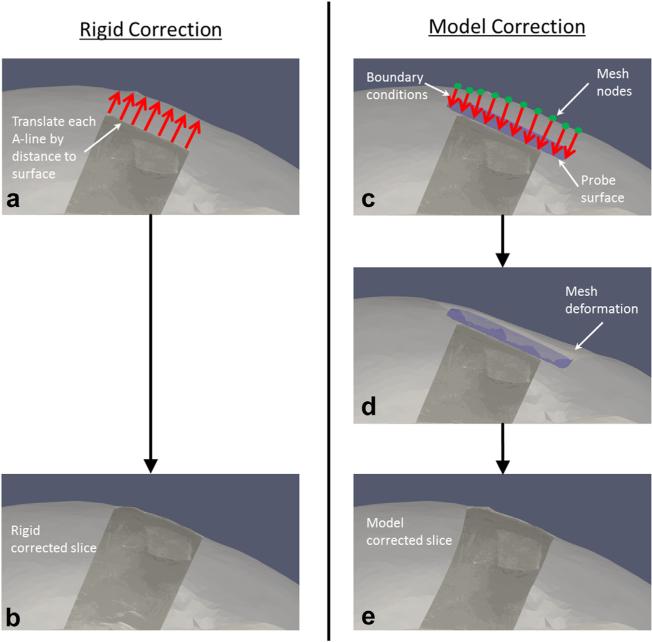
The goal of our project was to reduce the error associated with rigid registration of the tracked ultrasound data to pre-operative volumetric image data by additionally correcting for tissue compression. The general strategy was to use probe tracking information in combination with co-registered tomograms to calculate the distance into the tissue that the probe was pressed, and then use that distance to correct the tracked ultrasound image pose. We chose to first evaluate rigid translations of the ultrasound pixels based on this calculated compression distance as a simple, yet naive correction. This method would have the benefit of very low computational expense, and may be sufficient for aligning sub-surface targets to within a surgically relevant threshold. However, this rigid approach would not account for non-rigid compressional effects throughout the ultrasound image itself. Our proposed correction method instead used the compression distance as input to a more sophisticated tissue-mechanics model-based approach, which non-rigidly deformed the ultrasound image in a physically realistic fashion. Both the naive rigid correction and our model-based correction are outlined in Figure 3 and described below, and both methods were performed for comparison in terms of alignment error reduction during simulations, phantom experiments and a clinical case described in the next section.
Fig. 3.
Procedures for rigid correction and model-based correction. The rigid correction was performed by calculating the distances between the top of each A-line and the co-registered tomographic surface (a) and then translating the A-lines upward in the depth direction by those distances (b). The model-based correction was performed by calculating the distances from the tomogram mesh nodes to a digital representation of the ultrasound probe surface, and designating the distances as boundary conditions to a finite-element model (c). The model was used to solve for tissue displacements throughout the mesh (d) and then reversed to deform the ultrasound image to its pre-compressed state (e).
Rigid correction
The rigid correction procedure stems from the notion that, in the absence of registration error from tissue compression, the near-field row of each A-line in a tracked ultrasound image should ideally be aligned with the organ surface from the co-registered pre-operative tomogram. In the presence of compression error, our tracked ultrasound capabilities would predict that the near-field pixels in the image would typically be some distance below the organ surface. Thus, the correction consists of calculating the distances between the unperturbed surface and the near-field ultrasound image pixels representing the interface between transducer and organ, and then rigidly translating each A-line of the image by that distance opposite the direction of compression to render the ultrasound image in the appropriate pre-operative image space, as illustrated in Figure 3(a, b). The translation of each A-line is calculated by assuming that the compression occurred purely in the depth direction of the ultrasound image, and vectors are created for each pixel in the top row of the image with origin at that pixel and direction opposite of compression. The points of intersection on the surface are determined for each vector, and the distances from the pixels in the top row to these points are calculated to provide the translational correction vectors for the each A-line in the image.
Model-based correction
The model-based correction procedure consists of modeling the volumetric tissue displacement exerted by the ultrasound probe. Knowledge of the exterior geometry of the probe is a necessary component of this model. A laser range scanner (LRS) was used to scan the face of the ultrasound probe to create a 3-D point cloud representing the probe surface, as illustrated in Figure 2d. The accuracy of the LRS device was previously characterized and known to have geometric root mean square error of approximately 0.5 mm (Pheiffer et al. 2012). The LRS was tracked by the same tracking system as the ultrasound probe during the scan, and thus, the created point cloud had a known pose based on the pose of the probe. As a consequence of this relationship and the tracking of the ultrasound probe during data acquisition, the position and orientation of the digital probe surface were known for every ultra-sound image collected. The LRS point cloud of the probe geometry was converted to a smooth surface using radial basis functions, and this surface was used for all subsequent calculations (FastRBF, FarField Technology, Christchurch, New Zealand). It should be noted that the LRS scan of the probe surface was necessary only in the absence of 3-D geometry files from the ultrasound probe manufacturer, which could be used to provide an equivalent geometry.
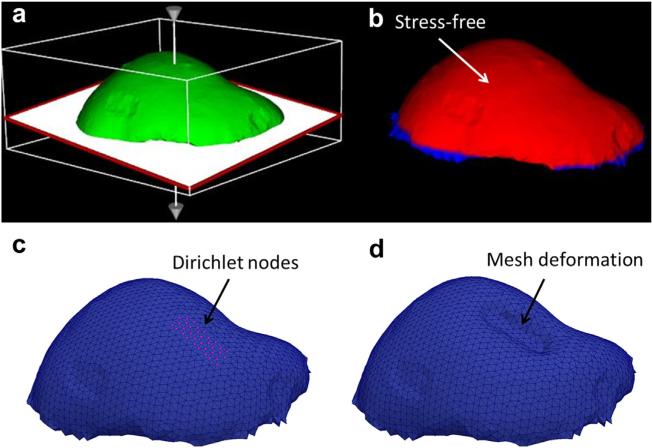
The model-based correction method is illustrated in Figure 3(c–e). The general approach is to use the pose of the probe surface to create boundary conditions for a forward finite-element model (FEM) solution to predict tissue deformation. Because of the standard image-to-physical registration that is done in image-guided interventions, the digital probe surface is placed in the same coordinate space as the patient-specific FEM mesh. Provided a good initial registration between the patient and pre-operative imaging, we assume that the probe surface is located within the mesh at some distance beneath the surface depending on the magnitude of compression exerted by the user. The distances from the probe surface opposite the direction of compression to the mesh surface are computed automatically in a similar fashion as in the rigid correction method. The computed distances are then assigned as Dirichlet boundary conditions to the model. This is accomplished by first generating initial mesh boundary conditions that describe the tissue at rest, without the influence of the ultrasound probe. For the phantom experiments, the far field of the mesh was set as fixed because of the phantom base enclosure, and the near field and surrounding regions of the mesh were set to stress free, as illustrated in Figure 4(a, b). The top of the phantom was considered stress free because that portion of the phantom was left exposed to the atmosphere and was not subjected to any external forces. The ultrasound probe was applied to the top of the phantom in the stress-free region. The set of initial boundary conditions was then altered to reflect the position of the probe in the tissue. Thus, for each ultrasound image, the appropriate mesh nodes were changed from stress free to Dirichlet with the probe displacement values, as illustrated in Figure 4(c).
Fig. 4.
Initial boundary conditions were assigned manually (a) to designate the bottom fixed and the top as stress free (b). These boundary conditions were then modified for each model-based correction by changing the appropriate nodes to Dirichlet displacement conditions (c) based on the position of the ultrasound probe surface, and then the model was solved to produce an approximation of the deformed tissue (d).
After the boundary conditions are generated, they are used to drive a FEM biomechanical model to solve for 3-D displacements throughout the tissue. A linear elastic model was used in the phantom experiments, as the displacements were relatively small and the phantoms were largely homogenous. The model consists of the standard 3-D Navier-Cauchy equations for the displacement field
| (1) |
where E is Young’s modulus, v is Poisson’s ratio, u is the 3-D displacement vector at a point in the tissue and F is the applied body force distribution. The partial differential equation is solved using the Galerkin weighted residual technique with linear basis functions. The system of equations that solves for the displacement vectors at every node in the mesh can be written as
| (2) |
where K is the global stiffness matrix, u is the vector of nodal displacements and f contains the contributions of any applied body forces or surface movement at each node. This system of equations is solved for the nodal displacements that satisfy static equilibrium for the supplied boundary conditions.
These nodal displacement vectors are used to deform the mesh nodes to the compression state exerted by the probe, as illustrated in Figure 4(d), giving a deformed mesh in which each node is associated with a displacement vector. We can then interpolate displacements corresponding to the pixels associated with the co-localized ultrasound image slice and apply the reversed field to simulate the un-compressed state; that is, the reverse displacement vectors are used to non-rigidly un-deform the ultrasound image to an estimation of the tissue in its un-compressed state.
Experimental validation
Simulations of proposed correction
The proposed model-based correction method relied primarily on the assumption that the ultrasound probe would be applied with pressure directly normal to the tissue surface during data collection. The limits of this assumption were tested using a simulation data set and applying the rigid and model-based corrections for a set of tissue compression scenarios in which the trajectory of the probe into the tissue was varied.
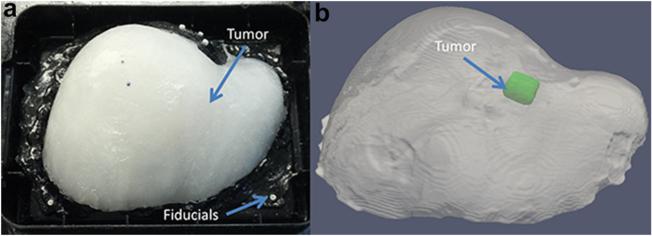
A patient-specific model was constructed from the pre-operative MR volume of a low-grade glioma patient at Vanderbilt University Medical Center who previously gave informed consent with approval of our institutional review board. The brain surface and contrast-enhanced tumor were segmented, and a patient-specific model was constructed as a tetrahedral mesh. For simplicity, the brain and tumor were approximated as homogenous linear elastic materials with Young’s modulus of 2100 Pa and Poisson’s ratio of 0.45, taken from the values used by Dumpuri et al. (2007) for white and gray matter. There are few consistent values reported in the literature for brain material properties in vivo, but the values reported here fall within a range of values proposed by our group in the past for model-updated neurosurgery (Miga 1998; Miga et al. 1998a, 1998b, 2000).
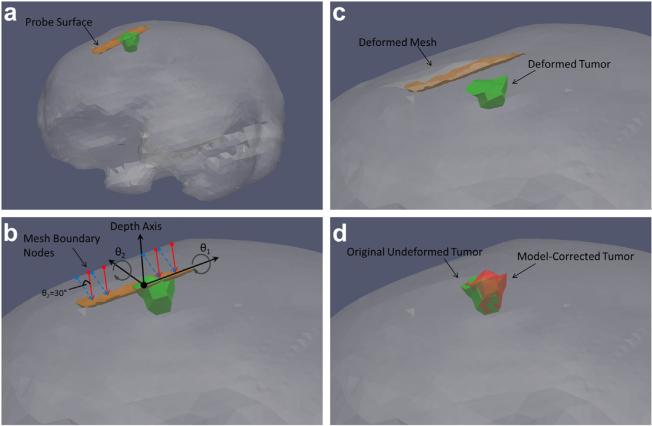
First, the digital probe surface was manually inserted into the mesh over the tumor to simulate misalignment between the tracked ultrasound and co-registered MR volume caused by tissue compression, as illustrated in Figure 5(a). The compression distance from the brain surface down to the probe surface was approximately 7.5 mm, which is within the 1-cm compression magnitude often observed in routine imaging (Artignan et al. 2004; Xiao et al. 2002). An initial set of boundary conditions were created for the brain mesh. A patch of boundary nodes corresponding to a hypothetical craniotomy region above the tumor was designated as stress free, the brain stem was set as fixed and then the rest of the brain surface nodes were designated to have zero normal displacement, with stress-free tangential components to allow slip along the skull. This slip condition has been observed and used in modeling brain shift previously (Chen et al. 2011; Coffey et al. 2013; Miga et al. 1999). Then, vector distances from the brain surface nodes to the probe surface were calculated and used as Dirichlet boundary conditions for a forward solve of the linear elastic model. To determine the impact of our assumption of purely axial probe compression, the orientation of these vectors was systematically altered across the pitch and yaw angles (θ1 and θ2 in Fig. 5b) of the probe surface from –30° to 30° in steps of 15°. For each of these vector alterations, the probe surface remained stationary, and the only change was the selection of brain surface nodes that were designated to displace toward the probe with Dirichlet conditions. These scenarios were intended to illustrate the primary limitation of our approach, which is a lack of known correspondence between the tissue surface and the ultrasound probe. Although tracking the probe gave knowledge of its location within the tissue, its trajectory into the tissue to arrive at that location was not necessarily known because of tissue contact uncertainty. These forward boundary conditions were used to deform the brain and tumor to simulate nine possible physical conditions (one for each of the angle rotations) during an ultrasound data acquisition.
Fig. 5.
Simulation methodology. The probe surface was inserted into the mesh to simulate its position during ultrasound imaging of the tumor (a). Nine sets of boundary conditions were then generated to simulate various possible probe-tissue contact scenarios by rotating the displacement vectors about angles θ1 and θ2 defined with respect to the probe orientation (b). The solid arrows descending from the brain to the surface represent the assumption of compression in the depth direction, whereas the dashed arrows are an example of how the displacement vectors were systematically rotated to test that assumption (here θ2 = 30°). Each set of boundary conditions was used to drive the forward model and deform the mesh and tumor (c). The proposed rigid and model-based corrections (using the assumption of compression perfectly parallel to depth direction) were then applied to each deformed tumor and compared with the original un-compressed tumor (d).
Finally, the proposed compression corrections were applied to each of the deformed tissue models generated from the boundary condition variants from above, and resulted in nine corrected tumor locations. The corrections incorporated the assumption that the probe was compressed purely in the depth direction of the image plane, even for the simulations in which the compression trajectory was at an angle not parallel to the depth direction. The average distance from tissue surface to probe surface was used in the rigid correction method to translate the entire tumor in the direction of the mesh surface. The model-based procedure was used as described previously to create an inverted displacement field and to correct the tumor. Each of the simulated tumor corrections was then compared with the gold standard un-compressed tumor from the original patient model before deformation, in terms of both the boundary node distances between the corrected and gold standard tumor and the distance between the tumor centroids.
Phantom experiments
We performed three validation tests of our method using phantoms. The first was to image a phantom through a layer of water with no contact between probe and phantom, to assess the baseline alignment accuracy of the system in the absence of compression. Second, to test our method we performed an experiment with an anthropomorphic phantom containing a stiff, contrast-enhanced lesion. We compared the tracked ultrasound tumor borders and centroid locations with the equivalent data from co-registered CT as a gold standard before and after compression correction. Third, we also evaluated the effect of tumor elasticity on our model-based correction by using the actual tumor-to-phantom stiffness ratio from material testing, and compared this with the correction using our assumption of tissue homogeneity.
The two phantoms were first constructed as described previously. The phantom fiducial markers were localized in physical space with a tracked stylus, and the corresponding marker positions in the CT volumes were also recorded. The image-to-physical registration was computed using a standard point-based method. The registration produced a transformation matrix that was then automatically applied to all tracked ultrasound images to align them with the CT data.
After the registration was calculated for each phantom, the first phantom, which was constructed in a cup-like container, was covered with a thin layer of water and then imaged with freehand tracked ultrasound for a total of 116 B-mode images in several sweeps while avoiding direct contact with the phantom surface. With respect to this contained phantom, the purpose was not to assess our compression technique with realistic geometries, but instead to quantitatively assess geometric accuracy of a reconstructed target based on tracked ultrasound images without the presence of deformation. Each captured image was stored along with the concatenation of calibration, tracking and registration transformations describing the 3-D location of each slice, and then was compared with the co-aligned CT surface with metrics described below.
The second phantom was then imaged normally with full contact between probe and phantom with the more realistic organ geometry. The tumor was first fully outlined with B-mode using several slow sweeps in approximately 1-mm increments. A total of 178 B-mode images were collected. Then, the elasticity software was used to create strain images of the tumor. A total of 83 strain images were collected. The tracking and registration transformations were applied to the LRS probe surface for each image to generate boundary conditions as described previously.
After collection of the ultrasound data from this phantom, the rigid and model-based correction methods were applied to each ultrasound image. The result was a collection of uncorrected and corrected images. Each type of correction was evaluated by comparing each population of images with the baseline CT images in terms of tumor geometry. In each B-mode and strain image, the tumor borders were segmented semi-automatically using an implementation of the Livewire technique. For each ultrasound image, the CT volume was re-sliced to provide a co-planar CT slice according to the 3-D location and orientation of the co-registered US slice. The CT tumor borders were segmented using intensity thresholding in Analyze 9.0. The tumor borders segmented from ultra-sound images and CT were then compared with each other in terms of the modified Hausdorff distance (MHD) between the two contours, as well as the average distance between the contour centroids (Dubuisson and Jain 1994). The MHD value is defined for two sets of points A and B as follows:
| (3) |
| (4) |
where d (A,B) is the mean closest point distance in the direction of A to B; a and b are respectively points in sets A and B; and Na is the number of points in set A. Thus, the MHD value is created by calculating the mean closest point distance from A to B, and then B to A, and then choosing the maximum of those two values. This metric was chosen as it was less likely to underestimate the error between tumor borders than calculating just a mean closest point distance from the ultrasound to CT contours. The MHD and centroid distance comparison was made for every slice before and after correction and were the primary metrics used to evaluate the improvement offered by our proposed model-based correction algorithm. In addition, the tumor volume measured during phantom construction was recorded for comparison with the CT tumor volume, the volume measured by tracked B-mode in the baseline accuracy test and the volume of the model-corrected B-mode and strain data.
The third phantom experiment was performed to test the effect of tumor elasticity on the model-based correction. As mentioned previously, one of the simplifications of the method is the assignment of homogenous material properties to the patient-specific FEM mesh, which implies that the tumor-to-bulk stiffness ratio in terms of Young’s modulus is assumed to be 1:1. The impact of this assumption was tested by instead using the material testing data done on the phantom materials during the correction, which was a tumor-to-bulk stiffness ratio of 9:1. The 1:1 and 9:1 model-based corrections for the 178 B-mode and 83 strain images were then compared with each other in terms of MHD and centroid distances. PVA is known to be nearly incompressible, so Poisson’s ratio was set to 0.49 for all corrections.
Clinical case
In addition to the phantom study, we also investigated the feasibility of our method on a preliminary clinical case. As in the case of the simulation data set, informed written patient consent was obtained for this work. A pre-operative MR volume was used to construct the patient model. The tumor in this case was determined to be a meningioma, located on the left side of the brain just beneath the surface. Material properties for the linear elastic model were those used in the simulation, based on the average brain tissue properties used by Dumpuri et al. (2007). Intra-operative tracked ultra-sound images were aligned to the patient model by first collecting a scan of the patient face with a tracked LRS and then registering the point cloud to the corresponding MR surface using the iterative closest point algorithm (Cao et al. 2008). After the craniotomy was completed, tracked B-mode images were obtained of the tumor. The rigid and model-based correction methods were then applied to the ultrasound data and were evaluated in terms of MHD between the co-aligned B-mode and MR tumor borders, as well as the distance between the co-planar tumor centroid locations.
RESULTS
Simulations
The results of the correction simulations are summarized in Table 1. These simulations were designed to validate the assumption of compression applied purely in the depth direction. The corrected tumor volumes were compared with the original un-compressed tumor volume in terms of node positional error around the tumor boundary and distances between tumor centroids. Table 1 indicates in every case that model correction out-performed the rigid-based method regardless of application inaccuracy. Boundary errors ranged between 2.7 and 4.3 mm for the rigid method and below 2.8 mm for all model corrections. Similarly, centroid errors were 2.4–3.8 mm and <2.6 mm, respectively. On average over all cases, the model correction improved localization over the rigid method by 55% and 50% for mean boundary node and centroid errors, respectively.
Table 1.
Simulation results used to assess the assumption of compression purely in the depth direction of the ultrasound image plane*
| Rigid correction |
Model correction |
||||
|---|---|---|---|---|---|
| θ1 (°) | θ2 (°) | Boundary node error (mm) | Centroid error (mm) | Boundary node error (mm) | Centroid error (mm) |
| 0 | 0 | 2.7 ± 1.5† | 2.4 | 0.0 ± 0.0 | 0.0 |
| 15 | 0 | 3.0 ± 1.3 | 2.5 | 1.1 ± 0.4 | 1.2 |
| –15 | 0 | 3.3 ± 1.3 | 2.8 | 1.2 ± 0.5 | 1.1 |
| 0 | 15 | 2.9 ± 1.4 | 2.4 | 1.0 ± 0.4 | 1.0 |
| 0 | –15 | 3.2 ± 1.2 | 2.7 | 1.0 ± 0.4 | 1.0 |
| 30 | 0 | 4.0 ± 1.0 | 3.6 | 2.5 ± 0.8 | 2.3 |
| –30 | 0 | 4.3 ± 1.1 | 3.8 | 2.8 ± 1.2 | 2.6 |
| 0 | 30 | 3.5 ± 1.0 | 2.9 | 2.2 ± 0.8 | 2.1 |
| 0 | –30 | 4.0 ± 0.9 | 3.4 | 2.3 ± 1.0 | 2.2 |
The two angles are the pitch and yaw of the ultrasound probe about which the displacement vectors were rotated when assigning Dirichlet boundary conditions. The mean and standard deviation of the boundary node error and the mean centroid distance were calculated in comparing each corrected simulation tumor with the original un-compressed tumor.
Mean ± SD.
Phantom experiments
The baseline accuracy test using the cup phantom provided an assessment of the best alignment of tracked ultrasound and CT that could be achieved using only tracking and point-based registration. By use of the 116 images from this test, the MHD between the B-mode and CT tumor contours was 1.2 ± 0.4 mm, and the average centroid error was 1.7 ± 0.6 mm. Additionally, the tumor volume enclosed by the ultrasound contours was found to be approximately 3.0 cm3, whereas the volume given by the CT segmentation was 3.3 cm3. For comparison, the volume of PVA mixture used for the tumor during construction was 3.2 cm3.
The results of the phantom experiments are illustrated in Figures 6 and 7. Figure 4 provided an example of the FEM mesh of the phantom organ in its original un-deformed state, as well as in its deformed state after the probe compression has been modeled for a particular ultrasound slice. We note qualitatively that the displacements displayed by the model match very well those observed in the physical phantom during data acquisition. In Figure 6 are examples of B-mode and strain images before and after compression correction using the rigid method and model-based method. The segmented tumor contour from each ultrasound image was outlined, and the CT tumor surface was overlaid for comparison. The MHD between the ultrasound borders and CT borders was 5.0 ± 1.6 mm for B-mode and 5.6 ± 1.1 mm for strain images before correction. The quantitative compression correction results in Figure 7 display the MHD and co-planar-centroid distances as error metrics in comparing the ultrasound tumor borders with the co-registered CT tumor borders. A Wilcoxon signed rank test was also computed for the null hypothesis that the median difference between the error metrics was zero. The alternative was that the median was not zero, with the implication that the correction method offered a statistically significant improvement to the data. The number of samples for each test was the number of corrected ultrasound images. In results not presented here, we also assessed the effect of discarding image slices that were within 1.5 mm (approximately the tracking system accuracy) of the previous slice in the image stream to enforce uniqueness of each observation in the statistical analysis, but no differences were observed in the resulting p-values compared with the use of every image, and so we included all images for the Wilcoxon tests (recall n = 178 B-mode and n = 83 strain).
Fig. 6.
Examples of B-mode (a–c) and strain image (d–f) contours. (a, d) Uncorrected images in 3-D space with the segmented tumor contour in red and the tomogram tumor volume in green. (b, e) Alignment after the rigid correction method. (c, f) Alignment after the model-based correction method.
Fig. 7.
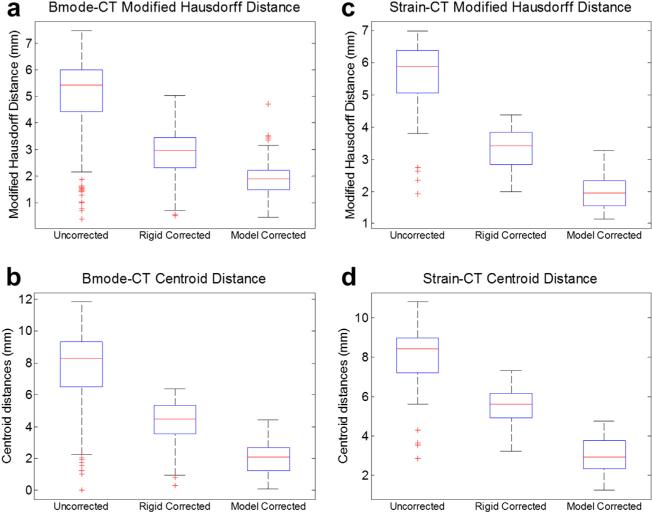
Alignment error results for the B-mode (a, b) and strain imaging (c, d) modalities for the organ-like phantom (n = 178 for B-mode, n = 83 for strain). The position of tumor borders in each modality was evaluated in terms of modified Hausdorff distance to the co-aligned computed tomography borders (a, c), as well as the distance between the centroid of the ultrasound tumor and the co-planar CT tumor border (b, d). The edges of the boxes are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points not considered as outliers.
With respect to contour boundary metrics, after the rigid correction, the MHD for the B-mode images dropped to approximately 2.8 ± 0.9 mm, which was a significant improvement (p < 0.01). The rigid correction also significantly improved the alignment of the contours in the strain images using this metric with an error of 3.3 ± 0.6 mm (p < 0.01). In the case of the model correction, the MHD was reduced to approximately 1.9 ± 0.6 mm for B-mode and 2.0 ± 0.5 mm for strain images. The model-based correction was found to make a significant improvement to the data compared with both the uncorrected and rigid-corrected data (p < 0.01).
With respect to centroid metrics, the mean uncorrected centroid distance was approximately 7.6 ± 2.6 mm for B-mode and 8.0 ± 1.6 mm for strain images, which conformed to typical deformation values of up to 1 cm reported in soft anatomy by others (Artignan et al. 2004; Xiao et al. 2002). After application of the rigid correction, the mean centroid distance was reduced to 4.3 ± 1.3 mm in B-mode images and was only reduced to 5.4 ± 0.9 mm in strain images, but was still significant according to the Wilcoxon test (both improved with p < 0.01). After application of the model-based correction, the mean centroid error was reduced to 2.0 ± 0.9 mm for B-mode and 3.0 ± 0.9 mm for strain images—a significant improvement over the uncorrected and rigid-corrected data (both p < 0.01).
The tumor volumes enclosed by the rigid-corrected and model-corrected ultrasound B-mode contours were found to be approximately 3.2 and 3.8 cm3 for this phantom, respectively, and the volumes enclosed in the rigid-corrected and model-corrected strain images were 2.5 and 2.9 cm3. Recall that in the baseline accuracy test using the cup phantom, the tumor volume (made from the same mold) was measured with tracked B-mode as 3.0 cm3, and the tumor mold was measured as 3.2 cm3.
The last phantom experiment was the comparison of model correction with the assumption of a tumor:bulk stiffness ratio of 1:1 against the known 9:1 ratio. These results are compiled in Table 2 and indicate that there was no measureable difference in how much the tumor border was corrected when the actual 9:1 ratio was used.
Table 2.
Results of phantom elasticity test comparing the effect on model correction of the assumption of a 1:1 tumor:bulk stiffness ratio against the known 9:1 stiffness ratio from material testing
| 1:1 Stiffness ratio |
9:1 Stiffness ratio |
|||
|---|---|---|---|---|
| MHD error (mm) | Centroid error (mm) | MHD error (mm) | Centroid error (mm) | |
| B-mode (n = 178) | 1.9 ± 0.6 | 2.0 ± 0.9 | 1.8 ± 0.8 | 2.2 ± 1.0 |
| Strain (n = 83) | 2.0 ± 0.5 | 3.0 ± 0.9 | 1.9 ± 0.5 | 3.1 ± 0.9 |
Clinical case
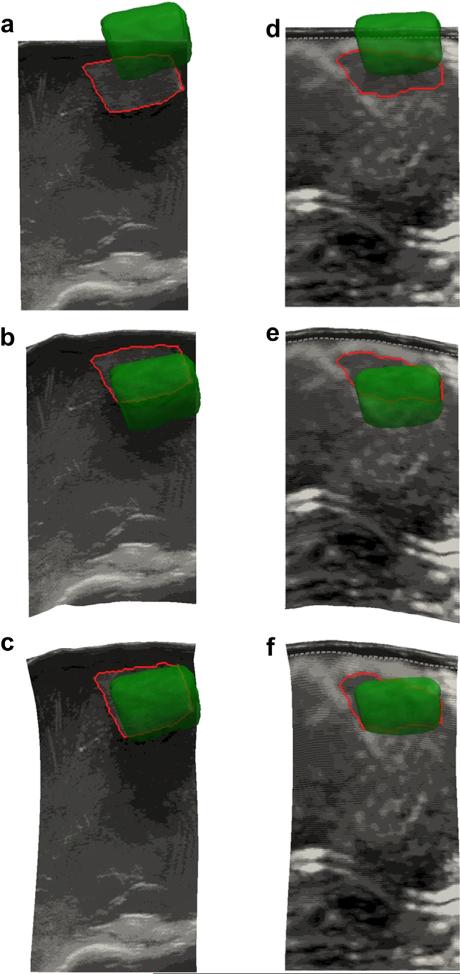
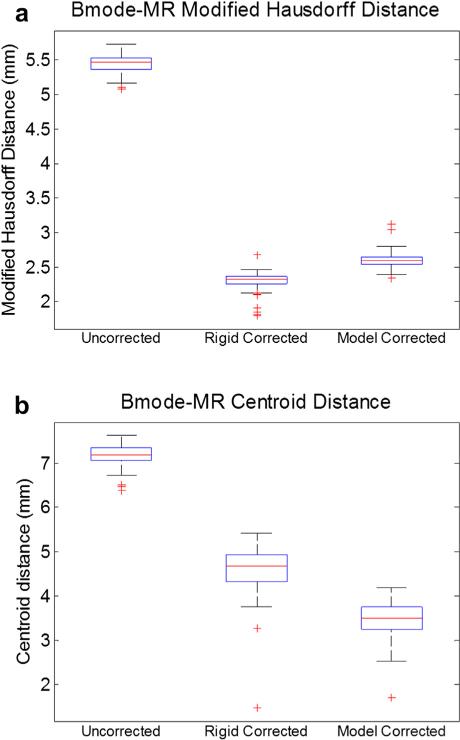
The results of the clinical case are illustrated in Figures 8 and 9. Figure 8 is an example of a B-mode image before and after compression correction using the rigid method and model-based method. The segmented tumor border in each ultrasound image was outlined for comparison with the co-aligned MR tumor surface. Quantitative compression correction results are illustrated in Figure 9 in the same manner as the phantom studies, with the error metrics being the MHD and co-planar centroid distances. The MHD error before any correction was approximately 5.4 ± 0.1 mm, and the average centroid error was approximately 7.2 ± 0.2 mm. A Wilcoxon signed rank test was also computed to assess the significance of the improvement offered by each method. The rigid and model-based corrections both offered substantial improvement compared with the uncorrected alignment (both p < 0.01) across the two error metrics. The rigid correction resulted in a reduced MHD error of 2.3 ± 0.1 mm and centroid distance error of 4.6 ± 0.5 mm, whereas the model-based correction resulted in an MHD error of 2.6 ± 0.1 mm and centroid distance error of 3.5 ± 0.4 mm. Because of the difficulty in maneuvering the large ultrasound probe in the craniotomy of this patient, only a few angles of insonation were achieved and so a meaningful ultrasound tumor volume could not be constructed.
Fig. 8.
Results of the clinical case in which tracked B-mode was used to localize a tumor border. Coronal and axial views are provided for no correction (a, b), rigid correction (c, d) and model correction (e, f), with the segmented tumor contour in red and the tomogram tumor volume in green. The segmented tumor surface in each B-mode slice is outlined for comparison with the magnetic resonance image tumor surface.
Fig. 9.
Alignment error results for the clinical case (n = 118 B-mode images). The position of tumor borders was evaluated in terms of modified Hausdorff distance to the co-aligned magnetic resonance image borders (a), as well as the distance between the centroid of the ultrasound tumor and the co-planar MR tumor border (b). The edges of the boxes are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points not considered as outliers.
DISCUSSION
Simulations
The results of the compression correction simulations in Table 1 illustrate the effect of deviating from the assumption that the user would always apply compression purely in the depth direction of the ultra-sound image. As expected, when the displacement vectors were actually parallel to depth (θ1 and θ2 of 0°), the model-based correction method essentially resulted in a corrected tumor that was equivalent to the original un-compressed tumor. The rigid correction method resulted in several millimeters of error in terms of both the tumor boundary and centroid location. However, when the displacement vectors used to create the simulated deformation were rotated to approach the probe surface from a different set of surface nodes (see Fig. 5), the average boundary node error after both corrections grew. The performance variations caused by the different angles can be attributed to the assumption made in assigning boundary conditions to the FEM, which is that the insertion trajectory of the probe into the tissue is perfectly parallel to the depth direction of the ultrasound images. The results in Table 1 indicate the sensitivity of the method to physical deviations from that assumption. Essentially, when the insertion trajectory is not perfectly perpendicular to the tissue surface, then the method creates inappropriate boundary conditions, which leads to model solutions that do not accurately reflect the actual tissue movement. These numbers represent a large error addition to an image-guidance platform, especially in procedures such as neurosurgery. It could be concluded that it is important that the user apply the probe primarily in the depth direction of the image plane for this compression correction method to be effective. This may not be a large limitation in practice, however, because of the typical presence of slip between the probe and tissue surface from ultrasound gel or other fluids. This would conceivably make it unlikely for the ultra-sound probe to apply enough friction to the tissue surface necessary for the “dragging” effect, which is described by the scenarios simulated above, in which the probe trajectory into the tissue is off-axis from the depth direction.
Phantom experiments
The results of the baseline accuracy test indicate that the tracked ultrasound system is capable of aligning the ultrasound and CT tumor borders with error between 1 and 2 mm when tissue compression is not a factor. This represents the best outcome that could potentially be expected from our correction. In addition, the tumor volume measured by tracked B-mode was quite similar to both the volume measured from the tumor mold and the CT volume.
The results of the compression correction methods illustrated in Figure 7 clearly indicate the improvement of the model-based method to the alignment between ultrasound and co-registered tomograms in the phantom experiments. The MHD error metric exhibits a decrease in misalignment after application of the rigid method and a further decrease when the model-based method is used instead. The varying magnitude in improvement between B-mode and strain image when using the rigid method highlights the differences in contrast mechanism between the two modalities, as well as the lack of tumor shape change, which both contribute to the delineation of mock tumor borders in this case. However, after application of the model-based compression correction, both modalities yield similar MHD error values. This indicates that shape change of the inclusion is significant and needs to be taken into account when correcting guidance systems. One interesting effect of the correction was the increase in B-mode tumor volume after model correction to 3.8 cm3, which is a slight overestimate compared with the tumor mold and CT volumes and is likely due to the stretching effect of the model displacements. The model-corrected strain volume was actually an underestimate of the volume, but this was primarily related to the sparser manner in which those images were collected to avoid out-of-plane movement. The discrepancy in rigid-corrected tumor volumes compared with the uncorrected volume was due to the movement of the tumor contours in non-uniform directions determined by the freehand insonation angles for the slices.
After application of the model correction, the centroid distance error metric exhibited an even clearer improvement compared with the uncorrected ultrasound images. A similar trend was again noted with respect to the rigid correction in that a modest improvement in both error metrics was observed, and model-based correction resulted in a large correction in both modalities. It can be seen that the rigid correction caused a slightly larger improvement in B-mode images than in strain images. This again points to the significance of contrast and shape change factors in our study. Overall, the results indicated that although the rigid method occasionally led to a modest improvement, the model-based correction consistently led to significant reduction in alignment error.
Clinical case
The results of the clinical case indicated a clear improvement in alignment between the tracked B-mode tumor and MR tumor borders, as illustrated in Figures 8 and 9. Interestingly, the rigid correction was slightly more effective than expected in improving the alignment given the results of the previous phantom experiments, which may be related to the location and structure of the tumor in this particular case. The model-based correction did offer a large improvement to alignment, especially along the region of the tumor closest to the surface, as illustrated Figure 8(d, f). One important note about this case was that the pre-operative brain surface was not updated to account for general intra-operative brain shift that may have occurred before applying our ultrasound compression correction methods. Typically our group employs a model-based shift correction driven by sparse surface data from a LRS or other instrumentation to update the pre-operative imaging to reflect intra-operative sag or swelling of the brain (Cao et al. 2008; Ding et al. 2011; Simpson et al. 2013a). However, qualitatively there was little brain shift observed at the time of ultrasound acquisition for this patient before resection of the dural membrane, so no LRS data were obtained so as to limit the amount of intra-operative data collected for this case. It is possible that there was some quantifiable amount of brain shift before the ultra-sound acquisition, which would directly affect our correction method and could be reflected in the error metrics reported in Figure 9. In the future, the pre-operative brain surface would ideally be corrected for brain shift before collection and correction of ultrasound data.
Limitations
It is worthwhile to note that although the model-based correction exhibited a marked improvement over the uncorrected alignment in both the phantoms and clinical case, the gold standard used in this comparison (the co-registered tomogram borders) had some bulk-to-lesion segmentation variability. It was also likely that because of our realistic guidance environment, several sources of error propagated through to the final analysis. For example, the optical tracking system used in this work had inherent error, which was imparted to each measurement made with a tracked device and was a primary contributor to the overall error. Propagating uncertainty in optical tracking is an open problem. We have recently proposed a solution to this problem (Simpson et al. 2011) and are working on an empirical evaluation (Simpson et al. 2013b) with encouraging results. The tracking error of our tracking system has been reported to have a root mean square error of approximately 0.2 mm when tracking a passive rigid body, although typically the tip of a stylus-like tool that is subject to lever-arm effects can be localized at 1 to 2 mm (Glossop 2009; Wiles et al. 2004). This influences fiducial localization error (FLE), which affects the accuracy of the image-to-physical registration between tomogram and tracked ultrasound data. Although fiducial localization errors can be difficult to directly quantify, the mean fiducial registration error in our phantom experiments was calculated as 0.4 ± 0.3 mm for the phantoms. It should be noted this error represents only the accuracy with which the fiducial markers in the tomograms could be matched to the physical fiducials localized with a pen probe, and does not necessarily imply that the target registration error throughout the phantoms was the same value. In addition, there was error associated with the tracked ultrasound calibration, which was found to be approximately 0.4 mm using the method of Muratore and Galloway (2001). It should be noted that the errors discussed above are somewhat inter-related and not necessarily additive, but in our experience a reasonable estimate of the error involved in using a passively tracked ultrasound system ranges from 1.5 to 2.5 mm.
There were also several assumptions and simplifications made in the development of the rigid and model-based corrections. Regarding the rigid correction, it would be intuitively more accurate to stretch the A-lines to approximate the deformation rather than simply translate them. However, without a known reference in the far field, it is difficult to choose an appropriate bounding condition as there is no guarantee of having a known fixed object in view. In the case of the model-based correction, the first assumption was that the user would apply the probe purely in the depth direction for each image acquisition. This simplified the creation of boundary conditions for the model, but this was not always accurate. It was challenging to avoid lateral and out-of-plane probe movement during freehand imaging. This type of movement would invalidate the assignment of Dirichlet boundary conditions based on the position of the digital probe surface, because the correspondence between the probe surface and the tomogram surface could potentially be lost in the absence of perfect slip at the boundary. The other assumption was the assignment of material properties to the FEM mesh. Overall, material properties are largely irrelevant in our approach because the model is driven by only Dirichlet conditions, and thus, only large stiffness ratios between tissue regions might have an effect. Absolute values for Young’s modulus do not affect the displacement solution in the scenarios described in this work, and Poisson’s ratio affects it only slightly. Possible future incorporation of force measurements into the model, however, would indicate a need for accurate material properties. In our phantom experiments, there was prior knowledge of the phantom material properties from mechanical testing data, and using the known properties was not shown to improve the correction. The phantoms were also highly homogenous compared with real tissue. In translating this method to the clinic, there is the challenge of assigning appropriate property values throughout the mesh. It is well recognized that determining patient-specific material properties in vivo is difficult, so one solution that has been employed is to use values from the literature, as well as those deduced through optimization experiments (Dumpuri et al. 2007). Lastly, one simplification that was made was the use of a simple linear elastic model to describe tissue movement. More sophisticated governing equations that better capture soft tissue mechanics could be employed to estimate displacements, such as Biot’s consolidation theory in the case of brain tissue (Nagashima et al. 1990; Paulsen et al. 1999). However, with added complexity comes added computational and integration burden that can affect adoption, yet despite these sources of model error, the improvement we found using this simple model was considerable. The model-based method offered consistent alignment error reductions of between 4 and 6 mm; that is, the final alignment error was approximately 2 mm, which has clinical utility in the case of brain, liver and breast surgery. These results suggest that our approach is a meaningful improvement to the utility of tracked ultrasound in image-guided surgery. In addition, anatomy with well-defined constitutive frameworks may provide an opportunity to improve this performance.
Other improvements can be made with respect to work flow. Currently, the correction cannot be run at real-time frame rates given that the model solution takes several seconds to calculate on an Intel i7 processor. However, updated ultrasound images can be provided in less than 10 s, which is not an unreasonable burden on normal surgical work flow. The system could potentially be made real time with the proper hardware and parallelization methods. Our method also made no use of the actual ultrasound images themselves to assist in realignment. One possible addition would be the utilization of either raw radiofrequency or B-mode pixel values to generate displacement fields by comparing frames in close proximity to one another and performing deformable registration, as other groups have proposed (Treece et al. 2005; Xiao et al. 2002). The inclusion of these smaller displacements could help address small inaccuracies caused by the tracking system, while still making use of the biomechanical model to provide an estimate of bulk displacements.
CONCLUSIONS
In this work we proposed and validated two very practical methods for correcting alignment error caused by tissue compression exerted by an ultrasound probe within the context of image-guided therapy. In one method, a simple rigid correction was applied. In a second more sophisticated method, patient-specific models were used to estimate physical tissue deformation as the direct result of pressing the tracked probe to the tissue surface. These model solutions were then used to transform the ultrasound images to an un-deformed state for assessing pathology. The method was validated in simulations, phantoms and a preliminary clinical case and indicated that alignment of freehand tracked ultrasound with co-registered tomographic images was improved to within clinically useful margins. Experimental results indicate that integration of this correction method into conventional image-guided therapeutic platforms could assist the clinicians in decision making by providing more accurate intra-operative data.
Acknowledgments
This work was supported in part by the National Institutes of Health award R01 NS049251 of the National Institute for Neurological Disorders and Stroke, and by the National Institute of Health award R01 CA162477 from the National Cancer Institute.
REFERENCES
- Artignan X, Smitsmans MH, Lebesque JV, Jaffray DA, van Her M, Bartelink H. Online ultrasound image guidance for radio-therapy of prostate cancer: Impact of image acquisition on prostate displacement. Int J Radiat Oncol Biol Phys. 2004;59:595–601. doi: 10.1016/j.ijrobp.2004.01.043. [DOI] [PubMed] [Google Scholar]
- Blackall JM, Rueckert D, Maurer CR, Penney GP, Hill DLG, Hawkes DJ. An image registration approach to automated calibration for freehand 3D ultrasound.. Lecture Notes in Computer Science; Medical Image Computing and Computer-Assisted Intervention—Miccai 2000:Third International Conference; Pittsburgh, Pennsylvania. 11–14 October 2000; Berlin/Heidelberg: Springer; 2000. pp. 462–471. [Google Scholar]
- Boctor EM, Iordachita I, Choti MA, Hager G, Fichtinger G. Bootstrapped ultrasound calibration. Stud Health Technol Inform. 2006;119:61–66. [PubMed] [Google Scholar]
- Boisvert J, Gobbi D, Vikal S, Rohling R, Fichtinger G, Abolmaesumi P. An Open-Source Solution for Interactive Acquisition, Processing and Transfer of Interventional Ultrasound Images. The MIDAS Journal - Systems and Architectures for Computer Assisted Interventions. 2008 [Google Scholar]
- Burcher MR, Lianghao H, Noble JA. IEEE Workshop on Mathematical Methods in Biomedical Image Analysi—MMBIA 2001. IEEE; New York: 2001. Deformation correction in ultra-sound images using contact force measurements. pp. 63–70. [Google Scholar]
- Cao A, Thompson RC, Dumpuri P, Dawant BM, Galloway RL, Ding S, Miga MI. Laser range scanning for image-guided neurosurgery: Investigation of image-to-physical space registrations. Med Phys. 2008;35:1593–1605. doi: 10.1118/1.2870216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen I, Coffey AM, Ding SY, Dumpuri P, Dawant BM, Thompson RC, Miga MI. Intraoperative brain shift compensation: Accounting for dural septa. IEEE Trans Biomed Eng. 2011;58:499–508. doi: 10.1109/TBME.2010.2093896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffey AM, Miga MI, Chen I, Thompson RC. Toward a preoperative planning tool for brain tumor resection therapies. Int J Comput Assist Radiol Surg. 2013;8:87–97. doi: 10.1007/s11548-012-0693-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding SY, Miga MI, Pheiffer TS, Simpson AL, Thompson RC, Dawant BM. Tracking of vessels in intra-operative microscope video sequences for cortical displacement estimation. IEEE Trans Biomed Eng. 2011;58:1985–1993. doi: 10.1109/TBME.2011.2112656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubuisson MP, Jain AK. Proceedings, 12th IAPR International Conference on Pattern Recognition:Vol. 1, Conference A. Computer Vision and Image Processing. IEEE; New York: 1994. A modified Hausdorff distance for object matching. pp. 566–568. [Google Scholar]
- Dumpuri P, Thompson RC, Dawant BM, Cao A, Miga MI. An atlas-based method to compensate for brain shift: Preliminary results. Med Image Anal. 2007;11:128–145. doi: 10.1016/j.media.2006.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fromageau J, Gennisson JL, Schmitt C, Maurice RL, Mongrain R, Cloutier G. Estimation of polyvinyl alcohol cryogel mechanical properties with four ultrasound elastography methods and comparison with gold standard testings. IEEE Trans Ultrason Ferroelectr Freq Control. 2007;54:498–509. doi: 10.1109/tuffc.2007.273. [DOI] [PubMed] [Google Scholar]
- Glossop ND. Advantages of optical compared with electromagnetic tracking. J Bone Joint Surg Am. 2009;91(Suppl 1):23–28. doi: 10.2106/JBJS.H.01362. [DOI] [PubMed] [Google Scholar]
- Hsu PW, Prager RW, Gee AH, Treece GM. Real-time freehand 3 D ultrasound calibration. Ultrasound Med Biol. 2008a;34:239–251. doi: 10.1016/j.ultrasmedbio.2007.07.020. [DOI] [PubMed] [Google Scholar]
- Hsu PW, Treece GM, Prager RW, Houghton NE, Gee AH. Comparison of freehand 3-D ultrasound calibration techniques using a stylus. Ultrasound Med Biol. 2008b;34:1610–1621. doi: 10.1016/j.ultrasmedbio.2008.02.015. [DOI] [PubMed] [Google Scholar]
- King AP, Blackall JM, Penney GP, Edwards PJ, Hill DLG, Hawkes DJ. Bayesian estimation of intra-operative deformation for image-guided surgery using 3-D ultrasound.. Lecture Notes in Computer Science; Medical Image Computing and Computer-Assisted Intervention—Miccai 2000:Third International Conference; Pittsburgh, Pennsylvania. 11–14 October 2000; Berlin/Heidelberg: Springer; 2000. pp. 588–597. [Google Scholar]
- Mercier L, Lango T, Lindseth F, Collins DL. A review of calibration techniques for freehand 3-D ultrasound systems. Ultrasound Med Biol. 2005;31:449–471. doi: 10.1016/j.ultrasmedbio.2004.11.015. [DOI] [PubMed] [Google Scholar]
- Miga M, Paulsen K, Kennedy F, Hoopes J, Hartov A, Roberts D. Initial in-vivo analysis of 3 D heterogeneous brain computations for model-updated image-guided neurosurgery.. Lecture Notes in Computer Science; Medical Image Computing and Computer-Assisted Intervention—Miccai 1998: First International Conference; Cambridge, Massachusetts. 11–13 October 1998; Berlin/Heidelberg: Springer; 1998a. pp. 743–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miga MI. Thesis. Department of Engineering, Dartmouth College; Hanover, NH: 1998. Development and quantification of a 3 D brain deformation model for model-updated image-guided stereotactic neurosurgery. [Google Scholar]
- Miga MI, Paulsen KD, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. Modeling surgical loads to account for subsurface tissue deformation during stereotactic neurosurgery. IEEE SPIE. 1998b;3254:501–511. doi: 10.1109/10.740884. [DOI] [PubMed] [Google Scholar]
- Miga MI, Paulsen KD, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. In vivo analysis of heterogeneous brain deformation computations for model-updated image guidance. Comput Methods Biomech Biomed Eng. 2000;3:129–146. doi: 10.1080/10255840008915260. [DOI] [PubMed] [Google Scholar]
- Miga MI, Paulsen KD, Lemery JM, Eisner SD, Hartov A, Kennedy FE, Roberts DW. Model-updated image guidance: Initial clinical experiences with gravity-induced brain deformation. IEEE Trans Med Imaging. 1999;18:866–874. doi: 10.1109/42.811265. [DOI] [PubMed] [Google Scholar]
- Muratore DM, Galloway RL. Beam calibration without a phantom for creating a 3-D freehand ultrasound system. Ultrasound Med Biol. 2001;27:1557–1566. doi: 10.1016/s0301-5629(01)00469-0. [DOI] [PubMed] [Google Scholar]
- Nagashima T, Shirakuni T, Rapoport SI. A two-dimensional, finite element analysis of vasogenic brain edema. Neurol Med Chir (Tokyo) 1990;30:1–9. doi: 10.2176/nmc.30.1. [DOI] [PubMed] [Google Scholar]
- Pace D, Gobbi D, Wedlake C, Gumprecht J, Boisvert J, Tokuda J, Hata N, Peters T. An open-source real-time ultrasound reconstruction system for four-dimensional imaging of moving organs.. Lecture Notes in Computer Science; Medical Image Computing and Computer-Assisted Intervention—Miccai 2009:Third International Conference; Pittsburgh, Pennsylvania. 11–14 October 2009; Berlin/Heidelberg: Springer; 2009. 2009. [Google Scholar]
- Paulsen KD, Miga MI, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery. IEEE Trans Biomed Eng. 1999;46:213–225. doi: 10.1109/10.740884. [DOI] [PubMed] [Google Scholar]
- Pheiffer TS, Simpson AL, Lennon B, Thompson RC, Miga MI. Design and evaluation of an optically-tracked single-CCD laser range scanner. Med Phys. 2012;39:636–642. doi: 10.1118/1.3675397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson AL, Burgner J, Glisson CL, Herrell SD, Ma B, Pheiffer TS, Webster RJ, Miga MI. Comparison study of intraoperative surface acquisition methods for surgical navigation. IEEE Trans Biomed Eng. 2013a;60:1090–1099. doi: 10.1109/TBME.2012.2215033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson AL, Dillon NP, Miga MI, Ma B. A framework for measuring TRE at the tip of an optically tracked pointing stylus. SPIE Medical Imaging: International Society for Optics and Photonics. 2013b:867114–1–867114-6. [Google Scholar]
- Simpson AL, Ma B, Ellis RE, Stewart J, Miga MI. Uncertainty propagation and analysis of image-guided surgery. Proceeings of SPIE medical imaging: visualization, image-guided procedures, and modeling. 2011;7964:79640, H-7. [Google Scholar]
- Sullivan JM, Charron G, Paulsen KD. A three-dimensional mesh generator for arbitrary multiple material domains. Finite Elem Anal Des. 1997;25:219–241. [Google Scholar]
- Sun S-Y, Anthony BW, Gilbertson MW. D'hooge J, McAleavey SA, editors. Trajectory-based deformation correction in ultrasound images. Proceedings of SPIE, Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy. 7629:76290A–1–76290A-9. [Google Scholar]
- Surry KJ, Austin HJ, Fenster A, Peters TM. Poly(vinyl alcohol) cryogel phantoms for use in ultrasound and MR imaging. Phys Med Biol. 2004;49:5529–5546. doi: 10.1088/0031-9155/49/24/009. [DOI] [PubMed] [Google Scholar]
- Treece GM, Gee AH, Prager RW. RF and amplitude-based probe pressure correction for 3 D ultrasound. Ultrasound Med Biol. 2005;31:493–503. doi: 10.1016/j.ultrasmedbio.2004.12.018. [DOI] [PubMed] [Google Scholar]
- Wiles AD, Thompson DG, Frantz DD. Galloway RL Jr., editor. Accuracy assessment and interpretation for optical tracking systems. Proceedings of SPIE Vol. 5367, Medical Imaging 2004: Visualization, Image-Guided Procedures, and Display. 2004:421–432. [Google Scholar]
- Xiao G, Brady JM, Noble JA, Burcher M, English R. Nonrigid registration of 3-D free-hand ultrasound images of the breast. IEEE Trans Med Imaging. 2002;21:405–412. doi: 10.1109/TMI.2002.1000264. [DOI] [PubMed] [Google Scholar]