In vivo Loads in the Lumbar L3-4 Disc during a Weight Lifting Extension

Abstract

Background

Knowledge of in vivo human lumbar loading is critical for understanding the lumbar function and for improving surgical treatments of lumbar pathology. Although numerous experimental measurements and computational simulations have been reported, non-invasive determination of in vivo spinal disc loads is still a challenge in biomedical engineering. The object of the study is to investigate the in vivo human lumbar disc loads using a subject-specific and kinematic driven finite element approach.

Methods

Three dimensional (3D) lumbar spine models of three living subjects were created using MR images. A 3D finite element model of the L3-4 disc, including the annulus fibrosus and nucleus pulposus, was built for each subject. The endplate kinematics of the L3-4 segment of each subject during a dynamic weight lifting extension was determined using a dual fluoroscopic imaging technique. The endplate kinematics was used as displacement boundary conditions of the subject specific finite element model of the L3-4 disc to calculate the in-vivo disc forces and moments during the weight lifting activity.

Findings

During the weight lifting extension, the L3-4 disc experienced maximum shear load of about 230 N or 0.34 bodyweight at the flexion position and maximum compressive load of 1500 N or 2.28 bodyweight at the upright position. The disc experienced a primary flexion-extension moment during the motion which reached a maximum of 4.2 Nm at upright position with stretched arms holding the weight.

Interpretation

This study provided quantitative data on in vivo disc loading that could help understand intrinsic biomechanics of the spine and improve surgical treatment of pathological discs using fusion or arthroplasty techniques.

Introduction

Knowledge on in vivo loadings of human lumbar spine is critical for understanding the lumbar function and for improving surgical treatments of lumbar pathology such as using pedicle screws, fusion, disc replacement, etc. (Rohlmann et al., 2000, Rohlmann et al., 2009a, Abe et al., 1999, Kumar et al., 2005). Numerous studies have investigated spinal loads using experimental measurements and computational simulations (Wilke et al., 1999, Nachemson, 1981, Shirazi-Adl et al., 2005, Kim et al., 2011, Rohlmann et al., 2009b, Shirazi-Adl, 1994a, Shirazi-Adl, 2006, Arjmand et al., 2011, Arjmand et al., 2012). Pressure transducers have been inserted into the nucleus pulposus (NP) in living human volunteers during sitting, standing and other daily activities (Wilke et al., 1999, Andersson et al., 1977, Nachemson, 1981, Polga et al., 2004), while overall disc loads were calculated from the intradiscal pressure and the total effective area of the disc. Rohlmann et al.(Rohlmann et al., 2000) and Ledet et al.(Ledet et al., 2005) have also placed telemeterized force sensors into posterior fixation or inter-body space to measure the in vivo forces on the lumbar spine. Although invaluable information was obtained, these techniques are invasive and could be risky and cause pain and injury (Rohlmann et al., 2000, Wilke et al., 1999). To overcome the difficulties of in vivo measurements, inverse dynamic optimization methods have been widely used to estimate the spinal load during functional motions of the body (Park et al., 2012, Han et al., 1995, Goel et al., 1993, Shirazi-Adl et al., 2005, Kim et al., 2011, Shirazi-Adl, 1994a, Shirazi-Adl, 2006). In these computational simulations, in vivo spinal kinematics was determined and input into the equilibrium equations of the spine; the inter-segmental forces of each motion segment and the forces of the surrounding muscles were estimated through an optimization process to estimate the spinal loads (Park et al., 2012, Shirazi-Adl et al., 2005, Arjmand et al., 2009). A few musculoskeletal models for the lumbar spine were developed using commercial software (Han et al., 2013, Christophy et al., 2012, de Zee et al., 2007) to calculate the spinal joint loads and muscle forces. While the computational methods have the advantage to be non-invasive, various assumptions, such as of the abdominal pressure, upper body mass center, segment joint center, etc., in the model make it difficult to validate the predicted results (Park et al., 2012, El Ouaaid et al., 2009).

Recently, a subject specific, kinematic driven finite element (FE) modeling approach has been validated to investigate the internal disc loads using cadaveric specimens and showed that the spinal loads could be predicted within 20% of the applied loads (Wang et al., 2012). In this study, the method was applied to calculate in-vivo disc loads during a weight lifting extension activity of living human subjects. Subject specific 3D anatomic spine models were constructed using MR images of the spinal segments. Six DOF kinematics of the spinal segments under functional loads was measured using a dual fluoroscopic imaging method (Li et al., 2009) and used as displacement boundary conditions to the 3D FE disc model. We hypothesized that the disc would experience maximal loads in a flexed position than at standing position of the body during the weight lifting activity.

Material and Methods

Three healthy asymptomatic male subjects (mean age 48.3, standard deviation (SD) 2.4yrs; mean height 177.0, SD 4.3cm; mean weight 70.6, SD 7.4kg) were recruited in this study with institutional review board (IRB) approval and written consent. The subjects did not perform any intense activity before the scans. Each subject was MRI scanned in a supine position using a 3T scanner (MAGNETOM Trio, Siemens, Erlangen, Germany) with a spine surface coil and a T2-weighted fat suppressed 3D spoiled gradient recall (SPGR) sequence for 3D vertebral model construction (TR: 3430ms; TE: 24ms; slice thickness: 1mm; bandwidth: 300-500Hz; echo-train: 7; FOV: 30cm, 512×512 resolution; duration: approximately 10 minutes). The MRI images were directly input in a commercial solid modeling software (Rhinoceros, Robert McNeel & Associates, Seattle, WA, USA) for 3D model reconstruction (Wang et al., 2008). The contours of the vertebrae and the intervertebral disc were digitized manually using B-Spline curves. Mesh models of the vertebrae were then created from the contour lines. A coordinate system was created for each disc. A transverse plane was determined by fitting a plane through the lower disc endplate. A mid-sagittal plane was determined by left-right symmetry of the disc. The direction of anterior-posterior axes was along the intersection of the two planes. The left-right and proximal-distal axis were perpendicular to the anterior-posterior direction and in the transverse and mid-sagittal plane, respectively.

After the MRI scan, each subject performed weight lifting of 15 lbs (67 N) using two hands, with 8 lbs in the right and 7 lbs in the left hands (Fig. 1) to simulate functional daily activities. The starting position was approximately 45° of flexion of the upper body from the vertical direction and the ending position was maximum extension about 20° from the vertical line. There were minimum motion in the arm and shoulder of the subject during the lifting activity. Therefore, at the upright position, the subject held the weights with the arms extended horizontally, similar to the extended arm position tested by Andersson et al. (Andersson et al., 1976).

Fig 1.

Weight lifting flexion-extension activity by holding 15lb dumbbells. a) Flexion; b) up-right standing; and c) maximal extension positions

The entire activity took about 3 seconds, while Images of the lumbar spine along the motion path were captured by a dual fluoroscopic imaging system (DFIS) at 30 frames per second with a pulse width of 8 millisecond (Wang et al., 2008, Li et al., 2009). The typical fluoroscopic setting for dynamic spine imaging is 77 kV and 13 mAs. Our Radiation Safety Committee estimated the overall radiation dosage during each lifting activity is about 0.4 mSv.

The virtual setup of the DFIS was reproduced in the Rhinoceros software. Pairs of fluoroscopic images of the spine were placed in calibrated orthogonal planes, reproducing the actual positions of the image intensifiers of the fluoroscopes. Two virtual cameras were created inside the virtual space to reproduce the positions of the X-ray sources with respect to the image intensifiers. The MR image-based 3D vertebral models were introduced into the virtual fluoroscopic system and viewed from the perspective views of the two virtual cameras. The 3D models of each vertebra could be independently translated and rotated in 6DOF until their projections match the osseous outlines captured on the two orthogonal fluoroscopic images (Wang et al., 2008, Li et al., 2009). The mean accuracy of our technique in determining translation has been shown to be 0.40 mm for the image matching technique. The repeatability of the method in reproducing in vivo human spine 6DOF kinematics was less than 0.3 mm in translation and less than 0.7° in orientation (Wang et al., 2008). The relative motion of the superior endplate with respect to the inferior endplate of the disc was determined at each motion segment unit (Wang et al., 2009) (Fig. 2). Three positions along the motion path were chosen for the FE analysis: Flexion (about half a second after the initial lifting, about 20° flexion), Upright position, and Extension (maximal extension of the body, about 20° extension).

Fig 2.

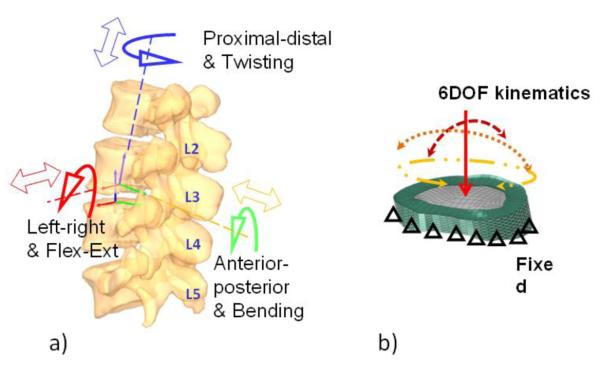
a) Determination of the 6 DOF kinematics of the disc endplates. b) Application of displacement boundary conditions in FE disc model

In this study, the L3-4 motion segment was analyzed. Subject specific FE models of the L3-4 disc were created using hexahedral elements from the 3D MR scans. The models consist of four parts (Wang et al., 2012, Rohlmann et al., 2009a, Rohlmann et al., 2006, Rohlmann et al., 2005, Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984): the NP, the annulus ground matrix (AG), the annulus fibres (AF), and the endplates (Table 1). The NP was estimated to occupy 40% volume of the whole disc and modeled as an incompressive hydraulic fluid with initial pressure of 70 kPa (Rohlmann et al., 2006, Rohlmann et al., 2009a, Rohlmann et al., 2005, Nachemson and Evans, 1968). The AG was divided into eight layers and was modeled as a hyper-elastic solid (Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984). Eight layers of AFs were inserted into the outer surface and between each two layers of the AG. Based on the anatomy, the angles between the AF and disc endplates were set to be 30° and 150° (Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984). The diameter of the AFs was set so to occupy 16% of the overall cross section area of the annulus to simulate a physiological condition (Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984). The AFs were modeled using tension only truss elements with a stiffness decreasing from outer to inner annulus layers (Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984). Inferior and superior endplates were modelled as rigid plates. The material properties of the disc were adopted from those widely used in the literature (Wang et al., 2012, Rohlmann et al., 2009a, Rohlmann et al., 2006, Rohlmann et al., 2005, Polikeit et al., 2003, Smit et al., 1997, Goel et al., 1995, Shirazi-Adl et al., 1984). There were totally about 10,000 elements and 4,000 nodes in each L3-4 disc model (Wang et al., 2012).

Table 1.

Material properties used in FE disc models

	Type of element		Elastic modulus (MPa)	Poisson’s ratio
Nucleus pulposus *	Hydraulic fluid element		-	-
Annulus ground matrix **	Neo-Hookean  Hexahedral solid element C10=0.348, D1=0.3		-	-
Annulus fibres ***	Tension only elastic truss element	Layers 1,2	550	0.3
		Layers 3,4	495	0.3
		Layers 5,6	421.5	0.3
		Layers 7,8	357.5	0.3
Endplates	Rigid shell element		-	-

^*Rohlmann, et al. 2005, Rohlmann, et al. 2006, Rohlmann, et al. 2009b

^**Rohlmann, et al. 2006

^***Shirazi-Adl, et al. 1984, Goel, et al. 1995, Smit, et al. 1997, Polikeit, et al. 2003

For the kinematic driven FE analysis, the inferior endplate was fixed in space, and the relative motion of the superior endplate during the weight lifting activity was input as the displacement boundary conditions (Fig. 2b). The forces and moments were calculated with respect to the coordinate system at the center of the disc using the Abaqus 6.10/Standard FE code (Simulia, Providence, RI, USA). Since the flexion-extension motion was rather slow, a quasi-static analysis was adopted to simulate the equilibrium of the motion segment at each selected position of the lumbar spine (Wang et al., 2012). The non-weightbearing supine position during the MRI scan was used as a reference position, where the forces and moments in the disc were assumed to be zero.

This kinematic driven FE simulation technique has been rigorously validated previously using a cadaveric setup and demonstrated that the forces and moments in all three principal directions could be predicted with an average error less than 20% (Wang et al., 2012). In this paper, we calculated intradiscal pressure; reaction forces and moments at each of the selected body positions of the 3 subjects.

Results

In vivo 6DOF displacement boundary conditions

The 6DOF displacement boundary conditions were similar, but with different magnitudes among the 3 subjects (Table 2). The anterior shear displacement was the largest at the flexion position among the 3 subjects (0.5 to 2.2mm). However, the maximum compression of the L3-4 was 1.4 to 1.7mm occurred at the upright position (Table 2). The average segmental range of flexion-extension motion was from 2.1 to 5.1° of the 3 subjects.

Table 2.

6DOF kinematic input boundary conditions

	Translation (mm)			Rotation (deg)
	left(+) right(−)	posterior(+) anterior(−)	proximal(+) distal (−)	flexion(+) extension(−)	left(+) right(−) bend	left(+) right(−) twist
Subject #1
flexion	1.39	−0.50	−0.80	2.49	−0.89	2.08
upright	1.09	0.44	−1.43	0.52	−0.52	1.11
extension	−0.45	−0.20	−0.71	−2.58	0.13	−1.00
Subject #2
flexion	0.58	−1.68	−0.38	0.19	1.12	0.94
upright	0.40	−0.05	−1.68	−0.25	1.89	0.07
extension	−0.77	−0.90	−0.58	−1.86	0.54	−0.51
Subject #3
flexion	−0.38	−2.16	−0.42	−0.17	0.83	0.88
upright	0.16	−0.39	−1.47	−1.84	0.93	1.13
extension	−0.07	−0.69	−0.68	−3.59	1.18	0.30
Average
flexion	0.53	−1.45	−0.53	0.84	0.36	1.30
upright	0.55	0.00	−1.53	−0.52	0.77	0.77
extension	−0.43	−0.60	−0.65	−2.68	0.62	−0.40

Intradiscal Pressure

The Intradiscal pressure of the L3-4 disc of the three subjects followed similar trend, with an average maximum pressure of 1.4 MPa (1.0 to 1.6MPa) at the upright position (Fig 3). The average minimum pressure is 0.6 MPa (0.4 to 0.8MPa), at the flexion position which is about 20° flexion of the body. The intradiscal pressure was slightly changed again to 0.6 MPa (0.5 to 0.7MPa) at the extension position.

Fig 3.

Intradiscal pressure during weight-lifting flexion-extension activity

Spine segmental forces and moments

At the flexion position, the compressive force at the center of the disc was 518 N (384 to 773 N), or 0.75 BW (0.51 to 1.11 BW) (Fig. 4). The maximal compressive load increased to 1544 N (1243 to 1704 N), or 2.28 BW (1.6 to 2.84 BW) at upright position. At extension position, the compressive force was reduced to 672 N (539 to 790 N), or 0.97 BW (0.88 to 1.13 BW).

Fig 4.

a) Anterior (−) Posterior (+) shear force, b) Compressive (−) force, and c) Flexion (+) Extension (−) moment during weight-lifting flexion-extension activity

The maximum anterior-posterior shear force was 233 N (86 to 347 N), or 0.34 BW (0.12 to 0.45 BW) at flexion. The shear force was decreased to 70 N (−74 to 187 N), or 0.11 BW (−0.11 to 0.24 BW) at upright standing position. At extension position, the shear force again increased to 119 N (29 to 171 N), or 0.17 BW (0.04 to 0.26 BW).

Maximum flexion moments were −1.0 Nm (0.5 to −2.1 Nm) at the flexion position (Fig. 4). However, extension moments were similar at maximum extension and upright position, and were −4.1 Nm (−3.2 to −5.6 Nm) and −4.2 Nm (−2.4 to −6.0 Nm), respectively.

Discussion

Determination of spinal forces is critical for the understanding spinal function and for the improvement of surgical treatments of spinal pathology. This study showed the applicability of the kinematic driven FE modeling approach to study in vivo disc loads using three healthy asymptomatic subjects. The results of the L3-4 disc loads indicated that the intervertebral disc experienced maximum compressive loads of about 2.28 BW (1544 N) and large compensatory extension moment of −4.2 Nm at upright position during the activity investigated in this study. Maximum shear forces were around 233 N at the flexion position. In general, the resultant forces and moments are highest at upright position.

Li et al. has studied the average overall ranges of motion of L3-4 disc of 10 healthy asymptomatic subjects in flexion-extension positions (Li et al., 2009). The current data obtained from the three subjects was during a dynamic motion comparable to the previous study. The average range of disc flexion-extension motion in our study is 3.1° (2.1 to 5.1°). This compares well to the mean flexion-extension range of 4.3 and SD of 3.4° in the previous study. However, the largest compression and AP shear displacements in the current study are about 1.5mm, which are larger than the previous in vivo study of up to 1 mm(Li et al., 2009, Pearcy, 1985). This might be explained by the differences of the dynamic and static experimental setups as well as the weight lifting and free flexion-extension loading conditions of the current and the previous studies Dynamic weight lifting activity could increase the loads thus deformation of the discs.

Intra-discal pressure has been measured using pressure transducers in vivo previously under various loading and posture conditions (Wilke et al., 1999, Andersson et al., 1977, Nachemson, 1981, Polga et al., 2004) and has served as an important standard for FE model validation. Due to different experimental setups, it is difficult to directly compare our data with those measured from these various studies. Nachemson et al. and Andersson et al. reported intradiscal pressures and disc loads at L3-4 level at a 20° body flexion with 20kg weight in hands (Nachemson, 1981, Andersson et al., 1977) and at an upright standing position with 5kg in extended arms (Nachemson, 1981, Andersson et al., 1976). These two loading conditions are close to those in our experiments. In their studies, the disc loads (calculated from intradiscal pressure) were about 1900 N at the upright position and 1200 N at about 20° flexion position for a subject of 70kg bodyweight (Nachemson, 1981, Andersson et al., 1977, Andersson et al., 1976) while holding the weight. These results were similar in trend to our data where we also observed higher disc load in the upright position than in the flexion position, where a large moment arm from the stretched arms may explain the higher disc load in the upright position. Han et. Al. (Han et al., 2013) used a validated musculoskeletal model, together with commercially available AnyBody software, to calculate the segmental loads. When lifting 100N with two arms, overall resultant force and moment were obtained at L3-4 level ranged from 926 to 1369 N and 2.0 to 4.3 Nm, respectively, with variations in subject weight and height. The results were similar in range to our in vivo findings. Arjmand et al. (Arjmand et al., 2011, Arjmand et al., 2012) recently derived predictive equations to estimate spinal loads in lifting tasks using FE models and optimization for muscle forces. Lifting and holding a 20 kg weight, compressive and shear forces were reported up to 1924 N and 686 N at L4-5 level, and up to 5474 N and 5026 N at L5-S1 (Arjmand et al., 2011). The overall forces were larger than our results and probably because of holding the 20 kg heavy weight, which is difficult to test in our in vivo lifting setup.

It should be mentioned that most occupational spine injuries occurred during lifting weights at a flexion position (Kingma et al., 2010, Shirazi-Adl, 1989). It is still unclear which loading mode, compression or shear or both, could represent the injury mechanism. Our data showed that L3-4 had a lower compression load, however a higher shear force, in the flexion position than at the upright standing position during the dynamic weight lifting extension motion. We speculated that an abnormal shear load might be related to the spinal injury. Previously published study has also reported low resistance of the lumbar spine structure to shear forces [30]. In addition, during weight-lifting the abdominal pressure could affect the load on the spine (Park et al., 2012, El Ouaaid et al., 2009). An appropriate abdominal pressure could effectively reduce the spinal load but loss of the pressure could enhance the load on the lumbar spine in a flexion position of the body while lifting a weight (Andersson et al., 1976).

In our study, the coordinate system was created at the center of the intervertebral disc. It is interesting to see that the disc load always coupled with an extension moment at the studied L3-4 segment in addition to the shear and compressive forces. It should be noted that the forces and moments only represented the response of the IVDs but not represent the overall forces in the lumbar segment. The moment may be resulted from the load sharing and the effect of different spinal structures such as ligaments, muscles and facet joints that keep the spine at a stable and balanced curvature. This observation might provide insights to the computational modeling methods (Park et al., 2012, Han et al., 1995, Goel et al., 1993, Shirazi-Adl et al., 2005, Kim et al., 2011) that are intended to estimate spinal loads based on various assumptions and boundary conditions. In traditional inverse dynamic optimization analysis, the disc was simulated as a ball-socket joint that bears no moment (Patwardhan et al., 1999, Kasra et al., 1992, Shirazi-Adl et al., 1986). The “follower load” concept assumed that the spinal load follows the lordosis curve of the spine (Rohlmann et al., 2009a, Rohlmann et al., 2001, Patwardhan et al., 1999, Kim et al., 2011). More recently, Park et al. (Park et al., 2012) introduced the global convergent method that determines the instantaneous rotation center of each motion segment in space. Our data implied that any computational simulation may need to consider the coupled forces and moments acting on the spinal discs in simulation of disc function.

Great efforts have been made to improve FE modeling by including various ligaments, muscle activities and realistic facet interactions (Shirazi-Adl, 2006) (Shirazi-Adl et al., 2005) (Natarajan et al., 2006) (Rohlmann et al., 2006) (Goel et al., 1993) (Woldtvedt et al., 2011) (Shirazi-Adl, 1994b). In our study, the kinematics of the each disc endplate was obtained from the net balance of all external and internal forces and moments, such as from the ligaments, muscles and facet joints. Therefore, by using the kinematics of the disc endplates as a displacement boundary condition, the FE modeling of disc could take into account the effect of all surrounding structures of the lumbar spine.

There are several limitations that need to be noted in future studies of spinal biomechanics using the kinematic driven FE modeling method. The disc was treated as linear elastic materials that neglected the viscoelastic behavior of the disc materials (Wang et al., 2012). Since the lifting extension activity did not involve rapid motion or impact, simulation of the disc as elastic materials may still provide a reasonable estimation of the disc function (Goel et al., 2005). For more sophisticated and time consuming activities, viscoelastic behavior of the discs (Rohlmann et al., 2006, Natarajan et al., 2006) can play an important role and should be included in the FE modeling. In addition, the intervertebral disc properties may be subject-specific and segment-specific in the in vivo physiological environment which may require further investigation. It is difficult to make every subject start at the same body position. In order to make data comparable, we choose to analyze the instance about half a second after the initial lifting, where all subjects had their body position at about 20° flexion. We also observed slight inter-subject variation in trend at extension, which could result from different extension ending conditions of the body such as the pelvis motion. Therefore, we chose to present the data of all subjects in this paper. Despite these limitations, this study was the first study to estimate the in vivo disc loads using a combined subject-specific and kinematic driven FE analysis technique. This technique can also be used to investigate various motion segments during various functional loading activities.

Conclusion

In conclusion, this paper used a combined subject-specific and kinematic driven FE analysis technique to investigate in vivo loads in the L3-4 disc of human lumbar spine. The data indicated that during a weight lifting extension, the disc experienced a higher shear load at a flexion position and higher compressive load at the upright position. The disc was also loaded with coupled moments along the motion path. These data may provide insights into the understanding of spinal function and the development of surgical treatments of disc pathology. In the future, we plan to use this technique to investigate different motion segments during various functional loading activities.