Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Feb 1.
Published in final edited form as: Hum Mov Sci. 2013 Nov 23;33:203–210. doi: 10.1016/j.humov.2013.11.004

Body size and countermovement depth confound relationship between muscle power output and jumping performance

Srdjan Markovic 1, Mirkov Dragan 1, Aleksandar Nedeljkovic 1, Slobodan Jaric 2,3
PMCID: PMC3943730  NIHMSID: NIHMS541043  PMID: 24280557

Abstract

A number of studies based on maximum vertical jumps have presumed that the maximum jump height reveals the maximum power of lower limb muscles, as well as the tested muscle power output predicts the jumping performance. The objective of the study was to test the hypothesis that both the body size and countermovement depth confound the relationship between the muscle power output and performance of maximum vertical jumps. Sixty young and physically active males were tested on the maximum countermovement (CMJ) and squat jumps (SJ). The jumping performance (Hmax), peak (Ppeak) and the average power output (Pavg) during the concentric phase, countermovement depth (only in CMJ) and body mass as an index of body size were assessed. To assess the power-performance relationship, the correlations between Hmax with both Ppeak and Pavg were calculated without and with controlling for the effects of body mass, as well as for the countermovement depth. The results revealed moderate power-performance relationships (range 0.55<r<0.64) that were comparable for CMJ and SJ jumps. When controlled for body mass, the same values were markedly higher (0.61<r<0.82; p<0.05 for Ppeak of both jumps). When controlled for both the body mass and countermovement depth, CMJ revealed r=0.88 and r=0.77 for Ppeak and Pavg, respectively. Both jumps revealed stronger relationships with Ppeak than with Pavg (p<0.05) when controlled for either body mass or both body mass and countermovement depth. We conclude that both body size (in CMJ and SJ) and countermovement depth (in CMJ) confound the relationship between the muscle power output with the performance of maximum vertical jumps. Regarding routine assessments of muscle power from jumping performance and vice versa, the use of CMJ is recommended, while Ppeak, rather than Pavg, should be the variable of choice.

Keywords: body mass, squat, force, peak power, average power

1. Introduction

Power is typically defined as a rate of performing mechanical work, or a product of force acting upon an object and the object’s velocity. Studies of muscle mechanical properties have often explored the ability of isolated muscles and muscle groups to exert power under various mechanical conditions (Cormie, McGuigan, & Newton, 2011a; Kaneko, Fuchimoto, Toji, & Suei, 1983; McMahon, 1984). However, since only external forces directly affect movements, the studies of human movements typically assess the power output produced in actions of the muscular system upon external objects, such as the ground and other external supports, added weights, etc (Nedeljkovic, Mirkov, Bozic, & Jaric, 2009; Samozino, Rejc, Di Prampero, Belli, & Morin, 2012). It has been generally accepted that the performance of ballistic movements depends upon the maximum power that our muscular system can exert under the given mechanical conditions (Bobbert, 2012; Cormie, McGuigan, & Newton, 2011b; Samozino, Morin, Hintzy, & Belli, 2010).

Maximum vertical jumps have not only been one of the most often applied movements in training and testing of particular physical abilities (Cormie, et al., 2011b; Cronin & Sleivert, 2005; Markovic, Dizdar, Jukic, & Cardinale, 2004), but also a frequent model for studying the fundamental properties and phenomena related to the human locomotor system (Jaric & Markovic, 2009; Markovic & Jaric, 2005; Samozino, et al., 2010; Samozino, et al., 2012). Therefore, the relationship between the jumping performance and the associated muscle power has been of particular importance. Specifically, the performance of various types of maximum vertical jumps have often been used to assess the maximum power of the lower body musculature. A number of authors have argued that the tested height of maximum vertical jump (Hmax) is a valid measure of the maximum power output of lower limb muscles (Baker, Nance, & Moore, 2001; Markovic & Jaric, 2007b; Samozino, Morin, Hintzy, & Belli, 2008). Conversely, muscle strength and power have been routinely considered as valid predictors of jumping performance (Baker, et al., 2001; Cronin & Sleivert, 2005). However, a possible effect of body size on the discussed power-performance relationship has been mainly neglected. For example, both the scaling models and most of the experimental data suggests that the muscle power output increases with body size, while the performance of rapid movements (such as Hmax) could be relatively independent of body size (Astrand, 1986; Jaric, 2003; Markovic & Jaric, 2004; McMahon, 1984). This concept has been supported by findings revealing that the Hmax could be a measure of muscle power output normalized for body size (Harman, Rosenstein, Frykman, Rosenstein, & Kraemer, 1991; Markovic & Jaric, 2007a; Nedeljkovic, Mirkov, Markovic, & Jaric, 2009). However, the discussed effect of body size has yet to be properly quantified. Namely, due to a relatively narrow range of human body sizes (Jaric, 2003; Markovic & Jaric, 2004; McMahon, 1984), the discussed effect may not be strong enough to play a meaningful role in routine assessments of muscle power output from the tested jumping performance, and vice versa.

In addition to the body size, one could argue that the jumping technique could also confound the discussed power-performance relationship of vertical jumps. For example, it is well known that the depth of the preceding countermovement can vary within a wide range in the natural maximum vertical jumps (Cormie, McGuigan, & Newton, 2010; Markovic & Jaric, 2007b; S. Markovic, Mirkov, Knezevic, & Jaric, 2013). Increased countermovement depth reduces the leg extension angles and leg stiffness, which inevitably decreases the ground reaction force due to a lower leverage of the leg extensor muscles (Bobbert, 2012; Gavrilovic, Ristanovic, & Jaric, 1981; Hunter & Marshall, 2002). The final outcome could be a reduced power output (i.e., the product of the force and velocity), while the jumping performance may remain relatively unaffected by the countermovement depth (Cormie, et al., 2010; Domire & Challis, 2007). However, although recent findings suggest that an increase in the countermovement depth could decouple a training associated increase in the jumping performance from the muscle power output of maximum vertical jumps (Markovic, et al., 2013), this phenomenon remains largely unexplored in the literature.

To address the discussed problems, we designed the present study to assess the relationship between the muscle power output and the vertical jumping performance. We recruited a large and relatively homogeneous sample of physically active subjects and tested them on the maximum jumps that either allow (i.e., the countermovement jump; CMJ) or do not allow for varying the countermovement depth (squat jump; SJ). We hypothesized that both the body size and the countermovement depth would confound the relationship between the maximum muscle power output and the jumping performance. The expected findings could contribute to refining the methodology and interpretation of the results of routine tests based on maximum vertical jumps, as well as to our understanding of the general role of muscle power in the performance of ballistic movements.

2. Methods

The sample of subjects included 60 male physical education students (age: 23.7 ± 1.7 years; body mass: 80.8 ± 8.2; body height: 182.2 ± 6.3; percent of body fat: 13.6 ± 5.6). They were free of any neurological disorders and recent injuries of the lower extremity. The subjects were physically active throughout their standard academic curriculum, but not involved in any other systematic physical training during the experiment. Before any of the tests were performed they signed an informed consent document containing the explanation of the measurement procedures, the aim of the study, as well as the potential risks. The study was conducted in accordance with the Declaration of Helsinki and the protocol was approved by the Ethical Committee of the School of Sport and Physical Education (02/1144-01).

The testing protocol consisted of 2 consecutive sessions conducted with at least two days of rest between them. The goal of the first session was to measure anthropometric characteristics and additionally familiarize subjects with the vertical jump tests. Namely, all subjects had already been familiarized with performing maximum vertical jumps through various activity classes (on average 9 hours per week). The body height was measured using Martin’s anthropometer with 0.1cm accuracy, while the body mass as the most often employed index of body size and body composition were measured by Biospace InBody 720 (USA) using DSM – BIA method (Direct Segmental Multi - frequency Bioelectrical Impedance Analysis). Thereafter, they practiced the jumping tasks through 10 squat jumps (SJ) and 10 countermovement jumps (CMJ). The second session served for recording the maximum jumping performance through the jump height (Hmax), as well as for the assessment of the associated muscle power through the peak (Ppeak) and average power output (Pavg).

Both CMJ and SJ were performed on a force plate (AMTI, BP600400; USA; sampling frequency 1000 Hz), and were mounted and calibrated according to the manufacturer’s specifications. Regarding CMJ, subjects were instructed to perform an unconstrained maximum vertical jump with their hands placed akimbo (i.e., without arm swing). No specific instructions were given regarding the depth of the countermovement. SJ were performed from a semi-squat position (knee angle set at 90°) with hands placed akimbo. SJ were repeated if a transient drop in the force signal revealed a downward movement at the jump initiation. Three consecutive trials of each jump were performed and the highest jump was taken for further analyses. One minute of rest was allowed between the consecutive trials.

Custom-designed Lab VIEW (National Instruments, Version 8.2) programs were used for the acquisition and processing of the vertical component of the ground reaction force. The signal was sampled at a rate of 1000 Hz and filtered by 2nd order Butterworth low-pass filter (10 Hz cut-off frequency). The signal and its consecutive integrations provided Hmax and the maximum lowering of the center of mass during the eccentric jump phase (i.e., countermovement depth; only in CMJ), while the product of GRF and vertical velocity allowed for the calculation of the peak power (Ppeak) and average power output (Pavg) during the concentric jump phase. Note that a high reliability of both the jumping performance and power output variables from various vertical jumps has been demonstrated (Markovic, et al., 2004; Markovic & Jaric, 2005).

Descriptive statistics were calculated as the mean and SD. None of the variables revealed deviations from normality (Kolmogorov-Smirnov test; all p ≥ 0.63). The first step of analysis was to calculate the correlations between Hmax and both Ppeak and Pavg using Pearson product-moment. Thereafter, the partial correlations between the same variables were calculated when controlling for body mass (in CMJ and SJ), as well as for both the body mass and countermovement depth (in CMJ only). The corresponding 95% confidence intervals of all correlation coefficients were also calculated. They served for the assessment of differences between the observed correlation coefficients. Finally, the relationships between the indices of the power output and either the body mass or countermovement depth were assessed using the allometric approach. In short, while the standard ratio scaling presumes a linear relation between the power output and body mass (i.e., the normalized power output data should be presented in W/kg), the allometric approach is based on presumably more accurate relationship depicted in W/kgb where b is allometric exponent different from 1. In line with standard procedures (Jaric, 2002; McMahon, 1984), we obtained b from the regression line fitted through the logarithmic values of power (P) and body mass (m) log P = log a + b log m. A standard linear model was used for the relationship between the power output and both body mass and countermovement depth (Jaric, 2003; McMahon, 1984).

3. Results

Table 1 shows descriptive data obtained from CMJ and SJ. Note that both the jumping performance as assessed through the jumps height and the recorded power output were higher in CMJ than in SJ.

Table 1.

Descriptive data obtained from CMJ and SJ

CMJ SJ
Hmax (cm) 43.1 ± 5.1 30.3 ± 4.0 a
ΔHcmd (cm) 29.9 ± 5.6 -
Ppeak (W) 3730 ± 521 3374 ± 474 a
Pavg (W) 2244 ± 345 1650 ± 287 a
Open in a new tab

Hmax – jump height; ΔHcmd – countermovement depth; Ppeak – peak power; Pavg – average power;

a

- significantly different from CMJ (p < 0.05)

Figure 1 presents the main findings of the study. Regarding the testing our hypothesis, we evaluated the values of particular correlation coefficients with respect of the 95% confidence intervals of others to claim significant differences. Controlling for body mass (in Ppeak of both CMJ and SJ), as well as controlling for the countermovement depth (in both Ppeak and Pavg of CMJ) resulted in significantly stronger power-performance relationships. However, the results also revealed 2 secondary findings. First, most of the recorded power-performance relationships proved to be stronger for Ppeak than for Pavg. In particular, this finding was observed from the partial correlations of both jumps (i.e., the relationships controlled for body mass and countermovement depth), but not from the Pearson’s correlations between the indices of power output and jumping performance. Second, although no differences in the strength of the studied relationships between CMJ and SJ were recorded when either the Pearson or partial correlations controlled for body mass were compared, when controlled for both body mass and countermovement depth, CMJ revealed stronger power-performance relationships than SJ when controlled for body mass. Note that SJ is controlled for the countermovement depth per se.

Figure 1.

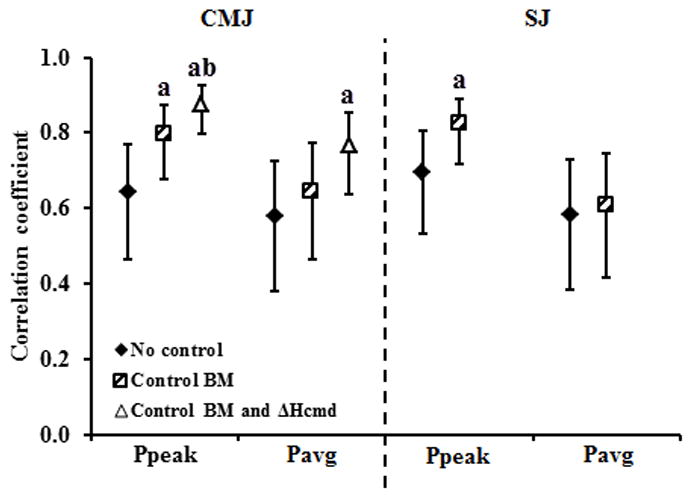
Figure 1

Open in a new tab

Pearson’s correlations coefficients (No control) and the partial correlations controlled for body mass (Control BM) and for both body mass and countermovement depth (Control BM and DEPTH) observed between the jump height and the peak, as well as the average power output (a - significantly above No control; b - significantly above Control BM). All correlation coefficients are shown with the corresponding 95% confidence intervals.

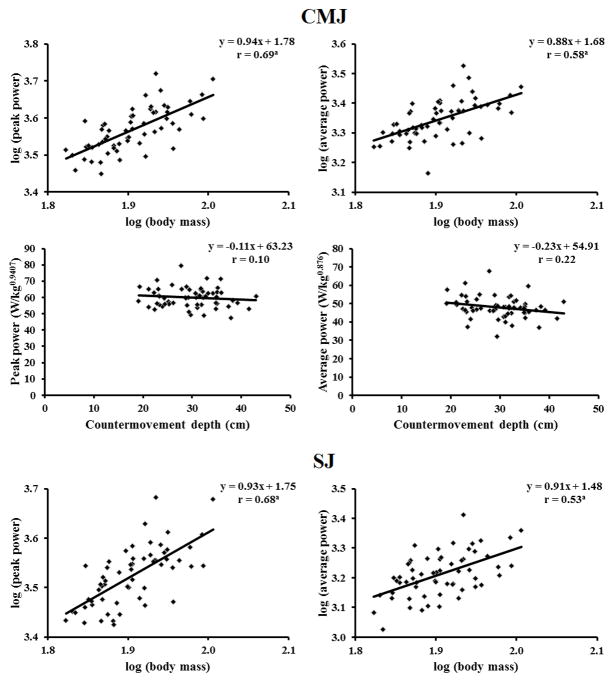
To explore the separate effects of the hypothesized confounding variables affecting the studied power-performance relationship, we assessed the effects of body mass (in both CMJ and SJ) and countermovement depth (in CMJ only) on the power output (Figure 2). The correlations between the log-transformed power output and body mass proved to be moderate (range from 0.534 and 0.691), but highly significant (all p < 0.01). Note that the regression slopes reveal the allometric coefficients within a relatively narrow interval from 0.876 to 0.941. Regarding the relationships between the power output and countermovement depth, they proved to be weak and only Pavg revealed a correlation coefficient close to the level of significance (p = 0.07). Nevertheless, of potential importance could be that fitted regression lines of both Ppeak and Pavg suggest a possibility that a decrease of power output could have a weak relationship with the countermovement depth.

Figure 2.

Figure 2

Open in a new tab

Relationships between the log-transformed values of the power output and either the body mass or the countermovement depth observed from CMJ (upper panels) and SJ (lower panels). The corresponding linear regression models are also shown (a p < 0.01).

4. Discussion

Within the present study we explored the relationships between the performance of maximum vertical jumps as assessed through the jump height (Hmax), and the associated muscle power as assessed by the peak (Ppeak) and average power output (Pavg). The findings mainly supported the hypothesis. Specifically, controlling for either the body mass (in both CMJ and SJ), or both the body mass and countermovement depth (in CMJ) resulted in stronger power-performance relationships. However, the results also revealed two secondary findings. Firstly, the peak power output (Ppeak) could provide a stronger relationship with the tested jumping performance than the average power output (Pavg). Secondly, CMJ performance could provide a similar assessment of the muscle power output as the SJ performance.

The observed relationships between the power output and body mass in the present study were not only significant (see Figure 2), but also comparable to previous studies (Markovic & Jaric, 2005; Nedeljkovic, Mirkov, Bozic, et al., 2009). This particular finding explains why most of the data reveals that the body mass markedly confounds the studied power-performance relationship in maximum vertical jumps (see correlations coefficients in Figure 1). In addition to supporting the findings obtained from both the principle component analysis (Markovic & Jaric, 2007a; Nedeljkovic, Mirkov, Markovic, et al., 2009), and the mathematical and theoretical models ((Astrand, 1986; Jaric, 2003; McMahon, 1984; Samozino, et al., 2008); see also Introduction for details), the observed findings related to body mass also reveal the magnitude of the effect of body size on the studied power-performance relationship. For example, when predicting Ppeak from Hmax, or vice versa, controlling only for body mass increases the coefficients of determination (i.e., the correlations coefficients squared; see Figure 1 for correlations) from 0.41 to 0.63 in CMJ, and from 0.48 to 0.68 in SJ. We believe that the main cause of the discussed phenomenon is the difference in the scaling mechanisms briefly reviewed in Introduction. Namely, while movement performance (such as the maximum jumping velocity and, consequently, the jumping height) could be relatively independent from body size, the maximum muscle power output increases with body weight, albeit at a somewhat lower rate (Astrand, 1986; Jaric, 2003). As a consequence, the confounding effect of body size on the studied performance-power relationship needs be accounted for by normalizing the power output for the differences in individual body masses (see also Harman, Rosenstein, Frykman, Rosenstein, & Kraemer, 1991; Markovic & Jaric, 2007a). We can only speculate on the role of other factors and mechanisms involved in the observed phenomenon, such as the general design of leg muscles (McMahon, 1984; Jaric, & Markovic, 2009) and their adaptation (Samozino, Rejc, Di Prampero, Belli & Morin, 2012).

Regarding the role of the countermovement depth in CMJ, note that its effect on the power output was markedly weak (see Figure 2). Nevertheless, the effect of the countermovement depth on the studied power-performance relationship as revealed by partial correlations was significant in Ppeak, and somewhat below the level of significance for Pavg. A negative, albeit week decrease in the power output associated with the countermovement depth could be explained by a decreases leverage of knee extensor muscle that should reduce leg stiffness (Hunter & Marshall, 2002) and the measured ground reaction force (Bobbert, 2012; Gavrilovic, et al., 1981). Recently published models also suggests that that the maximum jumping performance may not be only related with the power output, but also with the countermovement depth (Samozino, et al., 2008; Samozino, et al., 2012). Taken together, these findings strongly suggest that both the indices of body size (in both CMJ and SJ) and countermovement depth (in CMJ) need to be taken into account when relating the muscle power output to the jumping performance and vice versa. In addition to their practical implications (see further text for details), these findings could be of potential importance for understanding the relationship between the muscle power and performance of human ballistic movements in general.

The observed power-performance relationships also revealed two secondary findings of potential importance. First, note that either Ppeak (Baker, 2001; Cormie, McCaulley, Triplett, & McBride, 2007), or Pavg (Markovic & Jaric, 2007a; Samozino, et al., 2008), or both Ppeak and Pavg (Cormie, et al., 2007; Markovic, et al., 2013; Sleivert & Taingahue, 2004) have been indiscriminately used to assess the power output in vertical jumping and relate it to the jumping performance. Our data show that when controlled either for body mass or for both the body mass and countermovement depth, Ppeak consistently shows a stronger relationship with Hmax than Pavg. This is arguably a novel finding and one can only speculate on the mechanisms involved. A part of explanation could be based on prominent changes in force- and power-time profiles that could be associated with changes in jumping techniques (c.f., Markovic & Jaric, 2007b; Markovic, et al., 2013; Samozino, et al., 2012) that could alter Pavg more than Ppeak. Nevertheless, this finding apparently suggests that Ppeak should be the variable of choice when relating the jumping performance and muscle power, rather than Pavg.

Regarding another secondary finding, although several studies recommend using SJ instead of CMJ for the assessment of muscle power output (Baker, 2001; Sleivert & Taingahue, 2004), note that both the simple correlations and the partial correlations controlled for body mass suggest a comparable strength of the power-performance relationships in two jumps. However, CMJ data controlled for both the body mass and countermovement depth reveal a stronger power-performance relationship than SJ controlled for body mass (note that the ‘countermovement depth’ in SJ is typically prescribed). It should be also taken into account that CMJ is simpler to perform, requires shorter familiarization, and no control of the starting position is needed. Therefore, even when routine testing does not allow for controlling the countermovement depth, CMJ should be selected both for the assessment of muscle power output and for relating the assessed power to the jumping performance.

5. Conclusions

The results supported the hypothesis that both the body size and countermovement depth confound the power-performance relationship obtained from maximum vertical jumps. This finding could be of importance both for understanding the role of muscle power in the human ballistic performance and for the application of vertical jumps in routine training and testing procedures. We also found that peak power reveals a stronger relationship with the jumping performance than the average power recorded during the concentric jump phase. Finally, the strength of the power-performance relationship in natural CMJ could be comparable with the jumps performed from a prescribed semi-squat position (such as SJ), if not higher. Future research could address underexplored aspects of the studied power-performance relationship, such as the role of the force-velocity relationship pattern of the leg extensor muscles (Bobbert, 2012; Cormie, et al., 2011a; Samozino, et al., 2012) and the dependence of both the jumping performance and power output variables on the countermovement depth and other kinematic and kinetic variables of the tested jumps (Jaric & Markovic, 2009; Markovic, et al., 2013; Samozino, et al., 2010).

Highlights.

  • We tested the maximum countermovement and squat jumps.

  • We related the jump performance with the associated muscle power output.

  • Both body size and countermovement depth confound the studied relationship.

  • The peak, rather than average power, should be related with jumping performance.

  • Use of the countermovement jump for power testing is recommended.

Acknowledgments

The study was supported in part by NIH grant (R21AR06065) and grants from the Serbian Research Council (#175037 and #175012).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Astrand P-O, Rodhal K. Textbook of Work Physiology. 3. New York: McGraw-Hill; 1986. [Google Scholar]
  2. Baker D. A series of studies on the training of high-intensity muscle power in rugby league football players. J Strength Cond Res. 2001;15(2):198–209. [PubMed] [Google Scholar]
  3. Baker D, Nance S, Moore M. The load that maximizes the average mechanical power output during jump squats in power-trained athletes. J Strength Cond Res. 2001;15(1):92–97. [PubMed] [Google Scholar]
  4. Bobbert MF. Why is the force-velocity relationship in leg press tasks quasi-linear rather than hyperbolic? J Appl Physiol. 2012;112(12):1975–1983. doi: 10.1152/japplphysiol.00787.2011. [DOI] [PubMed] [Google Scholar]
  5. Cormie P, McCaulley GO, Triplett NT, McBride JM. Optimal loading for maximal power output during lower-body resistance exercises. Med Sci Sports Exerc. 2007;39(2):340–349. doi: 10.1249/01.mss.0000246993.71599.bf. [DOI] [PubMed] [Google Scholar]
  6. Cormie P, McGuigan MR, Newton RU. Changes in the eccentric phase contribute to improved stretch-shorten cycle performance after training. Med Sci Sports Exerc. 2010;42(9):1731–1744. doi: 10.1249/MSS.0b013e3181d392e8. [DOI] [PubMed] [Google Scholar]
  7. Cormie P, McGuigan MR, Newton RU. Developing Maximal Neuromuscular Power Part 1-Biological Basis of Maximal Power Production. Sports Med. 2011a;41(1):17–38. doi: 10.2165/11537690-000000000-00000. [DOI] [PubMed] [Google Scholar]
  8. Cormie P, McGuigan MR, Newton RU. Developing Maximal Neuromuscular Power Part 2-Training Considerations for Improving Maximal Power Production. Sports Med. 2011b;41(2):125–146. doi: 10.2165/11538500-000000000-00000. [DOI] [PubMed] [Google Scholar]
  9. Cronin J, Sleivert G. Challenges in understanding the influence of maximal power training on improving athletic performance. Sports Med. 2005;35(3):213–234. doi: 10.2165/00007256-200535030-00003. [DOI] [PubMed] [Google Scholar]
  10. Domire ZJ, Challis JH. The influence of an elastic tendon on the force producing capabilities of a muscle during dynamic movements. Comput Methods Biomech Biomed Engin. 2007;10(5):337–341. doi: 10.1080/10255840701379562. [DOI] [PubMed] [Google Scholar]
  11. Gavrilovic P, Ristanovic D, Jaric S. “In vivo” study on the effect of muscle length on its maximum force of contraction. Period Biol. 1981;83:135–137. [Google Scholar]
  12. Harman EA, Rosenstein MT, Frykman PN, Rosenstein RM, Kraemer WJ. Estimation of human power from vertical jump. J Appl Sport Sci Res. 1991;5:116–120. [Google Scholar]
  13. Hunter JP, Marshall RN. Effects of power and flexibility training on vertical jump technique. Med Sci Sports Exerc. 2002;34(3):478–486. doi: 10.1097/00005768-200203000-00015. [DOI] [PubMed] [Google Scholar]
  14. Jaric S. Muscle strength testing: use of normalisation for body size. Sports Medicine. 2002;32(10):615–631. doi: 10.2165/00007256-200232100-00002. [DOI] [PubMed] [Google Scholar]
  15. Jaric S. Role of body size in the relation between muscle strength and movement performance. Exerc Sports Sci Rev. 2003;31(1):8–12. doi: 10.1097/00003677-200301000-00003. [DOI] [PubMed] [Google Scholar]
  16. Jaric S, Markovic G. Leg muscles design: the maximum dynamic output hypothesis. Med Sci Sports Exerc. 2009;41(4):780–787. doi: 10.1249/MSS.0b013e31818f2bfa. [DOI] [PubMed] [Google Scholar]
  17. Kaneko M, Fuchimoto T, Toji H, Suei K. Training effect of different loads on the force-velocity relationship and mechanical power output in human muscle. Scand J Sports Sci. 1983;5:50–55. [Google Scholar]
  18. Markovic G, Dizdar D, Jukic I, Cardinale M. Reliability and factorial validity of squat and countermovement jump tests. J Strength Cond Res. 2004;18(3):551–555. doi: 10.1519/1533-4287(2004)18<551:RAFVOS>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  19. Markovic G, Jaric S. Movement performance and body size: the relationship for different groups of tests. Eur J Appl Physiol. 2004;92(1–2):139–149. doi: 10.1007/s00421-004-1076-7. [DOI] [PubMed] [Google Scholar]
  20. Markovic G, Jaric S. Scaling of muscle power to body size: the effect of stretch-shortening cycle. Eur J Appl Physiol. 2005;95(1):11–19. doi: 10.1007/s00421-005-1385-5. [DOI] [PubMed] [Google Scholar]
  21. Markovic G, Jaric S. Is vertical jump height a body size-independent measure of muscle power? J Sports Sci. 2007a;25(12):1355–1363. doi: 10.1080/02640410601021713. [DOI] [PubMed] [Google Scholar]
  22. Markovic G, Jaric S. Positive and negative loading and mechanical output in maximum vertical jumping. Med Sci Sports Exerc. 2007b;39(10):1757–1764. doi: 10.1249/mss.0b013e31811ece35. [DOI] [PubMed] [Google Scholar]
  23. Markovic S, Mirkov D, Knezevic O, Jaric S. Jump training with different loads: effects on jumping performance and power output. Eur J Appl Physiol. 2013;113(10):2511–2521. doi: 10.1007/s00421-013-2688-6. [DOI] [PubMed] [Google Scholar]
  24. McMahon TA. Muscles, Reflexes, and Locomotion. Princeton: Princeton University Press; 1984. [Google Scholar]
  25. Nedeljkovic A, Mirkov DM, Bozic P, Jaric S. Tests of muscle power output: the role of body size. [Research Support, Non-U.S. Gov’t] Int J Sports Med. 2009;30(2):100–106. doi: 10.1055/s-2008-1038886. [DOI] [PubMed] [Google Scholar]
  26. Nedeljkovic A, Mirkov DM, Markovic S, Jaric S. Tests of muscle power output assess rapid movement performance when normalized for body size. J Strength Cond Res. 2009;23(5):1593–1605. doi: 10.1519/JSC.0b013e3181a9ebce. [DOI] [PubMed] [Google Scholar]
  27. Samozino P, Morin JB, Hintzy F, Belli A. A simple method for measuring force, velocity and power output during squat jump. J Biomech. 2008;41(14):2940–2945. doi: 10.1016/j.jbiomech.2008.07.028. [DOI] [PubMed] [Google Scholar]
  28. Samozino P, Morin JB, Hintzy F, Belli A. Jumping ability: a theoretical integrative approach. J Theor Biol. 2010;264(1):11–18. doi: 10.1016/j.jtbi.2010.01.021. [DOI] [PubMed] [Google Scholar]
  29. Samozino P, Rejc E, Di Prampero PE, Belli A, Morin JB. Optimal force-velocity profile in ballistic movements--altius. Med Sci Sports Exerc. 2012;44(2):313–322. doi: 10.1249/MSS.0b013e31822d757a. [DOI] [PubMed] [Google Scholar]
  30. Sleivert G, Taingahue M. The relationship between maximal jump-squat power and sprint acceleration in athletes. Eur J Appl Physiol. 2004;91(1):46–52. doi: 10.1007/s00421-003-0941-0. [DOI] [PubMed] [Google Scholar]

RESOURCES