Feasibility study of red blood cell debulking by magnetic field-flow fractionation with step-programmed flow

Abstract

Emerging applications of rare cell separation and analysis, such as separation of mature red blood cells from hematopoietic cell cultures require efficient methods of red blood cell (RBC) debulking. We have tested the feasibility of magnetic RBC separation as an alternative to centrifugal separation using an approach based on the mechanism of magnetic field-flow fractionation (MgFFF). A specially designed permanent magnet assembly generated a quadrupole field having a maximum field of 1.68 T at the magnet pole tips, zero field at the aperture axis, and a nearly constant radial field gradient of 1.75 T/mm (with a negligible angular component) inside a cylindrical aperture of 1.9 mm (diameter) and 76 mm (length). The cell samples included high-spin hemoglobin RBCs obtained by chemical conversion of hemoglobin to methemoglobin (met RBC) or by exposure to anoxic conditions (deoxy RBC), low-spin hemoglobin obtained by exposure of RBC suspension to ambient air (oxy RBC), and mixtures of deoxy RBC and cells from a KG-1a white blood cell (WBC) line. The observation that met RBCs did not elute from the channel at the lower flow rate of 0.05 mL/min applied for 15 min but quickly eluted at the subsequent higher flow rate of 2.0 mL/min was in agreement with FFF theory. The well-defined experimental conditions (precise field and flow characteristics) and a well-established FFF theory verified by studies with model cell systems provided us with a strong basis for making predictions about potential practical applications of the magnetic RBC separation.

Introduction

Centrifugation plays an important role in the separation of blood into its basic components of red blood cells (RBCs), white blood cells (WBCs), platelets and plasma [1]. It is widely used for blood sample enrichment of nucleated cells (leukocytes) for use in diagnostic and therapeutic biomedical applications [2]. The separation mechanism is based on differential cell sedimentation due to the characteristically higher RBC mass density as compared to other blood cells (and the suspending fluid) [3]. Specialized centrifuges capable of processing a wide range of blood sample volumes from μL (to measure fractional RBC volume in blood, or hematocrit) to hundreds of mL (for blood banking purposes) to many liters of blood (by a continuous process used in clinical apheresis) are commercially available and are a staple in clinical laboratories and clinical apheresis hospital units. In particular, centrifugal split flow thin cell fractionation (SPLITT) has been shown to successfully fractionate blood into its main components [4]. However, centrifugal separation has drawbacks that become apparent in new applications to microfluidics and to separation of rare cells (such as circulating tumor cells, CTCs) [5–7]. The complexities of centrifuge integration with the microfluidic components for μL volume sample processing make such an approach difficult to implement [8]. Hypotonic RBC disruption has been the technique that has been resorted to, which is also suboptimal [9,10].

We set out to investigate if the effect of RBC motion in strong magnetic fields (magnetophoresis) could be used for RBC separation and to apply the mechanism of field-flow fractionation (FFF) to develop a theoretical and experimental basis for engineering the design of a practical magnetic RBC separator. In the course of previous studies we have measured the RBC magnetophoretic mobility (MM) using the technique of cell tracking velocimetry (CTV) and have shown that it depends on the presence of high-spin hemoglobin [11]. Our results were in agreement with earlier studies on the magnetic properties of hemoglobin and RBC, using other techniques (notably by Pauling in 1936 using a Gouy balance, who also provided the theoretical explanation of the hemoglobin magnetization mechanism) [12,13]. In the presence of oxygen in solution, the electron spin of the oxygen-heme complex with the adjacent globin bonds has a zero net value, resulting in their null contribution to the total RBC magnetic moment and leaving the cell slightly more diamagnetic than water because of the diamagnetic globin contribution. In the absence of oxygen, the net electron spin of the four heme groups in the hemoglobin is nonzero, resulting in their collective paramagnetic contribution that is almost equal, but of opposite sign to the total diamagnetic globin contribution, leaving the cell less diamagnetic than water. The net effect is such that the oxygenated RBCs in solution are pushed away from the magnet (have negative MM value) and the deoxygenated RBCs are attracted by the magnet (have positive MM value). The effect for the oxygenated RBCs is very weak and comparable to the effect for other (WBC) cells in the blood so that they could be considered non-magnetic (MM ≈ 0). The magnetic forces acting on a RBC are small as compared to the forces associated with centrifugation or the forces acting on synthetic magnetic nanoparticles used as tags or labels for current magnetic cell separation applications [14,15]. This demands a significant effort in designing and fabricating a practical magnetic RBC separator [16]. Nevertheless, the availability of high energy, low cost permanent magnets makes such label-free magnetic RBC separation methods possible in principle. We set out to investigate if it is feasible in practice.

Theoretical

The force on a RBC in a magnetic quadruple field used in this study is given by the equation [15]

$$F_m=\frac{V\mathrm{\Delta }\chi }{{\mu }_0}{\left(\frac{B_0}{r_0}\right)}^{2}r={\phi }_m{S}_m$$ (1)

where V is the volume of the RBC, Δχ is the difference in magnetic susceptibility of the RBC and the suspending fluid, and VΔχ is then the magnetic polarization of the RBC relative to the suspending fluid (also known as the particle-field interaction parameter, φ_m). B₀ is the magnetic field at the radius r₀ of the aperture, μ₀ is the magnetic permeability of free space equal to 4π × 10⁻⁷ H/m (or Tm/A), and B₀/r₀²r/μ₀ is the local magnetic potential energy density gradient at a distance r from the aperture axis which drives the separation (also known as the parameter S_m). For a creeping RBC motion in a viscous fluid of aqueous electrolyte solution, the RBC velocity induced by the magnetic field is

$$u_m=\frac{F_m}{f}$$ (2)

where f is the RBC friction coefficient. We define the magnetophoretic mobility, m, as the ratio of the particle magnetic polarization relative to the suspending fluid to the particle friction coefficient

$$m=\frac{{\phi }_m}{f}$$ (3)

Combining Eqs. (1) and (3), one obtains

$$u_m={mS}_m$$ (4)

For paramagnetic and diamagnetic media, the magnetic polarization, φ_m, is independent of the applied field and the friction coefficient, f, is independent of velocity in the creeping flow regime. Thus, the magnetophoretic mobility of the RBC is independent of the applied field and is strictly the property of the RBC and the suspending fluid. It follows that the field-induced RBC velocity, u_m, is directly proportional to S_m, and therefore directly proportional to the radial distance from the quadrupole field symmetry axis. This justifies the use of the term “centrifugal field” when analyzing the RBC motion inside the quadrupole magnet. The effect of the magnetic centrifugal field on the RBC is small in comparison to the sedimentation centrifugal field in rotating centrifuges because the difference in magnetic susceptibility of the RBC and the suspending fluid, Δχ, on the order of 10⁻⁶, is small compared to the difference in mass densities of the RBC and the suspending fluid (relative to that of the suspending fluid), Δρ/ρ_fluid = ρ_RBC/ρ_fluid − 1, on the order of 10⁻² [14]. This demands the application of high magnetic field and field gradients, which is most easily accomplished for small channel volumes and small aperture radius, and is compatible with the intended microfluidic applications.

Cells that are driven to the outer wall of the annular channel (the accumulation wall) before the fluid flow is restarted will elute from the channel according to the mechanisms of field-flow fractionation (FFF). The retention ratio R, defined as the elution velocity of the cells divided by the mean fluid velocity, is given approximately by the equation

$$R=6\gamma a+6\lambda$$ (5)

where α is the ratio of cell radius to channel thickness, γ is an empirical parameter that may be less than or considerably greater than unity and accounts for the effects of hydrodynamic lift forces and other hydrodynamic effects close to the wall [17,18], and λ is the so-called FFF retention parameter [19]. In the normal mode of FFF, the particulate sample materials are driven to the wall by their interaction with the applied field and the buildup of concentration next to the wall is countered by diffusion away from the wall. These opposing effects result in an equilibrium concentration profile that decays exponentially away from the wall. The characteristic length ℓ for the exponential decay is given by

$$\ell =\frac{D}{u}$$ (6)

where D is the particle diffusion coefficient and u is the field-induced velocity toward the wall. The retention parameter λ is equal to the ratio of ℓ to the channel thickness. In the normal mode of FFF the second term on the right hand side of Eq. (5) tends to dominate. In the steric mode of FFF the particulate sample materials tend to be larger than a micron in diameter, so that their diffusion away from the wall is suppressed and ℓ is negligible in comparison to particle radius. In this case the first term on the right hand side of Eq. (5) dominates.

Experimental

Measurement of RBC magnetophoresis

The magnetophoretic mobility, m, of human erythrocytes was measured by cell tracking velocimetry (CTV) [20–22]. The CTV apparatus measures the motion of cells on an individual basis, due to a nearly constant magnetic force directed orthogonal to gravity. The permanent magnet assembly with specially shaped pole pieces, produces a magnetic energy gradient, S_m (146 ± 1 TA/mm²), that is nearly constant (isodynamic) in the area where the measurement is made (1.05 mm wide × 0.79 mm high). Consequently, the horizontal cell velocity component induced by the magnetic force is constant. Displacements inside a 1 mm × 1 mm ID glass channel are observed using a microscope (Olympus BXFM-F, Tokyo, Japan) with attached 12-bit monochrome video camera (Retiga Exi, QImaging, Burnaby, BC, Canada). The image size is 640 × 480 pixels with 1 × 1 binning. The digital images are acquired to PC RAM using software (Video Savant, IO Industries, London, Ontario, Canada), and subsequently saved to the PC hard drive. The CTV algorithm uses five consecutive frames to establish the most probable paths of cells (N = 300 to 700 cells per sample). From this information, the algorithm reports 2D locations. With the aid of EXCEL macros, a linear fit of location-time data gives the velocity components of each particle. The cell magnetophoretic mobility is calculated as the horizontal component of cell velocity divided by S_m. Up to 1,500 cells can be measured in 20 minutes. The final outputs are mobility population statistics (including mean, standard deviation and 95% confidence interval) computed with the aid of additional macros.

Magnetic FFF system

Quadrupole magnet

An open gradient magnetic separator was assembled using permanent magnet blocks arranged in a special configuration producing centrifugal force on paramagnetic molecules (such as methemoglobin) inside its air bore [14]. Permanent magnets (neodymium-iron-boron, maximum energy product 42 MGOe, K&J Magnetics, Inc., Jamison, PA) and suitably shaped iron flux return pieces generated a quadrupole field with a maximum field of B₀ = 1.68 T at the pole tips and a constant field gradient of B₀/r_o = 1.75 T/mm. The aperture was 1.91 mm diameter, and its length was 76.2 mm plus a 3.81 mm tapered entrance region. It accommodated a cylindrical flow channel (Polyimide tubing, Cole-Parmer, ID = 1.8 mm, OD = 1.9 mm, L = 90 mm). The volume near the center of the channel, where the magnetic centrifugal force was the lowest, was excluded by insertion of a co-axial solid rod (enameled copper wire, 16 AWG, McMaster-Carr). This created an annular space accessible to the flowing cell suspension with an inner diameter of d_i = 1.3 mm and outer diameter of d_o = 1.8 mm, resulting in an open channel annular thickness of 250 μm that had a volume of 0.093 mL within the quadrupole field. The parameter S_m was equal to 2,200 TA/mm² at the outer annular radius and 1600 TA/mm² at the inner next to the enameled axial wire.

Fluidics

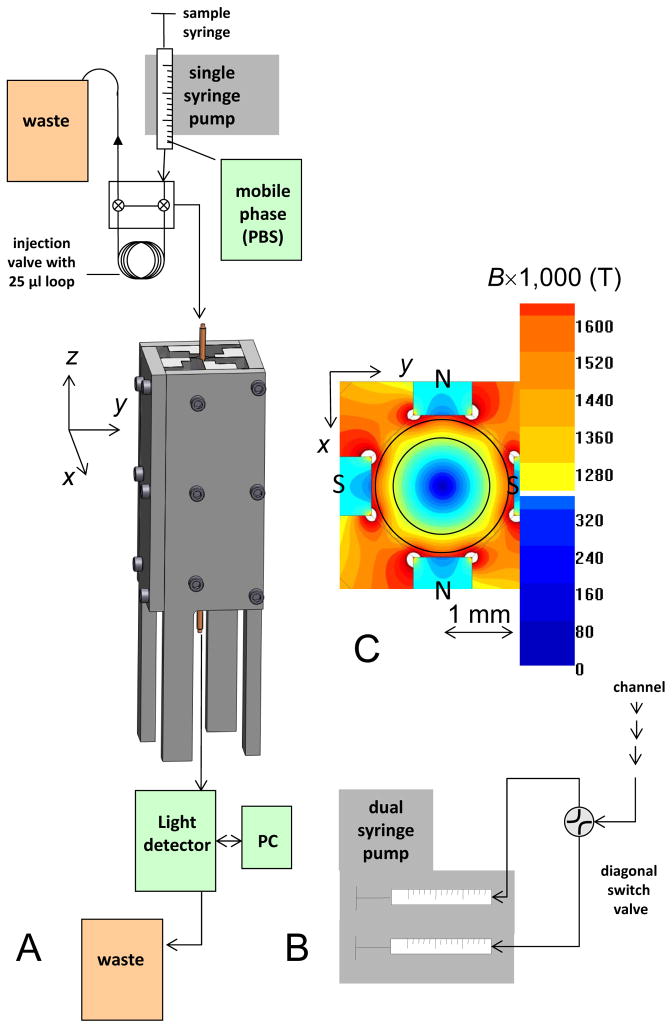
There were two different flow configurations used in this study. 1) The system fluidics of the “one-syringe” configuration (Figure 1A) consisted of a Rheodyne valve with 25 μL sample loop. The mobile phase was infused by a dual syringe pump (Harvard 33, Harvard Apparatus, Inc., Holliston, MA) with a single 5 mL syringe with flow rates varied from 0.025 to 5.0 mL/min. A light detector downstream of the magnet (between the magnet and the sample collection syringe) measured light attenuation caused by the cells eluting from the magnet. The light attenuation signal was used to determine cell elution profile from the magnet as a function of the elution time (fractogram). 2) The “two-syringe” configuration (Figure 1B) comprised dual syringes at the outlet where the light detector was replaced by a diagonal valve (between the magnet and the sample collection syringes) that directed the eluate to one of two syringes, in sequence with the changing flow conditions discussed below, as a means of fractionation of the cell sample into the eluted (“nonmagnetic” eluate) and the retained (“magnetic” retentate) cell fractions. The sample injection setup was replaced by a sample container in contact with a nitrogen gas tank to achieve complete RBC deoxygenation, equipped with the magnetic stirrer to prevent KG-1a cell sedimentation during separation runs exceeding 30 min. The container was connected to the channel via a diagonal valve that directed the flow stream to the channel or diverted to the waste container. The outlet flow was controlled by a dual syringe pump (Harvard 33, Harvard Apparatus, Inc., Holliston, MA) with 5 mL syringes with flow rates varied from 0.025 to 5.0 mL/min.

Fig. 1.

Magnetic FFF system schematic. A The quadrupole magnet (in perspective view) and the associated components set up for a “one-syringe” operation. The cylindrical flow channel with a coaxial rod is centered inside 2-mm magnet aperture. B The outlet portion of the system set up for “two-syringe” operation. The details of the inlet portion setup are described in the text (not shown). C B field heat map calculated midway the length of the magnet. The flow channel cylinder fits snugly between two pairs of N-S pole pieces. The coaxial rod left a 250-μm annulus serving as a flow channel (red-to-orange region between the pole pieces) exposed to 1,500 T/m field gradient. The outlines of the inner and outer annular channel walls are shown.

Sample fractionation sequence

Typical cell sample processing sequences were comparable for the two different flow configurations (involving one- or two- syringe operation, Figures 1A and B). The mobile phase volumetric flow rate was set to 0.05 mL/min. The sample was injected for 1 min, loaded into the channel for 2 min, followed by a stop-flow period of 5 min. The flow was then resumed at 0.05 mL/min for 15 min to allow for the elution of the unretained material (“eluate”) and then increased to 2 mL/min for 5 min for the elution of the retained material (“retentate”) that ended the data collection run. Between runs the system was purged of any residual cells by flushing with 20–30 mL PBS at a flow rate of 5 mL/min. The data gathered depended on the flow configuration. For one-syringe operation the fractograms were analyzed for differences in the elution profile between low flow rate (0.05 mL/min) and high flow rate (2 mL/min) periods, whereas for the two-syringe operation the syringe contents were collected for cell counts and compared with the cell count in the original sample. The cell count ratios post-to-prior separation were reported as fractional recoveries in the eluate and in the retentate. The mass balance was checked by adding fractional recoveries in eluate and retentate and comparing to 100%.

Model cell mixtures

Three different types of cells were used in the study: 1) RBC suspension obtained by dilution of whole blood, obtained from healthy volunteer donors (providing signed consent approved by the institutional ethics committee) in PBS and maintained in equilibrium with ambient air (“oxy RBC”); 2) aliquots of the same RBC suspension incubated with 10 mM sodium nitrite for approximately 1 hr for complete conversion of hemoglobin to methemoglobin (“met RBC”); and 3) mixtures of equal numbers of deoxygenated RBCs (“deoxy RBCs”) and cultured KG-1a cells. The KG-1a cell line is derived from human bone marrow and shares phenotype with a hematopoietic progenitor cell which makes it suitable for use in models of hematopoietic cell cultures that contain maturing RBCs [23]. The oxy RBC and met RBC samples were used with the one-syringe flow configuration to determine their retention ratios from fractograms and for comparison with FFF theory based on the difference in their magnetophoretic mobilities. The deoxy RBC + KG-1a cell mixtures were used to determine the cell fractionation capability of the magnetic system on mixed cell populations approximating practical applications, such as separation of maturing RBCs from hematopoietic cell cultures intended for in vitro blood production [23–25]. The two cell types were distinguished in the separated cell fractions by large differences in the mean cell diameter (6 to 8 μm for RBC and 15 μm for KG-1a). The differential cell counts were performed manually under the microscope using a hemacytometer or an automated cell counter (Z2 Coulter Counter). Typical sample injection volume was 50 μL and a typical cell number concentration was 5 × 10⁷ per mL, resulting in the total cell number processed of 2.5 × 10⁶ per injection.

Results and discussion

Cell motion analysis by tracking velocimetry in a high magnetic field gradient, S_m = 146 TA/mm², was capable of resolving differences in the RBC magnetophoretic mobility distributions resulting from differences in hemoglobin chemistry (Figure 2). In the oxygenated state, the RBC mobility distribution was centered on zero, whereas in the deoxygenated state or following chemical oxidation to methemoglobin, the RBC mobility distribution shifted towards a positive value. The magnitude of the mean mobility shift agreed with the calculated shift based on known values of the magnetic dipole moments of the oxygenated, deoxygenated, and the chemically oxidized form of methemoglobin (0, 5.46 and 5.80 Bohr magnetons per heme group, corresponding to 0, 4, and 5 unpaired electrons per heme group, respectively, with four heme groups per hemoglobin molecule) [11,12,13]. The shift was larger than observed before (5.1 × 10⁻⁶ as compared to 3.7 × 10⁻⁶ mm³/T.A.s [11], respectively) and larger than calculated from theory (4.3 × 10⁻⁶ mm³/T.A.s [11]) presumably due to cell suspension motion artifacts that may have increased the apparent cell velocity measured by cell tracking velocimetry. The calculated resolution between the different RBC mobility distributions was 0.8 (Figure 2). The magnetophoretic mobility distribution of the nucleated KG-1a cell line (devoid of hemoglobin) was also centered on zero, similar to the oxy RBC (results not shown). When extrapolated to high field gradient value, S_m = 1,500 TA/mm², available at the inner annular wall of the channel inside the quadrupole magnet used for cell separation, the expected field-induced RBC mean velocity, u_m, was comparable to the RBC hydrodynamic diameter per second (8 μm/s, Figure 2, third abscissa). Considering that the annular channel width was 250 μm, the mean time required for the RBC to traverse the channel width was calculated to be approximately 30 s. The results suggest that under well-controlled conditions of the magnetic field and viscous flow, such as prescribed by the field-flow fractionation method, one may develop a quantitative understanding of the magnetic separation process of weakly paramagnetic RBCs, verifiable by experiment. We have set out to use the FFF approach to analyze the magnetic RBC separation, firstly on a model of RBC with paramagnetic hemoglobin (deoxy and met) and oxygenated RBCs, and secondly on a mixture of met RBCs with nucleated KG-1a cells that could provide a model of label-free KG-1a magnetic separation from RBCs (by first converting hemoglobin to high-spin methemoglobin or by performing the separation in anoxic conditions). This type of the magnetic FFF analysis could be useful in applications to studies on hematopoietic progenitor differentiation [23–25].

Fig. 2.

RBC magnetophoretic mobility, m, histograms measured by the CTV. A Oxygenated RBCs. B Methemoglobin RBCs. The magnetophoretic mobility deoxygenated RBCs is approx. 20% lower than that of the met RBCs (not shown). Also shown are the corresponding field-induced RBC velocities measured inside the CTV apparatus (secondary abscissa) and calculated for the annular channel inside the quadrupole magnet (tertiary abscissa).

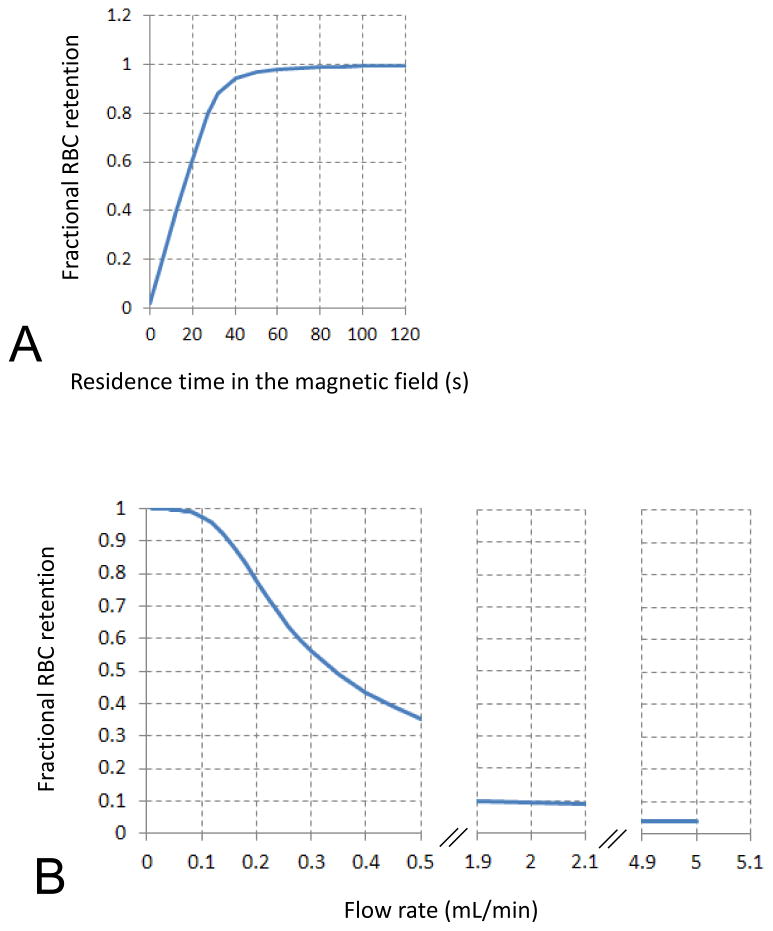
The experimentally determined RBC magnetophoretic mobility distributions were used to calculate the RBC residence time in the magnetic field required for RBC retention inside the separation column of the type used in this study, and to determine the effect of mobile phase flow rate, Figure 3. The convective and magnetic drift transport model of non-interacting, point mass, paramagnetic particles was used to calculate the fractional retention of the particles inside the column: firstly, as a function of time for the stop-flow conditions, Figure 3A, and secondly as a function of the mobile phase volumetric flow rate for the sample elution conditions, Figure 3B. For the latter calculations it was assumed that once a cell is carried to the outer wall of the annular channel it is either immobilized or it moves at such a low longitudinal velocity that it does not have time to migrate to the channel outlet before the end of the experiment. The stop-flow conditions resulted in nearly complete depletion of the deoxy RBCs from the cell suspension after 1 minute. Considering that the model did not take into account the volume effects of the RBCs migration in the magnetic field that would slow down the separation, such as increase in the effective, local viscosity of a thickening cake of the fluid and RBC mixture next to the accumulation wall and the fluid displacement by the RBCs approaching the wall, two minutes was considered a minimum time for stop-flow conditions. More than twice that, 5 min, was selected for the experimental part of the study. The deoxy RBC retention fraction decreased with the increasing volumetric flow rate of the mobile phase, Figure 3B. This was especially apparent for flow rates higher than 0.1 mL/min. In order to minimize losses of the retained deoxy RBC fraction, half that value, 0.05 mL/min was selected for the experiment. For practical reasons, in order to complete the separation in a realistic length of time that would not adversely affect viability of the cells, flow rates lower than 0.025 mL/min were not considered feasible. For the removal of the retained deoxy RBC fraction from the column, we selected a flow rate of 2 mL/min, sufficient to elute nearly all RBCs from the column. Even higher flow rate, 5 mL/min, was used to complete the experimental run and to wash the column between the sample injections.

Fig. 3.

Dependence of fractional RBC capture on A residence time in the magnetic field, and B the volumetric flow rate of the mobile phase (calculations based on the met RBC magnetophoretic mobility distribution shown in Fig. 2), subsequently used for selection of 0.05 mL/min for met (and deoxy) RBC capture.

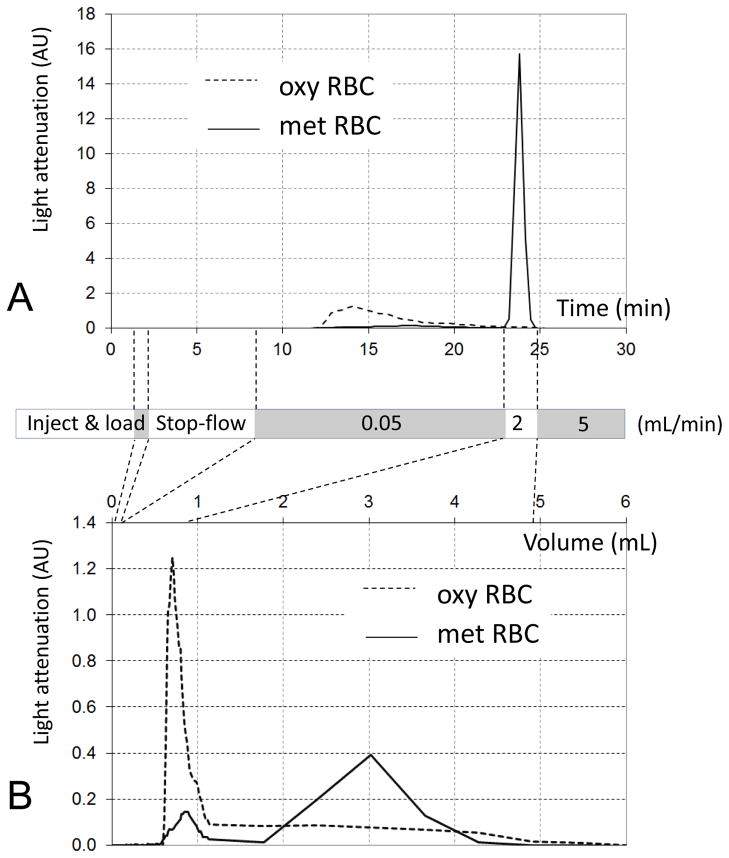
The time required for complete elution of the unretained, non-magnetic cell fraction (such as oxy RBCs or KG-1a cell line) was expected to be several times longer than the mean time for fluid to pass through the channel, the so-called void time. The void time is calculated from the ratio of the column void volume, 0.093 mL, and the volumetric flow rate of the mobile phase, 0.05 mL/min, and is equal to 1.9 min. This was corroborated by the experimentally measured elution profile of oxy RBCs from the column, Figure 4A. One notes that the oxy RBC light attenuation trace returns to baseline after about 15 min of flow following the stop-flow period, indicating complete elution of oxy RBCs, as predicted. In contrast, there was only marginal elution of paramagnetic met RBCs during the same time period and the same flow rate of the mobile phase, 0.05 mL/min, as indicated by a nearly flat light attenuation trace, Figure 4A. This confirmed the model predictions of the optimal mobile flow rate value of 0.05 mL/min, based on the met RBC magnetophoretic mobility distribution, Figures 2 and 3B. The met RBCs were eluted only after increasing the mobile phase flow rate 40-fold, to 2 mL/min, Figure 4A. The clear separation between oxy RBC and met RBC elution profiles is also apparent when they are presented as a function of the elution volume rather than the elution time, Figure 4B.

Fig 4.

Fractograms of pure oxy RBC and pure met RBC preparations combined into a single plot. A Measured as a function of the elution time. B Recalculated as a function of the elution volume. The grey & white box diagram indicates phases of the mobile phase flow. The data were obtained using a single-syringe magnetic FFF setup.

The characteristic length ℓ as given by Eq. (6) may be calculated for a met RBC close to the outer annular channel wall as follows. The diffusion coefficient for a RBC in aqueous suspension at room temperature may be calculated as kT/f where k is the Boltzmann constant (1.38 × 10⁻²³ J/K), T is the absolute temperature (298 K), and f is the RBC friction coefficient (= 3πηd_h = 7.26 × 10⁻⁸ kg/s [11]). The diffusion coefficient is thus calculated to be 5.7 × 10⁻¹⁴ m²/s. The field-induced velocity at the outer wall is given by Eq. (4), and taking mean mobility as 5.1 × 10⁻⁶ mm³/TAs and S_m = 2,200 TA/mm², and therefore u_m = 11 μm/s. The characteristic length ℓ is therefore equal to D/u_m = 5.1 × 10⁻³ μm. This is far smaller than the RBC radius and we can conclude that the met RBCs must elute in steric mode.

It was mentioned in relation to Eq. (5) that the parameter γ may take a value from less than unity to a considerably greater value. The actual value depends on experimental conditions. It is a function of the equilibrium distance from the wall where the force toward the wall due to interaction with the magnetic field is balanced by the hydrodynamic lift force. At low flow rates, the hydrodynamic lift will be small and the met RBCs will be driven close to the wall. In this case, the retention ratio may be considerably less than 6α = 0.096 (taking RBC radius to be 4 μm and channel thickness as 250 μm). Assuming a channel volume of 0.093 mL, the void time would be 1.9 min at a flow rate of 0.05 mL/min. At low flow rate we might expect met RBCs to elute in a time greater than 1.9 min/0.096 = 20 min. It is even possible that the met RBCs become immobilized at these low flow rates in which case γ = 0 and R = 0.

At the higher flow rate of 2 mL/min the hydrodynamic lift forces would be much larger and γ could be greater than unity as the balance between force toward the wall is balanced by hydrodynamic lift at some distance from the wall. It is clear that when the higher flow rate is applied to the channel the met RBCs elute from the channel very quickly. At this higher flow rate the void time falls to 0.047 min and we can expect met RBCs of mean magnetophoretic mobility 5.1 × 10⁻⁶ mm³/T.A.s to elute in a time less than 0.49 min. This is indeed seen to occur in Figure 4A. Note that the selection of the two populations of cells, here achieved in the steric mode, has much in common with the previously described selection of magnetic nanoparticle populations in the normal mode of magnetic FFF [26]. The selection was achieved in the normal mode by reducing the magnetic field in stepwise fashion rather than by increasing the flow rate.

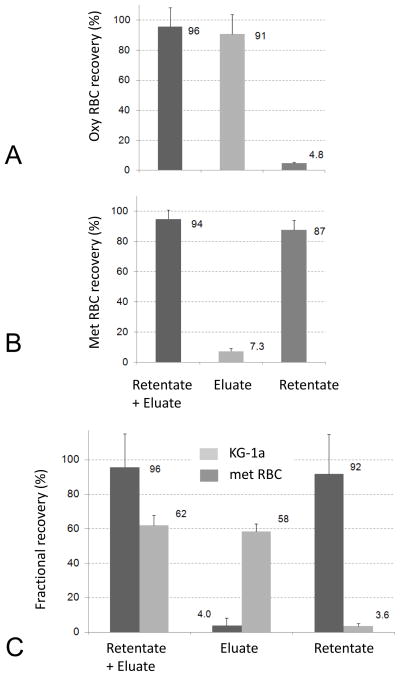
The cell number collected in the eluate following the low flow and high flow phases of the magnetic sorter operation agreed with expectations based on the RBC elution profiles, Figure 5. There was little retention of oxy RBCs in the magnetic field (approx. 5% of the injected cell number, Figure 5A) as expected from the evidence of their eluting early, at low flow rate conditions from the magnet (Figure 4). In contrast, there was a nearly complete retention of the met RBC in the magnetic field (approximately 90%, Figure 5B), again as expected from the evidence of their eluting late, at high flow rate conditions from the magnet (Figure 4). The residual, 5% fractional retention of the oxy RBCs could be related to the natural conversion of hemoglobin to methemoglobin in the blood, known to occur particularly in storage conditions, leading to capture of such RBCs in the magnetic field, even for an oxygenated cell sample. Conversely, the failure to capture ~10% of the met RBCs at low flow rate phase of the separation could be due to incomplete conversion of hemoglobin to methemoglobin during the sample preparation stage. The results of our previous study [11] would suggest that this was unlikely to have been the cause. A more likely cause may be the less than ideal behavior of cells approaching the accumulation wall resulting in lower than predicted fractional cell capture. The total fractional cell capture from both phases of the separation (low flow and high flow) was used as a cell number balance check before and after separation. It shows that all the cells were accounted for after the separation to within the experimental error (nearly 100% total fractional capture in Figures 5A and 5B).

Fig. 5.

A Quantitative distribution of oxy RBC between the eluted and retained fractions (relative to the injected cell number). B Quantitative distribution of met RBC between the eluted and retained fractions. C Fractionation of 50:50 mixtures of deoxy RBC and KG-1a cells inside the magnetic FFF sorter. The “retentate + eluate” columns show total cell recovery in both fractions relative to the injected cell number. The data were obtained using a dual-syringe magnetic FFF setup.

The magnetic RBC separation from 50:50 mixture with the hematopoietic cell line KG-1a showed cell fraction distributions as expected from their natural magnetization, that is KG-1a cells eluting early at low flow rate conditions and met RBC eluting late, only after application of high flow rate of the mobile phase, Figure 5C. The separation was efficient, with only less than 5% KG-1a cell losses in the met RBC fraction, and approximately 5% met RBC contamination in the KG-1a fraction. There was a difference in the recovery of those two, different types of cells, however: the total recovery of the RBCs from those two fractions was complete (to within the experimental error) whereas that for KG-1a cells was only 60%, Figure 5C. The reason for KG-1a losses inside the fluidics system of the magnetic RBC sorter were unclear: the likely causes were related to differences in cell size (larger KG-1a cells were more likely to be caught in the flow stagnation points due to their higher sedimentation rate) and the cell surface properties (the mobile phase composition may have been conducive to KG-1a cell adhesion to surfaces of materials used for the fluidics fabrication). It is also possible that KG-1a cells may be more susceptible to adhesion to channel walls during stop flow than RBCs. The decreased KG-1a recovery increased the undesirable RBC contamination of the KG-1a sorted fraction from 5% (relative to the number of RBCs injected) to 5/65 ≈ 0.077 or 7.7% (relative to the total number of cells sorted).

Conclusions

Taken together, the results of the magnetic field-flow fractionation with step-programmed flow allowed us to determine an upper limit of the magnetic RBC sorting throughput for a given target RBC debulking efficiency. The theory of RBC magnetophoresis and the RBC and KG-1a cell mixture fractionation experiments show that a 5 × 10⁷/mL cell suspension pumped at 0.1 mL/min through a strong, mean magnetic field of 1.5 tesla and gradient of 1,000 T/m is depleted to less than 5% of its original RBC number concentration (based on Figures 3B and 5C). This is equivalent to debulking of approximately 1 μL of whole blood of the RBCs in one minute (assuming normal mean RBC number concentration of 5 × 10⁹/mL). A 5% RBC residual contamination is comparable or better than that typically seen in white blood cell preparations obtained by blood centrifugation [1–3]. Such performance may be well-matched to applications of total analysis systems (TAS) that are based on microfluidics architecture and require on the order of 10 μL whole blood for analysis [6–8]. Thus, the magnetic RBC fractionation may provide simple means of RBC debulking in micro-analytical applications.