Network-assisted analysis to prioritize GWAS results: principles, methods and perspectives

Abstract

Genome-wide association studies (GWAS) have rapidly become a powerful tool in genetic studies of complex diseases and traits. Traditionally, single marker-based tests have been used prevalently in GWAS and have uncovered tens of thousands of disease-associated SNPs. Network-assisted analysis (NAA) of GWAS data is an emerging area in which network-related approaches are developed and utilized to perform advanced analyses of GWAS data in order to study various human diseases or traits. Progress has been made in both methodology development and applications of NAA in GWAS data, and it has already been demonstrated that NAA results may enhance our interpretation and prioritization of candidate genes and markers. Inspired by the strong interest in and high demand for advanced GWAS data analysis, in this review article, we discuss the methodologies and strategies that have been reported for the NAA of GWAS data. Many NAA approaches search for subnetworks and assess the combined effects of multiple genes participating in the resultant subnetworks through a gene set analysis. With no restriction to pre-defined canonical pathways, NAA has the advantage of defining subnetworks with the guidance of the GWAS data under investigation. In addition, some NAA methods prioritize genes from GWAS data based on their interconnections in the reference network. Here, we summarize NAA applications to various diseases and discuss the available options and potential caveats related to their practical usage. Additionally, we provide perspectives regarding this rapidly growing research area.

Introduction

Genome-wide association studies (GWAS) have become a powerful tool to study the genetic architectures of complex diseases and traits in humans. Since the first GWA study was published (Klein et al. 2005), more than 1650 publications of GWA studies, which have pinpointed tens of thousands of single nucleotide polymorphisms (SNPs), have been reported and deposited into the GWAS Catalog (as of August 1, 2013, http://www.genome.gov/gwastudies/) (Hindorff et al. 2009). Conventional GWAS analysis requires disease-associated SNPs to reach the genome-wide significance level (e.g., p < 5 × 10⁻⁸) due to multiple test correction. However, this stringent requirement has excluded many genuinely associated SNPs that have moderate or weak association signals (Wang et al. 2010). As a result, the discovered significant SNPs might only explain a small proportion of genetic risks for most complex diseases or traits, leaving the question of “missing heritability” open to further investigation (Manolio et al. 2009). A number of contributing factors have been hypothesized, such as joint effects of multiple SNPs/genes (Cantor et al. 2010; Wang et al. 2010), epistasis effects (e.g., SNP-SNP interactions and gene-gene interactions) (Hu et al. 2011; McKinney et al. 2009; McKinney and Pajewski 2011), epigenetic regulations, gene-environment interactions, and joint effects of rare variants and common/rare variants (Gibson 2011).

Among these expanded approaches to search for missing heritability, gene set analysis (GSA) of GWAS data, which assesses the combined effects of multiple SNPs/genes, has been of great interest to researchers due to its improved power and biologically interpretable results (Lee et al. 2011; Wang et al. 2010). The rationale of GSA recognizes that while many variants might contribute to complex diseases, with each variant individually creating weak to moderate effects, their combined effects could be significant (Gibson 2010; Yang et al. 2010; Yang et al. 2011). Throughout this review, GSA is denoted as an analytical approach that conducts an enrichment test of a set of genes. The gene set can be defined using canonical pathways (Kanehisa et al. 2010), Gene Ontology (GO) categories (Ashburner et al. 2000), or subnetworks. Pathway-based analysis (PBA) is one type of GSA that uses canonical pathways, GO biological process categories, or other pathway annotations as its gene set unit. So far, PBA approaches have been well-developed for GWAS analyses and successfully applied to the study of various complex diseases (Askland et al. 2009; Askland et al. 2012; Chen et al. 2010; Elbers et al. 2009; Fehringer et al. 2012; Holmans et al. 2009; Jia et al. 2012a; Jia et al. 2010b; Perry et al. 2009; Wang et al. 2007; Wang et al. 2009; Wang et al. 2011a). PBA utilizes pre-defined gene sets based on functional annotations, thereby providing well-annotated biological information and regulation. Readers may refer to several recent review articles (Ramanan et al. 2012; Wang et al. 2010; Wang et al. 2011b) for more detailed discussions.

In contrast to PBA’s reliance on pre-defined gene sets, network-assisted analysis (NAA) can define gene sets flexibly and dynamically using subnetwork search algorithms. Enrichment tests may also be included in NAA. In NAA’s structure, genetic data is overlaid onto a reference network. Then, a search for subnetworks is conducted with the guidance of the GWAS data. The first network-assisted study was reported in an analysis of multiple sclerosis (MS) in 2009 (Baranzini et al. 2009) using the plugin package jActiveModule in the software tool Cytoscape (Shannon et al. 2003). This plugin package was originally developed for the network analysis of gene expression. The authors superimposed genetic association data (p-values) onto a human protein-protein interaction (PPI) network and successfully identified subnetworks that were enriched with MS-associated genes as well as immune- and neurodevelopment-related pathways. Inspired by this successful application, several methods and tools have gained rapid publications. These methods vary in their data management, subnetwork search algorithm, hypothesis testing, and result interpretation. Considering the broadness of network approaches, NAA of GWAS can reach beyond the GSA principle of gene set-based enrichment analysis. Disease Association Protein-Protein Link Evaluator (DAPPLE) is one such expanded approach (Rossin et al. 2011). A set of association loci is required as DAPPLE’s input. Then, this method prioritizes genes based on connectivity in the PPI network (see details below). With the growing awareness of NAA’s advantages, many original GWA or genetic studies have included such analyses to help interpret their association results (Arning et al. 2012; Neale et al. 2012; Xu et al. 2012).

While promising, current development of NAA approaches for GWAS data is still in an early stage. In this article, we aim to review the strategies and methodologies in this emerging field of NAA of GWAS data, the issues that have arisen from real applications, and the challenges that accompany the deluge of new data. Notably, we discuss analyses that are based on networks in which nodes are typically proteins (e.g., PPI networks) rather than other genetic or statistical interaction systems such as SNP-SNP interactions, gene-gene interactions, or interactions built on SNP and expression quantitative trait locus (eQTL) relationships. The methods discussed in this review provide guidelines for future network-assisted analyses of GWAS data.

Demand and rationale in network-assisted analysis of GWAS data

As high-throughput technologies advance rapidly, many GWAS datasets have been published, and many more are expected in the near future. The demand on GSA, PBA, and NAA is strong, as investigators now often search for association signals beyond single markers. Both pathway and network approaches explore combined genetic association signals based on the existing biological knowledgebase. One advantage of these approaches is that the interpretation of the results (enriched pathways or networks) is straightforward. Both NAA and PBA each have their own strengths and weakness. Table 1 summarizes several representative features that distinguish NAA from PBA. PBA has been successfully applied in the study of many diseases. The enriched pathways uncovered by PBA provide insights that might be missed by single marker analysis. However, PBA has several limitations. (1) Results gleaned using different methods differ greatly (Fehringer et al. 2012; Wang et al. 2013). (2) Pathway annotations used in PBA are limited to our current knowledge. For poorly-studied diseases such as dental caries, there is a lack of appropriate canonical biological pathways for PBA. (3) Current pathway annotations cover many pre-defined pathways that may be too general in their delivery of disease-related biological functions (Ruano et al. 2010; Sun 2012). (4) Connections among many genes are lacking within major annotation databases used for PBA, such as the GO database (Farber 2013).

Table 1.

Features of pathway-based and network-assisted analysis approaches

Feature	Pathway-based analysis	Network-assisted analysis
Gene set annotation	Pathways or gene sets from knowledgebase	A reference network
Gene set component genes	Fixed	Dynamic
Search for sub-pathways/subnetworks	No	Yes
Available for topological characteristics	No	Yes
Assess combined association signals	Yes	Available but not required
Function	Focus on one specific function	No particular function boundaries
Correlation amongst genes (or molecules)	Not always available, e.g., GO does not have interactions amongst genes (or molecules)	Available
Hypothesis testing	Q1 vs. Q2*, pre-defined pathways	Multiple and dynamic

^*Details of Q1 and Q2 are provided in Figure 3 and the main text.

NAA provides complementary approaches that may expand the current advanced analysis of GWAS data. NAA relies on network annotations that present functional interactions among genes and their products. A variety of networks are available, such as PPI networks, gene co-expression networks, and regulatory networks. Compared to PBA, NAA is more flexible when defining gene sets throughout the whole network, allowing for the generation and testing of various types of hypotheses. Nevertheless, NAA is not flawless. The PPI data used in NAA tends to contain false positives and is dynamic under specific cellular conditions. The resultant subnetworks typically do not specify biological function as explicitly as canonical pathways.

The rationale behind NAA is the principle of “guilt-by-association (GBA)” (Farber 2013; Lee et al. 2011), which states that genes (or genes’ products) that are interconnected in the network are more likely to share the same or a similar function (Gillis and Pavlidis 2012). Accordingly, studying association signals pulled from GWAS data in the context of a biological network will likely help to uncover disease susceptibility genes and their interactions. A straightforward design for NAA of GWAS data is to search for subnetworks that are both enriched with association signals and contain functional relationships. Several methods have been published based on this concept. In the next section, we discuss the issues and features of these methods, thereby aiming to provide guidelines for the design and implementation of NAA of GWAS data.

Design and methodological issues

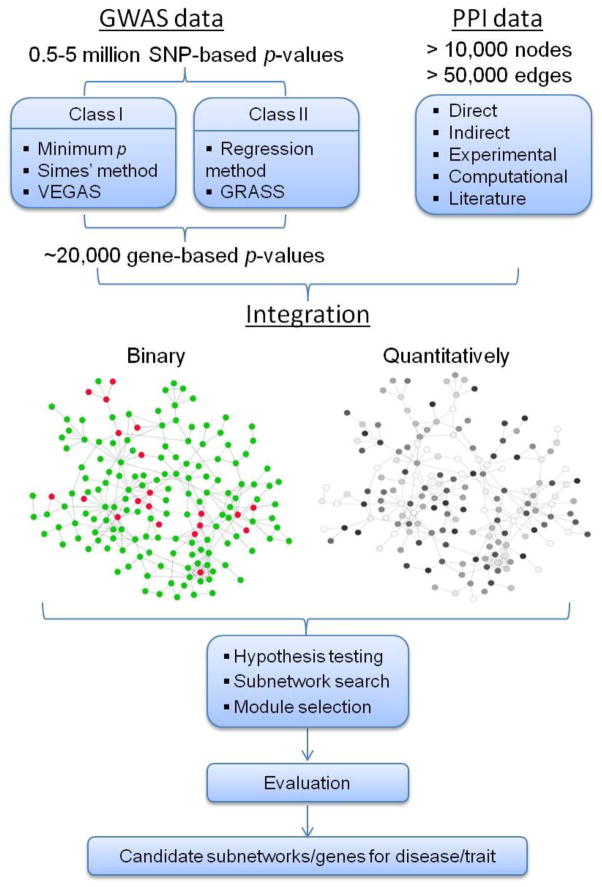
As illustrated in Figure 1, in general, the NAA of GWAS data has the following steps. First, GWAS data is preprocessed to compute SNP-based and gene-based statistical values, which represent their association levels related to the phenotype/disease under investigation. Second, the genetic signals (SNP- or gene-based p values or scores) are overlaid onto the network in a quantitative or qualitative manner. Third, a network-based integrative analysis is performed to explore the topological characteristics of the network, study the connections among genes of interest, and search for subnetworks, among other purposes. Finally, the results are postprocessed and evaluated through the use of significance tests, module selection, follow-up functional analyses of subnetwork genes, and other approaches.

Figure 1.

A general pipeline for network-assisted analysis of data from genome-wide association studies (GWAS).

Preprocess GWAS data: gene-based p-value computation

In GWA studies, association tests are performed for SNP markers, yet PPI network annotation data is based on genes’ products (proteins). Hence, one challenge in NAA is to map SNPs to genes and then compute gene-based statistical values. Accordingly, only SNPs mapped to genic regions are considered when estimating gene-based statistical values, while intergenic SNPs are typically discarded due to the nature of GSA. A genic region is defined by the gene (from gene’s start point to end point) plus its boundary regions (the flanking regions both upstream and downstream of the gene). SNPs that are mapped to their nearest gene region would belong to that gene. In practice, the length of the boundary regions varies from 0 to 500 kb. Using a schizophrenia GWAS dataset genotyped on the Affymetrix 6.0 chip, we previously demonstrated that the total number of informative genes (genes with at least one SNP in the GWAS dataset) increased from ~18,000 to ~20,000 when the gene boundary increased from 5 to 100 kb (Jia et al. 2011a). The SNPs mapped to genic regions increased accordingly from ~307,000 to 509,000 out of the 725,000 genotyped SNPs. Despite this increase, Lee et al. (2011) showed that a change of boundaries from 0 to 250 kb did not significantly affect the power of the related network analysis.

As shown above, the SNP-gene mapping process will result in a gene having multiple SNPs with genotype data. Thus, it is necessary to estimate a gene-based p-value to represent the overall association signal to the gene. So far, there have been many methods to calculate this estimation. They can be categorized into two classes depending on whether it requires raw genotyping data. The first class of methods does not require raw genotyping data. Rather, they use the SNP p-values to compute gene-based p-values (Curtis et al. 2008; Li et al. 2011; Liu et al. 2010; Wang et al. 2007; Zaykin et al. 2007). The most popular method in this class defines a gene-based p-value by using the smallest p-value from all SNPs mapped to its genic region (hereafter denoted as the MinP method). The advantages of the MinP method are its easy implementation and its sensitivity in capturing association signals. However, one disadvantage is that genes represented by more SNPs on genotyping arrays (SNP density, which is usually correlated to gene length) are more likely to have small p-values (Askland et al. 2012; Jia et al. 2012b), thereby introducing biases. Several methods were recently developed to overcome this major disadvantage of the MinP method, such as the Fisher’s method (Curtis et al. 2008), the truncated-product p-value method (Zaykin et al. 2007; Zaykin et al. 2002), the extended Simes’ procedure (Li et al. 2011; Wang et al. 2007), and the versatile gene-based test (VEGAS) (Liu et al. 2010). Among them, VEGAS performs a gene-based association test by considering either all SNPs that are mapped to the gene or a subset of SNPs ranked by significance (through function “Top-x% test” in VEGAS) while accounting for gene length and linkage disequilibrium (LD) structures. Given that a gene has n SNPs for the computation of the gene-based p-value, VEGAS simulates an n-element, multivariate, normally distributed vector using both SNPs’ p-values and pairwise LD values among these n SNPs. VEGAS has been implemented in both online and stand-alone tools. It is easy to use, and its computational time is moderate. One disadvantage is that VEGAS only allows for autosomal genes due to inaccurate LD information from sex chromosomes (Liu et al. 2010).

The second class of methods requires individual genotype and phenotype data and involves various regression-related strategies (Chen et al. 2010; Wang and Abbott 2008; Wu et al. 2010b). Many early works used multivariate regression to compute gene-based p-values. These methods involve a high dimensionality of data (thus, high degree of freedom) and ignore LD information (Mukhopadhyay et al. 2010; Wessel and Schork 2006). Recently, several sophisticated approaches have been proposed to deal with these problems, such as the kernel linear regression (Wu et al. 2010b) and penalized regression (Chen et al. 2010) methods. Because this review article focuses on NAA approaches, readers who are interested in gene based p-value methods are referred to several recent reviews for more details (Dering et al. 2011; Ma et al. 2013; Wu and Cui 2013).

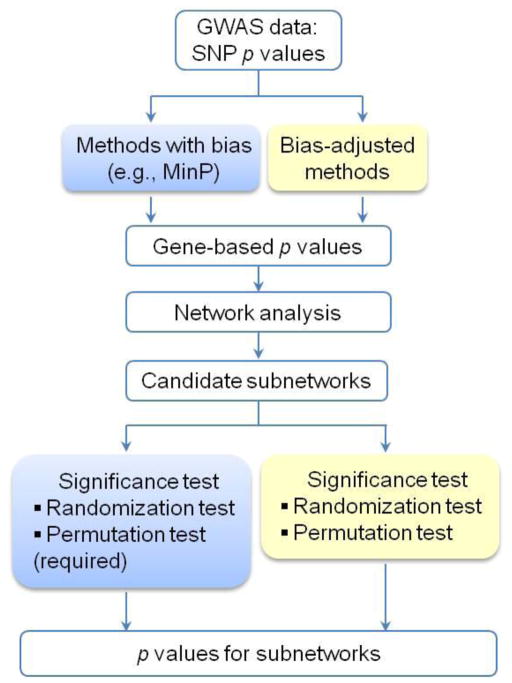
Computing gene-based p-values is critical because it is the first step in both PBA and NAA of GWAS datasets. As shown in Figure 2, if the MinP method is used, a permutation-based test is strongly suggested in the downstream pipeline to adjust for potential biases derived from SNP density and/or gene size. Alternatively, if a method can take into account the potential biases in the gene-based p-value computing step, the significance test in the downstream pipeline would not be necessary for the purpose of adjusting for potential biases (e.g., through permutation test). It is worth noting that intergenic SNPs, with the exception of those located in the boundary region of genes, are largely discarded. Furthermore, genes that currently do not have appropriate pathway or network annotations are excluded in PBA or NAA.

Figure 2.

Overall design of network analysis of GWAS data that addresses potential biases. On the top, the methods in the blue box (e.g., the MinP method) may introduce biases in the computation of gene-based statistics. Therefore, adjustments should be made in downstream steps (blue box in the bottom) by applying a permutation test or other tests. The methods in the yellow box compute gene-based statistics by considering the effects of gene length, LD structure, and SNP density. Thus, an adjustment is not required in those downstream analyses (yellow box in the bottom).

Features of network data

A variety of molecular networks have been actively explored in biological systems, such as the PPI network, metabolic network, regulatory network, gene co-expression network, and so on. We refer to a functional protein network to represent any interactions among proteins, including physical interactions, co-expression, and co-occurrence in literatures. The functional protein network represents a global view of connectivity among genes in terms of their protein interactions. It has been widely used in NAA of GWAS data, primarily because it is straightforward in its examination of the joint genetic effects of multiple related genes. Among the available functional networks, the PPI network has been the most popular resource for NAA. The major sources of the protein network data include (1) large-scale experiments, (2) computational predictions, and (3) literature mining and curation. All of these sources of network data have been exploited in NAA of GWAS. Table 2 lists four specific datasets, which either have previously been applied to the NAA of GWAS data or are suitable for direct applications in disease studies.

Table 2.

Summary of protein networks used in GWAS data analysis

Source	Curation from literature	Computational prediction	High-throughput experiment	Direct	Indirect		Reference
					Co-expression	Phenotype
PINA			•	•			(Wu et al. 2009)
HumanNet	•	•	•	•	•		(Lee et al. 2011)
Lage et al.	•	•	•	•		•	(Lage et al. 2007)
Wu et al.	•	•	•	•	•		(Wu et al. 2010a)

One caveat of PPI data is that most currently available PPI data sets are static and ignore the temporal and spatial dependence of protein interactions in real biological systems. Most of the currently available PPI data derives from large-scale high-throughput experiments in vitro and may not represent tissue-specific information (Barshir et al. 2013). In addition, PPI data is currently far from being complete. It accumulates and changes over time. For example, the BioGRID database (Chatr-Aryamontri et al. 2013), a comprehensive database that collects genetic and protein interaction data from human and model organisms, updates its interaction data monthly. Finally, PPI data is not error-free and may not specifically reflect real cellular conditions.

In addition to the direct and physical interactions gleaned from PPI data, indirect interactions relying on functional correlations could be useful for GWAS analysis (Barabasi et al. 2011; Braun 2012; Lage et al. 2007; Vidal et al. 2011). These indirect interactions include tissue-specific gene co-expression (Lee et al. 2011), literature co-citation, and genetic interactions (Hu et al. 2011), among others. Compared to physical interactions, these functional interactions are more biologically relevant to diseases or traits and, thus, instrumental to the discovery of meaningful subnetworks enriched with GWAS signals. For example, disease-relevant tissue data, such as gene co-expression correlations, may be of special interest due to its tissue-specific information, as demonstrated in specific studies of obstructive sleep apnea (Liu et al. 2011) and autism (Ben-David and Shifman 2012). Details of these data resources can be found in additional reviews elsewhere (Barabasi et al. 2011; Vidal et al. 2011).

Construction of subnetworks

In general, NAA of GWAS data starts with certain pre-defined “seed” genes from the original GWAS data. Seed genes can range from a small set of pre-selected interesting genes (e.g., genes with p < 5×10⁻⁸) to all genes mapped onto a reference network (i.e., iteratively take each gene as a seed). NAA expands from the seed genes to a subnetwork by searching the whole network and then assessing the statistical significance of the resultant candidate subnetworks. We summarized the subnetwork construction approaches in the following five points.

Binary versus quantitative

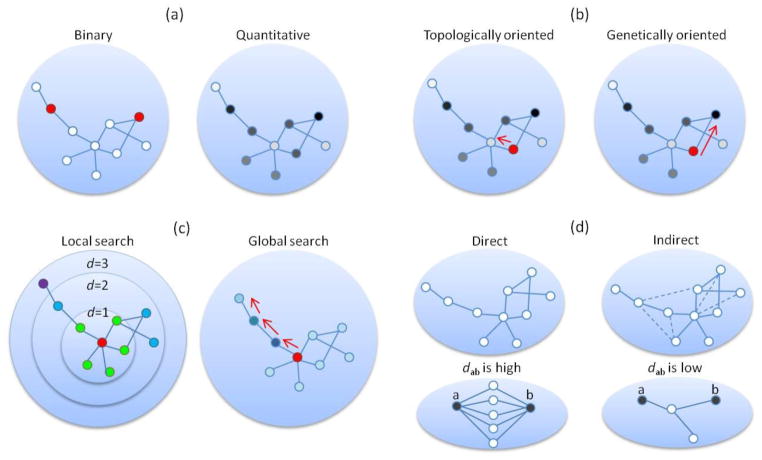
Each gene extracted from the GWAS data is denoted by a statistical value (e.g., gene-based p-value) to represent its disease-association level. Depending on how these quantitative genetic signals are used, NAA methods can be categorized into two groups (Figure 4a). The first group dichotomizes genes by selecting a set of interesting genes (e.g., genes with p < 5×10⁻⁸) and uses these interesting genes as input query genes (i.e., seed genes) (Rossin et al. 2011). In this group of methods, GWAS data is only used to select interesting genes, and the subsequent analyses generally do not require further information from the GWAS dataset (Rossin et al. 2011). The second group of methods overlays the quantitative signal of each gene onto the whole network to build a node-weighted network. The node weights are transformed from the association significance values (i.e., gene-based p-values) (Akula et al. 2011; Baranzini et al. 2009; Jia et al. 2011b; Liu et al. 2011). Then, the search process is guided by the node weights.

Figure 4.

Algorithms in network-assisted analysis of GWAS data. Nodes represent genes. Red nodes denote seed genes. (a) Two representations of gene association signals: binary (left) versus quantitative (right). Gene-based association signals are indicated by color and darkness: red/white for seed/non-seed genes (left) and darkness level proportional to the association strength (right). (b) Search methods guided by topological characteristics (left) or genetic signals (right). Starting from a seed gene (in red), the former method searches for candidate genes with significant topological characteristics (e.g., genes with high degree), while the latter method searches for candidate genes with strong association signals (nodes in dark color). (c) Search that is restricted by local paths or global paths. Nodes are categorized according to their distance (d, defined by shortest path) from the seed gene (in red), e.g., nodes with d=1 (in green), d=2 (in blue), and d=3 (in purple). In local searches, only nodes that are located within a pre-defined distance (e.g., d≤2) from the seed genes are considered. In global searches, the search space is not defined by d but could theoretically access every node in the network. (d) Search methods in the space of direct and indirect (dash lines) interactions. Suppose d_ab represents the closeness between two nodes, a and b, in the network. When many paths exist between the nodes, these nodes are considered to be close to each other in network space, and their closeness (d_ab) is high. On the other hand, if there are few paths (in the bottom right panel, only one path exists between nodes a and b), the d_ab of these nodes is low.

Topologically oriented versus genetically oriented

One advantage of network analysis is that the topological structure of a network reflects biological interactions among nodes (proteins encoded by genes). Previous studies in network medicine have explored a number of similarly expressed hypotheses based on the principle of guilt-by-association, such as “proteins involved in the same disease are more likely to interact with each other,” or, conversely, “proteins closely located in the network tend to lead to similar disease phenotypes” (Barabasi et al. 2011). Depending on how the topological structure is applied within the analysis of GWAS data, NAA methods can be categorized as topologically oriented, genetically oriented, or a combination of both (Figure 4b). Topologically oriented methods leverage topological features such as degrees and shortest paths to build disease-subnetworks (Lee et al. 2011). As illustrated in Figure 4b, in every subnetwork-expansion step, those nodes that have the most important topological signatures (e.g., those nodes with the largest degree) tend to be selected. Because of this feature, the resultant subnetwork gleaned using a topologically oriented method greatly depends on the reference network. Thus, topological features may be included in computation of subnetwork scores in these methods. Genetically oriented methods use genetic signals to guide the search for disease subnetworks (Baranzini et al. 2009; Jensen et al. 2011; Jia et al. 2011b). In the expansion step, genetically oriented methods recruit the nodes that have the most significant association signals (Figure 4b). Subnetwork scores are typically computed by combining the genetic signals of all the nodes in the subnetwork in genetically oriented methods. A third design leverages features from both types of methods. For instance, Akula et al. (2011) calculated a combined score of a subnetwork using the Liptak-Stouffer method: $z_{\mathit{comb}}=\frac{\sum w_i{z}_i}{\sqrt{\sum w_i^2}}$, where z_i is converted from a gene-based p-value of the component genes in the subnetwork, and w_i is the gene-based weight obtained from the modified Google PageRank algorithm. Thus, this approach accounts for both topological and genetic characteristics of the genes (Akula et al. 2011).

Global versus local search

Given a node-weighted reference PPI network, the search path of a disease-related subnetwork may either reach all the nodes in the network or be restricted to reach a certain distance from the seed genes (Figure 4c). Starting with the seed genes, a global search theoretically allows for access to every node in the network as long as there are available paths (Baranzini et al. 2009; Jia et al. 2011b; Lee et al. 2011). For local searches, only the nodes and edges that are located within pre-defined distances, e.g., 2 steps away from the query seed genes, are explored and evaluated (Akula et al. 2011; Rossin et al. 2011).

Prioritization versus combination

Some of the published methods prioritize candidate genes, while others assess the combined effect of a set of genes without accounting for the particular rank of each individual gene in the resultant subnetwork. The main purpose of gene prioritization is to find disease candidate genes. Many methods for gene prioritization (Bornigen et al. 2012; Kohler et al. 2008; Sun et al. 2009) can be adapted to GWAS data analysis. Starting with a list of reference genes (e.g., known disease genes), these gene prioritization methods uncover the features of the reference genes and rank the candidate genes to identify new, potentially disease-associated genes. In GWA studies with a multi-stage design, gene prioritization is particularly useful in the selection of candidate genes/markers at the initial stage. Then, the prioritized genes are recruited for deep and dense genotyping in the later stage(s) (e.g., stage 2 or stage 3 for replication). Representative prioritization methods, such as GRAIL (Raychaudhuri et al. 2009) and DAPPLE (Rossin et al. 2011), have the functions to facilitate candidate gene prioritization. On the other hand, methods that focus on combined gene effects evaluate genes in a subnetwork as a whole (Akula et al. 2011; Jia et al. 2011b) with no particular rank for each gene in the subnetwork. A permutation test is often implemented in these methods to assess disease associations.

Direct versus indirect interactions

Most network-based methods used for the analysis of GWAS data are built on direct interactions among proteins (Akula et al. 2011; Baranzini et al. 2009; Jia et al. 2011b; Liu et al. 2011). Recently, indirect connections have drawn increasing attention. These connections describe the closeness of nodes in a network rather than relying on direct interactions. Figure 4d illustrates the scenarios of direct and indirect interactions. For instance, two disconnected proteins in the network (nodes a and b) that are highly reachable through the paths between them are more likely to be involved in the same disease than two proteins that have only sparse paths between them (Figure 4d). The diffusion kernel-based network model is one of the emerging methods that incorporate indirect interactions (Barabasi et al. 2011; Kohler et al. 2008; Kondor and Lafferty 2002). This type of method has been widely used in network medicine but, to date, has been rarely applied in GWAS data. One pioneering application by Lee et al. (2011) explored six network methods to assess their capability to boost the statistical power of GWA studies and detect disease candidate genes. Considering their strength in the measurement of the global distance in a network (Kohler et al. 2008; Nitsch et al. 2009), kernel-based models warrant future expansion and applications.

Statistical significance tests

After obtaining candidate subnetworks, an important next step is to evaluate and select subnetworks by utilizing appropriate significance tests. Two hypotheses have been widely formulated and followed in most GSA of GWAS data (Wang et al. 2010; Wang et al. 2011b). The competitive null hypothesis (Q1) states that the genes in a gene set have the same association levels with the investigated disease compared with the genes outside of the gene set. The self-contained null hypothesis (Q2) states that the genes in a gene-set are not associated with the given disease (Figure 3). Because of the dynamics in subnetwork searches and due to different network algorithm features, the traditional multiple testing correction methods (e.g., Bonferroni correction) are generally not applicable to NAA. In practice, estimation of the null distribution through randomization or permutation tests is popular to assess the significance of the results. In general, a randomization test is typically adopted in Q1-related methods, while permutation analysis is more appropriate for assessing the results obtained by Q2-related methods (Figure 3).

Figure 3.

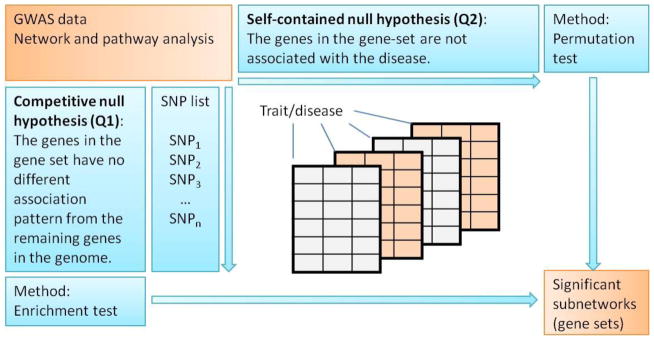
Two types of hypothesis testing in GWAS gene set enrichment analysis. Starting with the original GWAS data, the competitive null hypothesis (Q1) tests whether the genes in a gene set have the same association pattern compared with the remaining genes in the genome. The self-contained null hypothesis (Q2) tests whether the genes in a gene set are associated with the studied disease or not. To test Q1, a randomization of SNP markers or genes is typically adopted, and to test Q2, a permutation of case/control labels is utilized.

In randomization tests, random networks are first generated to estimate the null distribution. Then, the results obtained in the actual reference network are assessed for significance by comparing them with the null distribution. The approaches to generate random networks are quite diverse, including various node- and edge-related randomization strategies. A number of previous investigations have proved that the whole human PPI network behaves in a scale-free fashion. One feature of scale-free networks is that a small portion of nodes have numerous interacting partner nodes (i.e., “hub” nodes/genes). Accordingly, they are more likely to be included in subnetworks by chance in NAA. However, when generating random network data, many methods ignore the topological features of the nodes and treat all nodes equally. To control the potential biases, Li et al. (2009) suggested the generation of topologically-matched random networks according to degree and clustering coefficients. In another work by Rossin et al. (2011), random networks were built using matching node degrees.

In permutation tests, randomized phenotype data is generated to estimate the null distribution, e.g., by swapping case and control labels in the GWAS data. Then, subnetworks were assessed using both the actual and permuted GWAS datasets. Permutation tests, although often computationally intensive and requiring raw genotype data, have been found to be effective to adjust for various biases, such as the long gene bias, as discussed in a recent survey (Jia et al. 2010a). Permutation tests are especially applicable when the MinP method is used. Due to its computational intensity, a permutation test cannot be practically implemented in most online tools. However, it can be conveniently incorporated in stand-alone computer programs. We expect that the development of future NAA tools for GWAS data will take into consideration both computational efficiency and practical convenience.

Analysis procedures

GWAS datasets collected from different consortia, ethnic populations, or technical platforms are now available for many complex diseases or traits. New approaches are needed to take advantage of the multiple datasets for the same diseases or traits. In a recent publication, Jia et al. (2012c) proposed an approach using two schizophrenia GWAS datasets, one as discovery and another as an evaluation dataset, to find subnetworks that are consistently highly scored in both datasets. This approach may be applied to the same analysis method for multiple GWAS datasets (cross-dataset validation), different methods for the same GWAS dataset (cross-method validation), or both.

NAA Methods

There are a number of publications regarding the network analysis of GWAS data. These publications are either methodology-oriented or discovery-oriented (Table 3). Below, we selected several representative approaches for detailed discussion.

Table 3.

Published network-based methods for GWAS data analysis

Method	Genetic measurement	Strategy	Association test	Randomization test	Software	Reference
jActiveModule	Quantitative	Combinatory	No	Yes	Stand-alone	(Baranzini et al. 2009; Burcu and Osman Ugur 2011; Liu et al. 2011)
dmGWAS	Quantitative	Combinatory	Yes	Yes	Stand-alone	(Jia et al. 2011b)
NIMMI	Quantitative	Combinatory	No	No	Stand-alone	(Akula et al. 2011)
DAPPLE	Binary	Prioritization	No	Yes	Online	(Rossin et al. 2011)
Lee et al.	Quantitative	Prioritization	No	NA	NA	(Lee et al. 2011)
NetworkMiner	Quantitative	Combinatory	No	Yes	Online	(Garcia-Alonso et al. 2012)

Methods based on jActiveModule

jActiveModule is a plugin package in the software tool Cytoscape (Shannon et al. 2003) and was initially developed for gene expression data analysis (Ideker et al. 2002). The original model works on a node-weighted PPI network where node weights are represented by z-scores converted from gene-based p-values, e.g., z = Φ⁻¹(1−p). The underlying algorithm of jActiveModule relies on a greedy search. The algorithm starts with “seed” genes and recruits the best nodes in the neighborhood of the seeds in each expansion step. Module expansion stops when it does not satisfy the pre-defined criteria, e.g., if the module score increase is too small to reach the cutoff value. Then, modules are evaluated using a randomization test. In gene expression data and in most applications of jActiveModule to GWAS data, the module score (z_m) is computed by combining node weights using the Liptak-Stouffer z- score method (Ideker et al. 2002), $z_m=\sum z_i/\sqrt{k}$, where k is the number of nodes in the subnetwork, and z_i is the node weight. Recent studies have started to incorporate genotyping data features in the computation of network scores based on either the correlations among genes/SNPs (Pedroso et al. 2012) or the topological features of gene products (Akula et al. 2011).

jActiveModule is a well-developed model in Cytoscape, and it only requires a gene-based z-score. Thus, it can be easily adapted to GWAS data analysis. For example, node weights can be computed based on GWAS p-values instead of gene expression p-values. A protocol called PANOGA describes the details of using jActiveModule for GWAS data (Burcu and Osman Ugur 2012). So far, jActiveModule has been one of the most widely used network methods in GWAS data analysis (Table 4), with applications in multiple sclerosis (Baranzini et al. 2009), obstructive sleep apnea (Liu et al. 2011), and rheumatoid arthritis (Burcu and Osman Ugur 2011).

Table 4.

Network-assisted GWAS studies

Phenotype/disease	Method	Type	Epub. date	Reference
Multiple sclerosis	jActiveModule	Methodology	Mar. 2009	(Baranzini et al. 2009)
Multiple sclerosis	jActiveModule	Application	May 2010	(Baranzini et al. 2010)
Breast cancer and pancreatic cancer	dmGWAS	Methodology	Nov. 2010	(Jia et al. 2011b)
Obstructive sleep apnea	jActiveModule	Application	Dec. 2010	(Liu et al. 2011)
Rheumatoid arthritis, Crohn’s disease, height, lipids, and type 2 diabetes	DAPPLE	Methodology	Jan. 2011	(Rossin et al. 2011)
Crohn’s disease and type 2 diabetes	Label propagation algorithm	Methodology	May 2011	(Lee et al. 2011)
Seven immune-mediated and autoimmune diseases	DAPPLE	Application	Aug. 2011	(Cotsapas et al. 2011)
Mood disorders	Michigan Molecular Interactions (MiMI)	Application	2011	(Detera-Wadleigh and Akula 2011)
Height, Crohn’s disease	NIMMI	Methodology	Sep. 2011	(Akula et al. 2011)
Rheumatoid arthritis	PANOGA	Application	Oct. 2011	(Burcu and Osman Ugur 2011, 2012)
Bipolar disorder	Greedy search modified from jActiveModule	Methodology	Apr. 2012	(Pedroso et al. 2012)
Bipolar disorder	NetworkMiner	Methodology	Jun. 2012	(Garcia-Alonso et al. 2012)
Schizophrenia	dmGWAS	Application	Jul. 2012	(Jia et al. 2012c)
Alzheimer disease	DAPPLE	Application	Apr. 2012	(Raj et al. 2012)
Multiple sclerosis	DAPPLE	Application	Oct. 2012	(Ragnedda et al. 2012)
Pediatric stroke	dmGWAS	Application	Dec. 2012	(Arning et al. 2012)

While it is easy to run, jActiveModule was developed originally as a tool to analyze gene expression data rather than GWAS data. This fact creates several potential issues. First, in gene expression data, the majority of genes are not differentially expressed (DE) and these gene p-values are evenly distributed between 0 and 1, with an exception of DE genes. Therefore, the converted z-scores are expected to evenly fall into the intervals that are less than 0 and greater than 0. In GWAS data, however, the SNP p-values, instead of gene p-values, are presumably evenly distributed between 0 and 1, with the exception of disease-associated SNPs. Depending on how the gene-based p-values are computed, the results could be substantially skewed. For example, in the MinP method, gene-based p-values are biased towards 0, causing an uneven distribution of the converted z-scores (Jia and Zhao 2012). This outcome, in turn, results in extremely high module scores, making the selection of modules difficult (Baranzini et al. 2009; Jia et al. 2011b). To solve this problem, multiple strategies may be considered. For instance, gene-based p-values can be computed using more sophisticated methods rather than the MinP method (see above). Alternatively, additional steps can be introduced in the downstream analysis to adjust for biases (Figure 3) (Jia et al. 2012c). It should also be considered that, since jActiveModule was originally developed for analyzing gene expression data, the permutation test for GWAS data is not implemented in jActiveModule. When users perform an association test (Q2), additional work is needed to implement a permutation test on the resultant modules from jActiveModule.

dmGWAS

dmGWAS is the first tool to implement a network-based method specifically for GWAS data analysis (Jia et al. 2011b). It allows for a quantitative global search using the association signals for guidance. Although built initially on the design of jActiveModule, dmGWAS includes functions to facilitate the analysis of genetic data, such as the computation of gene-based p-values and implementation of permutation tests. dmGWAS implemented several methods for computing gene-based p-values, including the MinP method, the Simes’ method (Wang et al. 2007), the Fisher’s method, and the method that uses the smallest gene-based false discovery data value (Jia et al. 2011b; Peng et al. 2010). However, for sophisticated methods such as VEGAS (Liu et al. 2010), the user needs to compute gene-based p-values using independent tools first. Overall, the NAA strategy implemented in dmGWAS is to search for subnetworks that are significantly associated with a specific disease or trait.

NIMMI

The software tool Network Interface Miner for Multigenic Interactions (NIMMI) (Akula et al. 2011) applies a local search to find subnetworks that have high combined scores. NIMMI is the first NAA tool to integrate topological features with genetic signals. It computes a combined score using the Liptak-Stouffer method, i.e., $Z_{\mathit{comb}}=\sum w_i{z}_i/\sqrt{\sum w_i^2}$, where z_i is the z-score converted from gene-based p-values, and w_i represents topological features computed using a modified Google PageRank method (Akula et al. 2011). NIMMI requires nodes in the subnetworks to be within a certain distance (d) from the seed nodes. A distance of 2 was suggested in the original work (Akula et al. 2011) (Figure 4c). One disadvantage of NIMMI is that the resultant subnetworks contain all the nodes that are d steps away from the seed without further filtering. Correspondingly, the subnetworks would include many unrelated nodes and tend to be too large to prioritize genes for follow up investigations.

DAPPLE

DAPPLE performs local searches and evaluates whether genes located in association loci are significantly connected in the PPI network. In implementation, DAPPLE takes associated loci, or the genes located within the loci, as input seed genes. Importantly, DAPPLE’s search steps do not rely on quantitative genetic data. Two sets of interactions are defined in DAPPLE: (1) direct interactions among any two proteins encoded by the genes located in association loci and (2) indirect interactions, in which two association proteins are linked through a third protein. DAPPLE also implements a series of comprehensive randomization tests, including node-label randomization, to assess the significance of the interactions. Because DAPPLE only needs a set of interesting genes as its input, it can be easily extended to many other cases for the study of candidate genes that are not necessarily derived from GWAS (Neale et al. 2012; Sanders et al. 2012). In addition, DAPPLE provides a convenient online tool for users to upload the candidate gene list(s) for analysis.

One limitation of DAPPLE is that it heavily relies on how the association loci are defined, as only genes located in these loci are used. So far, 5×10⁻⁸ has been widely accepted as the genome-wide significance cutoff p-value to select disease-associated SNPs in GWA studies. However, for studies in which no significant loci were identified by this stringent threshold (Sullivan et al. 2008), the selection of association loci could be arbitrary. Of note, the GWAS signals are only used in the first stage to define input genes in DAPPLE. In fact, the search step for interactions in DAPPLE is independent of GWAS data but depends on the reference PPI network.

Perspectives for future work

With the rapid accumulation of GWAS data, investigators are now facing more challenges related to advanced analyses of multiple GWAS datasets for complex diseases or traits. These datasets were generated using different platforms, were sourced from different ethnic populations, or were initially analyzed by different groups or consortia. NAA approaches are expected to address issues involving multiple datasets, multi-dimensional data types, and different types of variants. Previous studies have demonstrated the utilization of multiple GWAS datasets to validate the discovered pathways in PBA (Fehringer et al. 2012; Wang et al. 2009). Based on these studies, NAA is suggested to incorporate cross-dataset designs as well. For example, candidate subnetworks identified in one GWAS dataset (discovery stage) could be further validated in an independent GWAS dataset (evaluation stage) for the same disease or trait using the same NAA method (Jia et al. 2012c).

Most NAA approaches discussed in this review focus on the integration of GWAS data with PPI data. In addition to PPIs, other data, such as gene expression data at pathway levels (Xiong et al. 2012; Zhang et al. 2012) and co-expression networks (Farber 2010), can also be used in NAA. One recent study constructed regulatory networks consisting of SNPs and genes as nodes and their correlations as edges (Zhu et al. 2012). Furthermore, a protein-interaction-network-based pathway analysis (PINBPA) was proposed and successfully applied to two large genetic studies of multiple sclerosis (International Multiple Sclerosis Genetics Consortium 2013). Many network-related approaches that have been applied to other biological data, such as somatic mutation data (Ng et al. 2012; Vaske et al. 2010), mRNA abundance data (Chuang et al. 2007), and methylation data, may be adapted and incorporated in the NAA of GWAS data. With the rapid accumulation of genetic and genomic data, multi-dimensional integration is expected to gain more attention in the near future than canonical single domain based approaches.

Expanding NAA to incorporate a full spectrum of genetic variants, including common, rare, and de novo SNPs, is another potential direction. Advances in next-generation sequencing technologies have revolutionized biological and biomedical research, including related search methods for association signals in complex diseases and traits. The high volume of single-nucleotide variants uncovered in each single human genome or exome creates both challenges and opportunities for genetic studies. The richness and variety of hypothesis testing methods in network medicine provide multiple directions to facilitate the study of genetic variants within network data. Rare variants are typically computed for each gene by collapsing them in gene regions. These gene-based p-values from rare variants can be integrated into the PPI network using the same approach that is used for common variants. For instance, one could search for subnetworks that are enriched with rare variants for a disease. It is also of interest to test whether the genes pulled based on rare variant associations are connected via PPIs in a non-random manner (Neale et al. 2012; Sanders et al. 2012). Gilman et al. (2012) designed an approach named NETBAG for NAA of rare de novo variants (Gilman et al. 2011), and they later successfully extended their approach to diverse types of genetic variants. These works demonstrate the tendency of genetic variants to converge on functional gene networks in schizophrenia. With this proof of concept, new NAA approaches that incorporate various genetic data are expected to be in high demand in the near future.

Conclusion

In summary, we discussed the main features of network-based analyses of GWAS data and highlighted key issues in the design, implementation, and application of these network-based methods. So far, the available methods vary in their hypothesis testing, search algorithm, integration strategy, and additional useful features. Specifically, we reviewed four NAA methods in detail. We expect more GWAS data at both genotyping array and sequencing levels to be generated in the near future. These new datasets, along with existing GWAS datasets, will help us to fine-tune network-based methods. Furthermore, these enhanced methods and computational tools will further help to uncover genes and subnetworks that might play a role in complex diseases or traits.