Enslaving in a serial chain: Interactions between grip force and hand force in isometric tasks

Abstract

This study was motivated by the double action of extrinsic hand muscles that produce grip force and also contribute to wrist torque. We explored interactions between grip force and wrist torque in isometric force production tasks. In particular, we tested a hypothesis that an intentional change in one of the two kinetic variables would produce an unintentional change in the other (enslaving). When young healthy subjects produced accurate changes in the grip force, only minor effects on the force produced by the hand (by wrist flexion/extension action) were observed. In contrast, a change in the hand force produced consistent changes in grip force in the same direction. The magnitude of such unintentional grip force change was stronger for intentional hand force decrease as compared to hand force increase. These effects increased with the magnitude of the initial grip force. When the subjects were asked to produce accurate total force computed as the sum of the hand and grip forces, strong negative co-variation between the two forces was seen across trials interpreted as a synergy stabilizing the total force. An index of this synergy was higher in the space of “modes”, hypothetical signals to the two effectors that could be changed by the controller one at a time. We interpret the complex enslaving effects (positive force co-variation) as conditioned by typical everyday tasks. The presence of synergic effects (negative, task-specific force co-variation) can be naturally interpreted within the referent configuration hypothesis.

Introduction

A central feature of the human motor system is the presence of redundancy (Bernstein 1967). It implies that the number of variables at a selected level of analysis (called elemental variables) is higher than the number of task-imposed constraints. Consequently, there are infinite ways in which a task can be accomplished. The phenomenon of redundancy is sometimes viewed as a problem for the central nervous system (CNS): It must come up with a unique way of executing a desired task, for example by minimizing some cost incurred by the system in executing that choice (Prilutsky and Zatsiorsky 2002). Conversely, motor redundancy is recast as motor abundance (Gelfand and Latash 1998; Latash 2012); this position assumes that the CNS facilitates a family of solutions that can accomplish a task.

Studies of joint moment coordination in a serial multi-joint chain present an interesting challenge related to the presence of bi- and multi-articular muscles (Ambike et al. 2013). Such muscles naturally couple moments in different joints and may be expected to produce unintentional joint moment changes when the person tries to perform an action by another joint of the chain. Similar phenomena have been described in studies of finger interaction and are addressed as lack of finger individuation or finger enslaving. Enslaving has been defined as unintentional fingertip force production (or motion) by a fingertip when another finger of the hand generates force (moves) intentionally (Kilbreath and Gandevia 1994; Zatsiorsky et al. 1998, 2000; Kim et al. 2008).

The human digits are served by two main muscle groups, intrinsic (with the bellies in the hand) and extrinsic (with the bellies in the forearm). The tendons of the extrinsic muscles, such as Flexor Digitorum Profundus (FDP), Flexor Digitorum Superficialis (FDS), Extensor Digitorum Communis (EDC) and Flexor Pollicis Longus (FPL), cross the wrist joint. As a result, these muscles act as wrist flexors and extensors. In this study, we focus on the interactions between isometric hand force (F_H) production via isometric wrist flexion or extension effort and grip-force (F_G) production. Grip force is the set of forces with zero resultant exerted by the digits on a hand-held object normal to the contact surfaces. The digit tips exert forces primarily due to the activation of the FDP and the FDS muscles, although all other muscles (intrinsic and extrinsic) naturally contribute to the generated force. The salient point in the present study is that the primary digit actuators are multi-joint, and therefore, they potentially affect grip force production as well as wrist action. These muscles also pass through the wrist joint, and they are important wrist flexors (Chao et al. 1989; Brand and Hollister 1999; Platzer 2004). Therefore, when a person tries to produce a change in F_G, wrist moment of force may be expected to change unintentionally due to the wrist-flexion action of the FDP. Along similar lines, when a person tries to exert isometric flexion or extension effort with the wrist (i.e., change F_H) while keeping a certain level of F_G, the latter force may show unintentional change. Our first goal has been to test this hypothesis and quantify such bidirectional enslaving effects between F_G and F_H.

In planar statics, a multi-joint serial chain with more than three joints is over-constrained in force production tasks (Zatsiorsky 2002). Indeed, if the vector of endpoint force/moment is defined, torques in all joints, no matter how many, can be unambiguously computed for a given configuration of the chain. The problem of motor redundancy emerges if only some components of the endpoint force/moment vector are prescribed by the task, for example the force vector, while other components (for example, the moment vector) are left unconstrained (Xu et al. 2012).

We used the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2002, 2007) to explore whether two effectors in a serial chain can co-vary their outputs, F_G and F_H, to produce an accurate common performance variable. The UCM hypothesis assumes that the CNS acts in the elemental-variable space and organizes a solution space (UCM) in that space corresponding to a desired value of a task-specified performance variable. Further, the CNS acts to minimize the variability orthogonal to the UCM (V_ORT) and allows large variability along the UCM (V_UCM). If V_UCM > V_ORT, both quantified per degree of freedom in the corresponding spaces, a conclusion can be drawn that the CNS organizes a synergy stabilizing the performance variable, for which the two variance components have been quantified (reviewed in Latash et al. 2002, 2007). Such synergies have been demonstrated for kinematic variables in serial chains during sit-to-stand and pointing movements (Scholz and Schöner 1999), and for kinetic variables in parallel chains during finger force and moment of force-production tasks (Latash et al. 2001; Park et al. 2010).

The wrist-hand system can be viewed as a two-element serial chain, and our second goal was to explore whether isometric actions of this chain can co-vary to stabilize a value of a certain commonly produced variable, for example total force (F_H + F_G). While there is little ecological value in producing a constant value of (F_H + F_G), we decided to use this artificial task motivated by earlier studies of parallel effectors, such as two digits pressing in parallel, that have shown strong synergies stabilizing the sum of the two forces (Latash et al. 2001; Wu et al. 2012). To our knowledge, this is the first study to explore such synergies in a serial chain. The mentioned presence of multi-articular finger flexors favors positive co-variation of the two forces, while a synergy stabilizing their sum requires their negative co-variation. We hypothesized that the CNS would be able to overcome possible effects of across-element force inter-dependence (enslaving) and organize a synergy stabilizing the total force such that V_UCM > V_ORT.

Methods

Subjects

Seven male subjects participated in this experiment. Their age (mean ± SD) was 30.9 ± 3.9 years, height 177.6 ± 5.7 cm, mass 77.1 ± 10.0 kg, hand length from the proximal palmar crease to the tip of the middle finger 18.5 ± 1.2 cm. All subjects were right-handed. None of them reported a history of neurological or upper extremity pathology. Each subject provided informed consent according to The Pennsylvania State University Institutional Review Board.

Apparatus

Subjects were seated with the right arm resting in the force measurement device (Figure 1). The shoulder was abducted at 45° and flexed at 0°. A wooden platform was constructed to support the right forearm horizontally in a mid-prone position with the elbow flexed at 90° and the wrist slightly extended in a comfortable position. The wrist position was kept the same across tests and subjects. The forearm was strapped to the platform to prevent relative motion.

Figure 1.

An illustration of the instrumented handle (left) and the hand position during the experiment (right).

The hand was placed between an aluminum rod and an aluminum plate, such that the palm was in contact with the rod and the back of the hand was in contact with the plate (shown in Figure 1). Both, the rod and the plate were attached to a six-component transducer (PY6, Bertec Co., Columbus, OH, USA) via a U-shape metal part. The six-component transducer was fixed to the wooden platform. This arrangement allowed the wrist to exert flexion or extension effort in isometric conditions. The sensor measured the hand force (F_H) as the force along the Z axis that results from isometric flexion or extension wrist effort. In addition, subjects held an instrumented aluminum handle (0.3 kg) with their digit tips. The tip of each digit (thumb T, index I, middle M, ring R, little L) was placed on a six-component (three forces and three moments) transducer (Nano-25 for T and Nano-17 for the four fingers, ATI Industrial Automation, Garner, USA) as shown in Figure 1. The distance between finger sensors (I, M, R and L) was 30 mm, and the distance between the face of the thumb sensor and the finger sensors was 60 mm. Grip force (F_G) was computed from the normal force components (measured along the finger sensor Z axis) as the absolute value of the sum of the normal forces of all fingers (Σ|F_Zi|, with i= T, I, M, R and L).

Procedures

The experiment had four parts. Part I (Baseline) consisted of a series of control tests: the subjects were instructed to hold the handle ‘naturally’ (Natural-grip). Next, they performed maximal voluntary contraction (MVC) task for F_G (“squeeze the handle as hard as you can”). During this task, visual feedback on F_G was provided. Next, subjects performed isometric MVC tasks for F_H produced by flexion or extension wrist effort while holding the handle (“press as strongly as possible on the rod/plate”). The feedback on F_H was provided. Three trials for each task lasting 5 s each were performed with 30 s rest intervals.

During Part II of the experiment (Ramp Task), subjects were required initially to produce a constant specified force for one force variable (F_G or F_H) and then follow a ramp profile depicted in Figure 2 with the other force variable, while ignoring possible changes in the former variable. The first force variable will be addressed as the enslaved variable and the second variable will be called the master variable in the rest of this paper. The following four conditions were tested. (1) The enslaved variable was F_G. Subjects held the instrumented handle with a specified grip force (F_G = N, with N = {Natural, 10%, 30%, and 50% of the F_G MVC}) and performed the ramp tasks with flexion F_H. (2) The same as condition (1), but the ramp task was performed with extension F_H. (3) The enslaved variable was F_H. Subjects applied a specified wrist flexion F_H (F_H = N, with N = {0, 10%, 30%, and 50% of flexion F_H MVC}) and performed the ramp tasks with F_G. (4) The same as (3) but the specified force was extension F_H. Three 15 s long trials for each level of force were performed with a resting time of 20 s between trials.

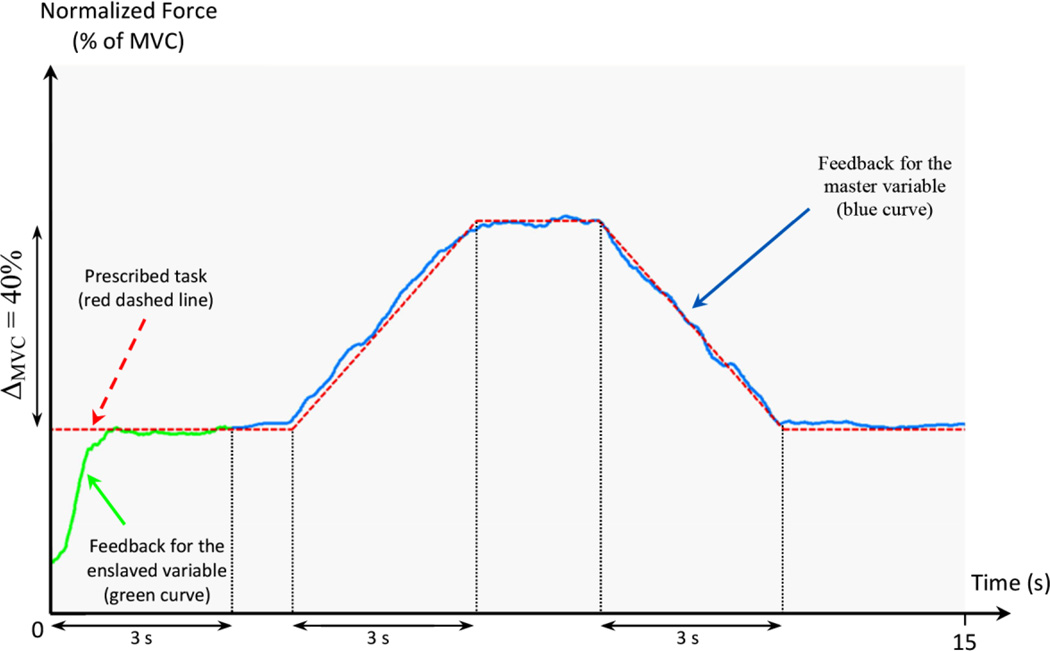
Figure 2.

An illustration of feedback for the ramp tasks. The green line represents the feedback on the enslaved variable. The blue line is the feedback on the master variable. The red dashed line specifies the time profile to be followed. A change in the Y-scale at t = 3 s ensured that no jump in the feedback happened when it switched from the enslaved to the master variable.

At the start of each trial, the subject was shown the target force profile (the red dashed line in Figure 2). For the first 3 s of each trial, the force exerted by the enslaved element was presented to the subject as feedback (green trace in Figure 2). The subject matched this force to the red dashed line. At 3 s, the feedback switched from the enslaved to the master variable and this was indicated by a change in the color of the feedback trace (blue trace in Figure 2). Simultaneously, the y-axis scale was translated vertically so that neither the feedback trace (now corresponding to zero force) nor the target profile jumped in the vertical direction. Then the subject followed the target profile with the master variable. The target profile was a 3 s ramp-up over 40% of the master variable MVC, 2 s steady state at the top of the ramp, a 3 s ramp-down to the initial level of the master variable, and a steady state until the end of the trial.

Part III of the experiment (Steady-state) consisted of trials wherein subjects held a specified level of either F_G or F_H for 15 s (duration matches that for task 2). The purpose of this part was to estimate the decline of the force due to the feedback removal in Part 2. The procedure was similar to the one described for the second part except that the force feedback was provided for the enslaved element for the first 3 s, and then the feedback trace disappeared and no change in the master variable took place. Three trials were performed for each level of force for F_G (F_G = N, with N = {Natural, 10%, 30%, and 50% of the F_G MVC}) and F_H (F_H = N, with N = {0, 10%, 30%, and 50% of flexion F_H MVC}) of the enslaved variable. The resting time was 20 s between trials. The goal of this part of the experiment was to quantify unintentional drop in the enslaved force when visual feedback is removed (cf. Slifkin et al. 2000; Vaillancourt and Russell 2002; Baweja et al. 2009).

For technical reasons, only six of the seven subjects that completed the first three parts of the experiment also performed Part IV (Total force production). Here, subjects were required to produce a 7-s steady-state specified level of total force F_T = F_G + F_H. The specified targets for F_T ranged from 10% to 60% of the sum of the MVC values for F_G and flexion F_H in steps of 10%. The feedback on F_T was provided. Fifteen trials for each level of force were conducted with a resting time of 20 s between trials. Note that while both Part IV and Part III involved steady-state force production, only Part IV provided feedback on the total force.

For parts II, III and IV, the trials were block randomized to avoid any possible effects of learning or fatigue. All parts were always performed in the order I, II, III, and IV.

Data analysis

For part I, the maximum force from each MVC trial was measured, and the average of these values across the three trials was used as the F_G and F_H MVC values. As mentioned earlier, F_G was defined as the sum of the absolute values of the five digit normal forces:

$$F_G≔\mathrm{\Sigma }|F_{Zi}|,$$ (1)

with i= T, I, M, R and L; the symbol “≔ “ means “by definition” throughout this paper.

Computing the enslaving matrix (E)

The data from the ramp tasks for the master and enslaved variables (data from part II) were averaged across repetitions. The enslaved variable was detrended using the across-repetition average of the force trace from the corresponding trials from part III. This was done to account for the slow drop in isometric force that occurs after turning visual feedback off, even when subjects try to keep the force constant (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008). Then, for each ramp task (ramp-up is considered separately from rampdown), the middle 2 s of data were used to construct the enslaving matrix (E) that reflects unintended force production by the enslaved variable as the master variable performs the ramp task (Zatsiorsky et al. 2000; Latash et al. 2001). We used the 2-s window to eliminate possible transition effects. The elements of the 2 × 2 E matrix were computed as the first-order coefficients of linear regressions performed between {F_G, F_H} and F_T over the ramp duration:

$$\mathit{E}=\left[\begin{array}{cc}{S}_{H,H/T,H}\hfill & S_{H,G/T,G}\hfill \\ S_{G,H/T,H}\hfill & S_{G,G/T,G}\hfill \end{array}\right]$$ (2)

$$F_{j,k}=a_j+S_{j,k/T,k}·F_T$$ (3)

where S_j,k/T,k is the slope of the force of the elemental variable j against F_T, when the master variable is k (j,k = {Hand (H), Grip (G)}), and a_j is a constant representing the intercept of the regression (not used to describe the enslaving). Note that since F_t,k = F_H,k + F_G,k, the columns in the enslaving matrix add to one. Sixteen E matrices were computed for each subject: 2 (ramp up/down) × 2 (hand flexion/extension) × 4 (initial load level of the enslaved variable).

The enslaving effect may induce co-variation between F_G and F_H unrelated to a particular task. To eliminate such enslaving-induced correlations between the elemental variables, we transformed the hand and grip forces, F_H and F_G, into a set of hypothetical variables that can be changed by the CNS one at a time, the so called force modes (cf. Latash et a. 2001; Danion et al. 2003) defined as:

$$\left[\begin{array}{c}{M}_H\hfill \\ M_G\hfill \end{array}\right]≔E^{-1}\left[\begin{array}{c}{F}_H\hfill \\ F_G\hfill \end{array}\right]$$ (4)

The term mode is used for a combination of forces produced when the subject tries to produce force with the hand only or the digits only.

Analysis of the structure of variance

The data from part IV were subjected to the analysis of the structure of variance within the space of elemental variables using the toolbox developed within the UCM hypothesis (Scholz and Schöner 1999). Such analysis was performed in both the Force and the Mode spaces. Here we describe the calculation of the two variance components, V_UCM and V_ORT (defined below), in the Force space. The Mode space analysis is conducted by performing the computations in Equations 5–11 by replacing the force values with the corresponding mode values obtained via Equation 4. Since the data in part IV were obtained by exerting flexion F_H force, the enslaving matrix for flexion F_H effort and ‘natural’ grip force condition during the ramp-up task from part II was used to compute the modes.

Trials from part IV were analyzed for each F_T level and each subject separately. For a given trial, {F_G, F_H} values were averaged over a 1-s time window during the steady state of the total force. The 1-s time window started at the same time for a given subject and was chosen in the middle part of the shortest steady state across all the trials the subject performed. This relatively short time window was selected to ensure that the data reflected steady state without any border effects.

We use bold face letters to indicate vector quantities (f⃗). For unit vectors, the overhead bar is replaced with a hat (ê). The notation a⃗ · b⃗ denotes the dot product of vectors a⃗ and b⃗, and the symbol d(․) indicates the derivative.

Changes in the elemental variables (F_G and F_H) sum up to produce a change in F_T:

$$d{F}_T=[1\cdots 1]{[d_{FH}\cdots d_{FG}]}^T$$ (5)

The UCM is a manifold in the space of elemental variables (F_H and F_G) such that any change in the elemental variables that lies within the UCM leads to no change in the performance variable. For the task of producing a constant sum of F_G and F_H, the UCM is one-dimensional and it is the null-space of the task Jacobian [1 1] obtained by solving the equation:

$$0=[11]\overrightarrow{\mathit{e}}$$ (6)

where ê is a unit vector spanning the null-space of the Jacobian. The forces from individual trials within a condition were projected onto ê to produce:

$${\overrightarrow{\mathit{f}}}_{\Vert }=(\mathit{ê}·\overrightarrow{\mathit{f}})\mathit{ê}$$ (7)

where, f⃗ ≔ F_H F_G^T. The component of the force orthogonal to the null-space is then given by:

$${\overrightarrow{\mathit{f}}}_{\perp }=\overrightarrow{\mathit{f}}-{\overrightarrow{\mathit{f}}}_{\Vert }$$ (8)

The amount of variance parallel to the UCM is:

$$V_{UCM}=\frac{|f_{\Vert }{|}^2}{N_{\mathit{\text{trials}}}}$$ (9)

The amount of variance orthogonal to the UCM is:

$$V_{ORT}=\frac{|f_{\perp }{|}^2}{N_{\mathit{\text{trials}}}}$$ (10)

A synergy index ΔV was computed as the normalized difference between V_UCM and V_ORT:

$$\mathrm{\Delta }V=\left(\frac{V_{UCM}+V_{ORT}}{V_{\mathit{\text{TOT}}}/2}\right)$$ (12)

where V_TOT ≔ V_UCM + V_ORT is the total variance. If ΔV is positive, V_UCM > V_ORT, which we interpret as a synergy stabilizing the total force. The synergy index is bounded: −2≤ΔV≤2. Therefore, ΔV was z-transformed prior to parametric statistical analysis:

$$\mathrm{\Delta }{V}_Z=\frac{1}{2}\text{ln}\left(\frac{1+\mathrm{\Delta }V/2}{1-\mathrm{\Delta }V/2}\right)$$ (13)

The output of the Fisher z-transform function can theoretically reach plus/minus infinity.

Statistical analysis

Most data are presented as means and standard deviations. Statistical analysis was performed for the enslaving matrix coefficients (obtained from parts II and III of the experiment) and for the variance indices V_UCM, V_ORT, and ΔV_Z obtained from the UCM analysis (part IV of the experiment). Since the columns of the enslaving matrices add to one, statistical analysis was conducted only on the off-diagonal elements of each matrix (enslaving coefficients). We performed a one-sample t-test to compare the mean of each condition to the zero value. The enslaving coefficients were potentially affected by four factors: enslaved variable (EV: F_H and F_G), F_H-direction (flexion and extension), Ramp-direction (up and down), and Load: the initial force level prescribed for the enslaved variable (four levels). A four-way, repeated measures ANOVA (EV × F_H-direction × Ramp-direction × Load) was performed to investigate the main effects. Further, two three-way, repeated measures ANOVAs (F_H-direction × Ramp-direction × Load) were performed: one when the enslaved variable was F_G and another one when it was F_H.

The variance indices obtained from the UCM analysis were potentially affected by two factors: Analysis (forces and modes), and the task total force (F_T-task: six levels). Two two-way, repeated measures ANOVAs (Analysis × F_T-task) were performed for V_UCM and ΔV_Z; a one-way ANOVA (F_T-task) was performed on VORT because changing the analysis space does not influence V_ORT (see Appendix A for a proof of this assertion). Tukey’s Honestly Significant Difference test was used for pairwise comparisons.

Results

Enslaving coefficients

When the subjects produced ramp changes in the hand force (F_H, master variable), the grip force (F_G, enslaved variable) changed unintentionally in the direction of F_H change. Specifically, an increase (ramp-up) in flexion F_H led to an increase in F_G and, conversely, a decrease (ramp-down) in flexion F_H led to a decrease in F_G. However, only a decrease in the magnitude of extension F_H (ramp-down) led to a decrease in F_G. In contrast, ramp changes in F_G (master variable) had no consistent effect on F_H (enslaved variable), except for one condition: F_G ramp-down led to a drop in flexion F_H.

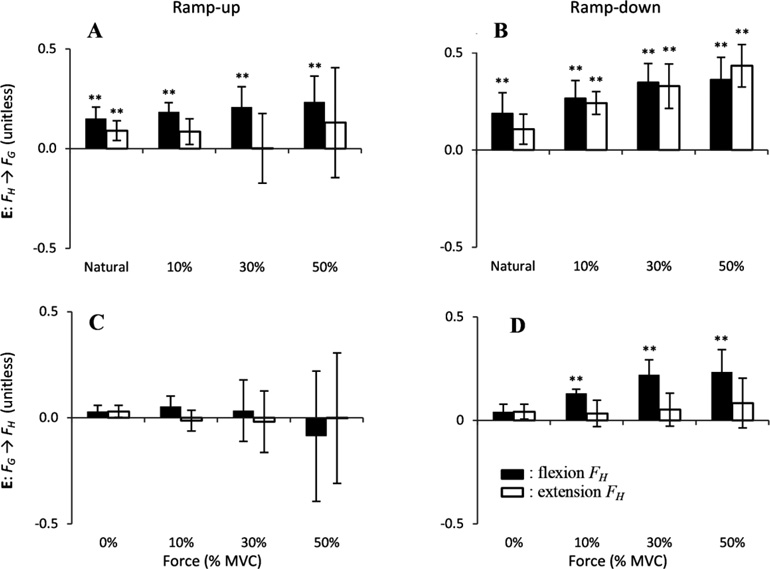
Figure 3 illustrates these findings with the enslaving coefficients (the off-diagonal entries of the E matrix, see Methods) averaged across subjects. In this Figure, the double stars (**) indicate the enslaving values that are significantly different from zero (p < 0.01). Note the relatively large enslaving coefficients in conditions when F_G was the enslaved variable (on average, 0.21±0.18, panels A and B in Figure 3). In contrast, the enslaving coefficients in conditions when F_H was the enslaved variable were small and mostly not different from zero (on average, 0.05±0.13, panels C and D in Figure 3). The enslaving coefficients were greater during flexion F_H (0.16±0.15) than during extension F_H (0.1±0.18), for ramp-down (0.20±0.15) than for ramp-up (0.05±0.16), and they also increased with the initial Load level (see Figure 3D). The four-way ANOVA showed that the enslaving coefficients were significantly affected by all four factors: EV [F_{(1, 6)} = 29.9, p<0.05], F_H-direction [F_{(1, 6)}=26.9, p<0.05], Ramp-direction [F_{(1, 6)} = 76.99, p<0.05], and Load [F_{(3, 18)} = 5.33, p<0.05].

Figure 3.

The enslaving index (E) (across-subject means ± SD) across all initial force values, directions of the ramp, and tasks. Panels A and B represent the enslaving effect of F_H onto F_G during ramp-up (A) and ramp-down (B). Panels C and D represent the enslaving effect of F_G onto F_H during ramp-up (C) and ramp-down (D). Black bars depict trials with flexion F_H and white bars depict extension F_H.

The ANOVA also revealed significant two-way interaction (Ramp-direction × Load) [F_{(3, 18)} = 10.3, p<0.05], three-way interaction (EV × F_H-direction × Ramp-direction) [F_{(1, 6)} = 17.5, p<0.05], and four-way interaction [F_{(3, 18)} = 4.41, p<0.05]. Rather than interpreting the 4-way interaction, two three-way, repeated-measures ANOVAs were performed, and the results of those are explained in detail in the two subsections below.

Effect of hand force modulation on grip force (enslaved variable: F_G)

Analysis of the trials with F_H ramp force production showed that enslaving coefficients were influenced by all three factors. Enslaving coefficients were higher for flexion (0.24±0.11) than extension F_H (0.17±0.22) (Figure 3, panels A and B); and for ramp-down (0.3±0.13) than for ramp-up (0.12±0.17) (compare the white and black bars in Fig. 3). The three-way ANOVA confirmed the main effects of F_H-direction [F_{(1, 6)} = 9.83, p < 0.05], Ramp-direction [F_{(1, 6)} = 58.2, p < 0.05] and Load [F_{(3, 18)} = 4.84, p < 0.05]. The enslaving coefficients during extension F_H were close to zero during Ramp-up (white bars, panel A), but were different from zero during Ramp-down (white bars, panel B). In contrast, the coefficients during flexion F_H were unaffected by direction (black bars, panels A and B). This resulted in a significant interaction [F_H-direction × Ramp-direction: F_{(1, 6)} = 1.9, p<0.05]. Finally, the enslaving coefficients increased with the Load during ramp-down of F_H but not during ramp-up of F_H (panels A and B). This resulted in an interaction Ramp-direction × Load: F_{(3, 18)} = 7.01, p<0.05.

Effect of grip force modulation on hand force (Enslaved variable: F_H)

Intentional changes in F_G influenced F_H only during ramp-down in flexion (black columns in Figure 3, panel D). While the plot suggests an increase in these effects with the initial F_H, the effect was non-significant. The enslaving coefficients were higher during flexion F_H (0.08±0.15) than extension F_H (0.02±0.08), and for ramp-down (0.1±0.1) than for ramp-up (0.0±0.12). The three-way ANOVA showed the main effects of F_H-direction [F_{(1, 6)} = 11.6, p<0.05] and Ramp-direction [F_{(1, 6)} = 12.9, p<0.05] on the enslaving coefficients. There were no interaction effects.

Analysis of variance in two-element tasks

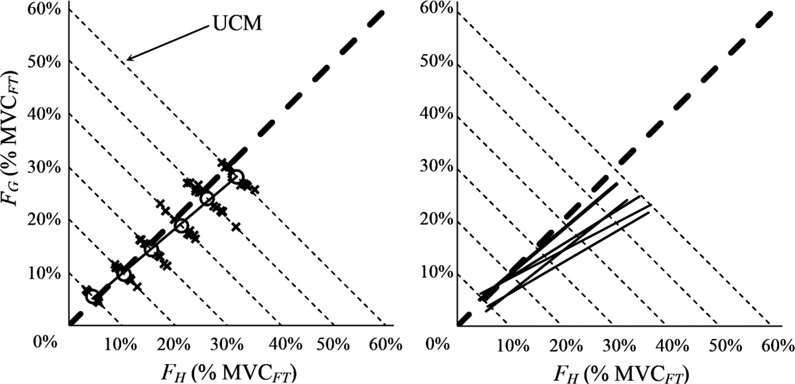
The goal of this analysis was to explore whether the two elemental variables (F_G and F_H) co-vary across trials to stabilize the value of the jointly produced task variable F_T = F_H + F_G. The data showed that F_G and F_H co-varied in such a way that most across-trials variance was parallel to the UCM computed for F_T. The left panel of Figure 4 shows the data for a representative subject across all task F_T levels. In Figure 4, each axis represents the percentage of MVC of F_T produced by each element (F_H on the horizontal axis and F_G on the vertical axis). Each slanted dashed line represents the UCM at a different level of F_T. The dashed thick line represents the sub-space orthogonal to each of the UCMs. The thin solid black line is the linear regression line fit to the centroids (white dots) of the performance at each load level, and it represents the average sharing pattern at that level. For all subjects the sharing pattern always favored the hand force: The regression lines all have slopes less than one (Figure 4, right panel).

Figure 4.

Left: Force magnitudes (F_H and F_G) for individual trials of a representative subject in the accurate total force (F_T) production task are shown with crosses. The white circles are the centroids of the data at each F_T level and the solid thin dark line is the linear regression line fit to the centroids for the subject. The thin dashed lines show the UCMs for different F_T magnitudes. The think dashed line shows the direction orthogonal to the UCMs. Right: The linear regression lines for all subjects. All the lines have slope less than one and, therefore, lie below the gray dashed line, which has unity slope.

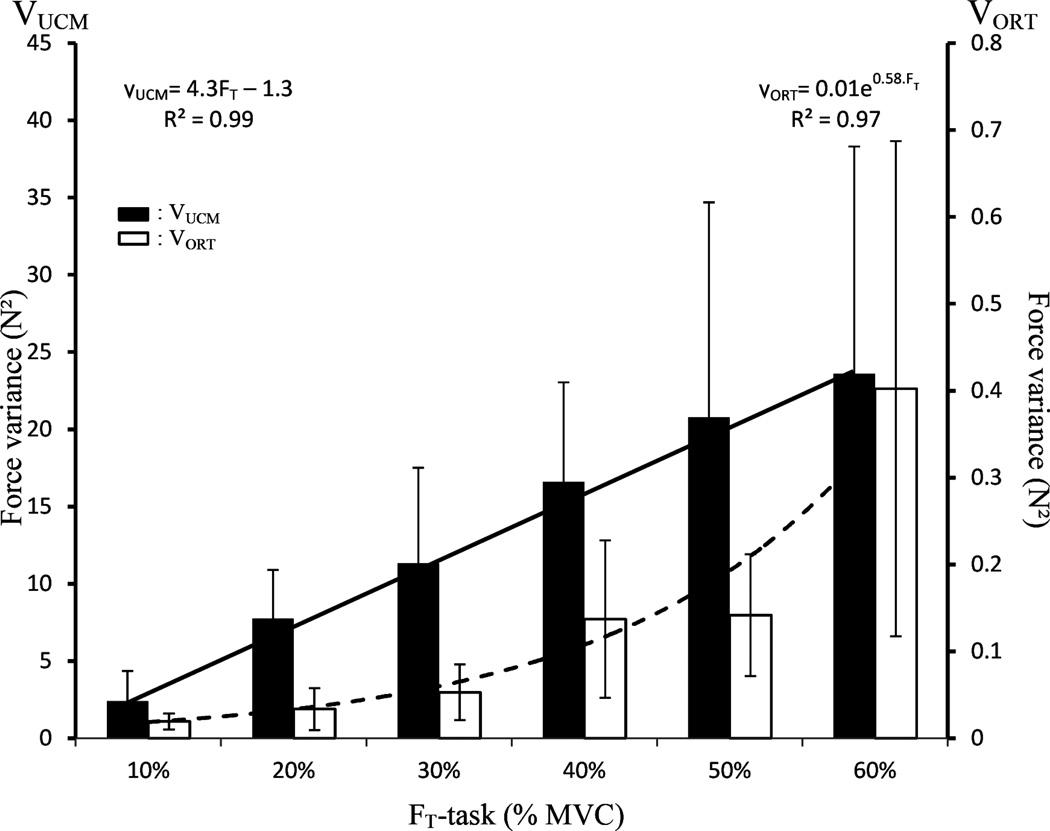
Overall, similar results were obtained for the analysis of the structure of variance in the Force and Mode spaces. In particular, variance compatible with the required F_T magnitude (V_UCM, 13.7±8.1 N²) was always greater than variance leading to a change in F_T (V_ORT, 0.13±0.14 N²) (Figure 5, note the large difference in the scales for the two Y-axes). V_UCM increased linearly with F_T in both Force and Mode spaces. This increase was faster in the Mode space [Analysis × F_T-task: F_{(5, 25)} = 5.48, p<0.05]. V_ORT also increased with F_T, but exponentially (Figure. 5); the increase was statistically significant (F_{(5, 35)} = 6.21, p < 0.05). Post-hoc tests revealed that V_ORT for the highest F_T-task level was greater than that for all others F_T magnitudes.

Figure 5.

Two components of variance, V_UCM (black) and V_ORT (white), computed across trials in the Mode space and their respective regressions shown by the dark solid line (linear fitting) and dark dashed line (exponential fitting). Regression equations are also presented. Means across subjects are shown with standard error bars. Note the very large difference in the scales of the left and right Y-axes.

The synergy index ΔV reflected the relative amount of V_UCM in the total variance. This index was always greater than zero, indicating a F_T-stabilizing synergy between F_G and F_H at all F_T levels (Figure 6). V_UCM was larger in the Mode space [F_{(1, 5)} = 24.5, p < 0.05]. Recall that V_ORT does not change between the Force and Mode spaces (Appendix 1).

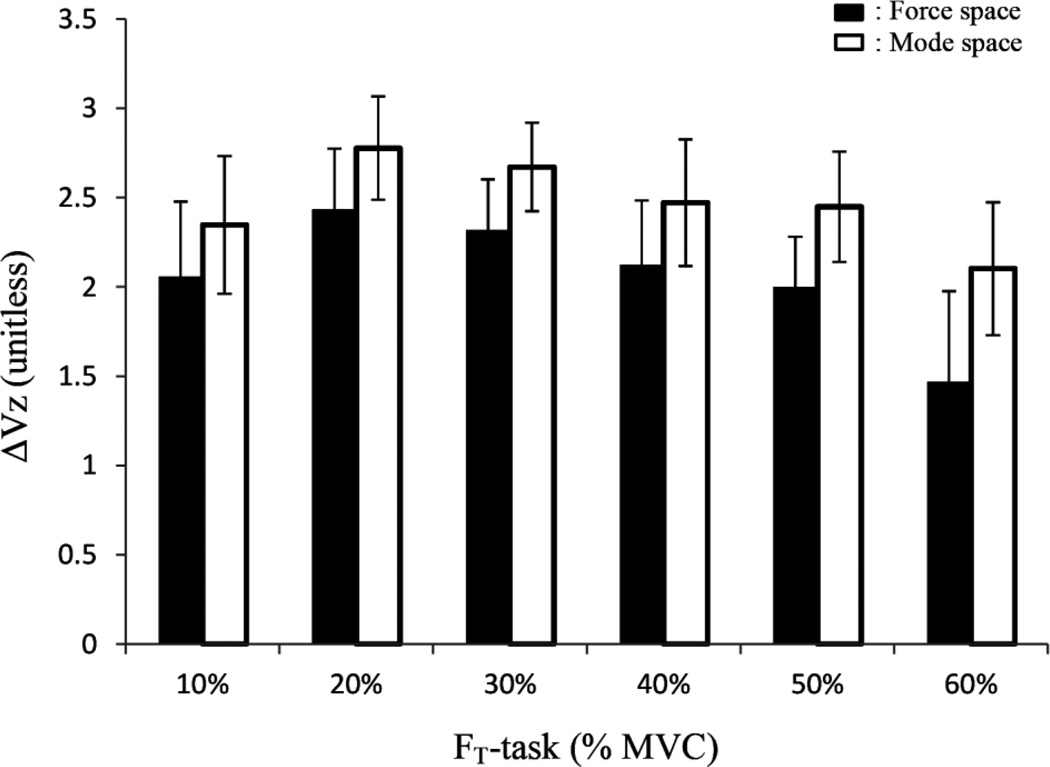
Figure 6.

The z-transformed values of the synergy index, ΔV_Z, in the Force space (black) and in the Mode space (white). Across-subject means ± SD are presented. Note that ΔV_Z > 0 across all force levels.

The z-transformed synergy index values, ΔV_Z (Figure 6), were greater in the Mode space (2.47±0.38) than in Force space (2.05±0.43) [F_{(1, 5)} = 139.3, p < 0.05]. There was also a significant effect of F_T-task on V_Z (F_{(5, 25)} =6.34, p < 0.05). Post-hoc analysis revealed that ΔV_Z for the 20% and 30% tasks was greater than for the 10%, 40%, 50% and 60% tasks.

Discussion

The first hypothesis formulated in the Introduction has been confirmed only partly. As predicted, we observed phenomena of enslaving (unintentional force production) between the grip force and hand force, F_G and F_H. The patterns of enslaving were, however, asymmetrical with much stronger and more consistent enslaving effects on F_G from F_H than on F_H from F_G. The indices of enslaving also showed significant effects of such factors as the direction of intentional force change and the baseline force level of the enslaved variable. These patterns are much more complex as compared to the enslaving effects across the fingers of the human hand (Li et al. 1998; Zatsiorsky et al. 2000).

Hypothesis-2 has been confirmed in the experiments. Indeed, we observed significantly more variance within the space that had no effect on the task variable (total force, F_T) as compared to variance in the orthogonal direction. In other words, there was a synergy between the two forces, F_G and F_H, stabilizing F_T. The synergy indices were larger when the analysis was performed in the space of hypothetical variables (modes, M_H and M_G) computed to eliminate the co-variation between F_G and F_H expected from the enslaving. The observed negative co-variation between F_H and F_G pointed at strong synergic mechanisms overpowering the effects of enslaving that favor positive co-variation between these two forces.

In summary, F_G and F_H showed both positive and negative co-variation: (a) Intentional increase/decrease of F_H/F_G induced similar changes in F_G/F_H. The effect strongly depended on the selected force and the direction of its change. Still, qualitatively, such changes correspond to force enslaving; and (b) Task-specific negative co-variation between F_H and F_G across repeated trials — a synergy stabilizing the sum of F_H and F_G.

Mechanisms of inter-joint enslaving

Several factors have been invoked as potential contributors to enslaving among human fingers (reviewed in Schieber and Santello 2004; Zatsiorsky and Latash 2008; van Duinen and Gandevia 2011). These include mechanical connections between fingers provided by connective tissue, the presence of multi-finger, multi-tendon extrinsic hand muscles, and neural factors such as overlaps in the finger cortical projections. A number of recent studies provided evidence for a dominant role in enslaving played by neural factors. These include the quantitative analysis of enslaving when the subjects pressed not with the fingertips but with proximal phalanges, where only digit-specific intrinsic muscle contributed to force production (Latash et al. 2002b), changes in enslaving in musicians (Slobounov et al. 2007) and in healthy older adults (Shinohara et al. 2003), and effects of a brief episode of specialized practice (on the order of one hour) on enslaving (Wu et al. 2012, 2013).

Across-joints effects of enslaving in a serial chain can also be due to both peripheral factors, such as links provided by connective tissue and those due to possible force transmission among the compartments of the extrinsic hand muscles, and neural factors. In particular, the presence of bi-articular and multi-articular muscles naturally couples actions across joints. Inter-joint reflexes, in particular those from force-sensitive receptors, have been known for a long time (reviewed in Nichols 2002); they are expected to produce inter-joint coupling via spinal mechanisms. And, as in the case of inter-finger enslaving, the divergence and convergence of descending cortical projections (reviewed in Schieber and Santello 2004) allows expecting effects on multiple joints when a person tries to perform an action with one joint only.

When a person changes grip force, extrinsic finger flexors change their forces. Since these muscles are also wrist flexors, consistent enslaving effects on F_H from F_G are expected. Since the wrist joint is also served by dedicated muscles, which do not produce finger action, enslaving effects on F_G from F_H may be avoided. Our observations, however, were opposite to this simplistic prediction: Stronger and more consistent enslaving effects were observed on F_G from F_H. These observations, as well as the dependence of the enslaving effects on other factors manipulated in the study, suggest that these enslaving effects were to a large degree defined by other factors such as the contribution of wrist/finger extensors that may be defined by neural mechanisms involved in everyday natural hand actions. Note that humans can easily change the grip force on a hand-held object without moving the wrist; this is reflected in the low enslaving effects from F_G on F_H. In contrast, varying wrist torques with a hand-held object can be seen in quick motion of the hand with the grasped object. In such cases, close coupling between the hand acceleration and grip force is commonly observed (Flanagan and Wing 1993; Flanagan and Tresilian 1994; Ambike et al., 2013); this phenomenon is reflected in our experiment in the consistent enslaving effects from F_H on F_G.

Inter-joint synergies

The word “synergy” has been used in movement studies in a variety of meanings (reviewed in Latash 2008). In clinical literature, this word has a negative connotation and implies pathological, stereotypical patterns of muscle activation (and joint action) typical of a variety of disorders including stroke (Bobath 1978; DeWald et al. 1995). Currently, the most common meaning of “synergy” in the literature is something close to “a group of variables that show parallel scaling in time or with variations of the task”. Parallel changes in kinematic, kinetic, and electromyographic variables have been documented in a variety of actions ranging from precise digit manipulation to whole-body tasks (Santello and Soechting 2000; Santello 2002; Ivanenko et al. 2004; Grinyagin et al. 2005; d’Avela et al. 2005; Ting and Macpherson 2005; Torres-Oviedo and Ting 2007; Vinjamuri et al. 2010; Tessitore et al. 2013). In contrast to the above term usage, we use the word “synergy” to mean a neural, task-specific mechanism that ensures stability of important performance variables.

For example, if several variables show consistent parallel changes, this by itself qualifies them as a synergy according to the most common definition but not according to our definition. In particular, typical finger force enslaving patterns leading to consistent positive co-variation among finger forces (Zatsiorsky et al. 2000) qualify as a synergy under the former definition but, according to our definition, these effects may act against a force-stabilizing synergy in an accurate multi-finger force production task. To claim the existence of a synergy, one has to demonstrate what aspect of performance is stabilized by the observed co-variation of elemental variables.

Synergies are reflected, in particular, in specific signatures of the structure of variance across repetitive trials with most variance in a sub-space compatible with desired patterns of important performance variables. A toolbox introduced within the UCM hypothesis (Scholz and Schöner 1999) allows quantifying synergies by estimation of the two variance components, within the UCM for a selected performance variable (V_UCM) and orthogonal to it (V_ORT).

A number of studies reported synergies across a range of tasks, sets of variables, and populations (reviewed in Latash 2008). In particular, kinematic synergies within a serial chain stabilizing such variables as the end-effector trajectory and orientation in space, and kinetic synergies within a parallel chain stabilizing such variables as the resultant force and moment of force have been described (reviewed in Latash et al. 2007; Zatsiorsky and Latash 2008). The task explored in our current study was rather unusual: The subjects were asked to produce a constant sum of two forces generated by different segments in a serial chain, F_T = F_H + F_G. Moreover, the enslaving effects acted against the F_T-stabilizing synergy by producing positive co-variation between the two forces. Nevertheless, after minimal practice, strong patterns of co-variation between F_H and F_G were observed (Fig. 5) corresponding to high synergy indices (Fig. 6).

The subjects were provided visual feedback on F_T. While this factor could help them reduce V_ORT, it did not, by itself, encourage subjects to produce higher or lower values of V_UCM. Hence, the presence of strong F_T-stabilizing synergies in this experiment is non-trivial. It suggests that humans are able to develop multi-joint kinetic synergies after only a handful of trials.

Is muscle anatomy a complicating factor in motor coordination?

Can one move one joint at a time (or produce net moment of force in one joint at a time)? The presence of bi- and multi-articular muscles and inter-joint reflexes suggests a negative answer to this question, while everyday experience suggests a positive answer. This non-scientific observation points at potential flaws of analyses of movements that try to analyze problems of the neural movement control starting with the design and properties of the elements. Problems with this reductionist approach have been emphasized by many authors (reviewed in Kugler and Turvey 1974; Feldman 2009; Latash 2010).

Within a recently developed scheme (Latash 2010), neural control is organized in a relatively low-dimensional task space and then it goes through a chain of few-to-many transformations resulting in changes in activation of numerous muscles. Task-related performance variables are drawn to their referent values (cf. Feldman 2009, 2011), and all muscles contribute to this motion. Specific patterns of muscle activation (and also patterns of elemental variables at other levels of analysis, such as joint torques) may not be crucial for success at the task resulting in large across-trials variability in the muscle activation space induced by irreproducible initial conditions. Within this scheme, specific anatomical design of the involved muscles may not matter too much as long as the muscle set remains redundant with respect to the important performance variables. Learning a novel task may be associated with organizing appropriate coupling from sensory signals reflecting a task-specific performance variable with neural signals driving shifts of the referent value of that variable.

This general scheme is supported by a number of observations. For example, fatigue of an effector (a subset of muscles) typically leads to a substantial increase in the variance of the fatigued effector while the effects on variance of a performance variable produced by a redundant set of effectors, including the fatigued one, are relatively small (Cote et al. 2002, 2008; Huffenus et al. 2006; Gates and Dingwell 2008; Singh et al. 2010, 2011). A reaching movement that may or may not involve the trunk shows very quick adjustments of the arm motion if the trunk is unexpectedly arrested in the initial condition, compatible with the same hand trajectory (Adamovitch et al. 2001). Another group of observations supporting this scheme includes the relatively quick adaptation of animals to tendon transfer operations when the function of a particular muscle group is changed rather dramatically (Ilert et al. 1986; Holmberg et al. 1997; Friden and Lieber 2002).

There is also neurophysiological support for some of the assumed features of the described scheme. Studies of single-neuron activity in the ventral premotor cortex and the inferior parietal lobule of monkeys showed association of the neuronal discharge with specific actions (such as manipulating an object), not with simple, isolated digit movements (Rizzolatti et al. 1988; Jeannerod et al. 1995; Fogassi et al. 2005). Besides, some neurons in the ventral premotor and inferior parietal cortical regions are sensitive to a motor action regardless of the specific grip used to accomplish it, while other neurons are more selective. However, even those, relatively selective, neurons discharge strongly only when the movement is performed as a component of a specific motor action, not when the same movement is performed in isolation or within a different motor goal (Rizzolatti et al. 2004; Rizzolatti and Sinigaglia 2008). These observations have also been corroborated by brain imaging studies (Grafton and Hamilton 2007).

Finally, the limitations of the study are as follows. First, we consider a simplified model of the hand muscle design without separating such potentially important factors as the action of the FDS and of the intrinsic hand muscles. Second, we tested a small number of subjects, which was nevertheless sufficient to reach significance in all the main tests.

Appendix A

The following is a proof for the equality of variance in the orthogonal subspace defined in the Force and Mode spaces. We denote vector quantities by a lower-case, bold font letters (f⃗). For unit vectors, the overhead bar is replaced with a hat (ê). The notation a⃗ · b⃗ denotes the dot product of vectors a⃗ and b⃗, and the symbol d(․) indicates the derivative.

Consider a system of n elemental variables f_i constrained by a single, linear equation: $f_{\mathit{\text{tot}}}={\sum }_{i=1}^{i=n}{f}_i$, and an enslaving matrix E ∈n × n such that all of the n columns add to 1. The matrix E has the form of a left stochastic matrix or a Markov matrix.

The mode is defined as:

$$\mathit{m̄}≔E^{-1}\mathit{f̄}$$

where m̄ is a n-dimensional column vector. Now assuming that the enslaving matrix is constant,

$$d\mathit{m}=E^{-1}d\mathit{f},\Rightarrow d\mathit{f}=Ed\mathit{m}\text{Therfore},d{f}_{\mathit{\text{tot}}}=Jd\mathit{f}=JEd\mathit{m}=Jd\mathit{m},$$ (A1)

where J is the task Jacobian given by 1 1 ⋯ 1. Equation A1 shows that the task Jacobian is identical in the Force and Mode spaces. Therefore, the orthogonal subspace of the task Jacobian in the two spaces is:

$$\mathit{ô}=\frac{1}{\sqrt{n}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill :\hfill \\ \hfill 1\hfill \end{array}\right]$$

It is evident that the vector v̄ 1 1 1 … 1 n is a left eigenvector of E, and v̄^T is a right eigenvector of E_T, each with the eigenvalue 1 (i.e., v̄ E = v̄ and E^T v̄^T = v̄^T). Also, ${\mathit{v̄}}^T=\sqrt{n}\mathit{ô},$, and therefore,

$$E^T\mathit{ô}=\mathit{ô}$$

Here we show that

$$\mathit{f̄}•\mathit{ô}=\left(E\mathit{m̄}\right)•ô=\mathit{m̄}•\mathit{ô}$$

It is well known that for two arbitrary vectors, p̄ q̄ ∈ℝⁿ, and a matrix A ∈ n × n,

$$A\mathit{p̄}•\mathit{q̄}=\mathit{p̄}•A^T\mathit{q̄}$$

Therefore, for any vector m̄ in the Mode space,

$$\left(E\mathit{m̄}\right)•\mathit{ô}=\mathit{m̄}\left(E^T\mathit{ô}\right),$$

$$(E\mathit{m̄})•\mathit{ô}=\mathit{m̄}•\mathit{ô}$$

$$\Rightarrow \mathit{f̄}•\mathit{ô}=\mathit{m̄}•\mathit{ô}=\frac{1}{\sqrt{n}}\sum _{i=l}^{i=n}{f}_i$$ (A2)

Equation (A2) demonstrates that the transformation of f̄ into m̄ leaves the projection of f̄ onto ô unaltered. It follows that the variances in the orthogonal subspaces of the Mode and Force spaces for such systems are equal.