Timing in a Variable Interval Procedure: Evidence for a Memory Singularity

Abstract

Rats were trained in either a 30s peak-interval procedure, or a 15–45s variable interval peak procedure with a uniform distribution (Exp 1) or a ramping probability distribution (Exp 2). Rats in all groups showed peak shaped response functions centered around 30s, with the uniform group having an earlier and broader peak response function and rats in the ramping group having a later peak function as compared to the single duration group. The changes in these mean functions, as well as the statistics from single trial analyses, can be better captured by a model of timing in which memory is represented by a single, average, delay to reinforcement compared to one in which all durations are stored as a distribution, such as the complete memory model of Scalar Expectancy Theory or a simple associative model.

There has recently been considerable interest in examining the link between the temporal control of behavior and associative learning processes. Gallistel and Gibbon (2000) proposed that a number of behavioral phenomena, typically understood by reference to associative processes, can be alternatively understood as resulting from decisions based upon a perception of time. Broadly, they argue that the decision to respond is based upon an estimate of rates of return. Specifically, they argued that the cumulative time until reward during a conditioned stimulus is compared to the cumulative time until reward when the conditioned stimulus is absent, and a decision of whether to respond depends on this ratio passing a response threshold. This proposal has resulted in a number of studies examining this relationship, with some reports supporting the theory (Balsam, Fairhurst, & Gallistel, 2006; Gottlieb, 2008; Harris, Andrew, & Livesey, 2012), and others finding discrepancies (Delamater & Holland, 2008; Golkar, Bellander, & Ohman, 2013; Gottlieb & Rescorla, 2010). Irrespective of whether this model proves to be an accurate predictor of associative learning, it has been eminently successful in highlighting the lack of temporal specification of most associative accounts, which have focused on whether, rather than when, responding should occur.

One issue that is critical to any attempt to bridge these two approaches to understanding behavior is to identify the form and content of the memory that is used to guide the temporal control of behavior. For example, in an operant timing task such as the peak-interval procedure, a subject is given a food reward for the first desired response after a criterion time has elapsed. After training, the average rate of responding ramps up as a function of time until the criterion duration, and declines thereafter, leading to maximal levels of responding around the time that the reward has been programmed to be available. What is the content and form of the memory that is in play here? One possibility that follows from a simple associative perspective is that the strength of responding at each moment in time is modified by excitation (and inhibition) resulting from reinforcement (and the lack thereof), and variability in “perceived” time results in a broad array of response strengths. Models such as the Behavioral Theory of Timing (Killeen & Fetterman, 1988), the Learning to Time Theory (Machado, 1997), and the Spectral Timing model (Grossberg & Schmajuk, 1989) are varied instantiations of this general idea. Thus, in such a model, no explicit expectancy of the time of reward is generated. Alternatively, Scalar Expectancy Theory (SET) proposes that the animal learns the time (in terms of an internal clock count) at which reward was obtained (Gibbon, 1977; Gibbon, Church, & Meck, 1984). Specifically, SET proposes that elapsed time is represented by the linear accumulation of pulses released from a pacemaker. When reinforcement is provided, the accumulated count, which is directly proportional to elapsed time, is stored in reference memory. However, due to variability in the speed of the pacemaker across trials, the subjective time at which reward occurs will vary across trials. As a result, a distribution of reward time memories will be created which reflect every time at which reinforcement was obtained. In addition, SET proposes that there is variability in the memory encoding process, which would also lead to a memory distribution. Responding is generated following a comparison of the elapsed pulse count in the accumulator with a random sample from the memory distribution. Specifically, high rate responding is proposed to occur throughout the interval during which the relative discrepancy (|memory sample-accumulator count|/memory sample) is smaller than a threshold level of similarity. This similarity threshold is also proposed to exhibit normal variability across trials. Together then, SET proposes four primary sources of variability between trials: variability in the clock rate, variability in the memory encoding process, variability in the memory sampling process and variability in the similarity threshold used in the decision process. In contrast to the associative account, in this framework, an explicit expectation of reward exists for every time at which reward has been obtained, and responding is based on a sample of this knowledge. While these models obviously differ in the content of memory, in both frameworks, the form of memory is a distribution (of response strengths or reward times).

An alternative possibility, suggested by recent work from our lab, is that temporal memory is composed of an average of past reinforcement times. Specifically, we showed that rats trained in a mixed-interval peak procedure in which two different modality cues predicted two different delays to reward availability (e.g., tone = 10s, light = 20s) will respond maximally at a time between the trained criterion durations (e.g., 16s) when presented with the compound cue (tone + light) in extinction (Swanton, Gooch, & Matell, 2009). Importantly, the breadth of responding to the compound cue was scalar (i.e., it had the same relative width as the response functions from the component cues). Similar results have been seen using a range of durations, duration ratios, and cues (Kurti, Swanton, & Matell, 2013; Matell & Kurti, 2013; Matell, Shea-Brown, Gooch, Wilson, & Rinzel, 2011; Swanton & Matell, 2011).

We interpreted these data as indicating that the onset of the two cues led to the simultaneous retrieval of the two component temporal memories, which due to their discrepancy, were then integrated or averaged, and the resulting expectation timed in an otherwise normal manner. Intriguingly, such scalar behavior to the compound cue constrains the possible ways in which temporal memories can be represented. For example, if temporal control is instantiated by the sequential activation of a distribution of response strengths following an associative model, then the compound response function would presumably result from the combined activation of the temporal generators activated by each cue. However, simulations of this scenario in which the two component response functions are pooled (with all possible combinations of weights) does not produce a scalar response form at an intermediate time (it is always wider than scalar), and frequently produces a multi-modal response function (depending on the component response rates and weights). Similarly, if the compound stimulus led to a (weighted) average of the each cue’s temporal memory distribution, the average distribution would be relatively wider than the component distributions and would potentially have multiple modes (again depending on the component memory spreads and weights). Thus, in scenarios in which response strength or entire memory distributions are pooled or averaged, compound responding should be broader than scalar.

In contrast, if the organism randomly sampled memories for each duration as proposed by SET (i.e., one from the short memory distribution and one from the long memory distribution), and then timed the average of these samples, the compound response function would be narrower than scalar. Such a result emerges because a random sample from one of the tails of the short distribution is highly likely to be offset by a less extreme sample or one biased in the other direction from the long distribution, thereby creating less variability in the average than that seen in the component distributions. More broadly speaking, this narrowing of the average expectation follows from the central limit theorem, in that the variability of a sample mean is always smaller than the variability of the sample distribution.

In summary, models of timing in which temporal memories are represented as a distribution (of either explicit expectations or response strengths) are generally unable to account for the scalar form seen in stimulus compounding situations. Instead, these results suggest that the mnemonic representation of time is composed of a single expectancy. Specifically, the average of two discrepant singular expectations will itself be a singular value. As such, responding will reflect the same sources and levels of variability as that of the component durations, and the response form will therefore be scalar. In information processing terms, this would imply that there is variability in the clock and decision stages, but not in the memory stage (i.e., there is either no memory distribution and only an average expectation, or the value sampled from the distribution is a single measure of central tendency, such as the mean).

While these compounding data suggest that the memory for a fixed interval schedule of reinforcement may be represented by a singular expectation, it is also important to investigate whether such integration processes may be at work when a single cue is associated with multiple, different times of reward, such as under mixed fixed-interval schedules or variable-interval schedules. Previous work using mixed fixed-interval schedules associated with a single cue typically demonstrated multi-modal response functions, unless the ratio of the two durations was small (Leak & Gibbon, 1995; Whitaker, Lowe, & Wearden, 2003), or the probability of reinforcement at the earlier duration was very low (Whitaker, Lowe, & Wearden, 2008). These multi-modal response patterns are obviously not consistent with the two (or more) different durations being integrated into a single expectation (note, however, that these data do not preclude each fixed-interval being represented by a singular expectation). Instead, the form of responding in these tasks was well accounted for by the simple summation of two independent peak functions, each centered near the respective fixed intervals (Whitaker et al., 2003, 2008).

Why should the single interval schedules be represented by a single average expectancy when the mixed-interval schedules generate multiple, potentially distinct, expectations? The obvious answer to this question is that in the mixed-interval schedule the animal experiences multiple durations to reinforcement, whereas there is only a single delay to reinforcement under a single fixed-interval schedule. However, a bit of reflection suggests that this is not a sufficient answer. An assumption made by all models of timing is that there is variability in the rate of the processes composing the clock. As a result, the subjective delay to reinforcement under a single fixed-interval schedule will vary across trials, and therefore, in both cases the organism experiences multiple delays to reinforcement. The difference then appears to be how much variation there is for the experienced durations. When there is a small amount of relative variability, the organism may conclude that this variation is a result of sensory error and form a single expectation, whereas when the relative variability is large, the organism may attribute the variation to the environment, and form multiple expectations. One simple way in which this could be implemented without forming a distribution is just computing the ratio between the expected and obtained reinforcement time. A similar suggestion was made by Jones and Wearden (2003) in their perturbation model in which reference memory is updated only when the proportional difference between currently experienced reinforcement time and the expected time passes a threshold level of dissimilarity (e.g., 20% difference).

In keeping with this idea, an examination of the pattern of responding to constrained variable intervals may be informative. In contrast to the multi-modal response functions seen with mixed FI schedules, work using a uniformly distributed 30–60s variable interval procedure found that the average response function was peak shaped (Church, Lacourse, & Crystal, 1998) which could imply that a single expectation was formed. However, the peak was broader than that obtained with a FI45s schedule due to earlier initiation of responding and later termination of responding (see also Brunner, Fairhurst, Stolovitzky, & Gibbon, 1997; Brunner, Kacelnik, & Gibbon, 1996). Thus, at first glance, these data are also inconsistent with an averaging process that results in a single temporal expectation (at least under the assumption that other processes, such as response thresholds, are unaltered). Similarly, the response form in random-interval procedures is well known to be flat, with the subject responding at a constant rate until reinforcement is delivered (Catania & Reynolds, 1968), and thus such data also appear inconsistent with a single average expectancy. On the other hand, performance on concurrent, but unequal, variable-interval schedules is well known to generate matching behavior, such that the proportion of responding on each alternative is equal to the proportion of reinforcement obtained from each alternative (Herrnstein, 1974). Such data are consistent with the idea that an average expectancy of the delay to reinforcement for each schedule might well be derived (i.e., molar choice, Williams, 1991).

We have recently found that scalar responding to a stimulus compound, indicative of integration processes, depends on the component cues having similar reinforcement densities, whereas selection processes appear to result when reinforcement densities differ across cues (Matell & Kurti, 2013). Although there is only a single cue in a uniformly distributed variable interval procedure, the receipt of reinforcement after a short duration may be deemed more valuable than receipt of reinforcement after a long duration, which may limit integration. Thus, it is important to examine the form of responding on a variable-interval procedure under conditions in which the durations have equal “value”. To this end, we compared the performance of rats trained on a ramping probability 15–45s variable-interval peak procedure (rVI) with rats trained on a 30s fixed-interval peak procedure (FI). In the ramping distribution, the probability of reinforcement increased in a linear manner as the duration increased. As part of another experiment run previously, we also tested rats using a uniform 15–45s distribution of reinforcement (uVI), and we present these data first to provide a comparison group.

Methods

Experiment 1 compared responding under a 30s FI schedule with that from a uniform 15–45s (uVI) schedule. Experiment 2 compared responding under a 30s FI schedule with that from a ramping 15–45s (rVI) schedule. The two experiments were performed at different times of the year (spring versus fall), in different rooms (dedicated testing room versus colony room), and used different food reinforcements (grain versus sucrose). Presumably as a result of these differences in experimental procedures, performance differed between the FI groups. As such, we present the methods and results of each experiment separately, and then discuss them in concert.

Experiment 1

Subjects and Apparatus

20 male Sprague-Dawley rats, approximately 4 months old at the beginning of the experiment were used. All subjects were kept at 85–90% free feeding weight by providing sufficient rodent chow (Harlan 2019 Rat Diet) immediately after each session. Subjects were run in 10 standard operant chambers (30.5 × 25.4 × 30.5 cm; Coulbourn Instruments), enclosed in moderately sound-attenuating cabinets in a dedicated testing room. Each chamber had aluminum front and back walls and ceiling, a metal stainless steel grid floor, and ventilated Plexiglas sides. An auditory stimulus was provided via a sonalert mounted outside the chamber, and they were reinforced with 45mg sucrose pellets delivered to a food magazine on the front wall of the chamber. Chambers were equipped with 3 infrared nosepoke response detectors on the back wall (only the center one was used here), and a houselight at the top of the front wall. The colony room was on a 12:12 hour (8am–8pm) light-dark cycle, and all training and trials took place during the light phase. Rats were run five days a week.

All subjects were given approximately 20 sucrose pellets in their home cage two days before nosepoke training began in order to acclimate them to the pellets used as reinforcement in the operant chamber.

Procedures

Nosepoke training

Rats were trained to nosepoke the center nosepoke aperture on a 2s fixed interval schedule (from the last reinforcement). The 2s interval was used to prevent the rats from earning rewards so rapidly that that the feeders jammed. Sessions ended after the rat received 60 reinforcements or 120 minutes had elapsed, whichever came first. Rats were trained on this procedure until they earned 60 reinforcements for two consecutive sessions.

Discrete Trial Fixed-interval Training

Rats in the FI groups were trained on a discrete trial fixed-interval (FI) procedure. Trials began with the onset of an auditory stimulus (the sonalert signal). The first nosepoke response subsequent to the 30s criterion duration was reinforced and the trial terminated. Nosepokes prior to the criterion duration had no programmed consequence. A variable, uniformly distributed, 30–60s inter-trial interval (ITI) separated the trials in this and all other procedures. All sessions for this and all other procedures lasted 2 hours.

Discrete Trial Uniform Variable-Interval Training

Rats in the uVI group were trained on a uniformly distributed 15–45s variable interval procedure. Trials began with the onset of the auditory stimulus. On each trial, a duration was randomly selected (with replacement) from a uniform 15–45s distribution with 1s resolution in the spacing (i.e., 15s, 16s, 17s,…,45s), and reinforcement was available for the first nosepoke response after this duration elapsed from trial onset, after which the trial terminated. Responses prior to the selected criterion duration had no programmed consequence.

Peak-interval training

After 7 sessions on the FI and VI training procedures, rats were put on a corresponding peak-interval (PI) procedure. The procedures were identical to the FI and VI procedures described above, with the addition of non-reinforced probe trials (50% of trials). All probe trials lasted three to four times the maximum duration of the VI (i.e., 135 – 180s) and terminated independently of response.

Data Analysis

The times at which the rat’s snout entered the nosepoke aperture were recorded with 20 msec resolution. For construction of the mean response functions, responses were pooled across five sessions, and binned into 1s bins. Because some of the rats had response functions that were skewed, instead of fitting Guassian curves to represent the data, we used a non-theoretical approach (see Church et al., 1998). Specifically, the data were smoothed with a 5s running mean to minimize the influence of noise, and the maximal rate of responding was identified (peak rate). The time at which the peak rate occurred was used as the peak time. The time at which the response function first reached half the maximal rate (computed from the minimal response rate during the trial) and the last time at which it descended to the half maximal rate were identified (left and right half max times). The spread of the response function was the difference in these times. We also conducted single trial analyses, in which we exhaustively fit a low-high-low step function to the response pattern on each trial (Church, Meck, & Gibbon, 1994) in order to identify the times at which a prolonged period of high rate responding began (start time) and ended (stop time). The spread (stop time-start time) and midpoint (start time + spread/2) of the step function were also computed. To minimize the contribution of temporally uncontrolled responding (most frequently seen as a burst of activity very late in the trial), we analyzed data from the first 90s of trials. Following Church et al. (1998), we used the median and interquartile range of the obtained step function statistics for statistical analysis to minimize the contribution of outliers.

Results

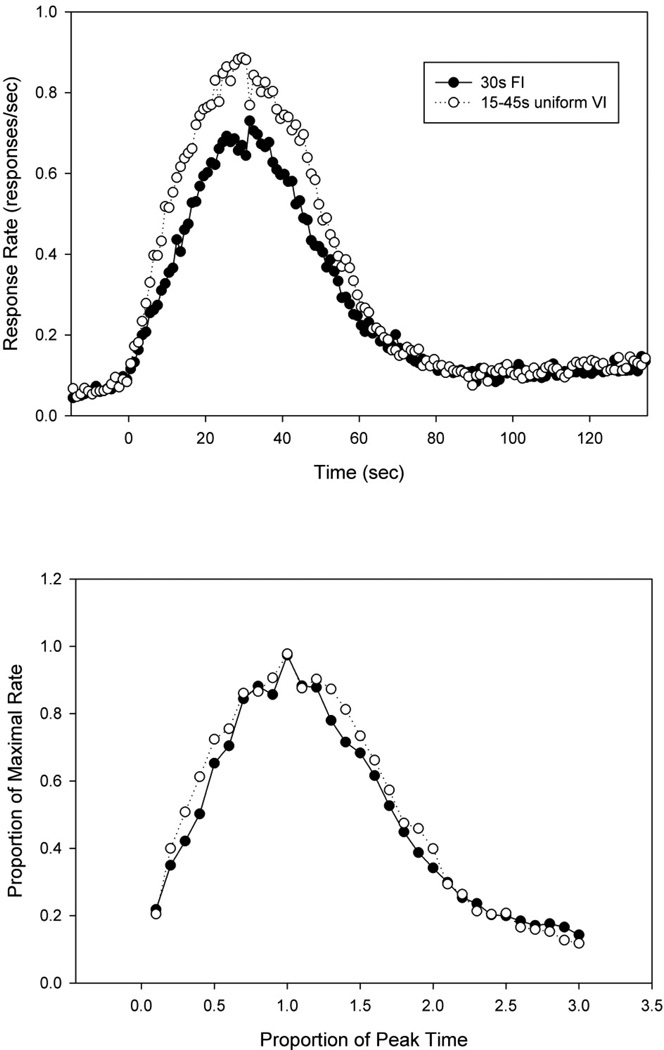
Response rate as a function of time from rats in the FI and uVI procedure are shown in Figure 1a. As can be seen, both groups responded in a peak-shaped manner, centered around the average reinforced duration, although responding appeared slightly broader and more robust in the uVI group than the FI group. Specifically, the mean peak times (standard deviation) were 30.7s (2.9) in the FI group and 29.6s (3.7) in the uVI group, which did not significantly differ from one another [F<1]. The left half max time in the uVI group (10.3s +/−3.6) was significantly earlier than that in the FI group (13.1s +/−1.4) [F(1,18) = 5.15, p < 0.05]. No significant difference was seen in the right half max times between the FI group (52.8s +/−4.3) and the uVI group (51.1s +/−3.0) [F(1,18)=1.06]. No significant differences were found for spread (FI: 39.7s +/−3.6; uVI: 40.8s +/−4.3), [F<1]. Peak rate was nearly, but not significantly [F(1,18) = 3.78, p = 0.053] greater in the VI group (0.89 resp/sec +/−0.18) than the FI group (0.71 resp/sec +/−0.20). Figure 1b shows the peak data after each rat’s responses were normalized by both peak rate and peak time. As can be seen, there was a slight increase in the relative width of the uVI group as compared to the FI group, but this impression was not borne out in the statistics [F<1].

Figure 1.

A) Average peak functions from rats on a 30s peak-interval procedure and rats on a uniformly distributed 15–45s variable-interval peak procedure. B) Average peak functions after the data has been normalized by each subject’s maximal rate and peak time.

Generally similar results were obtained in the single trial analyses. The statistics from the STA are shown in Table 1. As can be seen, the start time was significantly earlier in the uVI group as compared to the FI group, whereas no significant difference was seen in the stop times. As a result, there were trends for the midpoint to be earlier (p = 0.071), and the spread to be broader (p = 0.050), leading to a significantly larger relative spread of responding (spread/midpoint). The start times were significantly less variable in the uVI group (IQR = 18.3s) than the FI group (26.5s), but this diminished variability is likely accounted for by the earlier start time in this group, as the relative variability of the start times (i.e., start CV = interquartile range/median) did not differ. In contrast, the stop times were also significantly less variable in the uVI group (IQR = 25.2s & 20.5s in the FI and uVI groups, respectively), but this diminished variability remained in the normalized statistic (i.e., stop CV). The correlations between the start, stop, spread and midpoints are shown in Table 2 (analyses limited to trials in which the start and stop times bracketed the median midpoint to avoid spurious positive correlations - (see Church et al., 1998; Church et al., 1994). As can be seen, the start-stop correlation was significantly weaker in the uVI group than the FI group (ANOVAs performed on Fisher transformed r values). In addition, the start-spread correlation was significantly stronger in the uVI group.

Table 1.

Statistics from single trial analysis – Experiment 1

	Start	Stop	Spread	Midpoint	Relative Spread	Start CV	Stop CV	Spread CV	Midpoint CV
FI mean	19.23	47.17	23.65	32.82	0.73	1.38	0.54	0.90	0.73
VI mean	15.22	47.33	29.24	30.90	0.94	1.27	0.43	0.88	0.49
FI stdev	3.31	2.78	5.27	2.23	0.15	0.13	0.12	0.24	0.14
VI stdev	3.91	3.39	6.56	2.22	0.22	0.51	0.08	0.30	0.14
F value	6.13*	.01	4.40	3.69	6.63*	0.47	4.75*	0.02	14.59*

^*=p<0.05

Table 2.

Correlations of single trial analysis statistics – Experiment 1

Correlations	S1,S2	S1,SPR	S1,MID	S2,SPR	S2,MID	MID,SPR
FI mean	0.11	−0.33	0.61	0.39	0.67	0.05
VI mean	0.03	−0.34	0.46	0.56	0.64	0.05
FI stdev	0.07	0.11	0.19	0.18	0.10	0.15
VI stdev	0.04	0.09	0.13	0.10	0.07	0.06
F value	5.14*	0.04	5.10*	3.58	0.72	1.78

^*=p<0.05

Experiment 2

Subjects and Apparatus

30 male rats, approximately 4 months old at the beginning of the experiment were used. These subjects were run in 10 standard operant chambers (30.5 × 25.4 × 30.5 cm; Coulbourn Instruments), enclosed in highly sound-attenuating cabinets, which were located in the colony room. The discriminative stimulus for these subjects was a 4 kHz tone, played through a speaker on the back wall of the chamber. They were reinforced with 45mg grain pellets. 10 rats (n=5 rVI, 5FI) were run in the summer of 2012, and 20 rats (n=10rVI, 10FI) were run in the fall of 2012. All other details of the apparatus were identical to Experiment 1. One rat in the rVI group died from undetermined causes during training. In addition, 2 rats in the FI group and 1 rat in the rVI group had very low response rates and poor temporal control with peak times or right half max times more than 3 standard deviations away from the mean times of the remaining rats. They were therefore removed from further analysis.

Procedure

All aspects of the procedure were identical to Experiment 1, with two exceptions. First, both groups received only a single day of FI and VI training prior to implementing probe trials. This was done to ensure that the rats wouldn’t extinguish responding in the transition from the nosepoke training phase to the FI/VI phases due to exposure to probe trials, while at the same time, limiting their exposure to a non-ramping distribution of reinforcement. Second, we used a ramping probability of reinforcement for the VI group. Specifically, at trial onset, a possible interval in the range of 15–45s with 1s resolution spacing was selected with equal probability, and the nosepoke was primed at the end of that interval with a probability that co-varied with the selected duration (ranging from 25–75% computed with equal spacing that increased linearly as a function of duration (i.e., 1.667% increase in reinforcement probability for each 1s duration). If reinforcement was not primed, the trial continued as a probe trial for 3–4 times the longest VI duration (i.e., 135–180s). As a result of the random interval selection and reinforcement probability used for each interval, the actual probability of reinforcement for a particular duration increased in a linear manner from 0.008% (15s) to 0.024% (45s), with an overall probability of reinforcement on each trial of 50%, thereby matching the reinforcement probability of the FI group. Due to the resolution of the behavioral control system, the computed reinforcement probability was rounded to the nearest whole number (i.e., 25%, 27%, 28%, 30%,…, 75% reinforcement probability for 15s, 16s, 17s, 18s,…, 45s).

Results

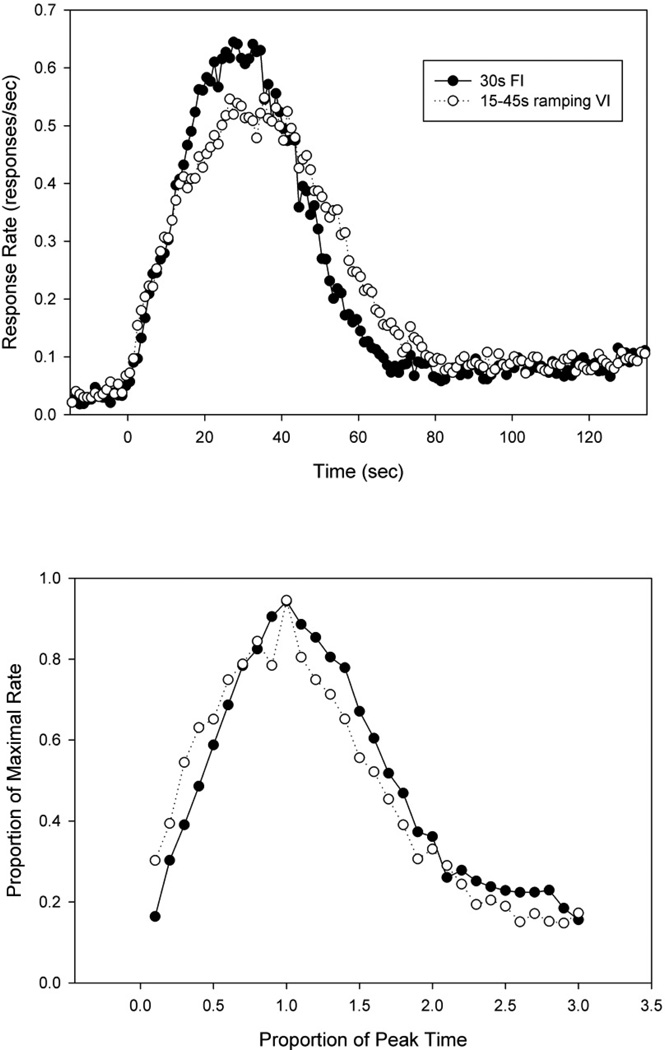
Response rate as a function of time from rats in the FI and rVI procedure are shown in Figure 2a. The mean peak times (standard deviation) were earlier in the FI group (27.8s +/−6.2) than the rVI group (33.8s +/−6.2) [F(1,24) = 6.17, p < 0.05]. The left half max times were 11.9s +/−2.8 in the FI group and 10.2s +/−4.7 in the rVI group, a non-significant difference [F (1,24) = 1.36]. The right half max times in the FI group (48.6s +/−4.0) were significantly earlier that in the rVI group (54.5s +/−5.4) [F(1,24) = 9.98, p < 0.005]. As a result, peak spread was smaller in the FI group than the rVI group (36.7s +/−5.4) & 44.3s +/−4.8), respectively) [F(1,24) = 14.56, p < 0.001)]. Also, peak rates did not differ (0.71 +/−0.36 responses/sec for the FI group, 0.58 +/−0.21 for the rVI group) [F(1,24)= 1.35]. In Figure 2b, the same data are replotted after being normalized by peak rate and peak time. There appears to be a failure of superimposition, resulting from differences in the form of the response functions (i.e., they are asymmetric around the peak time). However, there was no significant difference in normalized spread [F<1]. Results from the single trials analysis are shown in Table 3. As can be seen, while the start times did not differ, the stop time was significantly later in the rVI group as compared to the FI group. As a result, the midpoint was later. As in the mean functions, relative spread did not differ. Likewise, no differences were seen in the relative variability of these measures. Similarly, no significant differences were found in the correlations between these statistics (Table 4).

Figure 2.

A) Average peak functions from rats on a 30s peak-interval procedure and rats on a ramping probability distribution 15–45s variable-interval peak procedure. B) Average peak functions after the data has been normalized by each subject’s maximal rate and peak time.

Table 3.

Statistics from single trial analysis – Experiment 2

	Start	Stop	Spread	Midpoint	Relative Spread	Start CV	Stop CV	Spread CV	Midpoint CV
FI mean	17.19	44.11	21.84	30.31	0.73	1.27	0.47	0.96	0.62
VI mean	17.63	48.74	24.49	33.37	0.79	1.31	0.51	1.12	0.56
FI stdev	3.31	2.71	5.43	2.67	0.18	0.37	0.14	0.36	0.17
VI stdev	5.06	6.63	9.95	4.08	0.26	0.43	0.15	0.38	0.17
F value	0.07	5.44*	0.71	5.12*	0.62	0.06	0.39	1.30	0.76

^*= p<0.05

Table 4.

Correlations of single trial analysis statistics – Experiment 2

Correlations	S1,S2	S1,SPR	S1,MID	S2,SPR	S2,MID	MID,SPR
FI mean	0.04	−0.33	0.47	0.56	0.66	0.10
VI mean	−0.01	−0.43	0.40	0.60	0.58	0.06
FI stdev	0.09	0.19	0.18	0.17	0.15	0.13
VI stdev	0.09	0.16	0.15	0.16	0.14	0.12
F value	2.49	1.97	1.08	0.30	1.88	0.17

^*= p<0.05

Discussion

The results of Experiment 1 were generally similar to those reported by Church et al. (1998), as well as those of Brunner et al. (1996). Specifically, we found that the time at which the response rate function initially reached half-maximal levels (left half max time) started earlier in the uVI group than the FI group. This shift toward early responding was also seen in the start times identified by the single trials analysis. In contrast, we found little evidence to suggest that the time at which the rats terminated responding (i.e., right half max time and stop times) became later in the uVI group. We also found that the the relative variability of the stop time (i.e., variability of the stop time/median stop time) was smaller in the uVI group than the FI group, and there were significant decreases in the strength of the start-stop correlation and the start-midpoint correlation. In Experiment 2, the peak time and right half max time were later in the rVI group than the FI group, resulting in a broader absolute, but not relative, spread. Similarly, in the single trial analysis, the stop time was later in the rVI group, leading to a later midpoint. No significant differences were found for the correlations between the single trial statistics. These results were somewhat similar to those seen in the “backwards” condition of Brunner et al. (1997).

What conclusions can we draw from these results? Our primary goal was to examine the pattern of responding when the “value”, or reinforcement density (probability/delay), at each duration of the variable-interval schedule was equivalent. To this end, Experiment 2 used a ramping reinforcement schedule with the notion that the increasing likelihood of reinforcement would offset the diminished “value” that would result from the increased delay. This approach was carried out to test whether the subjects would average these durations and respond in a manner equivalent to the rats tested on the FI schedule, as we had previously found that rats would average temporal memories in response to stimulus compounds only when the reinforcement density of the component cues was equivalent (Matell & Kurti, in press). Intriguingly, under such conditions, the compound peak falls at the probability weighted average of the component cues (Kurti et al., 2013; Matell & Henning, 2013; Swanton & Matell, 2011). If the rats in Experiment 2 were generating a single expectation by computing a probability weighted average of the reinforced durations, we would expect a scalar peak at a slightly later duration (the probability weighted average is 32.6s, rather than 30s). Indeed, all of the changes (and lack of changes) in both the statistics of the mean function and single trials statistics are consistent with this interpretation. On the other hand, the plots of the data after normalizing by peak rate and peak time failed to reveal precise superimposition, instead suggesting some skew in the response profiles of the rVI group (it should be noted that a subset of rats showed narrow, symmetric responses). Intriguingly, the skew is somewhat reminiscent of the response form of rats trained with greater valued short durations in the stimulus compounding experiments described above, which tended to start responding as though they were timing the short duration, but terminate responding based upon the average of the component durations (Matell & Kurti, in press). As such, these data are somewhat inconsistent with the hypothesis that the rats exposed to a ramping VI schedule would respond in an equivalent manner to rats trained with a single duration. Unsurprisingly, we saw greater differences in the pattern of temporal control in the uVI rats. Taken together, these differences suggest that rats trained under conditions of variable reinforcement times engage in a different set of processes than what is utilized when trained with a single duration.

Can these results provide some illumination regarding what attributes of the timing processes differ between the fixed and variable conditions? In previous work by Brunner et al. (1997), they generated predictions about the form of responding on FI and VI schedules based on a single trial implementation of SET (Church et al., 1994). As described earlier, responding on each trial occurs when the relative discrepancy between currently perceived time and a single random sample from temporal memory is smaller than a threshold value. In their “complete memory model”, temporal memory is a replica of the distribution of reinforced times experienced by the animal. Because the animal experiences much greater variation in reinforced times on a VI schedule as compared to an FI schedule, and this increased variation is reflected in the memory sampled across trials, the “complete memory” model predicts increased relative variability of both start and stop times in subjects trained with VI schedules. However, their experimental results showed diminished stop time variability under VI schedules (as did we), thereby suggesting that the complete memory model was incorrect. A similar conclusion was reached by Church et al. (1998).

An alternative possibility, first proposed by Brunner et al. (1996) as the minimax model, is that subjects base their behavior on the earliest and latest times at which reinforcement has been obtained. Specifically, they proposed that only the earliest and latest times of reinforcement are remembered, thereby substantially lightening the memory requirements compared to the complete memory model. However, this model also has trouble accounting for the data. First, stop times are consistently less variable than start times on fixed interval schedules (Church et al., 1994) (Cheng & Westwood, 1993; Church & Broadbent, 1990; Matell, Bateson, & Meck, 2006) and variable interval schedules (present results and Brunner et al., 1997; Church et al., 1998), a finding that is not predicted by a dual memory model without additional assumptions. Specifically, recall that the decision rule in SET is based on the relative discrepancy between currently perceived time and the memory sample (i.e., responding occurs when the discrepancy/memory sample < threshold). If the response decision is based on two different memory samples (one to start and one to stop), the start decision will be normalized by a smaller memory value than the stop decision, and there should be no difference in relative variability between start and stop times. Second, the minimax model predicts earlier start times and later stop times in the two VI groups compared to the FI groups. In contrast, we saw no difference in start times between the rVI group and the FI group, and no difference in stop times between the uVI group and the FI group. While such an observation is potentially just a failure to disprove the null, we found a significant shift in start times in the uVI group and a significant shift in stop times in the rVI group, suggesting that we were not lacking power to identify such predicted changes. Third, the minimax model predicts that the start and stop times should be equivalent for the two VI groups in the present experiment despite the different composition of the intervals (i.e., uniform versus ramping distribution), whereas our results suggested differential effects. Finally, the minimax model is difficult to reconcile with data from multiple fixed interval schedules (Leak & Gibbon, 1995; Whitaker et al., 2003, 2008), in which responding starts and stops multiple times in a trial. If an organism used a minimax approach, there should only be a single long period of responding.

One possibility that was not considered by these investigators is the computation of an average delay to reinforcement, coupled with different thresholds for starting and stopping responding based on this average delay. This averaging situation is close to the minimax model in that it minimizes memory load compared to the complete model, and it also provides independently adjustable thresholds, which would be useful if the consequences of early or late responding were asymmetric. Additionally, the average memory model predicts the greater relative variability in start times than stop times that is consistently seen in the peak procedure. This prediction follows from using the same memory value as the normalizer in the decision stage discrepancy computations. Specifically by using the same normalizer, the computation for each decision becomes identical to an absolute decision rule, and timing gets more precise as more time elapses as expected for a Poisson timing process (Gibbon, 1992). Secondly, while we have not attempted to formulate a precise rule for the location and variability of the transition time thresholds, a rule that reflected the reinforcement distribution could permit different patterns of responses as a function of the composition of the reinforcement schedule as we saw here. Third, specifying thresholds around an average expectation would allow the average expectation to be used to generate preferences for one schedule over another, whereas utilizing just the minimum and maximum reinforcement times could easily lead to a failure in matching. Finally, the formation of an average expectation would not preclude multiple response transitions, as seen for the minimax model.

How well does such a model account for the present data? We conducted a simulation of an average memory version of SET as follows. On each trial (n=2000) of the simulations, we selected a clock speed from a normal distribution with a mean rate of 10 pulses/sec (SD = 1.0 across trials). The pulse count as a function of time on each trial was computed assuming a Poisson pacemaker running at the selected clock speed. The interval being timed was set at a constant value (e.g., 30s) for all trials for a particular schedule which represents the average expectation. The times at which responding would begin and terminate were derived by the passage of a threshold pulse count, one for starting, and an independent one for stopping. These thresholds were set at a specified proportion of the criterion memory (e.g., 50% and 160%), and were assumed to vary independently on each trial according to a normal distribution with a standard deviation of 15%. Lower bounds for these variables were used, such that clock speed could not drop below 1 pulse/sec, the start thresholds could not drop below 10% and the stop threshold had to be 10% larger than the start threshold. As shown in Tables 5 and 6, with regards to the uVI and FI data, lowering the average expected delay to 28s from 30s (which is consistent with the preference of a uniform VI over an FI of equal mean length (Killeen, 1968) and would result if the “value” of the reinforcement at each delay is taken into account), and broadening the thresholds in both directions, allows the model to capture the direction of all significant changes seen in the data. Similarly, simply increasing the average duration used as the memory, without changing the relative position of the thresholds, captured the limited differences seen in the rVI group as compared to the FI group (not shown). Thus, the use of a single memory which represents the average delay to reinforcement, coupled with independently scalable thresholds allows a version of SET to account for the current data.

Table 5.

Statistics from simulations of SET with a single average memory and two independent thresholds

	Start	Stop	Spread	Midpoint	Relative Spread	Start CV	Stop CV	Spread CV	Midpoint CV
FI sim	18.75	47.92	29.17	33.34	0.87	0.27	0.15	0.23	0.15
uVI sim	14.48	47.58	33.09	31.03	1.07	0.31	0.14	0.21	0.14

Table 6.

Correlations	S1,S2	S1,SPR	S1,MID	S2,SPR	S2,MID	MID,SPR
FI sim	0.13	−0.11	0.56	0.58	0.79	0.15
uVI sim	0.07	−0.14	0.48	0.63	0.78	0.17

In contrast to this conclusion, Jones and Wearden (2003) attempted to assess the form of reference memory by examining whether the extent of experience with the “standard” duration influences performance on a temporal generalization task in humans. Specifically, they compared performance levels after subjects received between one and five presentations of the “standard”. Their design was based on the argument that greater experience with the standard would be expected to improve performance if subjects computed an average, whereas no improvement would be obtained if subjects used a random sample from a distribution. As they found no difference in behavior as a function of level of experience, they concluded that an average memory model was incorrect, and a distributional model was more consistent with the data. However, as their human participants repeatedly learned and were tested with a new criterion duration on each block, with very limited experience (i.e., 1–5 presentations), it is unclear that the subjects would be utilizing the same reference memory system as used by the rats in the present experiment who had over a month’s worth of experience. Indeed, protein synthesis is necessary for long-term memory consolidation (i.e., over a few hours), whereas short-term memory does not require such processes (Davis & Squire, 1984; Nader, Schafe, & Le Doux, 2000).

One question relating to the use of an average expectation is how such an average is computed or updated upon reinforcement. We did not examine different update rules in our simulations, but simply assumed that the average expectation was “known” by the organism, and reflected sufficient experience with the reinforcement schedule. Such a situation would result if each reinforcement modified the average expectation weakly (i.e., the weight given to recent evidence is low). In contrast, if the influence of the most recent reinforcements were strong, this would produce results that would be equivalent to increasing clock speed (or memory sampling) variability. As such, the results would trend toward those predicted by the “complete memory model” described above, which has been ruled out as a possible model (at least for animal subjects trained on constrained variable interval procedures). We note, however, that it is likely the case that the degree of influence that a recent reinforcement has had on an average will depend on the reinforcement contingencies in place. Specifically, as mentioned above, it has been shown that both human and non-human animals can learn to track the most recent reinforcement in schedules that systematically change (Higa, Wynne, & Staddon, 1991; Lejeune, Ferrara, Soffie, Bronchart, & Wearden, 1998) or jump abruptly after being stable for a several trials (Higa, 1997; Simen, Balci, de Souza, Cohen, & Holmes, 2011), suggesting that subjects can be quite sensitive to individual experiences.

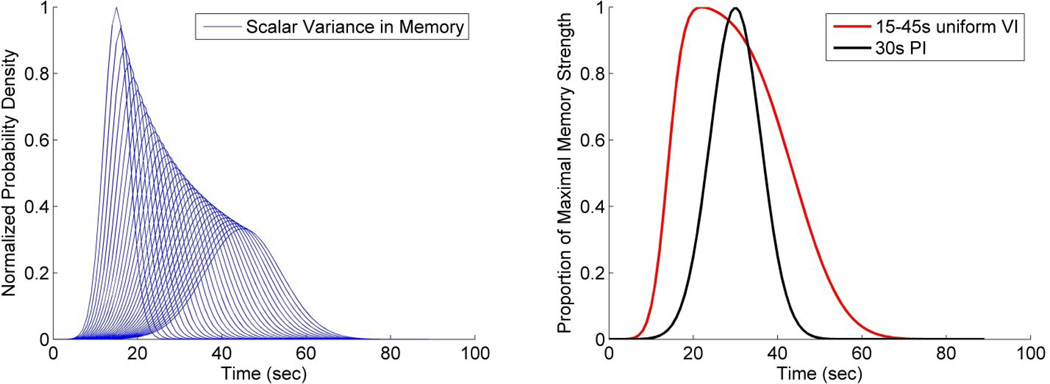
As it relates to the theme of this special issue, we also consider whether a basic associative model can account for these findings. As a result of scalar variability in “perceived” time, reinforcement that was scheduled in a uniform manner from 15s–45s would generate an array of perceived times of reinforcement (Figure 3a). Under the assumption that each reinforcing event strengthens the probability of future responding at that moment in time, a summation process provides the expected response pattern. The summed memory distribution is shown in Figure 3b. We also show the distribution associated with a single 30s reinforcement time. As can be seen, the uniform VI peaks earlier than the FI. This result was seen in the mean functions of Experiment 1. However, the right tail of responding is more skewed in the uVI summation curve than was seen in the data, and generally comes down later. It has been well established that the smooth response rate function result from averaging single trials with abrupt changes in responding (Church et al., 1994; Gibbon & Church, 1990). To account for the response pattern on a single trial, a response threshold would have to be implemented, and to account for the consistently obtained negative start-spread correlation, threshold variability must be incorporated (Church et al., 1994; Gibbon & Church, 1990). The use of such a threshold would capture the earlier start times seen in our data. Further, depending on the height of the threshold, the stop time in the VI group could be earlier, the same time, or later than that for the FI group, thus potentially capturing this aspect of the data as well. However, because the summation process generates data that are rightward skewed (i.e., the left tail of the simulated VI curve is steeper than the simulated FI curve, whereas the right tail of the VI curve is shallower than the FI curve), variability in the threshold would lead to decreased variance in the start time, but increased variance in the stop time. In contrast, our data, and arguably that of Church et al. (1998), showed decreased normalized stop time variability. Thus, like the complete memory model of SET considered by Brunner et al. (1997), a simple associative model of timing in which response strength is represented as a skewed memory distribution is incompatible with the data.

Figure 3.

A) Expected memory strength distribution associated with each reinforcement time on a uniform 15–45s variable interval procedure due to scalar variance. B) Summation of the strength of memories shown in panel A, as well as a single memory distribution associated with a 30s PI.

In sum, we suggest that a single memory of the average expectation of the delay to reinforcement, coupled with independent decision thresholds, may be sufficient to characterize temporally controlled responding across several different reinforcement schedules and offers some conceptual and empirical benefits as compared to both distributional models and the minimax model. Finally, an average delay to reinforcement provides a natural statistic for choice behavior showing equivalent preference of an FI and the harmonic mean of a VI (Killeen, 1968), as well as response strength in VI schedules under Pavlovian contingencies (Harris & Carpenter, 2011). Finally, a single memory value, perhaps encoded in firing rates through synaptic weights, may be easier to instantiate in neural models than sampling of a memory distribution, thereby lending a link between associative and cognitive architectures of timing models (e.g., Simen et al., 2011).

Key Points.

Rats on a uniform 15–45s VI peak procedure respond earlier and more broadly than rats on a 30s peak procedure.

Rats on a ramping 15–45s VI peak procedure respond later than rats on a 30s peak procedure.

These data are consistent with a model of temporal memory that represents the average delay to reinforcement.