Stochastic Fusion Simulations and Experiments Suggest Passive and Active Roles of Hemagglutinin during Membrane Fusion

Abstract

Influenza enters the host cell cytoplasm by fusing the viral and host membrane together. Fusion is mediated by hemagglutinin (HA) trimers that undergo conformational change when acidified in the endosome. It is currently debated how many HA trimers, w, and how many conformationally changed HA trimers, q, are minimally required for fusion. Conclusions vary because there are three common approaches for determining w and q from fusion data. One approach correlates the fusion rate with the fraction of fusogenic HA trimers and leads to the conclusion that one HA trimer is required for fusion. A second approach correlates the fusion rate with the total concentration of fusogenic HA trimers and indicates that more than one HA trimer is required. A third approach applies statistical models to fusion rate data obtained at a single HA density to establish w or q and suggests that more than one HA trimer is required. In this work, all three approaches are investigated through stochastic fusion simulations and experiments to elucidate the roles of HA and its ability to bend the target membrane during fusion. We find that the apparent discrepancies among the results from the various approaches may be resolved if nonfusogenic HA participates in fusion through interactions with a fusogenic HA. Our results, based on H3 and H1 serotypes, suggest that three adjacent HA trimers and one conformationally changed HA trimer are minimally required to induce membrane fusion (w = 3 and q = 1).

Introduction

Membrane fusion is an important process that enveloped viruses such as influenza use to enter host cells. The surface of influenza viruses contains hemagglutinin (HA) proteins that govern both the attachment of the virus to sialic acid receptors on a host cell and the fusion of the viral envelope with the host membrane. The HA protein is a trimer of three monomers; this protein unit will be referred to as an HA trimer. Below a pH of 5.8 (1), HA trimers can undergo conformational changes that insert hydrophobic fusion peptides into the target membrane to initiate membrane fusion (2). Despite extensive research on the fusion mechanism, the minimum number of HA trimers needed for fusion is still a matter of debate. In this work, we use simulations and experiments to resolve the possible roles of hemagglutinin in fusion.

Adopting the notation used by Bentz (3), we refer to the minimum number of HA trimers that are required for fusion as w, and the minimum number of HA trimers within the subset of w that must undergo conformational change as q. A direct way of determining w and q would be to observe distinct HA trimers inducing fusion in real time, but, as of this writing, such experiments are not yet possible. Therefore, w and q are extracted indirectly through the analysis of the kinetics of HA-induced membrane fusion, combined with electron-micrograph (EM) images (4–7) and crystallographic data (8–10) of intermediate states of membrane fusion. The general techniques used to study membrane fusion kinetics are discussed in Struck et al. (11) and Otterstrom and van Oijen (12). The kinetic data are often collected as a distribution of lag times between the acidification of HA trimers and the membrane fusion event, which is normally detected through the dequenching of membrane fluorophores. In past studies, different values for w and q were proposed depending on the experimental systems used to obtain the lag-time distributions and the statistical models used to interpret the data. Additionally, many past studies did not assume that w and q can have different values. Generally, values of w or q > 1 suggest that multiple HA trimers act cooperatively to induce fusion, whereas a value of 1 suggests HA trimers do not act cooperatively to induce fusion. Past studies have provided evidence for both cooperative and noncooperative behavior of HA trimers to induce fusion, which appears to be contradictory. Through simulations and the analysis of kinetic data, we propose that contradictory observations can be reconciled if conformationally changed HA trimers play an active role in fusion whereas unchanged HA trimers play a passive role.

Variations in approaches that have led to different conclusions for w and q

There are three common approaches for determining w and q using kinetic data from fusion experiments:

One approach is to monitor how the fusion lag times change as the ratio between the number of fusogenic HA trimers (HA_1,2) and nonfusogenic HA trimers (HA₀) is varied while the total HA density is kept constant. This method is referred to as the “Variable F” approach by Imai et al. (13) because the fusion (F) capacity of virions (or virosomes) is being varied and not their binding (B) capacity. The fusion rate, V, can then be extracted from the slope of the cumulative lag-time distribution. Considering the fusion event as a reaction, an nth-order reaction equation such as V = k[HA_1,2]ⁿ could be used to correlate V with the number of cooperating HA trimers, n. Note that many past studies did not consider w and q as separate values, hence, n is considered as being either w or q (n = w or q). Most kinetic data from the Variable F approach (13–16) support that HA trimers do not act cooperatively to induce fusion (n = 1).

A second approach, is to find the correlation between fusion rate and the total concentration of HA trimers, all of which are fusogenic (HA_1,2). This method is referred to as the “Variable FB” (13), Most results from past studies that used this approach (3,13,17–19) show that the fusion rate scales nonlinearly with fusogenic HA density, which indicates that HA trimers act cooperatively to induce fusion (n > 1).

A third approach, deduces n by analyzing the shape of the lag-time distribution obtained at a constant fusogenic HA density. This method is referred to as the “Constant FB” approach since the fusion and binding capacities of the virions (or virosomes) are not varied, though environmental conditions such as the pH to trigger fusion can be varied. Often, statistical models with n as the fitting parameter are used to fit the lag-time distribution. This approach usually concludes that n is >1 (3,19–25). Table S1 in the Supporting Material provides an extended summary of related works, along with their concluded values of w or q.

The work by Imai et al. (13) demonstrates that fusion kinetics proves sensitive to different approaches, despite the fact that the experimental system is otherwise the same. The Variable F approach suggests n is 1, whereas the Variable FB approach suggests n is >1. Because Imai et al. (13) did not consider that w and q can have different values, one value for n had to be chosen between the Variable F and FB results. They decided n = 1 according to the Variable F approach. However, we show that both of their results are consistent with each other if we allow w and q to take different values (w ≠ q). The interpretation that w and q are not equal is that fusion proceeds through the involvement of both conformationally changed and unchanged HA trimers.

We present a mechanistic model and simulation strategy that can generate kinetic data showing both cooperative and noncooperative behaviors of HA trimers in inducing fusion when w is 3 and q is 1. The results for w and q were validated using kinetic data from both the experiments of Imai et al. (13) and our own fusion experiments, which studied the membrane fusion behavior of the H1 and H3 serotypes of HA trimers, respectively. We note here that the obtained values for w and q may not extend across other experimental systems that use different HA serotypes or fusion conditions.

In addition to extracting w and q from kinetic data, our model is able to capture the dependence of fusion lag times on target membrane properties, as shown by other works (26–28). Our model is notably different from other simulation models (19,24,25), which do not generate kinetic data that agree with the data from all three approaches and do not explicitly consider how target membrane properties affect fusion.

Experiment Methods

Influenza virus labeling

To label the viral envelope with a fluorescent fluorophore, 5 μL of X31 A/Aichi/68 H3N2 (Charles River, Wilmington, MA) at a concentration of 2 mg/mL, along with 0.1 μL of 1.8 mM octadecyl rhodamine B chloride (R18; Invitrogen, Carlsbad, CA) in ethanol, and 250 μL of MES buffer (1 mM 2-(n-morpholino)ethanesulfonic acid, 150 mM NaCl, pH 7), were mixed in a vial for 1 h at room temperature using a water sonicator bath. Unincorporated R18 fluorophores were removed from solution using a G25 Sephadex spin column (GE Healthcare Biosciences, Pittsburgh, PA). The filtered virus solution was diluted in MES buffer by 10-fold before use.

Target bilayer compositions

DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine), POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine), LPC (1-stearoyl-2-hydroxy-sn-glycero-3-phosphocholine), and cholesterol (Avanti Polar Lipids, Alabaster, AL) were individually dissolved in chloroform. The sialic acid receptor, G_D1a (Sigma-Aldrich, St. Louis, MO), was dissolved in a 2:1 chloroform/methanol solution. Oregon Green DHPE (Invitrogen), an acid-sensitive membrane fluorophore, was dissolved in ethanol. Two different lipid compositions were then prepared, labeled as compositions A and B. Composition A was prepared by mixing lipid components at a molar ratio of 4:4:2:0.1:0.001 DOPC/POPC/Cholesterol/G_D1a/Oregon Green DHPE, and composition B was prepared similarly, but with LPC replacing POPC. The lipid solutions were dried under vacuum for 3 h and rehydrated in MES buffer to a concentration of 0.5 mg/mL. Lipids were extruded 10 times through a 50-nm pore size polycarbonate membrane filter (GE Healthcare Life Science, Pittsburgh, PA) to form vesicles that were ∼100 nm in diameter, determined by dynamic light scattering (Malvern Instruments, Worcestershire, UK).

Fusion assay

Fusion experiments were performed inside microfluidic devices. The device assembly procedure is provided in the Supporting Material. The outlet tubes of the microfluidic device were attached to a syringe pump while the inlet tubes were placed in a vial containing a loading solution. The first loading solution contained the lipid vesicles, which were drawn into the microfluidic device to form a supported lipid bilayer (SLB) over the course of 20 min. This SLB acts as the target membrane for the virus, and the SLB can either consist of composition A (SLB A) or B (SLB B). Excess vesicles were rinsed away by flowing MES buffer through the device channels. Virions were loaded into the channels and then allowed to bind to the G_D1a in the bilayer. Unbound virions were rinsed away with MES buffer. Fusion was triggered by flowing in a citric acid buffer (1 mM citric acid, 150 mM NaCl) at prescribed pH values at a flow rate of 500 μL/min for 30 s (see Fig. S1 in the Supporting Material).

Hemifusion lag-time data from experiments

The R18-labeled virus was observed through total internal reflection fluorescence microscopy using an inverted microscope (Carl Zeiss, Oberkochen, Germany) and a 100× oil-immersion objective. Two lasers (561-nm and 488-nm) illuminated the labeled virus and the Oregon Green in the bilayer. When the acid reached the bilayer, the Oregon Green fluorophores quenched in the target bilayer and the R18 fluorophores in the virus dequenched upon lipid mixing. The time between these events is the lag time for hemifusion. In this work, we use the terms “fusion” and “hemifusion” interchangeably to describe the merging of two outer leaflets of the viral and target membrane. Fig. S1 shows how the fusion lag time is determined; additional details about fusion lag-time acquisition can be found elsewhere (21,23,29).

Target membrane quality and lipid diffusivity

The diffusion coefficients of R18 fluorophores in the supported lipid bilayers at various pH conditions were determined using fluorescence recovery after photobleaching (FRAP). FRAP was performed to check the bilayer quality and detect changes in membrane properties. FRAP experiments and analyses are described in the Supporting Material and in Fig. S2.

Simulation Methods

Defining the spatial domain with a two-dimensional hexagonal lattice

The spatial domain of the simulation is defined as a two-dimensional plane representing the overlapped projection of the viral and target membrane, similar to the setup used by Schreiber et al. (19). To capture some three-dimensional aspects of fusion, such as the curvature of the viral membrane, we define two regions in the spatial domain: the contact area and the surrounding area. In the contact area, the viral and host membrane are located at an optimal distance from each other to allow HA trimers to mediate receptor binding and membrane fusion. In the surrounding area, the HA trimers are too far away from the target membrane to interact with the receptor. Note that due to the two-dimensional spatial system, fusion intermediate structures, such as the hemifusion stalk and membrane dimples, cannot be shown visually, but their formation can still be described kinetically by associating these structures with distinct species that occupy space within the simulation spatial domain.

The spatial domain was discretized into a lattice array as a coarse-graining strategy to reduce simulation time at the cost of losing spatial resolution. We used a hexagonal lattice, instead of a square lattice, because tightly-packed HA trimers tend to adopt a triangular arrangement (30,31). To simulate HA positions more realistically, a continuous spatial domain could be deployed using an off-lattice system. However, such a simulation method would be considerably more computationally expensive. If HA trimers must be close together to cooperatively induce fusion, then the hexagonal lattice suffices in capturing this arrangement of HA trimers.

The circumdiameter of one hexagonal unit was set at 6 nm to match the diameter of an HA trimer (7,10); this lattice element size ensures that HA trimers will not physically overlap. The total simulation space size was set at 25 × 25 grid elements (14,625 nm²), or roughly half the surface area of a spherical virus with a diameter of 100 nm. A larger spatial domain could be used, though this may be unnecessary because fusion occurs at a smaller contact area. The contact area was approximated as a 10 × 10 lattice domain (2338 nm²) positioned in the center of the entire simulation space. The influenza strains we are studying are generally spherical and span a range of diameters between 85 and 170 nm (32,33). To determine whether the contact area size has an impact on the values obtained for w and q, we also considered other contact area sizes. In short, w and q were not sensitive to contact area size (see the Supporting Material and Fig. S6).

Defining the simulation species

The total number of receptors, R, was set arbitrarily to 65, whereas the number of HA trimers was varied depending on the approach being used. All species were placed randomly across the entire spatial domain. The maximum number of HA trimers used in our simulation was set to 200, to be consistent with the HA density of a typical 100-nm-diameter virion that contains roughly 400 HA trimers (34). This maximum HA number density is referred to as ρ_HA,200. Note that Imai et al. (13) report the unit of HA density as a weight ratio of HA to lipid. Our ρ_HA,200 corresponds to their maximum HA density and a 3.4 HA/lipid mass ratio.

There are two types of HA trimers in our model, HA₀ and HA_1,2. Both can bind to receptor R, but only HA_1,2 can undergo conformational change to become an HA_1,2^∗ species. An HA species can move laterally to an adjacent free grid element that has no HA in it, and a similar rule applies for R as well. An HA and an R can overlap the same grid element because HA and R exist in two different membranes. An HA_1,2^∗ inside the contact area is interpreted as an HA trimer that has inserted its fusion peptide into the target bilayer, and this is then treated as an immobile species. Here, fusion peptide insertion can occur without receptor binding (1,35,36), which is also consistent with several reports showing that receptor binding is not required for fusion (22,37–41). Table S2 summarizes the species involved in our simulation and their permitted locations in the simulation space.

The positions of HA trimers are important when defining a fusible unit species. A fusible unit is defined by an arrangement of HA (HA₀ or HA_1,2) and HA_1,2^∗ species in adjacent grid elements that is characterized by w and q. An example of a w = 3 and q = 1 criterion for forming a fusible unit is shown in Fig. 1; examples of other arrangements that were tested are provided in Supporting Material and Fig. S4. Note that the actual number of conformationally changed HA trimers inside the fusible unit arrangement can exceed q and follow a distribution; however, q itself cannot follow a distribution because q represents the minimum number of conformationally changed HA trimers that are required for fusion.

Figure 1.

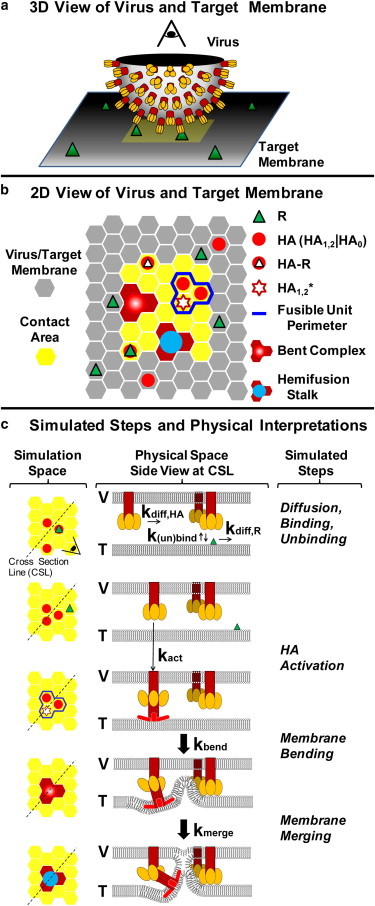
Virus-cell interaction represented in the simulation space. (a) A close-up, three-dimensional view of half of the virus bound to the host membrane. (b) Two-dimensional representation of the three-dimensional picture. The simulation space represents the viral membrane overlapping the target membrane. The HA and R species move within a hexagonal lattice domain. Any interaction between the virus and host membrane occurs within the contact area (yellow). An example of using a w = 3, q = 1 criterion for forming a fusible unit is outlined (blue perimeter). (c) Catalog of simulated events in the fusion model. The simulation species are shown on the left-hand side as a top-down view; the corresponding physical interpretations of the species are shown in the middle through cross-sectional side views. The viral and target membranes are labeled V and T, respectively. (Yellow ovals) HA₁ binding domain; (red objects) HA₂ fusion domain of an HA_1,2 trimer. (Brighter red) Portions of the HA₂ domain representing the hydrophobic fusion peptides that inserts into the target membrane. To see this figure in color, go online.

An unresolved issue remains whether or not the fusible unit consists of an irreversible aggregation of HA trimers. Based on the EM picture provided by Kanaseki et al. (6), aggregated HA trimers are not apparent before or after fusion. Aggregation has been theorized mainly due to the rosette seen after the acidification of HA trimers (4). The fusible unit in our model is not an aggregated HA trimer complex, but rather it is a transient configuration in the contact area where HA trimers can pinch the target bilayer into a dimple. Once a fusible unit is identified within the contact area, it is treated as a distinct simulation species that can transition into a bent complex intermediate, which is analogous to the fusion dimple observed in EM studies of influenza membrane fusion (5,6). The bent complex can then proceed to a merged state of the outer leaflets of the two membranes, defined as a hemifusion stalk. The time when the first hemifusion stalk appears dictates the fusion lag time in both the fusion simulations and experiments. Fig. 1 shows the simulated reaction/diffusion events and Table 1 summarizes the rate parameter values used in this work (17,19,42,43).

Table 1.

List of simulated reaction events and their associated symbols and values

Reaction event	Rate symbol	Rate value (s−1)
Diffusion of HA and R
HA(r1) → HA(r2)	kdiff,HA	740 (17)
R(r1) → R(r2)	kdiff,R (Glycoprotein) kdiff,R (GD1a)	[74] (19,42) 2000a
Actions of HA and R
HA + R → HA-R	kbind	0.20 (19)
HA-R → HA + R	kunbind	0.15 (19)
HA1,2 → HA1,2∗	kact (pH = 5.2) kact (pH < 4.9)	[0.067]b 5.78 (43)
Membrane events
[Fusible unit] → [bent complex]	kbend	Fitted parameter
[Bent complex] → [hemifusion stalk]	kmerge	0.10

HA refers to either HA₀ or HA_1,2. The bracketed rate parameter values were used only when matching the data of Imai et al. (13). The numbers in parentheses are the references from which these values were taken.

^aCapped value. See text and the Supporting Material for more details.

^bk_act values for the H1 serotype of HA in the virosomes of Imai et al. (13) are unknown. Values of 0.01 s⁻¹ and 0.067 s⁻¹ were tested. More details are provided in the Supporting Material.

Defining the reaction rate parameters

The hopping rate of HA or R from one grid element to an adjacent element is defined as k_diff,HA and k_diff,R, respectively. These parameters were calculated from their corresponding diffusion coefficients as described in the Supporting Material. The binding and unbinding rates between an HA trimer and receptor, defined as k_bind and k_unbind, respectively, were adopted from the work of Schreiber et al. (19). Note that Imai et al. (13) used glycoprotein on red blood cells as the viral receptor, whereas we used G_D1A glycolipid instead. Hence, the k_diff,R value for glycoprotein (i.e., 74 s⁻¹) was used to simulate the data of Imai et al., whereas the k_diff,R value for G_D1A (capped at 2000 s⁻¹) was used when simulating our own data.

The activation rate, k_act, of an HA trimer as a function of pH has been determined experimentally by Krumbiegel et al. (43) for the X31 virus (H3N2) that we are using. They report a k_act value of 5.78 s⁻¹ for pH conditions that are <4.9. Because Imai et al (13) performed experiments at a higher pH value of 5.2 and with a different HA serotype (H1), a different k_act value had to be used to simulate their data. But, to our knowledge, k_act is unknown for the H1 serotype of HA trimer, therefore as a starting point, we used the k_act value (0.067 s⁻¹) for the H3 serotype at a pH value of 5.2 that was found by Krumbiegel et al. (43). We then tested another arbitrary k_act value of 0.010 s⁻¹ to see how this affects our conclusion for w and q. Results for these tests are provided in the Supporting Material and in Fig. S7; in short, our conclusions on w and q did not depend on k_act within the tested range.

A lumped rate parameter that describes how fast a fusible unit can bend the target membrane is defined as k_bend. Parameter k_bend depends on both the HA trimer’s ability to bend the membrane as well as the properties of the target membrane that dictate its ability to bend. The value for k_bend is unknown and k_bend is an important fitting parameter in our model. An approximate value for k_bend, which we denote as k_bend,approx, is found by adjusting k_bend until the simulated distribution is not statistically different from the actual distribution according to a Kolmogorov-Smirnov (KS) test, as described below. When a more precise value of k_bend is necessary to make conclusions about membrane bending rates, which is the case when studying k_bend as a function of pH or membrane properties, k_bend is refined using a bootstrap method (44). This refinement method is described in the Supporting Material. The k_bend values reported later in Figs. 5 and 6 have been refined.

Figure 5.

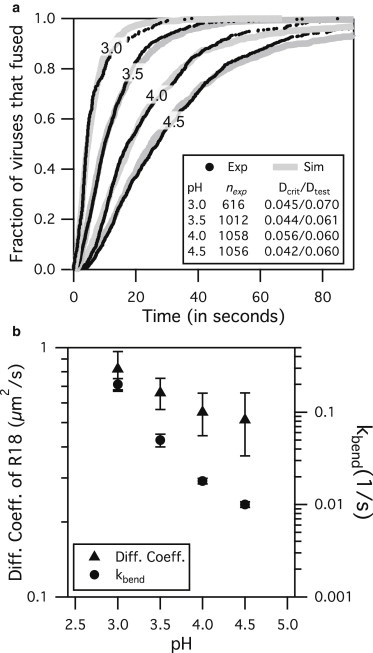
X31 fusion results at various pH conditions for SLB A at ρ_HA,200. (a) Simulations are able to fit experimental data by adjusting only k_bend while keeping w = 3 and q = 1. (b, right axis and circles) The mean k_bend values for pH 3.0, 3.5, 4.0, and 4.5 are 0.2, 0.05, 0.018, and 0.01 s⁻¹, respectively, with standard deviation shown in error bars. (b, left axis and triangles) The mean R18 diffusivity values for pH 3.0, 3.5, 4.0, and 4.5 are 0.82, 0.66, 0.55, and 0.51 μm²/s, respectively, with standard deviation shown in error bars. Mobile fractions of R18 were close to 1 for all cases. Both R18 diffusivity and k_bend decrease with increasing pH over this range.

Figure 6.

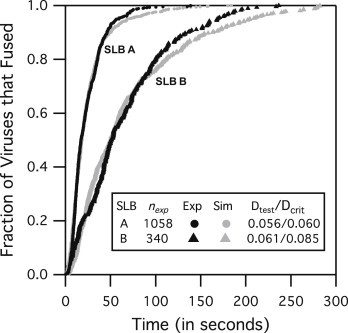
X31 virus fusion results at pH 4.0 using SLB A and SLB B. Simulations were able to match experimental data for two different target membranes membrane compositions by adjusting k_bend only. The values of k_bend from the fits are 0.018 (±0.001) s⁻¹ for SLB A and 0.0035 (±0.0002) s⁻¹ for SLB B.

The frequency rate at which a highly bent target membrane transitions into a hemifusion stalk, k_merge, is expected to be similar in magnitude to that for vesicle-vesicle fusion. Lentz and Lee (45) provided a comprehensive review on the similarities between PEG-induced and HA-induced fusion. The half-life for PEG-induced fusion is ∼10 s (45,46), which, if fitted to the equation k_merge = −ln(1/2)/t_1/2, gives an associated rate constant of 0.07 s⁻¹. To find a value for k_merge that is most representative of an influenza virus fusing with a host membrane, we look to existing fusion data in the pH range where HA conformational change is not limited by proton availability. Floyd et al. (21) showed that at pH 3, the fusion lag-time distribution reflects a single rate-limiting step with a rate constant of 0.1 s⁻¹. If the rate-limiting step is the merging of the membrane at this low pH, then the rate constant value of 0.1 s⁻¹ is in good agreement with that estimated from PEG-induced vesicle fusion studies. We therefore assigned k_merge to be 0.1 s⁻¹ in our simulation model.

Technique for simulating hemifusion lag time

Our simulation uses the stochastic simulation algorithm developed by Gillespie (47) to predict the lag time for a virus hemifusion event. Any changes to a simulation species or its position are treated as a reaction event. The probability of a reaction event occurring within a small time increment, [t, t + dt], is defined as a “propensity”. The propensity of a reaction event is calculated from both the rate parameters and the number of species involved for each reaction event. At a simulated time of t = 0, the system is considered to be acidified and fusogenic HA trimers are allowed to change conformation and participate in forming a hemifusion stalk. Using a random number generator and an iterative loop, all reaction events can be simulated based on their propensities. The formation of the first hemifusion stalk species dictates the fusion lag time and ends the simulation. Simulations are repeated 1000 times to collect a distribution of lag times. More details on the simulation algorithm are provided in the Supporting Material.

Matching simulated and actual fusion lag-time distributions

To determine if the simulated lag-time distribution is an acceptable fit for the experimental data, the two-population KS test (48,49) was used. The null hypothesis for the KS test is that two distributions are statistically the same. If the KS statistic (D_test), defined as the greatest vertical distance between two normalized cumulative lag-time distributions, is greater than the critical KS statistic (D_crit) for a 5% significance level, then the null hypothesis is rejected. The critical KS statistic is calculated using the equation below, where c(α) = 1.36 for the 5% significance level, n_exp = number of data points from experiment, and n_sim = number of data points from simulation:

$$D_{\text{crit}}=c\left(\alpha \right)\sqrt{\frac{n_{\text{sim}}+n_{\exp }}{n_{\text{sim}}{n}_{\exp }}}.$$

• •If D_test ≥ D_crit, simulation results are rejected.
• •If D_test < D_crit, simulation results are accepted.

The criteria for accepting a simulation result is that D_test must be less than D_crit, which means the simulated distribution is not statistically different from the experimental distribution within the 95% confidence interval. Values for D_test and D_crit are provided in the legends of the figures that show the lag-time distributions (Figs. 2, 5, and 6).

Figure 2.

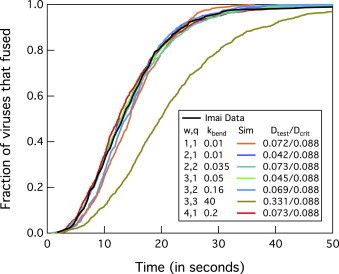
Determining possible solutions for w, q, and k_bend using the Constant FB approach on the fusion data of Imai et al. (13) at ρ_HA,200 and using rate values in Table 1 for pH 5.2. The ratio D_test/D_crit is used to determine if simulations match with the data of Imai et al. If D_test/D_crit is <1, simulations are accepted. An example of an invalid solution is shown when w = 3 and q = 3 (olive green line), as noted by D_test/D_crit being >1. To see this figure in color, go online.

Determining rate-limiting steps using sensitivity analysis

To determine the rate-limiting steps (RLSs) for fusion, the common strategy of comparing the magnitude of rate parameters could not be used because this neglects the fact that multiple HA trimers can act in parallel to induce fusion. Another way to determine the RLSs is to make use of the fact that the fusion lag-time output will be most sensitive to the RLSs; hence, a sensitivity analysis was performed for each rate parameter. To perform the sensitivity analysis, the rate parameter being evaluated was adjusted by 10 and 20% from the current value while other parameters were fixed, and simulations were run to extract the new, altered lag-time distributions. A sensitivity index, S_a, is calculated for each rate parameter using the formula (25,50)

$$S_a=\frac{\partial Y}{\partial p}=\frac{\left|Y_{\text{alt}}-Y_{\text{ref}}\right|}{\left|p_{\text{alt}}-p_{\text{ref}}\right|},$$

where Y_alt is the mean lag time obtained at the altered parameter value p_alt, and Y_ref is the mean lag time obtained at the original value of the parameter p_ref. The RLSs are associated with the rate parameters with the highest, relative sensitivity index values.

Results

Overview of the strategy for determining w and q

The unknown parameters in our model are w, q, and k_bend. We begin by using the Constant FB approach to find multiple valid combinations of w, q, and k_bend that allow the simulated lag-time distributions to match that of Imai et al. (13) when the HA_1,2 density is ρ_HA,200 (Fig. 2, black line). The rate parameters that were used for this step are listed in Table 1 for the experimental system of Imai et al., which involves virosomes with HA trimer (H1 serotype) binding to glycoprotein receptors and fusing with a cell membrane at a pH of 5.2. We then use the Variable F and FB approach to find a unique solution for w, q, and k_bend by matching the simulated trends in fusion rates versus HA densities with the trends of Imai et al. (13). After a unique solution of w, q, and k_bend is determined, we retain the w and q values and perform a model validation procedure to see if the model can predict the fusion kinetics of the H3N2 (X31) influenza virus.

The model is validated if simulated lag-time distributions match with those from X31 fusion experiments performed at different pH conditions and membrane compositions. Because the HA densities were not varied, this process is categorized under the Constant FB approach. The rate parameters that were used are listed in Table 1 for our experimental system, which involves the H3N2 virus binding to G_D1A receptors and fusing with a supported lipid bilayer at a pH between 3 and 4.5. We assumed w and q are constant across the H3 and H1 serotypes of HA trimers and for the experimental conditions used here. Parameter k_bend was left as the sole fitting parameter while all other parameters were held constant. If the simulations cannot match the lag-time distributions found from fusion experiments through the adjustment of k_bend, then the model assumptions are invalid and need to be revised. If simulations can match with experiments, then the model assumptions are validated and the resulting solution for w and q is accepted. The above simulation strategy is summarized in a flow chart provided in Fig. S5.

Finding potential solutions for w, q, k_bend using Constant FB

The Constant FB approach was used to simulated lag-time distribution from Imai et al. (13) when the HA_1,2 density is ρ_HA,200 and the pH is 5.2. The rate parameters (besides k_bend) used are shown in Table 1 for the experimental system of Imai et al. (13), which were held constant. Fig. 2 shows the matched cumulative fusion lag-time distributions for many combinations of w, q, and k_bend. Note that this also shows that the Constant FB approach cannot be used alone to find a unique solution for w and q. Variable F and FB approaches are needed to reduce the number of solutions.

Eliminating w, q, k_bend solutions using Variable F

For each possible solution of w, q, and k_bend found above, simulations were run to mimic the Variable F approach of Imai et al. (13) to see which set of values could recapitulate results from their experimental data set. In the simulation, the number of HA_1,2 trimers was incrementally decreased from 200 to 10 while the number of HA₀ trimers was incrementally added so that the total number of HA trimers in the simulation space remained constant at 200. The cumulative lag-time distributions for each concentration of HA_1,2 were then plotted and the maximum slope, V_max, was determined for each distribution for each HA_1,2 density. The slope value of Imai et al. (13) for a plot of log V_max versus log [HA_1,2] from the Variable F approach is 0.85 (95% confidence interval (CI), between 0.63 and 1.08). Simulation yields a slope value within the 95% CI from Imai et al. (13) when q is 1 (Figs. 3 a and 4) and w is 2 or 3. The slope value increased with higher q values (Figs. 3 a and 4), and therefore values of q > 3 did not need to be tested because this would cause simulation results to diverge further from the results of Imai et al.

Figure 3.

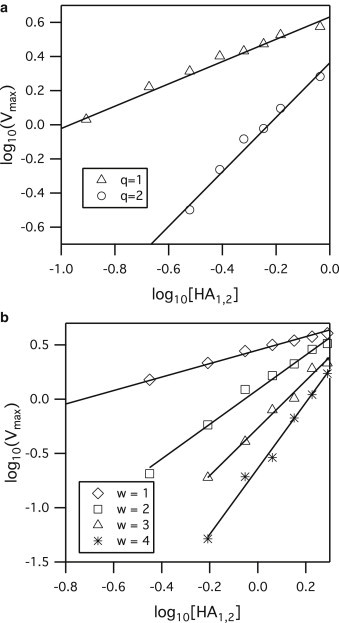
Sample simulation log-log plot of V_max versus HA_1,2 density for (a) Variable F approach for the condition that w = 3 while q is varied. The slopes of the best-fit lines are 0.65 and 1.6 for q = 1 and 2, respectively. (b) Variable FB approach for q = 1 while w is varied. The slopes of the best-fit lines are 0.62, 1.59, 2.19, and 3.03 for w values of 1, 2, 3, and 4, respectively. The r² values for all regression lines are at least 0.99. The unit of HA density, [HA_1,2], has been converted to its corresponding mass ratio of HA to lipid to be consistent with the results of Imai et al. (13).

Figure 4.

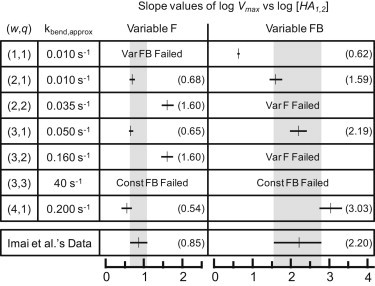
Slope values of log V_max versus log [HA_1,2] for various combinations of w and q values. Some simulations were unnecessary due to the inability to yield results that are consistent with the fusion data of Imai et al. (13). (Shaded bar) 95% confidence interval of the data of Imai et al. (13). The numerical values of the slopes are provided in parentheses.

Eliminating w, q, k_bend solutions using Variable FB

For each possible solution of w, q, and k_bend, simulations were also run to mimic the Variable FB approach (13). Here, the number of HA_1,2 trimers was incrementally decreased from 200 to 10 and no HA₀ trimers were present. The slope value of Imai et al. from the plot of log V_max versus log [HA_1,2] for the Variable FB approach is 2.2 (95% CI between 1.55 and 2.79). The simulation slope value falls within the 95% CI of Imai et al. (13) when w is 2 or 3 and q is 1 (Figs. 3 b and 4). The slope value increased with higher values of w; therefore, values of w > 4 did not need to be tested as this would cause simulation results to diverge further from the results of Imai et al.

The combinations of w and q that agree with both Variable F and FB results in Imai et al. (13) are either w = 3 and q = 1, or w = 2 and q = 1. Other combinations of w and q failed to match at least one data set of Imai et al. (13). We concluded that w is more likely to be 3 instead of 2 because for the Variable FB results, the 95% CI for simulation slope values falls completely inside that of the 95% CI from Imai et al. (13) only when w = 3. But regardless of whether the value of w is 2 or 3, any value of w > 1 suggests HA trimers act cooperatively to induce fusion.

Validating simulation model using Constant FB at varying pH conditions

Fusion experiments were performed with the X31 (H3N2) virus and SLB A at several pH conditions, and corresponding simulations were run to validate the model against this data. By adjusting only k_bend, while holding w and q constant and using the appropriate rate parameter values in Table 1 for our experimental system, the simulation model was able to replicate the kinetic data (Fig. 5 a) from fusion experiments. Note that k_diff,R is now 2000 s⁻¹ because we used G_D1A as the receptor, and k_act is 5.78 s⁻¹ because experiments were done at a pH < 4.9. The good agreement between simulations and experiments validates our model and assumption that w and q do not change over the range of pH values tested and across the HA protein serotypes of H1 and H3.

A closer look at the simulation results shows that the k_bend values for pH 4.0 and 4.5 are considerably smaller than those for pH 3.5 and 3.0, but k_bend is still a nonzero number (Fig. 5 b). Recall that k_bend represents both the HA trimer’s ability to bend the target membrane and the deformability of the membrane itself. One interpretation of a smaller k_bend value is that the HA trimers are having more difficulty bending the target membrane. Another possible explanation is that the target membrane itself is harder to bend due to changes in membrane properties, as suggested by the decreasing diffusion coefficient of R18 membrane fluorophores in the SLB at higher pH conditions (Fig. 5 b). We note that the diffusion coefficient itself is not a measure of membrane flexibility but is merely used here as an indicator to show that the target membrane has changed in some way. This change could be embodied as a change in lipid packing due to different pH conditions or ionic strengths (51,52).

Validating the simulation model using Constant FB at two target membrane compositions

To further confirm that fusion is affected by target membrane properties, we changed the composition of the target membrane by replacing POPC with LPC lipid (i.e., used composition SLB B). LPC lipid has been shown to impede fusion (27) by hindering the bending of membranes. Indeed, fusion experiments at pH 4.0 show that viruses fused much more slowly with SLB B than with SLB A (Fig. 6). In addition, simulations were able to match both SLB A and SLB B fusion lag-time data by adjusting only k_bend. Parameters w and q did not have to be altered to fit the data, suggesting that they are not sensitive to changes in membrane properties between SLB A and SLB B. The strong dependence of k_bend on target membrane properties agrees well with the finding of Chernomordik et al. (28) that fusion is sensitive to target membrane properties at a step after the HA activation, but before the merging of the membrane.

Note that for the same bilayer composition, higher lipid mobility is indicative of a more fluid membrane, which should be easier to bend. However, comparisons of membrane mobility across different SLB compositions to rank membrane flexibility are not appropriate because other factors such as lipid shape, bilayer elasticity, and bilayer thickness can also affect the membrane flexibility. We emphasize that the work here focuses on fluidlike membrane compositions; we have not simulated or examined other membrane types, e.g., raftlike membranes, which could cause the assumptions made earlier about the model to become invalid. Hence, we restrict our model results to apply only under such experimental conditions and fluid target membrane compositions as those used here and in the work of Imai et al. (13).

Sensitivity analysis result

A sensitivity analysis was performed on the simulation model to determine how sensitive the lag-time distribution is to slight perturbations to the rate parameters. In this case, the rate parameters that lead to the greatest change in fusion lag-time output when perturbed is associated with the rate-limiting steps of fusion, as described above in Simulation Methods. Sensitivity analysis was done for X31 fusion simulations at pH 3 and 4.5 conditions for when SLB A is the target membrane. The sensitivity index values for each of the simulation rate parameters (Fig. 7) were calculated according to the method described in Simulation Methods.

Figure 7.

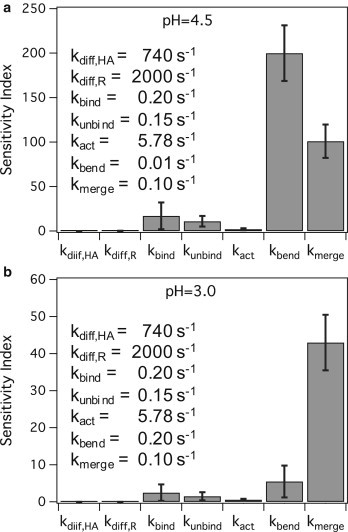
Sensitivity index values for rate parameters at (a) pH 4.5, where both k_bend and k_merge have large sensitivity index values relative to other parameters and (b) pH 3.0, where k_merge is the most sensitive parameter. The parameter values are provided in the legend of each plot.

At pH 4.5, both k_bend and k_merge are sensitive parameters relative to the other parameters, suggesting that two steps, membrane bending and merging, are dominating all the others and are rate-limiting. However, at pH 3.0, k_merge is the most sensitive parameter relative to other parameters, suggesting that one step, i.e., membrane bending, is rate-limiting. To confirm these results, we compared them to the number of rate-limiting steps predicted by the γ-distribution fitting strategy (21,53). The γ-distribution fits resolve parameters N and k, which represent the number of significant rate-limiting steps and the observed rate constant for each step, respectively. At pH 4.5, a γ-fit yields N = 2.04 ± 0.02 and k = 0.07 ± 0.01 s⁻¹, agreeing with our sensitivity analysis that shows two rate-limiting steps. At pH 3.0, a γ-distribution fit yields N = 1.12 ± 0.06 and k = 0.15 × 0.01 s⁻¹, agreeing with the sensitivity analysis showing one rate-limiting step. Note that when N is close to 1, the γ-fit k of 0.15 s⁻¹ is similar in value to that for k_merge of 0.1 s⁻¹. Recall that k_merge was estimated from the γ-fit data of Floyd et al. (21) at pH 3, in which N = 1 and k = 0.1 s⁻¹.

The remaining rate parameters, besides those of k_merge and k_bend, appear to be insensitive parameters that do not affect fusion lag times much for the X31 virus at pH conditions 4.5 or lower, as shown in Fig. 7. There are several explanations for these observations. The tight-packing of HA trimers and immobilization of HA trimers at the contact area due to receptor binding and membrane insertion may render HA diffusion negligible at the contact area. Fusion lag times are weakly sensitive to receptor binding and unbinding because HA trimers were allowed to participate in fusion regardless of receptor binding, to be consistent with prior work showing that binding is not necessary for fusion (22,37–41). Lastly, the HA activation rate does not contribute significantly to the fusion lag time because we are studying X31 fusion kinetics at a pH value <4.9 where the conformational change is fast (43) and is not expected to be rate-limiting.

Discussion

Due to some similarities between ours and the simulation model of Schreiber et al. (19), we provide a more detailed comparison between the two. The main similarities are that both used the stochastic simulation algorithm (47) to simulate fusion kinetics and the spatial domain was setup up similarly. The differences are many:

• 1.Our spatial domain distinguishes between a contact area and the surrounding area whereas the spatial domain of Schreiber et al. represents only the contact area.
• 2.Their model considers that all HA trimers have undergone conformational change a t = 0, whereas we simulate the conformational change through rate parameter k_act.
• 3.Contrary to the model of Schreiber et al. (19), we do not assume w = q and we allowed fusion to occur without receptor binding (22,37–41).
• 4.The model of Schreiber et al. (19) does not simulate the rate of membrane bending. Our model simulates membrane bending by including the transition rate of a fusible unit to a bent complex, granting us the ability to capture the dependence of fusion rate on target membrane properties (26–28).

According to our results, the minimum number of HA trimers required for fusion is three, but at least one HA trimer has to undergo conformational change (w = 3, q = 1). These results have not yet been tested against HA serotypes beyond H1 and H3, or for other experimental systems that do not involve virions or virosomes fusing to a fluid target membrane. Additionally, the results are valid only under the assumptions made when building the model. Whether or not this w and q pair applies for the other systems would be an interesting future study.

The practicality of q being 1 is reasonable when one considers the energy required to form a hemifusion stalk (54–57). The energy released by the conformational change of an HA trimer has been estimated to be ∼125 k_BT (58), which is more than enough energy to form a hemifusion stalk that requires ∼40 k_BT of energy (57).

The roles of the neighboring HA trimers that do not change conformation during membrane fusion, referred to as HA_adj, are unknown. We hypothesize that HA_adj trimers act as support structures that the conformationally changed HA_1,2^∗ trimer exploits to bend the target membrane into a sharp dimple that promotes fusion, as depicted in Fig. 1. To confirm this hypothesis, one possible experiment is to make virosomes containing inactive and active HA trimers, and observe them fusing to a target at various stages through electron microscopy. These inactive HA proteins could be one of the following:

• •Uncleaved HA₀ trimers; or
• •Mutated HA trimers with the fusion peptides removed; or
• •HA trimers that are deactivated with antifusogenic antibodies.

A visual confirmation that a fusion dimple exists between active and inactive HA trimers would support the idea that adjacent, unchanged HA trimers could act passively to induce fusion.

To postulate why different approaches result in different conclusions about the HA-induced fusion mechanism, we summarize the insight provided by each approach:

• •Variable F: Fusion experiments at varying number of fusogenic HA trimers at a constant total HA trimer density yield information about the level of cooperativity between only conformationally changed HA trimers.
• •Variable FB: Fusion experiments at varying total densities of fusogenic HA trimers reveal the number of HA trimers in a fusion complex.
• •Constant FB: Fitting fusion lag-time distributions, obtained at a single HA density, to statistical distributions yields quantitative information about the sequential and parallel steps leading to fusion.

The information obtained from all three approaches must be processed together to resolve the fusion mechanism from kinetic data.

Conclusion

The simulation model presented here demonstrates the importance of considering the differences between the three approaches for studying membrane fusion kinetics. The mechanistic insight this model provides is that some fraction of HA trimers could potentially act passively to assist in membrane fusion, which would explain why some experiments show that HAs act cooperatively to induce fusion whereas others do not. This simulation model is the first that we know of to explicitly capture the role of the host membrane into the model through the inclusion of rate parameter k_bend. Although we chose to focus on the influenza virus because of the plethora of data available to validate the model, the simulation and modeling approach is general enough that it could be extended to study other viruses. Whether the model is able to accurately recapitulate the fusion behaviors of other viruses will be an interesting future study.