The properties of the mesoscopic protein-rich clusters, within which protein crystal nuclei form, are reviewed. The cluster populations occupy from 10−7 to 10−3 of the solution volume; the cluster radii are of order 100 nm; the clusters exist owing to the formation of transient oligomers that, for some proteins, may be due to conformational flexibility.
Keywords: nucleation mechanism, crystallization, protein crystals, two-step nucleation, protein-rich clusters, partial unfolding
Abstract
Protein crystal nucleation is a central problem in biological crystallography and other areas of science, technology and medicine. Recent studies have demonstrated that protein crystal nuclei form within crucial precursors. Here, methods of detection and characterization of the precursors are reviewed: dynamic light scattering, atomic force microscopy and Brownian microscopy. Data for several proteins provided by these methods have demonstrated that the nucleation precursors are clusters consisting of protein-dense liquid, which are metastable with respect to the host protein solution. The clusters are several hundred nanometres in size, the cluster population occupies from 10−7 to 10−3 of the solution volume, and their properties in solutions supersaturated with respect to crystals are similar to those in homogeneous, i.e. undersaturated, solutions. The clusters exist owing to the conformation flexibility of the protein molecules, leading to exposure of hydrophobic surfaces and enhanced intermolecular binding. These results indicate that protein conformational flexibility might be the mechanism behind the metastable mesoscopic clusters and crystal nucleation. Investigations of the cluster properties are still in their infancy. Results on direct imaging of cluster behaviors and characterization of cluster mechanisms with a variety of proteins will soon lead to major breakthroughs in protein biophysics.
1. Introduction
Crystallization, including protein crystallization, as all other first-order phase transitions, starts with nucleation. Hence, the success of the search for protein crystallization conditions hinges on the ability to achieve and control nucleation. Nucleation determines the main properties of the crystal population, including the crystal polymorph, the number of crystals and their size and size distribution. The nucleation outcome favored in classical crystallography is to have a population consisting of one large crystal of a stable and robust polymorph or, failing that, of several well separated crystals of similar sizes and of a single polymorph. In the novel method of femtosecond X-ray protein nanocrystallography (Chapman et al., 2011 ▶), which relies on crystals as small as 200 nm, the need to grow the crystals after they have nucleated is nearly eliminated and nucleation emerges as the sole process to be controlled.
Nucleation has been studied since 1876, when J. W. Gibbs invented the method of thermodynamic potentials to describe nucleation; the papers, in which he laid the foundations of modern thermodynamics, were titled On the equilibrium of heterogeneous substances (Gibbs, 1876 ▶, 1878 ▶). With the work of Volmer (Volmer, 1939 ▶; Volmer & Schultze, 1931 ▶), the classical theory of crystal nucleation emerged (Kahlweit, 1969 ▶, 1975 ▶; Nielsen & Sohnel, 1971 ▶; Kashchiev, 1995 ▶, 2000 ▶), which, in application to solution crystallization, envisions that solute molecules form ordered nuclei directly as they assemble into a high-concentration cluster. A recent triumph of the classical theory is the partial correspondence of its nucleation-rate predictions to the results of simulations of a carefully formulated colloid crystal model (Blaak et al., 2004 ▶; Auer & Frenkel, 2004 ▶; Dorsaz et al., 2012 ▶). Still, to this day, nucleation, and in particular nucleation of crystals from solution, has remained one of the most poorly understood processes in nature. For any system of practical significance, theoretical predictions diverge from careful experimental determinations by many orders of magnitude. To make matters worse, nucleation-rate determinations are notoriously difficult and reliable data sets are scarce (Vekilov, 2012b ▶).
Several years ago, a two-step mechanism of nucleation of crystals in solution (Fig. 1 ▶) was put forth (Galkin & Vekilov, 2000 ▶; Vekilov, 2004 ▶; Filobelo et al., 2005 ▶; Pan et al., 2005 ▶; Vekilov, 2010 ▶). This mechanism posits that the first step of crystal nucleation is the formation of disordered protein-rich clusters of mesoscopic size. The second step is the formation of crystal nuclei inside the clusters (Galkin & Vekilov, 2000 ▶; Garetz et al., 2002 ▶; Vekilov, 2004 ▶). This mechanism explained the majority of the discrepancies between theory and experiment in crystal nucleation from solution, including nucleation rates that are ten or more orders of magnitude slower than the predictions of the classical nucleation theory (Garetz et al., 2002 ▶; Pan et al., 2005 ▶; Vekilov, 2010 ▶). Evidence of the action of this mechanism has been provided for protein crystals (Vekilov, 2010 ▶; Kuznetsov et al., 2001 ▶), sickle-cell anemia fibers (Galkin et al., 2007 ▶), amyloid fibrils (Lomakin et al., 1996 ▶; Krishnan & Lindquist, 2005 ▶), small-molecule organics (Aber et al., 2005 ▶; Garetz et al., 2002 ▶; Harano et al., 2012 ▶), colloids (Leunissen et al., 2005 ▶; Savage & Dinsmore, 2009 ▶; Zhang & Liu, 2007 ▶), biominerals (Pouget et al., 2009 ▶; Gebauer et al., 2008 ▶; Gower, 2008 ▶), polymers (Wang, Müller et al., 2009 ▶) and other substances. Convincing kinetic arguments support the action of the two-step mechanism for proteins and small-molecule organics (Vekilov, 2010 ▶; Erdemir et al., 2009 ▶). Direct imaging of crystal nuclei forming within dense liquid clusters have been provided for two types of systems: colloids (Savage & Dinsmore, 2009 ▶), which are larger and move more slowly than most molecules, and an ingeniously chosen organic system (Harano et al., 2012 ▶). The most powerful evidence for the general applicability of the two-step mechanism to proteins is the very slow rates of protein crystal nucleation despite the high supersaturations typically used in protein crystallization; no other mechanism accounts for such strong deviations from the predictions of classical theory.
Figure 1.
The two-step mechanism of nucleation of crystals: (i) a metastable cluster forms; (ii) a crystal nucleus may form inside the cluster. (a) Macroscopic viewpoint; the numbers denote the steps in the nucleation mechanism; after nucleation, a crystal irreversibly grows to macroscopic dimensions. (b) Microscopic viewpoint in the (concentration, structure) plane; the thick dashed line highlights the two-step pathway and the diagonal solid arrow highlights direct nucleation. (c) The free energy ΔG along three possible nucleation pathways: direct nucleation, the two-step mechanism and crystals forming within macroscopic dense liquid, as seen by Vivarès et al. (2005 ▶), following the Ostwald rule of stages (Ostwald, 1897 ▶).
The two-step mechanism highlights the significance of protein-rich clusters in protein crystal nucleation. Hence, understanding of the mechanisms of cluster formation and the phenomena that govern their properties is a crucial part of the rationalization of protein crystallization. Below, we review recent advances in the detection, characterization and mechanisms of the clusters.
2. Experimental methods for cluster detection and characterization
The requirements for the techniques employed in the investigation of protein-rich clusters are determined by the cluster properties. For the several proteins studied so far, the cluster radii have been in the range 50–500 nm, the fraction of the solution volume occupied by the cluster population has been in the range 10−7 to 10−3, the fraction of protein held in the clusters has been about 10× the cluster volume fraction (Li et al., 2012 ▶) and the protein concentration in the clusters has been about 500 mg ml−1 or higher (see below for further discussion). The cluster volume fraction and size indicate that the average separation between clusters in solution is of the order of micrometres.
The cluster size and separation precludes the use of small-angle neutron and X-ray scattering: these two methods detect structures with characteristic length scales in the angstrom and nanometre range (Stradner et al., 2004 ▶; Shukla et al., 2008 ▶; Porcar et al., 2009 ▶). The low fraction of protein held in the clusters suggests that the nuclear magnetic resonance (NMR) signal from the clusters may be too weak to be detected.
Scanning-probe and Brownian microscopies and dynamic light scattering (DLS) have provided the majority of the data on the clusters. Brownian microscopy (BM) and DLS rely on visible light scattered by the monomers and clusters. According to the Rayleigh law, the intensity scattered from an object is proportional to the sixth power of its radius. Hence, the clusters, which are about two orders of magnitude larger than the monomers, provide a scattering intensity stronger by 12 orders of magnitude. These considerations make DLS and BM particularly well suited for the detection and characterization of the mesoscopic protein-rich clusters.
The procedures used to characterize the clusters by scanning-probe techniques and BM are standard for the respective methods. In contrast, significant extensions and modifications of the DLS data-processing algorithms have been proposed. Since DLS has provided the vast majority of cluster data, it is discussed in detail below.
2.1. Scanning techniques: atomic force and scanning confocal microscopy
The typical atomic force microscopy (AFM) instruments and methods of imaging in protein crystallization have been discussed in numerous papers (Reviakine et al., 1998 ▶; Yau et al., 2000 ▶; Malkin & McPherson, 2004 ▶). The advantage of AFM for cluster detection and observation is the availability of images that allow determination of cluster sizes and of some cluster properties. The limitations of AFM are that AFM images are collected over periods of several tens of seconds to several minutes, which are often longer than the lifetimes of the clusters. Furthermore, the AFM view field is small (the imaged volume is only several cubic micrometres) and this severely reduces the probability of observing clusters, which have very low concentrations and occupy small fractions of the solution volume.
Fig. 2 ▶ is one of several that show clusters that land on the (001) face of a crystal of the protein lumazine synthase (Gliko et al., 2005 ▶). While the lateral dimensions of the clusters cannot be judged from the images, their height can be reliably determined: it varies between ∼100 nm and several hundred nanometres; in Fig. 2 ▶(a) the size is ∼120 nm. The clusters do not decay because of their interactions with the crystal, and spread sideways and become integral parts of the crystal, generating, in Fig. 2 ▶(b), five new layers.
Figure 2.
Direct imaging of clusters in a lumazine synthase solution by atomic force microscopy. (a, b) Sedimentation of a cluster and its development into a stack of five crystalline layers. Tapping-mode AFM imaging, scan size 20 × 20 µm; the time interval between (a) and (b) is 9 min. (c, d) Height profiles along a horizontal line crossing the three-dimensional object in (a) and (b), respectively, show an object height of ∼120 nm immediately after sedimentation in (a) and of ∼75 nm in (b). The arrows in (a), (b), (c) and (d) mark the same crystal layer. Reprinted with permission from Gliko et al. (2005 ▶), J. Am. Chem. Soc. 127, 3433–3438. Copyright 2005 American Chemical Society.
Scanning confocal microscopy has provided spectacular images of clusters in solutions of the proteins glucose isomerase, proteinase K, human recombinant insulin, hen egg-white lysozyme, xylanase, triosephosphate isomerase and RNAse IIIA (Sleutel & Van Driessche, 2014 ▶). This study demonstrates the role of the clusters in nucleation, as well as their participation in the generation of new crystal layers and the purification of crystal surfaces after impurity poisoning.
2.2. Dynamic light scattering
Several manufacturers provide high-quality instruments for dynamic light scattering. In all of them the solution is held in cylindrical cuvettes of volume from 0.5 to 1 ml. Dynamic light scattering (DLS) data are collected at times Δt ranging between 30 s and 2 min. If the long-term evolution of the scattering objects in a solution is of interest, numerous data sets can be collected in sequence for up to several days or even longer (Li et al., 2012 ▶).
The method relies on light scattered by concentration fluctuations. Since the rate of intensity decay is determined by the diffusion of the scatterers, this rate yields the diffusion coefficient of the scatterers and, using the Einstein–Stokes relation and the viscosity of the medium, their size (Berry et al., 2000 ▶). The concentration of individual species is determined from the intensity that each of them scatters.
The rate of intensity variation I(t) is determined from the intensity correlation function g 2(τ) of the scattered light. g 2(τ) is defined from the intensity at two times, t and t − τ, as (Schmitz, 1990 ▶)
where 〈〉Δt signifies averaging over time Δt and 〈I〉Δt is the average intensity. The normalized correlation function g 2(τ), illustrated in Fig. 3 ▶, can be represented as the square of the sum of exponential members representing the scatterers with different diffusion rates Γi. Our dynamic light-scattering experiments are aimed at identifying one or two scatterers: single molecules and, in some cases, larger clusters. Hence (Schatzel, 1993 ▶),
where τ1 = 1/Γ1 and τ2 = 1/Γ2 are the characteristic times of the diffusion of scatterers, whose contribution to the scattered light has amplitudes A 1 and A 2.
Figure 3.

Examples of the correlation function of the scattered light g 2(τ) and the intensity distribution function G(τ) of a hemoglobin S solution. The characteristic diffusion times τ1 and τ2 and the amplitudes A 1 and A 2 of the monomers and clusters, respectively, are indicated. Reprinted from Pan et al. (2007 ▶), with permission from Elsevier.
The characteristic times τ1 and τ2 and the amplitudes A 1 and A 2 are readily determined from the distribution function G(τ), as also illustrated in Fig. 3 ▶. The general form of G(τ) is
Hence, G(τ) is calculated by numerically inverting the Laplace transform with (g 2 − 1)1/2, using a software package based on the CONTIN algorithm (Provencher, 1982a ▶,b ▶). The deficiencies of the CONTIN-computed G(τ) and alternative ways to calculate the intensity distribution function are discussed in the next subsection.
To calculate the equivalent hydrodynamic radii from the values of the relaxation times τ1 and τ2, the Stokes–Einstein relation is used, modified with Γi = τi −1 = Diq 2,
where i = 1, 2 for single molecules or clusters, respectively, k B is the Boltzmann constant, T is the absolute temperature, ηi is the viscosity to which a diffusing object i is exposed, Di is its diffusion coefficient and the scattering vector q = 4πn/λsin(θ/2) (where n is the refractive index of the solvent, λ is the wavelength of the laser beam and θ is the scattering angle).
The amplitudes A 1 and A 2 are the basis for the determination of the concentration n 2 and volume fraction ϕ2 of the clusters. According to the Rayleigh law, the intensity of light scattered by an object is proportional to the sixth power of its size. On the other hand, the intensities scattered by the monomers and the clusters are proportional to the respective amplitudes in the intensity distribution function, A 2 and A 1 (Li et al., 2011 ▶; Pan et al., 2007 ▶). With this, one can estimate n 2 and ϕ2 as (Pan et al., 2007 ▶)
 |
In (5), P(qR 2) is the shape factor, assuming a spherical shape of the clusters, f(C 1) is a virial-type expression accounting for intermolecular interaction between protein molecules (the interactions between clusters are neglected because of low n 2). (∂n/∂Ci)T,μ is the refractive index n increment and ρ1 and ρ2 are the protein densities in the single molecules and in the clusters; the ratio ρ1/ρ2 can be estimated from the concentration of the protein in the clusters (Li et al., 2011 ▶; Pan et al., 2007 ▶). Note that (∂n/∂C 2)T,μ/(∂n/∂C 1)T,μ ≃ ρ1/ρ2, which somewhat simplifies (5).
2.3. Alternative methods of calculation of the DLS intensity distribution function
Although the CONTIN algorithm produces relatively consistent distribution functions, two features of these G(τ) values provoke significant questions about the veracity of the procedure: (i) the occasional appearance of more than one peak corresponding to scatterers larger than monomers and (ii) the nonzero width of both monomer and cluster peaks even under conditions where the monomer diffusion has a unique characteristic time (Li et al., 2011 ▶). Addressing these issues, we developed and tested two new models for G(τ).
- (i) In those cases where the fitting error was insensitive to the width of the cluster peak, the distribution function was modeled with a sum of two Dirac delta functions corresponding to the monomers and clusters, respectively,
where A 1 and A 2 are the amplitudes of the peaks corresponding to the monomers and clusters, respectively, and τ1 and τ2 are the respective diffusion times.
- (ii) In the cases where the superiority of fits with a finite width of the cluster peak was statistically significant, the following fitting form was used (σ2 is the cluster peak width):

Comparing the error of the distribution function G(τ) computed using (6) and (7) with that of G(τ) resulting from the numerical inversion of (3) using the CONTIN algorithm, we concluded that the extra peaks and the nonzero width resulting from the latter procedure are artifacts introduced to reduce the discrepancy between the computed and experimental g 2 to values below the inherent uncertainty of the experimental determination of g 2 (Li et al., 2011 ▶).
We fit the correlation function corresponding to the distribution functions in (6) and (7) to the experimentally measured correlation function and in this way evaluate τ1, τ2, A 1 and A 2. These parameters are used to determine the hydrodynamic radii of the clusters R 2 and, for verification, of the monomers R 1, the concentration of clusters n 2 and the fraction ϕ2 of the solution volume, analogously to the method discussed above.
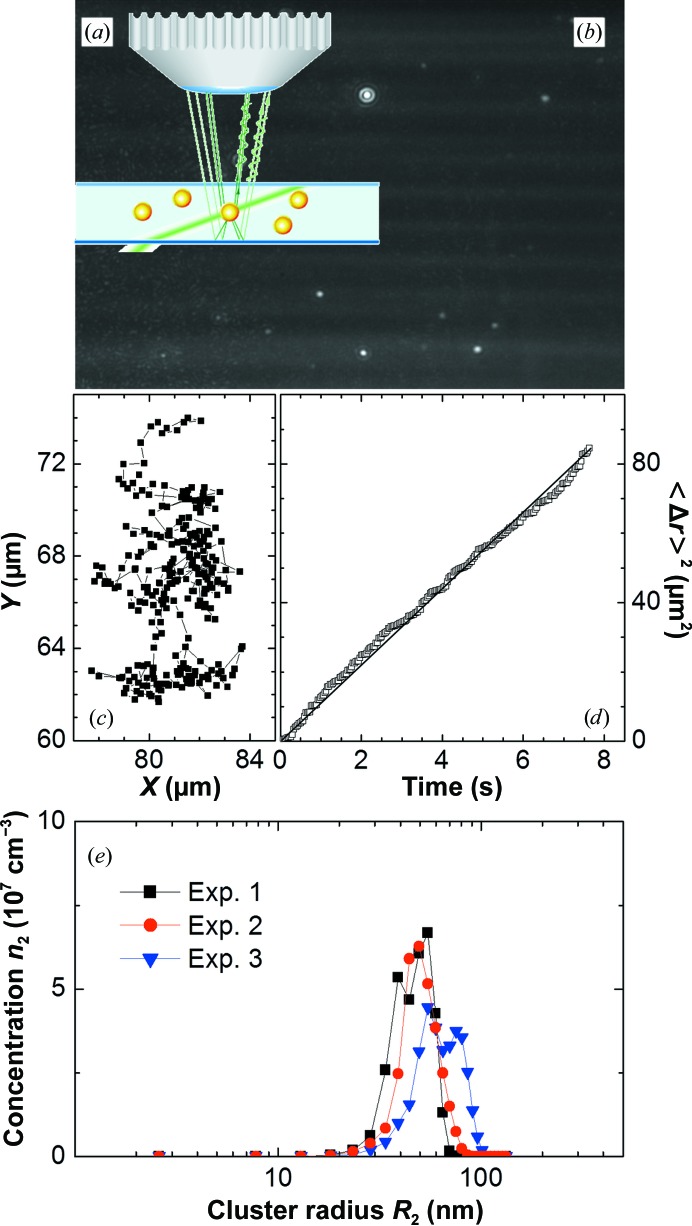
2.4. Brownian microscopy
In the BM method, about 100 µl of protein solution is held in a cuvette with thickness of about 500 µm. The solution is illuminated by a laser beam configured so that it does not enter the objective lens of an observation microscope (Fig. 4 ▶ a). The observation volume is determined by the focal depth of the objective lens and the view field of the microscope, and is typically 120 × 80 × 5 µm (width × length × height). This device detects the light scattered by the clusters. Since the protein molecules are smaller than the clusters, the light scattered from them is insignificant even at relatively high protein concentrations; the clusters are seen as bright spots (Fig. 4 ▶ b). Careful observation reveals that the cluster spots consist of concentric fringes (Fig. 4 ▶ b) that result from the interference of two beams of scattered light: one reflected from the cell bottom and a second directly entering the objective lens, as illustrated in Fig. 4 ▶(a). Since the wavefront of the scattered light is spherical, the resulting interference pattern represents a hologram of the imaged cluster.
Figure 4.
Brownian microscopy characterization of clusters in a lysozyme solution. (a) Schematic of the cuvette, the illuminating laser beam and the formation of a hologram of a cluster. (b) The clusters, which scatter light much strongly than the monomers, are seen as bright spots. (c) Brownian trajectory of a cluster. (d) The relation between the mean-squared displacement 〈Δr 2〉 and elapsed time Δt, from which the diffusion coefficient and size of the cluster are determined. (e) Characterization of the cluster population in a lysozyme solution by Brownian microscopy. Three independent determinations of the distribution of cluster size. Reprinted with permission from Li et al. (2011 ▶), Rev. Sci. Instrum. 82, 053106. Copyright 2011, AIP Publishing LLC.
The location of an individual cluster is determined from these images. The Brownian trajectories of the clusters are tracked by comparing the locations of the clusters in a sequence of images collected at the frame rate of the camera, and are illustrated in Fig. 4 ▶(c). The diffusion coefficients of the individual clusters D 2 are computed from the slope of the relation between the mean-squared displacement 〈Δr 2〉 and the time Δt, as displayed in Fig. 4 ▶(d). The sizes of the individual clusters are determined from D 2 using the Einstein–Stokes relation and the solution viscosity. The results are output as the concentration of clusters of a certain size as a function of this size (Fig. 4 ▶ e).
A Brownian microscopy device optimized for the determination of protein aggregates is commercially available from Nanosight Ltd. The BM method was tested using a solution of latex spheres of radius 200 nm in water and was found to faithfully reproduce the particle size and concentration. Fig. 4 ▶(e) displays the results of another test: the cluster size distribution was independently determined three times in the same solution. The distributions are consistent and, remarkably, agree within 10% with the sizes and concentration of the clusters in the same solution determined from DLS data as discussed in the preceding subsection (Li et al., 2011 ▶, 2012 ▶).
3. Cluster properties
3.1. The clusters are freely diffusing compact liquid objects
The slower process revealed by the DLS data, which has a characteristic time of the order of milliseconds, could represent the diffusion of either compact protein clusters suspended in the solution, schematically depicted in Fig. 5 ▶(a), or of single molecules embedded in a loose network structure constraining their free motion (Fig. 5 ▶ b). Loose networks of molecules could have a refractive index similar to that of the solvent and be optically undetectable. Such networks would increase the low-shear viscosity of the protein solution, but they would be destroyed by high-shear flow. The latter consideration allows tests for the presence of loose networks by determination of the low-shear viscosity of the solutions, determined, for instance, by monitoring the Brownian motion of latex spheres of known size (Pan, Filobelo et al., 2009 ▶). The low-shear viscosities of solutions of several proteins were in the range 2–4 mPa s, equal to the high-shear values (Ross & Minton, 1977 ▶; Fredericks et al., 1994 ▶). The equality of the low-shear and high-shear viscosities reveals that no networks of molecules exist in these solutions and suggests that the large scatterers are clusters of molecules of the respective protein.
Figure 5.
Characterization of clusters by dynamic light scattering. (a) Schematic illustration of the motion of clusters suspended in a solution; the clusters and monomers exhibit two distinct diffusion times. (b) Schematic illustration of the motion of molecules embedded in a loose network. The diffusion of the embedded molecules is slower than that for the free molecules in the network voids, resulting in two diffusion times. (c) The dependence of the decay rate of the intensity scattered from clusters in a lysozyme solution Γ2 on the scattering vector q. (d) The evolution of the mean cluster radius R 2 during 200 min immediately after solution preparation.
For another test to determine whether the slow shoulders in the correlation functions, such as that in Fig. 3 ▶, correspond to freely diffusing objects, we explored the dependence of the decay rate of this shoulder, Γ2 = τ2 −1, on the angle θ at which scattered light is recorded; this angle determines the scattering wavevector q. In the case of freely diffusing objects, we expect that Γ2 = D 2 q 2, while objects embedded in a network, as illustrated in Fig. 5 ▶(b), would violate this proportionality owing to the anisotropy of the constituent chains. Fig. 6 ▶(c) reveals that Γ2 is proportional to q 2, rendering strong support to the notion that the slow scatterers are compact clusters of protein molecules (Pan et al., 2007 ▶).
Figure 6.
The clusters and the phase diagram of the protein solution. Experimentally determined phase diagram of a lysozyme solution in 0.05 M sodium acetate buffer pH 4.5 and 4.0% NaCl. Liquidus, or solubility, from Cacioppo & Pusey (1991 ▶) and Howard et al. (1988 ▶); liquid–liquid (L–L) coexistence and respective spinodal from Petsev et al. (2003 ▶); solution–crystal spinodal from Filobelo et al. (2005 ▶); gelation line from Petsev et al. (2003 ▶) and Muschol & Rosenberger (1997 ▶). The shaded area denotes compositions at which dense liquid clusters were detected.
To address whether the clusters are liquid or solid, we observed the time dependence of their mean radius R 2 determined from τ2 as discussed above and as displayed for lysozyme in Fig. 5 ▶(d). The data in Fig. 5 ▶(d) and numerous other similar data sets (Gliko et al., 2005 ▶, 2007 ▶; Pan et al., 2007 ▶) reveal two features of the evolution of the cluster size R 2(t): (i) the clusters appear immediately after solution preparation and (ii) their mean radius is relatively unchanged over several hours of monitoring. Both features are incompatible with solid clusters: under the tested conditions protein solids take times of the order of 1 h to nucleate and grow to several hundred nanometres, and their size is not constrained but increases to dimensions visible with the naked eye within commensurate times (Malkin & McPherson, 1993 ▶; Malkin & McPherson, 1994 ▶; Gliko et al., 2005 ▶). We conclude that the clusters corresponding to the slow shoulder of the DLS correlation function consist of dense liquid in which the molecules move with respect to one another.
The liquid nature of the clusters in a lumazine synthase solution, as imaged in Fig. 2 ▶, is revealed by three AFM observations. (i) The clusters shrink in height as they rest on the crystal surface (compare Figs. 2 ▶ c and 2 ▶ d). (ii) The layers originating from the clusters merge continuously with each other and with the underlying lattice. (iii) The velocity of the layers originating from a cluster is the same as the velocity of the other layers on the surface of the crystal: compare the locations of the two types of layers in Figs. 2 ▶(a) and 2 ▶(b). If these were crystalline clusters, the probability of them landing with a (001) plane downwards and rotating to a perfect register with the underlying lattice would be negligible. Numerous examples of microcrystals landing on surfaces of growing crystals out of register and being incorporated with major stacking defects have been reported (Malkin et al., 1996 ▶; Yau et al., 2001 ▶). Disordered solid clusters would not shrink in size within the observation times, and the generation of new layers would be likely to be accompanied by the creation of a strained shell that would delay the spreading of the layers started by the clusters (Yau et al., 2001 ▶).
Determinations of the concentration and volume fraction occupied by the clusters using (5) show that the clusters occupy a low fraction of the solution volume: from ∼10−7 (below which they are not reliably detectable) to ∼10−3. The upper volume fraction limit of 10−3 is not exceeded even if the protein concentration in the bulk solution approaches that of the liquid within the clusters, i.e. 300–400 mg ml−1 (Pan et al., 2010 ▶; Uzunova et al., 2010 ▶). However, within these limits, the cluster volume fraction is a very sensitive, near-exponential function of the solution concentration (Li et al., 2012 ▶; Uzunova et al., 2012 ▶).
The lifetime of individual clusters can be directly determined in the BM technique; for lysozyme and glucose isomerase, it is longer than several minutes. Monitoring the disappearance and reappearance of the second shoulder of the DLS correlation function at low concentrations of lumazine synthase, at which the cluster concentration fluctuates above and below the detection limit, indicated that a cluster lifetime is about 10 s (Gliko et al., 2007 ▶).
3.2. The dense liquid clusters and the protein solution phase diagram
The phase diagram in the temperature, concentration (T, C) plane of the solution of the protein lysozyme, a favorite model in protein physical chemistry, is shown in Fig. 6 ▶. It contains the liquidus or solubility lines, which denote the concentration of a solution in equilibrium with a crystal phase, the lines characterizing the dense liquid phase, and a gelation line. A crucial feature of protein phase diagrams, also seen in Fig. 6 ▶, is that the liquid–liquid (L–L) coexistence line (also called a binodal) is submerged below the lines of liquid–solid equilibrium (Broide et al., 1991 ▶; Berland et al., 1992 ▶; Asherie et al., 1996 ▶; Grigsby et al., 2001 ▶); this is in contrast to the phase diagrams of binary mixtures of small molecules. Like all other liquid–liquid separations (Atkins & DePaula, 2002 ▶), the formation of the dense protein liquid phase is characterized by two phase lines: the co-existence line and a spinodal, below which the formation of the dense liquid proceeds without a nucleation barrier (Thomson et al., 1987 ▶; Shah et al., 2004 ▶). The spinodal and binodal touch at the so-called critical point for liquid–liquid separation: the highest temperature at which the coexistence of two liquid phases is possible. In Fig. 6 ▶, the critical point is at T = 19°C and C = 231 mg ml−1.
The phase area, in which clusters have been detected, is mapped on the lysozyme solution phase diagram in Fig. 6 ▶, where it is denoted by shading. Remarkably, mesoscopic clusters exist with similar characteristics both in the homogeneous region of the phase diagram of the protein solution (where no condensed phases, liquid or solid, are stable) and under conditions supersaturated with respect to ordered solid phases, such as crystals (Gliko et al., 2007 ▶) and fibers (Pan et al., 2007 ▶; Galkin et al., 2007 ▶). Note that the clusters are distinct from the dense liquid phase occupying the high-concentration and low-temperature region of the phase diagram in Fig. 6 ▶: DLS data collection from solutions held at conditions below the liquid–liquid binodal reveals consistent fast growth of the radius of the emerging new phase (Li et al., 2012 ▶). It is possible that the composition and structure of the dense liquid comprising the clusters is similar or identical to the long-lived protein-dense liquid. No evidence in favor or against this notion has been presented to date.
From the point of view of protein crystallization, the phase region under the solution–crystal spinodal, the line at which the barrier for crystal nucleation vanishes and the crystal nucleation rate is only limited by spatial and kinetic factors (Filobelo et al., 2005 ▶; Vekilov, 2010 ▶, 2012a ▶), is particularly intriguing. The presence of clusters that are nucleation precursors in this region indicates that this is a favorable set of conditions for crystal nucleation. These conditions would correspond to the top slice of the unstable zone for protein crystallization (Chayen et al., 2010 ▶). If the solution–crystal spinodal is hidden below the liquid–liquid binodal, dense phase formation with subsequent gelation and amorphous precipitation may precede and inhibit crystal nucleation; this would correspond to the unstable zone for protein crystallization.
At higher protein concentrations the protein solution may gel, even if the temperature is above the critical temperature for liquid–liquid separation (Muschol & Rosenberger, 1997 ▶; Galkin & Vekilov, 2000 ▶). Protein gelation is still relatively poorly understood; some recent theories attribute it to the action of additional long-range attractive forces (Noro et al., 1999 ▶; Sear, 1999 ▶; Kulkarni et al., 2003 ▶) or to the formation of weak, limited-lifetime networks of protein molecules (Pan, Filobelo et al., 2009 ▶). The increasing cluster volume fraction at high protein concentration discussed above suggests a novel mechanism of gel formation: the gel represents a three-dimensional network of interacting dense liquid clusters.
4. The cluster-formation mechanism
4.1. The excess free energy of the clusters
As demonstrated in the preceding subsection, clusters are observed outside the stability region of the dense protein liquid. Hence, increasing protein concentration is expected to lead to a free-energy excess ΔG. To evaluate the excess free energy ΔG of the clusters over that of the solution that hosts them, we use the dependence of the KC/R θ ratio on the protein mass concentration C (K is a constant that depends on the experimental parameters and R θ is the Raleigh ratio of the scattered to incident light; Schmitz, 1990 ▶); this ratio is output by static light scattering (Pan, Uzunova et al., 2009 ▶; Vekilov et al., 2002 ▶) and is displayed in Fig. 7 ▶. This ratio is directly related to the inverse osmotic compressibility of the solution: KC/R θ = (∂Π/∂C)/RT (Π is the contribution of the protein to the osmotic pressure and R is the universal gas constant). After obtaining the compressibility (∂Π/∂C), we can integrate it to compute the free energy,
needed to increase the concentration of N protein molecules from that in the dilute solution C L to that in the dense liquid C H. This allows us to determine ΔG as the free-energy difference between states with densities C L and C H (Pan et al., 2010 ▶).
Figure 7.
Evaluation of the free-energy density of the protein solution. Debye plot of the ratio M w KC/R θ as a function of protein mass concentration C. M w = 14 300 g mol−1 is the molecular mass of lysozyme, K is the instrument constant and R θ = I θ/I 0 is the Raleigh ratio of the intensity scattered at angle θ to the incident. Solid symbols, determination using static light scattering. Dashed line, fit of osmotic virial expansion to data. Solid line, integration of data according to (8) to determine the solution free energy ΔG. Reprinted with permission from Pan et al. (2010 ▶), J. Phys. Chem. B, 114, 7620–7630. Copyright 2010 American Chemical Society.
The experimentally determined dependence KC/R θ(C) for the protein lysozyme at concentrations of up to 300 mg ml−1, which is near the apparent solubility limit of the dry protein powder, is displayed in Fig. 7 ▶. The data are fitted using a cubic polynomial and then integrated. The resulting ΔG/k B T, shown in Fig. 7 ▶, varies between −9k B T at C L = 100 mg ml−1 and 0 at C H = 450 mg ml−1. If we assume that the protein concentration in the clusters C H is equal to that in a macroscopically stable dense liquid, 450 mg ml−1 (Petsev et al., 2003 ▶), the clusters possess an excess free energy of 9k B T over the host solution with concentration C L = 100 mg ml−1 (Pan et al., 2010 ▶).
4.2. The clusters are in a metastable equilibrium with the host solution
The conclusion that a metastable equilibrium exists between the clusters and the host solution comes from a correlation between the fraction of protein in the clusters ν2 and the excess free energy of the clusters ΔG evaluated in Fig. 7 ▶. We estimate ν2 = C Hϕ2/(C Lϕ1 + C Hϕ2), which yields ν2 ≃ (2.25–5.3)ϕ2/ϕ1 for lysozyme (Li et al., 2012 ▶); an analogous estimate for hemoglobin S yielded similar values for the relation between ν2 and ϕ2/ϕ1 (Uzunova et al., 2012 ▶). The value of the cluster volume fraction ϕ2 is likely to be underestimated: because of the Rayleigh law, larger clusters contribute more to the scattered intensity than smaller clusters and, as a result, the peak of the intensity scattered by clusters corresponds to a cluster size larger than the mean cluster size. (5) reveals that an overestimate of R 2, given a fixed A 2, leads to an underestimate of ϕ2 (Li et al., 2011 ▶). Accounting for this error, ν2 is about ten times higher than the ϕ2/ϕ1 ratio estimated from DLS data.
Using the Gibbs distribution v 2 ≃ exp(−ΔG/k B T) and experimental data for a lysozyme solution, ν2 ≃ 10ϕ2/ϕ1 = 7 × 10−5 at 200 mg ml−1 and ν2 ≃ 3 × 10−5 at 150 mg ml−1, we find that ΔG should decrease by about k B T as the concentration increases from 150 to 200 mg ml−1. Furthermore, since ΔG(C 1) in Fig. 7 ▶ is nearly linear, we extrapolate to find ΔG ≃ 6k B T for concentrations between 150 and 450 mg ml−1. Both of these estimates are in perfect agreement with the evaluation of ΔG in Fig. 7 ▶ (Li et al., 2012 ▶). A similar exponential relation between ν2 and ΔG was found for hemoglobin S solutions (Uzunova et al., 2012 ▶).
The correlation between ν2 and ΔG leads to two important conclusions. (i) Cluster formation is reversible and the clusters are in equilibrium with the solution; since the cluster free energy is higher than that of the solution, this is a metastable equilibrium. (ii) The fraction of protein molecules sequestered in the clusters is determined by the excess standard free energy of the cluster phase over that of the solution.
4.3. How do the clusters form and why do they exist?
The above findings about the cluster properties reveal two highly unusual features: (i) the clusters exist in the homogeneous region of the phase diagram, where single protein molecules should be the only stable state of the protein, and (ii) the clusters possess a significant excess of free energy, which should lead to their fast decay. The cluster mechanism should address these two puzzles.
Previous attempts to rationalize the finite size of clusters have focused on a balance of short-range attraction, owing to van der Waals, hydrophobic or other forces, and screened Coulomb repulsion between like-charged species (Sciortino et al., 2004 ▶; Groenewold & Kegel, 2001 ▶). While small clusters, containing tens of molecules, naturally appear in such approaches, large clusters are only expected if the constituent molecules are highly charged, with hundreds of elementary charges. These theories have been successfully applied to aggregation in colloidal suspensions (Liu et al., 2005 ▶; Mossa et al., 2004 ▶; Stradner et al., 2004 ▶). However, this mechanism appears to be inapplicable to solutions of proteins, in which the molecules carry fewer than ten net elementary changes.
The key to the cluster mechanism is the finding that they exist in what is viewed as a homogeneous region of the phase diagram. Clearly, clusters with sizes of up to several hundred nanometres represent a second phase, i.e. in reality the solution is not homogeneous but biphasic. On the other hand, the solution retains three degrees of freedom: temperature, pressure and concentration. According to the Gibbs phase rule, f = 2 + c − π, where f is the number of degrees of freedom, c is the number of components and π is the number of phases. With f = 3 and π = 2, we obtain c = 3. The first two components are trivial to list: protein and solvent. The presence of a third component is mandated by the presence of the cluster phase and it is natural to assume that this novel component underlies the cluster mechanism. Thus, the new component should be a new chemical form of the protein. The broad range of proteins for which clusters have been found excludes protein-specific modifications: oxidation, proteolysis, covalent dimerization and others. The new component should form in the region of high total protein concentration and decay at low concentrations, and this suggests that this component is a weakly bound protein dimer or another oligomer.
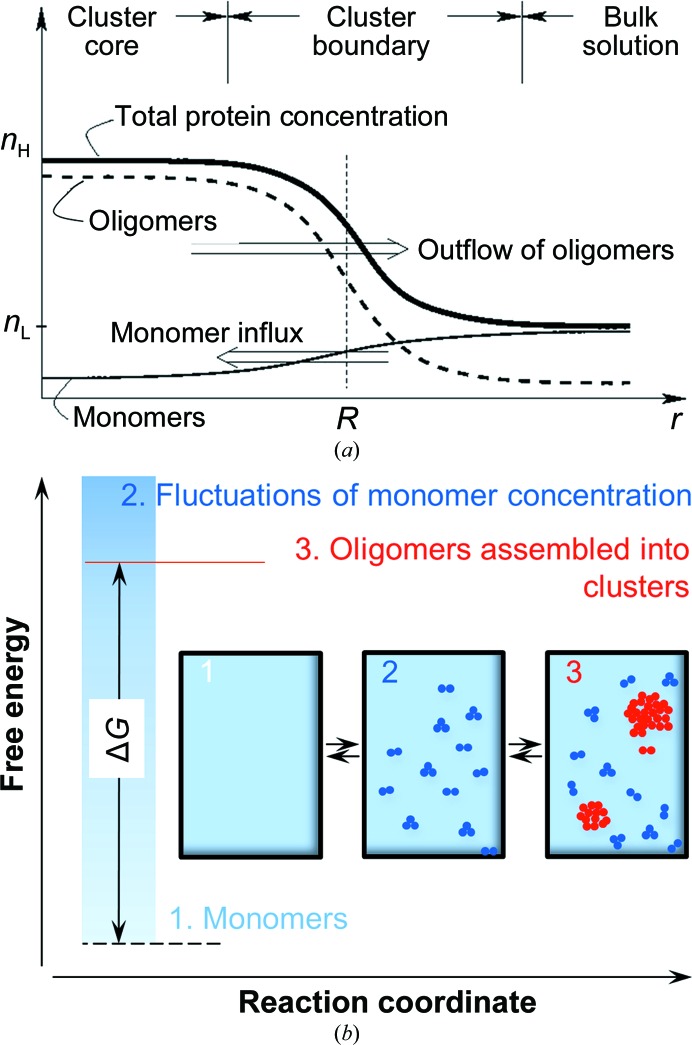
Following these considerations, we proposed that the clusters represent a mixture of protein monomers and transient oligomers (Pan et al., 2010 ▶). The oligomers are stabilized at the high protein concentration typical of the cluster core; as they diffuse out of the cluster core to the cluster periphery, they decay back into monomers, as illustrated in Fig. 8 ▶(a). The puzzling size of the clusters is determined by the lifetime τO and diffusivity D O of the transient oligomers, R cl ≃ (D OτO)1/2 (Pan et al., 2010 ▶). The nature of the oligomers is discussed below. However, the finite lifetime of the oligomers is crucial for the existence of the clusters: the above relation predicts that long oligomer lifetimes would lead to uninhibited protein aggregation into large macroscopic amorphous structures.
Figure 8.
The mechanism of cluster formation. (a) Concentration profiles in a cluster. n L, total protein concentration in solution; n H, total protein concentration in dense liquid inside clusters; r, distance from the center of the cluster; R, cluster radius. Reprinted with permission from Pan et al. (2010 ▶), J. Phys. Chem. B, 114, 7620–7630. Copyright 2010 American Chemical Society. (b) The free-energy variation along the reaction coordinate for formation of the anomalous mesoscopic clusters. Insets: schematic illustrations of the three steps of the cluster-formation mechanism.
The mechanism of cluster formation based on transient oligomers is summarized in Fig. 8 ▶(b). In a solution of protein monomers (step 1 in Fig. 8 ▶ b), concentration fluctuations lead to regions of high protein concentration (step 2). Straightforward thermodynamic evaluations reveal that the regions with concentration comparable to that in the dense liquid phase are small, containing at most several molecules, and very few, and do not survive over times longer than the diffusion time (Pan et al., 2010 ▶). However, in a few of these fluctuations protein oligomers form (step 3). Oligomer formation has two consequences: (i) it extends the lifetime of the region of high protein concentration to a time comparable to the lifetime of the oligomer, and (ii) it creates a gradient of monomer concentration that induces a flux of monomers towards this region. The arriving monomers convert to oligomers and this leads to cluster growth. The increased oligomer concentration accelerates the decay of oligomers into monomers. The balance between monomer influx and oligomer decay determines the steady-state R cl discussed above. The total protein concentration in the clusters is determined by the mass balance of the reversible monomer–oligomer reaction.
This mechanism yields several predictions that have been tested, such as the insensitivity of the cluster size to the bulk protein concentration. We have predicted and observed a crossover of cluster dynamics to critical-like density fluctuations at high protein concentrations, and that those dynamics obey a universal diffusion-like scaling with time and wavevector, including in the critical-like regime (Pan et al., 2010 ▶; Chan et al., 2012 ▶).
As evidence for the presence of oligomers in lysozyme solution, we consider the results of small-angle X-ray and neutron scattering investigations. The protein was held in HEPES buffer in the absence of precipitant; hence, the solution was undersaturated with respect to any solid or condensed liquid phases. The authors detected dynamic structures containing several protein molecules and with a lifetime of the order of milliseconds (Stradner et al., 2004 ▶; Porcar et al., 2009 ▶).
4.4. Oligomer formation by partial protein unfolding
The considerations in the preceding subsection reveal that the existence of transient protein oligomers is crucial for cluster formation. Several possible interactions that could underlie such oligomers have been tested: Coulomb interactions; ion bridges between positive and negative amino-acid residues; CO2 bridges between amine groups on lysine and arginine; disulfide bridges forming after the oxidation of the thiol groups of cysteine residues; and hydrophobic bonds after partial protein unfolding.
If protein molecules are viewed as particles with uniformly distributed charges, the formation of oligomers based on Coulomb interaction would be impossible owing to the repulsion between like charges. However, the charges on the protein molecular surfaces are discrete and the net charge is the balance of numerous positive and negative surface residues. A numerical model of the interactions between such discrete charges on the surface of lysozyme molecules revealed that dimer configurations in which positive residues face negative partners on an adjacent molecule are indeed possible (Chan et al., 2012 ▶). However, the resulting attraction is too weak to support macroscopic lifetimes of the dimer. The inevitable conclusion was that electrostatic interaction cannot support cluster formation through the stabilization of a protein dimer.
To test whether CO2 or intermolecular disulfide bridges could support the oligomerization needed for cluster formation, we bubbled He or air through a solution of lysozyme. We expected that He would purge the solution from dissolved CO2, lower its chemical potential and in this way disrupt the putative CO2 bridges, shorten the oligomer lifetime and decrease the cluster size. On the other hand, oxygen in air would increase the oxidative potential in the solution, leading to more intermolecular disulfide bridges, a longer oligomer lifetime and larger clusters. We found that after ∼1 h of bubbling, the size of the clusters increased significantly with both gases (Fig. 9 ▶ a). To reveal the mystery of the identical effects of the two gases, we lowered the bubbling rate of He by approximately threefold and found that the effect disappeared. The latter finding indicates that the gases do not exert a chemical effect on the clusters and imply that CO2 bridges between amino groups or intermolecular disulfide bridges between thiol groups are unlikely to be mechanisms of formation of cluster-supporting oligomers in lysozyme.
Figure 9.
The bonds in the transient oligomers. (a) Tests for the role of specific chemical bonds in cluster formation. The evolution of the cluster radius R 2 in a lysozyme solution as a result of bubbling with helium or air. (b) Schematic illustration of the domain-swapping mechanism of formation of protein oligomers. (c) The effect of urea on cluster formation. Correlation functions from lysozyme solutions at pH 7.8 in 20 mM HEPES buffer collected in the absence and presence of urea, as indicated in the plot. Reprinted with permission from Pan et al. (2010 ▶), J. Phys. Chem. B, 114, 7620–7630. Copyright 2010 American Chemical Society.
The independence of the increase in cluster size on the chemical nature of the gas indicates that mechanical agitation and ensuing solution flows may be the cause of the observed effect. Shear flows are known to unfold and, at high shear rates, denature proteins (Bekard et al., 2011 ▶). The lysozyme structure can be divided into two domains (McCammon et al., 1976 ▶). Shear flow may lead to separation of the domains, exposing their hydrophobic interfaces. In turn, an exposed interface of a domain may form a hydrophobic bond with a paired domain from another similarly unfolded molecule. An analogous phenomenon is well known in structural biology as ‘domain swapping’ (illustrated in Fig. 9 ▶ b; Bennett et al., 2006 ▶; Schlunegger et al., 1997 ▶). A recent study has demonstrated that dimers of partially unfolded proteins exhibit additional stabilization in a crowded environment (Wang, Xu et al., 2009 ▶). Thus, the data in Fig. 9 ▶(a) suggest that domain-swapped dimers or higher oligomers may be the cause of the clusters.
To test this hypothesis, we characterized cluster formation in the presence of urea. Urea has been used to controllably modify the degree of protein folding (Hua et al., 2008 ▶). We monitored the response of cluster formation to urea at 80 mg ml−1, where few clusters are present in the absence of urea. The results in Fig. 9 ▶(c) indicate that partial unfolding of lysozyme may contribute to cluster formation: clusters identifiable by the second shoulder in the correlation function in Fig. 9 ▶(c) appear upon adding a sufficient amount of urea (Pan et al., 2010 ▶).
The presence of protein oligomers or other chemically modified species in the clusters raises a crucial question: why is the formation of crystal nuclei, consisting of monomers, faster in the clusters, where the monomer concentration is lower than in the bulk solution? The nucleation rate depends linearly on the concentration of the crystallizing molecules and exponentially on their chemical potential. Importantly, the nucleation rate is inversely proportional to the exponent of the third power of the surface free energy of the nucleus. While we do not currently know the monomer concentration in the clusters, the mechanism presented by Pan et al. (2010 ▶) and illustrated in Fig. 8 ▶ suggests that it is lower than that in the bulk solution by a certain factor. This should lower the nucleation rate in the clusters from that in the solution by the same factor. Since the clusters are in equilibrium with the solution, the monomer chemical potentials in the clusters and solution are equal, avoiding a further huge suppression of nucleation. On the other hand, the high total protein concentration in the clusters, including monomers and oligomers, should significantly lower the surface free energy of a nucleus forming there. In view of the high sensitivity of the nucleation rate to the surface free energy of the nucleus, this may be the main reason for the accelerated nucleation in the clusters. Clearly, these considerations are somewhat speculative and should be subjected to further tests.
5. Summary and conclusions
Recent studies have suggested that the nucleation of crystals of the protein lysozyme, of polymers of sickle-cell hemoglobin and of crystals of other compounds of various molecular sizes follows a two-step mechanism. The low nucleation rates observed with numerous proteins even at very high supersaturations suggest that the two-step mechanism may be a general law for proteins.
A crucial part of the two-step mechanism is the existence of protein-dense liquid clusters. Above, we first reviewed the methods for cluster detection and characterization. Dynamic light scattering has provided the majority of the data, from which insights into the cluster properties and mechanisms have been gleaned. Atomic force and scanning confocal microscopies provided direct imaging of clusters and crucial verification of their liquid nature. Brownian microscopy is a recent method that has been used to test the processing routines developed for DLS data.
The most important cluster properties are consistent for all of the proteins studied in detail: lumazine synthase, hemoglobin S, oxyhemoglobin S, oxyhemoglobin A, lysozyme, glucose isomerase and insulin. The clusters are several hundred nanometres in size. They appear within seconds of solution preparation and their size does not increase, or increases very slowly, thereafter. The clusters occupy very low fractions of the solution volume: from 10−7 to 10−3. The cluster concentration and volume fraction are strong functions of the concentration of protein in the host solution.
Studies with lysozyme and sickle-cell hemoglobin have revealed that the standard chemical potential of the protein in the clusters is significantly higher than that in the host solution. Furthermore, the fraction of protein in the clusters is entirely determined by this standard chemical potential excess, indicating that the clusters are in a metastable equilibrium with the host solution.
Studies of the cluster mechanism with lysozyme indicate that the clusters exist owing to the formation of transient protein oligomers. These oligomers are bound not by Coulomb interactions or specific chemical bonds, but by hydrophobic interactions between internal protein interfaces exposed to the solution after partial protein unfolding (‘domain swapping’).
The investigation of dense liquid clusters in protein solutions is in its infancy: the first paper on the existence of clusters was published less than ten years ago. Most of the above mechanisms were deduced from data on the collective behavior of large cluster populations. The current challenge in the study of protein-rich clusters is to develop methods that allow the monitoring of individual clusters to directly answer questions about the behaviors of the clusters: Are the clusters liquid? What is their shape? Is the shape steady or variable? What is the viscosity of the liquid inside the clusters? Do the clusters always support crystal nucleation? What are the cluster characteristics that determine their suitability as nucleation precursors?
Another challenge is tests of the presence of clusters in solutions of different proteins. Do all classes of proteins allow cluster formation? Are clusters present in solutions of solubilized membrane proteins? Does protein conformational flexibility facilitate or hinder cluster formation? What structural and chemical characteristics of the protein molecules determine the presence and behavior of clusters?
Protein crystals hold the key not only to structural biology, but also to protein pharmaceuticals, protein-aggregation diseases and other fields of science, technology and medicine. The role that the clusters play in protein crystal formation places them at the pinnacle of these areas. Investigations of protein clusters have a clear potential for major breakthroughs.
Acknowledgments
Funding for this work was provided by NSF (grant MCB-1244568) and NASA (grant NNX13AH25G).
References
- Aber, J. E., Arnold, S. & Garetz, B. A. (2005). Strong DC Electric Field Applied to Supersaturated Aqueous Glycine Solution Induces Nucleation of the Polymorph. Phys. Rev. Lett. 94, 145503. [DOI] [PubMed]
- Asherie, N., Lomakin, A. & Benedek, G. B. (1996). Phase Diagram of Colloidal Solutions. Phys. Rev. Lett. 77, 4832–4835. [DOI] [PubMed]
- Atkins, P. & DePaula, J. (2002). Physical Chemistry, 7th ed. New York: W. H. Freeman & Co.
- Auer, S. & Frenkel, D. (2004). Numerical prediction of absolute crystallization rates in hard-sphere colloids. J. Chem. Phys. 120, 3015–3029. [DOI] [PubMed]
- Bekard, I. B., Asimakis, P., Bertolini, J. & Dunstan, D. E. (2011). The effects of shear flow on protein structure and function. Biopolymers, 95, 733–745. [DOI] [PubMed]
- Bennett, M. J., Sawaya, M. R. & Eisenberg, D. (2006). Deposition diseases and 3D domain swapping. Structure, 14, 811–824. [DOI] [PubMed]
- Berland, C. R., Thurston, G. M., Kondo, M., Broide, M. L., Pande, J., Ogun, O. & Benedek, G. B. (1992). Solid–liquid phase boundaries of lens protein solutions. Proc. Natl Acad. Sci. USA, 89, 1214–1218. [DOI] [PMC free article] [PubMed]
- Berry, P. S., Rice, S. A. & Ross, J. (2000). Physical Chemistry, 2nd ed. Oxford University Press.
- Blaak, R., Auer, S., Frenkel, D. & Löwen, H. (2004). Homogeneous nucleation of colloidal melts under the influence of shearing fields. J. Phys. Condens. Matter, 16, S3873–S3884.
- Broide, M. L., Berland, C. R., Pande, J., Ogun, O. O. & Benedek, G. B. (1991). Binary-liquid phase separation of lens protein solutions. Proc. Natl Acad. Sci. USA, 88, 5660–5664. [DOI] [PMC free article] [PubMed]
- Cacioppo, E. & Pusey, M. L. (1991). The solubility of the tetragonal form of hen egg white lysozyme from pH 4.0 to 5.4. J. Cryst. Growth, 114, 286–292.
- Chan, H. Y., Lankevich, V., Vekilov, P. G. & Lubchenko, V. (2012). Anisotropy of the Coulomb interaction between folded proteins: consequences for mesoscopic aggregation of lysozyme. Biophys. J. 102, 1934–1943. [DOI] [PMC free article] [PubMed]
- Chapman, H. N. et al. (2011). Femtosecond X-ray protein nanocrystallography. Nature (London), 470, 73–77. [DOI] [PMC free article] [PubMed]
- Chayen, N. E., Helliwell, J. R. & Snell, E. H. (2010). Macromolecular Crystallization and Crystal Perfection. Oxford University Press.
- Dorsaz, N., Filion, L., Smallenburg, F. & Frenkel, D. (2012). Spiers Memorial Lecture: Effect of interaction specificity on the phase behaviour of patchy particles. Faraday Discuss. 159, 9–21.
- Erdemir, D., Lee, A. Y. & Myerson, A. S. (2009). Nucleation of Crystals from Solution: Classical and Two-Step Models. Acc. Chem. Res. 42, 621–629. [DOI] [PubMed]
- Filobelo, L. F., Galkin, O. & Vekilov, P. G. (2005). Spinodal for the solution-to-crystal phase transformation. J. Chem. Phys. 123, 014904. [DOI] [PubMed]
- Fredericks, W. J., Hammonds, M. C., Howard, S. B. & Rosenberger, F. (1994). Density, thermal expansivity, viscosity and refractive index of lysozyme solutions at crystal growth concentrations. J. Cryst. Growth, 141, 183–192.
- Galkin, O., Pan, W., Filobelo, L., Hirsch, R. E., Nagel, R. L. & Vekilov, P. G. (2007). Two-step mechanism of homogeneous nucleation of sickle cell hemoglobin polymers. Biophys. J. 93, 902–913. [DOI] [PMC free article] [PubMed]
- Galkin, O. & Vekilov, P. G. (2000). Control of protein crystal nucleation around the metastable liquid–liquid phase boundary. Proc. Natl. Acad. Sci. USA, 97, 6277–6281. [DOI] [PMC free article] [PubMed]
- Garetz, B., Matic, J. & Myerson, A. (2002). Polarization switching of crystal structure in the nonphotochemical light-induced nucleation of supersaturated aqueous glycine solutions. Phys. Rev. Lett. 89, 175501. [DOI] [PubMed]
- Gebauer, D., Volkel, A. & Colfen, H. (2008). Stable Prenucleation Calcium Carbonate Clusters. Science, 322, 1819–1822. [DOI] [PubMed]
- Gibbs, J. W. (1876). On the equilibrium of heterogeneous substances, First Part. Trans. Connect. Acad. Sci. 3, 108–248.
- Gibbs, J. W. (1878). On the equilibrium of heterogeneous substances (concluded). Trans. Connect. Acad. Sci. 3, 343–524.
- Gliko, O., Neumaier, N., Pan, W., Haase, I., Fischer, M., Bacher, A., Weinkauf, S. & Vekilov, P. G. (2005). A Metastable Prerequisite for the Growth of Lumazine Synthase Crystals. J. Am. Chem. Soc. 127, 3433–3438. [DOI] [PubMed]
- Gliko, O., Pan, W., Katsonis, P., Neumaier, N., Galkin, O., Weinkauf, S. & Vekilov, P. G. (2007). Metastable liquid clusters in super- and undersaturated protein solutions. J. Phys. Chem. B, 111, 3106–3114. [DOI] [PubMed]
- Gower, L. B. (2008). Biomimetic Model Systems for Investigating the Amorphous Precursor Pathway and Its Role in Biomineralization. Chem. Rev. 108, 4551–4627. [DOI] [PMC free article] [PubMed]
- Grigsby, J. J., Blanch, H. W. & Prausnitz, J. M. (2001). Cloud-point temperatures for lysozyme in electrolyte solutions: effect of salt type, salt concentration and pH. Biophys. Chem. 91, 231–243. [DOI] [PubMed]
- Groenewold, J. & Kegel, W. K. (2001). Anomalously Large Equilibrium Clusters of Colloids. J. Phys. Chem. B, 105, 11702–11709.
- Harano, K., Homma, T., Niimi, Y., Koshino, M., Suenaga, K., Leibler, L. & Nakamura, E. (2012). Heterogeneous nucleation of organic crystals mediated by single-molecule templates. Nature Mater. 11, 877–881. [DOI] [PubMed]
- Howard, S. B., Twigg, P. J., Baird, J. K. & Meehan, E. J. (1988). The solubility of hen egg-white lysozyme. J. Cryst. Growth, 90, 94–104.
- Hua, L., Zhou, R., Thirumalai, D. & Berne, B. J. (2008). Urea denaturation by stronger dispersion interactions with proteins than water implies a 2-stage unfolding. Proc. Natl Acad. Sci. USA, 105, 16928–16933. [DOI] [PMC free article] [PubMed]
- Kahlweit, M. (1969). Nucleation in Liquid Solutions. Physical Chemistry, edited by H. Eyring, pp. 675–698. New York: Academic Press.
- Kahlweit, M. (1975). Ostwald ripening of precipitates. Adv. Colloid Interface Sci. 5, 1–35.
- Kashchiev, D. (1995). Nucleation. Science and Technology of Crystal Growth, edited by J. P. van der Eerden & O. S. L. Bruinsma, pp. 53–56. Dordrecht: Kluwer Academic Publishers.
- Kashchiev, D. (2000). Nucleation. Basic theory with applications. Oxford: Butterworth, Heinemann.
- Krishnan, R. & Lindquist, S. L. (2005). Structural insights into a yeast prion illuminate nucleation and strain diversity. Nature (London), 435, 765–772. [DOI] [PMC free article] [PubMed]
- Kulkarni, A. M., Dixit, N. M. & Zukoski, C. F. (2003). Ergodic and non-ergodic phase transitions in globular protein suspensions. Faraday Discuss. 123, 37–50. [DOI] [PubMed]
- Kuznetsov, Y. G., Malkin, A. J. & McPherson, A. (2001). The liquid protein phase in crystallization: a case study – intact immunoglobulins. J. Cryst. Growth, 232, 30–39.
- Leunissen, M. E., Christova, C. G., Hynninen, A. P., Royall, C. P., Campbell, A. I., Imhof, A., Dijkstra, M., van Roij, R. & van Blaaderen, A. (2005). Ionic colloidal crystals of oppositely charged particles. Nature (London), 437, 235–240. [DOI] [PubMed]
- Li, Y., Lubchenko, V. & Vekilov, P. G. (2011). The use of dynamic light scattering and Brownian microscopy to characterize protein aggregation. Rev. Sci. Instrum. 82, 053106. [DOI] [PubMed]
- Li, Y., Lubchenko, V., Vorontsova, M. A., Filobelo, L. & Vekilov, P. G. (2012). Ostwald-like ripening of the anomalous mesoscopic clusters in protein solutions. J. Phys. Chem. B, 116, 10657–10664. [DOI] [PubMed]
- Liu, Y., Chen, W.-R. & Chen, S.-H. (2005). Cluster formation in two-Yukawa fluids. J. Chem. Phys. 122, 044507. [DOI] [PubMed]
- Lomakin, A., Chung, D. S., Benedek, G. B., Kirschner, D. A. & Teplow, D. B. (1996). On the nucleation and growth of amyloid β-protein fibrils: detection of nuclei and quantification of rate constants. Proc. Natl. Acad. Sci. USA, 93, 1125–1129. [DOI] [PMC free article] [PubMed]
- Malkin, A., Kuznetsov, Y. G. & McPherson, A. (1996). Defect Structure of Macromolecular Crystals. J. Struct. Biol. 117, 124–137.
- Malkin, A. J. & McPherson, A. (1993). Light scattering investigations of protein and virus crystal growth: ferritin, apoferritin and satellite tobacco mosaic virus. J. Cryst. Growth, 128, 1232–1235.
- Malkin, A. J. & McPherson, A. (1994). Light scattering investigation of the nucleation processes and kinetics of crystallization in macromolecular systems. Acta Cryst. D50, 385–395. [DOI] [PubMed]
- Malkin, A. J. & McPherson, A. (2004). Probing of crystal interfaces and the structures and dynamic properties of large macromolecular ensembles with in situ atomic force microscopy. From Fluid–Solid Interfaces to Nanostructural Engineering, Vol. 2, Assembly in Hybrid and Biological Systems, edited by J. J. De Yoreo & X. Y. Lui, pp. 201–238. New York: Plenum/Kluwer Academic.
- McCammon, J. A., Gelin, B. R., Karplus, M. & Wolynes, P. G. (1976). The hinge-bending mode in lysozyme. Nature (London), 262, 325–326. [DOI] [PubMed]
- Mossa, S., Sciortino, F., Tartaglia, P. & Zaccarelli, E. (2004). Ground-State Clusters for Short-Range Attractive and Long-Range Repulsive Potentials. Langmuir, 20, 10756–10763. [DOI] [PubMed]
- Muschol, M. & Rosenberger, F. (1997). Liquid–liquid phase separation in supersaturated lysozyme solutions and associated precipitate formation/crystallization. J. Chem. Phys. 107, 1953.
- Nielsen, A. E. & Sohnel, O. (1971). Interfacial tensions electrolyte crystal-aqueous solution, from nucleation data. J. Cryst. Growth, 11, 233–242.
- Noro, M. G., Kern, N. & Frenkel, D. (1999). The role of long range forces in the phase behavior of colloids and proteins. Europhys. Lett. 48, 332–338.
- Ostwald, W. (1897). Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 22, 289–330.
- Pan, W., Filobelo, L., Pham, N. D. Q., Galkin, O., Uzunova, V. V. & Vekilov, P. G. (2009). Viscoelasticity in homogeneous protein solutions. Phys. Rev. Lett. 102, 058101. [DOI] [PubMed]
- Pan, W., Galkin, O., Filobelo, L., Nagel, R. L. & Vekilov, P. G. (2007). Metastable mesoscopic clusters in solutions of sickle-cell hemoglobin. Biophys. J. 92, 267–277. [DOI] [PMC free article] [PubMed]
- Pan, W., Kolomeisky, A. B. & Vekilov, P. G. (2005). Nucleation of ordered solid phases of protein via a disordered high-density state: Phenomenological approach. J. Chem. Phys. 122, 174905. [DOI] [PubMed]
- Pan, W., Uzunova, V. V. & Vekilov, P. G. (2009). Free heme in micromolar amounts enhances the attraction between sickle cell hemoglobin molecules. Biopolymers, 91, 1108–1116. [DOI] [PubMed]
- Pan, W., Vekilov, P. G. & Lubchenko, V. (2010). Origin of anomalous mesoscopic phases in protein solutions. J. Phys. Chem. B, 114, 7620–7630. [DOI] [PubMed]
- Petsev, D. N., Wu, X., Galkin, O. & Vekilov, P. G. (2003). Thermodynamic Functions of Concentrated Protein Solutions from Phase Equilibria. J. Phys. Chem. B, 107, 3921–3926.
- Porcar, L., Falus, P., Chen, W.-R., Faraone, A., Fratini, E., Hong, K., Baglioni, P. & Liu, Y. (2009). Formation of the Dynamic Clusters in Concentrated Lysozyme Protein Solutions. J. Phys. Chem. Lett. 1, 126–129.
- Pouget, E. M., Bomans, P. H. H., Goos, J. A. C. M., Frederik, P. M., de With, G. & Sommerdijk, N. A. J. M. (2009). The initial stages of template-controlled CaCO3 formation revealed by cryo-TEM. Science, 323, 1455–1458. [DOI] [PubMed]
- Provencher, S. W. (1982a). A constrained regularization method for inverting data represented by linear algebraic equations. Comput. Phys. Commun. 27, 213–227.
- Provencher, S. W. (1982b). CONTIN: a general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 27, 229–242.
- Reviakine, I., Bergsma-Schutter, W. & Brisson, A. (1998). Growth of Protein 2-D Crystals on Supported Planar Lipid Bilayers Imaged In Situ by AFM. J. Struct. Biol. 121, 356–361. [DOI] [PubMed]
- Ross, P. D. & Minton, A. P. (1977). Hard quasispherical model for the viscosity of hemoglobin solutions. Biochem. Biophys. Res. Commun. 76, 971–976. [DOI] [PubMed]
- Savage, J. R. & Dinsmore, A. D. (2009). Experimental Evidence for Two-Step Nucleation in Colloidal Crystallization. Phys. Rev. Lett. 102, 198302. [DOI] [PubMed]
- Schatzel, K. (1993). Single-photon correlation techniqes. Dynamic Light Scattering. The Method and Some Applications, edited by W. Brown, pp. 76–148. Oxford: Clarendon Press.
- Schlunegger, M. P., Bennett, M. J. & Eisenberg, D. (1997). Oligomer formation by 3D domain swapping: a model for protein assembly and misassembly. Adv. Protein Chem. 50, 61–122. [DOI] [PubMed]
- Schmitz, K. S. (1990). Dynamic Light Scattering by Macromolecules. New York: Academic Press.
- Sciortino, F., Mossa, S., Zaccarelli, E. & Tartaglia, P. (2004). Equilibrium cluster phases and low-density arrested disordered states: the role of short-range attraction and long-range repulsion. Phys. Rev. Lett. 93, 055701. [DOI] [PubMed]
- Sear, R. P. (1999). Phase behavior of a simple model of globular proteins. J. Chem. Phys. 111, 4800. [DOI] [PubMed]
- Shah, M., Galkin, O. & Vekilov, P. G. (2004). Smooth transition from metastability to instability in phase separating protein solutions. J. Chem. Phys. 121, 7505–7512. [DOI] [PubMed]
- Shukla, A., Mylonas, E., Di Cola, E., Finet, S., Timmins, P., Narayanan, T. & Svergun, D. I. (2008). Absence of equilibrium cluster phase in concentrated lysozyme solutions. Proc. Natl Acad. Sci. USA, 105, 5075–5080. [DOI] [PMC free article] [PubMed]
- Sleutel, M. & Van Driessche, A. E. S. (2014). Role of clusters in nonclassical nucleation and growth of protein crystals. Proc. Natl Acad. Sci. USA, 111, E546–E553. [DOI] [PMC free article] [PubMed]
- Stradner, A., Sedgwick, H., Cardinaux, F., Poon, W. C. K., Egelhaaf, S. U. & Schurtenberger, P. (2004). Equilibrium cluster formation in concentrated protein solutions and colloids. Nature (London), 432, 492–495. [DOI] [PubMed]
- Thomson, J. A., Schurtenberger, P., Thurston, G. M. & Benedek, G. B. (1987). Binary liquid phase separation and critical phenomena in a protein water solution. J. Chem. Phys. 84, 7079–7083. [DOI] [PMC free article] [PubMed]
- Uzunova, V. V., Pan, W., Galkin, O. & Vekilov, P. G. (2010). Free heme and the polymerization of sickle cell hemoglobin. Biophys. J. 99, 1976–1985. [DOI] [PMC free article] [PubMed]
- Uzunova, V., Pan, W., Lubchenko, V. & Vekilov, P. G. (2012). Control of the Nucleation of Sickle Cell Hemoglobin Polymers by Free Hematin. Faraday Discuss. 159, 87–104.
- Vekilov, P. G. (2004). Dense liquid precursor for the nucleation of ordered solid phases from solution. Cryst. Growth Des. 4, 671–685.
- Vekilov, P. G. (2010). Nucleation. Cryst. Growth Des. 10, 5007–5019. [DOI] [PMC free article] [PubMed]
- Vekilov, P. G. (2012a). The Two-Step Mechanism and The Solution–Crystal Spinodal for Nucleation of Crystals in Solution Kinetics and Thermodynamics of Multistep Nucleation and Self-Assembly in Nanoscale Materials, edited by G. Nicholls & D. Maes, pp. 79–109. Hoboken: Wiley.
- Vekilov, P. G. (2012b). Crystal nucleation: Nucleus in a droplet. Nature Mater. 11, 838–840. [DOI] [PubMed]
- Vekilov, P. G., Feeling-Taylor, A. R., Petsev, D. N., Galkin, O., Nagel, R. L. & Hirsch, R. E. (2002). Intermolecular Interactions, Nucleation and Thermodynamics of Crystallization of Hemoglobin C. Biophys. J. 83, 1147–1156. [DOI] [PMC free article] [PubMed]
- Vivarès, D., Kaler, E. W. & Lenhoff, A. M. (2005). Quantitative imaging by confocal scanning fluorescence microscopy of protein crystallization via liquid–liquid phase separation. Acta Cryst. D61, 819–825. [DOI] [PubMed]
- Volmer, M. (1939). Kinetik der Phasenbildung. Z. Phys. Chem. 156A, 208.
- Volmer, M. & Schultze, W. (1931). Kondensation an Kristallen. Z. Phys. Chem. 156A, 1–22.
- Wang, J. F., Müller, M. & Wang, Z.-G. (2009). Nucleation in A/B/AB blends: Interplay between microphase assembly and macrophase separation. J. Chem. Phys. 130, 154902. [DOI] [PubMed]
- Wang, W., Xu, W.-X., Levy, Y., Trizac, E. & Wolynes, P. G. (2009). Proc. Natl Acad. Sci. USA, 106, 5517–5522. [DOI] [PMC free article] [PubMed]
- Yau, S.-T., Petsev, D. N., Thomas, B. R. & Vekilov, P. G. (2000). Molecular-level thermodynamic and kinetic parameters for the self-assembly of apoferritin molecules into crystals. J. Mol. Biol. 303, 667–678. [DOI] [PubMed]
- Yau, S.-T., Thomas, B. R., Galkin, O., Gliko, O. & Vekilov, P. G. (2001). Molecular mechanisms of microheterogeneity-induced defect formation in ferritin crystallization. Proteins, 43, 343–352. [PubMed]
- Zhang, T. H. & Liu, X. Y. (2007). Multistep crystal nucleation: A kinetic study based on colloidal crystallization. J. Phys. Chem. B, 111, 14001–14005. [DOI] [PubMed]