Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 6;4:4294. doi: 10.1038/srep04294

Nanometer-thick lateral polyelectrolyte micropatterns induce macrosopic electro-osmotic chaotic fluid instabilities

M Wessling 1,2,a, L Garrigós Morcillo 1, S Abdu 1
PMCID: PMC3944711  PMID: 24598972

Abstract

Electro-convective vortices in ion concentration polarization under shear flow have been of practical relevance for desalination processes using electrodialysis. The phenomenon has been scientifically disregarded for decades, but is recently embraced by a growing fluid dynamics community due its complex superposition of multi-scale gradients in electrochemical potential and space charge interacting with emerging complex fluid momentum gradients. While the visualization, quantification and fundamental understanding of the often-chaotic fluid dynamics is evolving rapidly due to sophisticated simulations and experimentation, little is known whether these instabilities can be induced and affected by chemical topological heterogeneity in surface properties. In this letter, we report that polyelectrolyte layers applied as micropatterns on ion exchange membranes induce and facilitate the electro-osmotic fluid instabilities. The findings stimulate a variety of fundamental questions comparable to the complexity of today's turbulence research.

Ion transport out of an aqueous solution into an ion-selective solid surface, i.e. ion-selective membranes1 and beads2, nanochannels3 and electrodes4 can lead to convective fluid flows at severe ion concentration polarization above a critical current density. In desalination applications with ion exchange membranes, concentration polarization and overlimiting current transport has long been avoided since the overlimiting transport was assumed to be caused by detrimental water splitting causing irreversible metal hydroxide precipitation. However, water splitting occurs mostly only at anion exchange membranes, accounting only for a small fraction of the overlimiting current and has not been observed at cation exchange membranes5. In fact, overlimiting transport is often the superposition of various physico-chemical phenomena6, i.e. to a small extent water splitting, but especially gravitational convection and electro-convection7, and sometimes selectivity loss and current-induced membrane discharge8. The experimental deconvolution and proof of these effects has been difficult in the past. For instance, one would like to eliminate water splitting while being able to study fluidic instabilities at the interface unaffected by pH changes.

Electro-convective instabilities have been theoretically predicted as convection rolls in the diffusion boundary layer at the surface of the ion exchange membrane9. Such vortices have been optically proven to exist at ion exchange membrane surfaces where the vortex height increases with increasing potential drop over a concentration-polarized solution at the surface of the membrane10. The evolution of a sequence of such vortices in a flow channel at laminar flow conditions has been observed as well, and quantified by a scaling analysis11. While it is commonly understood that heterogeneity of the ion exchange surface can influence the overlimiting currents and fluidic instabilities12, there is no direct proof of a relationship between electrochemical surface topology and fluidic instabilities in the diffusion boundary layer. In fact, there is a complete lack of regio-selective methods to pattern the electrochemical surface properties of ion exchange membranes as well as a lack of systematic methods to suppress water splitting. Hence many experimental fluid dynamic studies of electro-convection phenomena still rely on experimental systems where water splitting and electro-convection are yet not decoupled. Evidence gives the recent paper of Kwak et al., where electro-convection rolls emerge distinctly at the cation exchange membrane, but only vaguely at the anion exchange membrane11.

Some experimental studies reveal that the surface properties indeed influence the overlimiting current transport and the electro-convection. A coating of poly(vinyl alcohol) with embedded ion exchange particles suppresses water splitting13. A heterogeneous layer increases the limiting current density and electro-convection is suggested to even occur in a liquid confined in the porosity14. Rubinstein predicted that a sinusoidal surface undulation would shorten the voltage plateau before overlimiting currents set in. This prediction has been reasonably proven using membranes having an imprinted micro-texture: depending on the orientation of the micro-texture with respect to the flow direction, the plateau before the onset of overlimiting currents shortened12. Whether or not chemical topography can trigger the convection rolls is still an unresolved question.

Here we discuss and prove that controlled adsorption of polyelectrolyte layers with well-defined ionic macromolecular properties at the interface between ionic solution and membrane surface triggers a significantly earlier onset of electro-convection at lower potential polarization. We also prove that their regio-selective adsorption imposed by a soft-lithography molecular printing transfer is even more effective.

Layer-by-layer macromolecular architectures are fuzzy nano-assemblies comprising layers of polycations and polyanions15. They are well known to switch surface properties and influence ion transport through membrane interfaces16. Recently, we reported that in electrodialysis such LBL-surface modifications even control ion selectivity17. In fact, the terminating layer with its electrochemical surface charge properties can tailor the membrane mono- or bivalent-ion-selective for Na+ vs Ca2+. In this report, we take the experimental methods of current−voltage curves and chronopotentiometry to deconvolute and quantify ohmic resistances and electro-convective contributions to the overall transport of ions as shown in Figure 1. We take the plateau length as a fingerprint of the electro-convective origin of the overlimiting current. At equal hydrodynamic conditions and inhibited water splitting, a shorter plateau length represents an earlier transition of a stable polarized diffusion layer into a transient, mixed boundary layer. We apply well defined LBL-layers to suppress any water splitting and analyze the polarization behaviour as a function of the electrochemical surface topology. This allows for the first time to establish experimental evidence that controlled electrochemical heterogeneity can introduce convection phenomena in the diffusion boundary layer adjacent to the membrane surface.

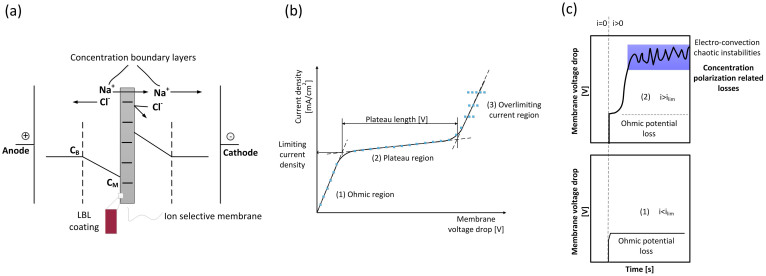
Figure 1.

Figure 1

Open in a new tab

(a) Concentration profiles of NaCl in the vicinity of a cation exchange membrane. The membranes facing the diluted side are modified with various assemblies of LBL-polyelectrolytes. (b) Current−voltage curve obtained from steady-stated measurements of membranes under polarization, showing: (1) the ohmic region of solution and membrane, (2) the plateau region, about which little is known today and (3) the overlimiting current region, in which superimposed effects, but in particular electro-convection is dominant. (c) Chronopotentiometric response upon a sudden start of current with: (1) the regular ohmic response when underlimiting current is applied and (2) when overlimiting current is applied; the voltage fluctuations being a fingerprint of the chaotic disturbances in the diffusion boundary layer.

Results

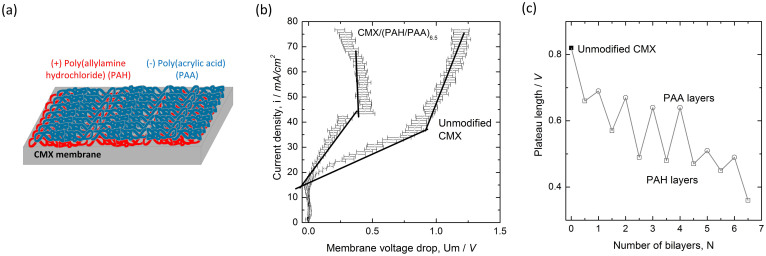
The polyelectrolytes poly(allylamine hydrochloride) (PAH) and poly(acrylic acid) (PAA) are identified to show no water splitting (See Figure S3(a) in the Supplementary Information). They were deposited from an aqueous solution onto a commercial CMX membrane by adsorption from the solution. The number of subsequent deposition steps for the different polyelectrolytes vary from 1 to 11, the latter being indicated as 6.5 double layers as shown in Figure 2. It is apparent from Figure 2(b) that the presence of the polyelectrolytes affects the plateau length significantly. It is also obvious from Figure 2(c) that the plateau length in general decreases with increasing number of polyelectrolyte layers. Superimposed onto this trend of shortening plateau length, a distinct switching pattern emerges between an upper bound for PAA-terminated surfaces as opposed to a lower bound for the PAH-terminated surfaces. This experimental observation for the first time establishes a quantitative correlation between a rigorously controlled and systematic surface modification with the induction of overlimiting currents at low polarization thresholds. The question whether lateral electrochemical surface heterogeneity can also influence the onset of electro-convective fluid motion will be answered below as well.

Figure 2.

Figure 2

Open in a new tab

(a) Schematic representation of a single LBL double layer on a commercial CMX cation exchange membrane. (b) A typical current−voltage curve, corrected for the ohmic resistance of membrane and solution, for the reference (unmodified CMX) membrane and the CMX membrane modified with an LBL coating, comprising 6.5 double layers. (c) Evolution of the plateau length with increasing number of LBL double layers terminated with either PAH or PAA layer.

In scanning electron micrographs, the membranes modified with 10 LBL double layers show a distinct layer at the surface of about 1 micron thickness (See Figure S5 in the Supplementary Information). This amounts to an average polyelectrolyte layer thickness of about 50 nm. While this is thick as compared to the thickness of layers on other very smooth and planar surfaces, this thickness analysis is very reproducible17. One may now apply a patterned electrochemical surface modification to the original membrane or the membrane carrying already an LBL modification. Such regio-specific surface modification is potentially possible using molecular printing techniques such as soft lithography.

Soft lithography is known to enable transfer of adsorbed macromolecules from a soft PDMS-based stamp to another surface18. We have applied this technique to print the PAH onto either the original CMX membrane or onto the CMX membrane modified with 6 double layers. Table 1 shows that applying the PAH micropatterns decreased the plateau length of the membranes. These results indicate that introducing surface micro-heterogeneities by microcontact printing is even more effective in diminishing the plateau lengths than increasing the number of homogenous LBL layers – comparing the results of the single PAH micropattern to the 6.5 homogenous double layers.

Table 1. Plateau lengths of the unmodified CMX membrane, and the CMX membrane modified by LBL assembly and microcontact printing.

Membrane Plateau length [V]
CMX 0.82
CMX/(PAH)0.5 0.66
CMX/μCP-(PAH)0.5 0.25
CMX/(PAH/PAA)6.5 0.36
CMX/μCP-(PAH/PAA)6.5 0.24
Open in a new tab

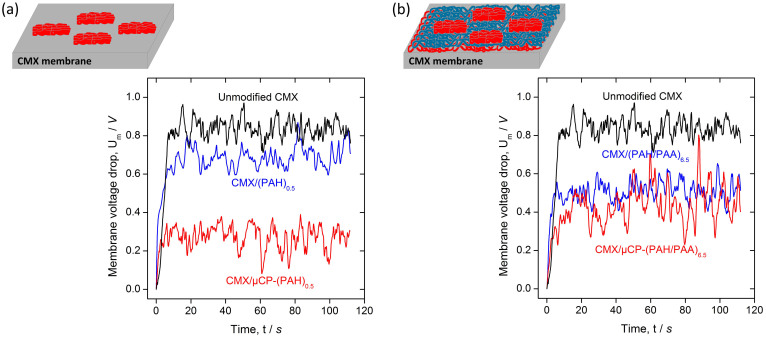
Rather than addressing the plateau length, Figure 3 shows the dynamic signal of the voltage drop over the membrane at a current above the limiting current density (30 mA/cm2) for the membranes modified with only one printed PAH layer. To focus on the fluid instability only, the voltage drop is corrected for the ohmic resistance of the membrane and the unpolarized solution, by subtracting it from the total voltage. Hence the only contribution to the signal stems from polarization in the diffusion boundary layer and the dynamic fluctuations associated with the fluid flow instabilities. From Figure 3(b), we can conclude that the average polarization resistance almost vanishes while the fluctuation is largest. Power spectral analysis of the fluctuations have been suggested in the past19, but they only give a broad distribution of fluctuation frequencies with little to no extra information to be extracted from the chaotic signal.

Figure 3.

Figure 3

Open in a new tab

Dynamic polarization signal obtained for: (a) the unmodified CMX membrane, and modified by applying a single homogenous PAH layer (CMX/PAH)0.5) or modified with a microcontact-printed PAH layer (CMX/μCP-PAH)0.5) on the original CMX (b) the unmodified CMX membrane, and modified by applying 6.5 homogenous double layers of PAH/PAA (CMX/(PAH/PAA)6.5) or modified with a microcontact-printed PAH layer on top of a 6 LBL double layer-modified CMX membrane (CMX/μCP-(PAH/PAA)6.5).

This observation in the chronopotentiometric experiments leads to the hypothesis that the combination of LBL layers and micropatterns is the most effective method to eliminate the detrimental effect of concentration polarization. Yet it poses the next question whether optimizing the geometric features of the molecularly printed polyelectrolytes can further attenuate this destabilization effect. Systematic variations in stamp pattern architecture are required in the future; however they go beyond the purpose of this report.

Discussion

While this report clearly indicates that adsorbed polyelectrolytes induce the onset of electro-convective flows at lower values of polarization, and while it also proves that lateral topological electrochemical heterogeneity even facilitates the onset, it becomes clear that the road to fully comprehend the phenomenon of interacting gradients in electrochemical potential, electrostatic potential, transient momentum gradients and surface heterogeneity will be challenging. The complexity of this phenomenon arises from the interaction of various materials and field gradients. Electrochemical lateral topology and heterogeneity as imposed by the printing can intuitively be accepted to interact with the concentration and flow gradients. However, in the absence of the printed patterns the polyelectrolyte layers still influence the onset of the overlimiting current. And the onset occurs earlier with increasing number of layers. Assuming that electrochemical inhomogeneity is the only material property responsible for the onset of electro-convection, one needs to relax the assumption of a lateral homogeneity in the LBL layers. In fact, recent literature indicates that electric fields can induce macroscopic morphological transitions in polyelectrolyte multilayers20. Microscopic phase separation is however more difficult to prove experimentally. Here, molecular simulations on the structure and interfacial softness of such layer architectures as a function of ionic effects may give deeper molecular insights21.

The extensive knowledge and methods in the field of turbulence research may offer important opportunities to further comprehend the complex fluidic phenomena of electro-convection22. Sophisticated simulations can guide the emerging community to the understanding of emergence of convection rolls and complex chaotic mixing phenomena in the diffusion boundary layer23, however, their extension into 3D simulations with a 2D membrane surface having micropatterned lateral electrochemical inhomogeneity will be a herculean task. Further sophistication of electrochemical characterization methods of the LBL architectures with microscopic resolution into the films thickness as well as at the fluid – LBL interface will be indispensable.

Methods

Membrane modification

In this study, the surface of the commercial cation exchange membrane CMX (Astom Corp., Japan) was modified by the layer-by-layer (LBL) assembly of polyelectrolyte multilayers as well as by the microcontact printing technique.

To introduce the polyelectrolyte multilayers, the CMX membrane (stored priorly in 0.5 M NaCl solution) was first rinsed with ultrapure water and coated on only one side with the desired polyelectrolyte multilayers. A summary of the screening experiments of the used polyelectrolytes is available in the Supplementary Information. For the main experiments, the CMX was sequentially dipped in 1 g/L solution of PAH (pH = 10) and 1 g/L PAA (pH = 3) solutions. Except the first layer, where the membrane was immersed in PAH for 45 min, the rest of the layers were formed each for 22 min, PAH as well as PAA. In between the coating steps, the membranes were thoroughly rinsed with ultrapure water to remove any loosely bound polyelectrolyte chains. The LBL layers were formed on the side that faces the anode (diluate side) in subsequent experiments.

The microcontact printing was conducted with a PDMS stamp with circular patterns (diameter = 350 μm and an edge-to-edge spacing = 1200 μm), either directly on the CMX membrane or on a previously assembled LBL layers (atop the CMX membrane), where the PAA was left as the outermost layer. To ink the PDMS stamp, it was immersed in PAH for 1 hour and then rinsed. The rinsing lasted for only few seconds to maintain the degree of ionization of the PAH. Then, the stamp and the membrane were blown dry with a gentle stream of nitrogen. The stamp was afterward pressed against the membrane for 1 min, to print the patterns.

Electrochemical characterization of the membranes

Polarization current−voltage curves and chronopotentiograms of the modified membranes were obtained with a six-compartment electrodialytic cell, using the four-point method: two working electrodes (a stainless steel cathode and a mixed-metal-oxide-coated titanium anode) were used to apply the current, while the voltage drop across the membrane was measured using two calomel reference electrodes. The reference electrodes were extended to a point as close to the membrane surface as possible using Haber-Luggin capillaries. A more detailed description of the setup can be found elsewhere17. The membranes, with an active membrane area of 10.5 cm2, were characterized in 0.1 M NaCl solution at a flow rate of about 1000 mL/min and the temperature was maintained at 25°C. Prior to the experiments, the membranes were equilibrated in 0.1 M NaCl solution for about 24 h outside the membrane module.

To obtain the current−voltage curves, the applied current density was increased stepwise, every 30 seconds, to allow the membrane reach steady state. The chronopotentiograms were obtained by applying a step input in current of 30 mA/cm2 (which is in the overlimiting region of the investigated membranes), and recording evolution of the voltage drop across the membranes at a sampling rate of 600/min. The plateau lengths were read off the current−voltage curves, which have had their ohmic parts subtracted. The transition of the current−voltage curves from the plateau to the overlimiting region is marked by the scatter of the voltage drop readings, but the transition was also determined with the aid of Cowan-Brown plots.

Author Contributions

M.W. conceived and supervised the project as well as wrote the manuscript. L.G.M. carried out many of the experiments and analysis. S.A. designed the experiments, performed part of the experiments and analysis as well as wrote part of the manuscript. M.W., L.G.M. and S.A. prepared the graphs and schemes. M.W. and S.A. reviewed and revised the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep04294-s1.pdf (455.1KB, pdf)

Acknowledgments

M.W. appreciates financial support from the Alexander-von-Humboldt Foundation. S.A. acknowledges support through the German Research Foundation (DFG) grant – SFB 985 “Functional Microgels and Microgel Systems”.

References

  1. Forgacs C. Deviations from the Steady-State in Ion Transfer through Perm-selective Membranes. Nature 190, 339–339 (1961). [Google Scholar]
  2. Nischang I., Reichl U., Seidel-Morgenstern A. & Tallarek U. Concentration Polarization and Nonequilibrium Electroosmotic Slip in Dense Multiparticle Systems. Langmuir 23, 9271–9281 (2007). [DOI] [PubMed] [Google Scholar]
  3. Zangle T. A., Mani A. & Santiago J. G. Theory and experiments of concentration polarization and ion focusing at microchannel and nanochannel interfaces. Chem. Soc. Rev. 39, 1014–1035 (2010). [DOI] [PubMed] [Google Scholar]
  4. Fleury V., Chazalviel J. N. & Rosso M. Theory and experimental evidence of electroconvection around electrochemical deposits. Phys. Rev. Lett. 68, 2492–2495 (1992). [DOI] [PubMed] [Google Scholar]
  5. Krol J. J., Wessling M. & Strathmann H. Chronopotentiometry and overlimiting ion transport through monopolar ion exchange membranes. J. Membr. Sci. 162, 155–164 (1999). [Google Scholar]
  6. Zabolotsky V. I. et al. Coupled transport phenomena in overlimiting current electrodialysis. Sep. Purif. Technol. 14, 255–267 (1998). [Google Scholar]
  7. Nikonenko V. V. et al. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 160, 101–123 (2010). [DOI] [PubMed] [Google Scholar]
  8. Andersen M. B. et al. Current-Induced Membrane Discharge. Phys. Rev. Lett. 109, 108301 (2012). [DOI] [PubMed] [Google Scholar]
  9. Rubinstein I. & Zaltzman B. Electro-osmotically induced convection at a permselective membrane. Physical Review E 62, 2238–2251 (2000). [DOI] [PubMed] [Google Scholar]
  10. Rubinstein S. M. et al. Direct Observation of a Nonequilibrium Electro-Osmotic Instability. Phys. Rev. Lett. 101, 236101 (2008). [DOI] [PubMed] [Google Scholar]
  11. Kwak R., Pham V. S., Lim K. M. & Han J. Shear Flow of an Electrically Charged Fluid by Ion Concentration Polarization: Scaling Laws for Electroconvective Vortices. Phys. Rev. Lett. 110, 114501 (2013). [DOI] [PubMed] [Google Scholar]
  12. Balster J. et al. Morphology and Microtopology of Cation-Exchange Polymers and the Origin of the Overlimiting Current. J. Phys. Chem. B 111, 2152–2165 (2007). [DOI] [PubMed] [Google Scholar]
  13. Kedem O., Schechtmann L., Mirsky Y., Saveliev G. & Daltrophe N. Low-polarisation electrodialysis membranes. Desalination 118, 305–314 (1998). [Google Scholar]
  14. Rubinstein I., Staude E. & Kedem O. Role of the membrane surface in concentration polarization at ion-exchange membrane. Desalination 69, 101–114 (1988). [Google Scholar]
  15. Decher G. Fuzzy Nanoassemblies: Toward Layered Polymeric Multicomposites. Science 277, 1232–1237 (1997). [Google Scholar]
  16. Stanton B. W., Harris J. J., Miller M. D. & Bruening M. L. Ultrathin, Multilayered Polyelectrolyte Films as Nanofiltration Membranes. Langmuir 19, 7038–7042 (2003). [Google Scholar]
  17. Abdu S., Martí-Calatayud M.-C., Wong J. E., García-Gabaldón M. & Wessling M. Layer-by-Layer Modification of Cation Exchange Membranes Controls Ion Selectivity and Water Splitting. ACS Appl. Mater. Interfaces 6, 1843–1854 (2014). [DOI] [PubMed] [Google Scholar]
  18. Braunschweig A. B., Huo F. & Mirkin C. A. Molecular printing. Nat Chem 1, 353–358 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Maletzki F., Rösler H. W. & Staude E. Ion transfer across electrodialysis membranes in the overlimiting current range: stationary voltage current characteristics and current noise power spectra under different conditions of free convection. J. Membr. Sci. 71, 105–116 (1992). [Google Scholar]
  20. Cho C., Jeon J.-W., Lutkenhaus J. & Zacharia N. S. Electric Field Induced Morphological Transitions in Polyelectrolyte Multilayers. ACS Appl. Mater. Interfaces 5, 4930–4936 (2013). [DOI] [PubMed] [Google Scholar]
  21. Rodriguez-Ropero F. & van der Vegt N. F. A. Ionic specific effects on the structure, mechanics and interfacial softness of a polyelectrolyte brush. Faraday Discuss. 160 (2013). [DOI] [PubMed] [Google Scholar]
  22. Grossmann S. & Lohse D. Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56 (2000). [Google Scholar]
  23. Druzgalski C. L., Andersen M. B. & Mani A. Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Physics of Fluids (1994-present) 25, 110804-110801-110804-110817 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep04294-s1.pdf (455.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES