Axonal Transport: How High Microtubule Density Can Compensate for Boundary Effects in Small-Caliber Axons

Abstract

Long-distance intracellular axonal transport is predominantly microtubule-based, and its impairment is linked to neurodegeneration. In this study, we present theoretical arguments that suggest that near the axon boundaries (walls), the effective viscosity can become large enough to impede cargo transport in small (but not large) caliber axons. Our theoretical analysis suggests that this opposition to motion increases rapidly as the cargo approaches the wall. We find that having parallel microtubules close enough together to enable a cargo to simultaneously engage motors on more than one microtubule dramatically enhances motor activity, and thus minimizes the effects of any opposition to transport. Even if microtubules are randomly placed in axons, we find that the higher density of microtubules found in small-caliber axons increases the probability of having parallel microtubules close enough that they can be used simultaneously by motors on a cargo. The boundary effect is not a factor in transport in large-caliber axons where the microtubule density is lower.

Introduction

Long-distance vesicular transport is critical for axonal function, and its failure may induce neurodegeneration (1,2). However, exactly what factors contribute to its robustness or failure is still not well understood. Much of the transport occurs along microtubules (MTs). Electron micrographs indicate that the packing density of MTs in axons increases as the axon caliber decreases, ranging from ∼ 150 MTs/μm² of cross-sectional area of axoplasm for small unmyelinated axons (which are less than 1 μm in diameter), to less than 15 MTs/μm² in the axoplasm of large myelinated fibers of ∼ 10 μm in diameter (3–6). In this study, we propose that the higher density of MTs found in small-caliber axons can compensate for confinement effects that can impede axonal transport in axons with a narrow diameter.

To date, it has been implicitly assumed that transport in axons is essentially the same as transport in the neuronal cell body. However, the previously unexplored effect of boundary conditions may make transport in these two areas quite different. In this paper, we propose that the long cylindrical geometry of the axon—with the close presence of the axonal membrane—leads to two classes of effects, both of which impair transport. These are 1), a wall effect (reflecting a “no-slip” boundary condition) in small-caliber axons and 2), an enhancement of macromolecular crowding.

The wall effect results from simple hydrodynamics: as a cargo moves along an MT in a small-caliber axon as shown in Fig. 1 A, it experiences a larger viscous drag than it would if it were moving in the cell body far from the cell walls. This is because of the no-slip or low-slip boundary condition of the cytosol at the axonal wall and also at the surface of the cargo, so that the closer the cargo is to the wall, the more shear there is, the larger the effective viscosity is, and the larger the opposition to motion. (The no-slip boundary condition refers to the fact that the fluid next to a surface cannot move or flow.) The second effect is an enhancement of the opposition to motion because of crowding, and conceptually results from an inability of large molecules to move out of the way of the cargo as it moves down the axon; as large molecules try to move away from the oncoming cargo, their motion is impeded by the presence of the nearby walls or boundaries. To illustrate these effects, we have used a simple model. We find that by walking along parallel MTs (see Fig. 1 A), multiple motors can be employed to dramatically improve transport by overcoming such opposition to motion.

Figure 1.

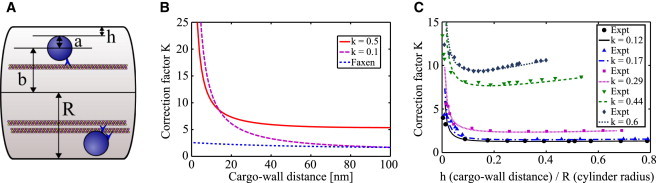
(A) Cargos being hauled by motors along MTs inside an axon. The spherical cargo has a radius a in a cylindrical axon of radius R. The center of the cargo is displaced a distance b from the axon’s axis. The distance h is the closest approach of the cargo to the axon wall. Two scenarios are shown. The top shows a single motor hauling a cargo along an MT. The key point of this paper is that the enhanced viscosity encountered by the cargo near the wall of the axon can be overcome by having multiple motors hauling the cargo along closely spaced parallel microtubules as shown at the bottom. (B) Correction factor K from Eq. 2 for a sphere of radius 250 nm for two axon diameters (k = 0.1 and k = 0.5) as a function of the cargo-wall distance h. As a comparison, we have also shown the correction factor obtained from the Faxén formula (blue dotted line) for the same parameters. Far away from the wall in a large axon (magenta dashed curve) our theory agrees well with Faxén’s law. Note that for a relatively large cargo (250 nm radius) in a relatively small axon (k = 0.5, corresponding to a 1 μm diameter axon, solid line), the “edge” effect, represented by the correction factor, extends over the width of the axon, even when the cargo is far away from the wall. (C) Comparison of the theoretical correction factor K given by Eq. 2 to experimental data (82) for a sphere moving through a fluid-filled cylinder for various values of k = a/R. To see this figure in color, go online.

Using a three-dimensional (3D) Monte Carlo simulation to model vesicular transport in an axon, we find that the single motor run length is significantly reduced because of the boundary or wall effect. This dramatic effect on axonal transport has not been considered before. We propose that axonal transport uses multiple motors moving along more than one MT to overcome this impediment (see bottom of Fig. 1 A). In particular, we suggest that the high density of MTs in small-caliber axons ensures that there will be a high probability of closely spaced parallel MTs that can promote multiple-motor-based transport along more than one MT, dramatically improving transport of cargos with multiple motors.

Our paper is organized as follows. We begin by showing that a sphere (cargo) moving through a fluid filled cylinder (axon) can experience significant drag if it is close to the wall of the cylinder. After describing our simulation procedure, we show that this viscous drag can reduce the run length of a cargo being hauled by a single motor along an MT in a cylinder, and describe how this effective viscosity in the fluid-filled cylinder can be further enhanced by macromolecules. We then show that a way to overcome this opposition to cargo transport is to use multiple motors to haul the cargo along two parallel MTs (see bottom of Fig. 1 A); if the MTs are close enough, because each motor’s “on” rate is effectively doubled, the presence of the second MT dramatically enhances the number of engaged motors. Thus, the high density of MTs found in small-caliber axons can help to compensate for the confinement effects of viscous drag on axonal transport. Interestingly, boundary effects should not impede cargo transport in large-caliber axons where there is a much lower MT density.

Heuristic approach: Wall correction increases as the cargo approaches the wall

Generally, the viscosity of axoplasm or cytosol depends on the length scale at which it is measured. For example, substances squeezed from nerves and assumed to be axoplasm were reported to have a viscosity 10⁶ times greater than that of water (7), though this can be attributable to the cross-linking and frictional interactions between neurofilaments and MTs in the axoplasm (8). On the other hand, electron spin resonance measurements of the microviscosity of mammalian nerve axoplasm found a value ∼ 5 times larger than the viscosity of water (9). This viscosity is not enough to seriously oppose motion, at least not in Drosophila embryos (10).

We considered the possibility that in the axon, the effective viscosity might be enhanced by the presence of the wall, attributable to both a direct effect of no-slip boundary conditions as well as the effect of the wall on the mobility of large macromolecules in the axoplasm. We first investigated the potential importance of a no-slip boundary condition. We considered a spherical cargo of radius a moving in a cylindrical axon of radius R (Fig. 1 A), with ${\eta }_{\infty }$ the viscosity of the axoplasm in an unbounded medium. The Stokes force experienced by the cargo moving with velocity v in the laboratory frame of reference can be expressed as (11) follows:

$$\mathit{F}=6\pi {\eta }_{\infty }a\mathit{v}K,$$ (1)

where K (>1) is the correction factor because of the wall effect. We assume a cargo velocity parallel to the axon axis; K depends on the position (relative to the axon wall) and radius of the cargo, as well as the axon diameter (2R).

The exact solution for K for a sphere moving on the axis of a cylinder filled with viscous fluid has been obtained numerically by solving a set of linear equations (11,12). Further, some special solutions can be found perturbatively when the sphere is near the axis of the cylinder (13–15). However, there is no general solution that applies over the entire range of positions and sizes of the sphere. Here, by exploiting the approximate behavior of the solutions near the axis and near the wall, we can write an approximate overall solution as a superposition of these solutions (Eq. 2), which is valid over a suitable range of the parameters (see the Supporting Material):

$$K=\exp \left(\mathrm{-}k\epsilon \right)K_0+k^2{\epsilon }^{2}f\left(\epsilon \right)\left(R/h\right)$$ (2)

This approximate solution is written in terms of the eccentricity parameter $\epsilon =b/R$ and the dimensionless radius of the sphere $k=a/R$, where b is the distance of the center of the sphere from the axis of the cylinder and R is the radius of the cylinder. Here, $K_0$ is the wall correction factor for rigid spheres moving in a still liquid along the axis of a cylindrical tube (b = 0) (11), and f(ε) is the Brenner eccentricity function (11). We give the approximations that we used for $K_0$ and f(ε) in the Supporting Material. H is the distance between the surface of the cargo and the inner surface of the axon. Eq. 2 recovers the previously obtained results for both limiting cases $\epsilon \to 0$ and $h\to 0$.

In Fig. 1, we show the correction factor K as a function of the sphere-cylinder surface to surface distance h. Two general features of our results are of interest. First, relatively close to the wall, the boundary effect is very large, and second, for cargos that are relatively large with respect to the caliber of the axon (i.e., roughly filling it by half), the “wall” effect is evident even quite far away from the wall. For example, if we think of ${\eta }_{eff}=K{\eta }_{\infty }$ as an effective viscosity, then ${\eta }_{eff}$ can be 50 times that of water for K = 5 and ${\eta }_{\infty }=10$ times that of water (9).

Methods

Modeling and numerical simulation

We used a previously developed 3D Monte Carlo model (16) to study the transport of cargos hauled by kinesin motor(s). Kinesin molecules were bound to a spherical cargo, and the “heads” of the motors were free to search for binding domains of the MT that were within reach. Once the head could reach the MT, we assigned a probability of the motor binding to the MT, based on an on-rate of 2 s⁻¹. We ignored head-head dynamics of a motor, and as others have done, simply modeled kinesin as a single head that hopped from one binding site to the next with step size of d = 8 nm, moving toward the plus end of the MT. Since modeling single-motor kinesin stepping followed previously published work, simulation details are left to the Supporting Material. However, we note that in addition to the forces acting on the cargo because of the molecular motors and viscous drag, it also underwent Brownian motion.

Cargo dynamics

In a viscous medium, a cargo hauled along an MT exhibits translational as well as rotational Brownian motion. Throughout our simulations, the motor-cargo system satisfied the following boundary conditions: 1) the motor(s) could not go into the cargo or the MT; 2) the cargo could not go into the MT; 3) the cargo had to be inside of the axon. Unless explicitly stated, the cargo radius was a = 250 nm whereas the MT radius was r = 12.5 nm. The coefficient of viscosity of the axoplasm was assumed to be 10 times that of water (9). All the physical properties were averaged over 1000 realizations. To avoid possible divergences in the numerical simulations, we introduced a 1 nm artificial clearance between the cargo-wall surfaces.

Modeling macromolecules in the axoplasm

To investigate theoretically how large macromolecules could hinder cargo transport through the cytoplasm and axoplasm, we included polymers in our simulations of a cargo moving in a fluid-filled axon. The study of the detailed molecular structure and dynamics of long chain molecules using a microscopic model such as a “molecular dynamics” approach is computationally challenging. To simplify this, we modeled each polymer as a chain of beads, coupled through massless springs. Each bead performed constrained diffusive motion and interacted with the cargo and with the beads of nearby chains. We assumed that the interactions could be approximated by a Lennard-Jones (LJ) type potential to take into account both the long-range attractive and short-range repulsive forces. The details of the model and calculations are given in the Supporting Material.

To quantify the effect of macromolecule-cargo interactions, we considered a spherical cargo being dragged through a cylindrical tube by an external force F through a fluid with polymers (see Fig. S3 A in the Supporting Material), i.e., the cargo was not being hauled by molecular motors. We calculated the (size-dependent) effective viscosity to which the cargo was subjected as follows:

$${\eta }_{eff}=\frac{F}{6\pi av}=K{\eta }_{\infty },$$ (3)

where F was the external driving force and v was the average velocity of the cargo. We solved the Langevin equation for the motion of a cargo driven by the external force (see Fig. S3 A). We randomly distributed the polymers in a tube of a given diameter and initially placed the cargo on the axis. The cargo interacted with each bead of the polymer as well as experienced the drag force because of proximity to the wall of the tube. The polymer-polymer interactions were also incorporated through bead-bead interactions. In this way, we measured the approximate time for a given fixed-travel distance along the axis and calculated the average velocity of the cargo.

Results

Wall effect on transport by a single motor

We first explored how the wall would modify axonal transport of a cargo hauled by a single kinesin motor. We modeled the axon as a long cylinder of uniform diameter with an MT centered along the axis of the axon. (In practice, electron micrograph images (17) show a wide variation both in the caliber size and longitudinal undulation.) We investigated the magnitude of the wall effect on cargo motion via our simulations (Fig. S2), and consistent with the analytic results in Fig. 1, found that the run length decreased as the diameter of the axon decreased. For a D = 1200 nm axon with ${\eta }_{\infty }=10$ times that of water, and with the 500 nm diameter cargo, the average load on the motor during the simulation was ∼ 0.84 pN; the effect of such a load in our simulations in the presence of Brownian motion was consistent with past experimental results (18) and previous force-processivity data (18). Thus, for some parameter values, the effect of the increased drag because of the wall effect can be enough to decrease by ∼ 50% the expected mean travel distance of a cargo that is hauled by a single motor. Such an effect would likely not be insignificant from a physiological point of view, since recent work (19) suggests that a roughly 25% decrease in motor processivity is enough to have significant consequences. Note that the parameters for the large cargo/small axon case considered are not unreasonable, since mitochondria are frequently on the order of 200 nm in diameter (20), and there are numerous axons on the order of 1 μm in diameter.

Potential effect of crowding

The biological medium differs from an idealized Newtonian fluid, in part because of large molecules or parts of large molecules that can impede cargo motion because of steric hindrance. For example, electron micrographs of MTs with MT-associated proteins (MAPs) bound to them have projections extending ∼ 100 nm away from the surface of the MT (21,22). Neurofilaments are oriented axially, parallel to the MTs. Quick-freeze deep-etch micrographs of frog axons reveal that the C termini of neurofilaments medium and heavy have long side arms that project 20 to 50 nm laterally outward from the filament core (22–24). There is also a family of very large cytoskeletal linking proteins called plectins that have globular multiinteractive end domains separated by an α-helical sequence dimerized with another molecule to form a 190 nm-long coiled coil rod domain (25). The major isoform found in neural cells is plectin 1c (26). It is not known if there are free-floating large molecules in the axon, partly because to extract the cytoskeleton to perform the quick-freeze deep etch, which is the gold standard for determining axoplasm structure, anything that is not anchored to the cytoskeleton is washed away. If there are such large molecules in the axoplasm, their movement could be restricted because of the confined geometry, resulting in a significant enhancement of their opposition to the cargos’ motion. MAPs, C termini of neurofilaments medium and heavy, plectin 1C, and other large molecules could result in increased average viscous drag, reducing the cargo’s run length.

To investigate theoretically how large molecules could hinder cargo transport through such effects, we simulated a spherical cargo moving through a cylindrical axon with a polymer-filled fluid under the influence of an external force as described in the Methods section. The results are shown in Fig. S3. We found that the higher the polymer concentration, the larger the viscosity was. In Fig. S3, we separated the wall effect from the viscous effect of the polymers alone on the cargo mobility (quantified in terms of effective viscosity) for different polymer concentrations. (We can turn off the wall effect by setting the viscosity correction factor K = 1 in Eq. 2.) As Fig. S3 B shows, without the wall effect, there was a significant enhancement of the “base” viscosity of the medium as the concentration of the polymer increased. This enhancement came from the excluded volume effect. When the wall effect was included (see Fig. S3 C), the effective viscosity remained fairly constant for a given volume exclusion (polymer concentration) in large-diameter axons. However, the wall effect became important and was the dominant factor inhibiting cargo mobility as the caliber size decreased, and the presence of the polymers increased the wall effect. The length scales for which the wall effect became important are discussed next.

Onset of the wall effect when the cargo radius and cargo-wall distance are comparable

Noting that the presence of long molecules dramatically enhanced the opposition to the motion for even a relatively small cargo in a small-caliber axon, we wanted to better understand how the onset of huge resistance depended on the different length scales of the system. So we varied the radius of the cargo (a), the diameter of the axon caliber (D), and the length of the polymers (L), and the distance of the surface of the cargo to the inner wall of the axon (h). The details of the simulation are given in the Supporting Material. Our results are shown in Fig. 2 where we see that, irrespective of the axon or cargo size, the effective viscosity dramatically increased when $h/a\le 1$ for all axon and cargo dimensions. Physically, small h meant that the cargo was close to the wall, and large a meant that there was a large amount of cargo surface area to enhance the viscous drag produced by proximity to the wall of the axon. Thus the wall effect became insignificant if the cargo-axon geometry satisfied the condition h/a ≫ 1.

Figure 2.

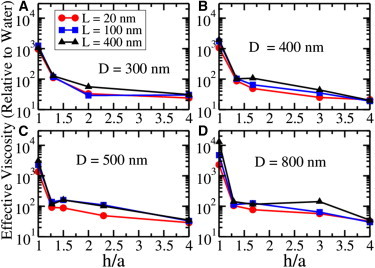
Effective viscosity of the medium in the presence of the macromolecules of length L as a function of the ratio of the cargo-cylinder surface-to-surface distance h to the radius a of the cargo. (A) Axon diameter D = 300 nm; (B) D = 400 nm; (C) D = 500 nm; and (D) D = 800 nm. Irrespective of the caliber D, there is dramatic increase in the effective viscosity when this ratio h/a is of the order of or less than one. Polymer concentration is fixed at 4.17% excluded volume. For L = 20, 100, and 400 nm, this excluded volume corresponds to concentrations of 16.5, 3.31, and 0.827 μM, respectively. To see this figure in color, go online.

For a moderate size axon (D ∼ 1 μm) and for small cargos (a ∼ 50 nm), the enhancement of viscosity merely came from the steric hindrances because of the cargo-polymer interactions, and the wall effect, in most of these circumstances, could be comfortably ignored. On the other hand, cargos can be relatively large membranous organelles such as mitochondria and lysosomes (a ∼ 0.5 μm). The wall effect and confinement becomes more relevant for such big cargos especially when $h/a\to 1$.

These studies, then, suggest that the presence of the axon membrane can in some circumstances contribute to significant opposition to cargo motion, especially for large cargos; the exact amount of resistance will depend on the size of the cargo relative to the axon diameter, on the cargo position relative to the axon wall, and also on the extent of large macromolecules/polymers locally present. We note that these effects likely vary spatially and temporally; e.g., even in a relatively large axon, when two large cargos pass each other, they may push each other against the side walls, temporarily decreasing h and satisfying the condition $h/a<1$ (see also Discussion). Such effects are potentially problematic because axons rely on long-distance transport, and its impairment would seriously compromise axonal health. Since groups of molecular motors can exert more force, and provide a more robust transport system under load, one axonal strategy to move given cargos further and more robustly might be to maximize the number of engaged motors. We therefore examined whether there were any structural features that might promote such increased motor engagement.

Transport along multiple microtubules enhances overall motor on-rates

Studies from multiple groups (27,28) indicate that the more molecular motors that move a cargo, the further the cargo is expected to move and the greater the force that moves it. In vivo, multiple motors typically move a cargo (19,29,30). Although multiple factors can affect exactly how many motors are engaged at any instant, one strong contributor is the motors’ on-rates, that is, how long it typically takes them to bind to the MT. The higher the average on-rate is, the more available motors there are that are engaged in hauling the cargo at any given instant (18,31).

Suppose that a single motor has an on-rate of $k_{attach}^{single}$, with a probability of binding in a time interval Δt equal to $k_{attach}^{single}\text{Δ}t$. If there are N total motors, with those bound to the MT denoted by $N_{bound}$, then the number of free motors is $N_{free}=N-N_{bound}$. In principle, the rate at which motors on a cargo can bind to an MT, i.e., the number of motors that bind per second, is determined by the state of the cargo, i.e., not only the number of free motors, but also the number of motors already bound to the MTs that could interfere with each other. However, for the simplest case (assumed here) all the motors were clustered at a point, and the motors did not directly interact with each other, so that the effective on-rate (number of motors that bind per second) was simply proportional to the number of free motors. Thus, when $N_{free}=1$, the on-rate is $k_{attach}^{single}$ but if $N_{free}=3$, for instance, the effective on-rate for any additional motor to bind is $3k_{attach}^{single}$, that is, three times as large. Now, in principle, if a second MT was parallel—and sufficiently close—to the first, any free motor could bind either to the first or the second MT, so that potentially, each motor had effectively twice as many chances to bind, that is, each motor’s on-rate is doubled.

Intriguingly, the magnitude of the hypothetical effect of having two parallel MTs increases with the number of motors present: if we imagine $N_{free}=1$, then when a single MT is present, the on-rate would be $k_{attach}^{single}$, but when two MTs are present, we might expect that the effective on-rate to be $2k_{attach}^{single}$. However, if $N_{free}=4$, then the on-rate goes from $4k_{attach}^{single}$ for a single MT to $8k_{attach}^{single}$ for two MTs. In other words, for the one-motor case, to double the on-rate, one can either add a second motor, or add a second MT; however to achieve an on-rate 8 times that of a single motor, one can either start from the $N_{free}=4$, and add an additional four motors, or simply add a second MT. This sort of argument suggests that clustering a few MTs close together might be a very efficient way to improve motor utilization, especially for cargos that potentially have more than two active motors. Note also that in any scenario where motors interfere with other motors binding (i.e., motors already bound decrease the on-rate of other free motors; this is not considered explicitly below), the presence of the second MT will be even more beneficial, because for the case where some motors are bound to one MT, but none to the second, all of the “free” motors will have higher on-rates for the second MT.

Theoretical modeling confirms that multiple close microtubules likely improve transport

To test this hypothesis that the clustering of parallel MTs might improve transport in the multiple motor case, we investigated the motility of a cargo driven by kinesin molecules clustered at a single attachment point on the cargo surface. We decided to cluster the kinesin motors on the cargo surface for two reasons. First, there is weak experimental evidence for kinesin clustering (32). Second, previous simulations (16) find that if motors are randomly placed on large cargos, achieving a reasonable number of engaged motors (i.e., three to six) would require a large number of motors (50 to 100) to be present on the cargo, which appears inconsistent with biochemical characterizations of cargo-bound MT motors (33). Note that recent studies show that in vivo cargos are frequently moved by more than one MT-based motor (10,29,33,34). Our simulated 3D model (16) took into account the Brownian motion of the cargo as well as the positions of the motors and MTs. We considered transport when the cargo was close to either one or two MTs, and incorporated the wall effect by renormalizing the effective viscosity of the medium. A diagram of the simulated geometry for multiple MT transport in an axon is depicted in Fig. S1. We fixed the position of the MTs symmetrically about the center of the axon, parallel to the axis of the axon, and let one of the motors bind to either of the two MTs randomly. The binding process, the position of the cargo and the diameter of the axon all satisfied the boundary conditions that were described above for a single MT. Initially, one motor was allowed to bind the MT and the rest were free. The algorithmic details of the motor processivity and switching between the MTs are described in the Supporting Material.

In Fig. 3, we show the run lengths, i.e., travel distances, of a cargo with N = 2 to 5 kinesin motors, moving along two parallel MTs, separated by MT center-to-center distances of d = 50, 75, and 275 nm as a function of viscosity. For simplicity, as discussed above, we assumed that the effect of axonal wall and/or the cargo-protein interactions was to modify the effective viscosity of the axoplasm. The MT separation of d = 275 nm approximately corresponded to the case of single MT transport since two kinesin motors, each 110 nm long and attached at a single point on the cargo, cannot reach two MTs simultaneously. In contrast, the motors could easily reach both MTs for the case of d = 75 nm. As we show in the next section, finding two MTs within 75 nm of each other is highly likely in small-caliber axons where the MT density is 150 MTs/μm² (3–6). It is evident that the second MT significantly enhanced the mean travel distance of the cargo, and the larger the number of motors, the stronger the enhancement.

Figure 3.

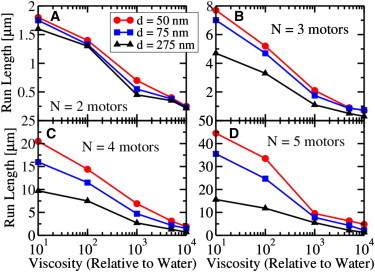
Cargo run length (i.e., cargo travel distance) along two parallel microtubules as a function of viscosity for a cargo (radius a = 100 nm) driven by a maximum of (A) N = 2 motors, (B) N = 3 motors, (C) N = 4 motors, and (D) N = 5 motors. For each number of (maximally engaged) motors, we investigated different microtubule-microtubule spacings d. The two microtubules were separated by center-to-center distances of d = 50 nm (upper curve); d = 75 nm (middle curve); and d = 275 nm (lower curve). To see this figure in color, go online.

The extreme values of the viscosity considered in some parts of the curves in Fig. 3 (>1000 × that of water), in general likely do not reflect what occurs in typical axoplasm. However, we demonstrated in an earlier section that under certain conditions (e.g., for the special class of cargo-axon geometry, $h/a\le 1$), the resistance to motion could be tremendously large. In such cases, clustering the MTs within a high load region of the axon might be a potential mechanism to overcome resistance to transport.

How close do the parallel MTs need to be to each other to effectively contribute to transport? Since a factor of 10 enhancement (because of wall effects and large molecules) over the base axonal viscosity (10 times that of water (9)) seemed reasonable from our above studies, we used this, and compared the run lengths, i.e., travel distances, of a cargo hauled by different numbers of motors, as a function of spacing between the MTs. As Fig. 4 shows, the enhancement of run length by decreasing MT separation for a small number of motors (N = 2) was not dramatic, even when the spacing between the MTs was very small. However, for a larger number of motors, the second MT had a considerable impact. For example, when five motors were present, there was almost a threefold enhancement of the run length as compared with the single MT value if the MT separation was ∼ 50 nm. The enhancement of the run length was significantly higher when the separation between the MTs was ∼ 100 nm or less.

Figure 4.

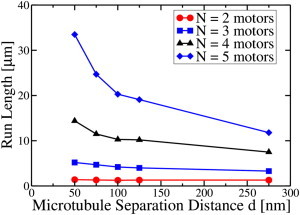
Cargo run length (i.e., cargo travel distance) as a function of the microtubule center-to-center separation for different numbers of motors. There are two microtubules. N is the number of motors on the cargo. Here the cargo radius is a = 100 nm, and the viscosity is 100 times that of water. In the simulations, a single motor binds to one of the microtubules and the system then evolves. The additional (free) motors can bind to either microtubule, governed by the prescribed binding rules implemented in the simulation (see the Supporting Material). To see this figure in color, go online.

High microtubule density in small-caliber axons ensures closely spaced MTs that can be used in cargo transport to overcome the wall effect

To overcome the enhanced viscosity because of the wall effect in small-caliber axons, our simulation results suggested that nearest-neighbor MTs should be spaced within ∼ 100 nm of each other so that both can effectively contribute to transport of a given cargo. (In large-caliber axons, the cargos are not subjected to the wall effect because they are sufficiently far away from the axonal wall.) If an axon has MTs randomly placed according to a Poisson distribution, how high does the MT density need to be to have a high probability of finding a pair of MTs within a certain distance? The answer is shown in Fig. 5 where we see that to have at least an 80% chance of having a pair of MTs with a separation of 75 nm, the axon needs to have an MT density of ∼ 100 MTs/μm². Thus the observation of 150 MTs/μm² of cross-sectional area of axoplasm for small unmyelinated axons (3–6) means that small-caliber axons will have a high chance of having MTs with a spacing of less than 100 μm. Note that in axoplasm of large unmyelinated axons of ∼ 10 μm in diameter, the MT density is less than 15 MTs/μm² (6), which implies that large-caliber axons with randomly placed MTs will have a rather low change of having MTs within 100 nm of each other and thus, cargo transport will tend to occur along single MTs. This is fine since the cargos in such large-caliber axons will not encounter the wall effect.

Figure 5.

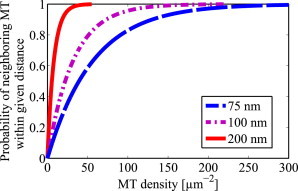
Probability of an MT having a neighbor within a given distance d versus MT density, where d = 75, 100, and 200 nm. Note that to have at least an 80% chance of having a pair of MTs with a separation of 75 nm (blue dashed line), the axon needs to have an MT density of ∼ 100 MTs/μm². To see this figure in color, go online.

Discussion

Axonal transport and its failure are of substantial interest with regard to neurodegeneration and neuropathy. In this study, we suggest that in small-caliber axons, the effect of the wall can be significant. Importantly, the effect is highly nonlinear, depending on the distance between the cargo to the wall, as well as on the size of the cargo; when h/a ∼ 1, the wall effect can dramatically increase opposition to motion.

We modeled the axonal membrane as a rigid wall even though one might expect it to be somewhat flexible and elastic, especially in unmyelinated axons. (Myelinated axonal membranes are more rigid because they are reinforced by the myelin sheath.) However, we believe that our approximation is reasonable for two reasons. First, Shlomovitz et al. have done microrheological measurements of the viscosity of in vitro phospholipid monolayers in which micron sized beads submerged a fixed distance beneath the monolayer are shaken parallel to the monolayer in an optical trap (35). The viscous drag experienced by the beads can be used to infer the viscosity or rigidity of the monolayer membrane. For membrane viscosities less than 10⁻⁹ N·s/m with the bead at a depth corresponding to barely touching the monolayer, the hydrodynamic forces on the bead produced by the monolayer are like that of a free fluid. For membrane viscosities greater than ∼ 4 × 10⁻⁷ N·s/m at a depth corresponding to barely touching the membrane, they find that the hydrodynamic forces produced by the membrane on the bead are like that of a rigid wall and show no evidence of membrane deformation. The rigid-wall membrane viscosity of 4 × 10⁻⁷ N·s/m is comparable with that of cellular membranes. For example, for erythrocytes the measured values of the membrane viscosity vary; it has been measured to be 3.4 × 10⁻⁷ N·s/m when high frequency electric fields induced transient deformation (36), and to be 3 × 10⁻⁶ N·s/m when a membrane tether was extruded (37). In another example, the membrane viscosity of a neuronal growth cone has been measured to be 2 × 10⁻⁷ N·s/m from studies where membrane tethers that were sliding over the cortical cytoskeleton were extruded (38). Even though 2 × 10⁻⁷ N·s/m is less than 4 × 10⁻⁷ N·s/m, Shlomovitz et al. still found significantly enhanced hydrodynamic drag at this value because of the presence of the membrane and no evidence of membrane deformation.

Second, cortical cytoskeletal filaments underlie the axonal membrane, increasing its effective stiffness. Importantly, very recent work by Xu et al. (39) found that actin forms ringlike structures that wrap around the circumference of axons and are evenly spaced along axonal shafts with a periodicity of ∼ 180 to 190 nm. The cytoskeletal protein spectrin also exhibited periodic structures alternating with those of the actin rings, and the distance between adjacent actin rings was comparable with the length of a spectrin tetramer (39). Thus, for a cargo to deform the membrane, it must also deform the underlying actin-spectrin-based cytoskeleton. Thus we believe that our approximation of the axonal membrane as a rigid wall is reasonable. Such a wall would provide opposition to cargos moving in close proximity to the wall. The point of this paper is to point this out, and to encourage experiments to test this hypothesis.

One would expect viscous drag to slow intracellular transport velocity with increasing vesicle size. This has been seen in axonal transport in the giant squid axon (0.5 mm diameter) where small vesicles, that typically had apparent diameters of 0.1 to 0.2 μm, had faster mean velocities (2.5 μm/s) than medium-sized (0.2 to 0.6 μm) and large (greater than 0.6 μm) vesicles (40). Another published example of size-dependent opposition to motion involves LIS1, which is a protein that enables dynein to produce sustained force generation (41). Inhibition of LIS1 arrested the motion of large lysosomes/late endosomes in axonal transport but had little effect on the transport of small vesicles (19). Importantly, these effects were not observed in nonneuronal cells (19), which is consistent with LIS1 playing a role in transport under high resistance conditions. However, viscous drag is not the only factor that can affect axonal transport, as implied by the broad distribution of velocities of similar-sized cargos, as well as the observation that anterograde motion tended to be more rapid than retrograde motion (40).

We suggested above that closely spaced pairs of MTs that result from high densities of randomly placed MTs in small-caliber axons can allow cargos to engage simultaneously motors on more than one MT. In an axon either the MTs are clustered or they are not. It may be that they are clustered in some axons as has been reported (23,42,43), and are not clustered in others as in the examples shown in the Supporting Material. If they are clustered, then there will be MTs within 100 nm of other MTs, by the definition of clustering. If they are not clustered but the MT density is high enough, then there is a very high probability that there will be at least two MTs within 100 nm of each other. Either way, clustered or not, there will be closely spaced MTs if the MT density is high enough in an axon. As we point out above, the MT density (3–6) is indeed high enough in small-caliber axons but not in large-caliber axons where our theory suggests that the wall effect does not hinder transport because the transported vesicles tend to be far from the axonal wall.

With regard to the mechanism that leads to a high density of MTs in small-diameter axons and a low MT density in large-caliber axons, we can say the following. Both neurofilaments (NFs) and MTs are found oriented along the length of axons, and the total number of neurofilaments and MTs together seems to be proportional to the diameter of the axon (43). Large-caliber axons are dominated by neurofilaments with roughly 5 to 10 times more NFs than MTs (44). As axons become smaller in diameter, this ratio decreases as the neurofilaments become fewer and less prominent, until in thin unmyelinated axons, neurofilaments are rare, leaving only a high density of MTs (6,43). Axon diameter decreases as axons branch. One can also follow the radial growth of axons after birth. After birth, peripheral nerves are small and unmyelinated (45). In mice, myelination is completed around postnatal day 21 (46). An axon that is fated to be 12 μm in diameter is ∼ 1 μm at birth (47). Radial growth will begin once myelination is complete (48). During this time of growth from 1 μm to 12 μm, neurofilaments will become the predominant cytoskeletal proteins, leading to a dilution of the MT density and the observed low density of MTs in large-caliber axons (43,44).

MTs that are close together can be used to improve motor function, by increasing each motor’s “on” rate, and thus, on average, increasing the average number of engaged motors at any instant. Several groups have suggested that the velocity of a cargo is determined by the number of motors hauling it for a given viscous drag (49–52). For a single motor, force-velocity curves show that the velocity decreases with increasing load on the motor (53–55), though in vitro measurements (55) indicate that the load on the motor needs to exceed ∼ 2 pN before there is a noticeable reduction of the velocity. Klump and Lipowsky (49) have suggested that the load resulting from high cytoplasmic viscosity could decrease the travel distance and velocity of cargos, and that the velocity of such cargos depends on the number of motors and the external load on the cargo. The observation that a given cargo can change its velocity during the course of its travel and that intracellular cargos of a given type have a distribution of velocities has led to the suggestion that velocity increases with the number of motors on a cargo to overcome the cytoplasmic viscous drag (50–52). However, Shubeita et al. (10) showed that reducing the number of engaged motors on lipid droplets in a Drosophila embryo changes neither the run lengths nor the velocities, implying that cytosolic drag in nonneuronal cells does not significantly limit transport. They found average plus-end transport velocities for lipid droplets were ∼ 550 nm/s, and average minus end velocities were ∼ 730 nm/s. This is comparable with average velocities in Chinese hamster ovary (CHO) cells of ∼ 1 μm/s in both plus and minus end directions for vesicles ranging in diameter from 30 to 300 nm (56). Average fast axonal transport speeds of mitochondria range from 1.4 μm/s (retrograde) and 1 μm/s (anterograde) in mice (57) to 0.4 μm/s in both directions in dorsal root ganglion cells (58). Thus a variety of cargo types and sizes are transported at roughly the same average speed, implying that cytosolic drag is not a limiting factor in intracellular transport.

However, in small-caliber axons, we hypothesize that the viscosity near the membrane is significantly increased, to the extent that it can hinder transport. We hypothesize that fast axonal transport rates are not lower in axons with small calibers because these axons have a higher density of MTs. Experimental studies involving radioactively labeled proteins have found that the rate of fast axonal transport in motor and sensory sciatic mammalian nerves of the cat, monkey, dog, rabbit, goat, and rat is ∼ 400 mm/day (59). These nerves consist of bundles of myelinated axons. Cross-sections of sciatic nerves from cats taken at the wave front, or forward part of the crest of the wave, show radioactively labeled proteins in axons ranging in diameter from 3 to 23 μm (59). This suggests that the rate of fast axoplasmic transport is independent of the axon caliber over this range of diameters. Furthermore, it has been observed that the average number of mitochondria moving within mouse axons is independent of the axonal cross-sectional area for areas ranging from ∼ 5 to 70 μm² (57), implying that on average, medium-caliber axons had many more mitochondria passing through a given volume of axoplasm than large-caliber axons. To test our assertion that fast axonal transport rates in small-caliber axons are comparable with those in large-caliber axons, there is a need for measurements of the speed of fast axonal transport in small axons with diameters of 1 μm or less. A further experimental test would be to knockdown the density of MTs in small-caliber axons to see if the cargo velocities decrease because of the enhanced viscous drag of the membrane.

With these effects in mind, our study then suggests a number of related routes to the impairment of transport. First, impairing motor function, e.g., mutating the kinesin heavy chain (Khc) (60) or LIS1 inhibition (19) as we mentioned earlier, can obviously affect transport. Second, any perturbation that alters the paired MT structure would be expected to have significant consequences, because of decreased per-cargo motor utilization. Such a perturbation could arise from a decrease in overall MT density (e.g., because of tau impairment) or directly because of a change in the pair-spacing distance (likely controlled by MT-associated proteins). Third, a number of different classes of perturbations could contribute to alteration of the h/a ratio. Changes in the effective size of individual cargos (swollen lysosomes, various cargos that aberrantly stick together and form “clumps,” etc.) could all increase the cargo radius a.

Similarly, any local constriction of the axon could result in decreasing the effective h. The diameter of myelinated feline axons decreases by 50% to 70% for a segment length of ∼ 10 μm at the nodes of Ranvier (61,62). Berthold et al. observed that axoplasmic organelles accumulate in the paranode-node-paranode regions in large-caliber (diameter ∼ 10 μm) myelinated axons of adult cats (63). At nodes of Ranvier in mouse axons, transported mitochondria often slow down and sometimes stall, especially those moving in the retrograde direction (57). When a mitochondrion is crossing a node, the average anterograde velocity is 0.7 μm/s compared with 1 μm/s without the node, and the average retrograde velocity is 0.6 μm/s compared with 1.4 μm/s in the absence of the node (57). Similar slowing of fast axonal transport in the vicinity of the node was observed for mitochondria being transported in small myelinated rat central nervous system axons where the average velocity in the internodal region was 0.47 μm/s in the anterograde direction compared with 0.27 μm/s in the nodal region, and 0.52 μm/s in the retrograde direction in the internodal region compared with 0.29 μm/s in the nodal region (64). Interestingly, in myelinated cat ventral root axons ranging in diameter from ∼ 1 to 12 μm, the MT density is ∼ 4 times higher in the nodal regions than in the intermodal regions, whereas the neurofilament density is essentially the same in these regions (65). This is consistent with our assertion that a higher density of MTs is needed for axonal transport, to allow the engagement of additional motors to overcome the increased viscosity near the axonal membrane.

Further, any stalled cargos also result in other (passing) cargos being “pushed” into the wall, again decreasing h. The result is organelle traffic jams. Mutations in the Drosophila kinesin heavy chain (Khc) disrupt anterograde fast axonal transport and leads to the stalling of organelles that depend on kinesin. This in turn probably disrupts retrograde transport, resulting in organelle traffic jams consisting of vesicles, synaptic membrane proteins, mitochondria and prelysosomal organelles that cause a dramatic swelling of axons (60). Similar traffic jams in axons have resulted from mutations of the Drosophila kinesin light chain (Klc) (66).

This leads us to ask whether there is evidence of such transport impairment in neuropathy and neurodegeneration found in disease processes (67–69). Our work implies that the increased viscous drag produced by the wall effect could be a factor in neurodegenerative diseases afflicting small fibers such as diabetes mellitus, Fabry’s disease, and chemotherapy-induced peripheral neuropathy (70). For example, it is known that the amount of material conveyed via fast axonal transport is reduced by ∼ 20% in the peripheral nerves of diabetic rats (71–73). In addition there is a 20% reduction in the cross-sectional area of axons in the peripheral nerves of diabetic rats (74,75), though the MT density of 25 to 28 MTs/μm² did not change in 3 μm diameter axons from sural nerves when compared with wild type rats (75). It is possible that the reduction in axonal caliber increased the influence of the wall effect and contributed to the reduction in fast axonal transport. It is also possible that the impairment of transport contributed to the decrease in axonal caliber.

The purpose of this paper has been to point out that there can be significant viscous drag on cargos moving close to the axonal wall, which effectively acts as a rigid wall. We have used a simple model of axonal transport to illustrate this, and some ways in which the model of axonal transport could be enhanced are described in the Supporting Material. This work thus provides a useful conceptual framework for viscous boundary effects but the extent to which such scenarios contribute to disease progression in the animal remains to be explored experimentally.