Robust estimation of pulse wave transit time using group delay

Abstract

Purpose

To evaluate the efficiency of a novel transit time (Δt) estimation method from cardiovascular magnetic resonance flow curves.

Materials and Methods

Flow curves were estimated from phase contrast images of 30 patients. Our method (TT-GD: transit time group delay) operates in the frequency domain and models the ascending aortic waveform as an input passing through a discrete-component “filter”, producing the observed descending aortic waveform. The GD of the filter represents the average time delay (Δt) across individual frequency bands of the input. This method was compared with two previously described time-domain methods: TT-point using the half-maximum of the curves and TT-wave using cross-correlation. High temporal resolution flow images were studied at multiple downsampling rates to study the impact of differences in temporal resolution.

Results

Mean Δts obtained with the three methods were comparable. The TT-GD method was the most robust to reduced temporal resolution. While the TT-GD and the TT-wave produced comparable results for velocity and flow waveforms, the TT-point resulted in significant shorter Δts when calculated from velocity waveforms (difference: 1.8 ± 2.7 ms; coefficient of variability: 8.7%). The TT-GD method was the most reproducible, with an intra-observer variability of 3.4% and an inter-observer variability of 3.7%.

Conclusion

Compared to the traditional TT-point and TT-wave methods, the TT-GD approach was more robust to the choice of temporal resolution, waveform type, and observer.

INTRODUCTION

Reduced arterial compliance (increased arterial stiffness) is one of the earliest detectable manifestations of adverse structural and functional changes within the vessel wall. The aorta accounts for most of global arterial compliance, contributing to 60–70% of its total value (1). Aortic stiffness is recognized as a major risk factor in coronary heart disease (2, 3) and is an independent predictor of cardiovascular mortality (4).

Aortic pulse wave velocity (PWV) is considered as the “gold standard” measurement of arterial stiffness, given its simplicity, accuracy, reproducibility, and strong prediction of adverse outcomes (5). PWV is a regional functional measurement of arterial stiffness, representing the speed of propagation of the pressure or the velocity waves along the artery. It is inversely related to vascular compliance: a stiffer vessel will conduct the pulse wave faster than a more distensible and compliant vessel.

The PWV is commonly calculated as the ratio between the distance separating two locations along the artery and the transit time (Δt) needed for the pressure or velocity wave to cover this distance. It is increasingly assessed by means of cardiovascular magnetic resonance (CMR) (6 - 9), given that steady-state free-precession (SSFP) cine acquisitions enable a precise measurement of the length of the aortic arch. Moreover, phase-contrast (PC) cine acquisitions allow the assessment of the blood flow velocities throughout different aortic sections during the cardiac cycle and consequently the estimation of flow or velocity waveforms. These waveforms are then used to estimate the transit time through a number of different algorithms, (6, 10 - 17) but there is no standardization.

The primary goal of this study was to describe a novel method for Δt estimation, based on the principle of group delay (GD) (18). The secondary goal was to compare this method with two previously described methods based on the commonly used point-to-point and wave-to-wave approaches. The comparisons among methods were performed in terms of dependence on the curves taken into account (velocity curves instead of flow), dependence on the temporal resolution and reproducibility.

MATERIALS AND METHODS

Study population

Our study population represents a sample of patients scanned for iron overload syndromes. In 2004 we began routinely measuring cardiac output at the sinotubular junction of the aorta using phase contrast (PC) cardiac magnetic resonance. Our routine clinical protocol reconstructs 20-30 frames per cardiac cycle. However, in a subset of patients, 100 temporal samples (phases) were reconstructed using one phase view per segment to determine if higher temporal resolution influenced cardiac output calculations. We retrospectively identified these exams for the present comparison; if more than one exam was present for the same patient, we chose the first one. We obtained a final cohort of 30 patients (25 with thalassemia major and 5 with sickle cell disease). Fifteen patients were females and mean age was 25.2 ± 9.8 years.

The protocol for was approved by the Committee for the Protection of Human Subjects. All patients gave written informed consent.

Image acquisition and analysis

All CMR examinations were performed on a 1.5 T scanner (GE Signa CVi running system 9.1; GE Healthcare, Waukesha, WI) using a phased array torso coil. The PC data were acquired continuously using a retrospectively ECG-gated breathhold gradient echo sequence with a velocity encoding gradient in the through-plane direction, which provided phase-related pairs of modulus and velocity-encoded images. The PC slice was set perpendicular to the axis of the aorta at sinotubular junction, simultaneously profiling the ascending and descending aorta in cross-section. The scan parameters were as follows: repetition time = 7.9 ms (range: 7.8–8.0 ms), echo time = 3.1 ms (range: 3.0–3.1 ms), flip angle = 20°, matrix acquisition = 256 × 256, field of view 320 × 320 mm, pixel bandwidth was 244 Hz/pixel, slice thickness = 8 mm, encoding velocity = 250 cm/s, and ECG trigger delay of the first phase = 10 ms. One view was collected per segment, creating a fundamental sampling frequency of the velocity waveform equal to twice the TR. The patient was instructed to breath shallowly through the three to four minutes long acquisition.

Images were transferred to a SUN Ultra Sparc I workstation (Sun Microsystems, Mountain View, California) and analyzed with the FLOW image analysis software (Medis, Leiden, the Netherlands). To extract ascending and descending aorta flow and mean velocity curves, aortic lumen contours were drawn manually on the modulus images of all cardiac phases. Contours were then superimposed on the velocity-encoded images. Flow (in milliliters per second) through each aortic level was calculated by using the areas on the modulus images and the velocity values of the corresponding velocity-encoded images (Figure 1). Vessel cross-sectional area, mean velocity and blood flow for each phase was exported in an ASCII file.

Figure 1.

Representative example of the analysis performed with the FLOW image analysis software. Images from our routine clinical protocol were used. Up: Contours of ascending (red circles) and descending (green circles) aorta drawn on the modulus image and replicated on the phase image. Bottom: Flow curves in the ascending and abdominal aorta.

Transit time calculation

The transit time was calculated from blood flow curves using a custom-built software platform developed in Matlab (The Mathworks, Natick, MA). Each curve was first interpolated 100-fold using cubic spline interpolation to improve temporal discrimination prior to Δt assessment using our approach and, for comparison, TT-point (6, 10, 11) and TT-flow (12 - 14) methods.

The TT-point method calculates the Δt as the time difference between arrival of the flow curves of the ascending and descending aorta at half of their maximum value (Figure 2A). The TT-wave method is based on the cross-correlation technique. It applies a time-shift to the normalized velocity curve of the descending aorta until the highest correlation with the normalized velocity curve of the ascending aorta is obtained. The Δt is the time shift corresponding to the best correlation (Figure 2B). Only the cross-correlation between the upstroke portions of the curves (normalized values between 0.2 and 0.4) was taken into account.

Figure 2.

A: TT-point method for Δt estimation. For each curve the point of 50% of maximum flow is represented by the asterisk and a vertical line passing thought it is traced. B: Normalized flow curves after the shift of the normalized flow of the descending aorta by the TT-wave method.

Since a trigger delay of 10 ms was applied, the TT-foot method, estimating Δt from the foot of the curves (5), could not be used for comparison.

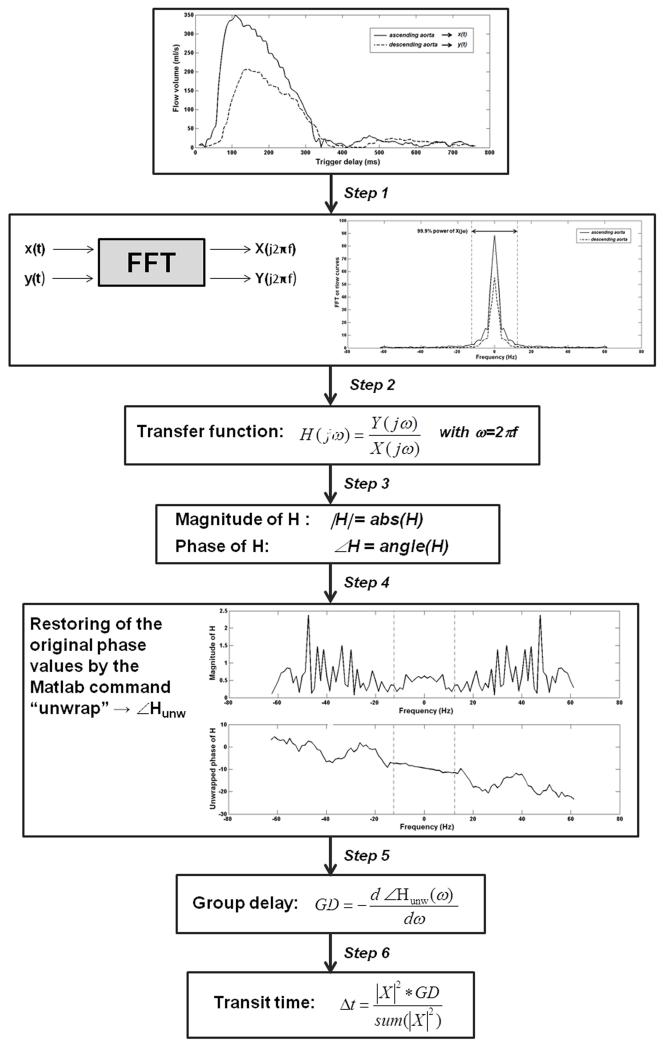
Our method is based on the GD concept and consequently we called it TT-GD. In signal processing, the group delay is a measure of the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component (18). We essentially model the ascending aortic waveform as an input passing through a discrete-component “filter”. The filter represents a computational process, or algorithm, transforming the input into another discrete sequence of numbers (the output) having a modified frequency domain spectrum. The produced output is the observed descending aortic waveform. The GD of that filter represents the average time-delay produced by the filter for a given signal.

The calculation of the Δt requires the following steps, represented also in Figure 3.

Figure 3.

Steps of the TT-GD method.

1. Application of the discrete Fourier transform using a fast Fourier transform (FFT) algorithm to convert the ascending and descending aorta flow curves (x(t) and y(t), respectively) from time to frequency domain (19, 20).

2. Calculation of the transfer function H as the ratio between the descending and the ascending aorta flow curves in the frequency domain.

3. Calculation of the magnitude and the phase of the transfer function (|H| and ∠H, respectively).

4. Phase unwrap to restore original phase values (∠H_unw) (21).

5. Calculation of the GD, expressed in seconds, by differentiating the phase response with respect to ω= 2πf, where f is the frequency.

6. Determination of the ΔT from the GD by “weighting” all of the delays properly, since most of the pulse wave power is concentrated in a couple of harmonics:

   $$\Delta t=\frac{{\mid X\mid }^2\ast GD}{sum\left({\mid X\mid }^2\right)}$$ [1]

Efficiency of the algorithms

All the algorithms were also revaluated using mean velocity curves instead of flow, in order to detect possible differences in Δt values.

Since the number of phases was kept constant, the temporal resolution of each patient depended on his/her heart rate (HR). The mean HR over the entire population was 77.4 ± 11.2 (range: 48-102 bpm) while the mean temporal resolution was 7.9 ± 1.2 ms (range: 6.1-11.8 ms). This temporal discrimination is better than what is typically used in clinical practice. In order to study the effect of the temporal discrimination on ΔT estimates, the original flow and velocity curves were decimated by a factor of two, three and four after anti-aliasing filtering with an 8^th order Chebyshev type 1 low pass filter. Therefore, all the algorithms were revaluated for each patient starting from flow curves utilizing 50, 34 and 25 phases, corresponding to temporal discrimination more typically encountered in clinical studies.

Reproducibility analysis was performed for all the algorithms. Images were reanalysed by the same observer (A. M., 5 years of experience) after at least 3 weeks to evaluate the intra-observer variability. To evaluate the inter-observer variability the images were presented to another operator (H. Z., one year of experience).

Statistical analysis

All data were analyzed using SPSS version 16.0 (SPSS Inc., Chicago, IL, USA) and MedCalc for Windows version 7.2.1.0 (MedCalc Software, Mariakerke, Belgium) statistical packages.

The data were tested for normal distribution using the Shapiro–Wilk test and since all variables were normally distributed, a parametric analysis was carried out. The transit times were provided for all methods as mean ± standard deviation (SD) for all subjects.

Values were compared across methods using the analysis of variance (ANOVA).

To quantify the dependence of Δt values on the used curve and the degradation in Δt estimation produced by downsampling, the following approach was adopted. Linear regression between Δt estimates was performed, providing slope, intercept, and R-squared estimates. A paired sample t-test was applied to detect significant differences between two datasets while the Pearson correlation coefficient was used to assess their relationship. The coefficient of variation (CoV) and the intraclass correlation coefficient (ICC) were calculated. The CoV was obtained as the ratio of the SD of the half mean square of the differences between the repeated values, to the general mean. A CoV < 10% was considered good (22). The ICC was obtained from a two-way random effects model with measures of absolute agreement. An ICC ≥ 0.75 was considered excellent, between 0.40 and 0.75 good, and < 0.40 unsatisfactory. The agreement between measurements was also evaluated through the use of Bland-Altman analysis by calculating the bias (mean difference) and the 95% limits of agreement (1.96 SD around the mean difference).

Reproducibility was evaluated using CoV, ICC and Bland-Altman statistics. The statistical significance was indicated by a P<0.05 on all tests.

RESULTS

Comparison among the three methods

Table 1 summarizes the distribution of transit times obtained from the flow data for the different methods and temporal discrimination. Mean Δt obtained with the GD method was higher than the values obtained with the other two methods, but the difference was not statistically significant.

Table 1.

Comparison among the Δts obtained from the original and the downsampled flow curves for the three different methods.

	TT-GD	TT-point	TT-wave	P
No downsampling (ms)	28.18 ± 5.36	27.02 ± 5.32	26.93 ± 4.41	0.561
Downsampling of 2 (ms)	28.11 ± 5.56	26.98 ± 5.83	26.32 ± 4.50	0.425
Downsampling of 3 (ms)	28.08 ± 5.29	26.51 ± 7.21	26.79 ± 4.67	0.520
Downsampling of 4 (ms)	29.16 ± 5.54	28.76 ± 6.63	27.97 ± 4.37	0.706

Comparison between velocity curves

Table 2 compares the Δt estimates obtained from the mean velocity curves to those obtained from mean flow curves. For all the methods the correlation was strong, the slope near unity, the CoV low and the ICC excellent. However, when the TT-point was used for the calculation, the TTs values obtained from the two curves were significant different and, accordingly, the Bland-Altman analysis demonstrated a small mean discrepancy (bias).

Table 2.

Comparison between the Δts estimated from flow and mean velocity curves for each algorithm.

	TT-GD	TT-point	TT-wave
Best-fitting line: slope     Intercept (ms)	1.044 ± 0.067 −0.872 ± 1.935	0.969 ± 0.097 −0.953 ± 2.361	1.005 ± 0.083 ±0.370 ± 2.254
R-squared for the linear fitting	0.895	0.782	0.841
Difference, mean ± SD (ms)	0.36 ± 1.93	−1.78 ± 2.73	−0.23 ± 1.93
P (paired test)	0.304	0.001	0.521
CoV (%)	4.81	8.71	5.04
ICC	0.970	0.914	0.955
Correlation, r (P-value)	0.946 (P<0.0001)	0.884 (P<0.0001)	0.917 (P<0.0001)
BA limits (ms)	−3.4 to 4.1	−7.1 to 3.6	−4 to 3.5

Influence of temporal discrimination

Table 3 demonstrates the results of the comparison between the Δts obtained from the original data and those obtained from downsampled data for the three methods. Both flow and velocity curves were taken into account.

Table 3.

Influence of temporal resolution on the Δts estimated from flow (A) and velocity (B) curves.

A) Δts estimated from flow curves
	Downsampling  by 2	Downsampling  by 3	Downsampling by 4
TT-GD
Best-fitting line: slope   Intercept (ms)	1.007 ± 0.047 −0.271 ± 1.361	0.929 ± 0.063 1.891 ± 1.810	0.923 ± 0.088 3.131 ± 2.519
R-squared for the linear fitting	0.941	0.886	0.798
Difference, mean ± SD (ms)	−0.08 ± 1.34	−0.10 ± 1.83	0.97 ± 2.52
P (paired test)	0.746	0.756	0.074
CoV (%)	3.33	4.52	6.57
ICC	0.985	0.970	0.937
Correlation, r (P-value)	0.970 (P<0.0001)	0.941 (P<0.0001)	0.893 (P<0.0001)
BA limits (ms)	−2.7 to 2.6	−3.7 to 3.5	−4.0 to 5.9
TT-point
Best-fitting line: slope   Intercept (ms)	0.722 ± 0.156 7.483 ± 4.287	0.927 ± 0.187 1.469 ± 5.147	0.506 ± 0.215 15.093 ± 5.921
R-squared for the linear fitting	0.434	0.467	0.165
Difference, mean ± SD (ms)	−0.03 ± 4.63	−0.52 ± 5.28	1.74 ± 6.6
P (paired test)	0.971	0.597	0.159
CoV (%)	11.91	13.78	17.04
ICC	0.798	0.794	0.559
Correlation, r (P-value)	0.659 (P<0.0001)	0.683 (P<0.0001)	0.406 (P=0.026)
BA limits (ms)	−9.1 to 9.0	−10.9 to 9.8	−11.2 to 14.7
TT-flow
Best-fitting line: slope   Intercept (ms)	0.917 ± 0.084 1.637 ± 2.303	0.926 ± 0.096 1.871 ± 2.622	0.809 ± 0.108 6.175 ± 2.939
R-squared for the linear fitting	0.808	0.768	0.668
Difference, mean ± SD (ms)	−0.61 ± 2.01	−0.13 ± 2.27	1.04 ± 2.66
P (paired test)	0.108	0.757	0.040
Correlation, r (P-value)	0.899 (P<0.0001)	0.876 (P<0.0001)	0.818 (P<0.0001)
CoV (%)	5.49	5.89	7.24
ICC	0.944	0.935	0.889
BA limits (ms)	−4.6 to 3.3	−4.6 to 4.3	−4.2 to 6.2
B) Δts estimated from velocity curves
	Downsampling  by 2	Downsampling  by 3	Downsampling  by 4
TT-GD
Best-fitting line: slope   Intercept (ms)	1.031 ± 0.043 −1.014 ± 1.258	0.956 ± 0.057 1.127 ± 1.660	0.930 ± 0.087 3.108 ± 2.529
R-squared for the linear fitting	0.953	0.910	0.804
Difference, mean ± SD (ms)	−0.14 ± 1.36	−0.12 ± 1.79	1.10 ± 2.75
P (paired test)	0.578	0.715	0.076
CoV (%)	3.33	4.44	7.08
ICC	0.988	0.977	0.939
Correlation, r (P-value)	0.976 (P<0.0001)	0.954 (P<0.0001)	0.897 (P<0.0001)
BA limits (ms)	−2.8 to 2.5	−3.6 to 3.4	−4.3 to 2.5
TT-point
Best-fitting line: slope   Intercept (ms)	0.671 ± 0.117 8.100 ± 3.024	0.927 ± 0.187 1.469 ± 5.147	0.829 ± 0.151 4.515 ± 3.913
R-squared for the linear fitting	0.541	0.467	0.518
Difference, mean ± SD (ms)	−0.19 ± 4.08	0.21 ± 4.77	2.25 ± 6.24
P (paired test)	0.798	0.814	0.058
CoV (%)	11.30	13.09	17.53
ICC	0.850	0.837	0.837
Correlation, r (P-value)	0.736 (P<0.0001)	0.720 (P<0.0001)	0.503 (P=0.005)
BA limits (ms)	−8.2 to 7.8	−9.1 to 9.6	−10.0 to 14.5
TT-Flow
Best-fitting line: slope   Intercept (ms)	0.904 ± 0.087 2.038 ± 2.371	0.929 ± 0.079 2.185 ± 2.140	0.790 ± 0.109 7.247 ± 2.966
R-squared for the linear fitting	0.793	0.832	0.668
Difference, mean ± SD (ms)	−0.51 ± 2.28	0.28 ± 2.05	1.63 ± 2.98
P (paired test)	0.108	0.757	0.005
Correlation, r (P-value)	0.890 (P<0.0001)	0.912 (P<0.0001)	0.807 (P<0.0001)
CoV (%)	5.17	5.37	8.63
ICC	0.941	0.955	0.868
BA limits (ms)	−5.0 to 4.0	−3.7 to 4.3	−4.2 to 7.5

The TT-GD method was slightly influenced by the temporal discrimination: regardless of the downsampling factor a strong correlation with the original data was always found, together with a slope near unity, a good CoV and an excellent ICC.

The TT-point method was the most sensitive to temporal discrimination, making the relationship between downsampled and reference datasets poorly linear. The CoV exceeded 10% and the ICC became was nearly unsatisfactory when only 25 phases of flow data were used. The Bland-Altman ranges were more than double those detected with the TT-GD method.

The TT-wave method was considerably more robust to downsampling than the TT-point method but not as tolerant as the TT-GD approach. In fact, for each dawnsampling size, the R-squared was lower, the CoV was higher, the ICC lower, and the Bland-Altman range wider. Moreover the paired t-test showed a significant difference between TTs values obtained from original high resolution data and those obtained from the data sampled using 25 phases.

Reproducibility

Table 4 shows the results of the reproducibility analysis. The intra-observer and the inter- observer reproducibility of Δt estimation by the three methods were excellent. The TT-GD did outperform the other methods with intra-observer variability of 3.38% and inter-observer variability of 3.67%.

Table 4.

Intra- and inter-observer reproducibility data for the Δts obtained with the three methods.

	TT-GD	TT-point	TT-wave
Intra-operator reproducibility
CoV (%)	3.38	5.66	3.40
ICC	0.982	0.954	0.978
BA bias (ms)	0.04	−0.42	0.10
BA limits (ms)	−2.8 to 2.9	−4.7 to 3.8	−2.5 to 2.7
Inter-operator reproducibility
CoV (%)	3.67	8.17	5.04
ICC	0.981	0.892	0.949
BA bias (ms)	0.06	−0.41	0.15
BA limits (ms)	−2.8 to 3.0	−6.6 to 5.8	−3.7 to 4

DISCUSSION

In this study we presented a new Δt estimation method called TT-GD, which exploits phase-differences in the frequency domain to reduce dependence on high temporal sampling rates. This method provides more robust Δt estimates across sampling rates and operators when compared with two previously described methods (TT-point and TT-wave). The TT-GD method gave slightly higher Δt (4.6%), but the difference was not statistically significant. The etiology of this difference is unclear but probably reflects different weighting of waveform frequency components.

Because this was a retrospective study, we did not have aortic length measurements in our study population. Assuming a mean aortic length of 10.5 cm (based on the literature data regarding healthy subjects with the same range of age (8, 23)), we would obtain with our method a PWV of 3.72 m/s. This value is consistent with those obtained in previous studies using CMR, when considering healthy subjects with comparable mean age. Groenink et al. used the TT-point method for the Δt estimation and found in 26 healthy subjects with a mean age of 28 ± 6 years a PWV of 3.80 ± 0.7 m/s (10). Lalande et al. introduced a method for Δt estimation based on a least squares minimization and reported for 21 subjects having a mean age of 25 ± 6 a mean PWV of 3.60 ± 0.64 m/s.

In our study we used the flow curves as reference standard curves for the Δt estimation, as frequently made by others (10, 17, 27). However some studies have used the mean velocity waveforms, instead (14, 25, 28). While the TT-GD as well as the TT-wave produced comparable results for velocity and flow waveforms, the TT-point resulted in significant shorter Δt values when calculated from velocity waveforms. This result is in agreement with a previous study performed in 50 healthy subjects and using a better temporal discrimination where the mean PWV was significantly higher when using the mean velocity curves (4.86 ± 1.61 m/s vs 4.73 ± 1.47 m/s; P=0.02) (26). While there is no consensus whether flow or velocity transit time more accurately reflect arterial stiffness, our results were qualitatively independent of the choice of methodology.

Sampling frequency is a potentially limiting factor defining accuracy of regional PWV assessment; temporal discrimination varies considerably among studies examining PWV. Rather than acquire multiple PC for the same patient, we chose to acquire a single high-temporal resolution phase-contrast data set that was subsequently downsampled to typical temporal discrimination. This approach is well-justified because more than 98% of the differences in the noise power spectrum produced by changing temporal resolution through view sharing is captured by simple linear filtering models (24). For accurate Δt estimation, time-domain methods often increase apparent temporal discrimination through interpolation (14, 25, 26). While cubic splines are stable and easy to calculate, they do oscillate near regions of rapid signal change. Since the TT-point method relies on a threshold transition, rather than on more global features of the flow waveform, it is not surprising that calculation of Δt using a half-maximum value (TT-point method) was more variable than Δt calculated using cross-correlation (TT-wave method).

Since the TT-GD method operates in the frequency domain, it is robust to reduced temporal discrimination. The underlying signal model is also a better description of underlying physics than simple correlation. That is, cross-correlation analysis is only “optimal” if the descending aorta waveform is a delayed but otherwise unmodified version of the ascending aortic waveform. While the TT-GD method ignores some complexities of pulse-wave propagation, such as reflection, it does compensate for dispersion (frequency-dependent wave-speed) by calculating a weighted-averaged of delay times across the spectral components of the ascending aortic waveform. This weighting, although empiric, emphasizes the dominant harmonics and suppresses frequency components that have lower signal to noise ratio. It is possible that other tuned-filtering approaches, such as Wiener filtering, could similarly improve time-domain estimation but this is beyond the scope of this manuscript.

The intra- and the inter- observer reproducibility for Δt estimation were quite good for all three methods, although the TT-GD yielded the best results. To be fair, we observed higher variability for the TT-point and the TT-wave than those found by Dogui et al (26). In that study, TT-point produced a mean difference of 0.2 ± 2.7 ms and a CoV of 5% and TT-wave yielded a mean difference of 0.08 ± 1.8 ms and a CoV of 4%. However their study population was limited to healthy volunteers, for whom automated contour detection may be more robust. It is also possible that their methods were optimized in a manner that we were not able to faithfully replicate.

This study has some important limitations. The first limitation was the relatively narrow range of transit time values observed in our study population; further studies should be conducted with the aim of proving that the new method displays similar advantages over a broader range of transit times. A second limitation is that we did not actually acquire low temporal resolution data, using filtered decimation to approximate this process. While the low-pass filtering produced by view-sharing is entirely explainable by simple linear filtering theory (24), it could potentially be vendor-specific. We tried to avoid potential vendor bias by using more traditional anti-aliasing filtering prior to downsampling. A third limitation is that we have not explored the method in any other vascular beds, such as the pulmonary artery, and cannot comment on its generalizability. Finally, due to the retrospective nature of this study, a direct comparison of transit times between PC CMR and tonometry, that is considered the “gold standard” and is the most widely used technique, was not performed. However, the consistency and robustness of the regional PWV calculated from CMR using the TT-wave method versus the tonometric measurements had been previously demonstrated (14).

In conclusion, we introduced a new method for the Δt assessment from PC CMR data. Compared to the traditional TT-point and TT-wave methods, this approach was more robust to the choice of temporal discrimination, waveform type, and observer.