Abstract
Small-angle x-ray scattering (SAXS) was used to study the behavior of equine metmyoglobin (Mb) and bovine pancreatic trypsin inhibitor (BPTI) at concentrations up to 0.4 and 0.15 g/mL, respectively, in solutions also containing 50% D2O and 1 M urea. For both proteins, significant effects because of interference between x-rays scattered by different molecules (interparticle interference) were observed, indicating nonideal behavior at high concentrations. The experimental data were analyzed by comparison of the observed scattering profiles with those predicted by crystal structures of the proteins and a hard-sphere fluid model used to represent steric exclusion effects. The Mb scattering data were well fit by the hard-sphere model using a sphere radius of 18 Å, only slightly smaller than that estimated from the three-dimensional structure (20 Å). In contrast, the scattering profiles for BPTI in phosphate buffer displayed substantially less pronounced interparticle interference than predicted by the hard-sphere model and the radius estimated from the known structure of the protein (15 Å). Replacing the phosphate buffer with 3-(N-morpolino)propane sulfonic acid (MOPS) led to increased interparticle interference, consistent with a larger effective radius and suggesting that phosphate ions may mediate attractive intermolecular interactions, as observed in some BPTI crystal structures, without the formation of stable oligomers. The scattering data were also used to estimate second virial coefficients for the two proteins: 2.0 ×10-4 cm3mol/g2 for Mb in phosphate buffer, 1.6 ×10-4 cm3mol/g2 for BPTI in phosphate buffer and 9.2 ×10-4 cm3mol/g2 for BPTI in MOPS. The results indicate that the behavior of Mb, which is nearly isoelectric under the conditions used, is well described by the hard-sphere model, but that of BPTI is considerably more complex and is likely influenced by both repulsive and attractive electrostatic interactions. The hard-sphere model may be a generally useful tool for the analysis of small-angle scattering data from concentrated macromolecular solutions.
Introduction
In recent years, increasing attention has been directed toward the behavior of proteins and nucleic acids under conditions of high macromolecular concentrations, in contrast to the relatively dilute solution conditions historically used for most biochemical and biophysical studies. Interest in the interactions among macromolecules at high concentrations has been motivated by the recognition that in vivo environments are highly crowded, as well as by practical concerns such as the preparation of protein pharmaceuticals (1,2) and optimization of conditions for protein crystal growth (3–7). Theoretical, computational, and experimental approaches have all been used to study the effects of crowding, with most experimental studies focused on a relatively small number of proteins, including hemoglobin (8), serum albumin (9–14), hen lysozyme (5,15–19), and ovalbumin (20,21). Studies of these proteins suggest that their behavior at high concentrations are influenced by both hard repulsive interactions and weaker interactions that can be either repulsive or attractive.
Among the experimental techniques used to characterize macromolecules at high concentrations, static light scattering and small-angle scattering of x-rays or neutrons (SAXS and SANS) provide information about intrinsically weak intermolecular interactions from the interference of electromagnetic radiation scattered from different molecules. In the case of light scattering, the wavelength of the radiation is much greater than the molecular dimensions, and only the interference between waves scattered from different particles is significant. For x-rays and neutrons, with much shorter wavelengths, interference can arise both from waves scattered from different atoms in the same molecule and waves scattered from atoms in different molecules. At low concentrations, the effects from within molecules dominate SAXS and SANS, and the scattering profiles reflect the molecular structure. At higher concentrations, interference between x-rays or neutrons scattered from different molecules (interparticle interference) can become significant. Whereas analysis of molecular structures is most easily carried out using SAXS or SANS profiles measured at, or extrapolated to, low concentrations, interparticle interference observed at higher concentrations can provide additional information about the distribution of molecules in solution and their influence on one another. Although the experimental implementations differ, the information about intermolecular interactions derived from light scattering and from small-angle scattering are fundamentally equivalent.
Mathematically, the intensity, I, of small-angle scattering as a function angle and concentration can be written as a product of two functions of the scattering angle (expressed as q, the scattering vector magnitude), P(q) and S(q,c) as follows:
| (1) |
where c is the particle concentration, expressed here in units of g/mL, and . θ is one half of the scattering angle, and λ is the x-ray or neutron wavelength. The function P(q), the form factor, represents the shape of the scattering profile in the absence of interparticle interference and is the Fourier transform of the distribution of intramolecular distances. At zero scattering angle, the form factor is unity. S(q,c), the structure factor, reflects the interparticle contributions to the scattering profile and is unity in the limit of low concentration. The dependence of the structure factor on q and c reflects the distribution of particles in the solution and can be derived analytically for simple models or calculated using Monte Carlo methods. The constant of proportionality, K, reflects the volume and scattering contrast of the particles.
In this study, SAXS was used to characterize the self-interactions of two globular proteins, equine metmyoglobin (Mb) and bovine pancreatic trypsin inhibitor (BPTI), as part of a more general study of the crowding effects among globular and disordered proteins (22–24). The experimental scattering profiles have been interpreted by direct fitting to the form factors predicted by the known three-dimensional structures of the proteins and the structure factor for a hard-sphere fluid. In addition, second virial coefficients, which reflect the strength of pairwise intermolecular interactions, were estimated from the zero-angle scattering intensities. Both analyses indicate that the behavior of Mb at high concentrations is well described by a hard-sphere model using an effective radius only slightly smaller than that estimated from the crystal structure. In contrast, the data for BPTI indicate significant attractive interactions, particularly in the presence of phosphate ions, which may act as bridges between nearby molecules. These results highlight the potential effects of specific structural features, even as manifested in the general behavior of macromolecules at high concentrations.
Materials and Methods
Protein samples
Bovine pancreatic trypsin inhibitor (Aprotinin) was purchased from Roche Applied Science, Indianapolis, IN. Myoglobin from equine heart was purchased from Sigma-Aldrich, St. Louis, MO (catalog number M1882) and was assumed to be in the metmyoglobin (Fe III) form (25). Both proteins were supplied as lyophilized powders and used without further purification. Concentrations of BPTI solutions were determined by absorbance at 280 nm, assuming an extinction coefficient of 5,400 cm−1M−1 (26). Myoglobin concentrations were determined by absorbance at 500 nm, assuming an extinction coefficient of 10,000 cm−1M−1 (25). BPTI and Mb samples for SAXS measurements were prepared by dissolving the lyophilized proteins in buffer solution containing 50% D2O (vol/vol), 1 M urea, and either 50 mM Na-Phosphate, pH 7, or 50 mM 3-(N-morpolino)propane sulfonic acid (MOPS), pH 7. The protein solutions were concentrated by ultrafiltration using Amicon Ultra-15 centrifugal filter units (Millipore, Billerica, MA) with Ultracel-3 cellulose membranes (3,000 or 10,000 Da cutoff for BPTI or Mb, respectively), and the flow-through fractions were used as reference samples for the SAXS measurements.
Small angle x-ray scattering
SAXS data were measured using an Anton Paar (Graz, Austria) SAXSess instrument with a sealed-tube x-ray source and line-collimation, as described by Jeffries et al. (27). The x-ray intensities were recorded using two-dimensional phosphor image plates, which were read using either a Perkin-Elmer (Waltham, MA) Cyclone scanner or a Molecular Dynamics Typhoon scanner (GE Healthcare, Pittsburgh, PA). The x-ray wavelength was 1.5418 Å (Cu Kα); the sample to detector distance was 264.5 mm; and the sample slit width was 10 mm. Data were recorded for 2 to 4 h. The image data were integrated using the program ImageJ (http://rsb.info.nih.gov/ij) with locally written macros. The width of the integration area (detector slit width) was 10 mm. Relative errors were calculated as the square root of the integrated intensities. For each sample, a reference scattering curve was recorded using a sample blank with identical buffer composition, and the reference curve was subtracted directly from the sample curve before any further analysis. Absolute scattering intensities, with units cm−1, were calibrated using a water reference as described by Orthaber et al. (28).
The experimental SAXS data for BPTI and Mb were fit to profiles predicted from the atomic coordinates of these proteins (Protein Data Bank (PDB) entries 4pti and 1ymb, respectively). The predicted profiles were calculated using the program CRYSOL with the default parameters, including a bulk solvent density of 0.334 electrons/Å3, a hydration layer 3 Å thick, and a scattering contrast of 0.03 electrons/Å3 for the hydration layer (29,30). To account for interparticle interference in solutions of high concentration, the predicted molecular scattering profiles (form factors) were multiplied by the theoretical structure factor for a solution of hard spheres, based on the Percus-Yevick treatment (31–33) (Eqs. 1–4 of (33)). The experimental data were fit to the model with four adjustable parameters: an overall scaling factor, a constant offset, and the two parameters defining the Percus-Yevick model, the radius of the particles (r) and their volume density (ϕ). The simulated SAXS curves were convolved with the experimental beam-length profile and the detector integration profile, so as to match the smearing effects attributable to the line-collimation geometry used in the experimental measurements.
To estimate the scattering intensities at zero angle, the slit-smeared data were corrected using a numerical algorithm based on the iterative method of Lake (34), with a smoothing step included at each iteration to minimize the introduction of excess noise. The correction incorporated both the experimental beam-length profile and the detector integration profile. No correction was introduced for the beam width, which was less than 5% of the beam length. For Mb and BPTI in phosphate buffer, estimates of the radius of gyration and the scattering intensity at zero angle were determined by fitting the data to the Guinier equation as follows:
| (2) |
where is the radius of gyration. The intensity data were weighted by their uncertainties, estimated from the relative scattering intensities, and the reported uncertainties in are the standard errors derived from the fitting procedure. For data from BPTI in MOPS buffer, which displayed a decrease in scattering intensity at very low q, the data were linearly extrapolated to .
SAXS data processing calculations and analyses were carried out using locally written software, the Utah SAXS Tools, available from http://bioweb.biology.utah.edu/goldenberg/software.shtml.
Other calculations
The constant K of Eq. 1 was calculated as follows:
| (3) |
where M is the molar mass, is the partial specific volume of the particles, is the scattering contrast between the particle and solvent, and is Avogadro’s number. The following parameter values were used: molar masses for BPTI and Mb, 6,513 and 17,800 g/mol, respectively; ; the solvent scattering density for 1 M urea in 50% D2O, ; and scattering densities for BPTI and Mb (calculated using the MULCH web server (35)), and , respectively; .
Second virial coefficients for BPTI and Mb were predicted using the program COVOL (36). The axial ratios used as inputs to COVOL were calculated from the crystal structures of BPTI and Mb using the PROTRUDER program (36,37). The axial ratios calculated for BPTI were and , and those for Mb were and . From their amino acid sequences, the net charge of BPTI at pH 7 was assumed to be +6, and Mb was assumed to be uncharged. The ionic strength of the 50 mM, pH 7.0 Na-phosphate buffer used in these studies was calculated to be 0.108 M.
To determine radii for equivalent spheres used to represent Mb and BPTI , the covolumes of the native proteins and spheres of radius 2.5 to 30 Å were calculated using a grid-search algorithm. The calculated covolumes were then plotted as a function of the probe-sphere radius and fit to the expression as follows:
| (4) |
Excellent fits were obtained , yielding values of 15.3 and 20.3 Å for the radii of BPTI and Mb, respectively, which were rounded to 15 and 20 Å for subsequent calculations.
Results and Discussion
The conditions for these measurements were chosen to be compatible with the SANS experiments described in the accompanying paper (24), including 50% D2O. The interpretation of our previous SANS measurements of λ N was complicated by the presence of aggregates, the formation of which was likely promoted by the presence of D2O (22). To counter this effect, urea was added to a concentration of 1 M in all of the samples used for the present study. Urea at this concentration does not significantly destabilize the native conformations of BPTI or Mb (38–40).
SAXS measurements of Mb and BPTI solutions were carried out using a laboratory-scale instrument with a slit-collimated x-ray beam. This geometry allows the use of low-beam intensities, thus minimizing radiation damage, while also providing adequate sensitivity over a range of protein concentrations. A disadvantage of this type of instrument, however, is that the recorded scattering profile is a convolution of the ideal scattering profile, as would be generated using a pin-hole collimated beam, and the linear beam profile. As described previously (23), we have used two approaches to analyzing the convolved, or smeared, data. The first method is to apply a numerical deconvolution of the data, commonly referred to as desmearing. The second is to directly compare the smeared experimental data with model data that have been numerically convolved to simulate the instrument effect.
Myoglobin
SAXS data for Mb at concentrations up to 0.4 g/mL are shown in Fig. 1 A. The experimental data for 0.09 g/mL Mb were well fit by the form factor predicted from the Mb crystal structure. At higher concentrations, however, there was a marked deviation from the predicted profile, which is most apparent from the nonlinear increase in the scattering intensity at zero angle, as plotted in Fig. 1 B. At 0.3 and 0.4 g/mL, the zero-angle intensity actually decreased.
Figure 1.
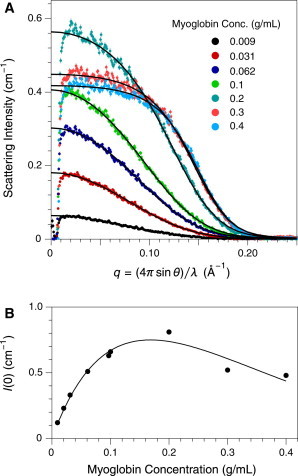
Small angle x-ray scattering from horse metmyoglobin in 50% D2O, 1 M urea and 50 mM Na-phosphate, pH 7.0. (A) SAXS data were recorded using a line-collimated x-ray beam, and the experimental data are uncorrected for smearing. The decrease in intensity below is attributable to absorption by the semi-transparent beam stop. Error bars represent relative uncertainties proportional to the square root of the measured intensities. The experimental data for 0.009 g/mL Mb were fit to the form factor predicted from the Mb crystal structure (PDB entry 1ymb), after numerically convolving the predicted profile with the beam profile. For the higher Mb concentrations, the SAXS data were fit using a model incorporating the Mb form factor and the structure factor, S(q,c), for a solution of hard spheres, as described in the text. (B) Scattering intensities at zero angle were estimated by extrapolation of Guinier plots of numerically desmeared data. The curve represents a fit of the experimental data to Eq. 7, which is derived from the model for a solution of hard spheres, yielding an estimate of 18 Å for the particle radius, as described in the text. To see this figure in color, go online.
For a hard-sphere fluid, the structure factor at zero scattering angle, , is predicted to depend only on the volume density of particles as follows:
| (5) |
where ϕ is the fraction of the solution volume occupied by the spherical particles. If the particle concentration, c, is specified in g/mL and is the sphere volume, then ϕ can be written as follows:
| (6) |
and the zero-angle scattering intensity can be written as follows:
| (7) |
The zero-angle intensities for Mb were fit to Eq. 7, with K and the only adjustable parameters (Fig. 1 B). The fit value of K was , in good agreement with the value calculated from Eq. 3 and the molecular parameters for Mb specified in Materials and Methods, . The fit value of was , corresponding to a spherical radius of 18 Å, compared with a radius of 20 Å calculated from the crystal structure.
To further analyze the Mb SAXS data, the full profiles were fit to a model based on the form factor, P(q), calculated from the crystal structure and the structure factor, S(q,c), for a solution of hard spheres (32,33). The expression for the structure factor includes two parameters, r, the sphere radius and ϕ, defined above. The SAXS data were fit with four adjustable parameters, r; ϕ; an overall scaling factor and a background intensity offset. As shown by the curves in Fig. 1 A, excellent fits to this model were obtained for all of the Mb solutions.
The structure factor functions defined by the fitting procedure are plotted in Fig. 2 A. As inferred from the scattering profiles, S(q,c) at low values of q progressively decreases as the protein concentration increases, reflecting destructive interference between x-rays scattered from different particles. The effect becomes more pronounced as the distribution of molecules becomes more constrained. At the higher concentrations, a peak in the structure factor also appears at , reflecting constructive interference of waves scattered from different molecules, primarily nearest neighbors. The position of this peak indicates a nearest neighbor distance of approximately (17). The fit parameters of the structure factor, r and ϕ, are plotted versus Mb concentration in Fig. 2 B. The average estimated radius was 18.7 Å and displayed very little change with protein concentration, and the estimated volume density of the solution, ϕ, increased linearly with protein concentration up to 0.3 g/mL. Thus, the scattering profiles for concentrated Mb solutions are well described by the hard-sphere model using physically reasonable parameters.
Figure 2.
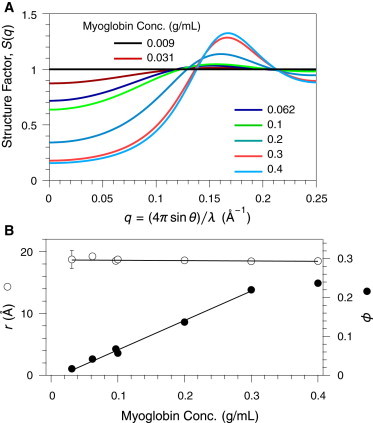
Structure factors for myoglobin solutions, determined by fitting to the SAXS data of Fig. 1A, assuming a solution of hard spheres. (A) S(q,c) plotted as a function of q at the indicated myoglobin concentrations. (B) Fit values of the parameters defining the hard-sphere solution structure factor, r the sphere radius, and ϕ the concentration expressed as the fraction volume occupied by the spheres. The lines represent least-squares fits to the data (excluding the value for ϕ at 0.4 g/mL myoglobin). To see this figure in color, go online.
BPTI
SAXS data recorded for 0.05, 0.1, and 0.15 g/mL BPTI, using the solution conditions described earlier, are shown in Fig. 3 A. The dashed curves in the figure represent fits of the experimental data to the form factor predicted from the crystal structure of BPTI (PDB entry 4pti), without incorporation of a structure factor to account for interparticle interference. As shown, the data for the 0.05 g/mL sample were well fit by the predicted form factor At higher protein concentrations, deviations from the predicted profiles were observed, but were much less pronounced than those seen for concentrated Mb solutions, suggesting a smaller degree of interparticle interference.
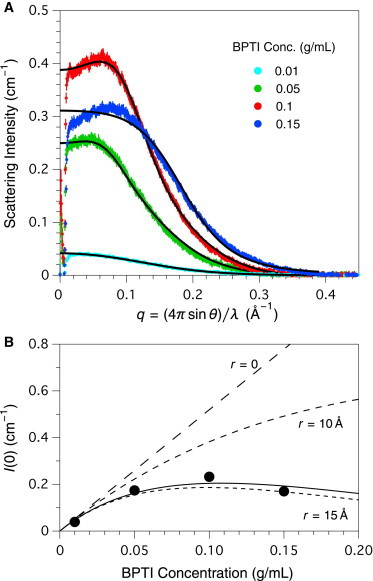
Figure 3.
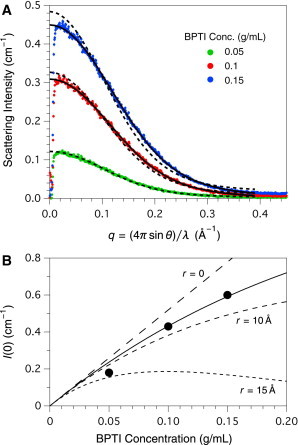
Small angle x-ray scattering from BPTI in 50% D2O, 1 M urea and 50 mM Na-phosphate, pH 7.0. (A) SAXS data were recorded and processed as described in the text and the legend to Fig. 1. The experimental data were fit to the scattering profile predicted from the crystal structure of BPTI (PDB entry 4pti), after numerically convolving the predicted profile with the beam profile. The dashed curves represent fits to the predicted form factor for BPTI, without incorporation of a structure factor. The solid curves represent fits to the BPTI form factor and the structure factor for a hard-sphere solution, with the fit parameters listed in Table 1. (B) The scattering intensities at zero angle were estimated by extrapolation of Guinier plots of numerically-desmeared data. The solid curve represents the fit of Eq. 7 to the experimental data, with a fixed value of the constant K = 5.2 cm2/g, and the fit sphere volume corresponding to a radius of 8.4 Å. The dashed curves are predicted from Eq. 7 using the same value of K and the indicated sphere radii. To see this figure in color, go online.
The BPTI SAXS profiles were also desmeared and analyzed using Guinier plots (not shown), which yielded estimates of 10.2 to 12.6 Å for the radius of gyration, in good agreement with the value predicted from the crystal structure, 11 Å. The extrapolated scattering intensities from BPTI at zero angle were found to display a nearly linear dependence on concentration, as shown in Fig. 3 B. When the extrapolated intensities were fit to Eq. 7 with both K and allowed to float, the parameters were inadequately determined by the data. With K constrained to the value 5.2 cm2/g (calculated from the molecular parameters specified in Materials and Methods), the data were well fit with the value of , as shown by the solid curve in Fig. 3 B. The estimated volume corresponds to a spherical radius of 8.4 Å, substantially smaller than the value predicted from the crystal structure, 15 Å. The dashed curves in Fig. 3 B represent the zero-angle scattering intensities predicted from Eq. 7, assuming radii of 0, 10, and 15 Å. Comparison of the observed and predicted intensities confirms that the degree of interparticle interference observed with BPTI is substantially less than expected for a solution of hard spheres with equivalent volumes.
The full scattering curves for the 0.1 and 0.15 g/mL BPTI solutions were also fit to the predicted profiles incorporating the hard-sphere structure factor with adjustable values of r and ϕ. The fit profiles are shown as solid curves in Fig. 3 A, and the fit parameter values are listed in Table 1. The fit values of the radius were 8–9 Å, in good agreement with the value estimated from the zero-angle scattering intensities, and the fit values of ϕ were 0.06–0.07, substantially smaller than expected from the BPTI concentration.
Table 1.
Hard sphere structure factor parameters for BPTI solutions
| [BPTI] (g/mL) | NaPO4 buffer |
MOPS buffer |
||
|---|---|---|---|---|
| ϕ | r (Å) | ϕ | r (Å) | |
| 0.05 | - | - | 0.06 | 33 |
| 0.1 | 0.06 | 8 | 0.09 | 25 |
| 0.15 | 0.07 | 9 | 0.13 | 14 |
All of the analyses described above indicate that the effects of steric exclusion on BPTI under these solution conditions are significantly less pronounced than expected for a solution of hard spheres. This pattern is particularly surprising in light of the large net charge (+6) expected for this protein at pH 7, which is predicted to enhance repulsion beyond that expected from steric effects. That the effective radius is smaller than predicted suggests that attractive interactions must compensate for the expected steric and electrostatic repulsion.
A possible explanation for these observations may lie in the use of phosphate as the pH buffer for these experiments. In two crystal forms of BPTI (the type II and III forms, represented by PDB entries 5pti and 6pti, respectively), a phosphate ion participates in intermolecular crystal packing contacts (41), suggesting that phosphate ions may facilitate attractive intramolecular interactions in solution. These interactions are illustrated in Fig. 4.
Figure 4.
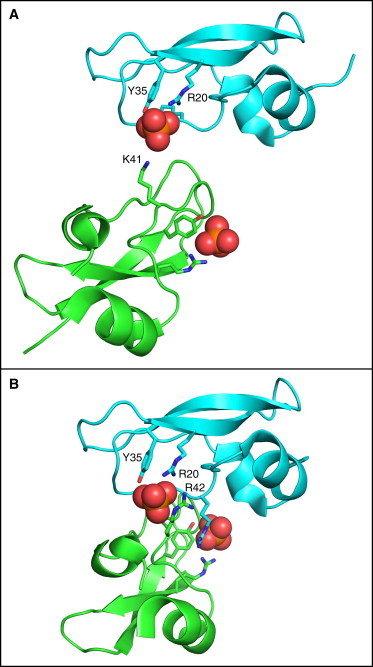
Phosphate-mediated intermolecular interactions in form II (A) and form III (B) crystals of BPTI. In each panel, the backbones of the two BPTI molecules are shown in a ribbon representation, and atoms of the phosphate ion are shown as spheres. The side-chains from each molecule that interact most directly with the phosphate are labeled and represented as sticks. Drawn from the atomic coordinates of PDB entries 5pti (A) and 6pti (B), using the program PyMOL (50) To see this figure in color, go online.
To test the possible influence of phosphate ions in solution, SAXS profiles were recorded for BPTI solutions buffered with 3-(N-morpolino)propane sulfonic acid (MOPS) rather than phosphate (Fig. 5 A). The scattering profile from 0.01 g/mL BPTI in MOPS closely matched the profile predicted from the crystal structure. At higher protein concentrations, however, the scattering profiles displayed a pronounced downward curvature at lower scattering angles, indicative of interparticle interference. After desmearing, the zero-angle scattering intensities were estimated by linear extrapolation and are plotted in Fig. 5 B. The extrapolated intensities were well fit to Eq. 7, with K constrained to the value and a fit value of , corresponding to a sphere radius of 14.5 Å, in good agreement with the effective radius calculated from the crystal structure.
Figure 5.
Small angle x-ray scattering from BPTI in 50% D2O, 1 M urea and 50 mM MOPS, pH 7.0. SAXS data were recorded and processed as described in the text and the legend to Fig. 1. The experimental data for 0.01 g/mL BPTI were fit to the form factor predicted from the crystal structure of BPTI, after numerically convolving the predicted profile with the beam profile. The data for the higher BPTI concentrations were fit to the predicted profile incorporating the BPTI form factor and the structure factor for a solution of hard spheres. The fit values for the sphere radius and volume fraction are listed in Table 1. (B) The scattering intensities at zero angle were estimated by linear extrapolation of numerically desmeared data. The solid curve represents the fit of Eq. 7 to the experimental data, with a fixed value of the constant K = 5.2 cm2/g and the fit sphere volume corresponding to a radius of 14.5 Å. The dashed curves are predicted from Eq. 7 using the same value of K and the indicated sphere radii. To see this figure in color, go online.
The full scattering profiles of 0.05 to 0.15 g/mL BPTI in MOPS buffer were fit to the form factor calculated from the 4pti crystal structure and the hard sphere structure factor. The fit profiles are shown as solid curves in Fig. 5 A, and the fit values of the hard-sphere parameters are listed in Table 1. Although the fit values for the volume fraction occupied by the spheres increased as expected with the BPTI concentration, the fit radius decreased with protein concentration, from 33 Å for 0.05 g/mL BPTI to 14 Å at 0.15 g/mL. In addition, the fit of the hard-sphere model to the experimental data was notably poorer for the highest concentration. These patterns suggest that the behavior of BPTI, even in the absence of phosphate, is more complex than observed with Mb.
Although the results described above strongly indicate a specific role for phosphate ions in mediating interactions among BPTI molecules in concentrated solutions, there is no evidence from the scattering profiles for a significant fraction of dimeric molecules or higher oligomers, as might be implied from the crystal interactions illustrated in Fig. 4. The models used to fit the data were based on the structure of a BPTI monomer, with the deviation from nonideal behavior described by the structure factor parameters listed in Table 1. Over the years, there have been several reports that BPTI can take on a variety of oligomeric forms (reviewed in (42)), but the most systematic studies of this question indicate that a decamer is the only oligimer that is significantly populated in solution, and only in the presence of high salt concentrations or pH values less than 5 or greater than 9 (42,43). The expected SAXS profile for the decamer is clearly distinguishable from those shown in Fig. 3 A, as illustrated in Fig. 1 C of our previous study (22). All of the available evidence thus indicates that the monomer is the predominant form under the conditions described in this study, with the phosphate ions contributing to transient interactions that shift the distribution of intermolecular distances toward shorter lengths, without leading to significant oligomerization.
Second virial coefficients
The observed effects of interparticle interference in the SAXS profiles of Mb and BPTI can also be interpreted in terms of a second-order virial expansion. Because the scattering intensity depends on transient fluctuations in the distribution of particles, the structure factor at zero angle is related to the osmotic compressibility of the solution as follows:
| (8) |
where is the osmotic pressure; R is the gas constant; and T is temperature. If the osmotic pressure is represented by a virial expansion, then the structure factor can be written as follows:
| (9) |
where , , and are the second, third, and ith virial coefficients, expressed in volume units. Common practice is to limit the expansion to the second term in the denominator and to express the second virial coefficient as , with units of cm3mol/g2. In this form, the zero-angle scattering intensity is written as follows:
| (10) |
The value of can be estimated by fitting experimental scattering intensity data measured at different concentrations to Eq. 10, an analysis that is analogous to the determination of from a Zimm plot of static light scattering data. The second virial coefficient is an intrinsic property of the particles in a given solvent and is usually interpreted as reflecting the tendency of the particles to interact pairwise, with attractive interactions giving rise to negative values and repulsive interactions (including steric overlap) leading to positive values. Interest in this parameter for protein solutions has been stimulated by the observation that measured values under conditions favorable for crystallization are typically negative and lie within a relatively narrow range, from approximately cm3mol/g2 to zero (4–7).
Fig. 6 A shows the results of fitting the zero-angle scattering intensities for Mb and BPTI to Eq. 10, with the values of K fixed to those calculated from the molecular properties. The fit values of were 2.0 cm3mol/g2 for Mb, 1.6 cm3mol/g2 for BPTI in phosphate buffer, and 9.2 cm3mol/g2 for BPTI in MOPS.
Figure 6.
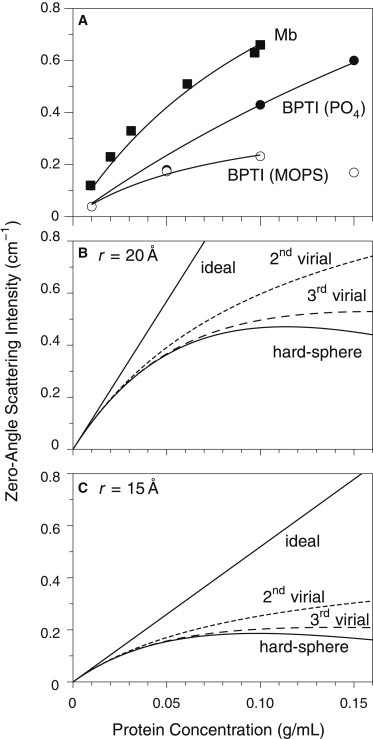
Analysis of zero-angle scattering intensities using the second-order virial representation. (A) The measured scattering intensities for Mb and BPTI were fit to Eq. 10, with the values of K fixed to those predicted by Eq. 3 and the molecular parameters specified in Materials and Methods. In each case, the curve indicates the range of concentrations used for the fit. The fit values for A2, the second virial coefficient, were 2.0 ×10-4, 1.6 ×10-4, and 9.2 ×10-4 cm3mol/g2 for Mb, BPTI in phosphate buffer and BPTI in MOPS, respectively. (B) Predicted dependence of I (0) for myoglobin, assuming ideal behavior, the analytic form of the hard-sphere structure factor (Eq. 7) or second- or third-order virial representations of S (0) (Eq. 9). In each case, a sphere radius of 20 Å was used, and K was assumed to have the value calculated from the molecular properties of Mb. (C) Predicted dependence of I (0) for BPTI, using the same representations as in panel B. For these calculations a sphere radius of 15 Å was used, and K was assumed to have the value calculated from the molecular properties of BPTI.
For a solution of hard spheres, is positive and is related to the sphere volume and molar mass according to . If Mb is treated as a sphere of radius 20 Å, the predicted value of is 2.6 cm3mol/g2, in reasonable agreement with the experimental result. For BPTI, the hard-sphere model (assuming a radius of 15 Å) predicts , close to the value measured in MOPS buffer but fivefold greater than that estimated in phosphate buffer.
Predicted values of the second virial coefficient were also calculated using the program COVOL, which estimates the steric contribution to by approximating the protein structure as a triaxial ellipsoid and calculates an electrostatic repulsion contribution using the Debye-Hückel theory and assuming a uniform distribution of net charge (36). For Mb, which has an isoelectric pH close to 7, the electrostatic component was assumed to be negligible, and the value of calculated for steric exclusion was , only slightly higher than that estimated from the hard-sphere model. Because BPTI carries a large net charge (+6) at neutral pH, electrostatic repulsion is expected to contribute further to a positive second virial coefficient, and the total predicted value of is , more than 10-fold greater than the value estimated from the SAXS data for BPTI in phosphate buffer and approximately twice that estimated in MOPS.
The discrepancy between the predicted values of for BPTI and those measured experimentally, under both buffer conditions, implies additional factors that compensate for both steric exclusion and electrostatic repulsion among BPTI molecules at high concentration. Factors that have been proposed to contribute to the second virial coefficient for proteins include van der Waals interactions, interactions with other solvent components, and specific electrostatic interactions that are not accounted for by simple models such as used in COVOLV. In addition to the apparent effect of phosphate ions, electrostatic interactions may be particularly important for BPTI, which has a markedly asymmetric distribution of charges that are likely to interact attractively when the molecules take on some relative orientations. The importance of orientation-specific attractive interactions have been emphasized by Neal et al. (44), and in a detailed modeling study of BPTI by Kim and Song (45).
Although the treatment of scattering data using a second-order virial expansion has the advantage of being independent of any specific structural model, it also suffers from some limitations. One difficulty lies in determining a range of concentrations for which the approximation is appropriate. To estimate a nonzero value of , the range must include concentrations for which deviations from ideal behavior are detectable, but higher-order terms may also be significant at these concentrations. This point is illustrated in panels B and C of Fig. 6, which shows the predicted dependence of on concentration assuming four models: ideal behavior, the hard-sphere fluid model represented by Eq. 7, and second- and third-order virial approximations to the hard-sphere model. For the calculations in panel B, and the constant K in Eqs. 7 and 10 was calculated from the molecular properties of Mb; the curves shown in panel C were calculated using and the properties of BPTI. Deviation from ideal behavior is seen at concentrations greater than ∼ 0.02 g/mL, but deviations between the second-order and full representations of the hard-sphere model also become apparent at concentrations greater than ∼ 0.05 g/mL, where higher-order terms become significant. Although the second-order approximation may be adequate to account for experimental data at the higher concentrations, as seen here with Mb and BPTI, the fit value of may not represent the true second virial coefficient or be easily interpreted. Winzor and colleagues have also argued that the second virial coefficients determined from scattering experiments do not truly represent the pairwise interaction potential between macromolecules when additional cosolvents species, such as buffers, are present (46–48). Although this argument has been disputed (49), the results shown here for BPTI in phosphate buffer clearly demonstrate the influence of another solution component on the apparent virial coefficient.
Conclusions
SAXS measurements of concentrated solutions of BPTI and Mb revealed distinctly different self-interaction properties of the two proteins. For Mb, the concentration dependence of the SAXS profiles was well accounted for by a model for a solution of hard spheres, with radii independent of protein concentration and comparable with that of the known Mb structure. For BPTI in phosphate buffer, the deviations from ideal behavior were found to be significantly smaller than expected from the known size and net charge of the protein, but could be accounted for by the hard-sphere model using a radius substantially smaller than indicated by the crystal structure. Replacing phosphate with MOPS increased the apparent radius of BPTI, as estimated by analysis of the zero-angle scattering intensities, to approximately that predicted from the crystal structure, consistent with the hypothesis that phosphate promotes attractive interactions between BPTI molecules. There were, however, no indications of the formation of stable dimers or higher oligomers under any of the conditions examined. The effective radii estimated from fitting the entire scattering profiles of BPTI in MOPS buffer were found to depend on protein concentration (Table 1), suggesting more complex behavior.
The analyses described in this study also highlight the utility of the hard-sphere fluid model in interpreting experimental studies of globular proteins at high concentrations, an approach suggested by Minton and Edelhoch more than 30 years ago (9). Although this model represents an extreme simplification, comparison with experimental data can suggest either that steric exclusion is the dominant factor determining intermolecular interactions, as with Mb, or that additional factors, such as electrostatic repulsion or attraction, are likely to play significant roles. Even for BPTI, the experimental scattering data for most of the conditions examined were well fit using the hard-sphere structure factor, and the deviations between the effective hard sphere radius derived from the fitting procedure and that expected from the known structure of BPTI provide a means of assessing the net effect of additional repulsive or attractive interactions. The effective hard-sphere radius can be considered an alternative to the second virial coefficient as a parameter for assessing nonideal behavior at high macromolecular concentrations, with the advantage of a simple physical interpretation. In addition, the hard sphere model can be applied over a very wide range of concentrations without introducing additional parameters. Further use of this model for the analysis of small angle scattering data will likely provide additional insights into its general applicability and the variety of macromolecular behaviors under highly crowded conditions resembling those found intracellularly.
Acknowledgments
We thank Drs. Jill Trewhella and Don Parkin for the use of the SAXSess instrument at the University of Utah, for their assistance in its use and for helpful discussions.
This research was supported by grant No. MCB-0749464 from the U.S. National Science Foundation.
References
- 1.Saluja A., Kalonia D.S. Nature and consequences of protein-protein interactions in high protein concentration solutions. Int. J. Pharm. 2008;358:1–15. doi: 10.1016/j.ijpharm.2008.03.041. [DOI] [PubMed] [Google Scholar]
- 2.Shire S.J. Formulation and manufacturability of biologics. Curr. Opin. Biotechnol. 2009;20:708–714. doi: 10.1016/j.copbio.2009.10.006. [DOI] [PubMed] [Google Scholar]
- 3.Wiencek J.M. New strategies for protein crystal growth. Annu. Rev. Biomed. Eng. 1999;1:505–534. doi: 10.1146/annurev.bioeng.1.1.505. [DOI] [PubMed] [Google Scholar]
- 4.George A., Wilson W.W. Predicting protein crystallization from a dilute solution property. Acta Crystallogr. D Biol. Crystallogr. 1994;50:361–365. doi: 10.1107/S0907444994001216. [DOI] [PubMed] [Google Scholar]
- 5.Bonneté F., Finet S., Tardieu A. Second virial coefficient: variations with lysozyme crystallization conditions. J. Cryst. Growth. 1999;196:403–414. [Google Scholar]
- 6.Bonneté F., Vivarès D. Interest of the normalized second virial coefficient and interaction potentials for crystallizing large macromolecules. Acta Crystallogr. D Biol. Crystallogr. 2002;58:1571–1575. doi: 10.1107/s090744490201418x. [DOI] [PubMed] [Google Scholar]
- 7.Veesler S., Lafont S., Boistelle R. Prenucleation, crystal growth and polymorphism of some proteins. J. Cryst. Growth. 1996;168:124–129. [Google Scholar]
- 8.Ross P.D., Minton A.P. Analysis of non-ideal behavior in concentrated hemoglobin solutions. J. Mol. Biol. 1977;112:437–452. doi: 10.1016/s0022-2836(77)80191-5. [DOI] [PubMed] [Google Scholar]
- 9.Minton A.P., Edelhoch H. Light scattering of bovine serum albumin solutions: extension of the hard particle model to allow for electrostatic repulsion. Biopolymers. 1982;21:451–458. [Google Scholar]
- 10.Minton A.P. A molecular model for the dependence of the osmotic pressure of bovine serum albumin upon concentration and pH. Biophys. Chem. 1995;57:65–70. doi: 10.1016/0301-4622(95)00046-z. [DOI] [PubMed] [Google Scholar]
- 11.Bendedouch D., Chen S.-H. Structure and interparticle interactions of bovine serum albumin in solution studied by small-angle neutron scattering. J. Phys. Chem. 1983;87:1473–1477. [Google Scholar]
- 12.Sjöberg B., Mortensen K. Interparticle interactions and structure in nonideal solutions of human serum albumin studied by small-angle neutron scattering and Monte Carlo simulation. Biophys. Chem. 1994;52:131–138. doi: 10.1016/0301-4622(94)00089-1. [DOI] [PubMed] [Google Scholar]
- 13.Sjöberg B., Mortensen K. Structure and thermodynamics of nonideal solutions of colloidal particles: investigation of salt-free solutions of human serum albumin by using small-angle neutron scattering and Monte Carlo simulation. Biophys. Chem. 1997;65:75–83. doi: 10.1016/s0301-4622(96)02251-x. [DOI] [PubMed] [Google Scholar]
- 14.Yousef M.A., Datta R., Rodgers V.G.J. Understanding nonidealities of the osmotic pressure of concentrated bovine serum albumin. J. Colloid Interface Sci. 1998;207:273–282. doi: 10.1006/jcis.1998.5789. [DOI] [PubMed] [Google Scholar]
- 15.Hubbard S.R., Doniach S. A Monte Carlo calculation of the interparticle interference in small-angle x-ray scattering. J. Appl. Cryst. 1988;21:953–959. [Google Scholar]
- 16.Minezaki Y., Niimura N., Katsura T. Small angle neutron scattering from lysozyme solutions in unsaturated and supersaturated states (SANS from lysozyme solutions) Biophys. Chem. 1996;58:355–363. doi: 10.1016/0301-4622(95)00078-x. [DOI] [PubMed] [Google Scholar]
- 17.Shukla A., Mylonas E., Svergun D.I. Absence of equilibrium cluster phase in concentrated lysozyme solutions. Proc. Natl. Acad. Sci. USA. 2008;105:5075–5080. doi: 10.1073/pnas.0711928105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu Y., Porcar L., Baglioni P. Lysozyme protein solution with an intermediate range order structure. J. Phys. Chem. B. 2011;115:7238–7247. doi: 10.1021/jp109333c. [DOI] [PubMed] [Google Scholar]
- 19.Velev O.D., Kaler E.W., Lenhoff A.M. Protein interactions in solution characterized by light and neutron scattering: comparison of lysozyme and chymotrypsinogen. Biophys. J. 1998;75:2682–2697. doi: 10.1016/S0006-3495(98)77713-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Minton A.P. Effective hard particle model for the osmotic pressure of highly concentrated binary protein solutions. Biophys. J. 2008;94:L57–L59. doi: 10.1529/biophysj.107.128033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ianeselli L., Zhang F., Schreiber F. Protein-protein interactions in ovalbumin solutions studied by small-angle scattering: effect of ionic strength and the chemical nature of cations. J. Phys. Chem. B. 2010;114:3776–3783. doi: 10.1021/jp9112156. [DOI] [PubMed] [Google Scholar]
- 22.Johansen D., Jeffries C.M.J., Goldenberg D.P. Effects of macromolecular crowding on an intrinsically disordered protein characterized by small-angle neutron scattering with contrast matching. Biophys. J. 2011;100:1120–1128. doi: 10.1016/j.bpj.2011.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Johansen D., Trewhella J., Goldenberg D.P. Fractal dimension of an intrinsically disordered protein: small-angle x-ray scattering and computational study of the bacteriophage λ N protein. Protein Sci. 2011;20:1955–1970. doi: 10.1002/pro.739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Goldenberg D.P., Argyle B. Minimal effects of macromolecular crowding on an intrinsically disordered protein: a small-angle neutron scattering study. Biophys. J. 2013 doi: 10.1016/j.bpj.2013.12.003. ms. no 2013BIOPHYSJ303324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Antonini E., Brunori M. North-Holland; Amsterdam: 1971. Hemoblobin and myoglobin in their reactions with ligands. [Google Scholar]
- 26.Creighton T.E. Renaturation of the reduced bovine pancreatic trypsin inhibitor. J. Mol. Biol. 1974;87:563–577. doi: 10.1016/0022-2836(74)90104-1. [DOI] [PubMed] [Google Scholar]
- 27.Jeffries C.M., Whitten A.E., Trewhella J. Small-angle x-ray scattering reveals the N-terminal domain organization of cardiac myosin binding protein C. J. Mol. Biol. 2008;377:1186–1199. doi: 10.1016/j.jmb.2008.01.080. [DOI] [PubMed] [Google Scholar]
- 28.Orthaber D., Bergmann A., Glatter O. SAXS experiments on absolute scale with Kratky systems using water as a secondary standard. J. Appl. Cryst. 2000;33:218–225. [Google Scholar]
- 29.Svergun D., Barberato C., Koch M.H.J. CRYSOL—a program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Cryst. 1995;28:768–773. [Google Scholar]
- 30.Svergun D.I., Richard S., Zaccai G. Protein hydration in solution: experimental observation by x-ray and neutron scattering. Proc. Natl. Acad. Sci. USA. 1998;95:2267–2272. doi: 10.1073/pnas.95.5.2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Percus J.K., Yevick G.J. Analysis of classical statistical mechanics by means of collective coordinates. Phys. Rev. 1958;110:1–13. [Google Scholar]
- 32.Ashcroft N.W., Lekner J. Structure and resistivity of liquid metals. Phys. Rev. 1966;145:83–90. [Google Scholar]
- 33.Ailawadi N.K. Possible generalization of the Ashcroft-Lekner hard-sphere model for the structure factor. Phys. Rev. A. 1973;7:2200–2203. [Google Scholar]
- 34.Lake J.A. An iterative method of slit-correcting small angle x-ray data. Acta Crystallogr. 1967;23:191–194. [Google Scholar]
- 35.Whitten A.E., Cai S., Trewhella J. MULCh: modules for the analysis of small-angle neutron contrast variation data from biomolecular assemblies. J. Appl. Cryst. 2008;41:222–226. [Google Scholar]
- 36.Harding S.E., Horton J.C., Winzor D.J. COVOL: an interactive program for evaluating second virial coefficients from the triaxial shape or dimensions of rigid macromolecules. Biophys. J. 1999;76:2432–2438. doi: 10.1016/S0006-3495(99)77398-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Taylor W.R., Thornton J.M., Turnell W.G. An ellipsoidal approximation of protein shape. J. Mol. Graph. 1983;1:30–38. [Google Scholar]
- 38.Vincent J.P., Chicheportiche R., Lazdunski M. The conformational properties of the basic pancreatic trypsin-inhibitor. Eur. J. Biochem. 1971;23:401–411. doi: 10.1111/j.1432-1033.1971.tb01634.x. [DOI] [PubMed] [Google Scholar]
- 39.Creighton T.E. Electrophoretic analysis of the unfolding of proteins by urea. J. Mol. Biol. 1979;129:235–264. doi: 10.1016/0022-2836(79)90279-1. [DOI] [PubMed] [Google Scholar]
- 40.Ahmad F., Bigelow C.C. Estimation of the free energy of stabilization of ribonuclease A, lysozyme, α-lactalbumin, and myoglobin. J. Biol. Chem. 1982;257:12935–12938. [PubMed] [Google Scholar]
- 41.Wlodawer A., Nachman J., Woodward C. Structure of form III crystals of bovine pancreatic trypsin inhibitor. J. Mol. Biol. 1987;198:469–480. doi: 10.1016/0022-2836(87)90294-4. [DOI] [PubMed] [Google Scholar]
- 42.Gottschalk M., Venu K., Halle B. Protein self-association in solution: the bovine pancreatic trypsin inhibitor decamer. Biophys. J. 2003;84:3941–3958. doi: 10.1016/S0006-3495(03)75122-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hamiaux C., Pérez J., Vachette P. The BPTI decamer observed in acidic pH crystal forms pre-exists as a stable species in solution. J. Mol. Biol. 2000;297:697–712. doi: 10.1006/jmbi.2000.3584. [DOI] [PubMed] [Google Scholar]
- 44.Neal B.L., Asthagiri D., Lenhoff A.M. Molecular origins of osmotic second virial coefficients of proteins. Biophys. J. 1998;75:2469–2477. doi: 10.1016/S0006-3495(98)77691-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kim B., Song X. Calculations of the second virial coefficients of protein solutions with an extended fast multipole method. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:011915. doi: 10.1103/PhysRevE.83.011915. [DOI] [PubMed] [Google Scholar]
- 46.Deszczynski M., Harding S.E., Winzor D.J. Negative second virial coefficients as predictors of protein crystal growth: evidence from sedimentation equilibrium studies that refutes the designation of those light scattering parameters as osmotic virial coefficients. Biophys. Chem. 2006;120:106–113. doi: 10.1016/j.bpc.2005.10.003. [DOI] [PubMed] [Google Scholar]
- 47.Winzor D.J., Deszczynski M., Wills P.R. Nonequivalence of second virial coefficients from sedimentation equilibrium and static light scattering studies of protein solutions. Biophys. Chem. 2007;128:46–55. doi: 10.1016/j.bpc.2007.03.001. [DOI] [PubMed] [Google Scholar]
- 48.Scott D.J., Patel T.R., Winzor D.J. A potential for overestimating the absolute magnitudes of second virial coefficients by small-angle x-ray scattering. Anal. Biochem. 2013;435:159–165. doi: 10.1016/j.ab.2012.12.014. [DOI] [PubMed] [Google Scholar]
- 49.Blanco M.A., Sahin E., Roberts C.J. Reexamining protein-protein and protein-solvent interactions from Kirkwood-Buff analysis of light scattering in multi-component solutions. J. Chem. Phys. 2011;134:225103. doi: 10.1063/1.3596726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Schrödinger, LLC. 2010. The PyMOL molecular graphics system, version 1.3r1.


