Spatiotemporal Evolution of Erythema Migrans, the Hallmark Rash of Lyme Disease

Abstract

To elucidate pathogen-host interactions during early Lyme disease, we developed a mathematical model that explains the spatiotemporal dynamics of the characteristic first sign of the disease, a large (≥5-cm diameter) rash, known as an erythema migrans. The model predicts that the bacterial replication and dissemination rates are the primary factors controlling the speed that the rash spreads, whereas the rate that active macrophages are cleared from the dermis is the principle determinant of rash morphology. In addition, the model supports the clinical observations that antibiotic treatment quickly clears spirochetes from the dermis and that the rash appearance is not indicative of the efficacy of the treatment. The quantitative agreement between our results and clinical data suggest that this model could be used to develop more efficient drug treatments and may form a basis for modeling pathogen-host interactions in other emerging infectious diseases.

Introduction

A goal of modern biomedical research is to develop patient-specific treatment plans. A potential step in this direction would be determining effective, noninvasive measures that correlate clinical observations with states of disease. In the case of infections, the ability to achieve this goal requires a clear link between the microscopic pathogen-host interactions and the macroscopic, observable host response. Quantitative modeling of pathogen-host dynamics can potentially bridge the gap between these seemingly disparate length scales. Here we explore this hypothesis in the context of Lyme disease, the most prevalent vector-borne illness in the United States and the sixth most notifiable disease in the nation, which, if untreated, can lead to complications in the heart, joints, or nervous system (1,2). Specifically, we consider how pathogen-host interactions lead to the spatial and temporal evolution of erythema migrans (EM), the characteristic rash that is typically the first indicator of the disease.

Lyme disease is transmitted to humans by a bite from Ixodes scapularis ticks infected with the bacterium Borrelia burgdorferi. In the tick, the spirochetes inhabit the midgut. During feeding, the bacteria replicate and a small fraction leave the midgut and migrate to the salivary glands, where they are then transported into the dermis of the host via the saliva (3). It takes at least 48 h for the spirochetes to move from the gut into the dermis (2,3), and the tick remains attached to the host for ∼4–5 days (2,3). Therefore, at the end of the bloodmeal, a small inoculum of spirochetes is introduced into the dermis at the bite site. In the dermis, the spirochetes replicate and begin to disseminate both locally and hematogenously. While migration through the dermis can be fairly rapid (at speeds of a few microns per second (4)), the spirochetes also bind to extracellular matrix (ECM) proteins and can become transiently adhered to the matrix (4,5). The tick bite along with the presence of the spirochetes in the dermis activates the innate immune response, which includes uptake of spirochetes by immune effector cells (2,6,7). Consequently, dendritic cells release cytokines that act as a signal to monocytes from the bloodstream to differentiate into phagocytic cells, such as macrophages (8,9). The release of proinflammatory cytokines by macrophages leads to further recruitment of innate immune cells and T cells to the infected region (2,7). This inflammatory cascade also causes hyperemia in the capillaries, leading to the characteristic rash that is usually the first symptom of infection (2,3).

The EM rash, then, serves as a marker for the innate immune response during the initial stages of Lyme disease and should be sensitive to the pathogen-host dynamics that accompany this disease. But what features of the spirochetal infection and immune response are the most important factors of the spread of this rash? Clearly, because most infections do not produce similar rashes, the behavior of the bacterium must be important. Here we hypothesize that the motility of the bacterium is a prime factor and that the details of the immune response are less important. To test this hypothesis, we developed a mathematical model that contains many of the basic features of the dynamics of each of these processes (Fig. 1 and Materials and Methods). We show that this minimalistic model is sufficient to explain the clinically observed progression of the early stages of Lyme disease and predicts which pathogen-host interactions are most relevant in determining the morphology and spreading rate of the EM rash. These results suggest that this simple yet quantitative model can be informative about the efficacy of antibiotics. Simulations then predicted the rate that spirochetes are cleared from the dermis under typical treatment.

Figure 1.

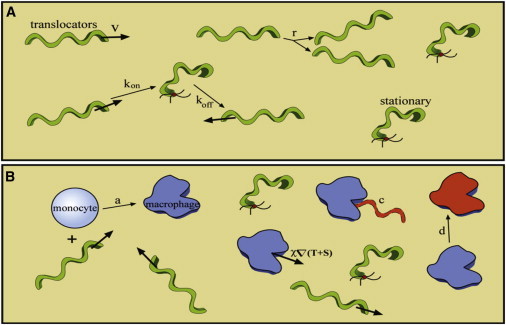
Schematic of the model. (A) The pathogen-specific dynamic processes that occur in the host. Our model includes translocation of the spirochetes through the dermis with velocity ν, binding and unbinding of the spirochetes to the ECM with rate constants k_on and k_off, respectively, and replication at a rate r. (B) The pathogen-host interactions. We consider macrophage activation from a pool of monocytes, which is proportional to the concentration of bacteria and a rate constant a. The macrophages then use chemotaxis to pursue the bacteria, which are cleared by the macrophages with a rate constant c. The macrophages are cleared or die at a rate d. Parameter values are given in the text and Table S1 in the Supporting Material. To see this figure in color, go online.

Materials and Methods

The mathematical model

Our model for pathogen-host dynamics captures the spread of the Lyme disease rash using parameters that have direct physical interpretations. The model contains spirochetes that grow with a replication rate, $r.$ As the spirochetes disseminate through the collagen-rich extracellular matrix, transient adhesions to the matrix result in the formation of two spirochete populations, a translocating population, which we denote as T, and a stationary population (4), S. The switch between these two states is defined by first-order reactions with transition rate constants k_on for binding to the matrix (T→S) and k_off for unbinding from the matrix (S→T). When stationary spirochetes release from the matrix and become translocating spirochetes, they often change direction. Therefore, on long timescales, the spirochetes exhibit diffusive behavior. The diffusion coefficient is then related to the average velocity of the translocators divided by the off rate, D = ν²/k_off, where ν is the velocity of the spirochetes.

The host’s innate immune system responds to these invading pathogens via a complex signaling pathway that involves recognition of the pathogen and activation and inhibition of immune cells by pro- and antiinflammatory cytokine release (10,11). Here we simplify this system by lumping many of these affects together into a local immune response. Proinflammatory cytokines activate monocytes from the blood, which differentiate into macrophage cells (8). These activated macrophages are significantly more effective at clearing spirochetes than the monocytes and are the first phagocytes to arrive at the site of spirochete inoculation (12). We denote the dermal density of active macrophages as M, and use this population to track the immune response. We assume that the pool of monocytes in the blood is fairly constant and that macrophage activation is proportional to the local spirochete burden. We, therefore, use a first-order reaction to describe the activation of the macrophages with an activation rate constant a. This assumption is consistent with in vitro data that cytokine release increases monotonically with the concentration of spirochetes (13). While these assumptions are an oversimplification, it can serve as a test for how important the details of the immune response are to the spread of the EM rash.

Macrophages migrate toward invading spirochetes. Movement of the macrophages is modeled using the Keller-Segel model for chemotaxis (14), which sets the speed that the macrophages migrate toward a population of bacteria as being proportional to the gradient of the bacterial concentration. A chemotactic rate constant, χ, defines the speed. Using that macrophages can move at a rate of microns per minute allows us to estimate χ. Active macrophages phagocytose the spirochetes. Experiments suggest that the rate of phagocytosis is dependent on the ratio of macrophages to spirochetes (15). We, therefore, model phagocytosis as a second-order reaction that depends on both the macrophage and spirochete concentrations with a clearing rate constant c. Finally, macrophages are cleared from the dermis with a clearing rate constant, d.

Other groups (see Segel et al. (16) and Penner et al. (17)) have derived complex reaction-diffusion equations to describe the innate immune signaling that leads to the formation of a skin rash. Our model is based on a highly reduced version of this previous work. Therefore, we propose the following model for the pathogen-host interactions that occur during the early stages of Lyme disease:

$$\frac{\partial T}{\partial t}=\underset{\text{Dissemination through host}}{\underbrace{D{\nabla }^{2}T}}+\underset{\text{Replication}\text{rate}}{\underbrace{rT}}+\underset{\text{Dermal}\text{release}}{\underbrace{k_{\text{off}}S}}-\underset{\text{Dermal}\text{binding}}{\underbrace{k_{\text{on}}T}}-\underset{\text{Clearing}\text{rate}}{\underbrace{cMT}},$$ (1)

$$\frac{\partial S}{\partial t}=rS+k_{\text{off}}T-k_{\text{on}}S-cMS,$$ (2)

$$\frac{\partial M}{\partial t}=\underset{\text{Chemotaxis}\text{toward}\text{bacteria}}{\underbrace{-\stackrel{\rightharpoonup }{\nabla }·\left(\chi M\stackrel{\rightharpoonup }{\nabla }\left(T+S\right)\right)}}+\underset{\text{Activation}\text{rate}}{\underbrace{a\left(T+S\right)}}-\underset{\text{Clearing}\text{rate}}{\underbrace{dM}}.$$ (3)

We assume circular symmetry about the bite site and that the dermis is thin compared to the lateral extent of the rash. Therefore, we simulated the dynamics of Eqs. 1–3 in axially symmetric, polar coordinates using a discrete finite volume method with a semiimplicit Crank-Nicholson time-stepping routine. The equations were solved in MATLAB (The MathWorks, Natick, MA) using a 40-cm grid of 300 nodes and a time-step of 10⁻² days, with runs simulated for a total time of 20–30 days.

Results and Discussion

To construct our model for the evolution of the EM rash, we first consider the spirochete-specific dynamic processes that occur in the host (Fig. 1 A). The bacteria translocate through the dermis with velocity ν, which is estimated to be ∼1–4 μm/s based on intravital imaging and in vitro measurements in gelatin matrices (4). Spirochetes also bind to the ECM using adhesion molecules expressed on the outer membrane with rate constant k_on. These stuck or stationary bacteria unbind with rate constant k_off and translocate away from this location, often in a new direction. The rate constants are likely of ∼0.01 s⁻¹ (4). Because the bacteria swim in roughly straight paths and can randomly change direction, dissemination through the dermis is modeled as a diffusive process, with diffusion coefficient D ∼ ν²/k_off. The bacteria also replicate at a rate r (∼1–2 days⁻¹) (18).

Next, we consider the pathogen-host interactions (Fig. 1 B). Identification of the invading spirochetes triggers cytokine release that causes monocytes from the blood to become activated macrophages. We lump this entire activation pathway into a single, first-order process with a rate constant a (∼1 days⁻¹) (8). The macrophages track the bacteria using chemotaxis; their speed is proportional to the gradient of the bacterial concentration. A rate constant c (∼5 days⁻¹) defines the rate that bacteria are cleared from the dermis by the macrophages. The macrophages are cleared or die at a rate d (∼0.2 days⁻¹) (19), which is likely comparable to the timescale associated with the antiinflammatory response. Parameters values are given in Table S1 in the Supporting Material.

Clinical observations of erythema migrans in patients with Lyme disease are classified into three separate morphologies: homogenous erythemas, which are solid, fairly uniform colored rashes (Fig. 2 a); central clearing rashes, which are rashes whose cleared center is surrounded by a single ring (Fig. 2 b); and central erythemas, which are the characteristic bull’s-eye rashes that can have single or multiple rings (Fig. 2 c). We used our model to simulate the spatiotemporal dynamics of spirochetes and activated macrophages in the dermis. Because inflammation causes the rash, we use the density of macrophages as an indicator of the rash appearance. Simulations of this model then reproduce all three rash morphologies (Fig. 2, d–f) and predict that the principle contributor to the formation of the different Lyme disease rashes is the rate at which active macrophages are cleared from the dermis. A fourfold increase in this parameter is sufficient to transform a homogenous erythema to a central clearing rash, and less than twofold further increase, leads to a central erythema. Combinations of the macrophage clearing rate with the bacterial replication rate and the incubation period for the infection were also found to affect the morphology of the Lyme disease rash (Fig. 2, j and k).

Figure 2.

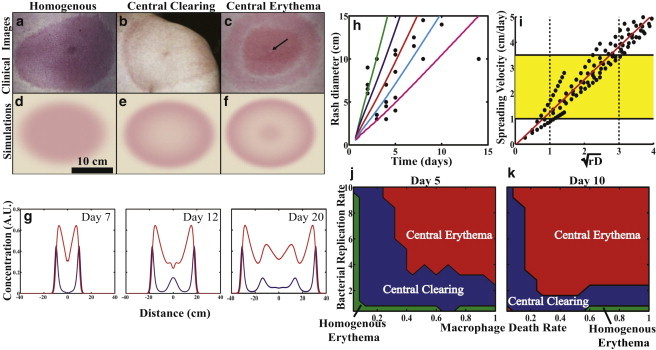
Pathogen-host dynamics recreate the Lyme disease rash. Clinical images of (a) homogeneous erythema, (b) central clearing, and (c) central erythema (arrow points at punctum) taken from Dandache and Nadelman (3) and Nadelman and Wormser (31), and reprinted with permission from Elsevier and Robert Nadelman. (d–f) The model recreates all three rash morphologies using realistic parameter values. (g) Time series of the spatiotemporal evolution of a central erythema, showing normalized bacterial (blue) and macrophage (red) densities at three separate time points. (h) Comparing the model results with different bacterial diffusion coefficients (2 cm²/day (green), 1 cm²/day (blue), 0.5 cm²/day (red), 0.25 cm²/day (cyan), and 0.1 cm²/day (magenta)) to clinical data on the spread of the rash (21) suggests that D ∼ 0.25 cm²/day. (i) The model predicts that spreading rate is proportional to the square-root of the replication rate and diffusion coefficient (yellow box). Clinically observed range of spreading velocities; (dashed lines) predicted range for the product of the bacterial replication and diffusion rates. (j–k) Phase diagrams for the rash morphologies at two time points illustrate that the primary parameters controlling rash morphology are the macrophage clearing rate, spirochete replication rate, and time since infection. (d–f) See Movie S1, Movie S2, Movie S3, Movie S4, Movie S5, and Movie S6 in the Supporting Material. To see this figure in color, go online.

One benefit of the model is that it allows us to predict the densities of the bacteria in relationship to the rash as a function of time during spreading. Fig. 2 g shows a radial slice through a simulated central erythema and shows how the spirochete and macrophage populations change as the rash progresses. The model predicts that the rash begins as a small homogeneous rash. Activation of the innate immune response is strongest at the center of the rash and clears most, but not all, of the bacteria from the center within ∼1 week. However, bacteria at the edge of the rash continue to spread outward, further activating the immune response away from the edge. Therefore, the rash grows, but the center becomes less inflamed. As time progresses, though, the spirochetes resurge at the center, leading to the characteristic bull’s-eye pattern often observed with Lyme disease (Fig. 2 g). This local resurgence near the site of the initial inoculation has been observed in experiments on mice where spirochete burden was measured in the dermis of an infected foot over the course of 55 days (20). Our simulations and these experiments both show an initial resurgence within approximately one week after infection.

A clinical trial with 24 Lyme disease patients measured the diameter of the Lyme disease rash after an incubation period (21). Fitting the clinical data with our model, we concluded that a diffusion coefficient ≤1 cm²/day was necessary to recreate the clinically observed spreading velocity range of 1–3 cm/day (3,21,22) (Fig. 2 h). This approximate value for the diffusion coefficient is exactly what is predicted based on the speed that the bacteria move through the dermis and the rate that they unbind from the ECM (4) (Fig. 1). An alternative mechanism driving the spread of the EM rash could be that cytokine reactions and diffusion are sufficient to account for the spatiotemporal dynamics. However, if spreading were controlled by cytokine diffusion, then any localized skin infection could lead to a large rash. In addition, measurements of cytokine mobility through epidermal mimics suggest that cytokine diffusion coefficients are ∼10-fold smaller than the coefficient that we estimate for B. burgdorferi (23). Therefore, it is unlikely that the EM rash is solely determined by cytokine dynamics.

Our model lets us further examine what pathogen-host interactions determine the rate at which the rash spreads. We find that the two most dominant parameters are the bacterial diffusion and replication rates. Indeed, we find that the spreading velocity is linearly dependent on the square-root of the product of these two parameters (Fig. 2 i). In addition, we find that macrophage chemotaxis toward the bacteria does not affect the rash appearance or the overall clearing of the bacteria. Instead, monocytes in the immediate vicinity must be activated into macrophages to clear the spirochetes from a given region. These findings suggest then that the rate of rash spreading is determined by pathogen-specific parameters. The model then suggests that strains of Borrelia found in Europe and Asia, which cause larger skin lesions, may replicate or disseminate faster than the strains that produce more slowly spreading rashes.

For B. burgdorferi to evade the immune response, it seems counterproductive that the spirochetes bind to the ECM. It was recently suggested, though, that this stationary population of bacteria could be beneficial, with the stationary state acting as a decoy that allows the translocating bacteria to escape (4). We used our model to explore this hypothesis and found that the stationary state does not assist immune evasion. However, the presence of the stationary state only leads to minor increases in the number of bacteria that get cleared and similarly small reductions in the spreading rate (see Fig. S1 in the Supporting Material). Therefore, binding to the ECM is not strongly detrimental to infection and likely provides some other benefit to the bacterium.

The standard treatment plan for a patient presenting with Lyme disease is doxycycline or amoxicillin administered for no more than 30 days (24). The dosage of these treatments is set to maintain the antibiotic concentration in the blood above the minimum inhibitory concentration over this time period. Although this treatment plan is usually successful in clearing the bacterial infection, our model provides a means for predicting the efficacy of different modes of antibiotic therapies on clearing spirochetes from the dermis. We therefore modeled antibiotic treatment by assuming that a patient presenting with a given rash morphology was administered antibiotic such that the effective antibiotic concentration in the dermis was maintained at the minimum inhibitory concentration. We then simulated the progression of each rash type over the course of four weeks of treatment. For all three rash morphologies, we found that bacteria were cleared from the dermis within roughly the first week of treatment; however, the dynamics of disappearance of the rash appearance varied depending on the type of EM with which the patient presented (Fig. 3).

Figure 3.

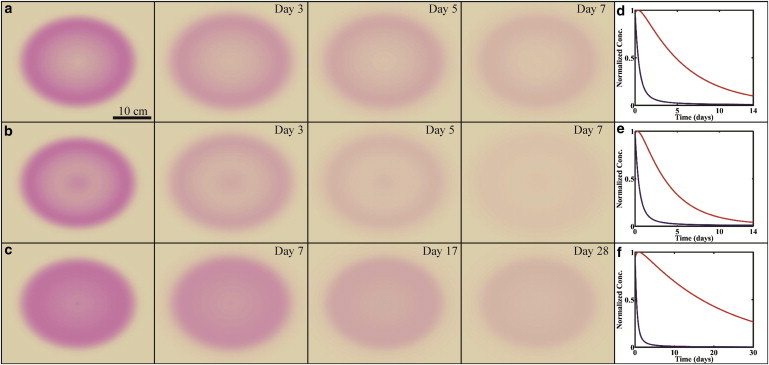
Effects of antibiotic therapy on the clearing of the three rash types. (a–c) Homogeneous rashes are predicted to take longer to clear than central clearing and central erythemas. (d–f) Normalized total number of bacteria (blue) and macrophages (red) as a function of time. For all rashes, the bacteria are mostly cleared within a few days; however, for homogeneous rashes, the macrophages take longer to clear due to the slower clearing rate. Parameter values for the rashes are the same as in Fig. 2. See Movie S7, Movie S8, and Movie S9 in the Supporting Material. To see this figure in color, go online.

Rashes characterized by central erythema or central clearing rashes resolved within the first week of antibiotic treatment, whereas homogenous erythemas were still present, in some cases, even after four weeks. The model suggests that the homogeneous EM will persist longer than the other rash types, because the appearance of this type of rash is predicted to depend most strongly on the clearing rate of the macrophages, which is slower for homogeneous erythemas. Therefore, the inflammation is predicted to persist longer in patients with homogeneous rashes. Clinical findings support some of these predictions. For example, studies done in the United States and Europe have found that 10-day antibiotic regimes are as effective as longer-term treatments and that the persistence of the EM rash beyond the treatment time-frame is not necessarily an indicator of the efficacy of the therapy (25,26).

Here we have described a simple model for the pathogen-host interactions that occur during the first weeks of Lyme disease. This model captures the spreading rate and morphological characteristics of EM rashes, which suggests that the series of fundamental processes that we consider, i.e., replication and migration of the spirochetes, activation and subsequent chemotaxis of phagocytic cells (such as macrophages) that then track down and kill the bacteria, and, finally, deactivation or death of the macrophages, are the dominant features affecting the spread of the infection through the host. Each of these processes is characterized by a single parameter, which can, in principle, be experimentally measured and/or clinically perturbed. Other models have also investigated skin rash dynamics but have focused primarily on describing the complex signaling that is involved in the innate immune response (10,11,16,17,27,28).

Our results suggest that, at least in the context of the Lyme disease rash, the details of the immune response are not as important as the fundamental processes that we considered. However, we expect that a full description of the innate immune response will produce quantitative differences to what we predict here and would provide a better description of the spreading of the rash. Therefore, our model can stand as a basis for subsequent work in this field. In addition, the quantitative agreement among the model, experimental data, and clinical findings suggest the possibility for developing mathematically guided treatment paradigms for this disease and possibly other emerging infectious diseases, similar to what has been done with HIV (29,30).