The Wall-stress Footprint of Blood Cells Flowing in Microvessels

Abstract

It is well known that mechanotransduction of hemodynamic forces mediates cellular processes, particularly those that lead to vascular development and maintenance. Both the strength and space-time character of these forces have been shown to affect remodeling and morphogenesis. However, the role of blood cells in the process remains unclear. We investigate the possibility that in the smallest vessels blood’s cellular character of itself will lead to forces fundamentally different than the time-averaged forces usually considered, with fluctuations that may significantly exceed their mean values. This is quantitated through the use of a detailed simulation model of microvessel flow in two principal configurations: a diameter $D=6.5$μm tube—a model for small capillaries through which red blood cells flow in single-file—and a $D=12$μm tube—a model for a nascent vein or artery through which the cells flow in a confined yet chaotic fashion. Results in both cases show strong sensitivity to the mean flow speed U. Peak stresses exceed their means by greater than a factor of 10 when $U/D\mathrm{\lesssim }10$ s⁻¹, which corresponds to the inverse relaxation time of a healthy red blood cell. This effect is more significant for smaller D cases. At faster flow rates, including those more commonly observed under normal, nominally static physiological conditions, the peak fluctuations are more comparable with the mean shear stress. Implications for mechanotransduction of hemodynamic forces are discussed.

Introduction

The mechanotransduction of hemodynamic forces into biochemical signals is well understood to be an essential factor in the development (1–9) and maintenance (10,11) of vascular systems. As such, its role is evident in several disease processes, including angiogenesis in cancerous tumors (12) and in atherosclerosis (10,13,14). The hydrodynamic forces exerted by the flowing blood are usually discussed in terms of its two main components: the shear stress exerted on the vessel walls by fluid friction and the normal stress, which is predominantly the pressure in the vessel. Of these, transduction of shear stresses is generally thought to be the principal driver for the response of endothelial cells (10), and it is usually quantified by its time-averaged mean value. With our detailed model, we consider both the mean and fluctuations of both components due to the flowing cells that make up the blood. In addition, for our round-vessel model, we also compute the instantaneous circumferentially directed shear traction. This component has zero mean because of the symmetry in our model but significant fluctuations because of the symmetry-breaking motion of the blood cells.

Experiments have demonstrated a remarkable sensitivity of vascular development to hemodynamic details. Lucitti et al. (15), for example, showed that sequestration of blood cells early in the development of the mouse yolk sac vasculature inhibits normal vascular network development via remodeling. Though shear stress was not directly measured, flow rates seemed unaffected by this sequestration. Thus, decreased stress because of the decreased resistance of the lower viscosity cell-free flow is implicated as the missing hemodynamic trigger for remodeling in the mice with sequestered red blood cells. In viewing these results, however, it is curious that the effective viscosity change is expected to be relatively small given the already low hematocrit $\left(H_c\right)$ of the nascent circulatory system. For example, measurements of embryonic chick blood viscosity as a function of hematocrit suggests less than a factor-of-two change in the effective viscosity (16). Data for low $H_c$ human blood show similarly modest changes (17). This implies a strong sensitivity to hemodynamic details. Remarkably, Lucitti et al. (15) show that increasing the viscosity of circulating plasma by introduction of hetastarch seems to recover superficially normal development, presumably because it increases hemodynamic stresses above some mechanosensing threshold. The present study considers the potential role of the time-fluctuating stress caused by the blood cells themselves, not only the mean shear.

Similarly, there is evidence from chick embryos that the endothelial cells are sensitive to the time-dependent character of the stress. Buschmann et al. (6) show that pulsatile flow augments mRNA expression of arterial (as opposed to venous) markers. They proposed a relative positive slope index (RPSI) as a metric for pulsatility that correlates with the establishment of artery versus vein identity. This metric is based on velocities deduced from the observed motion of red blood cells, which are relatively easy to see and provide a flow speed estimate that agrees reasonably well with more detailed velocimetry, even though the cells are too large to precisely track the flow in small vessels (18). Vessels with RPSI $>7.9$ correlate with their development as arteries, which suggests not only that endothelial cells can sense changes in wall shear stress, but also that they might be particularly sensitive to rapid changes. It was also noted in this study that upstream of a ligation in an artery, where it would then be exposed to pressure but not shear fluctuations, arterial marker expression was suppressed, with the implication that shear and not pressure fluctuations drive the identity selection. In the present study, we consider red-blood-cell-associated stresses, which are similarly time-dependent but less well studied in vivo.

Studies of cultured cells have similarly shown sensitivity to velocity waveform in regard to atherosclerosis (13,14,19) and the formation of the endothelial glycocalyx (20). Recently, detailed harmonic analysis suggests that different frequency components within a waveform might play distinct roles in gene expression (21), which further motivates the development of tools for studying the effects of the stress waveforms experienced by endothelial cells (22).

Given all these observations of sensitivity to the details of the hemodynamic stresses, we consider the possibility that in small vessels, even those in capillary beds that are shielded from the arterial pulse, the cellular character of blood per se might alter mechanosignaling by imposing stress fluctuations with particular space and time characteristics. This might be potentially important in tumor angiogenesis and in development, which is often used as a model for adult pathologies such as cancer. In particular, we consider the effects of the circulating red blood cells on the space-time character of wall stresses. A single-phase Newtonian Poiseuille flow model (Fig. 1 a) can provide useful rough estimates of mean shear stresses, but since hemodynamic details have been shown to be important in cases, such models might also neglect important factors. The addition of cells to plasma obviously increases its effective viscosity and introduces a non-Newtonian rheology that blunts velocity profiles (23). This leads to higher wall stresses (Fig. 1 b), which have been the subject of extensive experiments to quantify the nonmonotonic relationship between model-vessel diameter and the effective viscosity, which is directly related to the mean wall shear stress (24). Though surely more realistic that a Poiseuille model, a homogeneous-blood model that reproduces this behavior still neglects the fluctuating stress footprints of the cells. The cellular character will alter all components of the instantaneous wall stresses. Each passing blood cell, either alone or collectively with other cells, will exert a transient stress footprint on the wall (e.g., Fig. 1 c).

Figure 1.

Schematics showing the anticipated mechanism for wall stress τ to increase from (a) a plasma-only Poiseuille flow model, to (b) a mean cellular flow with higher effective viscosity and blunted mean flow profile, to (c) the instantaneous wall stress fluctuation because of a passing blood cell. To see this figure in color, go online.

We can anticipate that wall stresses associated with the cellular character of blood will be particularly pronounced in vessels of size comparable with the cells ($\sim 8$ μm). When so confined, blood cells are expected to be pressed close to the vessel wall or, more specifically in most cases, its glycocalyx lining. Where this happens, the relatively high rate of strain in the small plasma-filled space between the cell and the wall will exert a relatively high shear stress on the wall (Fig. 1 c). This will be most extreme in the smallest vessels, where the cells must deform to even fit within the lumen. Flow in such vessels has been studied in axisymmetric single-cell model configurations using the lubrication limit of the flow equations (25,26). Red blood cells can be deformed significantly by flow, but they elastically resist deformation in slow flows and are therefore relatively rigid in this limit (27). Slow-flow behavior is anticipated to be particularly relevant when considering the onset of vascular flow in development and as new vessels first lumenize. In this case, we anticipate the mean shear stress will be low because of the slow mean flow but instantaneously have strong peaks as relatively undeformed cells pass close to the vessel walls.

In vivo measurement techniques are advancing to the point where wall shear stresses can be deduced via the measurements of velocity profiles using particle image velocimetry (18). However, these methods do not yet have the resolution to quantify close interactions between blood cells and the vessel wall, as would be necessary to measure the time-dependent peak stresses that occur during these close encounters. Visualizing flow within the $\sim 1$ μm spacing between a red blood cell and the wall in a small vessel will challenge both the wavelength restrictions of standard optical methods and the visualization seeding, which is typically done with particles not much smaller than 1 μm (18). We therefore investigate this with a detailed simulation model, which has been validated against rheological measurements (27,28) and used to study various microcirculatory flows (29–31). Past simulation models that have considered the stress footprint of passing cells have been restricted to two dimensions and do not consider physiologically realistic close interactions between the cells and the vessel walls (32–34).

The next section summarizes the simulation model used for these investigations. The flow solver provides a particularly detailed description of the finite-deformation dynamics of the red blood cells, using a numerical discretization that provides an accurate representation of their dynamics, even when the cells approach closely to each other or the vessel walls. Results for the wall stresses, induced by the cellular blood flow, are provided in the Results section. These include the effects of flow rate, tube diameter, and hematocrit. Some possible implications for mechanotransduction are discussed along with the conclusions in the final section.

Simulation Model

Configurations

As a model for microvessels, we consider streamwise-periodic round tubes of length L and diameter D, as shown in Fig. 2. Streamwise periodicity provides a realistic and convenient way to represent segments of longer microvessels, away from the influence of any upstream or downstream conditions. This facilitates simulation of relevant configurations without the computational expense of simulating long vessels. The particular local stresses at vessel junctions are potentially important but are not considered in this study, which focuses on fully developed flow. A no-slip boundary condition is enforced on the vessel walls, which are assumed to be rigid based on observations of microcirculatory flow beyond the reach of the arterial pulse wave (35). In reality many vessels have a viscoporous glycocalyx lining, but it has been shown that the flow within it drops rapidly to zero (36,37). Thus, from the perspective of the flowing bloodstream a no-slip boundary condition provides a reasonable model. Potentially important effects of the glycocalyx are discussed in the final section.

Figure 2.

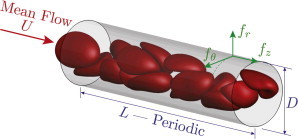
Simulation schematic showing streamwise $f_z$, wall-normal $f_r$, and circumferential $f_{\theta }$ wall traction components. To see this figure in color, go online.

The parameters for all cases simulated are summarized in Table 1. Vessel diameters between 6 and 12 μm were used to represent conditions from capillaries, in which the red blood cells flow in tight single-file formation, to larger capillaries or nascent arterioles or venules, where the blood cells are also highly confined but flow in an apparently random fashion. Mean flow speeds are selected to range from $U\approx 0.02$ mm/s, which is physiologically slow, up to $U\approx 20$ mm/s, which exceeds most observations of flow in vessels of these sizes. The slow flows represent cases in which the red blood cells are sufficiently stiff to resist significant flow-induced deformation. In contrast, for the faster flows deformations are pronounced. The corresponding pseudo-shear rates $U/D$, often used to quantify this, are also listed in Table 1 and span from 0.71 to 478 s⁻¹. We anticipate a potential change in behavior around $U/D\approx 10$ s⁻¹ because this is approximately the inverse relaxation time of a typical blood cell (38). Deformation-flow coupling has been studied in the single-file regime using semi-analytical models by Secomb et al. (39) and with simulations by Pozrikidis (40). Recently, simulations in a slightly larger diameter model, just large enough to permit the chaotic flow of blood cells, have been use to quantify the changes that occur with increasing flow rate in that case (27).

Table 1.

Simulation parameters

D [μm]	L [μm]	$H_c$	$N_{\text{rbc}}$	U [mm/s]	$U/D$ [s−1]	$N_p$	$N_w$
6.5	113.2	0.2	8	0.018	0.78	32	98,604
				0.10	4.5
				0.27	11.7
				1.1	49.0
				4.6	199.6
6.0	83.1	0.2	5	4.4	206.8	32	118,604
6.5	113.2		8	4.6	199.6	32	98,604
7.0	97.6		8	4.7	189.3	24	78,804
8.0	74.8		10	4.8	172.7	16	43,164
9.0	70.9		12	5.0	156.7	16	43,164
10.0	71.8		15	5.1	143.8	16	43,164
11.0	59.3		15	4.9	125.9	18	43,164
12.0	49.8	0.12	9	1.3	119.6	16	9,604
		0.16	12
		0.20	15
		0.24	18
	49.8	0.20	15	0.03	0.71	12	26,344
				0.31	7.3	16	26,344
				1.3	29.9	16	9,604
				5.1	119.6	18	9,604
			20.3	478.0	24	9,604

Hematocrits for most cases presented in this study were set to be $H_c=0.2$, which allows the cells to flow spaced out in their single-file line as is observed in the smallest tubes. We shall see in the Results section that each cell in this case seems to exert an independent stress footprint on the wall, which is expected to be insensitive to $H_c$. For the largest $D=12$ μm case, hematocrit was varied from $H_c=0.12$ to 0.24, spanning a range of typical microcirculatory values. Tube lengths and numbers of cells simulated $N_{\text{rbc}}$ were adjusted accordingly as listed in the table.

Flow solver

Full details of the finite-deformation model of the red blood cells and its coupling with the fluid mechanics of their cytosol and suspending plasma are reported elsewhere (28). Both the plasma (17) and cytosol (41) are assumed to be Newtonian fluids, a quantitatively accurate and widely used approximation. The slightly higher mass density of red blood cells relative to the plasma is neglected, which is a good approximation given that there is negligible inertia in the configurations we consider and settling velocities of blood cells are slow. Similarly, intermolecular forces, such as those that would lead to red blood cell agglomeration (42,43), are neglected because they are so short range and often of negligible strength (44). We next present only a synopsis of the particular features of the model. References are available that provide a thorough discussion of it in context of other simulation approaches (44,45).

To represent the cell-membrane dynamics, the Skalak et al. (46) constitutive model for shear and dilatational resistance is augmented with a curvature-based bending resistance. These effects are parameterized with the three independent elastic moduli selected by Pozrikidis (40) to match mechanical measurements. Given the availability of experimental data to calibrate models, this finite-deformation linear constitutive relation is expected to provide good quantitative predictions for ordinary deformation; only in limited cases are more detailed experimental data sufficient to calibrate more sophisticated constitutive models, the importance of which has not yet been established for flowing blood cells (44). The model we use has been shown to reproduce effective viscosity measurements for flow in round tubes such as considered in this study (28).

The flow of the cytosol inside the cells (viscosity $\lambda \mu$) and plasma (viscosity $\mu =0.0013$ Pa ⋅ s) is represented in the viscous limit by a boundary integral formulation of the flow equations (47), which includes an applied pressure gradient to maintain the flow. This formulation is advantageous because it only requires refinement of the cell surface discretization to resolve close cell-cell or cell-wall interactions. A fast solver based on a particle-mesh-Ewald (PME) Green’s function decomposition (48) is used to evaluate velocities, as described in detail elsewhere (28). It provides these accurately with $O\left(N\text{log}N\right)$ operations, where N is the number of discrete points representing the cells and vessel walls, rather than a direct approach that would have an $O\left(N^2\right)$ operation count.

The cell shapes are represented using a global spectral discretization, which provides both excellent accuracy and facilitates the use of a dealiasing procedure that provides numerical stability without artificial smoothing or dissipation, which would degrade the solution fidelity (28,44). Each cell is represented by a degree $N_p$ spherical harmonic expansion, which corresponds to $3N_p^2$ degrees of freedom per cell. The nonlinear operations required to evaluate the constitutive model are computed on a mesh with $M_p=3N_p$. Faster flows lead to larger deformations, which require more modes to be resolved. The tube walls were discretized with $N_w$ linear triangular elements. Both $N_p$ and $N_w$ are also listed for all cases in Table 1.

To start the simulation, cells were initialized as spheres randomly positioned in the tube for cases with $D=12$ μm and $D=7$ μm and $U\approx 5$ mm/s. These were then run until statistically stationary. To reduce the simulation time of start-up transients, the resulting cell configurations were then used as initial conditions for the other cases, all of which where run until wall stress statistics were converged.

Results

In quantifying the wall stresses, we generally normalize fluctuations relative to the mean streamwise shear tractions ${\overline{f}}_z$, averaged in time, z and θ. For specificity, we use traction to mean a vector force per unit area and stress formally to refer to the Cauchy stress tensor $\mathit{\sigma }$, with the usual relation $\mathbf{f}=\mathit{\sigma }\cdot \mathbf{n}$ for tractions acting on a surface from the side into which its unit normal $\mathbf{n}$ is directed. Wall traction components to be reported are the components of the traction vector $\mathbf{f}$, as shown schematically in Fig. 2. In discussion, however, we also use the term stress in a less formal capacity to simply mean force per unit area with recognition that any references to its components refer in truth to tractions.

As discussed in the first section, the $f_z$ component time average has been the most studied and seems in cases to be an important mechanotrigger. The symmetry of the round tube configuration dictates that the mean stress in the θ-direction is zero: ${\overline{f}}_{\theta }=0$. The mean wall-normal (radial) stress, ${\overline{f}}_r$ is nonzero, and in principal could also be used as a reference, but in general its time average is a function of position in the tube. High upstream pressures are needed to drive flow against downstream viscous resistance, which makes interpretation of mean wall-normal stresses more involved.

Cases with $D=12$μm: chaotic flow

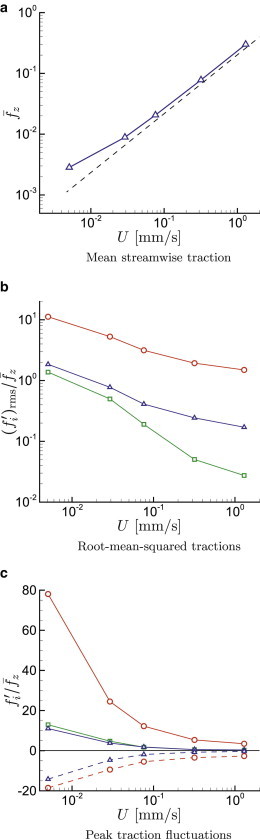
We first consider the $D=12$ μm cases with $H_c=0.2$. The visualization included in Fig. 2 shows an example of this case and suggests that the cells do seem to flow chaotically. The mean wall shear stress for our full range of flow rates increases, as expected, approximately linearly with flow rate (Fig. 3 a). Were this flow exactly Newtonian, this would be a linear relation reflecting the Poiseuille law. Here, the deviation from linear reflects blood’s well-known non-Newtonian character, which introduces a modest shear-rate dependence. This was considered in more detail using this simulation model elsewhere (27).

Figure 3.

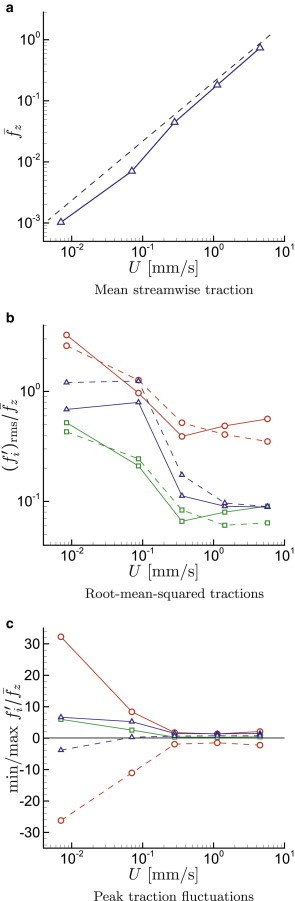
Cases with $H_c=0.2$, $D=12$μm from Table 1: (a) Mean streamwise wall traction ${\overline{f}}_z$; (b) relative root-mean-squared surface traction in the normal $f_r$$○$, circumferential $f_{\theta }$□, and streamwise $f_z△$ directions, for $\lambda =5$ (solid line) and $\lambda =1$ (dashed line); (c) for $\lambda =5$, the maximum (solid line) and minimum (dashed line) wall traction perturbations during simulations: $○$$f_r^{\prime }/{\overline{f}}_z$, □ $\left|f_{\theta }^{\prime }\right|/{\overline{f}}_z$, and $△f_z^{\prime }/{\overline{f}}_z$. To see this figure in color, go online.

Fig. 3 b shows the normalized wall-traction fluctuation intensities in the wall-normal r-, circumferential θ-, and streamwise z-directions. For these cases, in which the cells are continually distorting, their interior viscosity is potentially important, so we consider both the physiologically more relevant case $\lambda =5$ and, for reference, cases with $\lambda =1$. For slow flow, the wall-normal fluctuations $f_r^{\prime }\left(\theta ,z,t\right)\equiv f_r\left(\theta ,z,t\right)-{\overline{f}}_r\left(z\right)$ exceed the mean shear stress by about a factor of three. For the highest velocities considered, the fluctuations are still comparable with the mean, with ${\left(f_r^{\prime }\right)}_{\text{rms}}\approx 0.6{\overline{f}}_z$. Though not so large as the normal stress, the streamwise shear stress fluctuations $f_z^{\prime }\left(\theta ,z,t\right)\equiv f_z\left(\theta ,z,t\right)-{\overline{f}}_z$ have ${\left(f_z^{\prime }\right)}_{\text{rms}}\approx {\overline{f}}_z$ for the slow flows. However, these fluctuations become less significant for faster flows, dropping to ${\left(f_z^{\prime }\right)}_{\text{rms}}\approx 0.1{\overline{f}}_z$ for the fastest cases simulated. It is noteworthy that there is a significant change of behavior for $U/D\mathrm{\lesssim }10$ s⁻¹ versus $U/D\mathrm{\gtrsim }30$ s⁻¹, which spans the inverse cell relaxation time. The azimuthal shear stress fluctuations are comparable with the streamwise fluctuations, although they seem to decrease more gradually with increasing U than the streamwise shear stress. Similar to observations for the overall rheology of flow in vessels of this size (27), the cell interior viscosity does not seem to have a significant effect. The interior viscosity affects the stresses in detail, but lowering λ from 5 to 1 does not significantly change the statistical results.

Root-mean-square values offer only one measure of the fluctuation intensities, and it is unknown precisely what aspect of a stress signature will trigger any particular mechanotransduction mechanism. We can speculate that the most extreme stresses might also constitute an important mechanotransduction trigger and therefore also consider the stress peaks observed during the simulations. It turns out that the peak stresses exerted on the vessel walls are significantly more sensitive to flow conditions than the root-mean-square fluctuation intensities. These are plotted in Fig. 3 c. At slow flow rates, the peak normal stresses are particularly strong relative to the mean, deviating from the mean shear stress by about a factor of $\pm 30$. The streamwise and azimuthal fluctuations are relatively weaker, reaching a factor of six above the mean at the slowest flow speeds. For faster flow, with $U\mathrm{\gtrsim }0.3$ mm/s, as might be expected under normal fully developed conditions in a vessel of this size, the peak stresses do not much exceed the mean and become relatively insensitive to flow rate. This introduces the possibility that large fluctuations might trigger remodeling events that would lead to the low fluctuation stresses in nominally stable vascular networks.

It is interesting to note that the normal traction peaks are relatively symmetric, with nearly equivalent positive and negative values, but the streamwise shear has a distinct bias toward positive tractions. For the slowest flow, the streamwise wall traction actually reverses locally at times, which might of itself constitute a mechanical trigger.

Visualizations of the cells and the wall stresses confirm that in addition to their levels the wall stresses take on a significantly different character for the different speeds. For the slow $U/D=0.71$ s⁻¹ flow in Fig. 4 a, the cells appear as expected as relatively rigid bodies. As such, they are not so easily deformed away from the vessel walls by hemodynamic forces. Though there is no expectation that the lubrication limit of the flow equations would necessarily be accurate for such interactions, these results support similar underlying mechanisms. A hallmark of lubrication is a relatively strong dependence of stresses on separation distance h from the wall, which is consistent with both the strength of the observed fluctuations and their focal character under the points of closest approach. It is also clear in Fig. 4 c that the normal stresses have a positive (red) followed by negative (blue) pattern, as would be expected in the lubrication limit for any convex shape near a fixed wall. Lubrication would similarly predict the observed larger normal than shear stresses.

Figure 4.

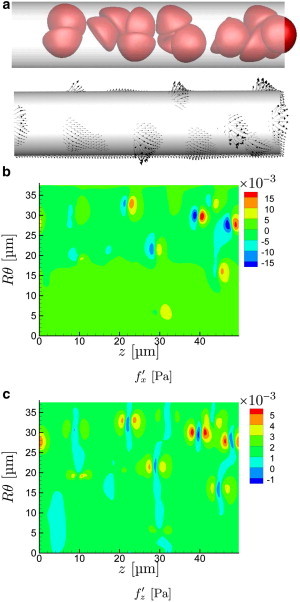
For a particular time in the $D=12$μm, $U/D=0.71$ s⁻¹ case, the frames show visualization of (a) cell positions and instantaneous tractions exerted on the wall, and (b) wall-normal and (c) streamwise fluctuation components. The angle $\theta =0$ in (b) and (c) is at the bottom and $\theta =3\pi /2$ is halfway up the in-view portion of the tube as oriented in (a). (An animation of this flow is shown in supplemental Movie S1.) To see this figure in color, go online.

With increasing flow rate, the cells are more drawn out in the streamwise direction and the near-wall cell-free layer increases in thickness, because of image-like interactions with the no-slip wall boundary (27,49). The character of their corresponding wall stress footprint also changes, as seen in Figs. 5 and 6. The wall stresses become both less intense and less focused, correlated over greater distances in both their streamwise z- and circumferential θ-directions. The close encounters that led to the particularly intense traction peaks for $U/D=0.71$ s⁻¹ are essentially absent in these cases.

Figure 5.

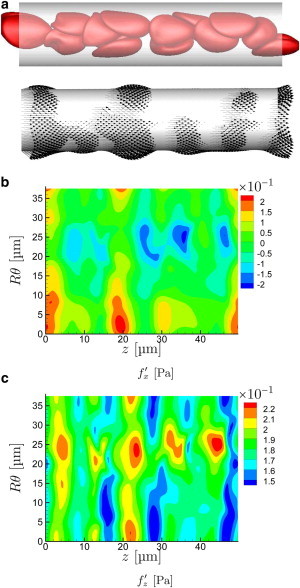
Same as Fig. 4 for $U/D=119$ s⁻¹. (An animation of this flow is shown in supplemental Movie S2.) To see this figure in color, go online.

Figure 6.

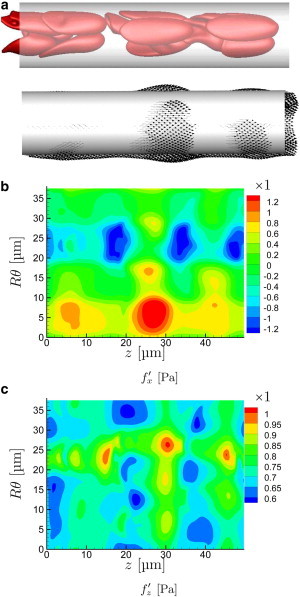
Same as Fig. 4 for $U/D=478$ s⁻¹. (An animation of this flow is shown in supplemental Movie S3.) To see this figure in color, go online.

The cases considered in detail thus far have hematocrit $H_c=0.2$. However, $H_c$ varies significantly in the microcirculation because of mechanisms such as plasma skimming (50). It is also necessarily lower at the onset of hematopoiesis, before which only plasma is circulating. In Fig. 7 we consider the effect of $H_c$, adjusting it as indicated in Table 1 by changing the number of cells in the same $D=12$ μm tube, and show that there is no strong sensitivity of ${\left(f_z^{\prime }\right)}_{\text{rms}}$ relative to mean ${\overline{f}}_z$. The only notable change is that the fluctuations become modestly more intense at $H_c=0.24$, the highest hematocrit considered, presumably because the increasing crowding in the center of the tube forces closer interactions with the vessel walls.

Figure 7.

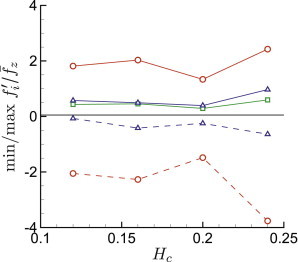
Relative peak wall tractions for $D=12$μm versus hematocrit $H_c$: normal $f_r○$, circumferential $f_{\theta }$□, and streamwise $f_z△$ directions components. To see this figure in color, go online.

Cases with $D=6.5$μm: single-file flow

The smallest capillaries require the cells to deform even to fit within their lumen. Thus, with decreasing D toward this limit, we expect closer interactions with the walls and therefore more pronounced wall-traction footprints. This is indeed seen in Fig. 8 for cases with $U\approx 4.5$ mm/s for $D=12$ μm down to $D=6$ μm. These velocities correspond to $U/D=120$ s⁻¹ for $D=12$ μm up to $U/D=207$ s⁻¹ for $D=6$, all of which are above the $U/D\approx 50$ s⁻¹ threshold noted by Pries et al. (24) above which effective viscosity is flow-rate insensitive. The figure shows that the wall-normal traction intensities increase by a factor of greater than three for $D\mathrm{\lesssim }8$ μm. This diameter approximately matches the resting dimension of a red blood cell. The shear traction also increases below this diameter, though only by about a factor of two.

Figure 8.

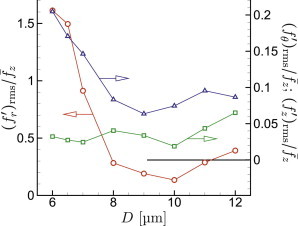
Relative root-mean-square wall traction for $U\approx 4.5$ mm/s versus vessel diameter: normal $f_r$$○$, circumferential $f_{\theta }$□, and streamwise $f_z△$ components. To see this figure in color, go online.

We focus on cases with $D=6.5$ μm as representative of flow in narrow capillaries. For this diameter, the cells line up in apparently stably translating columns, so there is little if any relative internal motion that negates any role of cytosol viscosity, so we only consider $\lambda =5$ cases in Fig. 9. As expected, the mean traction shows an approximately linear increase with increasing velocity, only deviating from this for very slow flows where their collective non-Newtonian character changes. For slower flow, the cell elastic resistance is relatively more significant, leading to thinner and more highly resistant lubrication layers (39), which increases the mean resistance as well.

Figure 9.

Cases with $H_c=0.2$, $D=6.5$μm from Table 1: (a) Mean streamwise wall traction ${\overline{f}}_z$; (b) relative root-mean-square wall traction in the normal $f_r$$○$, circumferential $f_{\theta }$□, and streamwise $f_z△$ directions, (c) for $\lambda =5$, the maximum (solid line) and minimum (dashed line) wall traction perturbations during simulations: $○$$f_r^{\prime }/{\overline{f}}_z$, □ $\left|f_{\theta }^{\prime }\right|/{\overline{f}}_z$, and $△f_z^{\prime }/{\overline{f}}_z$. To see this figure in color, go online.

The closeness of the cells to the wall in such a narrow tube increases their stress footprint intensity to be about three times larger than seen in the $D=12$ μm cases. For the slowest flow, the wall-normal tractions exceed the mean shear stress by a factor of greater than 10. The shear traction fluctuations are still large but only exceed the mean by at most a factor of two. This difference can be anticipated based on lubrication theory. For a lubrication layer of thickness h, pressure will scale as $1/h^2$ whereas shear stress will only scale as $1/h$, leading to more significant wall normal fluctuations for small h. The circumferential stresses are less pronounced; however, they are not zero because the cells do not flow exactly axisymmetricly down the center of the tube. Similar asymmetry has been observed both in previous experiments (51) and simulations (28,44).

In comparison with the $D=12$ μm results, which are shown in Fig. 3, the traction fluctuations shown in Fig. 9 exceed the mean shear for $D=6.5$ μm even more. The normal traction peaks are up to nearly 80 times greater than the mean shear. They are also asymmetric, presumably because of the streamwise-asymmetric geometry of the cells in these cases, with the positive fluctuation peaks ∼4 times as intense as the negative. Though the streamwise shear stress fluctuation intensity only exceeds the mean by about a factor of two in the slowest flows, the peaks exceed it by nearly a factor of 10. This is also true of the circumferential tractions. For the fastest flows, both $f_z^{\prime }$ and $f_{\theta }^{\prime }$ become negligible relative to their mean, but the normal fluctuations, per expectations based on lubrication theory, remain significant. These normal stresses are expected to be responsible for deforming the cells and thereby increasing the thickness of the lubrication layer between the cell and wall in a way that decreases the shear stress components.

Visualizations of the slowest- and fastest-flowing $D=6.5$ μm cases are shown in Figs. 10 and 11, respectively. These suggest that each cell creates its own seemingly independent stress footprint on the wall. Given the similarity of their shape, it is not surprising that these vary only in detail from cell to cell. For the fast flow velocity (Fig. 11 b), the obvious wedge shape plasma-filled gap between the cell and tube wall, thicker near the rounded leading side and thinner toward the rim-like trailing side, causes a positive pressure and thus a wall-normal force, as expected based on lubrication theory. This same trend is apparent for slower flow (Fig. 10 b), though it is significantly less pronounced since the cells are more rounded and do not take on so distinct a slider-bearing wedge-like geometry. In both cases, these wall-normal force reverses at the trailing edge. Similarly, wall shear stress is high immediately under the cells, as also expected based on lubrication theory. We again see that the most significant is the wall-normal component, again reflecting the lubrication scaling. At the trailing edge, where the cell’s trailing rim-like shape abruptly turns away from the wall, lubrication theory is expected to be at most only qualitatively correct. Here we see a sharp drop in the wall shear stress (Figs. 10 c and 11 c). For the slower flow cases, this is associated with a localized flow reversal and corresponding negative $f_z^{\prime }$.

Figure 10.

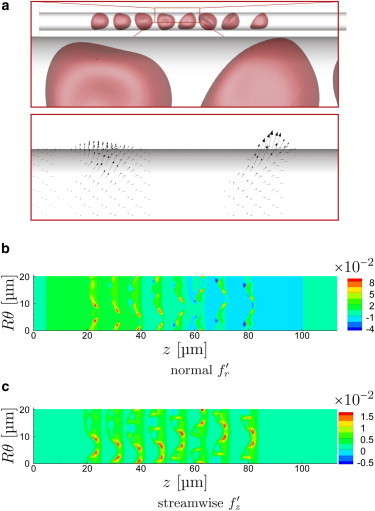
Same as Fig. 4 for $D=6.5$μm, $U/D=0.78$ s⁻¹. (An animation of this flow is shown in supplemental Movie S4.) To see this figure in color, go online.

Figure 11.

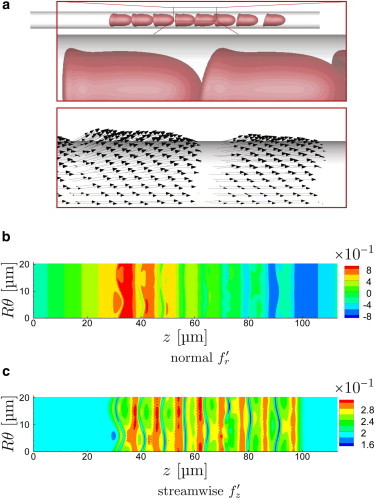
Same as Fig. 4 for $D=6.5$μm, $U/D=200$ s⁻¹. (An animation of this flow is shown in supplemental Movie S5.) To see this figure in color, go online.

Discussion and Conclusions

The principal conclusion is that in narrow vessels the cellular character of the blood significantly affects the instantaneous stresses on the vessel wall, introducing fluctuations that significantly exceed their mean values. This is true for all components of the wall traction: the wall-normal and circumferentially directed components in addition to the most often considered streamwise component. The strength of these fluctuations, relative to the mean streamwise shear stresses, is higher at slower flow rates, especially when $U/D\mathrm{\lesssim }10$ s⁻¹, which corresponds to the inverse relaxation time of typical red blood cells. For these slower flows, with lower shear rates, the elasticity of the cells resists flow-induced deformation, giving them a relatively rigid character in this low-flow-rate limit. In this case, they do not deform easily when brought close to the wall, either by the tight confines of the smallest vessels or through interactions with the other cells in larger vessels. This apparent change of character corresponds to the flow speeds at which we also see changes in the mean-stress/flow-rate relation associated with non-Newtonian behavior of the cellular suspension. We can anticipate that particularly rigid cells, perhaps brought on by senescence (38) or disease processes such as sickle-cell disease or malaria (52), might similarly play an outsized role in exerting fluctuating stresses for this same reason.

These fluctuations are particularly strong in vessels of diameter less than the resting cell shape. In such cases the cells must deform to flow through the vessel and are continuously in near contact with the vessel walls. Results show in this case that each cell has a distinct but similar traction footprint on the vessel wall, which is insensitive to the presence of the other cells. In such cases, the role of hematocrit is clear: for lower $H_c$ there will be fewer cells interacting with the vessel walls and fluctuating stress root-mean-square intensities will necessarily decrease. However, the peak stresses are expected to be nearly the same, corresponding to the peak within the footprint of any given cell. This feature is not shared by larger tubes, for which results indicate a relative insensitivity of the fluctuation intensities to $H_c$ between 0.12 and 0.24.

The goal of this study was to provide, with a detailed simulation model of realistic cellular blood flow, a measure of the stress fluctuations, with the expectation based on related observations that these might alter vascular responses. However, endothelial mechanotransduction mechanisms are not sufficiently understood to make any specific conclusions in this regard. Any altering of, for example, gene expression will depend on the specific transduction mechanism, of which there are thought to be many (53), each potentially sensitive to different components of the traction. No attempt is made to account for any particular microstructural mechanotransduction mechanism in our model. Furthermore, traction means, fluctuation frequencies, or peaks of any component might also each affect different mechanisms differently, or not at all. It is particularly intriguing that the slower flows show local reversal of the shear stress, which could of itself potentially constitute a mechanotrigger.

In interpreting our results, it should be recognized that we computed tractions on the no-slip wall boundary of a round tube. Such a geometry is often employed to provide a clear point of comparison between different cases in a vessel-like geometry. However, we also must recognize that mechanotransduction might involve more complicated structures than are included in our current model, such as the endothelial glycocalyx or cilia (7,53,54). The fluctuating character of the stresses we estimate are particularly salient for both. The glycocalyx will attenuate both temporal and spatial fluctuations, as anticipated by Secomb et al. (25) with an insightful theoretical model. They develop a wavenumber–frequency dependent transfer function that relates flow stresses to those experienced by the cells underlying the glycocalyx and show that short wavelength and high frequencies will be most attenuated. The glycocalyx also has the potential to affect the flow of cells near to it, particularly their wall proximity, which seems to be an important factor in the present study (55). Because a principal cilium can protrude away from the endothelium into the flow stream, it might be particularly sensitive to the shear stress footprints of passing cells, introducing its own space-time sensitivity. Evidence suggests that cilia-based mechanisms can indeed detect complex aspects of flow (56,57).

Given our low-flow-rate results, we can anticipate that the cellular character of blood might be particularly important in the mechanotransduction of fluid flow forces during luminization in angiogenesis of small vessels. At this point, red blood cells must deform significantly, and the resultant stresses might in part precipitate the formation of robust, fully open lumen or in the stabilization of the newly perfused branches (58).

Overall, these results suggest experiments to study the effect of red blood cells on the expression of genes that are known to respond to fluid shear in small vessels, such as in angiogenesis. A challenge in doing this is that the forces we consider depend on the confinement of the cells, and so might be missed by larger-scale in vitro devices or in any but the smallest in vivo vessels. It would seem that an in vivo and diagnostically accessible model will be required for definitive analysis. It is possible, for example, in the embryonic zebrafish model to suppress hematopoeisis at a stage where cellular oxygen transport is not yet necessary for oxygenation of tissue. Observing the effect of red blood cells on different stages of angiogenesis will provide evidence for any role of their transient induced tractions.