Sequence-Dependent Elasticity and Electrostatics of Single-Stranded DNA: Signatures of Base-Stacking

Abstract

Base-stacking is a key factor in the energetics that determines nucleic acid structure. We measure the tensile response of single-stranded DNA as a function of sequence and monovalent salt concentration to examine the effects of base-stacking on the mechanical and thermodynamic properties of single-stranded DNA. By comparing the elastic response of highly stacked poly(dA) and that of a polypyrimidine sequence with minimal stacking, we find that base-stacking in poly(dA) significantly enhances the polymer’s rigidity. The unstacking transition of poly(dA) at high force reveals that the intrinsic electrostatic tension on the molecule varies significantly more weakly on salt concentration than mean-field predictions. Further, we provide a model-independent estimate of the free energy difference between stacked poly(dA) and unstacked polypyrimidine, finding it to be ∼−0.25 k_BT/base and nearly constant over three orders of magnitude in salt concentration.

Introduction

The structure, mechanical properties, and function of nucleic acids in solution are strongly dependent on sequence-specific interactions. These interactions lead to secondary structure formation, which causes the highly charged phosphate backbone to form compact structures disfavored by electrostatics. Understanding the interplay between electrostatic repulsion and the attractive interactions that stabilize structure is a major goal in biopolymer research with implications for both our understanding of the folding of nucleic acids and proteins in vivo and our ability to exploit them in technical applications.

The two primary modes of secondary structure formation in nucleic acids are Watson-Crick basepairing and base-stacking. While base-pairing is known to be due to hydrogen bonding, the nature of the stacking interaction is considerably less well understood despite its direct relevance to a number of biological phenomena. For example, after transcription in eukaryotes, a highly base-stacked polyadenine (poly(A)) tail is added to the 3′ end of messenger RNAs to promote nuclear export and translation; these tails have been implicated in the regulation of protein expression (1). The stacked 3′ tail further protects the RNA from RNase in the cytoplasm, a phenomenon that has been exploited in DNA aptamer design (2). Further, many proteins utilize stacking interactions for single-stranded DNA (ssDNA) recognition (e.g., the OB-fold family of proteins (3)). In addition, ssDNA is now widely used to orchestrate the self-assembly of nanoscale objects (4). Thus, acquiring an understanding of the mechanical and thermodynamic properties of ssDNA as a function of sequence would be a step forward for contemporary understanding of certain biological processes, including regulation of gene expression and protein-DNA interactions, and our ability to rationally exploit ssDNA for technological purposes, from nanotechnology to drug delivery.

Certain sequences of nucleotides, particularly tracts of adenines, are known to exhibit strong stacking tendencies in single-stranded nucleic acids in the absence of a complementary strand (5). Stacking interactions between neighboring bases along the backbone cause the polymer to form single-stranded helices. From a modeling perspective, a given single-stranded nucleic acid lacking basepairing may be considered a statistical copolymer of helical (stacked) and unstructured (unstacked) polyelectrolyte domains (see Fig. 1) (6). Relative to the unstacked regions, the stacked domains are expected to be shorter—due to their helical geometry—and more rigid—due to the lack of conformational freedom of the backbone (7), but quantitative information regarding their mechanical properties is lacking.

Figure 1.

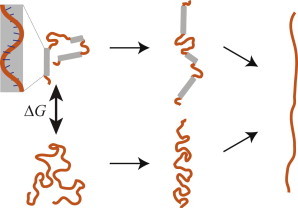
Cartoon depicting the stretching of an ssDNA capable of stacking (top) and an ssDNA incapable of stacking (bottom). Once the base-stacking is pulled out, the two polymers are in the same state. (Inset) Geometry of a base-stacked region. To see this figure in color, go online.

Single-stranded DNA’s conformation is dependent on ionic conditions due to its charged phosphate backbone. For example, the rigidity of heterogeneous sequences of denatured ssDNA—thought to be largely unstacked—has been shown to vary strongly with salt concentration (8,9). Here, we examine the salt-dependence of the elasticity of various sequences of ssDNA to explore the interplay between electrostatic repulsion and base-stacking in determining the mechanical and thermodynamic properties of the polymer. The applied force, in combination with electrostatic repulsion, disfavors stacking and this interplay leads to a variety of elastic phenomena. In particular, the low-force elasticity reveals that base-stacking significantly enhances the rigidity of the polymer, beyond that predicted by simple polymer models (6), and leads to our knowledge, a novel elastic regime at high salt concentrations. At higher forces, the stacked regions are unraveled by the tension in a weakly cooperative helix-to-coil transition (6). We measure the force at which this transition occurs as a function of salt to examine the intrinsic electrostatic tension on the polymer. We find qualitative agreement of the data with mean-field electrostatic theories (10,11), but poor quantitative agreement unless anomalously low charge densities are assumed for ssDNA. By integrating the force-extension curve through this transition, we quantify the salt-dependent work required to extend base-stacking competent and incompetent ssDNA species. We find that the difference between the two, attributed to the free energy contribution of base-stacking in the stacked sequence (see Fig. 1), to be ∼−0.25 k_BT/base and nearly independent of salt.

Methods

Sequence-specific ssDNAs were synthesized using a rolling-circle amplification strategy (12). The sequences studied here are referred to throughout this article as poly(dA), mixed base, and polypyrimidine. The 5′ phosphorylated template oligomers (with the complement of the desired product sequence) and 5′ biotin-labeled primer oligomers were purchased from Integrated DNA Technologies (Coralville, IA) (see Table 1). In the case of the polypyrimidine and mixed base sequences, the primer was designed to splint the template oligomer into a circle (13). For these two sequences, the primer and template were mixed in stoichiometric concentrations in 1× T4 ligase buffer (New England Biolabs, Ipswich, MA), heated to 95°C, and cooled to room temperature over 45 min. T4 ligase (New England Biolabs) was then added and incubated overnight at 4°C. For the poly(dA) substrate, splinting is not possible due to lack of specificity between the primer and template. In this case, the linear poly(dT) template was treated with Circligase II (Epicentre Biotechnologies, Madison, WI) to form the circular template followed by stoichiometric annealing with the poly(dA) primer. Rolling circle amplification reactions were carried out by incubating the primer-template complex at 5 nM with 0.2 mM dNTP and ϕ29 polymerase in 1× ϕ29 reaction buffer (New England Biolabs) at 30°C for 3 h followed by inactivation at 65°C for 15 min (12).

Table 1.

Identity of sequences discussed in text

Name	Template (5′ phosphate)	Product (5′ biotin)
Poly(dA)	(T)50	(A)n
Mixed base	ACTCTTCT3AT3CT4ACTTTCCAT	(AAGAGTATGGAA2GTA4GA3TA3G)n
Polypyrimidine	AGGAGAA4GA7GA3AGAAGG	(TCTCCTCCTTCTT3CT7CT4)n

The polypyrimidine and mixed-base sequences were designed and originally synthesized by Brockman et al. (13). The primer sequence is in bold in the product column and its complement is in bold in the template column. In the case of poly(dA), the primer is 5′-biotin-labeled (A)₂₀.

Magnetic tweezers protocols have been discussed elsewhere (14). Typically, a bifunctional polymer is stretched between an antidigoxigenin-coated cover glass and a streptavidin-coated paramagnetic bead. However, here we are interested in forces >20 pN, where the digoxigenin bond ruptures after only a short time (15). Thus, we use a simpler nonspecific-adsorption strategy. Briefly, the rolling circle amplification product (synthesis described above) is introduced to a cover glass with Sigmacote (Life Technologies, Carlsbad, CA) at ≈1–10 ng/μL and incubated for ≈2 h. We successfully use this procedure to tether all three ssDNA sequences from Table 1, indicating that the mechanism is independent of sequence. We posit that the ssDNA associates with the hydrophobic silanized glass via its exposed hydrophobic bases. The surface is then blocked with a solution of 2 mg/mL BSA for ≈20 min before introducing streptavidin-coated paramagnetic beads (Dynabeads; Life Technologies) which were also previously incubated in the BSA blocking buffer and which bind to the biotin moiety. Forces ranging from ≈0.05 to ≈15 pN are imparted using external magnets above the sample and 1-μm myOne beads (DynaBeads, Life Technologies). Forces approaching 100 pN can be achieved with 2.8 μm M280 beads (Dynabeads, Life Technologies). For both beads, we acquire data in the force range ≈5–15 pN.

We smooth the measured forces by fitting them to a fourth-order polynomial with respect to the magnet position (see Section S1 in the Supporting Material). The low-force extension data is then scaled to maximize overlap with the high-force extension data in the range for which the force measurements overlap (see Section S2 in the Supporting Material). A large fraction of tethers exhibited slowly increasing extensions at high force or hysteretic elasticity, effects that we attribute to the tether peeling off the surface, an artifact of our nonspecific attachment scheme; data exhibiting these behaviors were discarded. All data presented here were taken with the indicated amount of tris buffer (pH 7.5) and salt in deionized water (Millipore, Billerica, MA).

Throughout this article, we assume that the extension per base of ssDNA at 55 pN, X_{55 pN}, is independent of sequence. A simple model that fit the force-extension data for poly(A) ssRNA (6) indicates that the extension varies by <1% between stacking competent and incompetent species at forces above 50 pN, lending credence to this assumption. Due to the nonspecific nature of the ssDNA-glass interaction described above, the majority of ssDNA tethers do not persist long enough to enable taking a full data set over all salt concentrations studied here; the few that do indicate that the extension at 55 pN of each sequence varies by ≈5% from 1 mM to 1 M salt (see Fig. S3 A in the Supporting Material).

Results and Discussion

Force regimes in base-stacked ssDNA

The elasticity of ssDNA depends on its sequence. In Fig. 2, we present force-extension data at approximate physiological salt concentrations (150 mM KCl, 5 mM MgCl₂, 10 mM tris pH 7.5) for the polypyrimidine and poly(dA) sequences described above. Comparing the base-stacking competent poly(dA) and the base-stacking incompetent polypyrimidine sequence, we find a number of elastic regimes.

Figure 2.

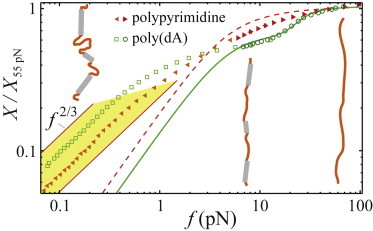
Sequence-dependent elasticity of ssDNA in approximately physiological salt conditions (150 mM KCl, 5 mM MgCl₂, 10 mM tris pH 7.5). Each sequence is represented by two force-extension curves, one at low force and one at high force. The low-force data is scaled to optimize the overlap of extensions with the high force data in the overlapping range. The full curves are normalized by the extension at 55 pN. (Solid curve) Plot of the weakly cooperative base-stacking model as fit to poly(A) data by Seol et al. (6). (Dashed curve) Unstacked state assumed by the model—a freely-jointed chain. Cartoons depict the elastic regimes of poly(dA). See text for details. To see this figure in color, go online.

The low-force elasticity indicates that base-stacking enhances ssDNA’s rigidity. Below a sequence-dependent force, the extension varies as a power law close to that expected for a self-avoiding polymer, X ∼ f^γ with γ ≈ 2/3 (16), as was previously reported for denatured ssDNA (8) (see below for a quantitative examination of this power law). Poly(dA) transitions out of the power-law regime at lower forces than the polypyrimidine sequence, consistent with scaling predictions: Long-range contacts due to polymer coiling are pulled out above a crossover force f_c ∼ k_BT/l, where l is the size of the effective Kuhn monomer (9). For ssDNA, l is sequence-specific. These data indicate that base-stacked sequences have smaller crossover forces and, therefore, longer effective Kuhn monomers. Thus, whereas the stacked regions in poly(dA) effectively reduce the polymer’s local length due to the helical geometry, this effect is more than compensated for by the base-stacking enhanced rigidity. Quantitatively, the power-law regime ends at f_c ≈ 0.2–0.4 pN. This implies that the effective Kuhn length l ∼ k_BT/f_c ≈ 10–20 nm. There is an unknown prefactor in the scaling equality for l, but we assume it to be of order unity here.

Our estimate of the Kuhn length compares well with a variety of bulk measurements of base-stacking-induced rigidity. In particular, a number of previous studies have estimated the persistence length of poly(A) ssRNA. An excellent review of these results was provided by Mills et al. (7); the values range from 3 to 8 nm, measured with a variety bulk techniques including x-ray scattering (17), viscometry (18), and transient electric birefringence (7). This would give a range of effective Kuhn lengths ≈6–16 nm, comparing favorably with our estimate. However, previous single-molecule data (8,9), molecular-dynamics simulations (19), and recent theory (20) all indicate that the persistence length is not necessarily a well-defined quantity for flexible polyelectrolytes. Indeed, we find that our poly(dA) data are not adequately fit by the Marko-Siggia wormlike chain model (21) over any substantial force range or for any salt concentration discussed in this article. Thus, though consistent with prior work on base-stacking-induced rigidity, our data further indicate that these quoted persistence lengths should only be considered phenomenological, and not with the usual interpretation pertaining to microscopic structure (e.g., an exponential decay of the tangent-tangent correlation function).

Due to the shorter effective contour length of the stacked regions (≈0.32 nm/base) compared to the unstacked regions (≈0.7 nm/base) (7), the applied force eventually unravels the single-stranded helices. A clear extension plateau at X/X_{55 pN} ≈ 0.6 indicates that a large fraction of the bases in poly(dA) are stacked at low force and that these stacked regions are robust to forces f ≤ 10 pN. Above 10 pN, the single-stranded helices unravel in a helix-to-coil transition (6). This transition displays no hysteresis for the conditions discussed here.

Comparison to poly(A) cooperative model

Buhot and Halperin (22) and Seol et al. (6) developed and applied a simple model for the force-induced helix-to-coil transition in poly(A) ssRNA. The similarity of ssRNA and ssDNA leads us to compare their model to our data. That model, as fit to the poly(A) data (6), is plotted in Fig. 2 along with the assumed elasticity of the unstacked state—a freely-jointed chain. The model captures the nature of the high-force unstacking transition in our poly(dA) data, indicating that the transition likely is weakly cooperative in poly(dA) as in poly(A). However, the data deviates at low forces. Indeed, the model qualitatively fails to predict that poly(dA) is longer than the polypyrimidine sequence at low forces. Discrepancies between the model and the data are at least partially expected: the naive nature of modeling the unstacked domains as freely jointed chains and the stacked domains as infinitely rigid rods should certainly lead to deviation. Further, the model neglects both long-range excluded volume interactions and electrostatic effects, both of which affect the elasticity particularly at low forces. Even at higher ionic strengths—conditions comparable to those used by Seol et al. (6)—the deviations from the data are significant up to ≈5 pN (see Fig. 3 D, inset).

Figure 3.

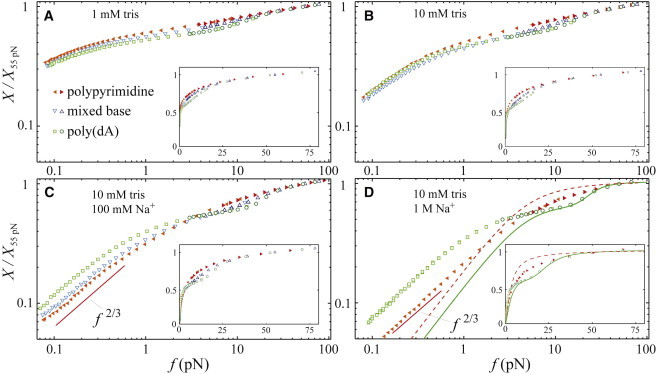
(A–D) Force-extension curves of the three different sequences of ssDNA from Table 1 in various ionic conditions, as indicated. Low- and high-force data are scaled as in Fig. 2. (Insets) Same data on linear axes to better visualize the area between curves. (In panel D, the solid and dashed curves are the same as in Fig. 2.) To see this figure in color, go online.

Salt-dependent mechanical properties of base-stacked ssDNA

To examine the electrostatic dependence of the mechanical properties of base-stacked ssDNA, we monitor the force regimes described above as a function of the monovalent salt concentration. In Fig. 3, we plot the elastic response of all three sequences for salt concentrations varying over three orders of magnitude. As the salt concentration increases, the extension for all three sequences decreases at any given force, as expected: enhanced screening of interphosphate repulsion causes the polymer to form more compact coils despite the force. Above 200 mM NaCl, the mixed base sequence displays irreproducible force-extension behavior. We attribute this to electrostatic stabilization of long-range hairpins formed via the adenines and the sparsely populated thymines in the sequence.

Low-force power law

At low ionic strength, electrostatic repulsion along the chain is large, enhancing the bending rigidity of all sequences. In fact, at the lowest salt concentrations used (≲10 mM), we do not observe a low-force power-law regime for any sequence, indicating the polymers are too stiff to coil significantly even at 0.1 pN. This implies that, for all sequences, l ≳ k_BT/(0.1 pN) ≈ 40 nm.

Beginning at moderate salt concentrations (>10 mM), a nonlinear power-law regime emerges in the low force data as discussed above. Scaling theory indicates that the power-law exponent γ (where X ∼ f^γ) reveals the solvent quality (9): In a good solvent, scaling theory predicts γ ≈ 2/3 (16), while γ = 1 in a θ-solvent (i.e., a solvent in which the polymer can be modeled as ideal). In Fig. 4, we quantify the power law in two independent ways. First, we examine correlations between the average extensions at different forces on a log-log plot (Fig. 4 A). Second, measurements of the fluctuations of the bead position at each force also reveal the effective power-law exponent at any force:

$$\gamma =\frac{dX}{df}\frac{f}{X}=k_{\perp }/k_{\parallel }$$

(this relation follows directly from the relation X ∼ f^γ), where k_⊥ (k_||) is the spring constant associated with motion perpendicular to (parallel to) the direction of applied force, which may be measured using standard magnetic tweezers protocols (14,23).

Figure 4.

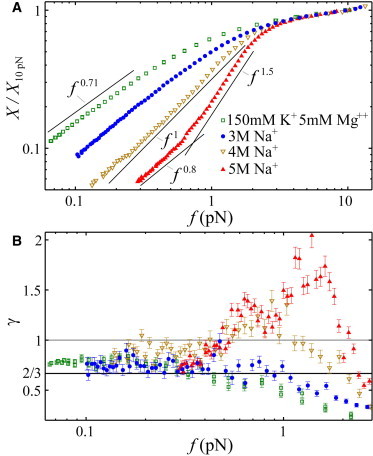
(A) Force-extension curves of poly(dA) under various conditions (salt conditions in the legend are in addition to 10 mM tris). The curves are scaled by their extension at 10 pN. At high salt, a believed novel elastic regime emerges at intermediate force. (B) Analyzing the fluctuations of the bead at each force permits a second estimate of γ, confirming the regimes observed in panel A. To see this figure in color, go online.

Closer inspection of poly(dA) at moderate salt concentrations reveals that 2/3 < γ < 1 using both methods (see Fig. 4 at approximate physiological salt concentration—150 mM KCl, 5 mM MgCl₂). Averaging over all measured γ-values <0.2 pN for eight different tethers at approximate physiological salt conditions, we find γ = 0.71 ± 0.02. This is a small, but significant, deviation from γ = 2/3. We posit that this exponent may result from a combination of good-solvent behavior, γ ≈ 2/3, from the flexible, unstacked regions (8) and ideal behavior, γ = 1, from the stacked regions.

At very high salt concentrations, electrostatic repulsion is screened away and a believed novel elastic regime emerges due to the rigidity of the base-stacked regions. In Fig. 4 A, we plot representative force-extension curves for poly(dA) at c > 1 M. Beginning at ≈4 M salt, a distinct sharpening in the force-extension curve emerges at intermediate forces; this sharpening is confirmed in Fig. 4 B where a peak begins to appear in the exponent γ in the same force range. This effect is expected for a polymer approaching a θ-point: as the excluded volume interaction gets weaker, v → 0, an ideal, thermal blob regime appears at forces k_BTv/l⁴ < f < k_BT/l (9) and manifests itself as a Hookean-spring-like behavior (X ∼ f¹). While this regime has been measured for charge-neutral poly(ethylene glycol) (24), this is the first confirmation of such a transition for polyelectrolytes of which we are aware. At these salt concentrations, denatured, mixed-sequence ssDNA was also shown to transition through a θ-point, but a thermal blob regime never appeared. In that case, we argued that denatured ssDNA was highly flexible with v ∼ l³ (9); the enhanced rigidity of poly(dA) causes the monomers to appear as effective cylinders with v ∼ l², d < l³, causing the thermal blob regime to appear. As we further increase the salt concentration to 5 M, the steepening of the power law continues to γ ≈ 1.5–2 while still reducing to γ < 1 at low force, an effect not predicted by the simple scaling analysis.

Elasticity of mixed-base sequences: broken cooperativity

The mixed-base sequence demonstrates intermediate elasticity at high force, consistent with an intermediate amount of base-stacking. However, the extension of the mixed-base sequence is unexpectedly small at low force; indeed in Fig. 3 B, it is shorter than both the polypyrimidine sequence and poly(dA). Given the intermediate nature of this sequence’s design, this result is unintuitive, but it can be explained via the weak cooperativity of the base-stacking effect: The mixed-base sequence has several short adenine tracts; stacking of these tracts locally shortens the contour length and enhances the rigidity of the polymer as with poly(dA). However, these tracts are separated by other bases, which we posit act as flexible hinges whose entropic freedom also acts to shorten the polymer’s extension. Thus, compared to poly(dA), the mixed base is shorter due to the flexible hinges breaking up the helices; whereas compared to polypyrimidine, the mixed base is shorter due to the loss of contour length. This effect is most salient at low salt, where the Debye length is significantly larger than the base-stacked adenine tracts in the sequence. At higher salt, the flexibility of the unstructured polypyrimidine out-competes the contour length loss in the mixed-base sequence (see Fig. 3 C). A systematic study of this broken cooperativity effect should be possible, varying the number and location of these single nucleotide hinges within a given sequence; however, that study is beyond the scope of this work. A similar hinging effect was proposed in 2000 to explain the rapid closing of poly(dA) hairpin loops with defects (25).

Quantifying the electrostatic tension

In addition to modulating the bending rigidity of the polymer, the salt concentration also determines the polymer’s intrinsic electrostatic tension, f_el—the tension along the polymer’s contour due to solvent-mediated electrostatic repulsion between phosphates. We exploit the unstacking transition in poly(dA) to measure this effect. From Fig. 3, it is clear that the transition from the partially stacked (low force) to fully unstacked (high force) states is salt-dependent. This suggests that unstacking is facilitated at low ionic strengths by the enhanced repulsion between phosphates on the backbone. After the treatment of the overstretching transition of double-stranded DNA by Manning (11), we assert that the structural transition in poly(dA) occurs at a force f_tot = f_applied + f_el, the sum of the applied force at the transition and the electrostatic tension, with f_el being appreciably larger at low ionic strengths, facilitating unstacking. Lacking the complicating factors of double-stranded DNA’s overstretching transition (including its sequence-dependence (26) and structurally ambiguous final state (27)), the helix-to-coil transition of poly(dA) is likely a better candidate for comparison with electrostatic theories. We estimate f_applied from the data by interpolating our high-force data with cubic splines and finding the point at which the curvature of the force-extension data changes sign (i.e., when the second derivative of the spline interpolation function vanishes; see Section S3 in the Supporting Material). As predicted above, f_applied increases with increasing salt concentration (see Fig. 5).

Figure 5.

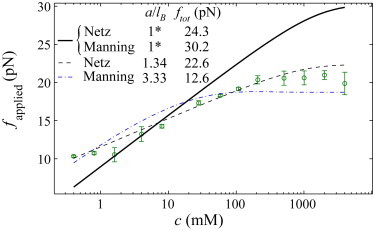
Plot of the applied force at the unstacking transition of poly(dA) as a function of ionic strength. Error bars represent the standard error of the mean of two to three measurements at each salt concentration. Also plotted are fitted expressions f_applied = f_tot = f_el, where f_el is the electrostatic tension as predicted by Netz (10) and Manning (11). Best-fit parameters are indicated in the legend. Parameters with an asterisk (^∗) are fixed in the fit. To see this figure in color, go online.

Models for the electrostatic tension have been reported recently by Netz (10) and Manning (11). Both are derived from a mean-field picture in which uniformly spaced charges on a linear backbone repel one another via a screened Coulomb potential. In the model by Netz (10), the electrostatic tension is calculated by summing Debye-Hückel potentials along the backbone and differentiating with respect to charge separation, yielding

$$f_{\text{el}}^{\text{Netz}}=\frac{k_{\text{B}}T{l}_{\text{B}}}{a^2}\left(\kappa a\frac{e^{-\kappa a}}{1-e^{-\kappa a}}-\text{ln}\left(1-e^{-\kappa a}\right)\right),$$ (1)

where k_BT is the thermal energy, l_B is the Bjerrum length (0.7 nm in water), κ⁻¹ is the Debye length, and a is the effective charge separation along the backbone—the separation after accounting for counterion condensation. Manning (11) further accounted for the entropy of condensed counterions, finding

$$f_{\text{el}}^{\text{Manning}}=\frac{k_{\text{B}}T}{{\ell }_{\text{B}}}\left(\left(2\frac{l_{\text{B}}}{a}-1\right)\kappa a\frac{e^{-\kappa a}}{1-e^{-\kappa a}}-1-\text{ln}\left(1-e^{-\kappa a}\right)\right).$$ (2)

Interestingly, accounting for the entropy of the counterions leads to negative electrostatic tensions for some values of a/l_B and κ⁻¹ in this model (11). Accounting for Manning condensation (28), we fix a = l_B and fit the models to the data (f_applied = f_tot = f_el) using f_tot as the only free parameter and setting f_el = f_el^Netz or f_el^Manning. This approach leads to poor agreement with the experimental data (both fits converge to the solid line in Fig. 5). Further reducing the charge density to that of ssDNA before counterion condensation only increases the slope of the predicted line, causing greater discrepancy with the data. If we fit the data adding the change density as a free parameter, the fits significantly improve. However, the best-fit charge density for both models is significantly smaller than that expected for ssDNA (see legend of Fig. 5). This apparent charge reduction may be the result of enhanced ion adsorption, for example, due to charge regulation effects beyond Manning condensation (29) or the hydrophobicity of the nucleotides (30). Additional deviations may be expected due to thermal fluctuations of the polymer away from the linear conformation assumed by the models.

Quantifying the free energy of stacking

The force-extension data presented above can be further used to extract sequence-specific thermodynamic properties of ssDNA. By integrating the area between the force-extension curve and the extension axis, we measure the work required to stretch each ssDNA to an elongated conformation. The error associated with extrapolating this quantity to zero force using our data is negligible; the insets of Fig. 3 demonstrate this by plotting the force-extension curves on linear axes. The work required to extend each ssDNA is plotted in Fig. 6 A as a function of the salt concentration. As the salt concentration increases, electrostatics are screened away and the polymers bend and coil more as discussed above, making them more difficult to extend. Thus, W increases with c for all sequences.

Figure 6.

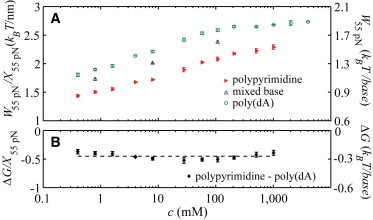
(A) The work required to extend each sequences to a force of 55 pN. We integrate using a trapezoidal rule. Error bars are the standard error of the mean of 2–13 force-extension curves. (Left axis) Measured work, W_55pN, normalized by the extension at 55 pN, X_55pN. (Right axis) X_55pN = 0.6 nm/base. (B) The difference between the work performed extending the polypyrimidine and poly(dA) sequences—an estimate of the free energy of base-stacking. (Left axis) Measured work, W_55pN, normalized by the extension at 55 pN, X_55pN. (Right axis) X_55 pN = 0.6 nm/base. (Dashed line) Average across salt concentrations: ΔG = −0.270 ± 0.021 k_BT/base. To see this figure in color, go online.

We posit that the difference in works required to extend the polypyrimidine and poly(dA) is a measure of the free energy difference between the two sequences at zero force due to the base-stacking prevalent in the poly(dA) sequence (see Fig. 1). This free energy is nearly independent of salt (see Fig. 6 B). The average across salt concentrations is ΔG/X_{55 pN} = −0.450 ± 0.036 k_BT nm at 298 K. Assuming an extension at 55 pN of 0.60 nm/base (31), we obtain a free energy difference of ΔG = −0.270 ± 0.021 k_BT/base = −0.159 ± 0.013 kcal/mol/base. It should be noted that this ΔG is the free energy of a highly base-stacked state (poly(dA)) referenced to an unstacked state (polypyrimidine). In contrast, ΔG values frequently reported elsewhere (5,32–37) are typically referenced to a state where half of the bases are stacked. For comparison with those values, we approximate the free energy to be linear with the fraction of stacked bases (because the helix-to-coil transition is only weakly cooperative, this is likely a reasonable approximation) and use the estimate that ≈80% of the bases are stacked in poly(dA) (36). Thus, our estimate for comparison with other studies (5,32–37) is ΔG = −0.169 ± 0.013 k_BT/base = 0.099 ± 0.008 kcal/mol/base.

The base-stacking free energy of dinucleotides containing only a single phosphate (e.g., ApA) has been measured to be independent of salt concentration (38). In contrast, we expect stacking in polynucleotides to be more strongly affected by salt through screening of phosphate-phosphate repulsion. Screening would reduce the energetic cost of forming the compact stacked state, such that increasing salt concentration favors stacking by decreasing the relative enthalpy of the stacked versus unstacked state. However, this enthalpic trend could be counteracted by an entropic trend: at higher salts, we have shown the flexibility of the unstacked state greatly increases (8,19). This would create an entropic trend that favors the unstacked state at higher salt. We thus posit an entropy/enthalpy compensation mechanism in which increasing salt enthalpically favors stacking, but entropically favors unstacking, leading to the measured salt-independent free energy difference.

Our estimate of the base-stacking free energy compares favorably with other estimates from bulk methods (5,32–37), while having the advantages of being model-independent and precise. Typical methods used to study the thermodynamic properties of single-stranded base-stacking are calorimetry (32–34) and the temperature-dependence of spectroscopic properties (e.g., absorbance (33,37) and optical rotary dispersion (35)). These methods estimate the standard changes in enthalpy and entropy upon structural changes by fitting multiparameter models to melting data (5). There is particular difficulty in applying this strategy to the unstacking transition of single-stranded nucleic acids because the transitions typically occur over a broader range of temperatures than is achievable in the experiments and thus require extrapolation of the data (5). Consequences of this include some ambiguity with regard to the measured thermodynamic parameters. For example, estimates of the base-stacking enthalpy ΔH of poly(A) ssRNA vary from −3 to −13 kcal/mol (5,32–37), yielding estimates of ΔG at 298 K varying from −0.02 to −0.67 kcal/mol. Whereas these results are for poly(A) ssRNA, it is reasonable to expect the thermodynamic parameters of poly(dA) to be comparable—for example, the free energy of single nucleoside association in water is approximately equivalent for both adenosine and deoxyadenosine (5). In contrast to these bulk measurements, our estimate of the free energy is model-independent and relies on a transition that occurs over a small, fully accessible range of forces compared with the large range of temperatures.

Conclusions

We report the electrostatic dependence of mechanical and thermodynamic properties of ssDNA as a function of the base-stacking propensity of its sequence. We demonstrate rational control of base-stacking to manipulate these properties through design of the sequence. The weakly cooperative base-stacking effect significantly enhances the rigidity of ssDNA as evident by the low-force elasticity, which differs qualitatively from that predicted by simple models (6). The enhanced rigidity is further confirmed by screening away electrostatic repulsion using high salt concentrations. Under these conditions a believed novel elastic regime emerges due to the interplay between excluded volume and polymer rigidity. Exploiting the high-force unstacking transition in poly(dA), we examine the salt dependence of the intrinsic electrostatic tension, a quantity that has been modeled (10,11), but not subject to experimental investigation. While the models agree qualitatively with the data, they deviate quantitatively unless relatively low charge densities of ssDNA are assumed. Finally, we obtain a precise, model-independent estimate of the free energy difference between base-stacking competent and incompetent ssDNAs by integrating the area between their force-extension curves: ΔG = −0.270 ± 0.021 k_BT/base = −0.159 ± 0.013 kcal/mol/base, nearly independent of salt concentration.

Our results indicate a need for further work to fully understand the electrostatic properties of ssDNA. Models of electrostatic tension appear to have some shortcomings, perhaps because more ions are adsorbed by the polymer than predicted by Manning condensation, and/or because mean-field electrostatics are not sufficient to describe the remaining intrastrand repulsion. Given the comparability of various length scales in the problem (e.g., the Bjerrum length, Debye length, interphosphate distance of ssDNA, and size of hydrated ions are all ≈0.5–1 nm), simulations, which have already shown considerable value in studying DNA electrostatics (19,39), may be more fruitful than analytic theory in pursuing a further understanding of these interactions. Finally, the lack of salt-dependence of the base-stacking free energy, and our suggestion that this is caused by an entropy/enthalpy compensation, could be probed by performing stretching experiments at various temperatures.