On the GFP-Based Analysis of Dynamic Concentration Profiles

Abstract

Studies with GFP-tagged proteins can be used to investigate the dynamics of concentration profiles of regulatory proteins in cells and tissues. Analysis of these experiments must account for the finite rate with which the GFP-tagged proteins mature to the fluorescent state. Toward this end, we present an analytical framework that provides an explicit connection between the apparent kinetics of concentration gradients and the rates of GFP maturation.

Discovery of green fluorescent protein (GFP) revolutionized the studies of protein dynamics in cells and tissues (1). Using recombinant DNA technology, GFP and its engineered derivatives can be fused to any protein, offering a noninvasive way to monitor protein dynamics in vivo. While there is always a chance that the fluorescent properties of GFP or the functional properties of the tagged protein are affected, GFP-fusion constructs provided new insights into essentially all aspects of cell biology (2). In particular, a number of recent studies used the GFP-tagged proteins to visualize morphogen gradients, defined as the concentration profiles of dose-dependent regulators of gene expression and cell differentiation (3).

Morphogen gradients can result from the localized production and uniform degradation of diffusible molecules (4). Such mechanisms have been established for intracellular proteins, such as Bicoid, an intracellular protein that controls gene expression in Drosophila embryo (5,6), and Nodal, an extracellular protein that patterns developing tissues in zebrafish (7,8). In both of these cases, the spatiotemporal distribution of GFP fluorescence was used to infer the distribution of tagged proteins. Note, however, that because GFP has an appreciable maturation time, which can be as long as 1 h (9,10), the pattern of GFP fluorescence may significantly differ from protein distribution. To quantify this effect, we present an analytical framework that accounts for the localized synthesis of the tagged protein in the immature nonfluorescent form and subsequent processes of maturation, diffusion, and degradation. The key quantity of our analysis is the local accumulation time that provides a timescale at which concentration reaches its steady-state value at a given location (11,12).

Let C(x,t) denote the concentration of a morphogen, which monotonically increases from zero at t = 0 to its steady-state profile C_s(x), as t → ∞. The approach to the steady value at a given location x can be characterized using the relaxation function, R(x,t), defined as

$$R\left(x,t\right)=1-C\left(x,t\right)/C_s\left(x\right).$$ (1)

As time increases from zero to infinity, R(x,t) monotonically decays from one to zero. The expression 1 − R(x,t) can be viewed as the probability that concentration at point x reaches its steady-state value C_s(x) by time t. Then the time derivative −∂R(x,t)/∂t may be interpreted as the probability density of establishing the steady state at point x at time t (see the Supporting Material). Based on this, one can define the mean local accumulation time, τ(x), which provides a characteristic timescale of the approach to the steady state at a given location x (11,12):

$$\tau \left(x\right)={\int }_0^{\infty }t\left(\partial R\left(x,t\right)/\partial t\right)dt={\int }_0^{\infty }R\left(x,t\right)dt.$$ (2)

Along with the steady-state concentration, the local accumulation time provides a compact characterization of morphogen kinetics in a large class of source-diffusion-degradation models. Below, we use this description to analyze the effect of finite maturation rate.

Consider a two-state model in which the tagged protein is synthesized in the nonfluorescent form and becomes fluorescent after it undergoes maturation (Fig. 1 A). The total concentration C(x,t) is the sum of the concentrations of immature and mature forms denoted by C_b(x,t) and C_g(x,t),

$$C\left(x,t\right)=C_b\left(x,t\right)+C_g\left(x,t\right),$$ (3)

where the subscripts b and g mean black (nonfluorescent) and green (fluorescent), respectively. Introducing the relaxation function of the nonfluorescent and fluorescent forms of the protein,

$$R_{b\left(g\right)}\left(x,t\right)=1-C_{b\left(g\right)}\left(x,t\right)/C_{b\left(g\right),s}\left(x\right),$$ (4)

where C_b(g),s (x) are the steady-state concentration profiles, one can readily show that

$$R_g\left(x,t\right)=\mu \left(x\right)R\left(x,t\right)-\nu \left(x\right)R_b\left(x,t\right).$$ (5)

Here μ(x) and ν(x) are time-independent functions defined by

$$\mu \left(x\right)=C_s\left(x\right)/C_{g,s}\left(x\right),\nu \left(x\right)=C_{b,s}\left(x\right)/C_{g,s}\left(x\right).$$ (6)

Integrating both sides of Eq. 5 with respect to time from zero to infinity, we obtain the local accumulation time of the fluorescent form as a linear combination of the corresponding times of the total concentration, given in Eq. 3, and the concentration of the nonfluorescent form,

$${\tau }_g\left(x\right)=\mu \left(x\right)\tau \left(x\right)-\nu \left(x\right){\tau }_b\left(x\right),$$ (7)

where ${\tau }_b\left(x\right)={\int }_0^{\infty }{R}_b\left(x,t\right)dt$. This result does not depend on the details of the kinetics, spatial distribution of the source, or the boundary conditions.

Figure 1.

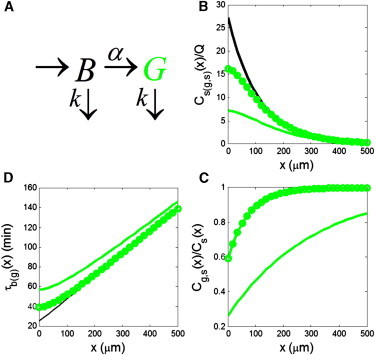
(A) Kinetic scheme of GFP maturation. (B) Comparison of the steady-state distributions of the total (black) and mature (green) forms of the protein. (Solid line and circles) Maturation times of 60 and 10 min, respectively. (C) Steady-state fraction of the mature form of the protein, for the same two maturation times. (D) Local accumulation times of the total and mature forms of the protein for the same set of parameters.

When maturation is instantaneous, C_g(x,t) = C(x,t), because C_b(x,t) = 0. In reality, this is not the case, and C_g(x,t) differs from C(x,t) because of the finite maturation rate. The difference is most pronounced at small x, and vanishes sufficiently far away from the source, because morphogen molecules reaching such distant locations have enough time to mature. To quantify the difference, consider the case where morphogen is produced at a constant rate Q at the boundary of the semi-infinite interval x > 0. The diffusivity and degradation rate constants are denoted by D and k, respectively. The steady state and local accumulation time in this case are given by (11,12)

$$C_s\left(x\right)=\frac{Q}{k\lambda }{e}^{-x/\lambda },\tau \left(x\right)=\frac{1}{2k}\left(1+\frac{x}{\lambda }\right),$$ (8)

where $\lambda =\sqrt{D/k}$ is the mean distance to which a morphogen molecule diffuses before its degradation.

Maturation is commonly described by the first-order kinetics. Let us denote the maturation rate constant by α. If the diffusivity and the degradation rate do not change upon maturation, then the concentration of the nonfluorescent form, C_b(x,t), is a solution of the same problem as C(x,t), in which the degradation rate constant k is replaced by k + α. As a consequence, the steady state and local accumulation time can be found from Eq. 8, simply replacing k by k + α and λ by $\sqrt{D/\left(k+\alpha \right)}$.

Based on Eq. 3, the steady-state profile of the green/mature form is given by the difference between the steady profiles of the total and dark concentrations:

$$C_{g,s}\left(x\right)=\frac{Q}{\lambda }\left(e^{-x/\lambda }-\frac{e^{-x\sqrt{1+\alpha /k}/\lambda }}{\sqrt{1+\alpha /k}}\right).$$ (9)

Using this and the relation μ(x) = 1 + ν(x), which follows from the definitions of μ(x) and ν(x) in Eq. 6, we arrive at the following expression for the local accumulation time of the mature protein:

$${\tau }_g\left(x\right)=\tau \left(x\right)+\frac{\alpha \nu \left(x\right)}{2k\left(\alpha +k\right)}\left[1+\frac{\sqrt{1+\alpha /k}}{1+\sqrt{1+\alpha /k}}\frac{x}{\lambda }\right].$$ (10)

The difference between C(x,t) and C_g(x,t) vanishes as α → ∞ (instantaneous maturation) and becomes larger and larger as α decreases. The same is true for the difference between the local accumulation times τ_g(x) and τ(x). The effect of the finite maturation rate is controlled by a dimensionless ratio α/k.

To illustrate these results for a specific morphogen, we apply them to Bicoid (Bcd), which patterns the anterior-posterior axis of Drosophila embryo (6). Bcd distribution in live embryos was studied with Bcd-GFP constructs, with the GFP maturation time of ∼1 h (13). Bcd diffusivity and degradation rate constants were measured using fluorescence correlation spectroscopy and pulse-chase experiments with photoconvertible Bcd, respectively (5,14). Based on these studies, we take D = 4 μm²/s, 1/k = 50 min, and 1/α = 60 min.

In Fig. 1, B–D, these numbers are used to compare the steady-state profiles and local accumulation times of total and fluorescent forms of Bcd. Clearly, a finite rate of maturation affects both the steady-state profile and kinetics with which this profile is approached. In this case, the steady state profile of the fluorescent form is significantly nonexponential close to the source (Fig. 1 B). Furthermore, plotting the ratio of the steady states of the fluorescent and total concentrations, we see that their shapes become the same only at a considerable distance from the source (Fig. 1 C). The local accumulation time of the fluorescent form is a nonlinear function of position and becomes linear only far from the source (Fig. 1 D). The shortest time for maturation is ∼10 min (9,10). While this leads to the fluorescent concentration profile which is much closer to that of the total concentration, the difference between the distributions of the total and fluorescent concentrations is still appreciable.

In summary, we presented a simple analytic framework for comparing the spatiotemporal patterns of GFP fluorescence and protein concentrations. Application of this framework to a morphogen with measured diffusivity and degradation rate constant shows that the difference between the two patterns can be significant and should be accounted for in the GFP-based studies of other experimental systems. Finally, our work considers a two-state fluorescent reporter. A dual labeling system, where a protein is tagged with two fluorophores, maturing with different kinetics has been recently used as a new tool for studies of protein dynamics (15). Our formalism can be readily extended to this case, by taking into account three states of a tagged molecule.