Essential role of conformational selection in ligand binding

Abstract

Two competing and mutually exclusive mechanisms of ligand recognition – conformational selection and induced fit - have dominated our interpretation of ligand binding in biological macromolecules for almost six decades. Conformational selection posits the pre-existence of multiple conformations of the macromolecule from which the ligand selects the optimal one. Induced fit, on the other hand, postulates the existence of conformational rearrangements of the original conformation into an optimal one that is induced by binding of the ligand. In the former case, conformational transitions precede the binding event; in the latter, conformational changes follow the binding step. Kineticists have used a facile criterion to distinguish between the two mechanisms based on the dependence of the rate of relaxation to equilibrium, k_obs, on the ligand concentration, [L]. A value of k_obs decreasing hyperbolically with [L] is seen as diagnostic of conformational selection, while a value of k_obs increasing hyperbolically with [L] is considered diagnostic of induced fit. However, this simple conclusion is only valid in the rather unrealistic assumption of conformational transitions being much slower than binding and dissociation events. In general, induced fit only produces values of k_obs that increase with [L] but conformational selection is more versatile and is associated with values of k_obs that increase, decrease with or are independent of [L]. The richer repertoire of kinetic properties of conformational selection applies to kinetic mechanisms with single or multiple saturable relaxations and explains the behavior of nearly all experimental systems reported in the literature thus far. Conformational selection is always sufficient and often necessary to account for the relaxation kinetics of ligand binding to a biological macromolecule and is therefore an essential component of any binding mechanism. On the other hand, induced fit is never necessary and only sufficient in a few cases. Therefore, the long assumed importance and preponderance of induced fit as a mechanism of ligand binding should be reconsidered.

1. Introduction

The interaction between a ligand, L, and its macromolecular target, E, forms the basis of function and regulation in all biological systems. Understanding how ligands recognize their targets in terms of structure, energetics and kinetics remains a central issue to biochemistry and biophysics and a prerequisite to rationally design efficient enzymes, effective drugs, and new therapeutics (1). The interaction involves two components: specific binding of L to E, and linked conformational changes that may precede and/or follow the binding step. The combination of binding steps and conformational transitions in any given mechanism of recognition generates the repertoire of kinetic behaviors accessible to experimental measurements. The challenge facing the experimentalist is to decipher the nature of conformational transitions involved in the recognition process from analysis of the transient behavior of the system relaxing to equilibrium (2, 3). A system of N independent species gives rise to N independent relaxations, some of which may be too fast to measure by conventional stopped-flow techniques or may be spectroscopically silent. Analysis of a ligand binding interaction must therefore rely only on the relaxations accessible experimentally and interpretation of the underlying mechanism should be based on the simplest kinetic scheme consistent with the observations.

2. Simplest binding mechanism: The lock-and-key model

Over the years, our interpretation of binding interactions has evolved alongside the emerging view of the plasticity of biological macromolecules buttressed by the successes of x-ray crystallography and NMR spectroscopy (4) Energy landscapes portraying the conformations available to the macromolecule have replaced the static view of a single “species” converting from free to bound upon ligand binding (Figure 1), as envisioned by the classic lock-and-key model introduced by Fischer (5). In this model, binding of L to E is cast in terms of the single step reaction scheme

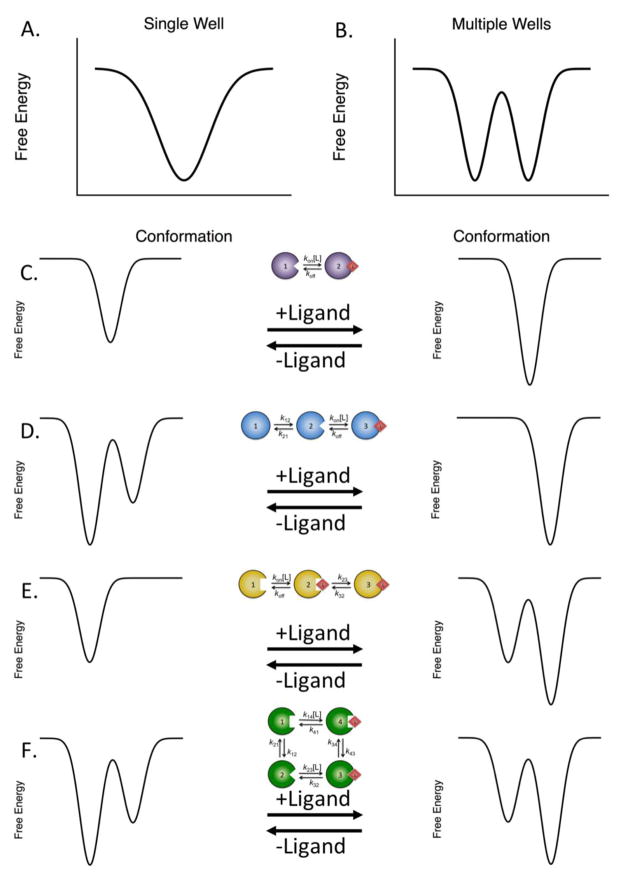
Figure 1. Free energy landscape view of macromolecular structure and binding.

(A) Single low energy well, indicating a single dominant conformation. (B) Multiple low energy wells separated by a free energy barrier. In this instance, two dominant conformations are present. (C) Lock-and-key mechanism of binding, where the macromolecule exists as the same species in both the free and bound states. Binding may stabilize the macromolecule, but does not alter its conformational distribution. (D) Conformational selection, where the free macromolecule exists in multiple conformations in the absence of the ligand. The ligand selectively binds to a single conformation, stabilizing it. (E) Induced fit binding, in which the macromolecule exists as a single conformation in the absence of ligand. After binding, the ligand induces conformational rearrangements in the macromolecule to optimize the interaction. (F) Linkage scheme for binding. The macromolecule exists as multiple conformations capable of interacting with the ligand. After binding, the ligand may change the relative stabilities of the two conformations or may alter the barrier for conversion between the two bound conformations.

$$\mathrm{E}\underset{k_{\text{on}}[\mathrm{L}]}{\overset{k_{\text{off}}}{\leftrightarrows }}\text{EL}$$

where k_on (M⁻¹s⁻¹) is the second-order rate constant for ligand binding and k_off (s⁻¹) is the first-order rate of dissociation of the EL complex into the parent species E and L. The strength of the interaction is quantified by the equilibrium dissociation constant K_d (M) defined as k_off/k_on. The lock-and-key model predicts a relaxation of the system to equilibrium that is linear in [L], i.e.,

$$k_{\text{obs}}=k_{\text{off}}+k_{\text{on}}[\mathrm{L}]$$ (1)

Measurements of k_obs as a function of [L] yield both k_off and k_on as the intercept and slope of the plot, respectively. Hence, for a simple binding interaction, the value of k_obs equals the rate of ligand dissociation for [L]=0 and grows without limits as [L] increases.

It has been argued for a long time that the lock-and-key model is too crude an interpretation of ligand binding because it envisions a rigid body collision between the ligand and its target, thereby neglecting the conformational flexibility of the macromolecule (2, 3, 6) recently supported by x-ray crystallography (7), NMR spectroscopy (8, 9) and single-molecule fluorescence detection (10). Although this argument has important merits, it is not completely rigorous. The existence of multiple conformations is not necessarily incompatible with the lock-and-key model. An ensemble of conformations that interconvert on a time scale faster than binding and dissociation events is indistinguishable from a single species as far as the equilibrium and kinetic properties of the system are concerned. The partition function of a system capable of binding L at a single site, as in the lock-and-key model, is linear in [L] regardless of the number of conformations accessible to the macromolecule (11, 12). Likewise, the transient properties of the system depend only on the slowest kinetic steps in the mechanism and replacing E or EL in the lock-and-key model with an ensemble of rapidly interconverting conformations does not change the observed relaxation kinetics (6). Therefore, the lock-and-key model describes the behavior of a macromolecule that exists in a single conformation but also applies to an ensemble of rapidly interconverting conformations, in which case k_on and k_off represents ensemble averages of rate constants over the entire population. In general, any individual species in a kinetic scheme can be replaced by an ensemble of rapidly interconverting species without changing the kinetic properties of the system. Therefore, the dynamic nature of proteins and the existence of an ensemble of conformations will not produce a departure from the simple properties predicted by the lock-and-key model, unless the conformational transitions take place over time scales that eventually affect events of functional significance.

3. Binding coupled to conformational transitions: conformational selection and induced fit

Consider next the relevant case of the macromolecule existing in multiple conformations interconverting on the ms-μs time scale, which is directly relevant to binding/dissociation reactions (10). Two limiting cases should be considered, depending on whether the conformational transitions precede or follow the binding step. In both cases, relaxation to equilibrium no longer follows a straight line as in the lock-and-key model because the macromolecule assumes alternative conformations over a time scale comparable to the binding/dissociation events of functional significance. In the first case (Figure 1), originally discussed by Eigen as pre-equilibrium (2, 3) and more recently referred to as conformational selection (13–15), the macromolecule is assumed to undergo a transition between multiple conformations from which one is selected for binding by the ligand. In this scheme, the number of conformations accessible to the macromolecule decreases upon ligation as the ligand singles out the one with optimal fit from the pre-existing ensemble. In the second case (Figure 1), introduced by Koshland as induced fit (16), the macromolecule is assumed to first bind the ligand and then change its conformation in the bound form to optimize the complex. Here, the conformational flexibility of the macromolecule does not pre-exist. Rather, association with the ligand generates it. Two mutually exclusive philosophies emerge in the analysis of ligand binding to biological macromolecules: one where the complexity necessary to accommodate a ligand pre-exists in the ensemble of conformations available to the macromolecule, and the other where such complexity is generated after ligand binding to optimize the initial encounter. Accordingly, two distinct scenarios are expected. In the case of conformational selection, the macromolecule is expected to be trapped in different conformations when free and to retain one of these conformations when bound. In the case of induced fit, the macromolecule is expected to be trapped in a single conformation when free and to assume multiple conformations when bound. Structural information is useful when evidence of multiple conformations is obtained for the free (conformational selection) or bound (induced fit) forms. More relevant to the function of the macromolecule is identification of the underlying mechanism from relaxation kinetics. As we have pointed out, the only conformational transitions relevant to function are those that occur on time scales comparable to those of ligand binding and dissociation. Ideally, information derived from structural biology and relaxation kinetics must converge to the same conclusion. Kinetic data are also necessary to derive information on the rate constants governing the recognition process.

Unlike the lock-and-key model, conformational selection and induced fit introduce a conformational transition in the kinetic scheme (Figure 1) that increases the number of independent relaxations from one to two. The fast relaxation increases without limits with [L] because it reflects the binding step, as in the case of the lock-and-key model. The slow relaxation, on the other hand, is saturable and spans two finite asymptotes in the plot of k_obs vs [L]. For several decades, kineticists have endorsed a facile litmus test for conformational selection and induced fit based on the dependence of this slow, saturable relaxation on the ligand concentration [L] (2, 3, 17–19). An increase of k_obs vs [L] has been considered diagnostic of induced fit, with a decrease of k_obs vs [L] being diagnostic of conformational selection. In turn, the vast preponderance of systems relaxing to equilibrium with a k_obs increasing with [L] to a saturable level has been used for decades as evidence of induced fit as a dominant mechanism of ligand binding (2, 3, 17–19). This facile conclusion is only valid under the rather unrealistic assumption of conformational transitions being rate-limiting in the kinetic mechanism. In fact, when such assumption is dropped and the kinetic scheme is analyzed in terms of its general properties, conformational selection easily accounts for a k_obs increasing with [L] to a saturable level (20). To reveal this important conclusion, we look at the kinetic scheme for conformational selection in some detail.

Consider the relaxations associated with the conformational selection mechanism in Scheme 1 (Figure 2), i.e. (20),

Figure 2. Mechanisms of ligand binding discussed in the text with corresponding asymptotic values for k_obs.

Shown are the limits [L]=0 and [L]=∞. Schemes 1 and 2 correspond to conformational selection and induced fit, respectively. Scheme 3 is the linkage scheme, of which schemes 1 and 2 represent special cases (see also Figure 3).

$$k_{\text{obs}1,2}=\frac{k_{-r}+k_r+k_{\text{off}}+k_{\text{on}}[\mathrm{L}]\pm \sqrt{{\left(k_{\text{off}}+k_{\text{on}}[\mathrm{L}]-k_{-r}-k_r\right)}^2+4k_{-r}{k}_{\text{on}}[\mathrm{L}]}}{2}$$ (2)

We see from eq 2 above that the condition k_r=k_off generates a second relaxation that becomes independent of [L] and equal to k_r. Elementary rearrangements show that this slower k_obs saturates at k_r regardless of the kinetic rate constants in the scheme and that the value at [L]=0 is the smaller of k_off, the rate constant for ligand dissociation, or the sum k_r+k_−r. When k_r+k_−r<k_off, the value of k_obs can only decrease with [L] from k_r+k_−r for [L]=0 to k_r for large [L]. This is the scenario generated by the “rapid equilibrium approximation” where conformational transitions are slower than the rate of ligand dissociation. However, when k_r+k_−r>k_off a different scenario unfolds. When k_off>k_r, the value of k_obs decreases with [L], but it otherwise increases with [L] if k_off<k_r. Basically, the condition k_off=k_r acts as a demarcation between the decrease and increase of k_obs with [L]. As a result of that, conformational selection covers the entire repertoire of kinetic properties of a system whose kinetics obey a single saturable relaxation. The richness of such repertoire comes at the expense of an exact resolution of the kinetic parameters involved in the mechanism. In general, when k_obs decreases with [L], only the asymptote at saturating [L] is defined exactly as k_r. The asymptote for [L]=0 becomes ambiguous as it may reflect either k_off or the sum k_r+k_−r, whichever is smaller. Hence, great care should be taken in the interpretation of such plots in practical applications. When k_obs increases with [L], on the other hand, the lower asymptote always reflect k_off giving a direct measurement of the dissociation rate constant of the ligand from its target. Likewise, when k_obs is independent of [L], both k_off and k_r are assigned unambiguously from the plot.

The richness of kinetic behaviors associated with conformational selection is not shared by induced fit, that always produces a saturable relaxation that increases with [L]. That is readily seen from the relaxations associated with Scheme 2 (Figure 2), i.e. (20),

$$k_{\text{obs}1,2}=\frac{k_{-r}^L+k_r^L+k_{\text{off}}^{\ast }+k_{\text{on}}^{\ast }[\mathrm{L}]\pm \sqrt{{\left(k_{\text{off}}^{\ast }+k_{\text{on}}^{\ast }[\mathrm{L}]-k_{-r}^L-k_r^L\right)}^2+4k_{-r}^L{k}_{\text{off}}^{\ast }}}{2}$$ (3)

Although eq 3 is quite similar to eq 2 for the case of conformational selection, a difference in the last term under the square root expression produces two relaxations that always increase with [L]. There is no combination of rate constants that makes the relaxation independent of [L]. The saturable relaxation equals the sum $k_{\mathrm{r}}^{\mathrm{L}}+k_{-\mathrm{r}}^{\mathrm{L}}$ for large [L] and a more convolute expression for [L]=0 (Figure 2) that is however always less than $k_{\mathrm{r}}^{\mathrm{L}}+k_{-\mathrm{r}}^{\mathrm{L}}$.

The properties encapsulated by eqs 2 and 3 refer to the case where conformational transitions involve only the macromolecule E. Extension to include conformational flexibility in the ligand L becomes biologically relevant in the case where the ligand is itself a macromolecule, as observed in enzymatic cascades (21). However, whenever the ligand is in large excess, its properties do not change significantly upon interaction with the macromolecule and the results of eqs 2 and 3 remain valid. The case where the macromolecule and ligand are present at comparable concentrations require modifications of the entire set of differential equations associated with the system and is beyond the scopes of this review.

4. Is induced fit necessary as a mechanism of ligand binding?

The foregoing analysis has very important implications for the interpretation of relaxation kinetics. A plot of k_obs decreasing with or independent of [L] is unambiguous proof of conformational selection and disproves induced fit automatically. On the other hand, a plot of k_obs increasing with [L] may be associated with induced fit or conformational selection and neither proves, nor disproves either mechanism. Therefore, conformational selection can never by disproven as a mechanism of ligand binding when a single saturable relaxation is measured experimentally, but induced fit can. Conformational selection is always sufficient and in some cases necessary to explain the relaxation kinetics for systems associated with a single saturable relaxation. On the other hand, induced fit is only sufficient in some cases and never necessary.

In addition to its limited kinetic repertoire, induced fit poses an intriguing challenge to the thermodynamicist. Validity of the induced fit hypothesis rests entirely on the assumption that the optimal bound conformation (EL in Scheme 2, Figure 2) does not exist in the free state. However, from a thermodynamic standpoint, it is not possible to rule out that such conformation, no matter how energetically unfavorable, could pre-exist in solution prior to ligand binding. This scenario is illustrated in Figure 3 where induced fit and conformational selection can be seen as special cases of a more general scheme (Scheme 3, Figure 2) linking the E*-E isomerization to ligand binding. The equilibrium properties of this scheme are well known and form the basis of linkage thermodynamics (11, 12). The steady state properties have also been discussed in great detail first by Botts and Morales (22) in connection with the action of a modifier on enzyme activity and then by Hill (6) in the context of energy transduction. The linkage scheme shows that for any induced fit step in a kinetic mechanism generating a new conformation of the macromolecule in the bound form, a perfectly legitimate thermodynamic cycle can be constructed including the same conformation in the free form. Hence, the basic tenet of the induced fit hypothesis, i.e., that the ligand induces a new conformation of the macromolecule that does not pre-exist in solution, is difficult to defend on thermodynamic grounds. On the other hand, conformational selection is not invalidated by the existence of multiple bound conformations in the linkage scheme because its basic hypothesis rests on the existence of multiple conformations in the free form from which the ligand selects the optimal one for binding. Preferential rather than exclusive binding to one of the two conformations in the linkage scheme does not invalidate existence of the pre-equilibrium between E and E*, which is the pillar of the conformational selection hypothesis. Although the linkage scheme in Figure 3 encompasses both conformational selection and induced fit as special cases, it is not the result of equal contributions from these mechanisms. Indeed, we have recently shown (23) that much of the kinetic repertoire of the linkage scheme (Scheme 3, Figure 2) is recapitulated by conformational selection (Scheme 1, Figure 2), but not by induced fit (Scheme 2, Figure 2).

Figure 3. Schematic diagram of the linkage scheme and its component mechanisms.

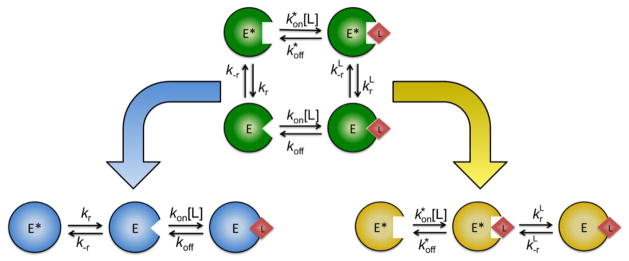
Linkage scheme containing four species is depicted in green. Here, two free species exist in equilibrium, interconverting according to the first-order rate constants k_r and k_−r. Both the E* and E forms are capable of binding the ligand with second-order rates of association $k_{\text{on}}^{\ast }$ and k_on and first-order dissociation rates $k_{\text{off}}^{\ast }$ and k_off. The bound conformations E*L and EL interconvert according to the first-order rate constants $k_{\mathrm{r}}^{\mathrm{L}}$ and $k_{-\mathrm{r}}^{\mathrm{L}}$. Conformational selection and induced fit, two special cases of the linkage scheme, are shown in blue and yellow. The asymptotic values of the relaxations of these schemes are summarized in Figure 2.

Analysis of the kinetic properties and thermodynamic underpinnings of induced fit raises questions about this mechanism being dominant or even necessary to explain the interaction of a ligand with its biological target. The well documented preponderance of systems associated with a single saturable relaxation that increases with [L] (18, 24) can no longer be used as unequivocal evidence of induced fit and the dominance of this mechanism (20, 23). We have analyzed the relaxation kinetics of glucose binding to glucokinase, a textbook example of a protein obeying the induced fit mechanism (25), and have shown that the same experimental data fit to conformational selection (20). The original interpretation of the binding mechanism of glucokinase has been called into question recently (26) and it is now accepted that glucokinase exists in alternative conformations in equilibrium prior to the binding of any ligands (27). This conclusion is strongly supported by recent x-ray structures of glucokinase that reveal how ligand binding does not result in conformational changes of the enzyme but only in stabilization of the E form (28). It is expected that several other cases previously assigned with certainty to induced fit because of a saturable relaxation increasing with [L] would allow for an alternative explanation based on conformational selection. Furthermore, the number of systems directly disproving induced fit with k_obs decreasing with [L] is rapidly expanding and includes alkaline phosphatase (29), glucokinase (26), several trypsin-like proteases (19, 20, 30–35), the immunoglobulin IgE (36), and DNA in its B to Z transition (37). The case of trypsin-like proteases is particularly striking and biologically relevant.

5. Trypsin-like proteases obey conformational selection, not induced fit

Historically, trypsin-like proteases have been portrayed as the active embodiment of the irreversible conversion of an inactive zymogen precursor via a tightly regulated transition aimed at preventing unwanted proteolysis in the compartments where the zymogen is stored (38, 39). A key element of this conceptual framework is that the zymogen transitions to the protease through structural changes that can also be induced by binding of specific ligands or cofactors (40). A recent extension of this view to the protease itself posits a continuum transition from zymogen-like to proteinase-like states upon ligand binding (41), based on the assumption that the protease in the free form is zymogen-like (42). These views have fueled the expectation that the zymogen and protease would behave according to the induced fit mechanism, which is a conclusion directly refuted by a large body of structural and kinetic data (7, 20, 31, 43, 44). Trypsin-like proteases and their zymogens behave according to conformational selection and not induced fit, as first reported for chymotrypsin more than forty years ago (30). Both the zymogen and protease exist in equilibrium between inactive (E*) and active (E) forms (7) whose distribution changes upon activation or the binding of cofactors. The active form of the protease is not induced by binding of the ligand but pre-exists in solution along with the inactive form (43, 44). Likewise, the zymogen exists mainly in the inactive form E* and, to a smaller extent, in the active form E (43, 44). The case of thrombin is particularly instructive. The enzyme crystallizes in alternative conformations when free (43) and the active E form remains unchanged upon binding of ligands at the active site, exosite I, or the Na⁺ site (Figure 4). The structure of thrombin bound to Na⁺ and hirudin to the active site and exosite I, covering 20% of the accessible surface area, shows that the enzyme retains the same E form observed when free in solution even when all three relevant binding sites are occupied (Figure 4). Recent NMR measurements of thrombin free and bound have revealed the dynamic nature of the enzyme (45, 46) and argued for the existence of conformational ensembles as a new, defining property of thrombin that should replace the static view based on a pre-equilibrium between distinct species. Although these developments are noteworthy, they do not invalidate the mechanism of thrombin function that is fully explained by two pre-existing conformations in equilibrium (see below). Each of these conformations, nicely trapped as single species by x-ray crystallography, may well be considered an ensemble of rapidly interconverting conformers, as suggested by NMR measurements. The distinction, however, is inconsequential on the properties of the kinetic scheme (see section 2).

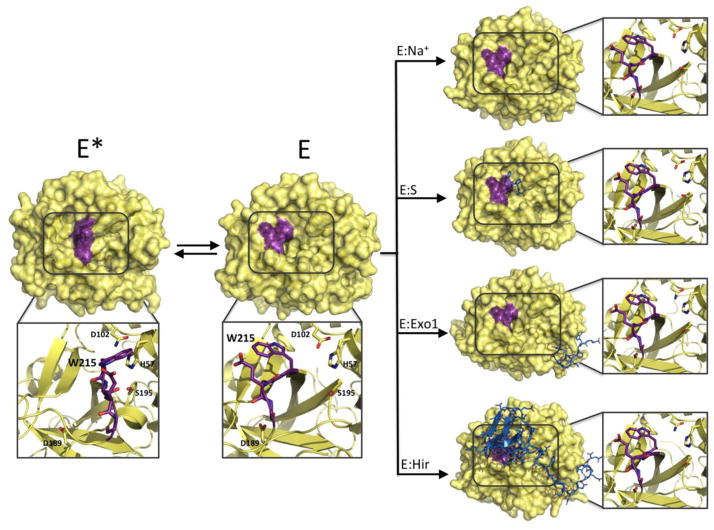
Figure 4. Structural evidence for conformational selection in the trypsin-like protease thrombin.

When thrombin is free in solution, two dominant forms exist in equilibrium. In the inactive E* form (3BEI, 1.55 Å resolution) the side chain of W215 and the entire segment 215–219 (purple) collapse in the active site. In the active E form (1SGI, 2.3 Å resolution), the indole ring of W215 moves back 11 Å along with the entire 215–219 segment to make the active site wide open and accessible to substrate. As postulated by the conformational selection mechanism, the ligand binds to a pre-existing conformation of the protease. In the case of thrombin, Na⁺ (E:Na⁺, 1SG8, 2.3 Å resolution), the active site inhibitor H-D-Phe-Pro-Arg-CH₂Cl (E:S, 1SHH, 1.55 Å resolution), hirugen binding at exosite I (E:Exo1, 3BEF, 2.2 Å resolution) and hirudin binding to an extended surface area of the enzyme (E:Hir, 4MLF, 2.2 Å resolution) select and stabilize the E form of the protease. The average calculated r.m.s.d. between all bound and free E forms is only 0.26 Å, supporting the conclusion that ligand binding does not alter significantly the conformation of the active free form E.

Kinetically, binding of different ligands to thrombin obeys the prediction of conformational selection (Figure 5). Binding of the inhibitor p-aminobenzamidine (PABA) and the substrate H-D-Val-Pro-Arg-p-nitroanilide (VPR) to the active site and Na⁺ and K⁺ to the cation binding site produces saturable k_obs dependencies consistent with conformational selection. All four ligands produce a saturable k_obs that approaches the same value (60 s⁻¹) when [L] becomes large (Figure 5A), consistent with the ligand-independent rate of isomerization from E* to E, k_r. When [L]=0, PABA and K⁺, which bind at two sites separated by more than 15 Å, have nearly identical asymptotic values for k_obs (400 s⁻¹), suggesting that this asymptote represents the ligand-independent isomerization of the free species, k_r+k_−r. The value of k_obs for Na⁺ binding is equal to 130 s⁻¹ when [L]=0. Since this value is lower than k_obs at [L]=0 for PABA and K⁺ binding, we infer that it represents k_off. The asymptotic value of k_obs at [L]=0 for VPR binding (2.5 s⁻¹) is actually lower than k_r, causing k_obs to increase with [L]. Using multiple ligands to probe the conformational landscape of thrombin allows us to accurately determine both the mechanism and the individual rate constants governing binding (20). The same strategy has been applied to two additional trypsin-like proteases present in the coagulation cascade: factor Xa (FXa) and activated Gla-domainless protein C (aPC). FXa binding to PABA and Na⁺ produces saturable k_obs values that decrease from approximately 350 s⁻¹ at [L]=0 to 45 s⁻¹ as [L] approaches saturation (Figure 5B). Again, the decreasing k_obs provides unequivocal proof of conformational selection. Both ligands, binding to different sites, produce identical values of k_obs when [L]=0 and when [L] becomes large providing strong support for the identification of these asymptotes as k_r+k_−r when [L]=0 and k_r when [L] is large. The presence of conformational selection in FXa with rates of isomerization k_r and k_−r that are remarkably consistent with those of thrombin suggests that this mechanism of binding is conserved in trypsin-like proteases. Binding of Na⁺ and Ca²⁺ to aPC confirms these suspicions. Na⁺ binds to aPC at a site analogous to that found in thrombin and FXa, while Ca²⁺ binds to a site defined by the 70-loop, in close proximity to exosite I in thrombin. The binding of Na⁺ to aPC produces a saturable k_obs that decreases from 50 s⁻¹ to 25 s⁻¹ with increasing [Na⁺]. Ca²⁺ binding produces a saturable k_obs that increases from 5 s⁻¹ to 20 s⁻¹ as [Ca²⁺] goes from zero to saturation. The convergence of k_obs values at high [L] suggests that both ligands are binding to the same E form of the enzyme, but the lack of agreement when [L]=0 makes clear assignment of the sum k_r+k_−r impossible for aPC (Figure 5C). The [L]=0 asymptote of k_obs for Ca²⁺ binding is clearly assigned to k_off, but for Na⁺ binding that asymptote could be equal to either k_off or k_r+k_−r. The unmistakable kinetic and structural signatures of conformational selection present in this large family of proteases provides a strong case for the ubiquity of this mechanism in biological systems.

Figure 5. Rapid kinetics of ligand binding to the trypsin-like proteases thrombin, FXa, and aPC.

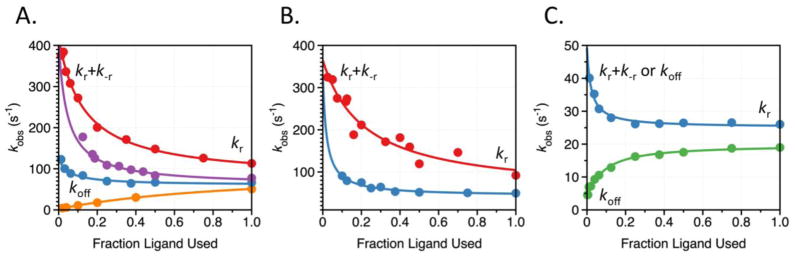
Rates of approach to equilibrium, k_obs, determined from stopped-flow fluorescence measurements of binding of PABA (red), KCl (magenta), NaCl (blue), VPR (orange), and CaCl₂ to (A) thrombin, (B) FXa, and (C) aPC. Reaction conditions were as follows: (A) 5 mM Tris, 0.1% PEG8000, pH 8.0 at 15 °C, with ionic strength kept constant at 400 mM with ChCl; (B) 50 mM Tris, 0.1% PEG8000, pH 8.0 at 15 °C, with no ChCl used due to specific inhibition of FXa by choline; (C) 5 mM Tris, 0.1% PEG8000, pH 8.0 at 15 °C, with ionic strength kept constant at 800 mM with ChCl. Solid lines were drawn according to the equation k_r+k_−r/{1+[L]/K_d} for PABA and KCl in thrombin, PABA and NaCl in FXa, and NaCl in aPC, or according to eq. 2 in the text. Best-fit parameters for thrombin binding to ligand (A) are: (PABA) k_r=70±10 s⁻¹, k_−r=340±10 s⁻¹, K_d=52±8 μM; (K⁺) k_r=60±10 s⁻¹, k_−r=340±10 s⁻¹, K_d=19±2 mM; (Na⁺) k_r=60±10 s⁻¹, k_−r=340±10 s⁻¹, k_on=3.2±0.3 10⁴ M⁻¹s⁻¹, k_off=130±20 s⁻¹; (VPR) k_r=80±10 s⁻¹, k_−r=340±10 s⁻¹, k_on=1.7±0.1 10⁷ M⁻¹s⁻¹, k_off=2.4±0.2 s⁻¹. Best-fit parameters for FXa binding to ligand (B) are: (PABA) k_r=48±36 s⁻¹, k_−r=327±29 s⁻¹, K_d=44±2 μM; (Na⁺) k_r=43±4 s⁻¹, k_−r=240±20 s⁻¹, K_d=10±1 mM. Best-fit parameters for aPC binding to ligand (C) are: (Na⁺) k_r=25±1 s⁻¹, k_−r=24±4 s⁻¹, K_d=9±1 mM; (Ca²⁺) k_r=20±1 s⁻¹, k_−r=25±4 s⁻¹, k_on=16±1 10³ M⁻¹s⁻¹, k_off=5.0±0.3 s⁻¹. Because k_−r was not well determined in FXa binding to Na⁺, it was restricted by the values derived from PABA binding. A similar procedure was used for k_on for Ca²⁺ binding to aPC. To facilitate comparison, the values of [L] for each ligand are expressed as the fraction of maximal ligand used.

6. More complex kinetics

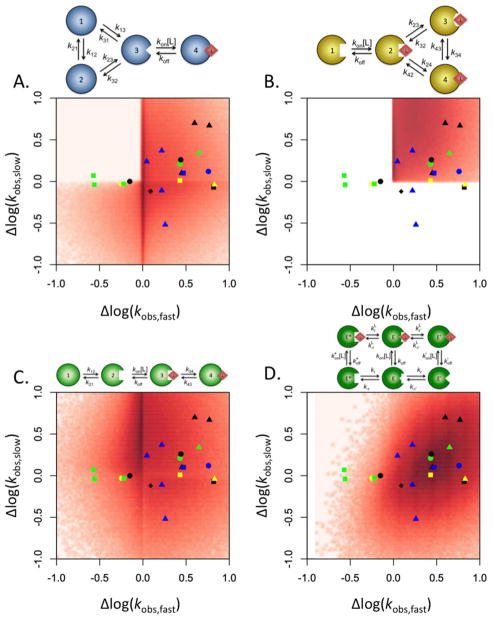
Conformational selection and induced fit exhaust the repertoire of two-step kinetic mechanisms linking ligand binding to conformational transitions when a single saturable k_obs is measured experimentally. Numerous biological systems such as the immunoglobulins IgE (47) and IgG (48), protein kinase A (49), DnaC (50), CheA (51), histone deacetylase-like amidohydrolase (52), polymerase X (53), 3-hydroxybenzoate 6-hydroxylase (54), 3-chloroacrylic acid dehalogenase (55), proline utilization A protein (56), ACTR and CREB-binding protein (57), G-quadruplex folding (58) and DnaB (59) exhibit multiple k_obs that saturate in the presence of high concentrations of their respective ligands. These data dictate expanded binding mechanisms containing a minimum of four species and requiring a more complex interpretation of the relaxation kinetics. When multiple saturable k_obs are present, four diagnostic scenarios are of interest: both k_obs increase with [L], the faster k_obs increases while the slower k_obs decreases with [L], both k_obs decrease with [L], and the faster k_obs decreases while the slower k_obs increases with [L]. These four scenarios are shown as the quadrants of a plot where the range of the smaller k_obs is plotted as a function of the range of the larger k_obs (Figure 6). The range is defined as ratio of the values of k_obs when [L]=∞ and [L]=0. Adopting this approach to investigating the behavior of k_obs with respect to [L], the majority of the experimental systems with multiple saturable k_obs fall into three quadrants of the plot, leaving the quadrant where the faster k_obs decreases with [L] while the slower k_obs increases almost completely unpopulated. What mechanisms of binding are capable of explaining the experimental data? The linkage scheme, of which conformational selection and induced fit are special cases, produces three independent relaxations. The two fastest of these k_obs increase linearly, reflecting the two independent binding steps present in the binding mechanism. The slowest k_obs is saturable and may either increase or decrease with increasing [L]. Because this mechanism produces only a single saturable k_obs, it is incapable of explaining the experimental data displayed in Figure 6. An extension of the conformational selection scheme to include three ligand free species in equilibrium with each other with selective ligand binding occurring for a single species also produces three independent relaxations. The fastest k_obs once again increases linearly as [L] increases, but the remaining two slower k_obs are both saturable. Numerical simulations of these k_obs reveal that the two saturable k_obs can either increase or decrease with increasing [L], but never in the combination where the faster k_obs decreases while the slower k_obs increases (23). In general, extensions of the conformational selection mechanism with any number of free species and only a single bound species produce qualitatively similar results. The largest k_obs will always increase linearly, reflecting the binding step while the remaining k_obs can either increase or decrease, but a decreasing faster k_obs is never coupled to a slower k_obs that increases with [L] (Figure 6A). An analogous extension of the induced fit mechanism where a single free species binds to a ligand to form a complex that interconverts between three bound species fails to account for the variety of kinetic behavior seen experimentally. As with conformational selection, the first of the three relaxations increases linearly with [L]. However, the remaining two saturable k_obs can only ever increase, limiting the general induced fit mechanism to the upper right quadrant of the plot (Figure 6B). The only mechanism containing four species that is capable of populating the upper left quadrant of the plot in Figure 6 is one in which conformational selection is followed sequentially by induced fit. This mechanism, discussed previously under certain approximations (29, 50), produces two saturable k_obs that may either increase or decrease independently of each other, thus allowing them to populate all four quadrants of the plot (Figure 6C). Enzymes with lid-gated active sites such as ribokinase (60), adenosine kinase (61) and glucokinase (62), where a conformational change must follow the binding step (63), are particularly good candidates for application of this scheme. However, an extension of the linkage scheme to include a third free species, also capable of binding, is sufficient to replicate this behavior entirely (Figure 6D) and without the need of induced fit. The important conclusion is that all of the kinetic behaviors of a system with multiple saturable k_obs can be explained by a mechanism in which all possible conformations are contained within the free ensemble. Conformational selection alone is sufficient to explain the overwhelming majority of the experimental systems displaying one or more saturable k_obs, proving essential in a wide array of them. On the other hand, induced fit is never necessary as a mechanism of ligand binding and frequently insufficient.

Figure 6. Mapping of the kinetic behavior of the general conformational selection and induced fit schemes.

Distribution of the range of the two saturable k_obs, computed as the ratio between the values for [L]=∞ and [L]=0, and plotted as the slow relaxation vs the fast. Density maps were created by running 10⁶ numerical simulations of the k_obs for each scheme presented, as described elsewhere (23). Four different mechanisms of binding are compared: (A) general conformational selection, (B) general induced fit, (C) sequential conformational selection and induced fit, and (D) extended linkage scheme. The results from thirteen experimental systems discussed in the text are superimposed above the density maps for comparison. Symbols are as follows: IgE (green squares), IgG (green circle), protein kinase A (black circles), DnaC (yellow circle), CheA (yellow triangle), histone deacetylase-like amidohydrolase (blue square), polymerase X (yellow square), 3-hydroxybenzoate 6-hydroxylase (green triangle), 3-chloroacrylic acid dehalogenase (black square), proline utilization A protein (blue circle), ACTR and CREB-binding protein (black diamond), K⁺-mediated G-quadruplex folding (black triangles), and DnaB (blue triangles). The extended linkage scheme gives the best fit of the experimental data, followed by the general conformational selection model.

7. Conclusion

Kinetic data that constitute the foundation for the induced fit hypothesis are actually consistent with conformational selection as a mechanism of binding (20, 23). The kinetic signature previously ascribed solely to induced fit can be entirely recapitulated by conformational selection, but the signature of conformational selection can never be reproduced by induced fit. A simple model of conformational selection in which one bound conformation is generated from multiple free conformations is sufficient to explain any set of experimental data where a single saturable relaxation is observed and is necessary for a large fraction of those systems. Remarkably, when multiple saturable relaxations are observed, inclusion of additional complexity in the free ensemble is sufficient to explain over 95% of existing relaxation kinetics and a scheme in which all bound conformations pre-exist in the free ensemble is entirely sufficient. The rich repertoire of kinetic behaviors associated with conformational selection makes this mechanism a far simpler unified solution to ligand binding. The complexity of the conformational ensemble pre-exists in the free form with the ligand selecting those conformations with the optimal fit. The ensemble view of the macromolecule agrees well with the fact that conformational selection can never be disproved as a mechanism of ligand binding, and with the fact that conformational selection is always sufficient and often necessary to account for the relaxation kinetics of simple and more complex systems. Pre-existence of alternative conformations is likely a fundamental property of all macromolecules.

Highlights.

• Conformational selection is always sufficient and often necessary to account for the relaxation kinetics of ligand binding to a biological macromolecule.

• Induced fit is never necessary and only sufficient in a few cases.

• The long assumed importance and preponderance of induced fit as a mechanism of ligand binding should be reconsidered.

• Conformational selection is an essential component of any mechanism of ligand binding.