Microdomain Effects on Transverse Cardiac Propagation

Abstract

The effect of gap junctional coupling, sodium ion channel distribution, and extracellular conductivity on transverse conduction in cardiac tissue is explored using a microdomain model that incorporates aspects of the inhomogeneous cellular structure. The propagation velocities found in our model are compared to those in the classic bidomain model and indicate a strong ephaptic microdomain contribution to conduction depending on the parameter regime. We show that ephaptic effects can be quite significant in the junctional spaces between cells, and that the cell activation sequence is modified substantially by these effects. Further, we find that transverse propagation can be maintained by ephaptic effects, even in the absence of gap junctional coupling. The mechanism by which this occurs is found to be cablelike in that the junctional regions act like inverted cables. Our results provide insight into several recent experimental studies that indirectly indicate a mode of action potential propagation that does not rely exclusively on gap junctions.

Introduction

Although gap junctions have been traditionally considered to be the primary mediator of action potential propagation, recent experimental evidence has suggested another means of coupling that supports conduction. In recent laboratory studies, Steven Poelzing and his colleagues have found that interstitial volume modulates the action potential propagation velocity and its dependence on gap junctional coupling (1). In conflict with classical bidomain theory, which predicts propagation speeds that increase monotonically with extracellular conductivity, Poelzing’s experimental results show that decreased extracellular volume increases propagation velocity and increased extracellular volume decreases velocity. This inverted relationship shows that there is a strong dependence of conduction speed on the structure of the extracellular space, an effect called ephaptic coupling (2,3). Ephaptic effects, or field coupling, arise due to inhomogeneities of extracellular space, such as the microdomain narrow junctional clefts between cells. Neighboring cells communicate through the extracellular space by way of strong localized gradients, a phenomenon that cannot occur in homogenized models such as the bidomain model.

We previously introduced a microdomain model that incorporates some features of the complex cellular geometry while remaining relatively computationally efficient (4,5). Our model, of intermediate complexity, includes microdomains, unlike homogenized models (6,7), yet has simplifications that allow for more efficient numerical simulations compared to highly detailed 3-dimensional (3D) models (8–14). These studies have found profound differences in longitudinal propagation because of the ephaptic coupling resulting from strong gradients in the extracellular space. Here, we extend this model to a sheet of 3D cells and focus on transverse propagation. We compare our results to those from the bidomain model, which considers a homogenized tissue sheet, to quantify the differences due to ephaptic effects.

Theory

Microdomain model

For our microdomain model, we assume conservation of current in the extracellular space, summing over capacitive and ionic transmembrane currents. The extracellular space is treated as a thin domain enclosing the cells and extracellular potential is assumed to be isopotential across the shortest distance, the width of which is denoted $W\left(x\right)$ at any point x in the extracellular space. For each x, there are $k\left(x\right)$ neighboring intracellular potentials, where $k=1$ on the exterior boundary and $k=2$ on the interior of the tissue. We sum over these neighbors to find the capacitive and ionic currents that depend on the transmembrane potential. Thus, the governing equation is

$$-\nabla \cdot \left(W\left(x\right){\sigma }_e\nabla {\varphi }_e\right)=\sum _{j=1}^{k\left(x\right)}\left(C_m\frac{\partial }{\partial t}\left({\varphi }_i^j-{\varphi }_e\right)+I_{\text{ion}}\left({\varphi }_i^j-{\varphi }_e,x\right)\right),$$ (1)

where $C_m$ represents membrane capacitance, ${\sigma }_e$ extracellular conductivity, and $I_{\text{ion}}$ is the current from the transmembrane ionic channels. Note that since the extracellular potential is uniform across the shortest width, the gradient and divergence operators are in two spatial dimensions tangent to the cell surface.

On the other hand, the intracellular equations for each cell with domain $\text{Ω}$ and boundary $\partial \text{Ω}$ are

$${\nabla }^2{\varphi }_i=0\text{in}\text{Ω},$$ (2)

$${\sigma }_i\nabla {\varphi }_i\cdot \hat{n}=-C_m\frac{\partial \left({\varphi }_i-{\varphi }_e\right)}{\partial t}-I_{\text{ion}}\left({\varphi }_i-{\varphi }_e,x\right)+g_{in}\left(x\right)\left({\varphi }_n-{\varphi }_i\right)\text{on}\partial \text{Ω},$$ (3)

where ${\sigma }_i$ is the intracellular conductivity, $\hat{n}$ the unit outward normal on the surface $\partial \text{Ω}$, and $g_{in}\left(x\right)$ represents the gap junctional conductance between cell i and a neighboring cell n at position x on the boundary.

Bidomain model

For purposes of comparison, we use the classical bidomain model (see for example (15)). By homogenizing the microstructure, the cardiac tissue is treated as a two-phase medium. At every point in the tissue there is an intracellular and extracellular potential ${\varphi }_i$ and ${\varphi }_e$. Using conservation of current, the bidomain equations are as follows:

$$\nabla \cdot \left({\sigma }_i^{\text{∗}}\nabla {\varphi }_i+{\sigma }_e^{\text{∗}}\nabla {\varphi }_e\right)=0,$$ (4)

$$\chi \left(C_m\frac{\partial \left({\varphi }_i-{\varphi }_e\right)}{\partial t}+I_{\text{ion}}\left({\varphi }_i-{\varphi }_e,x\right)\right)=\nabla \cdot \left({\sigma }_i^{\text{∗}}\nabla {\varphi }_i\right),$$ (5)

where ${\sigma }_i^{\text{∗}}$ and ${\sigma }_e^{\text{∗}}$ denote the effective intracellular and extracellular conductivity tensors of the homogenized tissue, and χ is the ratio of cellular surface area to volume.

Plane wave solutions to the bidomain model in Eqs. 4 and 5 give rise to plane wave speeds c of

$$c=\frac{\text{Λ}\left(\hat{n}\right)}{C_m{R}_m}{c}_0,\text{Λ}{\left(\hat{n}\right)}^2=\frac{R_m}{\chi }\frac{\left(\hat{n}\cdot {\sigma }_i^{\text{∗}}\hat{n}\right)\left(\hat{n}\cdot {\sigma }_e^{\text{∗}}\hat{n}\right)}{\hat{n}\cdot \left({\sigma }_i^{\text{∗}}+{\sigma }_e^{\text{∗}}\right)\hat{n}}.$$ (6)

where $R_m$ is the membrane resistivity (in units of cm²/mS), $\hat{n}$ is the direction of propagation, and $c_0$ is a unitless constant dependent on the ionic current model.

Methods

Cardiac tissue physiology

Table 1 provides the physiological parameters, based on reasonable experimental values, that remain unchanged in our simulations.

Table 1.

Simulation parameter values

Parameter	Symbol	Value
Cell length	l	0.01384 cm (18)
Cell width	w	0.00241 cm (18)
Cell height	h	0.00241 cm (18)
Membrane capacitance	Cm	1 μF/cm2 (19)
Extracellular conductivity	${\sigma }_e$	20 mS/cm (7)
Intracellular conductivity	${\sigma }_i$	6.7 mS/cm (20)

Each cell is idealized as a rectangular prism with a corner inclusion. The longitudinal and transverse offsets of the inclusion are taken to be 20% and 50% in the longitudinal and transverse directions, respectively, as shown in a top-down view in Fig. 1 A. These cells were arranged in a periodic structure, as in Fig. 1 B, to form a cardiac tissue sheet, and then extended periodically in the vertical ($x_3$) direction. We also assume that gap junctions couple cells only in the longitudinal (end-to-end) direction. This 3D cellular structure, two cells of which are shown in Fig. 1 C, captures some of the complex features of intracellular connectivity between neighboring cells.

Figure 1.

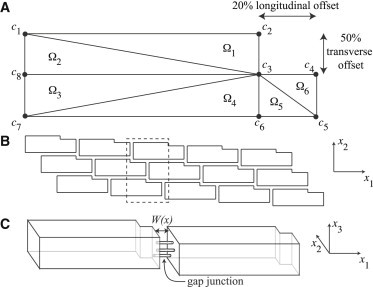
(A) Schematic of the physiological cellular structure, which has a 20% inclusion in the longitudinal direction and a 50% inclusion in the transverse direction. The finite-element discretization of the intracellular space has eight nodes per cell and six domains. (B) Periodic tiling of the cells, shown as a tissue sheet. (C) Two neighboring cells depicted as 3D structures.

Microdomain model numerics

Since the available cross-sectional area, and thereby the conductance of the intracellular space, is larger than that of the extracellular space, gradients in the intracellular potential are not as large as those in the extracellular space. As a result, the intracellular space need not be discretized to the same refinement as the extracellular space. However, some discretization is necessary for numerical accuracy. We choose to use a finite-element discretization of the cell, with eight nodes aligned with the corners of the indented cell, which is then divided into six domains as shown in a top-down view of the cell in Fig. 1 A. In assuming an overall structure of cardiac tissue shown in Fig. 1 B, we take the intracellular potential in the vertical ($x_3$) direction to be uniform.

Using the Galerkin method, we solve ${\nabla }^2{\varphi }_i=0$ in the weak sense, looking for solutions to

$$\langle {\nabla }^2{\varphi }_i,{\psi }_j\rangle ={\iiint }_{\text{Ω}}{\psi }_j{\sigma }_i{\nabla }^2{\varphi }_{i}dV=0,$$ (7)

where ${\varphi }_i={\sum }_{k=1}^8{c}_k{\psi }_k$, ${\psi }_k$ are piecewise linear interpolating functions, $k=1,2,\dots ,8$, and the inner product $\langle u,v\rangle ={\iiint }_{\text{Ω}}uvdV$, so that $c_k$ represents the value of the intracellular potential at node k.

Using the Divergence Theorem and some simplification, we find that

$${\sigma }_i{\iiint }_{\text{Ω}}\nabla {\psi }_j\cdot \nabla {\psi }_{k}dV=-\underset{\partial \text{Ω}}{\iint }{\psi }_{k}JdA,$$ (8)

where J are the boundary currents specified by the right side of Eq. 3.

In computing the gap junctional current term in Eq. 8, we assume that gap junctional proteins are exclusively end to end between cells (i.e., in the $x_1$ direction) and are evenly distributed along the end plate of the cell. The intracellular potentials are linearly interpolated along the edges of cells. The relationships between all intracellular potentials, $c_k$, coupled through gap junctions can be thought of as describing a network of nodes and resistors, with a corresponding electrical circuit diagram (Fig. 2 A).

Figure 2.

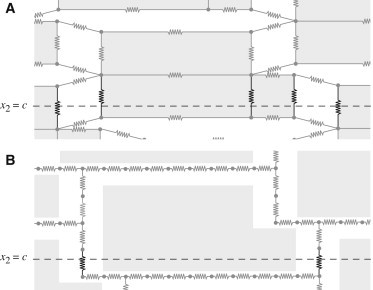
Discretization of the cardiac cells as a network of nodes and resistors. The total current through a cross section, shown at $x_2=c$ was calculated by summing over the individual currents in the resistors in bold to find the effective conductivity of the tissue in the intracellular (A) and extracellular (B) spaces.

We use cell-centered finite differences for spatial derivatives to discretize the current balance equation (Eq. 1) for extracellular space. Then, letting u represent a vector of the unknown intracellular potentials, $c_k$, and extracellular potentials, ${\varphi }_e$, we find that Eqs. 1 and 8 can be written in the form

$$A\frac{\partial u}{\partial t}-I_{\text{ion}}\left(u,x\right)-Lu=0,$$ (9)

where A and L are matrices. Because the matrix L is a discrete Laplacian operator, we use the Crank-Nicolson scheme for time derivatives and solve the equation

$$\left(A-\frac{\text{Δ}t}{2}L\right)u^{\left(n+1\right)}=\left(A+\frac{\text{Δ}t}{2}L\right)u^{\left(n\right)}+I_{\text{ion}}\left(u^{\left(n\right)},x\right)$$ (10)

for the unknowns $u^{\left(n\right)}$ at each time step n using a basic Jacobi preconditioner and LU factorization for the matrix $\left(A-\left(\text{Δ}t/2\right)L\right)$.

For the ionic currents, $I_{\text{ion}}\left(u^{\left(n\right)},x\right)$, we use a modified Hodgkin and Huxley formulation governing the action potential upstroke:

$${\alpha }_m\left(v\right)=\frac{0.1\left(25-v\right)}{\text{exp}\left(\frac{25-v}{10}\right)-1},{\beta }_m\left(v\right)=4\text{exp}\left(\frac{-v}{18}\right),m_{\infty }\left(v\right)=\frac{{\alpha }_m\left(v\right)}{{\alpha }_m\left(v\right)+{\beta }_m\left(v\right)},$$ (11)

$$I_{\text{ion}}\left(v,x\right)=-{\overline{g}}_{\text{K}}{n}_0^4\left(v+12\right)-\theta \left(x\right){\overline{g}}_{\text{Na}}{m}_{\infty }{\left(v\right)}^3{h}_0\left(v-115\right)-{\overline{g}}_{\text{L}}\left(v-10.6\right),$$ (12)

for which ${\overline{g}}_{\text{K}}=36$, ${\overline{g}}_{\text{Na}}=120$, and ${\overline{g}}_{\text{L}}=0.3$, and we assume resting-state values of $n_0=0.3176$ and $h_0=0.596$ for the gating variables.

In Eq. 12, $\theta \left(x\right)$ determines the distribution of the sodium ion channels, which for this study is uniform on the ends and the sides of the cells. No matter the distribution, the total number of sodium ion channels per cell is kept constant. For example, in what follows, 100% Ends indicates that on the sides of the cells $\theta \left(x\right)=0$, and on the ends of the cells $\theta \left(x\right)=11.9$, is the ratio of the total surface area of a cell to the surface area of the ends of the cells. Likewise, 100% Sides indicates that on the ends of the cells $\theta \left(x\right)=0$, and on the sides of the cells $\theta \left(x\right)=1.1$, is the ratio of the total surface area of a cell to the surface area on the sides of the cells. A uniform distribution of sodium ion channels on the cell is represented by $\theta \left(x\right)=1$ everywhere on the cellular membrane. Here, we study the two extreme cases in which sodium ion channels are located entirely on the sides or entirely on the ends of the cells to explore the full range of possible ephaptic behavior. In experiments, sodium ion channels have been shown to be preferentially localized on the ends of the cells (3,14,16,17). Even if all the sodium ion channels are on the ends of the cells, we find sodium ion depletion in the cleft due to an action potential to be negligible. For our particular cellular geometry, and assuming a sodium ion concentration of 150 mM, we estimate that there are approximately $7.8\times {10}^8$ molecules of sodium ions in the junctional cleft. Approximately $8.6\times {10}^7$ molecules of singly charged ions are required to depolarize the cell by 100 mV, and if all of those ions were sodium ions from the junctional region without inflow of ions into the junctional region, the junctional sodium concentration would decrease by only 12%. This leads to a decrease in the sodium Nernst potential of at most 4 mV. Since these changes are an overestimate of the junctional sodium decrease, it is safe to ignore this effect when calculating action potential propagation. A similar calculation with the same conclusion was previously done by Kucera et. al. (14).

To simulate action potential propagation, the overall tissue was taken to be periodic on the boundaries parallel to the direction of propagation. On the other two boundaries, equal and opposite voltages were applied until an action potential was initiated, after which no flux boundary conditions were imposed. All potentials were assumed to be periodic in the vertical ($x_3$) direction.

Bidomain model numerics

For a particular tissue structure and set of parameter values, we first compute the effective intracellular and extracellular conductivities in the longitudinal and transverse directions. We use the numerical discretization scheme for the microdomain model without ionic currents, solving the electrostatic problem ${\nabla }^2\varphi =0$ with imposed voltages at the boundaries, similar to the calculations of Hand et al. (6). For effective conductivities in the transverse direction, we take a cross section at $x_2=c$ (see Fig. 1 for directionality), and considering the discretization scheme as a network of nodes and resistors, we compute the total current through the intracellular, $I_i$, and extracellular, $I_e$, space, as shown in Fig. 2, A and B, respectively.

Thus, the transverse intracellular and extracellular effective conductivities ${\sigma }_i^{\left(t\right)\text{∗}}$ and ${\sigma }_e^{\left(t\right)\text{∗}}$ of a homogeneous tissue can be computed using

$${\sigma }_{e,i}^{\left(t\right)\text{∗}}=\frac{l}{A\text{Δ}V}{I}_{e,i},$$ (13)

where $\text{Δ}V$ is the voltage drop across the tissue, l is the transverse length of the tissue, and A is the total cross-sectional area at $x_2=c$. Similar calculations are done for the intracellular and extracellular effective conductivities ${\sigma }_i^{\left(l\right)\text{∗}}$ and ${\sigma }_e^{\left(l\right)\text{∗}}$ in the longitudinal direction, taking a cross section at $x_1=c$.

In Fig. 3, we show how these effective conductivities change with our parameters of interest. Fig. 3 A shows the effective extracellular conductivities normalized by the nominal extracellular conductivity, ${\sigma }_e$, as a function of extracellular volume fraction. The junctional cleft width is taken to be the nominal value of $1.5\times {10}^{-6}$ cm, and extracellular lateral width is varied. The longitudinal and transverse ratios are similar and change almost linearly with extracellular volume fraction in the range reported. Similar curves for the effective intracellular conductivities are shown in Fig. 3, B and C, plotted against gap junctional coupling, g. Although ${\sigma }_i^{\left(l\right)\text{∗}}/{\sigma }_i$ varies strongly with gap junctional coupling, ${\sigma }_i^{\left(t\right)\text{∗}}/{\sigma }_i$ is relatively small, reflecting the fact that gap junction connections are only end to end between cells. The inverse ratio ${\sigma }_i/{\sigma }_i^{\left(l,t\right)\text{∗}}$ is well represented by the linear relationship in $1/g$,

$$\frac{{\sigma }_i}{{\sigma }_i^{\left(t\right)\text{∗}}}=\left(7.04\times {10}^4\text{mS}/{\text{cm}}^2\right)\frac{1}{g}+13.1,$$ (14)

$$\frac{{\sigma }_i}{{\sigma }_i^{\left(l\right)\text{∗}}}=\left(7.71\times {10}^2\text{mS}/{\text{cm}}^2\right)\frac{1}{g}+\mathrm{1.25.}$$ (15)

To properly compare the velocities of propagation in our microdomain model with those from the bidomain model, we must remove discrete cell effects. To do this, we use Eq. 6 with velocities matched to the microdomain model in the nonephaptic limit. For a fixed structure, Eq. 6 can be rewritten as

$$c=k^{\left(l,t\right)}{\left(\frac{{\sigma }_i^{\left(l,t\right)\text{∗}}{\sigma }_e^{\left(l,t\right)\text{∗}}}{{\sigma }_i^{\left(l,t\right)\text{∗}}+{\sigma }_e^{\left(l,t\right)\text{∗}}}\right)}^{\frac{1}{2}},$$ (16)

where $k^{\left(l,t\right)}$ is a constant particular to the cardiac tissue structure and l and t indicate values for the longitudinal and transverse directions, respectively. When the extracellular conductivity is large, this velocity reduces to

$$c=k^{\left(l,t\right)}{\left({\sigma }_i^{\left(l,t\right)\text{∗}}\right)}^{\frac{1}{2}}.$$ (17)

Likewise, as ${\sigma }_e\to \infty$ in the microdomain model, the microdomain effects disappear as the extracellular potential becomes homogeneous, and we have a velocity $v_{\infty }^{\left(l,t\right)}$, which we refer to as the nonephaptic velocity. Equating this with Eq. 17, we find the constants of interest,

$$k^{\left(l,t\right)}=\frac{v_{\infty }^{\left(l,t\right)}}{{\left({\sigma }_i^{\left(l,t\right)\text{∗}}\right)}^{\frac{1}{2}}}.$$ (18)

For the tissue structure in this study, we determine the corresponding $k^{\left(l\right)}$ and $k^{\left(t\right)}$ (with units cm^3/2/mS^1/2/ms) for each parameter set studied, reported in Fig. 4, and, along with the computed effective conductivities, we are able to find the nonephaptic bidomain propagation speed in Eq. 6.

Figure 3.

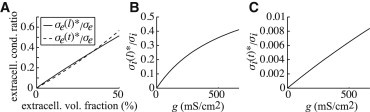
(A) The ratio of extracellular effective conductivities in the transverse and longitudinal directions to nominal extracellular conductivity, ${\sigma }_e$, with junctional cleft width fixed at $1.5\times {10}^{-6}$ cm with lateral extracellular width changing such that the extracellular volume fraction ranges up to 50%. (B and C) The ratios of intracellular effective conductivities in the longitudinal (B) and transverse (C) directions to nominal intracellular conductivity, ${\sigma }_i$, plotted against gap junctional coupling, g.

Figure 4.

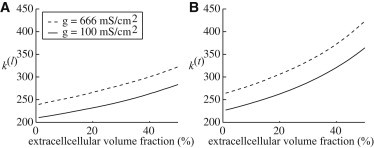
The constants in units of cm^3/2/mS^1/2/ms computed from Eq. 18 as a function of changing lateral extracellular width such that the extracellular volume fraction ranges up to 50%.

Results

To explore ephaptic effects in the microdomain model with varying physiological parameters, we vary the sodium ion channel distribution, the gap junctional coupling (typically 666 mS/cm (14)), junctional cleft width (typically $1.5\times {10}^{-6}$ cm wide (3,9,21)), and lateral extracellular width such that the total extracellular volume (ratio of the extracellular volume to the sum of the intracellular and extracellular volumes) ranges up to 50%.

Fig. 5 shows the comparison of the bidomain model (gray lines) to the microdomain model when sodium ion channels are distributed entirely to the sides (dashed black lines) or the ends (solid black lines) of the cell, plotted as a function of the extracellular volume fraction. The longitudinal velocities, transverse velocities, and anisotropy ratios were computed over a lateral extracellular width that changed the extracellular volume fraction up to 50%. In the left column, the gap junctional coupling and junctional cleft width are at the nominal values of 666 mS/cm² and $1.5\times {10}^{-6}$ cm, respectively. In the middle column, the gap junctional coupling is reduced to 100 mS/cm², and in the right column, the gap junctional coupling is still 100 mS/cm² whereas the junctional cleft width is increased to $1.5\times {10}^{-5}$ cm.

Figure 5.

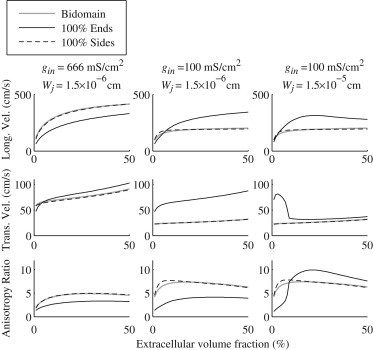
Longitudinal velocities, transverse velocities, and anisotropy ratios at a gap junctional coupling of 666 mS/cm² and 100 mS/cm² for extracellular junctional cleft widths of $1.5\times {10}^{-6}$ cm and $1.5\times {10}^{-5}$ cm with lateral extracellular width changing such that the total extracellular volume ranges up to 50%.

In all cases, the bidomain model and the microdomain model closely agree when the sodium ion channels are located entirely on the sides of the cells, indicating that ephaptic effects occur when the sodium ion channels are on the ends of the cells. However, with low gap junctional conductivity, and with sodium ion channels on the sides of the cell, ephaptic effects are seen again in the longitudinal velocities, as explored in our previous work (5). At nominal gap junctional coupling, ephaptic effects decrease velocities in the longitudinal direction, but enhance velocities at lower $g_{in}$, also as noted previously (4).

In the transverse direction, the microdomain model shows an increase in speed over the bidomain model when sodium ion channels are on the ends of the cells, regardless of gap junctional coupling or junctional width. When gap junctional coupling is low and junctional cleft width is large, transverse ephaptic propagation has an interesting biphasic behavior, also seen in our longitudinal study (4). With nominal junctional cleft size, the ephaptic enhancement of the transverse velocity brings the anisotropy ratio below that predicted by the bidomain model.

Although velocities for the bidomain model increase monotonically with increasing extracellular conductivity, the microdomain model exhibits a biphasic effect in both the transverse and longitudinal velocities in certain regimes (low gap junctional coupling and large junctional cleft width). The significant difference in the behavior of the velocities depending on sodium ion channel distribution also is not predicted by the bidomain model.

Transverse propagation without gap junctions

It has already been established that the microdomain model can have longitudinal conduction in the absence of gap junctional coupling (4,5). Here, we discuss the ephaptic effects for transverse propagation.

The bidomain model, which is entirely nonephaptic, predicts conduction failure in the absence of gap junctional coupling. Without gap junctional coupling, ${\sigma }_i^{\left(t\right)\text{∗}}=0$ in Eq. 16 and the transverse velocity is zero. However, the microdomain model allows for conduction in certain regimes due to the strong potential gradients in the extracellular space. In Fig. 6 A, velocities are shown for the case where the gap junctional coupling is zero, with sodium ion channels entirely on the ends of the cells. When junctional cleft width is at the nominal value of $1.5\times {10}^{-6}$ cm, transverse conduction velocity is relatively constant with respect to extracellular volume fraction and transitions to a biphasic curve with larger junctional cleft sizes. At large extracellular and junctional conductances, the microdomain model must agree with the bidomain model, and so the approach to zero is seen at larger extracellular widths as the junctional cleft width increases.

Figure 6.

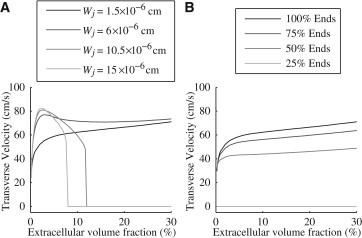
Transverse velocities with zero gap-junctional coupling for extracellular volume fractions ranging up to 50% (A) with the junctional extracellular cleft width changing from $1.5\times {10}^{-6}$ cm to $15\times {10}^{-6}$ cm and sodium ion channels entirely on the ends of the cells and (B) with the junctional extracellular cleft width fixed at $1.5\times {10}^{-6}$ cm and different distributions of sodium ion channels.

Also seen in Fig. 6 A is a biphasic trend in velocity as a function of extracellular lateral widths when sodium ion channels are on the ends of the cells. That is, transverse velocity increases and then decreases as extracellular volume fraction increases. This trend is also seen in Fig. 5, as the velocities for 100% Ends increase when $W_j$ increases to $15\times {10}^{-6}$ cm for smaller extracellular volume fraction.

Fig. 6 B shows the transverse velocity at several different levels of sodium ion channels on the sides of the cell, again without gap junctional coupling. The solid black line indicates the velocity when the sodium ion channels are entirely on the ends of the cell, matching that of Fig. 6 A. When more sodium ion channels are on the sides of the cell, the velocities (shown in increasingly lighter shades of gray) are driven to zero, i.e., there is conduction failure.

Mechanism of transverse propagation

To study the mechanisms behind transverse propagation, we examine the transmembrane potentials along the junctional cleft path in the $x_2$ direction. This region, indicated by the dashed box in Fig. 1 B, is magnified in the left side of Fig. 7. On the right side of Fig. 7, we plot the depolarization time of the nodes along the junctional cleft path as a function of vertical position as an action potential propagates up the tissue. On the left side of the path (dashed line and circles), each cell has four nodes (one at each corner, with two at the same vertical position), and on the right side (gray line and circles), each cell has three nodes. For this figure, we chose $W_j=1.5\times {10}^{-6}$ cm and an extracellular volume fraction of 25%.

Figure 7.

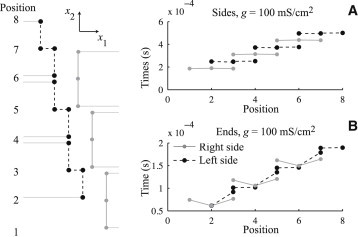
Activation sequence in transverse propagation with junctional cleft width of $1.5\times {10}^{-6}$ cm and extracellular volume fraction of 25% along the junctional cleft path shown on the left as a function of vertical position for 100 mS/cm² gap junctional coupling and sodium ion channels entirely on the sides (A) and entirely on the ends (B) of the cells.

For Fig. 7 A, all the sodium ion channels are on the sides of the cell and the gap junctional coupling is 100 mS/cm². The entirety of each cell depolarizes at the same time, and the depolarization follows linearly up the path of the junctional cleft, alternating between the right and left sides, in zig-zag fashion. This is the mode of transverse propagation that is classically understood as being mediated by gap junctions. When sodium ion channels are all placed in the ends of the cell, the propagation shows significant ephaptic effects, as depicted in Fig. 7 B. The middle of the cells on the righthand side cause the lower nodes on the upper left cells to depolarize. An added effect occurs when the remaining nodes on the left cells depolarize, which in turn causes the middle of the neighboring upper right cells to depolarize. In this propagation, driven by ephaptic effects, the left and right sides of the junctional cleft path are depolarized simultaneously through the extracellular space. This effect is illustrated in Fig. 8, where nodes that are simultaneously depolarized are circled. When sodium ion channels are entirely in the sides of the cells (Fig. 8 left), only nodes belonging to the same cell depolarize together. When sodium ion channels are in the ends of the cells (Fig. 8 right), simultaneous depolarization occurs in nodes belonging to three different cells, emphasizing the ephaptic coupling between cells. One way to understand this mode of propagation is to view the junctional space as an inverted cable, which supports propagation along its length, i.e., transverse to the longitudinal axis of the cell.

Figure 8.

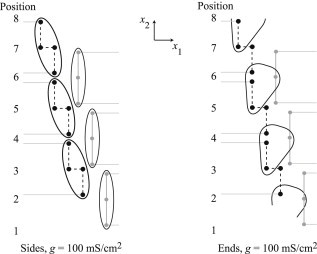
Encircled nodes indicate those in Fig. 7 that depolarize simultaneously for sodium ion channels entirely in the sides of the cells (A) and entirely in the ends of the cells (B).

Discussion

We have developed a microdomain model (Eqs. 1–3) that incorporates some features of the complex geometry and microdomain effects due to the small extracellular spaces and sodium ion channel distribution. Our numerical simulations show ephaptic effects that enhance the velocity (Fig. 5) above that of the nonephaptic bidomain model (Eqs. 4 and 5). Unlike the bidomain model, which has monotonically increasing velocity trends as a function of extracellular conductance or extracellular volume fraction, the microdomain model can show a nontrivial biphasic effect in both lateral and junctional extracellular space size that also changes behavior with sodium ion channel distribution and depends on the amplitude of gap junctional coupling. The bidomain model does not include microdomain inhomogeneities necessary to exhibit this complex behavior.

Our microdomain model allows for moderately fast numerical computations while also including the effects of the complex geometry in the cellular tissue. The ephaptic effects are enhanced by lowered gap junctional coupling, which can support conduction even in the absence of gap junctions. For propagation in the transverse direction with zero gap junctional coupling, ephaptic effects are most pronounced when sodium ion channels are distributed on the ends of the cells, as well as when lateral and junctional extracellular conductivities are lowered, as seen in Fig. 6. When sodium ion channels are distributed to the sides of the cell, or when extracellular conductivities are increased, the velocities decrease to zero, matching the nonephaptic prediction. Further, we found that when sodium ion channels are distributed to the ends of the cells, the junctional space acts like a transverse cable along which cablelike propagation can occur. Thus, ephaptic coupling provides for a believed new mode of transverse propagation.

Thus, we find that for transverse propagation, much like what has been established for longitudinal conduction (4,5), ephaptic effects are enhanced by a combination of end-dominant sodium ion channel distribution and lowered gap junctional coupling. A biphasic effect with changing extracellular sizes is necessary to explain the decrease in velocity with increased extracellular volume, observed by Steven Poelzing and colleagues (1). Such behavior is not possible for the classic formulation of the bidomain model.

Modifying sodium and potassium currents has been found experimentally to change the anisotropy ratio (22,23). However, in the bidomain model, the anisotropy ratio is independent of ion channel densities, as these are folded into the constant $c_0$ in Eq. 6. Future studies will further explore how microdomain effects are affected by transmembrane ionic currents.

In conclusion, our mathematical studies have shown that there can be nonnegligible microdomain effects on transverse propagation that depend strongly on transmembrane ion channel distribution and gap junctional coupling. Such insight is necessary to understand the role of structure and physiological characteristics of cardiac tissue in action potential propagation and its failure.