Temporal Dynamics of Microbial Rhodopsin Fluorescence Reports Absolute Membrane Voltage

Abstract

Plasma membrane voltage is a fundamentally important property of a living cell; its value is tightly coupled to membrane transport, the dynamics of transmembrane proteins, and to intercellular communication. Accurate measurement of the membrane voltage could elucidate subtle changes in cellular physiology, but existing genetically encoded fluorescent voltage reporters are better at reporting relative changes than absolute numbers. We developed an Archaerhodopsin-based fluorescent voltage sensor whose time-domain response to a stepwise change in illumination encodes the absolute membrane voltage. We validated this sensor in human embryonic kidney cells. Measurements were robust to variation in imaging parameters and in gene expression levels, and reported voltage with an absolute accuracy of 10 mV. With further improvements in membrane trafficking and signal amplitude, time-domain encoding of absolute voltage could be applied to investigate many important and previously intractable bioelectric phenomena.

Introduction

Any lipid membrane can, in principle, support a membrane voltage. This voltage modulates the free energy landscape of all charged proteins and small molecules associated with the membrane (1). Although membrane voltage is well known to regulate the activity of ion channels, voltage also regulates activity of phosphatases (2), G-protein coupled receptors (3), and redox proteins (4). Bacteria, fungi, plants, and animal cells dynamically regulate voltage in the plasma membrane and in intracellular organelles. Resting potentials range from as low as −300 mV in Neurospora crassa (5), −180 mV in mitochondria (6), −140 to −80 mV in Escherichia coli (7), −90 mV to −65 mV in cardiomyocytes and neurons, to near 0 mV in undifferentiated stem cells (8–10).

Genetically encoded fluorescent reporters of membrane voltage enable noninvasive optical monitoring of electrical dynamics in live cells. With recent advances in speed and sensitivity, one can now visualize single action potentials in neurons and cardiomyocytes, in vitro (11–13) and in vivo (14–16). These intensity-based measurements report relative changes in membrane voltage, not its precise numerical value. This approach is appropriate for detecting fast action potentials and subthreshold events, but not for measuring slower shifts in resting voltage, such as occur during embryonic development (17), stem cell differentiation (18), wound healing (19), programmed cell death (20), and plant responses to herbivory (21,22).

One would like a means to map the numerical value of the membrane voltage in a sample over space and time. A reporter of absolute voltage should meet several criteria. The measurement should be insensitive to variations in reporter concentration, photobleaching, and background autofluorescence. The measurement should also be insensitive to the precise intensity of the illumination or the efficiency of the optical collection, as these parameters often differ between experiments. The reporter should be genetically targeted to facilitate measurements in defined subclasses of cells within a heterogeneous population.

Dual-wavelength ratiometric imaging is sometimes used in attempts at accurate measurements. This strategy has been employed in fluorescent measurements of pH (23), Ca²⁺ (24,25), kinase activity (26,27), and voltage (28,29). The dye di-8-ANEPPS undergoes a voltage-dependent shift in emission spectrum that can be detected by simultaneous imaging in two emission bands. Fluorescence resonance energy transfer-based voltage indicators in principle enable ratiometric measurements of absolute voltage (30,31), but differential rates of photobleaching between the donor and acceptor make this difficult in practice. Dual-wavelength ratiometric measurements require careful spectral calibration of the apparatus and can be confounded by spectrally or spatially inhomogeneous background fluorescence. Due to the technical challenges of accurately quantifying fluorescence across multiple wavelengths, ratiometric indicators are not widely used for absolute voltage measurements.

In contrast to measurements of intensity, measurements of time can be both precise and accurate. A common strategy for detecting a small signal on a large and inhomogeneous background is to encode the information in the time domain. Fluorescence lifetime imaging microscopy uses changes in the electronic excited state lifetime to report on subtle environmental changes that are not apparent from the raw fluorescence intensity. This technique has been used effectively to measure calcium concentrations and enzymatic activity in dendritic spines (32,33). We sought to encode voltage information into a time-domain optical signal.

Retinal-binding proteins are emerging as a new class of genetically encoded optical reporters (34). We recently reported that microbial rhodopsins can serve as fast and sensitive, but dim, fluorescent voltage indicators (11,35). Electronic excited state lifetimes of rhodopsins are <100 ps (36), too short to use as a contrast mechanism in imaging. However, these proteins also undergo slower dynamics: they have a complex conformational landscape, with states connected by voltage- and light-dependent transitions (37–39). In wild-type Archaerhodopsin 3 (Arch), continuous illumination produces a voltage- and wavelength-dependent photostationary distribution among the states. A change in voltage alters the photostationary distribution and leads to a change in fluorescence. We reasoned that a change in illumination wavelength, with constant voltage, would also change the photostationary distribution. The trajectory of the relaxation to the new distribution might report absolute membrane voltage.

In the mutant Arch(D95H), voltage affected both the amplitude and timecourse of the fluorescence response to a step change in illumination wavelength. These quantities provided a measure of absolute voltage that was insensitive to expression level, precise illumination intensity, or precise collection efficiency. We demonstrated this technique in human embryonic kidney (HEK) cells.

Materials and Methods

Molecular cloning

Arch(D95H)-eGFP was created during the generation of an Arch(D95X) mutant library in pET-28b via saturation point mutagenesis. Arch(D95H) was moved (Gibson Assembly, New England Biolabs) into a lentiviral mammalian expression vector (Addgene plasmid 22051 cut with the restriction enzymes BamHI and AgeI). The final construct consisted of Arch(D95H) fused to C-terminal eGFP, driven under an ubiquitin promoter. The construct is available on Addgene.

HEK293 cell culture

HEK293T cells were cultured and transfected as previously described in (37).

Electrophysiology

Patch-clamp experiments were performed under conditions similar to those described in (37). Briefly, pipettes were pulled from borosilicate glass capillary tubes (World Precision Instruments, 1.5 mm OD, 0.84 mm ID) via a Flaming/Brown style micropipette puller (Sutter Instruments, P-1000) and filled with intracellular buffer (125 mM potassium gluconate, 8 mM NaCl, 0.6 mM MgCl₂, 0.1 mM CaCl₂, 1 mM EGTA, 10 mM HEPES, 4 mM Mg-ATP, and 0.4 mM Na-GTP at pH 7.3; adjusted to 295 mOsm with sucrose). Pipette resistances were 5–10 MΩ. The silver pipette electrode and ground were rechlorided daily before experimentation. HEK293 cells were bathed in Tyrode’s buffer (125 mM NaCl, 2 mM KCl, 3 mM CaCl₂, 1 mM MgCl₂, 10 mM HEPES, and 30 mM glucose at pH 7.3; adjusted to 305 mOsm with sucrose) for patch-clamp recordings. The liquid junction potential was compensated with the pipette immersed in the extracellular solution at zero pressure, before making a gigaseal with the cell membrane. Patch-clamp electrical parameters (pipette capacitance, access resistance, and membrane resistance) were recorded to ensure accurate control of the membrane voltage. All patch-clamp data were acquired in voltage-clamp mode under whole cell conditions, with a patch-clamp amplifier (Molecular Devices, Axopatch 200B).

Microscopy and image analysis

Fig. 1 a shows the experimental apparatus. This system comprised a spinning disk confocal microscope with up to four independently modulated laser lines. A patch-clamp apparatus controlled the membrane voltage in HEK cells expressing candidate indicators. Beams from solid-state lasers at 488 nm (Coherent Obis, 50 mW, Coherent, Santa Clara, CA), 532 nm (Coherent Compass 315M, 100mW), 594 nm (Cobalt Mambo, 100 mW), and 638 nm (CrystaLaser, 100 mW) were combined using dichroic mirrors (Semrock, Rochester, NY) and passed through an acousto-optic tunable filter (AOTF; Gooch & Housego 48058, Ilminster, UK) that allowed for spectral and temporal control of sample illumination. Illumination was directed into a modified Yokogawa spinning disk confocal imaging system (CSU-X1) attached to an Olympus IX71 inverted base. Imaging was performed with a custom dichroic optimized for 405, 488, 594 nm excitation (Chroma, Bellows Falls, VT). Maximum intensities after the objective (Zeiss 20× Plan-Apochromat NA 1.0) were 43 and 82 W/cm² for 488 and 594 nm, respectively. Emission fluorescence passed through a dual-band filter (Chroma) optimized for 488 and 594 excitation and was collected on an EMCCD camera (Andor iXon X3, 512 × 512 pixels, Andor, Belfast, UK).

Figure 1.

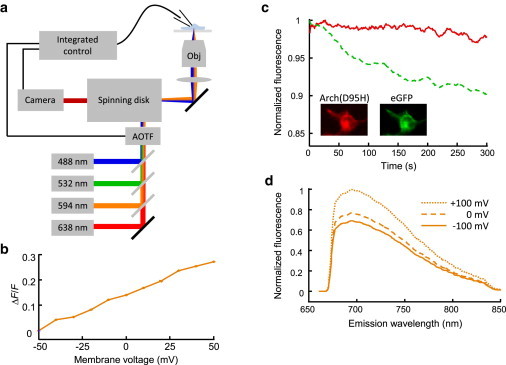
Experimental apparatus and characterization of voltage indicator Arch(D95H)-eGFP. (a) Imaging scheme with temporal control of illumination, patch-clamp amplifier, and camera for automated data acquisition. (b) Fluorescence from Arch(D95H) was sensitive to voltage when illuminated with 594 nm light. ΔF/F, normalized to fluorescence at −50 mV, was ∼30% per 100 mV. (c) Dual-indicator ratiometry was not robust to differential photobleaching. Under simultaneous illumination at 488 and 638 nm, eGFP (green dashed) photobleached faster than Arch(D95H) (red solid). Laser intensities were adjusted to achieve similar initial photon count rates from the two chromophores. (Inset) Dual-view spinning disk confocal images of HEK293 expressing Arch(D95H) (left) and eGFP (right). (d) Emission spectra of Arch(D95H) changed only in amplitude, and not shape, when membrane voltage was varied from −100 (solid), 0 (dashed), and +100 (dotted) mV. Panels (b) and (c) show representative traces from n = 10 measurements; panel (d) shows representative data from n = 3 measurements. To see this figure in color, go online.

Alternatively, illumination was directed onto the sample via widefield epifluorescence with a 650 nm long-pass dichroic mirror (Semrock). Intensities at the sample were 175, 80, 184, 193 W/cm² for 488, 532, 594, 638 nm light, respectively. Emission fluorescence was filtered through a 664 nm long pass filter (Semrock) before collection by the same Andor camera.

A custom LabView (National Instruments, Austin, TX) script along with a National Instruments DAQ (PCIe-6323) controlled the AOTF, patch-clamp amplifier, and camera for data acquisition. Data from images and current recordings were analyzed in MATLAB (The MathWorks, Natick, MA). Membrane-localized protein was separated from intracellular protein by selecting voltage-sensitive pixels corresponding to the plasma membrane via the method described in (11).

Voltage-dependent emission spectra

Emission spectra of Arch(D95H) were measured by placing an imaging spectrograph (Horiba iHR320, Horiba, Kyoto, Japan) at the image plane of the microscope. Samples under voltage-clamp control were illuminated by 594 nm light (184 W/cm²) via epifluorescence. Fluorescence was dispersed on a grating (100 grooves/mm) and then reimaged on an EMCCD camera.

Results and Discussion

Voltage-sensitive fluorescence in microbial rhodopsins is believed to arise from changes in protonation of the retinal Schiff base. The protonated state is fluorescent, the deprotonated state is not, and voltage controls the local electrochemical potential of protons and hence this acid-base equilibrium (37). Aspartic acid 95 in Arch (homologous to Asp-85 in bacteriorhodopsin) is the counterion to the Schiff base, and thus plays a key role in modulating protonation of the Schiff base. In a search for improved fluorescent voltage indicators, we generated a library of 20 Arch mutants by saturation mutagenesis at Asp-95. We screened the 20 mutants for voltage-sensitive fluorescence by expressing and imaging them in spiking HEK cells that had been genetically engineered to generate spontaneous electrical action potentials (41). Seven showed voltage-sensitive fluorescence. Of these, Arch(D95H) was the most sensitive.

We expressed the fusion Arch(D95H)-eGFP in standard (nonspiking) HEK293 cells and tested the response of Arch fluorescence (λ_ex = 594 nm, λ_em > 664 nm) to a ramp in membrane voltage applied via a patch pipette. Fluorescence increased 30% from V_m = −50 mV to V_m = 50 mV (Fig. 1 b). Arch(D95H) responded to a step in voltage with a biexponential rise in fluorescence, with time constants of 5 ms (34%) and 31 ms (66%) (41); the protein generated an outward photocurrent of 5 pA, which perturbed membrane voltage by <1 mV. In contrast, wild-type Arch excited at its absorption peak has been reported to pass a proton current of nearly 1 nA (42). This large proton current perturbed intracellular pH by 0.15 pH units; thus we infer that the pH perturbation from the 200-fold smaller Arch(D95H) photocurrent was negligible.

Ratiometric voltage indicators are confounded by differential photobleaching

We explored several strategies for using Arch(D95H) as an absolute voltage indicator. We first tested the eGFP fusion as a prospective dual-wavelength ratiometric indicator. We simultaneously imaged the fluorescence of Arch(D95H) (λ_ex = 638 nm, λ_em = 660–875 nm) and of eGFP (λ_ex = 488 nm, λ_em = 510–530 nm) using a dual-view spinning disk confocal imaging system. We adjusted laser intensities to achieve similar photon count rates in both channels. Fig. 1 c shows fluorescence of Arch(D95H) and of eGFP as a function of time under constant membrane voltage. eGFP photobleached faster than Arch(D95H), so this ratio could not be used as a robust measure of absolute voltage.

We further tested whether voltage-dependent shifts in the emission spectrum of Arch(D95H) could provide a measure of absolute voltage. We used an imaging spectrometer to record fluorescence emission spectra of Arch(D95H) at −100, 0, and +100 mV (λ_ex = 594 nm, λ_em > 664 nm). The emission spectrum did not exhibit detectable voltage-dependent shifts, and thus was unsuitable as a measure of absolute voltage (Fig. 1 d). This finding was consistent with a model of microbial rhodopsin fluorescence in which emission is dominated by a single state whose population is regulated by voltage (37).

We next tested the seven fluorescent and voltage-sensitive D95X mutants for dynamic changes in fluorescence in response to changes in illumination wavelength. We hypothesized that such changes indicated a photocycle topology in which the photostationary distribution depended on illumination as well as voltage, a possible route to a time-domain encoder of absolute membrane voltage. Arch(D95H) showed the biggest fluorescence transients and so we characterized its dynamics in more detail.

Optimization of a robust absolute voltage measurement

We tested whether the relaxation between different photostationary distributions in Arch(D95H) contained information on the membrane voltage. Our goal was to discover some measure, M, that could be computed from the time-dependent fluorescence and that would have a robust one-to-one mapping to absolute membrane voltage.

We used whole cell patch-clamp to set the membrane voltage of an isolated HEK cell to one of three constant values (V_m = −50, 0, or +50 mV). The cell was illuminated at wavelength λ_pump for time t_pump, immediately followed by wavelength λ_probe for time t_probe (Fig. 2 a). Fluorescence of Arch(D95H) was recorded throughout the pump and probe intervals. We searched for wavelength pairs (λ_pump, λ_probe) where the relaxation of the fluorescence during the probe interval showed voltage dependence.

Figure 2.

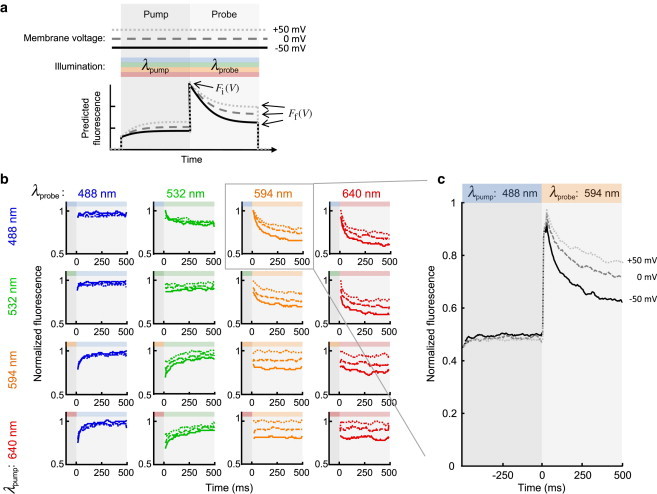
Optimization of pump and probe wavelengths. (a) Schematic of pump-probe experiment. Sample was held at constant membrane voltage V_m and illuminated sequentially by light of wavelengths (λ_pump, λ_probe). Fluorescence relaxation during the probe interval depended on V_m, λ_pump, and λ_probe. (b) Probe intensity traces of HEK293 expressing Arch(D95H)-eGFP, voltage-clamped at three voltages: −50 (solid), 0 (dashed), +50 (dotted) mV. We tested 16 (λ_pump, λ_probe) pairs using 488, 532, 594, and 638 nm light to find the largest differential fluorescence response between high and low V_m. (c) The wavelength pair (λ_pump, λ_probe) = (488 nm, 594 nm) resulted in intensity traces with the largest sensitivity to absolute membrane voltage. Data in (b) and (c) are representative traces from n = 5 cells. To see this figure in color, go online.

We measured relaxation of the fluorescence for 16 pairs of pump and probe wavelengths, each at three voltages (Fig. 2 b). We quantified the fluorescence transient during the probe by the dimensionless metric

$$M\left(V_{\text{m}}\right)\equiv \frac{F_{\text{i}}\left(V_{\text{m}}\right)-F_{\text{f}}\left(V_{\text{m}}\right)}{F_{\text{f}}\left(V_{\text{m}}\right)},$$ (1)

where F_i(V_m) and F_f(V_m) represent the initial and final fluorescence intensities during the probe interval, respectively. This metric was designed to be independent of the illumination intensity and expression level, i.e., multiplying F_i and F_f by the same constant does not change M. However, variations in voltage-insensitive background could confound measurements of M(V_m), i.e., adding a constant to F_i and F_f changes M. For the present measurements on HEK cells via confocal microscopy, background was negligible. An alternative metric based on a voltage-dependent rate constant is insensitive to background and is explored below.

Sensitivity to membrane potential was characterized by ΔM = M(V_m = −50 mV) - M(V_m = +50 mV). The wavelength pair (λ_pump, λ_probe) = (488 nm, 594 nm) gave the largest value of ΔM (Fig. 2 c). Under blue illumination, the fluorescence showed almost no sensitivity to voltage. This insensitivity to voltage did not change immediately upon switching to orange illumination. Instead, the fluorescence became sensitive to voltage with a time constant of ∼100 ms. This observation suggests that the blue photostationary distribution was not influenced by voltage, whereas the orange one was influenced by voltage.

We noticed that the initial fluorescence upon illumination at 594 nm depended on the previous illumination, even when the two illumination periods were separated by a dark interval (Fig. 3 a). This observation implied that the conformational landscape divided into two regions that only interconverted slowly, if at all, in the dark, but that reached a voltage- and illumination-dependent equilibrium in the light. Thus, we adapted the illumination scheme to include a dark interval between pump and probe pulses (Fig. 3 b). We reasoned that a dark interval would facilitate relaxation within each submanifold, and could allow voltage-dependent processes to occur in the dark. A dark interval could potentially increase the influence of voltage on the temporal dynamics of fluorescence during the probe.

Figure 3.

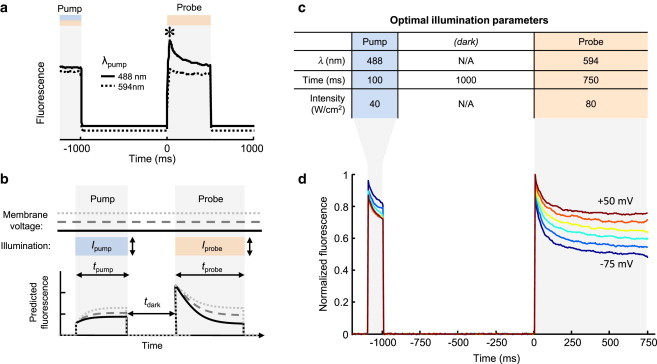
Optimization of pump-probe timing and intensity parameters. (a) Optical bistability in Arch(D95H). Initial fluorescence upon illumination at 594 nm (^∗) depended on the wavelength of the preceding illumination, even when separated by a dark interval. Traces are vertically offset for clarity. (b) Schematic of pump-probe experiment with the inclusion of a dark interval. Parameters t_pump, t_dark, t_probe, I_pump, and I_probe were explored. (c) Optimal parameters of time, wavelength, and intensity for sensitivity to voltage. (d) Normalized fluorescence traces of Arch(D95H) during the optimized pump-probe experiment showed desired voltage sensitivity. Each trace represents an average over 12 trials with the sample voltage-clamped at the indicated membrane voltage. The membrane voltage was incremented from −75 mV to +50 mV in 25 mV steps. The single-trial standard deviation in M was δM/M = 13%. To see this figure in color, go online.

We measured fluorescence transients as a function of t_pump, t_dark, t_probe, intensities I_pump and I_probe, and membrane voltage V_m (Fig. 3 b), using (λ_pump, λ_probe) = (488 nm, 594 nm). Over the range of t_pump explored (1–500 ms), fluorescence during the probe interval depended only on I_pump and t_pump through their contribution to the total fluence, f_pump = I_pump × t_pump. ΔM increased with f_pump but showed saturation behavior with a half-maximal fluence of 1 J/cm². By choosing a pump fluence well into the saturation regime (I_pump = 40 W/cm², t_pump = 100 ms), measurements of M became robust to variations in I_pump. We varied t_dark from 0 to 2 s and found that ΔM was maximal for t_dark = 1 s, but varied by only 10% over this range.

To achieve adequate fluorescence intensity during the probe interval, we operated at I_probe ≥ 80 W/cm². In this regime, fluorescence was directly proportional to I_probe, so M was independent of probe intensity. The probe interval was selected to be long enough for fluorescence to reach steady state; we used t_probe ≥ 750 ms.

With these optimal pump-probe parameters (Fig. 3 c), we measured the fluorescence relaxation during the probe at six voltages from V_m = −75 mV to 50 mV (Fig. 3 d). We observed a twofold change in M(V_m) over this range.

To test the robustness of our absolute voltage measurement, we measured M(V_m) in six cells from three dishes, using the illumination and timing parameters shown in Fig. 3 c. For each cell, we used patch-clamp to vary V_m between −75 mV and 50 mV. Expression levels of the indicator varied widely between cells; and hence, the plots of steady-state fluorescence versus membrane voltage also varied widely between cells (Fig. 4 a).

Figure 4.

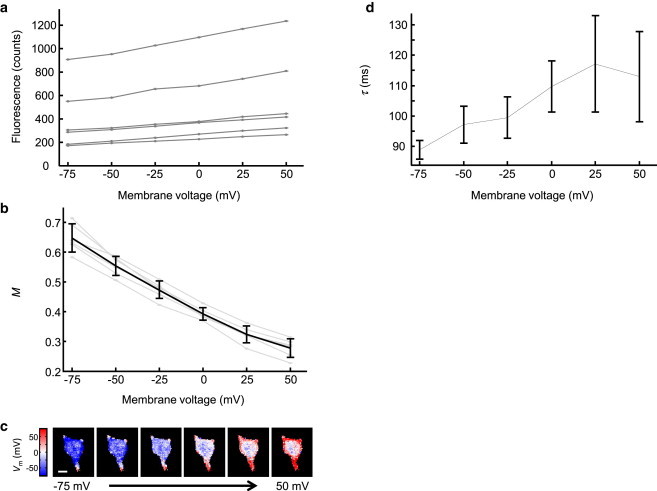
Time-domain response of Arch(D95H) gives a robust measure of absolute voltage. (a) Steady-state fluorescence of Arch(D95H) in six cells as a function of membrane voltage. Due to wide variations in protein expression levels, absolute fluorescence was not a robust measure of absolute voltage. (b) Time-domain response of Arch(D95H) under the illumination parameters of Fig. 3c. The fractional amplitude of the fluorescence relaxation, M, reported voltage with an absolute accuracy of σ_V = 9.8 mV. Gray lines show M(V_m) for the same six cells plotted in (a). (c) Map of voltage in a spinning disk confocal image of a single cell. Colormap indicates distribution of V_m at six values of the applied voltage, as calculated from calibration in (b). The voltage-dependent pixels are predominantly localized to the periphery of the cell, as one would anticipate for a voltage sensor. Values in the interior of the cell are determined by a combination of fluorescence from internalized Arch(D95H) (not sensitive to membrane voltage) and out-of-focus Arch(D95H) localized to the dorsal and ventral plasma membranes. Scale bar represents 10 μm. (d) Voltage-dependent time constant of fluorescence relaxation in Arch(D95H). The time constant, τ, was sensitive to membrane voltage, but not sufficiently so to serve as a reliable measure of absolute voltage. To see this figure in color, go online.

The dimensionless measure M(V_m) showed significantly less cell-to-cell variation than did the raw fluorescence (Fig. 4 b). We asked how accurately one could estimate V_m from M in a cell given no prior information. The error in the voltage estimate, σ_V, depends on the error in the measurement of M, σ_M, by

$${\sigma }_V={\langle \frac{{\sigma }_M}{\left|\text{d}M/\text{d}{V}_{\text{m}}\right|}\rangle }_{V_{\text{m}}}.$$ (2)

The plot of M(V_m) was approximately a straight line between −75 and +50 mV, so it was acceptable to take the average over all cells and all voltages. The accuracy of voltage measurements was σ_V = 9.8 mV.

The resistance of the plasma membrane is much greater than that of the cytoplasm, so HEK cells are expected to be electrotonically compact, i.e., the membrane voltage should be uniform throughout the plasma membrane. We used a spinning disk confocal microscope to acquire fluorescence images of the midplane of a HEK cell expressing Arch(D95H) and under patch-clamp voltage control. Due to variations in the density of protein, raw fluorescence was not able to test for electrical homogeneity. We applied the illumination scheme of Fig. 3 c and calculated a pixel-by-pixel map of M. From the map of M, we made a map of V_m via the calibration in Fig. 4 b. Fig. 4 c shows a homogeneous membrane voltage throughout the plasma membrane. Inside the cell, the membrane voltage was not a well-defined quantity. The calculated values were not sensitive to plasma membrane voltage, and were dominated by fluorescence from protein that had not trafficked to the plasma membrane.

Alternative parameterizations of fluorescence transients

The timecourse of the fluorescence transient also encoded information on the underlying membrane voltage. In principle, this timecourse might show complex multiexponential voltage-dependent kinetics. For simplicity, we initially fit the transients to a single exponential decay, with voltage-dependent time constant τ. Fig. 4 d shows τ(V_m). The dependence of τ on V_m is weak. Thus, for Arch(D95H), relaxation rate was not a useful measure of absolute voltage.

The definition of M (Eq. 1) was chosen to capture the observed voltage-dependent shifts in the fluorescence dynamics. However, one might imagine that in Arch(D95H) or in other candidate indicators, the fluorescence dynamics could vary with voltage in a complex way. In the absence of a detailed kinetic model (which can be laborious to infer for each mutant), it is not a priori obvious how to parameterize voltage-dependent changes in the transient waveforms. We sought a means to achieve this parameterization in a model-independent way.

We used principal component analysis (PCA) to find a basis of reduced dimensionality that accounted for the voltage-dependent variation in the fluorescence transients. This approach does not assume a particular response function. We generated the principal components from a training set of fluorescence transients F(V_m, t) in n = 6 cells, measured at membrane voltages V_m = −50, −25, 0, 25, 50 mV. We calculated the covariance

$$E(t,t\mathit{\text{'}})=\underset{V_{\text{m}}}{\Sigma }\left(F(V_{\text{m}},t)-\overline{F}\left(t\right)\right)\left(F(V_{\text{m}},t\mathit{\text{'}})-\overline{F}\left(t\mathit{\text{'}}\right)\right),$$ (3)

where $\overline{F}\left(t\right)$ is the mean of F(V_m, t) averaged over all tested values of V_m. The eigenvectors of the covariance matrix E(t, t′) yielded the set of principal components P_i(t) that represent the variations between the individual fluorescence transients and the mean. For Arch(D95H), >98% of the variation was accounted for by the first principal component P₁(t). Using $\overline{F}\left(t\right)$ and P₁(t) as basis functions (Fig. 5 a), we described the time-domain fluorescence F(V_m, t) of Arch(D95H) by two parameters a and b:

$$F(V_{\text{m}},t)=a\overline{F}\left(t\right)+b\left(V_{\text{m}}\right)P_1\left(t\right).$$ (4)

For each data trace, we used a least-squares linear regression to determine the values of a and b that minimized the residual

$$\sum _t{\left(F(V_{\text{m}},t)-\left(a\overline{F}\left(t\right)+b\left(V_{\text{m}}\right)P_1\left(t\right)\right)\right)}^2.$$ (5)

Both a and b(V_m) depend on the illumination intensity and collection efficiency with the same prefactor. Therefore, the quantity M_PCA(V) = b(V_m)/a, is expected to be a robust measure of absolute voltage, independent of probe intensity or expression level. We found that M_PCA reported absolute voltage with accuracy σ_V = 10.5 mV, similar to the quantity M with the phenomenological definition of Eq. 1 (Fig. 5 b).

Figure 5.

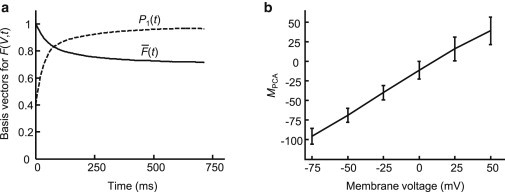
Parameterization of time-domain response using PCA. (a) Mean $\overline{F}\left(t\right)$ (solid) and first principal component P₁(t) (dashed) time-domain responses of Arch(D95H) during the probe interval. >98% of the variation due to differences in membrane voltage was accounted for by the first principal component. (b) Time-domain response of Arch(D95H) parameterized by M_PCA was a robust measure of absolute voltage. PCA provided a general approach for extracting absolute voltage measurements from a fluorescence time trace.

In this study, we accounted for variations in background by a combination of confocal imaging to reject out of focus fluorescence and background subtraction. However, in cases where these techniques are not possible, one could add a constant offset c to the fit in Eq. 4 to account for background. This approach requires that the background not show fluorescence transients too similar to those of membrane-bound protein—ideally the background should be static. In the case of Arch(D95H), the fluorescence background was dominated by improperly trafficked protein, which still showed fluorescence transients. Under widefield epifluorescence imaging, improperly trafficked protein could confound the signal. Ultimately, the solution should be to improve the trafficking of the protein.

The PCA-based analysis of fluorescence transients is applicable to any time-resolved measurement where the complexity of the underlying kinetics may prevent simple parameterization. This analytical approach will be useful in characterizing other reporters that encode absolute voltage in time-domain signals.

Conclusions

Fig. 6 contrasts the voltage-sensing mechanisms of traditional intensity-based voltage reporters and our absolute voltage reporter. In these schematics, we highlight the key transitions relevant to voltage-sensitive fluorescence; each cartoon structure could correspond to a submanifold of conformational states. In an intensity-based reporter (Fig. 6 a), membrane voltage affects the equilibrium between a dark state D and a fluorescent state F, but the populations are independent of illumination. Continuous monochromatic illumination probes the population of F.

Figure 6.

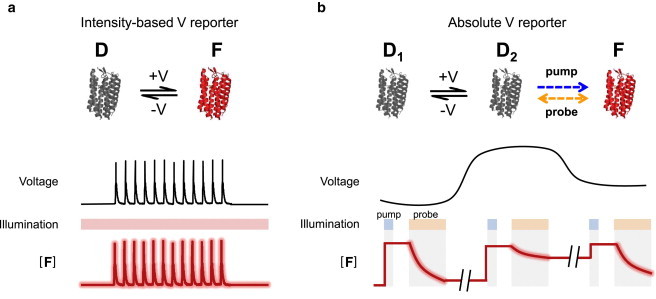
Comparison of intensity-based and absolute voltage reporters. (a) In an intensity-based voltage reporter, the membrane voltage determines the population of the fluorescent state F. Constant illumination excites fluorescence, but does not otherwise shift the equilibrium between F and dark state D. Fluorescence intensity serves as a reporter of voltage changes, but depends on illumination intensity, probe concentration, collection efficiency, and membrane voltage. (b) In an absolute voltage reporter, membrane voltage influences the equilibrium between two dark states D₁ and D₂. Illumination drives transitions between D₂ and fluorescent state F, toward a wavelength-dependent photostationary ratio of [F] to [D]. Time-varying illumination produces nonstationary distributions whose relaxation kinetics reports a slowly varying absolute voltage. To see this figure in color, go online.

Fig. 6 b proposes a simple photocycle topology for an absolute voltage sensor. A voltage-dependent equilibrium exists between two nonfluorescent states, D₁ and D₂. The state D₂ can be optically interconverted into a fluorescent state, F. Blue light drives only the transition into F, whereas orange light drives transitions in both directions. In a measurement of absolute voltage, the blue pump pulse drives the whole population into F. This population persists in the dark and thus the initial fluorescence during the probe pulse is insensitive to voltage. The orange probe pulse gradually establishes a photostationary distribution between D₂ and F, whereas voltage establishes equilibrium between D₁ and D₂. By the end of the probe pulse, the steady-state fluorescence of F thus depends on voltage. Fig. 6 b illustrates three voltage measurements in a slowly changing sample: the first at a low voltage, the second at a high voltage, and the third at an intermediate voltage. The fractional change in fluorescence during the probe pulse, M, is a function of voltage but not of illumination intensity or protein concentration.

The simple photocycle topology of Fig. 6 b occurs as a motif within the voltage-dependent photocycle of wild-type Arch described in (37). In the wild-type photocycle, the voltage-dependent equilibrium happens between nonfluorescent photocycle intermediates, whereas the optically generated fluorescent state (termed Q) thermally relaxes back to the main photocycle. We propose that the mutation D95H preserved the overall photocycle topology but changed the rates. Many microbial rhodopsins show optical bistability (43), therefore the bidirectional optical switching in our model is biophysically plausible.

Measurements of membrane voltage using membrane-embedded reporters are subtly different from electrode-based measurements. Molecular reporters probe local electric fields; electrodes probe the total potential difference between the aqueous reservoirs on opposite sides of the membrane. These two quantities are not the same for two reasons. First, ionization of lipid headgroups induces a potential difference between the lipid surface and the adjacent bulk aqueous phase. This surface potential can differ between membrane faces as a result of differences in the density of ionizable lipid headgroups, or differences in ionic composition of the bulk phases. Second, oriented polar species at the lipid-solution interface induce a dipole potential between the aqueous phase and the inside of the membrane. Asymmetry in the dipole potential can also induce an internal electric field. Thus, when the lipid composition or ionic environment differs between the two faces of the membrane, a strong unidirectional electric field can permeate the membrane even in the absence of a macroscopically measurable membrane potential (44).

Which parameter is correct—the local field or global potential? The answer depends on the process being studied. Equilibrium distribution of ions between the bulk phases depends only on the global potential difference. But conformational changes in transmembrane proteins depend on the local electric field. Interactions of soluble ions with transmembrane proteins are also sensitive to the potential profile in the double layer and in the membrane. Thus, one should not anticipate perfect correspondence between optical and electrode-based voltage measurements. Indeed, differences between local field and global potential have been observed with organic voltage-sensitive dyes and are proposed to be a means by which neurons generate spatially varying thresholds for ion channel activation (45,46). Internally generated membrane fields vary slowly compared to the timescale of an action potential, and thus are difficult to detect with reporters of relative voltage. Reporters of absolute voltage promise to elucidate mechanisms by which cells regulate intramembrane electric fields.

What phenomena might one study with the present accuracy of 10 mV? Bacterial resting membrane potential ranges from −80 to −140 mV depending on growth state and many environmental factors. Bacterial membrane voltage also undergoes spikes, which may last up to tens of seconds and likely have voltage swings >100 mV (35). Direct electrode-based calibration of voltage reporters in bacteria has not been feasible, so an absolute reporter could quantify these phenomena. In the context of embryonic development, stem cells with membrane voltages near zero differentiate into electrically diverse tissues: fibroblasts with voltage near −65 mV, neurons with voltage near −70 mV, and cardiomyocytes with voltage near −90 mV. The dynamics and modifiers of these transitions in embryonic development are largely unexplored.

For absolute voltage measurements to become more broadly applicable, several aspects of the reporter need to be improved. Primarily, improved membrane trafficking will prevent conflation of intracellular membrane voltages with plasma membrane voltage, thereby simplifying data analysis and improving accuracy. Overall brightness and voltage-sensitivity are also important parameters to improve. Finally, the protein should have voltage- and illumination-dependent rates in its photocycle, and at least one fluorescent state. Although we searched exhaustively at position 95 in Arch, a near-infinite variety of other Arch mutants await exploration; and Arch is but one of >5,000 known microbial rhodopsins (47). It is likely that mutants with better performance can be found.

Photogenerated states of microbial rhodopsins have absorption spectra that are typically broad and overlapping. Thus, continuous illumination at a single wavelength likely induces a mixed population of states, not all of which might be desirable for our purposes. In principle, one could apply an arbitrarily complex sequence of pump wavelengths and intensities to steer the population toward a particular distribution of states or even a single state (48). The dynamics of fluorescence under such an optical control scheme could provide improved measures of absolute membrane voltage.

Our PCA-based parameterization of the relaxation can account for an arbitrary temporal response without need for an underlying model of the protein’s spectroscopic dynamics. Time-domain approaches to absolute voltage measurement hold promise to map subtle shifts in membrane voltage and local electric fields in many biologically important phenomena.