Transported Substrate Determines Exchange Rate in the Multidrug Resistance Transporter EmrE

Background: EmrE transports a broad range of compounds.

Results: EmrE converts between open-in and open-out states with rates that vary over 3 orders of magnitude, depending on substrate.

Conclusion: Substrate affects both ground-state and transition-state energies for conformational exchange, emphasizing the coupling between substrate binding and transport.

Significance: Drug identity determines its own rate of transport by EmrE.

Abstract

EmrE, a small multidrug resistance transporter, serves as an ideal model to study coupling between multidrug recognition and protein function. EmrE has a single small binding pocket that must accommodate the full range of diverse substrates recognized by this transporter. We have studied a series of tetrahedral compounds, as well as several planar substrates, to examine multidrug recognition and transport by EmrE. Here we show that even within this limited series, the rate of interconversion between the inward- and outward-facing states of EmrE varies over 3 orders of magnitude. Thus, the identity of the bound substrate controls the rate of this critical step in the transport process. The binding affinity also varies over a similar range and is correlated with substrate hydrophobicity within the tetrahedral substrate series. Substrate identity influences both the ground-state and transition-state energies for the conformational exchange process, highlighting the coupling between substrate binding and transport required for alternating access antiport.

Introduction

Multidrug transporters are an ideal system for investigating the proposed alternating access model because their diverse substrates provide a natural toolkit of small molecules to probe the molecular mechanism. At the molecular level, active transport of a substrate against its electrochemical gradient requires two distinct conformations of the transporter, one open to the inner side of the membrane and one open to the outer side of the membrane, and the ability to convert between these two states to move bound substrate across the membrane (1) (Fig. 1B). Within this alternating access framework, stoichiometric antiport can be achieved with two simple conditions: (i) the counter-transported substrates compete for a single binding site such that the transporter cannot bind both substrates simultaneously, and (ii) the transporter is able to interconvert between the inward- and outward-facing states only when a substrate is bound. Energetically, substrate binding must lower the barrier for conformational exchange between the inward- and outward-facing states. This tight coupling between substrate binding and conformational exchange is important for secondary active transporters that use a proton gradient to drive transport, so that the proton motive force needed for ATP synthesis is not dissipated unnecessarily.

FIGURE 1.

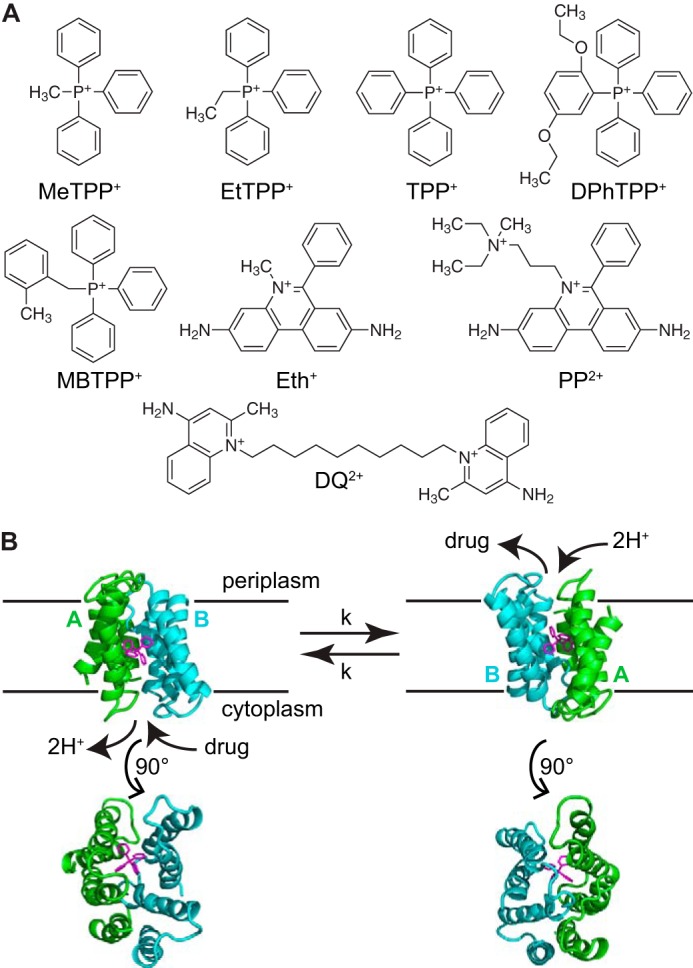
EmrE binds and transports a broad range of ligands. A, chemical structures of the tetrahedral and planar ligand series. B, the EmrE dimer exchanges between an AB and BA conformation (state A in green; state B in blue) as it converts between the inward- and outward-facing conformations. A 90° rotation permits a view of the open and closed faces of EmrE (Protein Data Bank code 3B5D, PyMOL).

But how is substrate binding and conformational exchange coupled in the context of a small multidrug resistance transporter such as EmrE, which recognizes and transports many different substrates? EmrE imports two protons across the inner membrane of Escherichia coli for each polyaromatic cation substrate exported, conferring resistance to a broad range of drugs that meet this chemical description (2–4). The simple single-site alternating access model of antiport described above is consistent with the biochemical data available for EmrE (5–8). Recent solid-state NMR studies of tetraphenylphosphonium⁺ (TPP⁺)² and methyltriphenylphosphonium⁺ (MeTPP⁺) binding to EmrE in liposomes have confirmed that TPP⁺ binds directly to the active site glutamate, Glu-14, and both substrates compete for the same binding site as proposed (9). Polyaromatic cation substrates of EmrE vary in charge (i.e. +1 versus +2), geometry (i.e. planar versus tetrahedral), and overall size. Their binding affinities vary widely, reflecting this substrate diversity (2), yet binding of any of these substrates must trigger the same open-in to open-out conformational exchange process for transport to occur. Does this important interconversion between open-in and open-out states occur on the same time scale for different substrates? If not, are there substrate properties that determine the conformational exchange rate and ultimately the ability of EmrE to confer resistance to a particular substrate?

The very small size of EmrE, which functions as a homodimer with only 110 residues per monomer, raises an additional question. How does such a small protein recognize and actively transport this diverse array of compounds? Multidrug resistance (MDR)² proteins are unique in their ability to bind a wide range of ligands and different families of MDR proteins appear to have evolved distinct strategies to recognize diverse compounds. Large MDR transporters from several superfamilies and MDR gene regulators appear to bind different drugs with distinct subgroups of residues within a large, hydrophobic binding pocket, and some can even bind multiple substrates simultaneously (10–12). As a member of the smallest family of MDR transporters, EmrE has a small binding pocket that must accommodate its entire wide range of substrates within a limited space. Multidrug recognition in a single small binding pocket has already been established in one case, the MDR transcription factor BmrR (13). In BmrR, the same set of active site residues interacts with its full array of ligands in a highly rigid binding pocket (13). This is in contrast to the canonical concept of multidrug recognition (11, 12), which postulates a key role for flexibility in accommodating diverse ligands in a single site. However, the requirements for coupling substrate binding to function are fundamentally different in transcription factors and transporters. Indeed, low-resolution cryo-EM data indicates that EmrE alters its structure when bound to planar or tetrahedral substrates (2). Thus, we expect flexibility is important in multidrug recognition by EmrE and that nature has successfully adopted different strategies for multisubstrate recognition in multidrug-binding proteins of different sizes and functions. Here we experimentally test how multidrug recognition is achieved by EmrE and coupled to functional transport.

We have previously directly monitored the dynamics of the conformational interconversion between the open-in and open-out states of EmrE bound to the well studied substrate TPP⁺ (14). Now we expand this work to test the hypothesis that the rate of conformational exchange between inward- and outward-facing states, the key step in moving substrate across the membrane, depends on the identity of the transported substrate. By combining NMR dynamics techniques with binding and efflux assays, we directly observe structural details, thermodynamics, and kinetics to link multisubstrate binding with functional motions.

EXPERIMENTAL PROCEDURES

Expression, Purification, and Reconstitution of EmrE

EmrE was expressed, purified, and reconstituted as previously described (14, 15). Isotopically labeled samples were extensively deuterated by growing in D₂O M9 media supplemented with 1 g/liter of ¹⁵NH₄Cl, 0.5 g/liter of ²H/¹⁵N-labeled ISOGRO (Sigma), and 2 g/liter of d-[¹H/¹²C]glucose. Purified EmrE was reconstituted into 1:3 DLPC/DHPC or DMPC/DHPC (mol/mol) isotropic bicelles at a 1:100 molar ratio of protein:long-chain lipid in 20 mm potassium phosphate, 20 mm NaCl, pH 7.

Partition Coefficients

Partition coefficients were measured via the HPLC method (16). Reference and sample compounds were dissolved in 75% MeOH, 25% buffer at roughly 2 mg/ml. 5-μl samples were injected onto an analytical Waters Sunfire C18 reverse-phase column with isocratic flow of 70% MeOH, 30% buffer at 1 ml/min. The dead time (t₀) of the column was taken as the retention time of the highly polar thiourea. A capacity factor, c, for each ligand was calculated from retention time (t_R): c = (t_R − t₀)/(t₀). A reference curve of log(c) versus well established experimental values of logP for phenol, p-cresol, 4-chlorophenol, 1-naphthol, 4-phenylphenol, and naphthalene was fit to: logP = a + b × log(c) (16). The logP values for the ligands were then calculated from this standard curve.

The propidium²⁺ (PP²⁺) retention time increases with increasing methanol and decreasing sample concentration, most likely reflecting aggregation of the ligand. The asymptotic value (logP = 4.3) of a dilution series was taken as the true logP, and error bars are larger for this ligand to reflect the greater uncertainty in logP. Repeating the logP determination at 50% methanol does not significantly alter the outcome for any of the tetrahedral ligands or dequalinium²⁺ (DQ²⁺). However, PP²⁺ does shift to logP = 2.5, as the asymptote of a dilution series.

Extinction Coefficient Determination for Ligands

Extinction coefficients were determined for TPP⁺ derivatives for accurate concentration determination. Extinction coefficients for TPP⁺ determined in the same manner matched literature values (i.e. 3750 m⁻¹ cm⁻¹ at 275 nm, 4400 m⁻¹ cm⁻¹ at 268 nm, and 3350 m⁻¹ cm⁻¹ at 262 nm), confirming the accuracy of this method. Extinction coefficients were determined in H₂O for MeTPP⁺ chloride (Sigma), ethyltriphenylphosphonium (EtTPP⁺) chloride (Acros Organics), and 2-methylbenzyltriphenylphosphonium (MBTPP⁺) bromide (Acros Organics). Due to its low solubility, stocks of 2,5-diethoxyphenyltriphenylphosphonium (DPhTPP⁺) iodide (Aldrich Chemicals) were prepared in methanol, and dilutions were made into water for measurements. The molar extinction coefficients were determined from 5 to 6 independently weighed and prepared samples: (a) MeTPP⁺: 2460, 2875, and 2150 m⁻¹ cm⁻¹ at 274, 267, and 261 nm; (b) EtTPP⁺: 2470, 2980, and 2260 m⁻¹ cm⁻¹ at 274, 267, and 261 nm; (c) DPhTPP⁺: 4480, 3040, 3390, and 2870 m⁻¹ cm⁻¹ at 321, 275, 268, and 262 nm; and (d) MBTPP⁺: 3720, 4270, and 3340 m⁻¹ cm⁻¹ at 276, 268, and 263 nm. The extinction coefficients of the planar ligands are: 5680 m⁻¹ cm⁻¹ at 478 nm for ethidium (Eth⁺) (17) and 5900 m⁻¹ cm⁻¹ at 493 nm for PP²⁺ (EMD Millipore). The absorbance of DQ²⁺ is 27,500 m⁻¹ cm⁻¹ at 329 nm in aqueous solutions (18) and 28,875 m⁻¹ cm⁻¹ in decylmaltoside solution (determined by dilution of aqueous stocks).

Isothermal Titration Calorimetry

All ITC experiments were performed with EmrE reconstituted into q_effective = 0.33 (19) DLPC/DHPC isotropic bicelles under NMR conditions (20 mm potassium phosphate, 20 mm NaCl, pH 7, 45 °C). Isotropic bicelle solutions were matched between protein and ligand samples, with at least a 100:1 DLPC:protein ratio, never going below 40 mm total lipid to preserve bicelle morphology (19). Triplicate titrations were carried out for each of the seven ligands. Injections ranged from 1 to 2.5 μl, with stirring at 300–350 rpm. Ligand concentrations were determined using extinction coefficients determined as described above. Titrations were performed for each ligand using an average of 900, 600, 40, 35, 30, 650, and 700 μm EmrE and 5, 3, 0.2, 0.14, 0.13, 4, and 4 mm ligand for MeTPP⁺, EtTPP⁺, TPP⁺, DPhTPP⁺, MBTPP⁺, PP²⁺, and DQ²⁺ titrations, respectively. Due to limitations on sample concentrations, the weakest (MeTPP⁺, PP²⁺, and DQ²⁺) and tightest (MBTPP⁺) binders have greater error in the determination of K_D.

ITC was performed on a TA Instruments Low Volume Nano calorimeter using ITCRun software and analyzed using ITCAnalysis software (TA Instruments, Lindon, UT). Data were fit to a model of ligand binding to n independent and identical sites on EmrE, as described in Ref. 14. Blank titrations of ligand and bicelles into bicelles always yielded equivalent heats across the titration, but it is difficult to precisely match to each sample. Therefore, the data were fit simultaneously to the binding model and a constant to represent the baseline of bicelle mixing.

In-cell Transport Assay

In-cell Eth⁺ efflux assays based on work from the laboratories of Le Pecq (20) and Schuldiner (21) were carried out in BL21(DE3) and BL21(DE3) Gold strains of E. coli transformed with EmrE in pET15b or an empty pET15b control vector in M9 media supplemented with 100 μg/ml of ampicillin. At an A₆₀₀ = 0.4, overexpression was induced with 0.33 mm isopropyl 1-thio-β-d-galactopyranoside for 30 min. 40 μm CCCP and 2.5 μm ethidium bromide were added, followed by incubation at 37 °C for an additional hour. Individual 2-ml aliquots were spun down and resuspended immediately in 2 ml of M9 media with or without 40 μm CCCP and 2.5 μm ligand (Eth⁺, MeTPP⁺, EtTPP⁺, TPP⁺, MBTPP⁺, or DPhTPP⁺). Eth⁺ fluorescence was measured with excitation at 545 nm and emission at 610 nm. Normalized fluorescence (F_N) was plotted as F_N(t) = (F(t) − F₀)F₀.

NMR Spectroscopy and Data Analysis

Data were collected on 0.8–1.0 mm ²H/¹⁵N EmrE reconstituted into q = 0.33 DLPC/DHPC isotropic bicelles in 20 mm potassium phosphate (+30 mm cacodylate for PP²⁺ sample), 20 mm NaCl, pH 7, at 45 °C. Ligand was added to 10, 5, 16, and 2 mm for MeTPP⁺, EtTPP⁺, MBTPP⁺, and TPP⁺, respectively. Due to the low solubility of DPhTPP⁺, PP²⁺, and DQ²⁺, these samples were incubated with excess ligand at 45 °C to push the samples to saturation. Most of the NMR data were collected on a 700 MHz Varian Inova spectrometer with a room temperature probe. Temperature was calibrated from ethylene glycol peak splitting. The DQ²⁺ data were collected on the Rocky Mountain Regional 900 MHz Varian DD2 spectrometer with room temperature probe. The data for EmrE in DMPC/DHPC isotropic bicelles bound to TPP⁺ was collected on the Varian 900 MHz spectrometer with a cryo probe at NMRFAM. ¹H/¹⁵N TROSY HSQCs were collected with 24 scans and 128 complex increments, with recycle delays of 2 s for standard spectra and 6 s for line shape analysis. The TROSY-selected ZZ-exchange experiment (22) was modified and run as described previously (14). Spectra were collected with 144, 128, 176–256, 128, and 288 scans and 144, 128, 128, 128, and 150 complex increments for EtTPP⁺, MBTPP⁺, DPhTPP⁺, PP²⁺, and DQ²⁺, respectively. NMR spectra were processed with NMRPipe (23) and analyzed in NMRViewJ (24), Sparky³, and CcpNmr analysis (26). ZZ-exchange and line shape data analysis was carried out in Igor Pro (Wavemetrics).

Assignments were transferred from TPP⁺-bound EmrE (14) to EmrE bound to the other four TPP⁺ derivatives using data from the HSQC and ZZ-exchange spectra. The ZZ-exchange data significantly reduces the ambiguity of transferred assignments. Only assignments that could be transferred with certainty were used in the analyses.

To extract the conformational interconversion rate, k_conf, the ZZ-exchange data for EmrE bound to each ligand were analyzed in the style of Miloushev et al. (27) as described previously for TPP⁺-bound EmrE (14). With equal populations in the inward- and outward-facing conformations of EmrE (14), the forward (k_f) and reverse rates (k_r) in this two-state exchange are equal and denoted by k_conf = k_f = k_r. The composite peak ratio is a complex ratio of the auto (I_AA, I_BB) and cross (I_AB, I_BA) peak intensities as a function of delay time given by Equation 1.

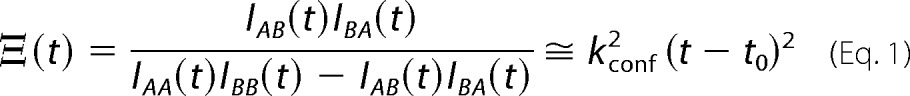The data were fit with an 11.1 ms time offset (t₀), which was determined by globally fitting the most intense residues from EmrE complexes with each of EtTPP⁺, TPP⁺, and MBTPP⁺ with a global time offset and individual rates between ligands. This delay time offset matches the calculated back-transfer time in the pulse sequence, confirming that exchange during back transfer must be accounted for with these short ZZ delay times and relatively fast exchange rates (28). This does not affect the determined rate for EmrE-ligand complexes with slow exchange rates, as exemplified by EmrE-DPhTPP⁺, which fit with k_conf = 0.4 ± 0.1 s⁻¹ with or without the time offset. However, exchange during back transfer is significant for faster exchanging complexes when the back transfer time is comparable with the ZZ delay with fitted rates of 30 ± 6 versus 25 ± 5 s⁻¹ for EtTPP⁺, 14 ± 3 versus 13 ± 3 s⁻¹ for MBTPP⁺, and 4.7 ± 0.5 versus 4.4 ± 0.4 s⁻¹ for TPP⁺ when determined without or with time offset, respectively. The quality of the fit improved when the time offset was included for these ligands, as judged by reduced residuals. The residues used for the global fits for each ligand-bound EmrE sample were: 9, 26, 58, 77, 80, 82, 83, and 106 for EtTPP⁺; 10, 17, 26, 49, 58, 79, 80, 82, 83, and 106 for MBTPP⁺; 9, 80, 82, 83, and 90 for DPhTPP⁺; 58, 80, 82, 106, and 108 for DQ²⁺; and 17, 26, 58, 80, 82, 83, and 106 for PP²⁺. The standard deviation of the collective individual fits was used to estimate the error of the global fits for each ligand-bound sample.

The relaxation properties of EmrE reconstituted into isotropic bicelles are not conductive to long experiments. As a result, at delay times past 300 ms the signal-to-noise was too low to be usable, which limits the accuracy of the rate constant determined for EmrE bound to DPhTPP⁺, the slowest under exchange conditions, as reported in the text.

The natural abundance ¹⁵N of the planar ligands caused significant streaking, which prevented the use of cryo probes. The dynamic properties of EmrE bound to these same ligands made the ZZ-exchange data analysis difficult. Due to these factors, EmrE bound to Eth⁺ could not be analyzed quantitatively. Better quality spectra were obtained for EmrE bound to PP²⁺ in DMPC/DHPC rather than DLPC/DHPC bicelles. Therefore, the rate is reported under these conditions because the conformational exchange rate of EmrE bound to TPP⁺ does not change between DLPC and DMPC bicelles (Table 1, Fig. 5B, and Ref. 14).

TABLE 1.

Summary of thermodynamics and kinetics of EmrE bound to range of tetrahedral and planar ligands

Ligand	Binding constant (KdpH7)a	ΔH	n	Interconversion rate (kconf)	Relative transportb	LogP
	μm	kJ/mol		s−1
MeTPP+	130 ± 20	−12.7 ± 0.2	0.60 ± 0.04	190 ± 80	1	1.8 ± 0.1
EtTPP+	21.8 ± 0.7	−16.6 ± 0.2	0.57 ± 0.04	25 ± 5	2	1.9 ± 0.1
TPP+	0.45 ± 0.01	−22 ± 1	0.49 ± 0.05	4.4 ± 0.4, 4.7 ± 0.6c	4	2.2 ± 0.1
DPhTPP+	0.16 ± 0.02	−39.4 ± 0.3	0.53 ± 0.05	0.4 ± 0.1	5	3.0 ± 0.2
MBTPP+	0.04 ± 0.01	−38 ± 2	0.544 ± 0.009	13 ± 3	3	2.5 ± 0.1
DQ2+	100 ± 20	−5.7 ± 0.3	0.58 ± 0.02	11 ± 2	N/A	3.4 ± 0.1
PP2+	90 ± 10	−16.3 ± 0.7	0.58 ± 0.06	13 ± 3c	N/A	4.3 + 0.5/−1.0

^a Observed binding constant from ITC at pH 7, 45 °C.

^b Determined via in-cell assay. Ranked 1 through 5, from fastest to slowest EmrE-dependent ethidium efflux in the presence of each competing ligand.

^c Reconstituted into DMPC/DHPC isotropic bicelles.

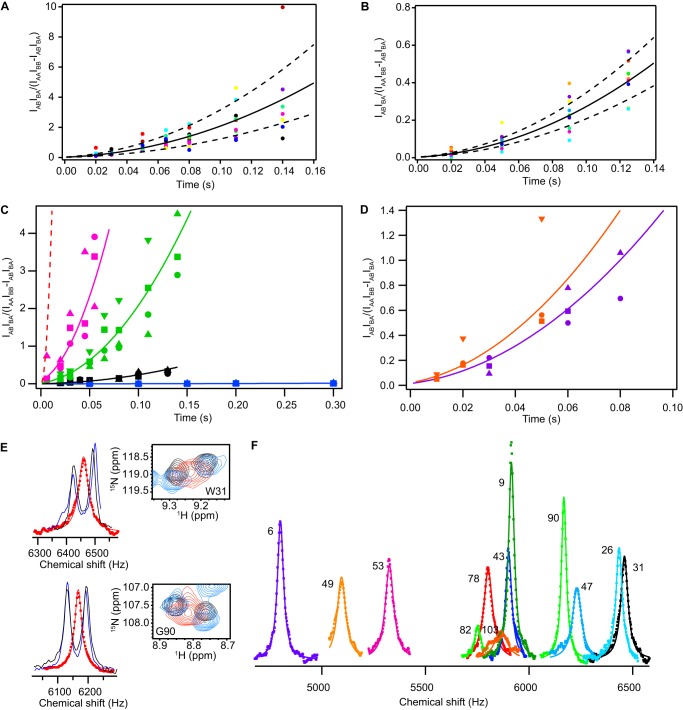
FIGURE 5.

Substrate identity determines the rate of EmrE conformational exchange. Plots of the full composite peak ratio analysis are shown for EmrE bound to MBTPP⁺ in DLPC/DHPC bicelles (A) and bound to TPP⁺ in DMPC/DHPC bicelles (B). The solid line represents the global fit of all residues used in the analysis, and the dashed lines represent a simulation of the fit rate ± S.D. of the fits to individual residues. C, composite peak ratio analysis of ZZ-exchange data shows significantly different exchange rates for EmrE bound to TPP⁺ (black) and the other slow-exchanging derivatives, EtTPP⁺ (magenta), MBTPP⁺ (green), and DPhTPP⁺ (blue). Global fits are depicted with solid lines, along with data points for several representative residues from each ligand. The dashed red line corresponds to a simulation of the composite peak ratio of MeTPP⁺ using the rate of conformational interconversion determined via line shape analysis (E and F). D, a similar plot is shown for the planar ligands PP²⁺ (DMPC bicelles; orange) and DQ²⁺ (purple), with representative residues plotted. E, representative fits from line shape analysis for residues Trp-31 (top) and Gly-90 (bottom) alongside the ¹⁵N/¹H TROSY HSQC overlay for EmrE bound to TPP⁺ (black), DPhTPP⁺ (blue), and MeTPP⁺ (red). F, global fit to 12 residues in the line shape analysis of the MeTPP⁺-bound EmrE data (see “Experimental Procedures”), giving a fit of k_conf = 190 ± 80 s⁻¹.

Spectra for line shape analysis were processed with exponential line broadening to maintain a Lorentzian line shape. Analysis was carried out by first extracting integrated one-dimensional slices of TPP⁺- and DPhTPP⁺-bound EmrE from ¹H/¹⁵N TROSY HSQC spectra using the Integrative Data Analysis Platform Sparky extension (29). The ¹H line shapes for all ligand-bound samples were fit to the analytical solution of the two-state Bloch-McConnell equations with equal populations in each state (30). The peak positions (ω_A, ω_B) and intrinsic relaxation rates (R₀^A, R₀^B) were set as adjustable parameters, whereas the conformational interconversion rate (k_conf) was held using the value determined by ZZ-exchange spectroscopy. One-dimensional slices from MeTPP⁺-bound EmrE spectra were extracted in the same manner and fit with the separation between the chemical shift end points (Δω) and intrinsic line width values constrained based on the results of the TPP⁺- and DPhTPP⁺-bound EmrE fits. Where values varied between ligands, the fitting parameter was allowed to float within constraints that spanned the entire range of values to allow for differences in chemical shift and intrinsic line width between ligands. To determine the conformational exchange rate, MeTPP⁺-bound EmrE line shapes were globally fit with a single k_conf and individual Δω, R₀^A, and R₀^B. The global fits was performed using 12 residues: Tyr-6, Gly-9, Gly-26, Trp-31, Ser-43, Leu-47, Gln-49, Tyr-53, Phe-78, Arg-82, Gly-90, and Leu-103.

Chemical shift differences (Δδ_tot) were calculated as a weighted average of the differences in amide proton (Δδ_H) and nitrogen (Δδ_N) chemical shifts with respect to TPP⁺-bound EmrE (31).

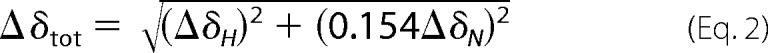Because MeTPP⁺-bound EmrE only has a single set of peaks, the chemical shift difference was taken with respect to the average of the two TPP⁺ peaks for each residue.

The energetic barrier to conformational interconversion was estimated using transition-state theory,

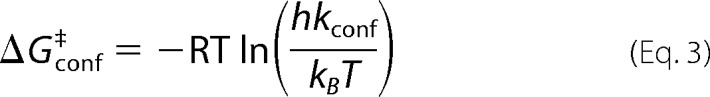where R is the universal gas constant, T is the temperature, h is Planck's constant, k_conf is the conformational exchange rate determined via NMR methods, and k_B is the Boltzmann constant.

RESULTS

Multidrug Recognition and Efflux by EmrE

EmrE binds a wide variety of polyaromatic cation substrates. To dissect key ligand properties, we began by examining a simple series of five compounds that all share a +1 charge and tetrahedral geometry and differ only by substitution of one phenyl ring: TPP⁺, MeTPP⁺ (also known as TPMP⁺), EtTPP⁺ (also known as TPEP⁺), DPhTPP⁺, and MBTPP⁺ (Fig. 1A, Table 1). Because this simple chemical series has not been previously studied, we first confirmed that these compounds are substrates of EmrE based on direct binding experiments via ITC and in-cell efflux assays.

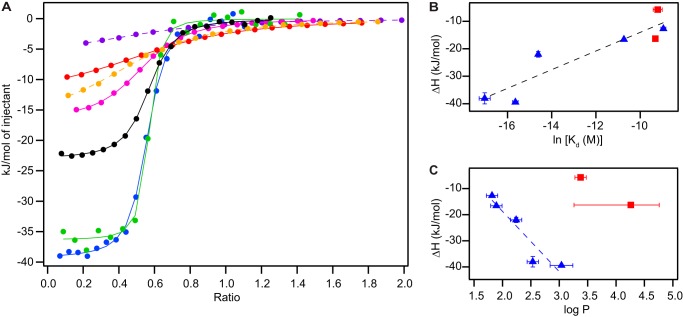
We used ITC to determine the relative affinity of each of the five tetrahedral substrates for EmrE reconstituted into DLPC/DHPC isotropic bicelles. Surprisingly, the binding affinity varies over 3 orders of magnitude (Fig. 2A). Upon further inspection, within this series of identically charged tetrahedral substrates, binding affinity is roughly correlated with enthalpy (Fig. 2B). In addition, the binding enthalpy is correlated with the hydrophobicity of the substrate, as assessed by the measured partition coefficients (Fig. 2C). Multiple mutational studies have identified key residues important for substrate binding in EmrE (32–34), and these aromatic and hydrophobic residues line the binding site in the crystal structure (35) (Fig. 7C). Thus, the data are consistent with hydrophobicity dominating the binding interaction between the substrate and the active site, provided other ligand properties are similar.

FIGURE 2.

Variation in binding affinity of EmrE substrates. A, overlay of representative ITC binding curves of the five TPP⁺ derivatives (fits in solid lines), MeTPP⁺ (red), EtTPP⁺ (magenta), TPP⁺ (black), MBTPP⁺ (green), and DPhTPP⁺ (blue), along with the two planar substrates (fits in dashed lines), DQ²⁺ (purple) and PP²⁺ (orange). The fit baseline for each titration was subtracted. B, binding affinity is correlated with enthalpy, regardless of ligand geometry (tetrahedral in blue triangles, planar in red squares, R² = 0.84). C, partition coefficients, a measure of ligand hydrophobicity, correlate with enthalpy within the tetrahedral ligand series (blue triangles, R² = 0.89) but not between ligand series.

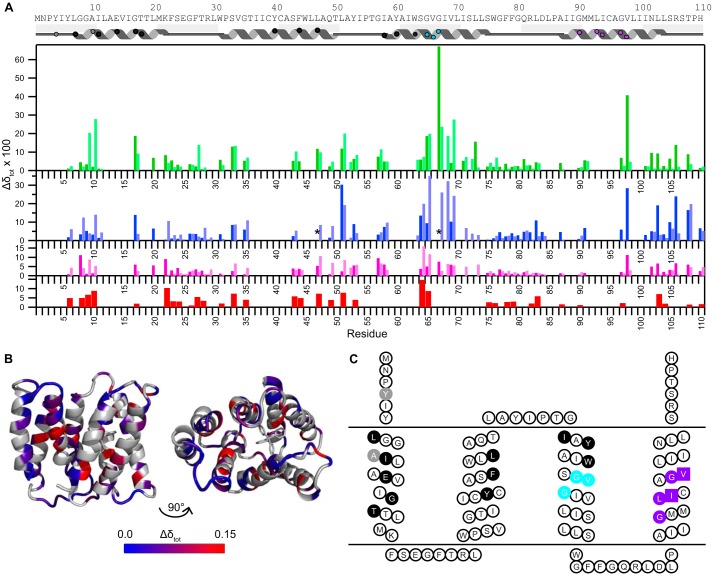
FIGURE 7.

Chemical shift differences highlight important functional residues. A, chemical shift changes between TPP⁺-bound EmrE and EmrE bound to other TPP⁺ derivatives (MeTPP⁺, red; EtTPP⁺, magenta; DPhTPP⁺, blue; MBTPP⁺, green), as described under “Experimental Procedures.” States A and B are distinguished via the dark and light shades, respectively. Due to a lack in connectivity, state A versus B is not certain for residues 17, 31, 67, 98, and 108. The asterisk (*) indicates that the peak moves significantly, but the exact assignment is uncertain. Residues with no data indicate a lack of transferred assignment. The approximate secondary structure according to the crystal structure (35) is shown at the top and includes symbols to allow easy comparison with C. B, chemical shift differences between MBTPP⁺- and TPP⁺-bound EmrE, plotted onto the TPP⁺-bound structure (Protein Data Bank code 3B5D, PyMOL) reveal regions sensitive to ligand identity. Residues in gray indicate a lack of data. C, EmrE topology diagram highlighting specific functional regions of EmrE based on previously published mutagenesis studies: direct substrate binding and substrate specificity (black), TPP⁺/H⁺ coupling (gray), GVG helix kink motif (cyan), and GG7 dimerization motif (purple, squares represent the pivot point) (4, 5, 25, 35, 37–39). Fig. made using TOPO2.

To see whether these trends were generalizable to a wider range of EmrE substrates, we looked at two planar divalent substrates, PP²⁺ and DQ²⁺ (Table 1, Fig. 2A). The affinity of Eth⁺ for EmrE was too weak to be measured quantitatively via ITC, but Eth⁺ clearly binds EmrE with a weaker affinity and lower enthalpy than PP²⁺ and DQ²⁺. Comparison between the planar and tetrahedral substrate series suggests that binding affinity is always correlated with enthalpy (Fig. 2B). However, binding enthalpy does not depend simply on substrate hydrophobicity, because ligands with differing charge and geometry do not follow the same trend (Fig. 2C). Both charge and geometry may have significant effects on substrate binding for two reasons. First, ligand charge will affect the interaction of the substrates with the critical residue Glu-14 in the binding pocket. Second, the structure of EmrE, and thus its binding pocket architecture, is known to change to accommodate different substrate geometries (2). Therefore, multiple ligand properties affect the structure of the transporter-substrate complex and substrate binding affinity.

It is important to investigate how this all comes together in the context of the cell. An in vivo assay allows us to monitor the competitive efflux of Eth⁺ and the tetrahedral substrates in E. coli (Fig. 3). Cells overexpressing EmrE efflux Eth⁺ considerably faster than control cells (Fig. 3A, dashed and solid orange lines, respectively), indicating that a significant portion of the active efflux is due to EmrE. Cells are unable to efflux Eth⁺ in the absence of a proton gradient (Fig. 3A, orange line, “+CCCP”). The non-EmrE-driven efflux rate is independent of the identity of the competing substrate, with the exception of DPhTPP⁺ (Fig. 3A). On the other hand, cells overexpressing EmrE have a decrease in Eth⁺ efflux when one of the TPP⁺ derivatives is added (Fig. 3B). All five of the tetrahedral substrates compete with Eth⁺, indicating that they are transported by EmrE in its native E. coli environment. The effect varies with the substrate, demonstrating that the in vivo transport rate depends on the identity of the bound substrate (Table 1, “relative transport”). This is not simply blockage by binding of competing substrate to the transport pore, because the effect does not correlate simply with binding affinity (Table 1) and MeTPP⁺ even enhances the final extent of ethidium efflux (Fig. 3B, red line).

FIGURE 3.

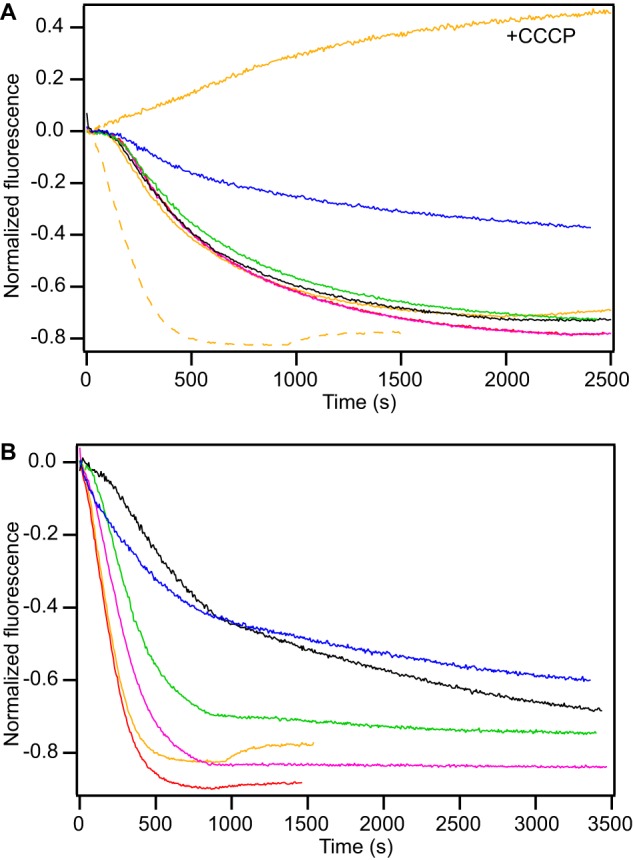
Substrate identity determines the transport rate in E. coli. In this competitive transport assay in E. coli, Eth⁺ efflux is monitored upon induction of (A) empty vector or (B) EmrE in BL21(DE3) with addition of external Eth⁺ (orange) or the competing ligands MeTPP⁺ (red), EtTPP⁺ (magenta), TPP⁺ (black), MBTPP⁺ (green), and DPhTPP⁺ (blue). The data shown are from a single batch of cells, to ensure equal protein expression levels between traces. Results were reproducible between batches of cells and were qualitatively similar between two BL21 cell lines. In A, the Eth⁺ trace from cells overexpressing EmrE was re-plotted as a dashed orange line for reference. Addition of CCCP inhibits Eth⁺ efflux (A, +CCCP).

Differences in the overall transport rate may be a result of changes in several steps in the transport cycle. Both substrate off-rate and conformational exchange rate have been suggested as likely candidates for rate-limiting steps for EmrE transport. Off-rates have been determined previously for several substrates of EmrE (7), but the rate of conformational exchange has only been measured for TPP⁺ (14). Therefore, we directly measured the rate of this important step for all the substrates in our ligand series using NMR.

Multidrug Conformational Exchange

Large-scale global motion, such as exchange between the inward- and outward-facing states of EmrE, can be directly monitored using solution NMR dynamics methods. ¹⁵N/¹H TROSY HSQC spectra of EmrE bound to EtTPP⁺, MBTPP⁺, and DPhTPP⁺ indicate that EmrE bound to these compounds has the same two sets of peaks previously described for TPP⁺-bound EmrE (Fig. 4A) (14). This corresponds to the two monomers in an asymmetric dimer, with inward- to outward-facing transitions occurring via AB to BA exchange as predicted by Fleishman et al. (5) (Fig. 1B). The overall pattern of the peaks is similar in each case, indicating the same overall-fold. However, local chemical shift changes do occur and are discussed below. Qualitatively, the different extent of line broadening in each spectrum results from differences in the conformational exchange time scale. This rate is quantified using TROSY-selected ZZ-exchange experiments (22), as demonstrated previously for TPP⁺-bound EmrE (14). The data are presented in the style of Miloushev et al. (27) (Fig. 5A), which allows easy comparison of global exchange between different substrate-bound states (Fig. 5C, Table 1). It is clear that the rate of conformational interconversion varies significantly with the identity of the bound substrate.

FIGURE 4.

NMR spectra of EmrE bound to the tetrahedral and planar substrates indicate the same overall protein structure but varying dynamics. A, ¹⁵N/¹H TROSY HSQC spectra of EmrE bound to EtTPP⁺ (magenta), TPP⁺ (black), DPhTPP⁺ (blue), and MBTPP⁺ (green), are similar, with two peaks per residue corresponding to slow exchange of the asymmetric dimer. The assignments for TPP⁺-bound EmrE are displayed for states A (red) and B (black). B, ¹⁵N/¹H TROSY HSQC spectrum of EmrE bound to MeTPP⁺ (red) has a single set of peaks at the average chemical shift, revealing faster conformational exchange of EmrE bound to this ligand than TPP⁺ (black). C, overlay of TPP⁺-bound EmrE (black) with EmrE bound to the two planar ligands, PP²⁺ (DMPC bicelles; orange) and DQ²⁺ (lavender). All spectra were collected identically at pH 7 and 45 °C, with 2-s recycle delay for all ligands except for MeTPP⁺ (6-s recycle delay).

Amazingly, when EmrE is bound to the remaining member of the series, MeTPP⁺, it reveals only a single set of peaks in a ¹⁵N/¹H TROSY HSQC (Fig. 4B). Thus, when bound to this substrate, EmrE is pushed into intermediate-fast exchange. Under these conditions, each peak represents the average chemical shift of the exchanging states for each residue, and line shape analysis is used to extract the conformational exchange rate. This requires prior knowledge of the chemical shift difference between the two states in the absence of exchange and the intrinsic line widths. We determined these parameters by fitting the line shapes for EmrE bound to TPP⁺ and DPhTPP⁺ using the known conformational exchange rates determined by ZZ-exchange spectroscopy as described under “Experimental Procedures.” Because EmrE in complex with these two substrates has the slowest exchange rates, these will be the closest to exchange-free conditions and thus have the lowest extrapolated error. By fitting data sets for multiple substrates, we were able to determine which parameters are sensitive to substrate identity and adjust the constraints and error bars appropriately. The MeTPP⁺-bound line shapes of 12 residues were then fit globally to determine the conformational exchange rate (Fig. 5, E and F).

The rate of conformational exchange for EmrE bound to the two planar substrates was also quantified (Table 1, Figs. 4C and 5D). Interestingly, even though the two planar substrates are structurally dissimilar, they have quite similar conformational exchange rates. This is in contrast to the large variation within the tetrahedral substrate series. Overall, the conformational interconversion rate of substrate-bound EmrE varies over almost 3 orders of magnitude (Fig. 5, C and D, and Table 1). How can EmrE move between its inward- and outward-facing states with such greatly varying kinetics? Because these are slow dynamics overall, are they an important factor in transport rate?

Previous measurement of several substrate on- and off-rates for detergent-solubilized EmrE suggests that substrate association rate is diffusion-limited and dissociation determines affinity (7). Using the on-rate at pH 7 (7) corrected for the temperature dependence of diffusion and our measured binding affinities (45 °C, pH 7), we calculated off-rates for each substrate. The estimated off-rates are within an order of magnitude of the conformational exchange rate for all but one substrate. Thus, both processes may contribute to the overall turnover rate for EmrE with the rate-limiting step depending on the transported substrate. Future experiments to test this hypothesis will require precise measurements under identical conditions.

The significant differences in conformational exchange rate (k_conf) when EmrE is bound to different substrates indicate that substrate binding alters the energy landscape. This is illustrated in Fig. 6 by approximating the complex energy landscape as a simple two-state process along a single reaction coordinate. Compared with TPP⁺, most of the substrates lead to faster conformational exchange rates in EmrE. A faster exchange rate may be due to higher ground-state (substrate-bound state) energy, lower transition-state energy for the conformational exchange process, or some combination thereof. To distinguish the relative importance of these effects, the apo state of the protein provides a convenient substrate-independent reference state to anchor the energy landscape. This approximation assumes that differences in the free energy of the unbound ligands are small relative to the binding energy. Differences in ground-state energy of EmrE bound to different substrates are determined relative to the apo reference state by the free energy of binding (ΔG_bind) as calculated from the experimentally determined binding affinities (Fig. 6, left side). This highlights the significant effect of substrate identity on the free energy of the complex, which is particularly interesting in light of the known changes in EmrE structure when bound to different substrates (2).

FIGURE 6.

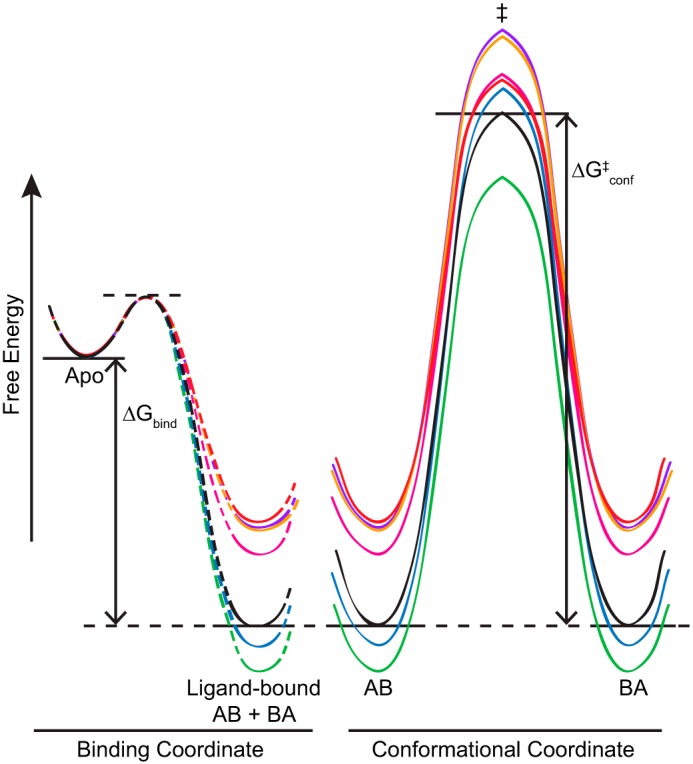
A simplified energy diagram illustrates the connection between ligand binding (left) and conformational exchange between the open-in (AB) and open-out (BA) states of ligand-bound EmrE (right). The free energy of binding, ΔG_bind, was calculated from measured binding affinities. The dashed lines indicate that nothing is known about the transition state connecting the apo and bound states of EmrE. The two ligand-bound ground states (AB and BA) have equal energy and are separated by the transition state, ‡, with energetic barrier of height ΔG_conf^‡ calculated from the rates of conformational interconversion and transition-state theory. The diagram shows the tetrahedral series, MeTPP⁺ (red), EtTPP⁺ (magenta), TPP⁺ (black), MBTPP⁺ (green), and DPhTPP⁺ (blue), as well as the planar substrates DQ²⁺ (purple) and PP²⁺ (orange).

We then used transition-state theory and the conformational exchange rate determined by NMR to estimate the height of the transition state barrier (ΔG_conf^‡) relative to the ground state for each of the substrates (see “Experimental Procedures”). It is clear that both the ground and transition states are affected by bound substrate (Fig. 6). This is why there is not a simple correlation between binding affinity and conformational exchange rate across all substrates (Table 1), as would be expected if only the ground-state energy (free energy of substrate-bound EmrE) were affected by substrate identity and the transition-state energy was the same for all ligands. Within the tetrahedral series, there is less variation in the transition-state energy than in the ground-state energy (note in particular the clustering of the transition-state energy for MeTPP⁺, DPhTPP⁺, TPP⁺, and EtTPP⁺ despite their wide variation in bound-state energy), and there is general correlation between binding energy and exchange rate within this subset. This suggests that the protein is an important but not exclusive factor in determining the energy of the conformational exchange transition state. Substrate properties also affect this barrier height, particularly when there are differences in substrate charge and geometry (note the higher barrier for the same ground state for the +2 planar substrates versus MeTPP⁺). It is this combination of effects that keeps the energy barrier for conformational exchange from becoming too large and enables EmrE to be a multidrug transporter.

DISCUSSION

Structural Implications

Structural studies have given some insight into the mechanism of multidrug recognition in EmrE. The first three transmembrane helices from each monomer come together to form a hydrophobic binding pocket, whereas the two TM4 helices form a dimerization arm (35, 36). The correlation we observe between ligand hydrophobicity and binding affinity within the tetrahedral substrate series confirms the importance of this property for substrate interaction with the hydrophobic binding pocket. However, this correlation does not hold across more diverse substrates (Fig. 2, B and C), indicating that ligand charge and shape are also important for substrate recognition by EmrE. Low-resolution cryo-EM data indicate that the structure of EmrE changes when bound to tetrahedral TPP⁺ and three planar substrates (Eth⁺, PP²⁺, and DQ²⁺) (2). Thus, multidrug binding by EmrE results from a complex interaction between substrate and protein, with ligand properties affecting the structure of the binding site and the free energy of the complex. Because helix tilt depends on the identity of the substrate, and the helices must reorient for alternating access, structural, and dynamic changes are likely to be linked.

Throughout these experiments, we observed how relatively small differences in the substrate cause large changes in binding, dynamics, and functional transport by EmrE. Hints at the structural changes induced in EmrE by the different substrates are provided by chemical shift changes in the ¹⁵N/¹H TROSY HSQC spectra (Fig. 7, A and B). Residues in TM1 such as Ala-10, Gly-17, and Ile-11 that affect substrate binding and specificity (32, 37) (Fig. 7C) show significant shifts between EmrE bound to TPP⁺ and the four other related compounds as expected for residues in close proximity to the substrate. Ile-94 and Val-98 are thought to form a “pivot point” in TM4 of the SMRs with importance not only for dimerization, but also a direct role in the mechanism of multidrug efflux (38). Although Ile-94 is not assigned, Val-98 does shift with substrate. Interestingly, Val-98 has very large shifts in one state and negligible shifts in the other, indicating an asymmetric role for this residue. In the crystal structure, Val-98 from one monomer faces into the interface between the two TM4 helices near the TM3 kink, whereas in the other monomer it is rotated into a more outward-facing position. The kink in TM3, caused by the GVG motif (residues 65–67), is also expected to play a key role in conformational interconversion (5, 14, 39), and this kink changes conformation upon substrate binding, as shown by solid-state NMR PISEMA spectra of Val-66 and Val-69 (40). Intriguingly, this region has some of the largest chemical shift changes when different substrates are bound, suggesting an important role for this hinge region in translating substrate identity into distinct rates of exchange for the common conformational interconversion process.

Further inspection of the spectra highlights some unique features of the C-terminal region of EmrE. The C termini are missing from the crystal structure (35), indicating they do not have a single well defined conformation under those conditions. However, residues in this region, including 104–108, have unique, well resolved chemical shifts that do not match random coil chemical shifts, indicating that the C terminus is not simply a floppy tail. In agreement with EPR studies that show a loss in helical periodicity after residue 103 (39), these chemical shifts are not typical of helical secondary structure, as might be expected if the final helix extended beyond the point where it is resolved in the crystal. Additionally, at least one of each pair of peaks for residues 105, 106, and 108 is highly sensitive to bound substrate (Fig. 7A and 4A). Arginine 106 (Fig. 4A) provides a particularly well resolved example of the behavior of residues in this region. Examination of the crystal structure reveals that on the open face of EmrE, the entrance to the transport pore extends between the TM3 helices (Fig. 1B) and there is space for C-terminal residues from monomer A to extend into this region. Using differential water accessibility to identify monomers A and B (14), it is precisely the peaks corresponding to the C-terminal tail of monomer A that are sensitive to substrate identity. Although its exact role is not known, the C terminus of EmrE is as sensitive to bound substrate identity as other key regions of EmrE and should not be ignored when considering the structure and function of the protein despite its absence in the crystal structure.

Implications for Protein Dynamics

The importance of protein motions on different time scales for biological function is well established (41, 42). The large-scale inward- to outward-facing conformational change of EmrE is key to the biological activity of this multidrug resistance transporter. As we have shown, the dynamics of this large-scale structural change are modulated over several orders of magnitude by the identity of the substrate being transported. Global domain motions that are modulated (in a non switch-like fashion) to this extreme have not been extensively reported. Only one similar example of a transporter exists: LeuT interconversion dynamics differ when bound to either alanine or leucine (43). However, the differences in rates do not vary as significantly as reported here, and the extreme differences in rate observed for EmrE may reflect the unique properties required for multidrug recognition and transport. Thus, we propose that large changes in dynamics with substrate identity may occur in many MDR transporters.

The coupled effects of substrate binding on EmrE structure and dynamics provide important insight into the transport mechanism. For EmrE, our results are consistent with large structural differences when bound to diverse substrates (2) leading to significant differences in the free energy of the bound state that are dependent on ligand geometry, charge, and hydrophobicity. This bound state is the ground state for the conformational transition between open-in and open-out states. The observation that there is less variation in the transition state energy within the tetrahedral series indicates the importance of EmrE itself in influencing the conformational exchange transition. This is reminiscent of the finding that partially active mutants and phosphorylation of NtrC alter the rate of exchange between the active and inactive states of this signaling protein by changing the ground-state energy and have very little effect on the transition state energy. Mutations of NtrC residues participating in the transition pathway do affect the transition state energy (44). However, in EmrE, there is structural overlap between the regions involved in substrate binding and interconversion. The chemical shift differences between EmrE bound to different substrates (Fig. 7, A and B) reveal significant effects in TM3 and TM4. TM3 forms part of the hydrophobic binding pocket and contains the critical binding residue Trp-63. The TM3 kink structure is sensitive to substrate binding (40), and together with the TM4 hinge is believed to play a critical role in conformational interconversion (5, 14, 38, 39). Based on this data, changes in helix tilt upon ligand binding alter the ground-state energy for the complex. Ligand can also affect the transition-state energy via the effect of altered helix tilt on the TM3-TM4 hinge point or direct ligand interaction with TM3. Thus, we propose that TM3 plays a central role in coupling substrate binding to conformational exchange between inward- and outward-facing states in EmrE.

The influence of substrate on the transition-state energy for EmrE converting between inward- and outward-facing states is consistent with the alternating access model of antiport. Unlike soluble enzymes, which have frequently been found to pre-sample the enzymatically active conformation in the apo state (45–49), EmrE should not undergo transport-related motions when not bound to substrate to achieve coupled antiport. This is more similar to PKA-C, where nucleotide binding is required to achieve a state with both structure and dynamics primed for catalysis (50). For single-site alternating access antiport, the transition state for conformational exchange cannot be determined solely by the protein and must have a significant influence from the substrate, in agreement with our data for EmrE. This suggests a mechanism for transport inhibition. A very tight-binding substrate may stabilize the ground state sufficiently to create a nearly insurmountable energetic barrier for conformational exchange, thus trapping a single state of EmrE and preventing efflux.