Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2013 Jun 11;8(2):151–156. doi: 10.1007/s11571-013-9260-2

Synchrony based learning rule of Hopfield like chaotic neural networks with desirable structure

Nariman Mahdavi 1,✉, Jürgen Kurths 1
PMCID: PMC3945457  PMID: 24624234

Abstract

In this paper a new learning rule for the coupling weights tuning of Hopfield like chaotic neural networks is developed in such a way that all neurons behave in a synchronous manner, while the desirable structure of the network is preserved during the learning process. The proposed learning rule is based on sufficient synchronization criteria, on the eigenvalues of the weight matrix belonging to the neural network and the idea of Structured Inverse Eigenvalue Problem. Our developed learning rule not only synchronizes all neuron’s outputs with each other in a desirable topology, but also enables us to enhance the synchronizability of the networks by choosing the appropriate set of weight matrix eigenvalues. Specifically, this method is evaluated by performing simulations on the scale-free topology.

Keywords: Synchrony based learning, Chaotic neural networks, Structure inverse eigenvalue problem, Scale-free networks

Introduction

Oscillations and chaos have been the subject of extensive studies in many physical, chemical and biological systems. Oscillatory phenomena frequently occur in the living systems as a result of rhythmic excitations of the corresponding neural systems (Wang et al. 1990). Chaos can occur in a neural system due to the properties of a single neuron and the properties of synaptic connectivities among neurons (Wang and Ross 1990). Some parts of the brain, for example, the cerebral cortex, have well-defined layers structures with specific interconnections between different layers (Churchland and Sejnowski 1989). (Babloyantz and Lourenco 1994) have studied an Artificial Neural Network with a similar architecture which has chaotic dynamics and performs pattern discrimination and motion detection. These studies have shown that interactions of neural networks are not only useful, but also important, in determining the cognitive capabilities of a neural system (Wang 2007).

In usual neural networks, there are not different kinds of dynamics. The idea of chaotic neural networks is proposed by Aihara from neurophysiologic aspects of real neurons (Aihara et al. 1990). In (Wang et al. 2007), it has been shown that by adding only a negative self-feedback to the cellular neural network, a transiently chaotic behavior can be generated. Moreover, Ma and Wu (2006) have proved that the bifurcation phenomenon appears only by applying a non-monotonic activation function. They have used this fact to increase the networks capacity for the memory storage. However, many different types of chaotic neural networks have been appeared (Nakano and Saito 2004; Lee 2004).

On the other hand, one of the interesting and significant phenomena in dynamical networks is the synchronization of all dynamical nodes in the network. In fact, synchronization is a kind of typical collective behaviors in nature (Watts and Strogatz 1998). Synchrony can be good or bad depending on the circumstances, and it is important to know what factors contribute to the synchrony and how to control it. For example, partial synchrony in cortical networks is believed to generate various brain oscillations, such as the alpha and gamma EEG rhythms. Increased synchrony may result in the pathological types of activity, such as epilepsy (Izhikevich 2007). Furthermore, some synchronization phenomena of coupled chaotic systems are very useful in our daily life and have received a great deal of attention (Lü et al. 2004; Li and Chen 2006).

In the aforementioned papers, some sufficient conditions on the coupling strengths have been derived to ensure the synchronization of the whole network without specifying how to find the appropriate weights. Therefore, a learning rule to completely synchronize the whole network is still needed, whereas only a few papers have addressed this matter (Li et al. 2008; Liu et al. 2010; Xu et al. 2009). Moreover, none of them discussed about the issue of synchronizability and as far as we know, there is not any learning rule for the tuning of the coupling strengths so that, finally, the whole network is synchronized in a desirable structure while the synchronizability is also enhanced. The synchronizability can be usually assessed by the eigenratio 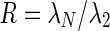Inline graphic, in the continuous case. If this value is small enough, then the synchronization is easier to achieve (Comellas and Gago 2007; Ponce et al. 2009; Wang et al. 2009). Current researches show that the value of R in the weighted networks has a great reduction with respect to the unweighted networks (Zhou and Kurths 2006). However, the value of R for the weighted networks could be calculated after the adaptation and therefore, we have no idea about its value until the completion of adaptation (Zhou and Kurths 2006; Wang et al. 2009).

Motivated by the above comments, this paper further investigates the issue of synchronization in the dynamical neural networks with a neuron of logistic map type and self-coupling connections. By utilizing the idea of Structured Inverse Eigenvalue Problems (Moody and Golub 2005) and expanding our previous results about the synchronization criteria on the coupling weights of a network (Mahdavi and Menhaj 2011), we propose a learning rule which brings about synchronization in a desired topological structure and also enhance the synchronizability of the network. Specifically, by assigning the scale-free structure to the network, one can reach to the benefits of this topology. For example, the number of tunable coupling weights is much less than the complete regular neural network and hence, it would be easier for implementation.

Problem formulation and preliminaries

As is well known, a variety of complex behavior, including chaos, is exhibited by some nonlinear mappings when iterated. A coupled map chain is the simplest possible collection of coupled mappings which can be looked upon as a neural network with several layers, each containing only one element, with the elements being both self-coupled and executing a non-monotonic function. A coupled map chain consists of N cells, in which the state of ith cell at time t, denoted by xi(t), can be written as:

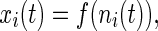graphic file with name M2.gif 1

where the net input for ith cell is a weighted sum of the state of this cell at previous time step, and the state of other cells at a former time step, say 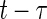Inline graphic. Then we have

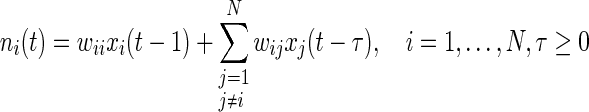graphic file with name M4.gif 2

Generally, there are various possible values for 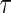Inline graphicwhich could be different for each cell. However, if f in (1) is a sign function, f(.) = sgn(.), and the parameters in (2) are set to: wii = 0, wij = wji, and Inline graphic; this leads to the binary Hopfield Neural Network. In fact, connections between cells are symmetric and there are no self coupling connections. In this study, the Hopfield like neural network consists of N neurons of logistic map type is considered as follows

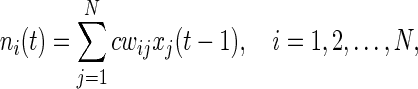graphic file with name M7.gif 3
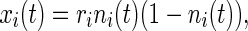graphic file with name M8.gif 4

where ni(t) is the net input, xi(t) is the output, 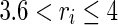Inline graphic is the controlling parameter of each neuron that ensure its chaotic behavior and the initial condition 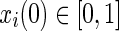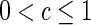Inline graphic. Inline graphic is a constant for the whole network. The coupling matrix 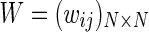Inline graphic which will be found by our proposed learning rule, represents the coupling strength and the coupling configuration of the network, in which wij is defined in such a way that if there is a connection from neuron j to neuron i, then 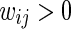Inline graphic; otherwise wij = 0. Moreover, the sum of all elements in each row of the matrix W should be equal to one, that is,

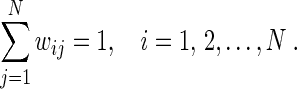graphic file with name M14.gif 5

Remark 1

The above row one sum assumption, Eq. (5), is a sufficient condition for the synchronization of a network described by the discrete chaotic maps (3)–(4) (Mahdavi and Menhaj 2011). This assumption is equivalent to the diffusive couplings for the continuous case which described by the row zero sum assumption. Based on these assumptions and the irreducibility of the coupling matrix W, it can be verified that one is an eigenvalue with multiplicity 1, denoted as λ1, of the coupling matrix W in the discrete maps (3)–(4) (Moody and Golub 2005). Similarly, zero is an eigenvalue with multiplicity 1 for the continuous case (Lü et al. 2004).□

It is assumed that when synchronization happens in the neural network (3) and (4) with identical neurons, all states become equal, i.e., x1(t) = x2(t) = … = xN(t) = s(t) as t goes to infinity, where s is an emergent synchronous solution of the network and will be created collaboratively by all neurons. In fact, we have no idea about s(t) in advance. For the main result of the next section, the following definitions and theorems are required.

Definition 1 (Moody and Golub 2005):

A matrix W is called nonnegative if all of its entries are nonnegative.

Definition 2 (Moody and Golub 2005):

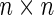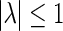An Inline graphic nonnegative matrix W is a Stochastic (Markov) Matrix if all its row sums are 1. Then, it is possible to show that every eigenvalue of a Markov Matrix satisfies Inline graphic.

The Stochastic Inverse Eigenvalue Problem (StIEP) concerns whether a Markov chain can be built with the desirable spectral property. This problem is stated in the following.

StIEP

(Moody and Golub 2005): Given a set of numbers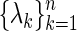Inline graphicthat is closed under the complex conjugation and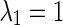Inline graphic, construct a stochastic matrix W so that

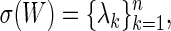graphic file with name M19.gif 6

where σ represents the spectrum of a matrix. Therefore, this problem is sometimes called an inverse spectrum problem.

Theorem 1

(Moody and Golub 2005): (Exsistence) Any n given real numbers 1, λ1,…, λn−1with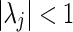Inline graphicare the spectrum of some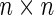Inline graphicpositive stochastic matrix if the sum of all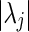Inline graphicover those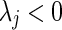Inline graphicis less than 1. If the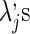Inline graphicare all negative the condition is also necessary.

Theorem 2

(Mahdavi and Menhaj 2011): All outputs of the network (3), (4) with identical neurons, i.e., ri = r, i = 1,2,…,N, c = 1 and nonnegative coupling strength wijbecome synchronous, if the coupling matrix W is a stochastic matrix and its eigenvalues satisfy the following condition.

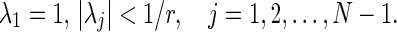graphic file with name M25.gif 7

Corollary 1:

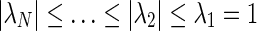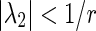if the eigenvalues of the coupling matrix W rewritten in the form ofInline graphic, then the sufficient synchronization criterion of theorem 2 could be replaced withInline graphic.

It can be seen from theorem 2 that the sufficient condition for the network synchronization is obtained but there is no systematic way for finding the coupling strengths. Moreover, the structure is usually considered as a fully connected topology which is far from any practical implementation. In the next section, both of these problems will be solved simultaneously.

Synchrony based learning

Theorem 2 only discusses about the case of c = 1, while the general case of 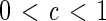Inline graphic could be formulated as follows.

Corollary 2:

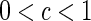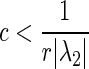All outputs of the network (3), (4) with identical neurons, i.e., ri = r, i = 1,2,…,N,Inline graphicand nonnegative coupling strength wijbecome synchronous, if the second greatest eigenvalue of the stochastic coupling matrix W satisfiesInline graphic.

Proof

It could be easily obtained by merging the parameters r and c to a single parameter and following the same procedure which has been done by Mahdavi and Menhaj (2011).□

Corollary 3:

According to the corollary 2, the following two cases could be easily deduced. (1) if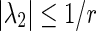Inline graphic, then for any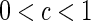Inline graphicthe network is synchronized, (2) if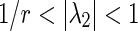Inline graphic, then for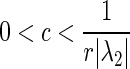Inline graphicthe network is synchronized.

Remark 2

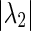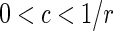By increasing the value of Inline graphic to 1 (closer the second largest eigenvalue to the unit circle), the interval of the synchronizable constant reduced to Inline graphic.□

Remark 3

For this kind of discrete chaotic maps, the value of 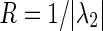Inline graphic could be considered as a measure of synchronizability. Therefore, the greater the value of 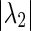Inline graphic, the stronger the synchronizability of the network, which means that the whole network could be synchronized with the smaller value of the constant c.□

The diagonal matrix 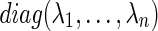Inline graphic of the prescribed eigenvalues can be transformed similarly, if necessary, into a diagonal block matrix Λ with 2 × 2 real blocks if some of the given values appear in complex conjugate pairs. The set 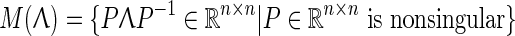Inline graphic denotes isospectral matrices parameterized by nonsingular matrices P. The cone of nonnegative matrices 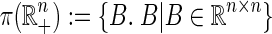Inline graphic is characterized by the element-wise product of general square matrices. 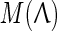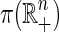If a solution exists, it must be at the intersection of Inline graphic and Inline graphic. Therefore, the following constrained optimization problem is introduced

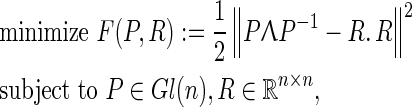graphic file with name M44.gif

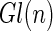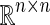where Inline graphic denotes the general linear group of invertible matrices in Inline graphic.

Let us recall that 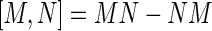Inline graphic is the Lie bracket and we abbreviate

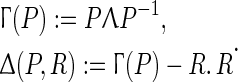graphic file with name M48.gif

Then, the differential system

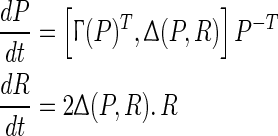graphic file with name M49.gif 8

provides a steepest descent flow on the feasible set 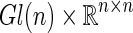Inline graphic for the objective function F(P,R). This method has an advantage that deserves notice. Observe that the zero structure, if there is any, in the original matrix R(0) is preserved throughout the integration due to the element wise product. In other words, if it is desirable that node i is not connected into node j, we simply assign 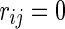Inline graphic in the initial value R(0). Then that zero is maintained throughout the evolution

Learning rule

Now, we are in the position to state the coupling strengths tuning mechanism such that synchronization is achieved by maintaining a desirable structure for the network and enhancing the synchronizability. To reach the above mentioned goals, the following steps are required.

  • Step 1: Choose the proper, in the sense of synchronizability, real eigenvalues λ1 = 1, λ2,…, λN, such that the theorem 1 and corollary 1 are satisfied.

  • Step 2: Assign 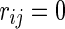Inline graphic in the initial value R(0) according to the desirable network structure and P(0) should be an invertible matrix.

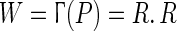  • Step 3: Numerically solve the differential system (8) and stop the iterations when the value of cost function becomes lower than a predefined threshold. If step 1 is done in a proper way, then the convergent solution of (8) always exists and could be considered as a coupling matrix W, i.e., Inline graphic.

  • Step 4: Due to the numerical calculations, there is always a little amount of errors between the spectrum of the founded weight matrix and the desired spectrum in the step 1. Moreover, because of the stopping criterion, the cost function never reaches to zero exactly. Therefore, we have to employ a synchronizable constant 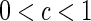Inline graphic according to the corollary 3.

Simulation results

In this section, the effectiveness of the proposed synchrony based learning rule is verified by an illustrative example. In this example, the network structure obeys the scale-free topology. Here, the numerical simulation is done in MATLAB environment.

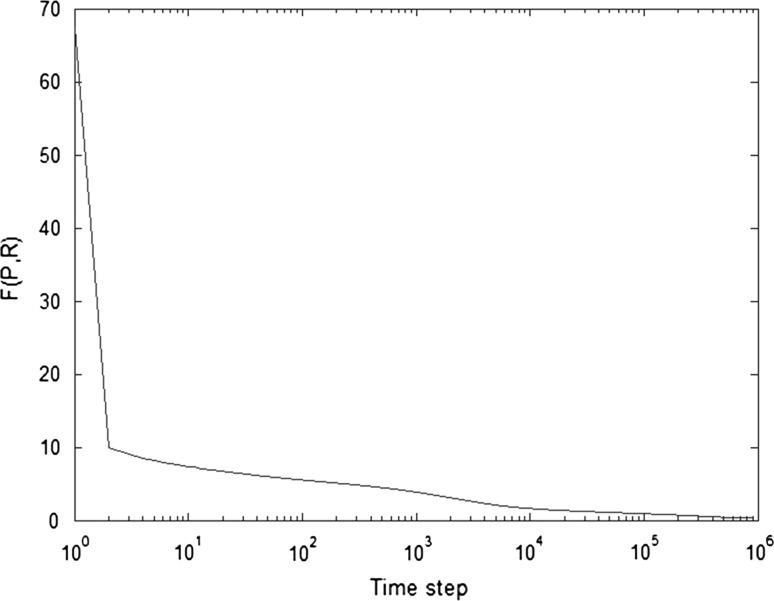
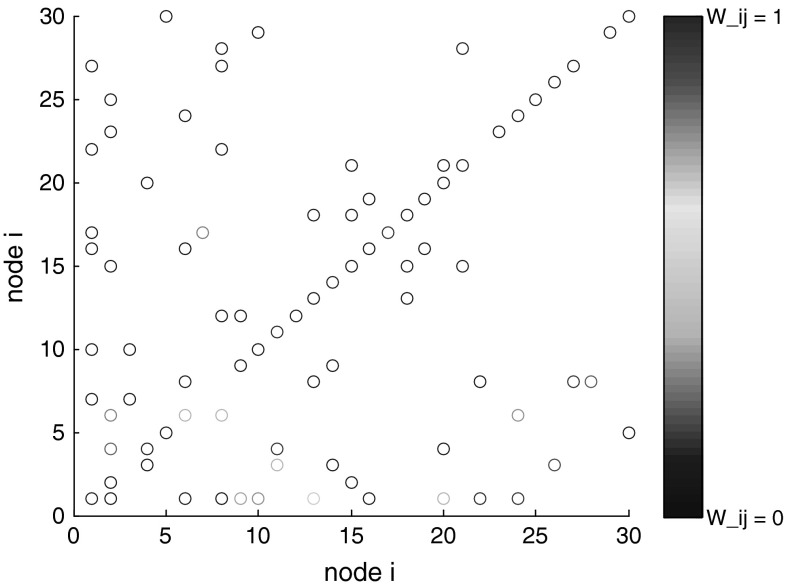
Consider the neural network (3), (4) with N = 30, ri = 3.9, i = 1,2,…,N, and initial random coupling matrix W. According to the step 1, the desired eigenvalues are chosen as λ1 = 1, λ2 = −0.1, λ3 = −0.15, and the others are generated by a uniform random number between 0 and 0.2 which satisfy both theorem 1 and 2. The initial value R(0) is generated by the BA scale-free method with m = m0 = 5 (Barabasi and Albert 1999) and P(0) is a random matrix. Afterwards, the differential system (8) is solved numerically which finally converges to the coupling matrix 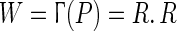Inline graphic. The objective function F(P,R) for this simulation is represented in Fig. 1. That shows the rapid decay in the beginning but a heavy tail in the end. Therefore, the speed of the convergence in this method is not enough and one should think about this important issue in the future. The final weights of the networks are shown in Fig. 2. It is interesting to note that the network structure is assumed to be symmetric; however, there is no necessity to have the symmetric weights, which is obvious from this figure. Although the coupling weights are asymmetric, the increasing or decreasing of the coupling weights behave symmetrically, which is interesting because the learning rule is completely offline and only based on the desired set of eigenvalues.

Fig. 1.

Fig. 1

Open in a new tab

Objective function decays to reach the true coupling strength required for synchronization of all neurons in scale-free structure

Fig. 2.

Fig. 2

Open in a new tab

The final coupling weights, which obtained from numerical solution of StIEP. These weights are asymmetric

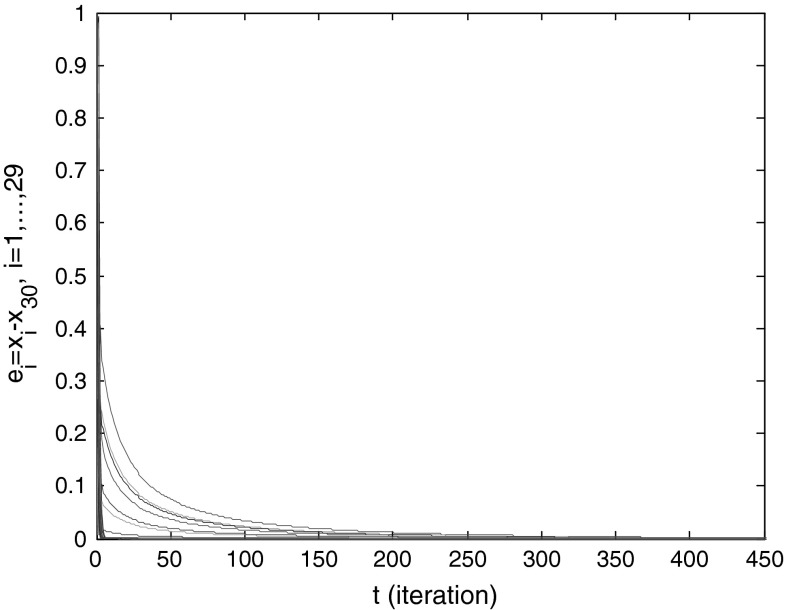
Afterwards, one can use the above founded weight matrix in the network and be sure that the synchronization happened. Here, we assumed the value of c = 0.25. As shown in Fig. 3, as the system evolves, the synchronization errors between the output of the last node and the other nodes converge to zero. This phenomenon also occurs if we select any other nodes as a master node, which means that all of the neurons reach to a synchronous state evolutionary.

Fig. 3.

Fig. 3

Open in a new tab

Synchronization errors between the output of the last node and the other nodes, by selecting the value of c = 0.25

Conclusions

In brain anatomy, the cerebral cortex is the outermost layer of the cerebrum and the part of the brain that is the center of unsupervised learning and the seat of higher level brain functions including perception, cognition, and learning of both static and dynamic sensory information. The cortex is composed of a sequence of discernable interconnected cortical networks (patches). Each concerned network has a specific functionality and is an ensemble of a large number of asymmetrically connected complex processing elements (CPEs) whose state–space orbits exhibit periodic orbits, as well as bifurcations and chaos (Mpitsos et al. 1988a). These networks of interconnected CPEs are responsible for the generation of sparse representations and efficient codes that are utilized during perception and recognition processes. Implementation of a microscopic model of the cortex that incorporates small details of neurons, synapses, dendrites, axons, nonlinear dynamics of membrane patches, and ionic channels is prohibitively difficult even with the computational resources and the nanofabrication technologies available today or predicted for the future. Consequently, a realizable model should emulate such neurobiological computational mechanisms at an aggregate level.

The computational units of the cortex are named netlets, which are composed of discrete populations of randomly interconnected neurons (Harth et al. 1970; Anninos et al. 1970). The similarity between the netlet’s return map and that of logistic map has been noted by Harth (1983). The fascinating conjecture is that the cortical networks can be modeled in an efficient way by means of populations of logistic processing elements that emulate the cortical computational mechanisms at an aggregate level. In addition, the idea of parametric coupling has been previously adapted to transmit the chaotic signals originating in one part of the nervous system to another part (Mpitsos et al. 1988b) and to improve the performance of the associative memories such as Hopfield model (Lee and Farhat 2001; Tanaka and Aihara 2005) and biomorphic dynamical networks that are used for cognition and control purposes (Farhat 1998, 2000).

In other words, the cortical networks could be modeled with networks of parametrically coupled nonlinear iterative logistic maps each having complex dynamics that represents populations of randomly interconnected neurons possessing collective emergent properties (Pashaie and Farhat 2009). Moreover, symmetrically coupled logistic equations are proposed to mimic the competitive interaction between species (Lopez-Ruiz and Fournier-Prunaret 2009).

In conclusion, in this paper, an effective tuning mechanism of coupling strengths in a Hopfield like chaotic neural networks with logistic map activation functions has been studied which not only synchronizes the whole neurons’ output in any desirable topology, but also enhances the synchronizability of the network. Our proposed method is obtained by utilizing the Stochastic Inverse Eigenvalue Problem and some sufficient conditions on the network couplings strength which guarantees that all neurons collaboratively reach to a synchronous state eventually. Synchronous behavior of neural assemblies is a central topic in neuroscience. It is known to be correlated with cognitive activities (Singer 1999) during the normal functioning of the brain, while abnormal synchronization is linked to important brain disorders, such as epilepsy, Parkinson’s disease, Alzheimer’s disease, schizophrenia and autism (Uhlhaas and Singer 2006). An illustrative example has been considered, taking the scale-free matrix as initial weight matrix of an asynchronous neural network. The numerical simulations showed that the proposed method can synchronize this network effectively with less tuning weights as well as more robustness.

As an interesting topic for the future works, one should think about possible extension of this method to other types of recurrent or feed forward neural networks and take the advantages of a desirable structure like scale-free topology. Moreover, the speed of convergence should be increased for the practical use of this method in the large networks.

Contributor Information

Nariman Mahdavi, Email: nariman.mahdavi@gmail.com.

Jürgen Kurths, Email: kurths@pik-potsdam.de.

References

  1. Aihara K, Takada T, Toyoda M. Chaotic neural networks. Phys Lett A. 1990;144:333–340. doi: 10.1016/0375-9601(90)90136-C. [DOI] [Google Scholar]
  2. Anninos P, Beek B, Harth E, Pertile G. Dynamics of neural structures. J Theor Biol. 1970;26:121–148. doi: 10.1016/S0022-5193(70)80036-4. [DOI] [PubMed] [Google Scholar]
  3. Babloyantz A, Lourenco C. Computation with chaos: a paradigm for cortical activity. Proc Natl Acad Sci USA. 1994;91:9027–9031. doi: 10.1073/pnas.91.19.9027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
  5. Churchland PS, Sejnowski TJ. The computational brain. Cambridge: MIT press; 1989. [Google Scholar]
  6. Comellas F, Gago S. Synchronizability of complex networks. J of Phys A: Math and Theor. 2007;40:4483–4492. doi: 10.1088/1751-8113/40/17/006. [DOI] [Google Scholar]
  7. Farhat NH. Biomorphic dynamical networks for cognition and control. J Intell Robot Syst. 1998;21:167–177. doi: 10.1023/A:1007989607552. [DOI] [Google Scholar]
  8. Farhat NH. Corticonics: the way to designing machines with brain like intelligence. Proc SPIE Critical Technol Future Comput. 2000;4109:103–109. doi: 10.1117/12.409209. [DOI] [Google Scholar]
  9. Harth E. Order and chaos in neural systems: an approach to the dynamics of higher brain functions. IEEE Trans Syst Man Cybern. 1983;13:782–789. doi: 10.1109/TSMC.1983.6313072. [DOI] [Google Scholar]
  10. Harth E, Csermely TJ, Beek B, Lindsay RD. Brain function and neural dynamics. J Theor Biol. 1970;26:93–120. doi: 10.1016/S0022-5193(70)80035-2. [DOI] [PubMed] [Google Scholar]
  11. Izhikevich EM. Dynamical systems in neuroscience. Cambridge: MIT Press; 2007. [Google Scholar]
  12. Lee RST. A transient-chaotic auto associative network based on Lee oscilator. IEEE Trans on Neural Networks. 2004;15:1228–1243. doi: 10.1109/TNN.2004.832729. [DOI] [PubMed] [Google Scholar]
  13. Lee G, Farhat NH. Parametrically coupled sine map networks. Int J Bifurcat Chaos. 2001;11:1815–1834. doi: 10.1142/S0218127401003048. [DOI] [Google Scholar]
  14. Li Z, Chen G. Global synchronization and asymptotic stability of complex dynamical networks. IEEE Trans on Circuits and Systems-II. 2006;53:28–33. doi: 10.1109/TCSII.2005.854315. [DOI] [Google Scholar]
  15. Li Z, Jiao L, Lee J. Robust adaptive global synchronization of complex dynamical networks by adjusting time-varying coupling strength. PhysicaA. 2008;387:1369–1380. doi: 10.1016/j.physa.2007.10.063. [DOI] [Google Scholar]
  16. Liu H, Chen J, Lu J, Cao M. Generalized synchronization in complex dynamical networks via adaptive couplings. PhysicaA. 2010;389:1759–1770. doi: 10.1016/j.physa.2009.12.035. [DOI] [Google Scholar]
  17. Lopez-Ruiz R, Fournier-Prunaret D. Periodic and chaotic events in a discrete model of logistic type for the competitive interaction of two species. Chaos, Solitons Fractals. 2009;41:334–347. doi: 10.1016/j.chaos.2008.01.015. [DOI] [Google Scholar]
  18. Lü J, Yu X, Chen G. Chaos synchronization of general complex dynamical networks. PhysicaA. 2004;334:281–302. doi: 10.1016/j.physa.2003.10.052. [DOI] [Google Scholar]
  19. Ma J, Wu J. Bifurcation and multistability in coupled neural networks with non-monotonic communication. Toronto: Technical report Math dept, York University; 2006. [Google Scholar]
  20. Mahdavi N, Menhaj MB. A new set of sufficient conditions based on coupling parameters for synchronization of Hopfield like chaotic neural networks. Int J control Auto and Syst. 2011;9:104–111. doi: 10.1007/s12555-011-0113-7. [DOI] [Google Scholar]
  21. Moody TC, Golub GH. Inverse eigenvalue problems: theory, algorithms and applications. Numerical mathematics and scientific computation series. Oxford: Oxford press; 2005. [Google Scholar]
  22. Mpitsos GJ, Burton RM, Creech HC, Soinila SO. Evidence for chaos in spike trains of neurons that generate rhythmic motor patterns. Brain Res Bull. 1988;21:529–538. doi: 10.1016/0361-9230(88)90169-4. [DOI] [PubMed] [Google Scholar]
  23. Mpitsos GJ, Burton RM, Creech HC. Connectionist networks learn to transmit chaos. Brain Res Bull. 1988;21:539–546. doi: 10.1016/0361-9230(88)90170-0. [DOI] [PubMed] [Google Scholar]
  24. Nakano H, Saito T. Grouping synchronization in a pulse-coupled network of chaotic spiking oscillators. IEEE Trans Neural Networks. 2004;15:1018–1026. doi: 10.1109/TNN.2004.832807. [DOI] [PubMed] [Google Scholar]
  25. Pashaie R, Farhat NH. Self organization in a parametrically coupled logistic map network: a model for information processing in the Visual Cortex. IEEE Trans on Neural Networks. 2009;20:597–608. doi: 10.1109/TNN.2008.2010703. [DOI] [PubMed] [Google Scholar]
  26. Ponce MC, Masoller C, Marti AC. Synchronizability of chaotic logistic maps in delayed complex networks. Eur Phys J B. 2009;67:83–93. doi: 10.1140/epjb/e2008-00467-3. [DOI] [Google Scholar]
  27. Singer W. Neuronal synchrony: a versatile code for the definition of relations? Neuron. 1999;24:49–65. doi: 10.1016/S0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
  28. Tanaka G, Aihara K. Multistate associative memory with parametrically coupled map networks. Int J Bifurcat Chaos. 2005;15:1395–1410. doi: 10.1142/S0218127405012673. [DOI] [Google Scholar]
  29. Uhlhaas PJ, Singer W. Neural synchrony in brain disorders: relevance for cognitive dysfunctions and pathophysiology. Neuron. 2006;52:155–168. doi: 10.1016/j.neuron.2006.09.020. [DOI] [PubMed] [Google Scholar]
  30. Wang L. Interactions between neural networks: a mechanism for tuning chaos and oscillations. Cogn Neurodyn. 2007;1:185–188. doi: 10.1007/s11571-006-9004-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wang L, Ross J. Interactions of neural networks: model for distraction and concentration. Proc Natl Acad Sci USA. 1990;87:7110–7114. doi: 10.1073/pnas.87.18.7110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wang L, Pichler EE, Ross J. Oscillations and chaos in neural networks: an exactly solvable model. Proc Natl Acad Sci USA. 1990;87:9467–9471. doi: 10.1073/pnas.87.23.9467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wang L, Yu W, Shi H, Zurada JM. Cellular neural networks with transient chaos. IEEE Trans on circuits and systems-II: express briefs. 2007;54:440–444. doi: 10.1109/TCSII.2007.892399. [DOI] [Google Scholar]
  34. Wang WX, Huang L, Lai YC, Chen G. Onset of synchronization in weighted scale-free networks. Chaos. 2009;19:013134. doi: 10.1063/1.3087420. [DOI] [PubMed] [Google Scholar]
  35. Watts DJ, Strogatz SH. Collective dynamics of small-world networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
  36. Xu YH, Zhou WN, Fang JA, Lu HQ. Structure identification and adaptive synchronization of uncertain general complex dynamical networks. Phys Lett A. 2009;374:272–278. doi: 10.1016/j.physleta.2009.10.079. [DOI] [Google Scholar]
  37. Zhou C, Kurths J. Dynamical weights and enhanced synchronization in adaptive complex networks. Phys Rev Lett. 2006;96:164102. doi: 10.1103/PhysRevLett.96.164102. [DOI] [PubMed] [Google Scholar]

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES