A review of EEG and MEG for brainnetome research

Abstract

The majority of brain activities are performed by functionally integrating separate regions of the brain. Therefore, the synchronous operation of the brain’s multiple regions or neuronal assemblies can be represented as a network with nodes that are interconnected by links. Because of the complexity of brain interactions and their varying effects at different levels of complexity, one of the corresponding authors of this paper recently proposed the brainnetome as a new –ome to explore and integrate the brain network at different scales. Because electroencephalography (EEG) and magnetoencephalography (MEG) are noninvasive and have outstanding temporal resolution and because they are the primary clinical techniques used to capture the dynamics of neuronal connections, they lend themselves to the analysis of the neural networks comprising the brainnetome. Because of EEG/MEG’s applicability to brainnetome analyses, the aim of this review is to identify the procedures that can be used to form a network using EEG/MEG data in sensor or source space and to promote EEG/MEG network analysis for either neuroscience or clinical applications. To accomplish this aim, we show the relationship of the brainnetome to brain networks at the macroscale and provide a systematic review of network construction using EEG and MEG. Some potential applications of the EEG/MEG brainnetome are to use newly developed methods to associate the properties of a brainnetome with indices of cognition or disease conditions. Associations based on EEG/MEG brainnetome analysis may improve the comprehension of the functioning of the brain in neuroscience research or the recognition of abnormal patterns in neurological disease.

Introduction

The brainnetome and the EEG/MEG network

Because the brain is an adaptable and efficient system that integrates a large number of neurons, axons and astrocytes so that they function concordantly, one of the challenges in the field of neuroscience is the examination of brain function. Exploring brain function increases scientists’ comprehension of this mysterious system and may facilitate the diagnosis of neuropsychological diseases. Neurologists and clinicians have attempted to determine the underlying mechanisms of brain function since the 18th century. For many years, the central theme of brain function was that of functional localization, i.e., each separate region of the cerebral cortex dictates a specific function. Thus, it would be hypothetically feasible to delineate the region of the cortex that implements a certain function. Electrophysiological techniques were applied to validate such functional localization. However, investigations that showed a high level of electrical conduction between different regions of the brain ultimately revealed that the evidence for functional localization was insufficient and thus that localizing a specific brain function to an individual region of the brain may not be possible (Başar 2011; Fehr 2013; Fuster 2006; Poldrack 2006).

Advances in electrophysiology and neuroimaging increased the comprehension of brain function by findings such as synaptic connections between neurons (Gerstein and Perkel 1969) and neural assemblies (Fingelkurts et al. 2010), in which distributed neural activity is thought to be integrated into dynamic connections (Eichenbaum 1993; Varela 1995). The brain is no longer considered to work via individual regions but rather by several regions working cooperatively (Varela et al. 2001). This concept is also consistent with microscopic observations of the brain. Neurons were found to be connected by axons in ways that allowed their individual actions to be synchronized. Similarly, the functional integration of distinct brain regions, which had been analyzed using various imaging modalities, could be deduced at a macroscopic level (Frackowiak et al. 2004; He and Liu 2008; Pockett et al. 2007). This functional integration means that segregated brain regions are integrated and coordinated to perform a particular function (Fingelkurts et al. 2010; Tononi et al. 1994).

Because of this progress from functional localization to functional integration, both the academic community and governments now understand the importance of the neural network. A series of projects, such as the “Human Connectome Project” in the U.S. and the “CONNECT Project” in Europe, were launched across the world to delineate this complex network. The Brainnetome Project is a similar project for China but is focused on the unique structural and dynamic features of the brain network and provides a longitudinal perspective. The brainnetome concept, as a new –ome, covers not only the brain connectivity based on brain structural/functional data but also the potential relationship between certain parts of the network with genetics. A review by Jiang (2013) presented details of the Brainnetome Project and enumerated these contemporary international projects. We refer readers to this work for more information regarding related projects. The brainnetome concept was designed to integrate a variety of neuroimaging techniques, methods and models as well as to merge fragmented findings into a uniform research framework to further clarify the organization of the brain. Song and Zuo, respectively, provided reviews of the use of functional magnetic resonance imaging (fMRI) and diffusion MRI (dMRI) to develop the brainnetome (Song and Jiang 2012; Zuo et al. 2012). Although the brain network, the brainnetome, has been studied in a number of publications, the majority of them focused on networks constructed using fMRI data. A few studies provided networks based on EEG/MEG data (Gavit et al. 2001; Michel et al. 2004; Michel and Murray 2012), but few introduced a method for constructing an EEG/MEG network in both sensor space where the measurements occur and source space in the brain itself or explained how neuroscientists and clinicians can apply this type of network analysis (Lemieux et al. 2011). This manuscript is designed to complement current brainnetome analyses by adding electromagnetic network information and applying its network properties to neuroscience research and clinical applications.

Traditional electrophysiological techniques that recorded electrical currents in a single region have been improved by multi-channel EEG and MEG systems which can record 256 channels simultaneously with superb temporal resolution. Taking advantage of multiple channels with this level of resolution, the functional integration of the brain can be analyzed across multiple regions by this system. The association between channels can be intuitively defined as their connectivity. Based on this definition of connectivity, the brain activity can be organized into networks. Adding this type of network system to those derived from fMRI and relating electromagnetic network features to psychiatric, behavioral, or clinical performance could advance neuroscience and clinical research (Britz et al. 2010) (Schoffelen and Gross 2009).

To encourage the adoption of EEG or MEG for studying the brainnetome, this review introduces EEG/MEG in Subsection “Usefulness of EEG/MEG in brainnetome analysis” of the Introduction. Because graph theory is the basis for brainnetome analysis, the basics of graph theory analysis will be introduced in Subsection “Graph theory”.

Usefulness of EEG/MEG in brainnetome analysis

EEG uses electrodes attached to a subject’s scalp to measure voltage fluctuations in the ionic current that accompanies neuronal activity (Lewine and Orrison 1995a). It is a common non-invasive technique used to record the electrophysiological signals resulting from brain activity. EEG is also free of ionic radiation or constrictive head fixation, which are unavoidable in computed tomography and MRI. This means that an EEG system can easily be administered in either research or clinical settings. Moreover, experimental paradigms that use EEG are not limited by stringent recording requirements. The most important factor with respect to the study of the brainnetome is that the most advanced EEG systems can detect signals with a sampling rate faster than 1 kHz. Equipped with this resolution, an EEG system can record subtle and swift changes in neuronal activity, an important advantage, since some activities, such as epileptiform spike waves, may occur in less than 50 ms. Hence, EEG can provide precise measurements of brain activity.

MEG is another non-invasive technique for the measurement of brain activity, but it records the magnetic fields produced by naturally occurring electrical currents from the brain using arrays of superconducting quantum interference devices. MEG data reflect the magnetic field flux directly produced by intra-cellular current flow in the asymmetrically organized dendritic tree arborizations that are principally found in the isocortical layers of the gray matter (Lewine and Orrison 1995b). MEG has a temporal resolution comparable to EEG. But because the different structures of the head (brain, cerebrospinal fluid, skull and scalp) influence the magnetic fields less than the volume current flow that affects EEG, MEG has a higher localization accuracy than EEG. Additionally, MEG is reference free, so localizing sources at a given level of precision is more easily done with MEG data than it is with EEG data (Bastiaansen et al. 2001; Kristeva-Feige et al. 1997; Scherg 1992).

Not only does their temporal resolution make EEG/MEG suitable for a brainnetome analysis, but also EEG and MEG systems can simultaneously provide signals in multiple channels. For example, EEG can support up to 256 electrodes to record signals at different sites on the subject’s scalp. Because the hypothesis about brain activity has progressed from functional specification to functional integration, a time series of simultaneous recordings in several regions of the brain is needed to investigate the integration of the various brain areas contained in these data.

In summary, both their superb temporal resolution and multiple-channel recording ability qualify EEG and MEG for the performance of brainnetome analysis. This is especially true in the context of source estimation or connectivity analyses, both of which require a high degree of temporal resolution (Darvas et al. 2004; Schoffelen and Gross 2009).

Graph theory

The neural network can be represented as a complex network due to the involvement of multiple brain regions and their multi-scale organization (Başar 2011; Bassett and Gazzaniga 2011). Its network representation inevitably demands graph theory analysis to investigate the properties of the brainnetome, such as small-worldness and scale invariance (Sporns et al. 2000). Studies of brain small-worldness suggested that the brain may be represented simultaneously by both a highly segregated and a highly integrated networks (Bullmore and Sporns 2009). This is in line with the phenomenon of metastability of brain activity demonstrated earlier (for the review, refer to the work by Fingelkurts (2004)). Metastability represents brain functioning where the individual parts of the brain exhibit tendencies to function autonomously at the same time as they exhibit tendencies for coordinated activity (Kelso 1995).

Graph theory originated three 100 years ago from physics, but has advanced significantly over the last century because of studies of social networks, for which the critical properties of specific networks were defined. In graph theory, a network is composed of nodes and the edges between the nodes. We will introduce methods for defining nodes and edges for the EEG/MEG brainnetome in detail in the next section. First, it is useful to enumerate the properties of graph theory that characterize a network. Graph topology can be quantitatively represented by a variety of measures. Among them are three elementary measures of brainnetome analysis. Node degree is the number of connections that link the node to the rest of the network. This reflects the relationship of a node to the rest of the network—the higher the node degree, the closer the relationship. The clustering coefficient is the proportion of the connections between nearest neighbors relative to the maximum possible number of connections. This coefficient can be used to detect a hub node, which directly associates with more nodes than other types of nodes. Path length is the minimal number of edges that must be traveled from one node to another (Bullmore and Sporns 2009). The path length reflects the efficiency of information communication in a network.

The construction of EEG/MEG networks

The construction of an EEG/MEG network first requires the definitions of nodes and edges. The sensor space where multi-channel EEG and MEG record signals and the source space where brain activity actually occurs are two separate spaces, in which we can define nodes and edges. Thus, an EEG/MEG network can be constructed within either or both of them.

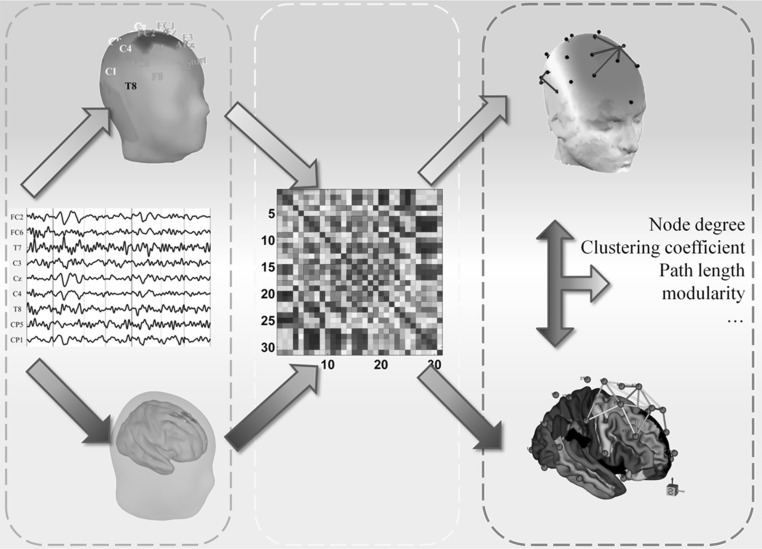
Although a network may be rendered in either of these two different spaces, the approaches to constructing a network consist of three similar steps (Lei et al. 2011a). As illustrated in the green dashed box in Fig. 1, the first step is to compute a measure of the associations between pairs of nodes (channels in the sensor space are indicated in the upper light blue part of the figure, and regions of interest in the source space are indicated in the lower light blue part of the figure)(Bonita et al. 2013). The correlation coefficient is the most frequently used metric for evaluating these associations, and we will use it in our example here. Subsequently, these coefficients are organized into a correlation matrix (the strength of each correlation is indicated by a black–red–yellow–blue scale). Next, a threshold is applied, and all correlations above the threshold are considered to be edges connecting nodes. Thus, the correlation matrix is converted to a binary adjacency matrix, i.e., an unweighted graph. Finally, the graph is analyzed using a number of graph metrics, including the clustering coefficient, modularity and efficiency.

Fig. 1.

Schematic illustration of a brainnetome analysis applied to multi-channel recordings of brain activity (EEG or MEG). The lower light red region indicates the steps in the source space, and the upper light blue region indicates those in the sensor space. The left green dashed box is the first step, the definition of nodes; the middle yellow dashed box is the second step, the acquisition of the adjacency matrix; and the right red dashed box is the third step, the calculation of the metrics for the graph. (Color figure online)

For a scalp EEG measurement, the potential in each channel is recorded with respect to a reference, i.e., an arbitrarily chosen “zero level”. The reference may have an effect on the network. A reference standardization method can be adopted to overcome this limitation (Qin et al. 2010; Yao 2001). The method proposed by Yao (2001) bypassed the selection of an arbitrary reference by first computing which signals had an equivalent probability of being the source signal from the scalp EEG on a virtual cortex. This step was not affected by the choice of a reference. Then signals obtained in each channel from the person’s scalp were reconstructed from these sources. Ultimately, these signals were free from the effects of an arbitrary reference.

Definition of nodes

The first step in initiating network analysis is to define its nodes. Depending on the space in which the network is constructed, nodes can be defined either by channels in the sensor space or by regions of interest in the source space. Setting each channel as a node is the more direct method. However, some evidence indicates that estimating causality using the cortical activity in the source space provides a more accurate estimation of brain-associated activity (Ewald et al. 2012; Michel et al. 2004). In addition, constructing a network in either space shares similar steps, as mentioned above, but the network in the source space is more complex than that in the sensor space. Therefore, we will present additional details for the construction of a source-space network.

The construction of a source-space network includes three crucial elements: the source reconstruction model, source estimation methods and spatial a priori assumptions. To reconstruct signals within the source space, a model must be chosen in advance. Hence, a source reconstruction model will be introduced first; an estimation method will then be presented to obtain a solution for the model. Finally, we will introduce spatial a priori information, which has recently been included to improve source estimation.

Source reconstruction model

Scalp EEG is the summation of the synchronous activity of large assemblies of neurons across the cortex, and the summation of each channel is weighted differently, even from the same source, owing to the volume conduction effect. Constructing a network based on scalp EEG directly suffers from this effect. Therefore, building a network in the source space, where brain activity actually occurs, is more reasonable. Translating the measurements of channels into time series of sources requires source reconstruction, a typical inverse problem in EEG source analysis (Grech et al. 2008). The problem can be modeled as follows: 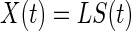, where 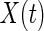denotes the vector of the measurements of the channels; L is the lead field matrix; and 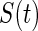denotes the vector of the source activity. Source reconstruction localizes the neuronal signal generator in the brain. One of the most crucial aspects of source reconstruction is the selection of source models. In current practice, the equivalent current dipole (He and Musha 1992) or the distributed (dipole or charge) source model (Dale and Sereno 1993) is often applied in this field. The equivalent current dipole model estimates the localization and orientation of a few dipoles that could be used to create the best possible scalp map to match the representation of the EEG electrodes. The reconstructed time-course can be further employed to build the brainnetome. In contrast, the distributed source model estimates the activity of every dipole distributed across the cortex. This model is suitable for non-local sources but requires assumptions to solve an ill-posed problem, as the number of unknown parameters is significantly greater than that of the measurements. Both the equivalent dipole model and the distributed source model have their own advantages. Recently, we proposed an integration of these models: the Gaussian source model (GSM) (Lei et al. 2009). The GSM can flexibly imitate the equivalent dipole and distributed source models by adopting the extreme supporting range parameter of the Gaussian function. For the distributed source model, because the brain is divided into a large number of sub-regions, each sub-region can be employed as a node of a network.

Source estimation methods

Constructing a network using the distributed source model involves source reconstruction based on the forward theory of electrical fields of the brain (Yao 2000). With the Laplacian weighted minimum l₂-norm constrained, low resolution electromagnetic tomography (LORETA) reconstructs brain electric activity at each point on a 3D grid of solution points (Pascual-Marqui et al. 1994). The l₂-norm can constrain the smoothness of a solution. The underlying assumption of LORETA is that neighboring grid points are more likely to have a similar orientation and activation strength compared to distant grid points. The weighted minimum norm solution can also be solved iteratively under the l₁-norm (Xu et al. 2007) and based on the distributed charge source model (Xu et al. 2008). The l₁-norm constrains the sparsity of a solution. After recomputing the surface signal into a cortical regional source time series, the functional connectivity between regions can be computed at each frequency band (Lehmann et al. 2012).

In addition to the above three-step network construction methods, alternative approaches for constructing networks in the source space have been proposed. The conventional three-step method can be represented by two equations: state and space. The state equation represents the cortical dynamics, while the space equation (a.k.a., the observation equation) describes the physics that correlates the cortical signals to the measured EEG. The cortical signals can be assumed to originate from known regions of the cortex, while the spatial distribution of the activity within each region is unknown. Hence, connectivity analysis of the cortex source based on scalp EEG/MEG can be modeled using a state-space function (Carmeli et al. 2005). This integrated approach, which estimates spatial distribution and temporal connectivity simultaneously, is less sensitive to noise than the three-step approach (Cheung et al. 2010). Recently, a l₀-norm based method provides a new window for viewing the scalp EEG (Xu et al. 2010). In fact, source reconstruction removes the effect of volume conduction on the network and the dependence on the reference (Yao 2001). Finally, the problem of EEG/MEG source localization can be cast as an optimization problem. Jiang et al. (2003) proposed a hybrid algorithm that combines a genetic algorithm (GA) and a local search strategy to solve the global optimization. The GA algorithm mimics the process of natural selection and can be used to generate useful, optimized solutions.

Spatial a priori assumptions

Although cost functions using l₂-norm, l₁-norm or both penalties improve the estimation of the source reconstruction, information from other neuroimaging modalities can provide further improvements. Previous studies used fMRI activity to constrain the spatial locations of EEG sources (Bledowski et al. 2006; Dale et al. 2000) or to initialize the dipole seeds (Auranen et al. 2009; Stancak et al. 2005). For example, the hemodynamic information provided by fMRI data could be taken into account when determining the weighted minimal norm estimator. By evaluating the partial directed coherence between regions of interest according to the Brodmann Atlas, a small-scale network can be constructed on the cortical surface (Astolfi et al. 2007b; Astolfi et al. 2009). When followed by graph analysis, this method can identify the functional connectivity pattern alternatively elicited by different tasks. Using this technique, Astolfi and colleagues compared the performance of various connectivity pattern estimators. They found that multivariate frequency domain methods, such as the directed transfer function (DTF), the direct DTF (dDTF) and the partial directed coherence (PDC), can all effectively estimate the functional connectivity patterns of cortical activity (Astolfi et al. 2007a).

Nevertheless, this a priori information produced undesirable effects when fMRI was considered as the “truth” with respect to spatial information (Dale et al. 2000). The relationship between EEG and fMRI has not been thoroughly evaluated (Gonzalez Andino et al. 2001). Thus, fMRI and biosignal (EEG/MEG) approaches should be used in a complementary rather than a redundant manner. A Bayesian framework is an easy way to combine these modalities, because it does not require a direct correspondence between modalities (Henson et al. 2010). This framework makes it possible to utilize multiple spatial priors from fMRI when constructing an EEG/MEG brainnetome. In our recently developed method, network-based source imaging (NESOI), measurements of intrinsic brain activity were combined with blood oxygenation level dependent (BOLD) fluctuation data to introduce the first model that constrained the spatial locations of EEG sources (Lei et al. 2011b). This method employs multiple fMRI functional coherent networks as source location priors. Improved estimation of the cortical activity could increase the accuracy of connectivity pattern estimates.

Definition of edges

Recently, scientists have reached a consensus that brain connectivity is a critical tool for understanding the organized behavior of cortical regions. Two main types of brain connectivity, functional and effective, are frequently utilized to construct the edges between nodes for EEG/MEG measurements. Functional connectivity can be evaluated via the temporal correlations between spatially remote neurophysiologic events (Fingelkurts et al. 2005; Friston et al. 1993; Güntekin and Başar 2010; Ghosh et al. 2008; Wilmer et al. 2010). Traditionally, coherence and correlation (Thatcher et al. 1986) have been the primary methods for assessing the degree of functional connectivity between brain regions. Several methods for calculating functional connectivity between cortical regions have been published: partial directed coherence (Baccala and Sameshima 2001), dynamic imaging of coherent sources (Gross et al. 2001), phase synchrony based on wavelet transform (Lachaux et al. 1999) and operational synchrony (Fingelkurts and Fingelkurts 2008). Effective connectivity, however, provides a direct insight into the causality between signals, which is the influence that one signal exerts over another (Friston et al. 1993; Kiebel et al. 2008). Valdes-Sosa et al. (2011) provided a seminal work about causality connectivity. Here, we focus on the synchronization likelihood (SL) and the Granger causality to introduce the two different kinds of connectivity in the brainnetome, as the two functional connectivity metrics are frequently used in either EEG/MEG or fMRI brainnetome in the functional network and causal network, respectively.

Synchronization likelihood

A popular method for assessing functional connectivity is to calculate the SL, which was defined by Stam and van Dijk (2002). Supposing that M channels record EEG signals for N samples, 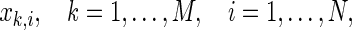then embedded vectors with a time delay can be represented as,

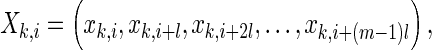1

where l is the delay and m is the dimension. At a given time point i of each channel k, a probability, 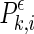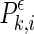, which measures the likelihood of vectors closer to one another than a distance ϵ, can be defined as,

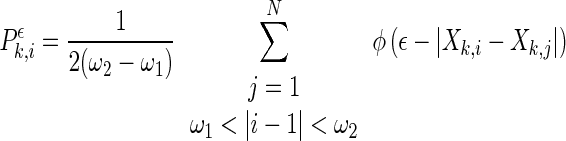2

Here, 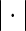is the Euclidian distance, 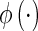is the unit step function 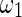and and 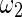are the widths of windows that can correct the autocorrelation effects and sharpen the time resolution of the synchronization measure, respectively, satisfying 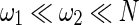. Given 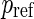, , 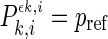it is possible to determine 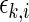. The number of channels, 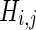, for each pair (i,j) within 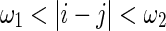is represented by the equation.

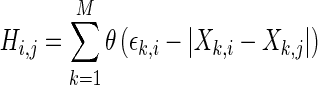3

Then, the SL 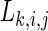for each channel k and each time pair (i,j) is

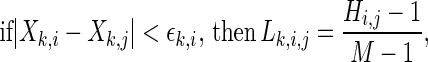4

5

After averaging over all the js, the SL becomes

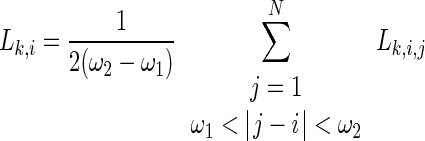6

The synchronization likelihood 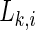evaluates the strength of the synchronization of the channel k with all the other M−1 channels at a time point i. 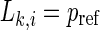means that all M time series are uncorrelated, and 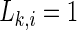corresponds to the maximal synchronization.

Granger causality

Effective connectivity is constructed by using the directed edges of the EEG network. One popular method is Granger causality (GC), which estimates the direct influences between nodes based on temporal information. Supposing two signals, S_i and S_j, a statistical interpretation of causality can be implemented in which S_i “Granger causes” S_j if knowing the past value of S_i can help predict S_j better than knowing the past value of S_j alone (Ding et al. 2006; Granger 1969). The standard implementation of GC is achieved via vector autoregressive (VAR) modeling, in which a set of time series are modeled as the weighted sums of past values. Let S(t) = [s₁(t), s₂(t),···,s_k(t)]^T be a k-dimensional random process defined in a segment of windowed time series data, where T stands for matrix transposition. Assuming the stationarity of the process S(t), 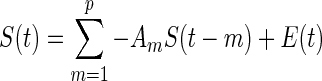, one can describe S(t) by a pth-order autoregressive process:

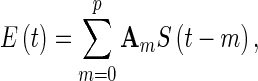7

where A₀is the identity matrix and A_m (m = 1, 2,…, p) are k × k coefficient matrices. E(t) is a k-dimensional, zero mean, uncorrelated noise vector. A_m matrices can be estimated using the Levinson-Wiggins-Robinson (LWR) algorithm (Haykin 2002). The covariance matrix of the noise (E(t)) is estimated by the Yule-Walker equations of the model. The multivariate Bayesian Information Criterion (BIC) is calculated to determine the VAR model order, p. Once A_m and the covariance matrix of the noise (E(t)) are estimated, the Granger causal influence from S₂ to S₁ can be inferred if knowing S₂ reduces the variance in the prediction error of S₁ when all other variables S₃ … S_n are also included in the regression model. The derivation of GC is not reviewed here; for details, please refer to the literature (Ding et al. 2006; Geweke 1984).

Frequency-domain method

Equation (7) is transformed to the frequency domain to investigate the spectral properties of the brainnetome:

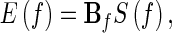8

where

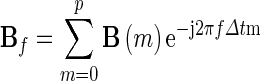9

Note that Δt is the temporal interval between two samples. Eq. (9) can further be rewritten as

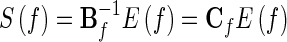10

The element C_f(i, j) represents the connection between the ith input and the jth output of the network. The DTF, which describes the causal influence of the ith waveform on the jth waveform, is defined as in Kaminski et al. (2001):

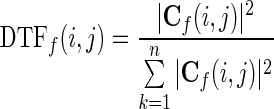11

Another estimator of direct causal relationships is the PDC, defined as in Baccala and Sameshima (2001):

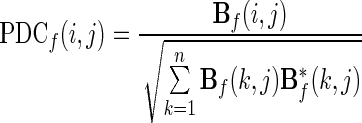12

The element 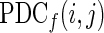describes the directional flow of information from the activity in the ith channel to the activity in jth channel.

Fusing the brainnetome of EEG/MEG with other modalities

The dynamic information provided by an EEG/MEG-derived network might allow for a precise definition of the timing and location of cognitive processes. For example, noninvasive dynamic imaging of the epileptic brain can enhance our understanding of seizure generation and propagation (Tyvaert et al. 2009). However, because individual EEG/MEG information provides limited results, advancing the EEG/MEG network requires the integration of EEG/MEG with other imaging modalities. The brainnetome can be utilized as a bridge to span the distinction between modalities and link them together.

Fusion of EEG and fMRI based on neural networks

To reconstruct the dynamics of large-scale neuronal systems, measurements with both high temporal and spatial resolution are essential. In addition, complementary neuro-electric and hemodynamic signals are helpful for explaining the complex relationships between different brain regions. For fMRI, the temporal dynamics of the components obtained by independent component analysis (ICA) have been utilized to examine causality between various brain networks (Demirci et al. 2009; Jafri et al. 2008). Unlike functional connectivity, which focuses upon the relationships between single nodes, functional network connectivity (FNC) is emerging as a powerful method for characterizing the relationships between distributed brain networks (Stevens et al. 2009). A straightforward extension of fMRI analysis, FNC also can be useful for analyzing the interaction between EEG components. The interactions between independent components (ICs) in each modality can be determined via Granger Causality Analysis. Based on the NESOI-estimated matching between the EEG and fMRI ICs, multimodal FNC (mFNC) facilitates the fusion of data into a large-scale brain network (Lei et al. 2011a; Lei et al. 2012). mFNC may help explain the complex relationships between distributed cerebral sites in the brain and possibly provide new insights into neurological and psychiatric disorders (Lei et al. 2011a). In addition to the fusion of fMRI and EEG/MEG functional signals, a bimodal system, called the Near infrared spectroscopy and electroencephalography (NEG) system, which is designed to be able to measure neuronal electrophysiological signals and the cerebral circular hemodynamic response simultaneously, is under development in the Brainnetome Center.

A systematic perspective for network integration

Although EEG and MEG data are not only generated by pyramidal cell activity, the activity of these cells appears to contribute a considerable portion of each signal. Moreover, because EEG has a high temporal resolution and provides recordings from multiple regions, EEG networks can be constructed from these abundant dynamic information. This combination of dynamic information with the involvement of pyramidal cells allows for a precise definition of the timing of a cognitive process. Although the relationship between postsynaptic potentials and other physiological information is unknown, network integration among modalities will provide valuable complementary information for understanding the brainnetome. Conventional approaches tend to examine converging evidence between EEG networks and other modalities. However, some neural processes are independent between modalities; that is, some types of brain networking may be visible in only one modality. Analysis of these components would be equally important for our understanding of various cognitive processes (Lei et al. 2010).

Applications of the EEG/MEG network

The EEG/MEG network has been employed in neuroscience research and in exploring the prognosis or pre-surgical brain mapping of neurological disorders. Here, we will introduce the applications of these networks to the brainnetome.

The EEG/MEG network in brain disorders

Simultaneous functional and effective networks derived from EEG/MEG data have been used to study neurological disorders (Başar 2011; Fingelkurts and Fingelkurts 2010), although conventional ERP analysis was also used in one study (Wang et al. 2013; Yener and Başar 2010). Its application to Alzheimer’s disease (AD) dates back to 1998 when Wada et al. (1998) employed EEG coherence to evaluate the functional correlation between patients and normal aging and found that the functional correlation was significantly reduced in AD patients. Babiloni et al. (2009) examined abnormalities in EEG directionality in mild cognitive impairment (MCI) and AD based on the effective connectivity of the fronto-parietal network. The loss of gamma band synchronization in AD patients was detected from a MEG network analysis by Stam et al. (2002).

Peled et al. (2001) used functional connectivity to detect the disconnection syndrome in schizophrenic patients and demonstrated that patients failed to activate networks in the fronto-temporal regions. Effective connectivity has also been utilized to analyze schizophrenia. A study by Winterer et al. (2003) showed a reduction in fronto-temporal coherence in schizophrenia patients. In addition researchers have performed a number of studies related to epilepsy. For example, Lemieux et al. (2011) reviewed the current publications related to the characterization of the propagation of epileptic activity using regional EEG networks and suggested the full characterization of epileptic networks using neuroimaging data.

The EEG/MEG network in cognition

Depending on individually applied strategies, complex mental processes such as mental arithmetic, art perception, and mental rotation are discussed to both share widespread neural network resources, but also recruit distinct neural network-parts (Fehr 2013; Fingelkurts and Fingelkurts 2010). Specificities in the respective functional network coupling as, for example, reported for experts as compared to non-experts in a particular domain (Bhattacharya and Petsche 2002), provide important insights in how the respective mental processes and involved mental sub-processes are organized at the neural level (Başar 2011; Fehr 2013). Based on these results, these researchers suggested that measuring the couplings between different brain regions might provide a good measure of the cognition state. Since then, evidence has accumulated that higher cognitive functions require functional interactions, or connectivity, between multiple, distinct neural networks (Stam and Reijneveld 2007). Functional networks revealed by a graph analysis of EEG or MEG data represent a physiological substrate for high-speed processing of segregated and distributed information.

In the resting state, the ‘basic’ brainnetome gives rise to constantly changing, weakly synchronized networks. This process of constantly creating and dissolving functional networks is called ‘fragile binding’ and is thought to underlie spontaneous information processing. The optimal normal brain dynamics are thought to be near the phase transition between low and high levels of synchronization (Stam and Reijneveld 2007). Another study, using a method to extract cerebral networks from the EEG data described previously by Stam (2004), showed that (un-weighted, undirected) networks produced more small-world characteristics during all sleep stages compared to the awake state and that these features were even more pronounced during special cyclic alternating pattern sleep phases (Ferri et al. 2007). Thus, network features can change during a cognitive task, as well as under the influence of sleep.

Future research directions

Methodological issues

Converting a correlation matrix into a binary matrix necessitates the selection of a threshold. However, the proper method for determining the appropriate threshold is not yet known. One alternative may be the direct analysis of weighted graphs, although only a few measures are currently available (Onnela et al. 2007). Studying the entire range of thresholds and test graph theoretical properties is typically performed in many studies. Another problem is that some nodes may become disconnected from the whole network when converting a binary matrix into a graph. This leads to difficulties in estimating clustering coefficients and path lengths.

Conceptual issues

Future studies are justified for some conceptual issues regarding the use of EEG and MEG to elucidate the brainnetome. First, verifying which EEG (or MEG) network properties are the best predictors of cognitive disturbances is difficult. A popularly accepted, but not entirely supported, hypothesis is that a “diseased” network is far from the optimal small-world network and that combining local segregation with global integration for optimal cognition is difficult in the disease state. Second, how to describe human brain development with respect to network properties is unclear. Using a large genetic information sample of twin families, the synchronization likelihood of the alpha frequency appears to be highly heritable (Posthuma et al. 2005).

Relationships between brain rhythms

The brain rhythms of different frequency bands have been reported to interact with each other in several contexts, suggesting the possibility that different frequency oscillations might carry different dimensions of the integration process (Varela et al. 2001). In decision-making, the amplitudes of high-frequency oscillations were dynamically modulated by the phase of concurrent theta-band oscillations (Tort et al. 2008). One important conclusion of a cross-frequency coupling analysis is that the beta rhythm is robust for long-distance synchrony, whereas gamma rhythms tend to be more stable for local patches of synchrony (Foster and Parvizi 2012). Cross-frequency coupling may be a pervasive mechanism used by the brain to perform the network-level dynamic computations that underlie brain integration. Furthermore, the extension of the brainnetome will consider the cross-talk between frequencies and develop more novel methods of analysis.

Conclusions

Brainnetome analysis indicates that the brain’s functions do not operate solely within specific regions. Concentrating on individual brain regions cannot possibly reveal the operations underlying a person’s brain function nor clarify the abnormal mechanisms of specific neuropsychiatric diseases. The consensus that functional integration is the main feature of mental processing stimulated the evolution of neuroimaging modalities in order to capture dynamic information across individual brains. Among these modalities, EEG and MEG were designed to measure the electromagnetic signals generated by neuronal activity at a high level of temporal resolution and with multiple-region recording.

Because of these properties, as well as because they are free of radiation and easy to set up, EEG and MEG are generally accepted in both neuroscience research and clinical applications as a source of data for performing brainnetome analyses. Networks derived from EEG/MEG data can be built in either sensor space or source space, but those formed using source space data may provide more accurate information about interacting sources than those formed using sensor space data. Both functional and effective connectivity can be used to define edges between nodes. The former reflects the coherence or correlation among nodes, while the latter represents the causal relationship of one node over another. The properties of a brainnetome analysis can be related to any of a number of factors that are important in either neuroscience research or clinical applications. For example, these properties may be able to be utilized to indicate differing levels of cognition or to reflect the conditions present in a neurological disease. Although EEG and MEG have been applied to the analysis of the brainnetome, methodological and conceptual issues as well as the relationship with other applications should be investigated further.