Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 7;4:4281. doi: 10.1038/srep04281

Light induced conch-shaped relief in an azo-polymer film

Mizuki Watabe 1, Guzhaliayi Juman 1, Katsuhiko Miyamoto 1, Takashige Omatsu 1,2,a
PMCID: PMC3945491  PMID: 24603295

Abstract

We have discovered that a novel chiral structured surface relief (termed ‘conch'-shaped surface relief) with a height of over 1 μm can be formed in an azo-polymer film merely by employing circularly polarized optical vortex irradiation with a total angular momentum of j = ±2. The temporal evolution of the conch-shaped surface relief in the azo-polymer film was also observed. The results provide physical insight into how the angular momentum of light is transferred to a material through mass transport by cis-trans photo-isomerization. Such conch-shaped surface reliefs with chirality, in which functional chemical composites can be doped, enable new applications, such as planar chiral metamaterials, plasmonic holograms, and identification of chiral chemical composites.

Surface relief holograms1,2,3 on azo-polymer films have been widely investigated through mass transport owing to a driving force based on an optical gradient force, anisotropic photo-fluidity, and cis-trans photo-isomerization4,5,6. They allow for unique optical devices, such as active waveguides7 and photonic circuits, by the doping of functional chemical composites, such as laser dyes and metal (or semiconductor, magnetic) nano-particles into the films.

In general, the mass transport driving force acts to direct the azo-polymer from a bright fringe toward a dark fringe along the polarization direction of the light. Thus, a spiral surface relief formation in the azo-polymer film is mostly inhibited by the irradiation of linearly polarized light.

An optical vortex, i.e. light with a helical wavefront due to an azimuthal phase singularity, exp(imϕ) (where m is an integer known as the topological charge), has been widely studied in a variety of fields, such as optical trapping and guiding8,9,10, optical telecommunications11, and a super resolution microscope12,13, because of its unique characteristics, such as its annular intensity profile and orbital angular momentum, 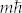Inline graphic14,15,16,17.

Recently, Ambrosio et.al. demonstrated spiral surface relief (termed “spiral relief” in their work) formation produced through linearly polarized higher-order optical vortex irradiation18. Tightly focused higher-order optical vortices can create a spiral surface relief with a shallow depth (10 ~ 20 nm) through slight mass-transport along an azimuthal direction owing to interference between longitudinal and transverse optical fields. However, there are still no reports on a single-arm chiral surface relief with depth and height on the micro-scale formed in azo polymer films, so far.

Circularly polarized light with a helical electric field exhibits spin angular momentum, 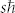Inline graphic. Thus, the circularly polarized optical vortex has a total angular momentum (the sum vector of the orbital and spin angular momenta), 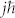Inline graphic, associated with its helicities of both the wavefront and the polarization19,20,21. These angular momenta of light are evidenced by the orbital and spinning motions of trapped particles in optical tweezers.

Recently, together with another co-worker, we first demonstrated the formation of chiral metal nanostructures by irradiation with circularly polarized optical vortex pulses22,23,24,25. This phenomenon originated in the orbital angular momentum of the optical vortex being transferred to the melted metal upon irradiation, forcing it to revolve around the axial core of the optical vortex. The spin angular momentum of the circularly polarized optical vortex then reinforced the chiral structure of the thus created nanoneedle.

In this paper, we present the first demonstration, to the best of our knowledge, of a single-arm chiral surface relief (we have termed this a conch-shaped surface relief) with a height of over 1 μm formed in an azo-polymer film using a lower-order optical vortex with a small dark core, utilizing the spin angular momentum associated with the circular polarization. We also address the temporal evolution of the conch-shaped surface relief in the azo-polymer film. Such conch-shaped surface reliefs have the potential to be used to create new optical devices, including planar chiral metamaterials26,27 and plasmonic holograms28. They also potentially enable identification of the chirality of chemical composites at the nanoscale29,30,31.

Results

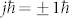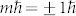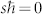Figure 1 shows an atomic force microscope (AFM; SHIMADZU, SPM-9700) image of a surface relief formed by irradiation with a linearly polarized optical vortex beam having a total angular momentum, Inline graphic (orbital angular momentum, Inline graphic and spin angular momentum, Inline graphic).

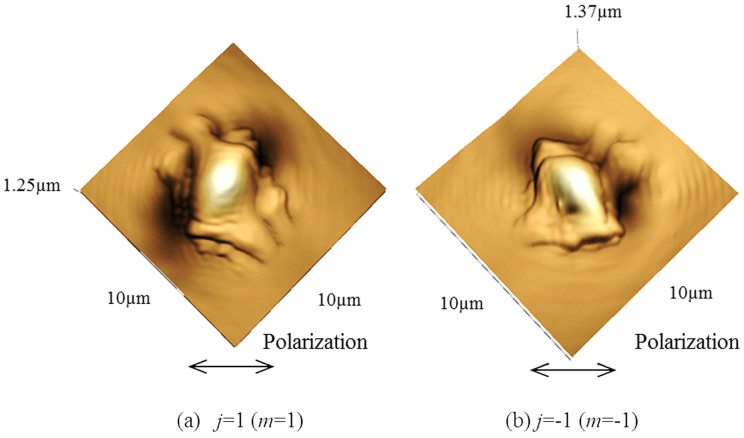
Figure 1. (a), (b) AFM images of the surface relief formed by optical vortex irradiation with j = ±1.

Figure 1

Open in a new tab

Spiral surface relief formation with a shallow depth obtained in a previous study18 was ascribed to interference between the longitudinal and transverse optical fields created by tight focusing with a high numerical aperture (NA = 1.3) objective lens. In our present experiments, the numerical aperture of the objective lens was too low to sufficiently produce a longitudinal optical field. Thus, the mass transport driving force acts to direct the azo-polymer toward the dark core along the polarization direction of the light, thereby creating only crescent surface reliefs in the azo-polymer film.

To suppress the polarization dependence of the mass transport driving force, we introduced a quarter-wave plate placed in the optical path so as to convert the linearly polarized optical vortex to a circularly polarized optical vortex. The sign of the orbital angular momentum was then the same (or opposite) to that of the spin angular momentum. The resulting total angular momentum of the optical vortex was characterized by j = ±2 (or j = 0). To reverse the sign of j, the spiral phase plate and the quarter-wave plate were also inverted. The vortex beam was focused into a ϕ8-μm annular spot on the azo-polymer film using an objective lens (NA ~ 0.65) system, and its power was measured to be approximately 600 μW. The corresponding intensity of the focused vortex beam was estimated to be ~1.2 kW/cm2. The morphology of the azo-polymer surface during exposure of the optical vortex beam was observed by a computer-based digital CCD camera.

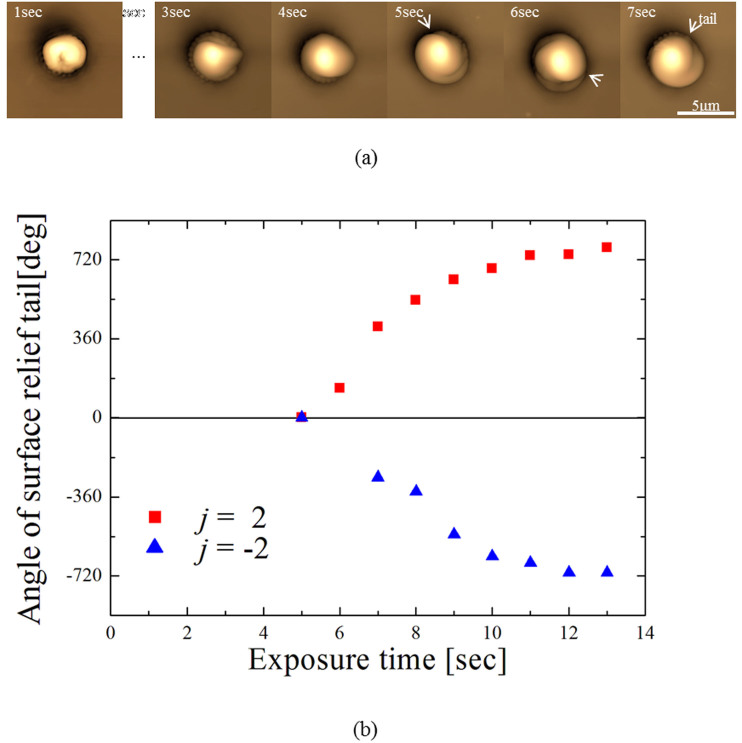
As shown in Fig. 2, in the case of j = +2, a surface relief with a clockwise-arm chiral structure (clockwise conch) was formed within an irradiation time of 5 seconds. The exposure energy density required for the conch-relief formation was ~6 kJ/cm2, which is comparable with the energy density (~18 kJ/cm2; power, ~5 μW; spot size, ~ϕ3.2 μm; exposure time, ~90 seconds) required for spiral relief formation using the focused vortex beam reported in the previous publication18.

Figure 2.

Figure 2

Open in a new tab

(a) Temporal evolution of the surface relief with a clockwise-arm chiral structure formed by circularly polarized optical vortex irradiation with j = 2. (b) Temporal dynamics of chiral surface reliefs formed by circularly polarized optical vortex irradiation with j = ±2.

Subsequently, the relief revolved axially in a clockwise direction. The initial rotation speed of the relief, defined as the time required for the relief tail to make one revolution, was estimated to be ~2 sec/cycle. The rotation of the surface relief was damped within several seconds, so as to complete the relief formation. Figures 3 (a) and (b) show AFM images of conch-shaped reliefs formed by optical vortex irradiation.

Figure 3.

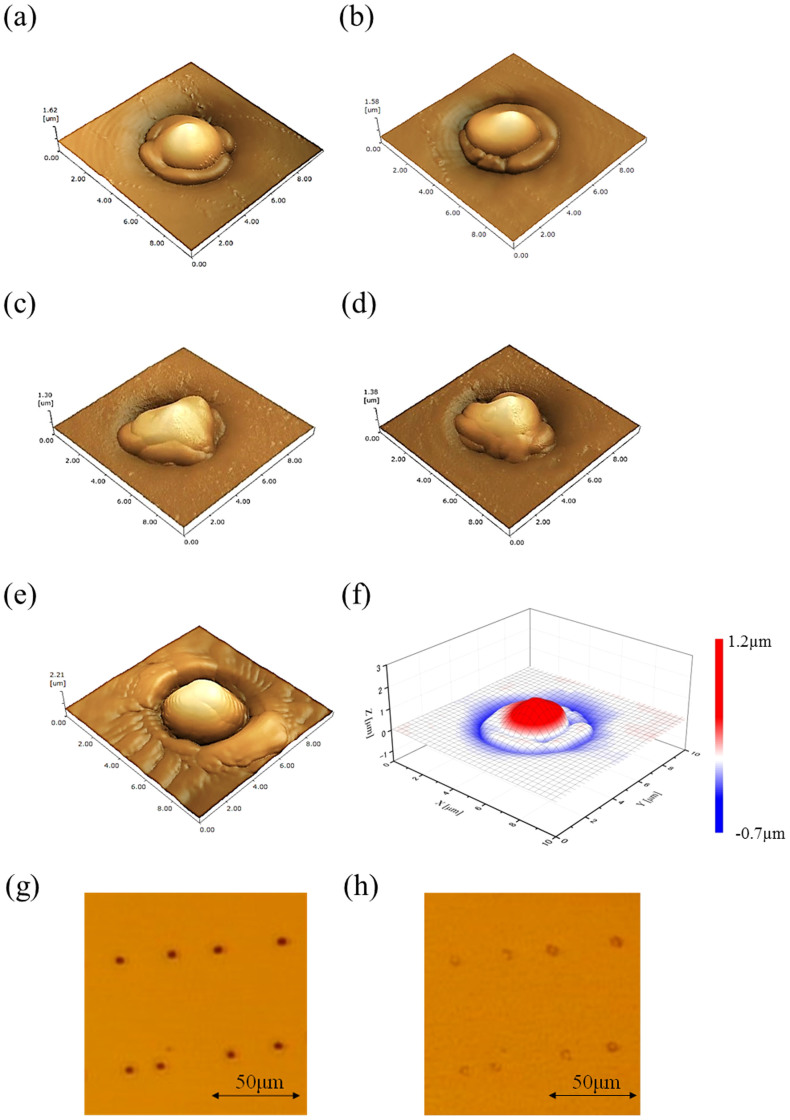
Figure 3

Open in a new tab

(a), (b) AFM images of surface reliefs formed by optical vortex irradiation with j = 2 (m = 1, s = 1) and j = −2 (m = −1, s = −1) respectively. (c), (d) AFM images of surface reliefs formed by optical vortex irradiation with j = 0 (m = 1, s = −1) and j = 0 (m = −1, s = 1) respectively. (e) AFM image of surface relief formed by optical vortex irradiation with j = 7 (m = 6, s = 1). (f) In the conch-shaped relief, the dump (hollow) is shown in red (blue). The volume of the red region was within 0.001 μm3 of that of the blue region. (g) Microscope image of surface relief before uniform green laser irradiation. (h) Microscope image of surface relief after uniform green laser irradiation.

When the sign of j was inverted, a counter-clockwise conch-shaped relief was also completed, and it revolved axially in the counter-clockwise direction. The height and diameter of the formed relief were measured to be 1.3 μm and 4.5 μm, respectively. The tip curvature was also measured to be ~0.5 μm.

In contrast, the conch-shaped relief was not formed when using optical vortex irradiation with a total angular momentum j = 0 (m = ±1, s = ∓1) (Fig. 3(c), (d)). When the higher-order optical vortices (m = 6) with larger dark cores were used, chiral conch-shaped relief formation was similarly prevented despite the spin angular momentum (Fig. 3(e)). A resulting non-chiral bump with a height of 1 ~ 2 μm was formed. These results indicate that the formation of the conch-shaped relief requires circularly polarized lower-order vortices with non-zero total angular momentum. A resistance force, such as viscosity, might force the azo-polymer to be confined within the narrow outer regions of the higher-order optical vortex, and thus preventing its orbital motion. The low light intensity due to the larger inner core of the optical vortex might also impact the orbital motion of the azo-polymer.

To fully understand the reason why higher-order vortices cannot create chiral conch-shaped reliefs, further investigation is needed.

Discussion

Mass-transport owing to the photo-isomerization occurs at a temperature below the glass transition temperature of the polymer, meaning that the polymer volume before and after the relief formation remains unchanged32. In the conch-shaped relief, the volume of the dump was within 0.001 μm3 of that of the hollow (Fig. 3 (f)), thus evidencing that the mass transport of the azo-polymer from the hollow to the dump preserved the polymer volume during relief formation. In addition, the conch-shaped relief was erased by irradiation with a spatially uniform green laser (0.36 W/cm2) for an exposure time of 50 minutes (Fig. 3 (g), (h)). These results indicate that it is not heat-induced effects (melting, expansions, ablation etc.), but rather photo-isomerization that predominantly induces conch-shaped relief formation.

The optical intensity profile |um(r)|2 of the optical vortex with orbital angular momentum, m, and spin angular momentum, s, is given by

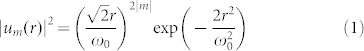graphic file with name srep04281-m1.jpg

where r is the radial coordinate in cylindrical coordinates and ω0 is the beam waist. The spatial distribution of the total angular momentum density, Jm,s(r), is then written as

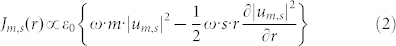graphic file with name srep04281-m2.jpg

where ε0 is the dielectric constant of a vacuum, and ω is the lasing frequency of the optical vortex.

Under the assumption that the spatial distribution of cis isomers created by photo-isomerization is determined by the optical intensity profile, we investigated the spatial overlap, ηm,s, between the total angular momentum density, Jm,s(r), and the optical intensity profile, |um(r)|2, to evaluate the efficiency of the angular momentum transfer from the optical field to the cis isomers. Here, ηj( = m + s) is defined as,

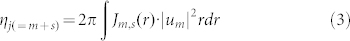graphic file with name srep04281-m3.jpg

By substituting m = 1 into Eqs. (1)–(3), the general relationship of the angular momentum transfer ratio, r(s) (defined as ηj = 1 + s/ηj = 0) = 2 + s, is established. Thus, the angular momentum ratio r(1)( = ηj = 2/ηj = 0) is estimated to be 3. As shown in Fig. 4, in the case of j = 2, the angular momentum of the optical vortex appears within the optical field, and is transferred efficiently to the cis (soft) isomers so as to revolve and form a chiral relief. In contrast, when j = 0, the angular momentum is localized near the dark core of the optical vortex, where the azo-polymer is mostly trans (solid). Thus, conch-shaped relief formation originating from angular momentum transfer is prevented.

Figure 4.

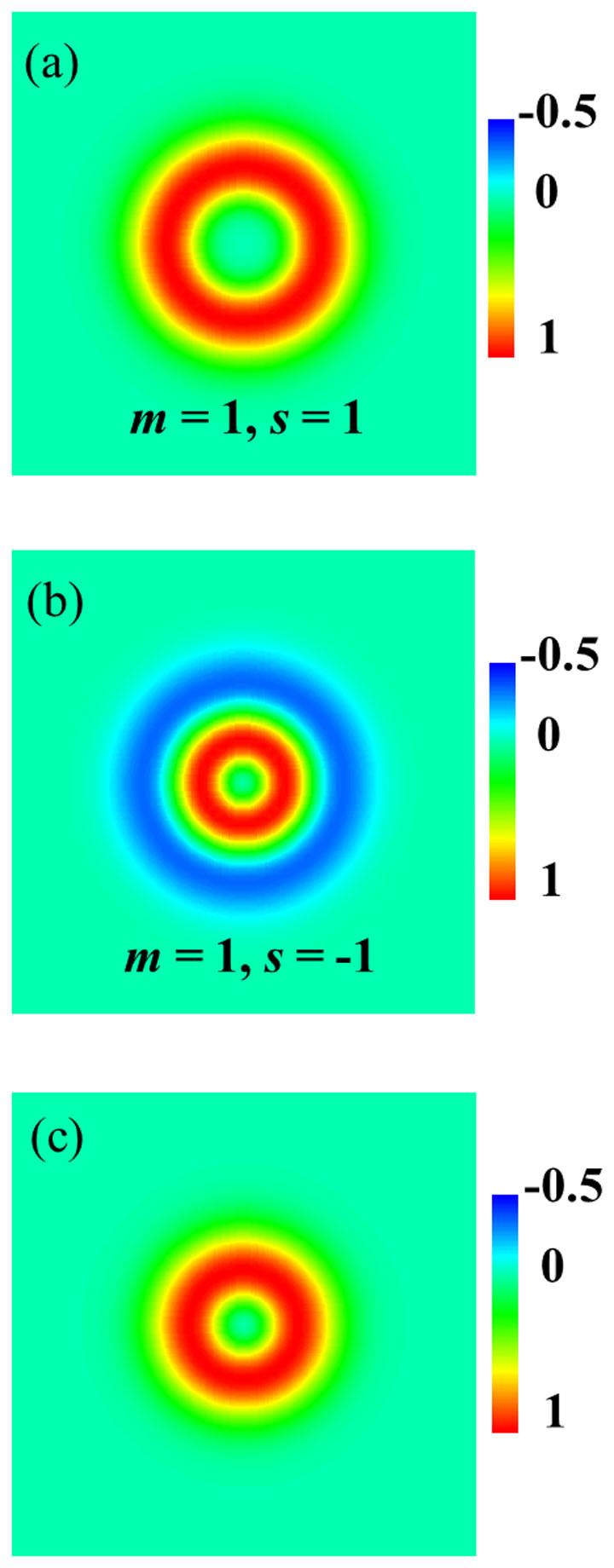
Figure 4

Open in a new tab

Simulated total angular momentum density of the circularly polarized optical vortex with (a) j = 2 (m = 1, s = 1) and (b) j = 0 (m = 1, s = −1). (c) Spatial intensity profile of the circularly polarized optical vortex.

These experimental results suggest the following mechanism. Photo-isomerization of the azo-polymer occurs as a result of the optical vortex irradiation. Subsequently, the resulting cis (soft) azo-polymer receives the orbital angular momentum of the optical vortex with the help of the spin angular momentum associated with the circular polarization, revolving in a clockwise (or counter-clockwise) direction. Following this, the cis (soft) azo-polymer is directed toward the dark core of the optical vortex by the mass transport driving force. The azo-polymer then turns back from cis (soft) to trans (hard) so as to form the conch-shaped structure.

In conclusion, we have achieved the first demonstration of conch-shaped chiral surface relief formation with a height of >1 μm formed in an azo-polymer film by using a circularly polarized optical vortex with a total angular momentum 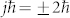Inline graphic. The formation of the conch-shaped surface relief requires circularly polarized optical vortices with non-zero total momentum.

We also directly observed that the cis (soft) azo-polymer produced by photo-isomerization receives the orbital angular momentum of the optical vortex, revolving in a clockwise (or counter-clockwise) direction, so as to form a conch-shaped surface relief. The chirality (spiral direction) of the conch-shaped surface relief can be controlled by merely varying the sign of the total angular momentum, 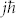Inline graphic, of the optical vortex.

These phenomena mainly originate because the orbital angular momentum of the optical vortex with the help of the spin angular momentum forces organic materials, such as the azo-polymer, to form chiral nano-structures.

Azo-polymers containing impurities, such as functional chemical composites (e.g., laser dyes) and metal (or semiconductor, magnetic) nanoparticles, can potentially be used to create unique optical devices such as planar chiral photonic devices as well as high-dimensional and hierarchic structures. In addition, they can also be covered with a thin metal film through a sputtering process to serve as chiral plasmonic devices and metamaterials, such as plasmonic holograms. They will also enable us to selectively identify chiral chemical composites.

Methods

The spin-coated azo-polymer film (mostly the trans isomer) used in this study was formed from a Poly-Orange Tom-1(POT)33 with the absorption band in the wavelength range of 300–550 nm, and its thickness was measured to be ~4 μm. The azo-polymer exhibits a photo-isomerization behavior upon green laser irradiation.

A continuous-wave frequency-doubled Nd:YVO4 laser with a wavelength of 532 nm was used, and its output was converted to be a linearly polarized first-order optical vortex (m = 1) with an annular intensity profile by a polymer spiral phase plate (RPC photonics, VPP-1c) providing an azimuthal 2π phase shift34. To generate a higher-order optical vortex with a topological charge, m, of 6, a computer-generated hologram displayed on a spatial light modulator (Hamamatsu photonics, X10468-03) was used. With this system, the mode conversion efficiency from the Gaussian output to the vortex output was measured to be ~50%. All experiments were performed with an exposure time of 12 seconds at room temperature and atmosphere.

Author Contributions

T.O. planed and organized the project. He also conducted the experiments and analysis. M.W., G.J. and K.M. performed all experiments. M.W. and T.O. wrote the main manuscript text. G.J. and K.M. prepared figures 1–4. All authors reviewed the manuscript.

Acknowledgments

The authors acknowledge financial support from the Japan Science and Technology Agency, and a Grant-in-Aid for Scientific Research (No. 24360022) from the Japan Society for the Promotion of Science.

References

  1. Viswanathan N. K. et al. Surface Relief Structures on Azo Polymer Films. J. Mat. Chem. 9, 1941–1955 (1999). [Google Scholar]
  2. Barrett C. J., Natansohn A. L. & Rochon P. L. Mechanism of Optically Inscribed High-Efficiency Diffraction Gratings in Azo Polymer Films. J. Phys. Chem. 100, 8836–8842 (1996). [Google Scholar]
  3. Natansohn A. & Rochon P. Photoinduced Motions in Azo-Containing Polymers. Chem. Rev. 102, 4139–4175 (2002). [DOI] [PubMed] [Google Scholar]
  4. Rohrbach A. & Stelzer E. H. K. Trapping Forces, Force Constants, and Potential Depths for Dielectric Spheres in the Presence of Spherical Aberrations. Appl. Opt. 41, 2494–2507 (2002). [DOI] [PubMed] [Google Scholar]
  5. Harada Y. & Asakura T. Radiation Forces on a Dielectric Sphere in the Rayleigh Scattering Regime. Opt. Commun. 124, 529–541 (1996). [Google Scholar]
  6. Ishitobi H., Tanabe M., Sekkat Z. & Kawata S. The Anisotropic Nanomovement of Azo-Polymers. Opt. Express 15, 652–659 (2007). [DOI] [PubMed] [Google Scholar]
  7. Hirose T. et al. Azo-Benzene Polymer Thin-Film Laser Amplifier with Grating Couplers Based on Light-Induced Relief Hologram. Opt. Commun. 228, 279–283 (2003). [Google Scholar]
  8. Gahagan K. T. & Swartzlander Jr G. A. Optical Vortex Trapping of Particles. Opt. Lett. 21, 827–829 (1996). [DOI] [PubMed] [Google Scholar]
  9. Simpson N. B., Dholakia K., Allen L. & Padgett M. J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Letters 22, 52–54 (1997). [DOI] [PubMed] [Google Scholar]
  10. Paterson L. et al. Controlled Rotation of Optically Trapped Microscopic Particles. Science 292, 912–914 (2001). [DOI] [PubMed] [Google Scholar]
  11. Bozinovic N. et al. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 340, 1545–1548 (2013). [DOI] [PubMed] [Google Scholar]
  12. Bretschneider S., Eggeling C. & Hell S. W. “Photoswitching microscopy with standard fluorophores.”. Phys. Rev. Lett. 98, 218103 (2007). [DOI] [PubMed] [Google Scholar]
  13. Watanabe T. et al. Formation of a Doughnut Laser Beam for Super-Resolving Microscopy using a Phase Spatial Light Modulator. Opt. Eng. 43, 1136–1143 (2004). [Google Scholar]
  14. Allen L., Beijersbergen M. W., Spreeuw R. J. C. & Woerdman J. P. Orbital angular momentum of light and the transformation of laguerre-gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992). [DOI] [PubMed] [Google Scholar]
  15. Padgett M., Courtial J. & Allen L. Light's orbital angular momentum. Phys. Today 57, 35–40 (2004). [Google Scholar]
  16. Lavery M. P. J., Speirits F. C., Barnett S. M. & Padgett M. J. Detection of a spinning object using light's orbital angular momentum. Science 341, 537–540 (2013). [DOI] [PubMed] [Google Scholar]
  17. Yao A. M. & Padgett M. J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon. 3, 161–204 (2011). [Google Scholar]
  18. Ambrosio A. et al. Light-Induced Spiral Mass Transport in Azo-Polymer Films Under Vortex-Beam Illumination. Nature Commun. 3, 989 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. O'Neil A. T., MacVicar I., Allen L. & Padgett M. J. Intrinsic and extrinsic nature of the orbital angular momentum of a light beam. Phys. Rev. Lett. 88, 536011–536014 (2002). [DOI] [PubMed] [Google Scholar]
  20. Zhan Q. Properties of circularly polarized vortex beams. Opt. Lett. 31, 867–869 (2006). [DOI] [PubMed] [Google Scholar]
  21. Zhao Y. et al. Spin-to-Orbital Angular Momentum Conversion in a Strongly Focused Optical Beam. Phys. Rev. Lett. 99, 073901 (2007). [DOI] [PubMed] [Google Scholar]
  22. Hamazaki J. et al. Optical-Vortex Laser Ablation. Opt. Express 18, 2144–2151 (2010). [DOI] [PubMed] [Google Scholar]
  23. Omatsu T. et al. Metal Microneedle Fabrication using Twisted Light with Spin. Opt. Express 18, 17967–17973 (2010). [DOI] [PubMed] [Google Scholar]
  24. Toyoda K. et al. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Letters 12, 3645–3649 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Toyoda K. et al. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 110, 143603 (2013). [DOI] [PubMed] [Google Scholar]
  26. Decker M., Klein M. W., Wegener M. & Linden S. Circular dichroism of planar chiral magnetic metamaterials. Opt. Lett. 32, 856–858 (2007). [DOI] [PubMed] [Google Scholar]
  27. Zhang S. et al. Negative Refractive Index in Chiral Metamaterials. Phys. Rev. Lett. 102, 023901 (2009). [DOI] [PubMed] [Google Scholar]
  28. Ozaki M., Kato J. & Kawata S. Surface-Plasmon Holography with White-Light Illumination. Science 332, 218–220 (2011). [DOI] [PubMed] [Google Scholar]
  29. Garcia R., Martinez R. V. & Martinez J. Nano-chemistry and scanning probe nanolithographies. Chem. Soc. Rev. 35, 29–38 (2006). [DOI] [PubMed] [Google Scholar]
  30. Piner R. D., Zhu J., Xu F., Hong S. & Mirkin C. A. ‘Dip-pen' nanolithography. Science 283, 661–663 (1999). [DOI] [PubMed] [Google Scholar]
  31. Binning G., Rohrer H., Gerber C. & Weibel E. Surface studies by scanning tunneling microscopy. Phys. Rev. Lett. 49, 57–61 (1982). [Google Scholar]
  32. Fang G. J. et al. Athermal photofluidization of glasses. Nature Commun. 4, 1521 (2013). [DOI] [PubMed] [Google Scholar]
  33. Harada K. et al. Holographic Recording and Control of Diffraction Efficiency using Photoinduced Surface Deformation on Azo-Polymer Films. Jpn. J. Appl. Phys. 41, 1851–1854 (2002). [Google Scholar]
  34. Oemrawsingh S. S. R. et al. Production and Characterization of Spiral Phase Plates for Optical Wavelengths. Appl. Opt. 43, 688–694 (2004). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES