Meteorological Influences on the Seasonality of Lyme Disease in the United States

Abstract

Lyme disease (Borrelia burgdorferi infection) is the most common vector-transmitted disease in the United States. The majority of human Lyme disease (LD) cases occur in the summer months, but the timing of the peak occurrence varies geographically and from year to year. We calculated the beginning, peak, end, and duration of the main LD season in 12 highly endemic states from 1992 to 2007 and then examined the association between the timing of these seasonal variables and several meteorological variables. An earlier beginning to the LD season was positively associated with higher cumulative growing degree days through Week 20, lower cumulative precipitation, a lower saturation deficit, and proximity to the Atlantic coast. The timing of the peak and duration of the LD season were also associated with cumulative growing degree days, saturation deficit, and cumulative precipitation, but no meteorological predictors adequately explained the timing of the end of the LD season.

Introduction

Lyme disease is a tick-borne zoonotic disease caused by the bacterial spirochete Borrelia burgdorferi.¹ Since its initial description in 1977,² Lyme disease has been increasing in both incidence and geographic distribution, and it is now the most common vector-transmitted infectious disease in the United States.³ The occurrence of Lyme disease in the United States is concentrated in the northeast from Maine south to Virginia and in the Midwestern states of Wisconsin and Minnesota. Like many vector-transmitted diseases in temperate regions, the occurrence of Lyme disease is highly seasonal. Approximately two-thirds of the cases from 1992 to 2006 had a reported onset date in June, July, or August.³ The seasonality of case occurrence varies geographically with the beginning of the main transmission season (and the peak) occurring earlier in southern endemic states (Virginia and Maryland) and later in the northern endemic states (Maine, New Hampshire, and Minnesota). Seasonality might also vary from year to year, with the timing of the beginning and peak of the period when the majority of infections occur differing depending on environmental factors.

The seasonality of Lyme disease case occurrence is driven in part by the life cycle of Ixodes scapularis, the main vector of Lyme disease spirochetes in the eastern United States. Ixodid ticks have four life stages (egg, larva, nymph, and adult), and only require one blood meal per host-seeking life stage.⁴ The life cycle of I. scapularis typically takes 2 years to complete in the northern United States latitudes where Lyme disease occurrence is most common. Nymphal ticks typically emerge and quest (seek hosts) in the late spring and early summer, although the majority of adults seek a blood meal in late summer and early autumn.⁴ The majority of human Lyme disease cases are believed to be transmitted by nymphal ticks because of their small size, which prevents timely detection, and the strong overlap in the timing of nymphal activity and Lyme disease occurrence.⁵ The timing of peak nymphal activity depends on both temperature and moisture. Ixodid tick development rates increase with temperature,^6–9 and temperature also influences nymphal questing activity.^10–12 Nymphal questing activity may also be reduced when relative humidity is low or saturation deficit is high,^11–13 or when precipitation is heavy.

Although influenced by meteorological conditions, tick activity is not the sole determinant of human illness. Human infection requires contact between infectious ticks and susceptible humans, and patterns of human activity can potentially augment or decrease the risk of disease transmission. Late spring through early fall is also the time period when humans are most active outdoors, which increases the contact rates between questing ticks and humans. Nevertheless, it is essential to recognize that human behavior may be independently influenced by temperature and precipitation in ways that also affect disease.

Strategies for preventing Lyme disease include reducing the abundance of ticks in the environment and modifying human behavior to reduce tick exposure and pathogen transmission.^14–16 One common control method in the northeast is the area-wide application of acaricides in the peridomestic setting to reduce the number of host-seeking nymphal ticks.^17,18 A single springtime application of synthetic acaricide timed to coincide with nymphal emergence can significantly reduce the number of questing ticks for several months.¹⁹ Natural, plant-based acaricides, which may be more acceptable to some homeowners^17,20,21 can also reduce the abundance of I. scapularis nymphs; however, their efficacy begins to wane after several weeks.^19,22,23 Knowledge regarding the time period when humans have a high risk of acquiring infection could therefore be used to target the timing of application of conventional or natural acaricides. Public awareness campaigns emphasize the avoidance of high-risk habitat for tick exposure, the use of clothing and repellents to avoid tick bites, and tick checks and bathing after outdoor activity to prevent pathogen transmission.^15,24 A better understanding of the seasonality of Lyme disease could be used to target when these awareness campaigns would be most effective, and also provide the public with a better sense of when risk levels are highest. The timely transfer of information regarding the level of risk to the medical community is also important because early diagnosis and treatment with antibiotics reduces complications and improves clinical outcome.^25,26 The goal of our study was to identify the meteorological factors associated with the timing of the primary Lyme disease season, with the goal of using this knowledge to improve the timing of control and prevention efforts.

The first objective of this study was to develop a measure of the seasonality of Lyme disease occurrence in humans by identifying the period or season when the majority of Lyme disease cases occur. This was accomplished using novel methods to calculate the beginning, peak, end, and duration of the season when the majority of cases occur. Next, we identified which meteorological variables are associated with seasonal patterns of Lyme disease, particularly the beginning of the period when the majority of cases occur, across all states where Lyme disease is highly endemic. Other studies of vector-borne diseases have linked seasonal variation in incidence or occurrence to climate and meteorology in general,^27–31 but have not tried to predict or explain temporal variation in the timing of the seasonal onset and peak, or the length of the season when the majority of cases occur. In addition to examining the association between meteorological factors and seasonality across a broad region of 12 highly endemic states, we also tested whether these associations held for 4, multi-state sub-regions. The meteorological variables connected to the variability in the timing of the Lyme disease season both geographically and annually in different regions of the United States could then be used to help forecast the annual timing of the Lyme disease season in highly endemic areas.

Materials and Methods

Epidemiological data.

Human Lyme disease cases have been voluntarily reported to the Centers for Disease Control and Prevention (CDC) by state and territorial health departments as part of the National Notifiable Disease Surveillance System (NNDSS) since 1991. A total of 275,518 human cases of Lyme disease were reported between 1992 and 2007.^3,32 During this period, a case of Lyme disease was defined as either 1) a physician-diagnosed erythema migrans rash of ≥ 5 cm in diameter or 2) at least one objective late manifestation (i.e., muscoskeletal, cardiovascular, or neurologic) with laboratory evidence of infection with B. burgdorferi.³³ The national surveillance case definition was revised in 2008 to include probable cases, so we limited our analysis to 1992–2007. However, we did use the confirmed case data from 2008 to 2010 to evaluate our model results. State or local health departments are responsible for ensuring that cases reported to CDC meet the case definition, and during the time period of our study state health officials used various methods to ascertain cases including provider-initiated passive surveillance, laboratory-based surveillance, and enhanced or active surveillance.³ These differences affect the completeness of case ascertainment but should not influence the seasonal trends among cases that are reported. Because we were interested in the seasonality of Lyme disease occurrence we excluded all cases where the suspected county of exposure was not reported or where the date of illness onset was either not reported or was more than a year before the case report date. We performed all analyses using either all confirmed cases that met our criteria or only confirmed cases with an erythema migrans diagnosis. Both analyses identified the same meteorological variables as statistically significant. Therefore, we present only the results of the analysis with all confirmed cases, which draws upon a much larger sample size (195,765 versus 112,501 cases).

Over 95% of Lyme diseases cases in the United States occurred in 13 states during our study period, primarily in the Northeast and Upper Midwest (Connecticut, Delaware, Maine, Maryland, Massachusetts, Minnesota, New Hampshire, New Jersey, New York, Pennsylvania, Rhode Island, Virginia, and Wisconsin). During the time period of our study, reports from Delaware did not include an illness onset date and were therefore excluded from our analysis. In the remaining 12 states, Lyme disease cases for each state were aggregated on a weekly timescale for each year based on the reported date of illness onset. We analyzed every year with ≥ 100 cases in a state (Table 1 ; total number of cases = 195,765). Years with fewer than 100 cases in a particular state were excluded because we could not accurately calculate seasonal statistics for that year.

Table 1.

Seasonal mean values, measured in weeks, for the 12 states (grouped into four regions) included in our analysis^*

State (Region)	Years	Start (SD)	Peak (SD)	End (SD)	Duration (SD)
North	21	22.1 (1.1)	27.6 (0.8)	35.5 (1.1)	13.4 (1.5)
Maine	6	22.0 (1.8)	27.8 (1.2)	36.5 (1.0)	14.5 (2.1)
Massachusetts	13	22.2 (0.7)	27.5 (0.7)	35.1 (1.0)	12.9 (1.0)
New Hampshire	2	22.0 (1.4)	27.5 (0.7)	35.5 (0.7)	13.5 (2.1)
East	66	21.3 (1.2)	27.1 (0.7)	35.1 (0.9)	13.8 (1.7)
Connecticut	16	21.9 (1.0)	27.2 (0.4)	34.6 (0.7)	12.7 (1.4)
Rhode Island	14	22.1 (1.1)	27.6 (0.9)	35.1 (0.8)	13.1 (1.2)
New Jersey	7	20.7 (1.4)	27.0 (0.6)	35.9 (1.3)	15.1 (2.6)
New York	15	21.1 (0.9)	27.2 (0.4)	35.5 (0.7)	14.3 (1.4)
Pennsylvania	14	20.2 (0.9)	26.4 (0.5)	34.9 (0.9)	14.6 (1.3)
South	26	18.6 (1.3)	25.4 (0.6)	35.5 (2.9)	16.9 (3.4)
Maryland	16	19.2 (0.9)	25.6 (0.5)	34.9 (1.9)	15.8 (2.4)
Virginia	10	17.7 (1.3)	25.1 (0.7)	36.4 (4.0)	18.7 (4.0)
Midwest	32	22.3 (1.6)	27.6 (1.5)	34.8 (1.8)	12.4 (2.0)
Minnesota	16	23.1 (1.5)	27.7 (1.2)	34.3 (1.2)	11.2 (1.6)
Wisconsin	16	21.6 (1.4)	27.4 (1.7)	35.3 (2.1)	13.7 (1.4)
Mean (SD)	145	21.2 (1.8)	27.0 (1.2)	35.2 (1.7)	14.0 (2.6)

^*Years are the number of years between 1992 and 2007 where > 100 Lyme disease cases occurred in a state and included in analysis. Start, peak, and end are the week when the Lyme disease season starts, reaches its peak, and ends, respectively; duration is the length of the Lyme disease season in weeks. Numbers in parentheses are standard deviations (in weeks) for each variable.

Seasonal response variables.

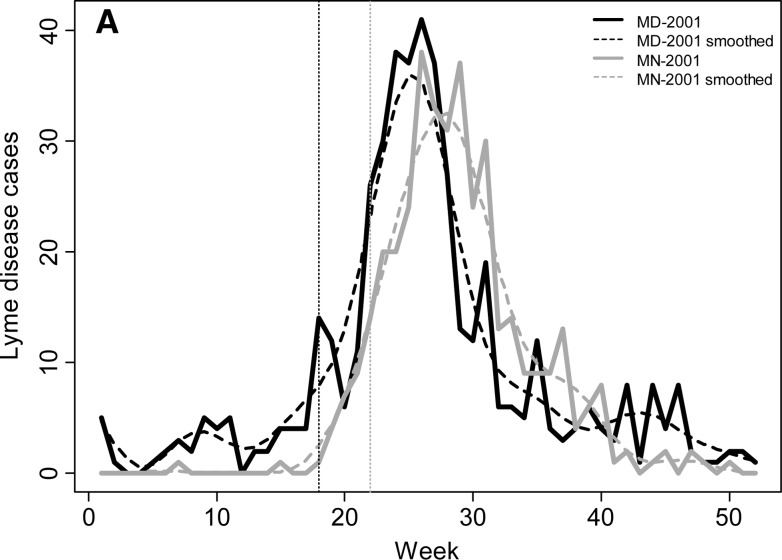
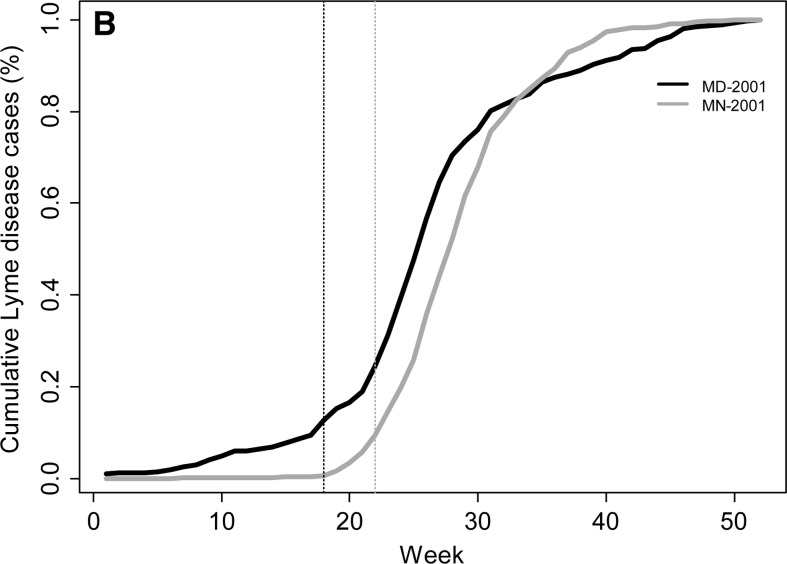
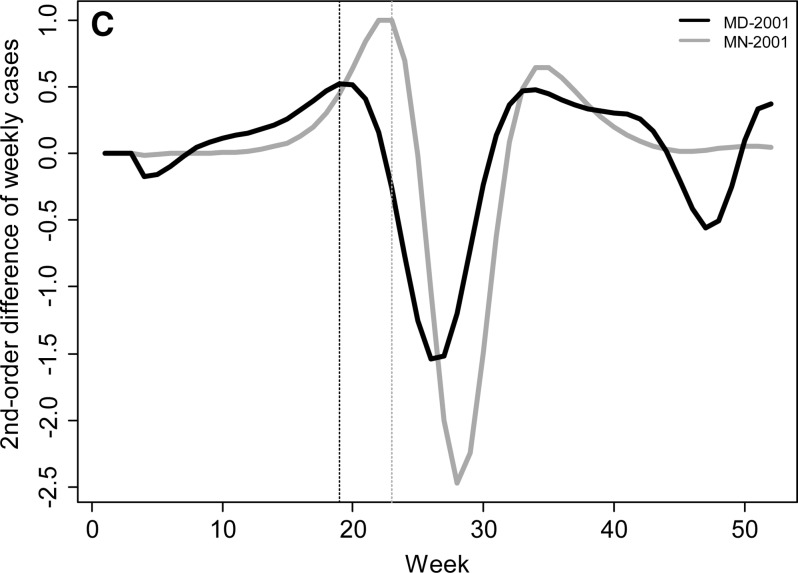
To examine seasonal variability in Lyme disease occurrence we calculated the beginning week of the primary Lyme disease season, the peak week of occurrence, and the week ending the primary Lyme disease season. In addition, we calculated the percentage of cases that occurred before, within, and after the primary season. The beginning of the primary Lyme disease season was defined as the week when the number of Lyme disease cases increased (accelerated) at its most rapid pace (i.e., not the week with the largest increase in the number of cases, which occurs a few weeks later in the season, but the week with the maximum percent increase in number of cases over the previous week). This variable is calculated by maximizing the second derivative of the weekly case curve (or the third derivative of the cumulative weekly case curve). The number of cases recorded in a given week is subject to stochastic factors independent of any meteorological drivers, which can inflate the change in the number of cases from one week to the next and lead to errors in calculating the beginning week of the Lyme disease season. To minimize the influence of this stochasticity on our assessment of seasonal variables, a fifth-order polynomial regression function was fit to the cumulative weekly case curve for each year for each state. A fifth-order polynomial was necessary to represent the non-normality in both tails of the annual case curve (R² > 0.994 for each year; Figure 1). The beginning week was then calculated by maximizing the second-order weekly difference in case counts, which approximates the second-order derivative, from this fifth-order polynomial function (Figure 1C).

Figure 1.

Weekly Lyme disease cases (A) and cumulative percentage of annual cases (B) for Maryland and Minnesota in 2001. Solid lines in (A) represent actual number of weekly cases for each state and dashed lines represent the smoothed number of cases using a fifth-order polynomial. (C) The second-order finite difference of the weekly case count for each state was used to calculate the beginning and end of the Lyme disease season for each state and year. The dotted lines in (A–C) represent the beginning week for each state.

The week with the most cases (peak) was also calculated from the fifth-order polynomial function. The end week of the primary Lyme disease season was calculated using the same method as the beginning week calculation, except we identified the week when the maximum deceleration in cases occurred following the annual peak. The seasonal duration (in weeks) was calculated by subtracting the beginning week from the end week.

Meteorological variables.

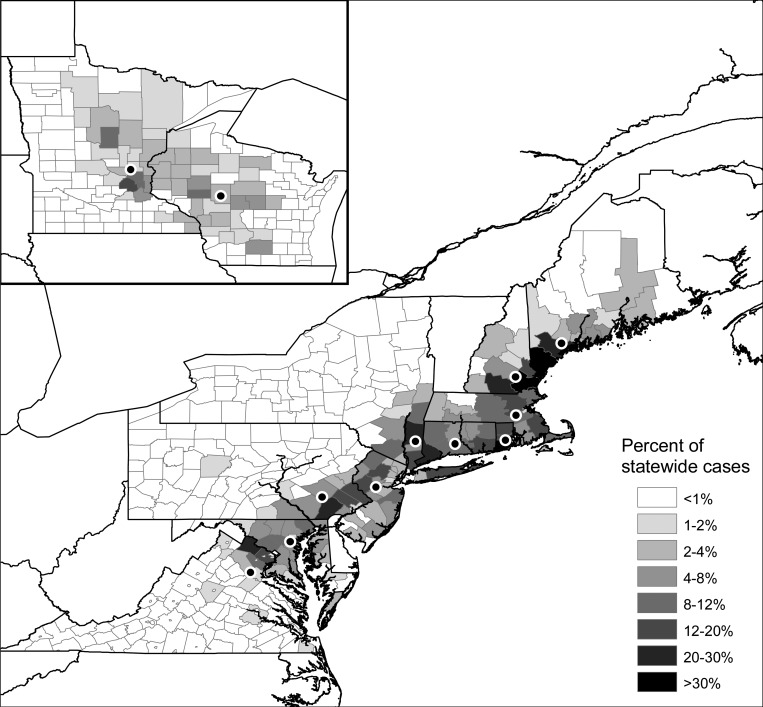
All meteorological variables were obtained from primary forcing data for Phase 2 of the North American Land Data Assimilation System (NLDAS-2).³⁴ The primary forcing data were originally developed to provide a high-quality, long-term dataset to drive a suite of research-grade land-surface models,^35,36 but have subsequently been used for a variety of climate research applications over central North America. The non-precipitation NLDAS-2 forcing data were interpolated to 1/8th degree spatial resolution and disaggregated to hourly temporal resolution from the 32-km, 3-hourly North American Regional Reanalysis (NARR), which has been shown to represent near-surface climatic fields with high fidelity.³⁷ Precipitation fields in the NLDAS-2 forcing data are not from NARR, but rather directly from gauge data augmented with satellite- and radar-derived precipitation estimates. Hourly meteorological fields from the NLDAS-2 forcing data were used to calculate the weekly minimum, mean, and maximum temperatures, saturation deficit, relative humidity, weekly precipitation, and cumulative precipitation from the beginning of the year for each grid cell (Table 2 ). Temperature data were used to calculate the weekly growing degree days (GDD) above a particular temperature threshold, and the cumulative growing degree days above that temperature threshold from the beginning of the year. Because several aspects of tick biology and human behavior may respond to different temperature thresholds we examined potential GDD thresholds of 5, 6, 10, 14, and 18°C by using the model selection techniques described below to determine which threshold value provided the best estimate of Lyme disease seasonality. The beginning of the Lyme disease season was strongly correlated with GDD at each threshold value, but model fit was maximized using a GDD threshold of 10°C. A threshold of 10°C has also been used in several studies of ixodid tick populations^38,39; therefore, we used a GDD threshold of 10°C for all of our analyses. A county-level mean value for each weekly meteorological variable was calculated using the Zonal Statistics tool in ArcGIS 9.3 (Environmental Systems Resource Institute, 2010; ESRI, Redlands, CA). A statewide average was then derived by calculating a weighted average of the county-level values within each state. Each county-level statistic was weighted by the percentage of 1992–2007 Lyme diseases cases from a state occurring in that county, so that meteorological variables from the counties with the most cases within a state had the highest weights (Figure 2). The latitude and distance from the Atlantic coastline were calculated in a similar fashion for each state by weighting the mean latitude and coastline distance of each county by its percentage of statewide cases.

Table 2.

Description of meteorological variables used in the analysis of Lyme disease seasonality. All variables were obtained from primary forcing data for Phase 2 of the North American Land Data Assimilation System (NLDAS-2)³⁴

Variable	Description
Weekly minimum temperature	Minimum temperature during the week
Weekly maximum temperature	Maximum temperature during the week
Weekly mean temperature	Mean temperature for the week
Weekly precipitation	Total precipitation for the week
Cumulative precipitation	Total cumulative precipitation from the beginning of the year
Growing degree days (GDD)	Total degrees above 10°C for the week calculated using daily mean temperatures
Cumulative growing degree days (GDD)	Total degrees above 10°C since the beginning of the year calculated using daily mean temperatures
Saturation deficit	Index of humidity that measures how far the amount of water vapor is below saturation for a given temperature and pressure
Relative humidity	Weekly mean of the ratio of the measured water vapor pressure to the saturation vapor pressure

Figure 2.

Percentage of statewide Lyme disease cases from 1992 to 2007 occurring in each county for the 12 highly endemic Lyme disease states included in our analysis. Dots represent the center of each state weighted by the county case percentages. State latitude and distance to the Atlantic coastline were calculated from these weighted centers.

Statistical analysis.

Analysis of variance was conducted to determine whether there was a significant difference in each of the seasonal statistics among states or among years. Individual states were compared using pairwise t tests with a Bonferroni correction to adjust for multiple comparisons. Linear multiple regression models were constructed to identify meteorological predictors of the beginning, peak, end, and duration of the Lyme disease season. The leaps package version 2.9 in R.⁴⁰ was used to perform an exhaustive search of the best fit models using Akaike's information criterion (AIC) as the model selection criterion. The mean beginning of the Lyme disease season across all states was 21.2 weeks. Therefore, we considered weekly values of saturation deficit, relative humidity, GDD, and precipitation from Weeks 1 to 20 as potential explanatory variables for the beginning of the Lyme disease season. Cumulative precipitation and cumulative GDD through Weeks 1 to 20, latitude, and distance to coastline were also included as potential explanatory variables. In addition to weekly meteorological variables, we calculated the saturation deficit, relative humidity, GDD, precipitation, cumulative precipitation, and cumulative precipitation after Week 8 (because the amount of precipitation that occurs as rain versus snow in the first few months of the year varies significantly) in the 5 weeks before the beginning of the Lyme disease season. We also calculated the week at which a cumulative threshold of 100 to 500 GDD was reached (in increments of 50). For the analysis of the duration and end of the Lyme disease season, we also included all weekly meteorological variables through Week 40 as potential explanatory variables. Several of the meteorological variables were highly correlated, so the predictors in the model were tested for multicollinearity by comparing variance inflation factors (VIF). All models with a VIF > 5 were excluded from analysis. Because of the relatively high correlation between relative humidity and saturation deficit, models including both variables from the same week were also excluded. All statistical analyses were performed in R 2.11 (R Development Core Team 2010).

Regional analysis.

The 12 states were grouped into different regions based on the similarity of their climate using k-means cluster analysis. K-means cluster analysis partitions observations from each state into k clusters, where k is a predetermined value, by placing each observation in the cluster with the nearest mean. The means for each cluster were calculated using the annual GDD, annual precipitation, and mean weekly saturation deficit for each observation. Because several states had a few years with > 100 Lyme disease cases between 1992 and 2007, we included every year from 1992 to 2007 from each state for clustering purposes (N = 192). The number of clusters was varied from three to six, with the appropriate number of clusters determined by which grouping had the best combination of precision and percent of variance explained by the cluster groupings. Precision was determined by the percent of annual observations from each state that were included in the same cluster. An optimum grouping of four clusters (regions) was chosen because only k = 3 and k = 4 had at least 50% of observations from each state (except MA) in one cluster, and the percentage of variance explained (ratio of between-group variance to total variance) was higher for k = 4 than k = 3 (75.8% versus 69.0%). The four regions roughly correspond to the upper midwest (MN and WI), northern New England (MA, NH, and ME), southern New England and the northern mid-Atlantic (RI, CT, NY, NJ, and PA), and the southern mid-Atlantic (MD and VA) (Table 3 ).

Table 3.

Results of k-means cluster analysis with the number of clusters set to k = 4^*

Region	CT	MA	MD	ME	MN	NH	NJ	NY	PA	RI	VA	WI
North	2	7	0	15	1	10	0	2	0	2	0	3
East	9	3	1	0	0	2	10	10	9	11	0	0
South	0	0	15	0	0	0	5	0	5	0	16	0
Midwest	5	6	0	1	15	4	1	4	2	3	0	13

^*Each column represents the number of years from 1992 to 2007 for each state that were clustered within a particular region based on the annual growing degree days (GDD), annual precipitation, and mean weekly saturation deficit for that year. Bolded values indicate the region into which each state was grouped.

The beginning week of the Lyme disease season was analyzed using a generalized linear mixed-effects regression model (GLMM) with region, state, and year as nested random effects to provide an estimate of the variance associated with each factor after accounting for variance at the other hierarchical levels (variance components analysis) using the lme4 package in R.⁴¹ The best fitting linear regression model(s) for all states were then fit separately for each region to determine whether the overall relationship between Lyme disease seasonality and climate held within the different regions. An exhaustive search of the best fit models of the beginning of the Lyme disease season for each region was also conducted using the same approach outlined for the overall model.

Results

Seasonal statistics.

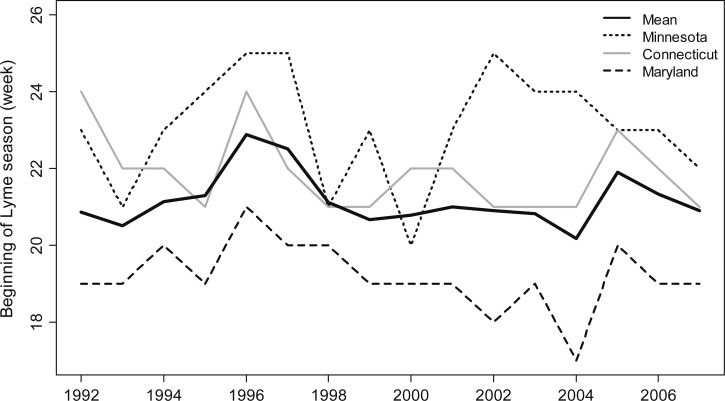
Across all states and all years, the beginning of the season when a majority of Lyme disease cases occur varied from Week 16 to Week 26 (mean = 21.2 weeks, SD = 1.8 weeks; Figure 3 ; Table 1). The mean duration of the season was 14.0 weeks (SD = 2.6 weeks). An average of 71.6% of cases occurred within the main Lyme disease season (12% occurred before, 16.4% after). The mean seasonal peak occurred at week 27.0 (SD = 1.2 weeks). The average timing of the beginning of the Lyme disease season varied significantly across states (F_11,132 = 19.8; P < 0.0001). The beginning of the Lyme disease season occurred significantly earlier in Virginia (mean = 17.7 weeks) than in any other state (expect Maryland which had a mean of 19.2 weeks; P = 0.12). Minnesota had the latest beginning to the Lyme disease season (mean = 23.1 weeks). The peak of the Lyme disease season also varied significantly among states (F_11,132 = 11.3; P < 0.0001), as did the duration (F_11,132 = 12.0; P < 0.0001). The end of the Lyme disease season also varied among states (F_11,132 = 1.8; P = 0.052), but differences among the states only explained 13.1% of the variance in the end week. The duration of the Lyme disease season in Virginia was significantly longer than in all of the other states (mean = 18.7 weeks), whereas Minnesota had the shortest season at 11.2 weeks. No state had a significantly earlier or later end week compared with the mean of week 35.2.

Figure 3.

The overall mean beginning of the Lyme disease season from 1992 to 2007, along with the annual beginning weeks for three states: Minnesota, Connecticut, and Maryland.

Beginning of the Lyme disease season.

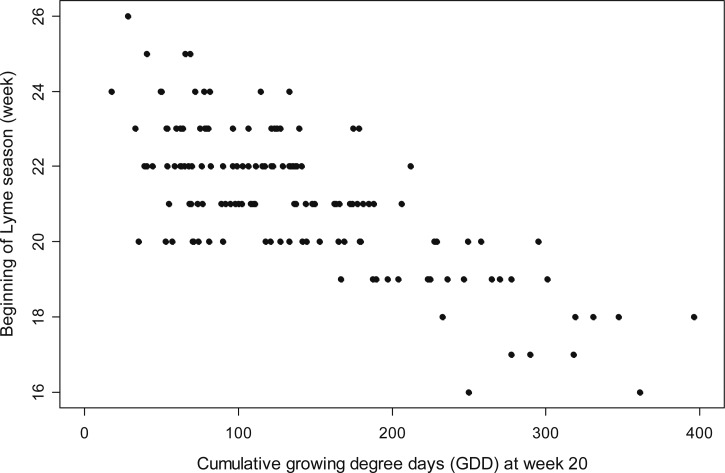
The strongest univariate predictor of the beginning of the Lyme disease season was the cumulative GDD through Week 20 (r² = 0.54), with higher cumulative GDD associated with an earlier start week (Figure 4 ). Cumulative GDD through Weeks 10 to 19 were all highly significant as well (R² = 0.41 to 0.53), as were the 100–400 GDD threshold weeks (R² = 0.47 to 0.51). The best fit model included four variables in addition to the intercept: the cumulative GDD through Week 20, the mean saturation deficit in the 5 weeks before the beginning of the Lyme disease season, the cumulative precipitation from Week 8 through the beginning of the Lyme disease season, and the distance to the Atlantic coastline (adj-R² = 0.79; Table 4 ). The only other model with a ΔAIC < 2 included longitude instead of the distance to the Atlantic coastline. All of the models with ΔAIC < 10 included the mean saturation deficit in the 5 weeks before the beginning of the Lyme disease season, the cumulative precipitation from Week 8 through the beginning of the Lyme disease season, and either the cumulative GDD through Week 20 or the number of weeks to 150 GDD as explanatory variables. An increase in the cumulative GDD through Week 20 (or an earlier 150 GDD threshold week) was associated with an earlier beginning of the Lyme disease season (Figure 4). The Lyme disease season is predicted to begin 1.4 weeks earlier for each additional 100 cumulative GDD through Week 20. Alternatively, the beginning of the Lyme disease season is 0.5 weeks earlier for each decrease in the week that 150 cumulative GDD are reached (model 3 in Table 4). An earlier start to the Lyme disease season was also negatively associated with the mean saturation deficit before the beginning of the season, the cumulative precipitation since Week 8, and the distance to the Atlantic coastline (Table 4).

Figure 4.

Beginning week of Lyme disease season across all states and years as a function of the cumulative growing degree days (GDD) above 10°C through Week 20 for that state and year (r² = 0.54).

Table 4.

Best fit models with the beginning week of the Lyme disease season as the response variable^*

Model	Number of parameters	Adj. R2	AIC	ΔAIC	Model parameters	Parameter estimates	95% Confidence interval
1	4	0.785	368.4	0	Week 20 cumul. GDD	−0.014	−0.016 to −0.011
					Mean SD before onset	0.945	0.696–1.194
					Cumul. precip. after Week 8	0.009	0.007–0.011
					Distance to coastline	0.093	0.055–0.131
2	4	0.784	369.4	1.0	Week 20 cumul. GDD	−0.014	−0.016 to −0.012
					Mean SD before onset	0.932	0.683–1.181
					Cumul. precip. after Week 8	0.009	0.008–0.011
					Longitude	−0.052	−0.090 to −0.014
3	4	0.773	376.7	8.3	Weeks to 150 GDD	0.530	0.445–0.614
					Mean SD before onset	1.062	0.801–1.322
					Cumul. precip. after Week 8	0.010	0.008–0.012
					Distance to coastline	0.098	0.059–0.137
4	4	0.772	377.3	8.9	Weeks to 150 GDD	0.568	0.487–0.648
					Mean SD before onset	1.055	0.792–1.318
					Cumul. precip. after Week 8	0.010	0.008–0.012
					Longitude	−0.056	−0.078 to −0.033

^*Number of model parameters, model adjusted r², AIC, and ΔAIC values and parameter estimates with 95% confidence intervals for all models with ΔAIC < 10. ΔAIC represents the difference between a model's AIC value and the AIC value of the best fit overall model. Italicized parameters are not statistically different from 0 at α = 0.05 confidence level.

Model validation was performed using climate and case data from 2008 to 2010 from each of the 12 states (N = 35; Rhode Island, 2008 was excluded from model validation because 40% of cases had a reported onset date of 3/22). Our best-fit model performed well for the 2008–2010 period (adj-R² = 0.70), with the cumulative GDD through Week 20 and mean saturation deficit variables remaining highly statistically significant (P < 0.001), but the cumulative precipitation since Week 8 and distance to the Atlantic coastline variables were not significant at a P value of 0.05 (P = 0.08 and P = 0.12).

Seasonal peak and duration.

The timing of the peak and duration of the Lyme disease season were explained by similar variables as the beginning of the season. The strongest univariate predictors of the peak and duration of the Lyme disease season were the cumulative GDD through Week 22 and Week 21, respectively (R² = 0.50 and 0.31). The best model for the peak week included cumulative GDD through Week 22, the saturation deficit 1 week before the beginning of the season, the cumulative precipitation after Week 8, and the distance to the Atlantic coastline (R² = 0.59). The best model of the duration of the Lyme disease season included cumulative GDD through Week 20, the mean saturation deficit before the beginning of the season, the cumulative precipitation up to 1 week before the beginning of the season, and the distance to the Atlantic coastline (R² = 0.54). None of the meteorological variables were strong predictors of the end of the Lyme disease season. No single predictor explained more than 5% of the variance in the end of the season, and no multi-variable model had an adjusted R² > 0.15.

Regional analysis.

The majority of the variation in the beginning of the Lyme disease season was determined by factors at the regional scale (59.8%), with differences among states within a region accounting for less of the variation (11.2%). The remainder of the variation in the beginning of the season was a result of differences among years within each state (29.0%). The beginning of the Lyme disease season started significantly earlier in the southern mid-Atlantic (mean = 18.6 weeks) than in the other regions, and earlier in the east (mean = 21.3 weeks) than in the north (mean = 22.1 weeks) or midwest (mean = 22.3 weeks). The best-fit overall model (model 1 in Table 4) performed relatively well in the southern mid-Atlantic (r² = 0.784), east (r² = 0.614), and midwest (r² = 0.614) regions, but not in the north (r² = 0.375). All four variables were significant for the southern mid-Atlantic region model, distance to coastline was the only variable that was not statistically significant in the east and midwest regions, and only cumulative precipitation after Week 8 was significant in the north region model. The best-fit model for the north region included cumulative precipitation before the beginning of the Lyme disease season, precipitation 4 weeks before the Lyme disease season, Week 5 saturation deficit, and Week 3 precipitation (Table 5 ). All of the other regional best-fit models included variables representing cumulative GDD, saturation deficit before the beginning of the Lyme disease season, and cumulative precipitation as three of the four model parameters (Table 5).

Table 5.

Best fit models for the beginning week of the Lyme disease (LD) season in each of the four regions of high Lyme disease occurrence^*

Region	Model	Model parameters	Adj. R2	AIC	ΔAIC
North	1	(+) Cumulative precip. before LD season	0.832	34.9	0
		(−) Precip. 4 weeks before LD season
		(+) Week 5 saturation deficit
		(−) Week 3 precip.
	2	(+) Cumulative precip. before LD season	0.827	35.5	0.6
		(−) Precip. 4 weeks before LD season
		(−) Week 7 relative humidity
		(−) Week 5 precip.
East	1	(−) Week 20 cumulative GDD	0.723	137.2	0
		(+) Mean SD before onset
		(+) Cumulative precip. after Week 8
		(−) Week 9 precipitation
South	1	(−) Week 17 cumulative GDD	0.852	42.9	0
		(+) Mean SD before onset
		(+) Cumulative precip. before LD season
		(+) Week 17 relative humidity
Midwest	1	(−) Cumulative GDD from Week 16–21	0.819	72.7	0
		(+) Mean SD before onset
		(+) Cumulative precip. after Week 8
		(−) Week 8 saturation deficit
	2	(−) Cumulative GDD from Week 16–21	0.809	74.4	1.7
		(+) Mean SD before onset
		(+) Cumulative precip. before LD season
		(−) Week 8 saturation deficit

^*Model adjusted r², AIC, and ΔAIC values for all models with ΔAIC < 2. The (+/–) signs indicate whether parameter coefficients are positive or negative. ΔAIC represents the difference between a model's AIC value and the AIC value of the best fit overall model.

Discussion

Previous research has linked the development and seasonal activity patterns of Ixodes ticks^6,9,42–44 to meteorological variables, specifically temperature and humidity. However, because non-entomologic factors can also influence the occurrence of tick-borne disease in humans,⁴⁵ the degree of coupling between meteorological factors and human Lyme disease has been open to question. Here, we showed that the geographical and annual variation in the timing of human Lyme disease can also be largely explained by meteorological factors. The beginning, peak, and duration of the Lyme disease season were associated with several meteorological variables, including cumulative GDD, cumulative precipitation, and saturation deficit at both the national and regional levels. The strongest predictor at the national level was the cumulative GDD above 10°C through the first 20 weeks of the year, with higher cumulative GDD associated with an earlier beginning to the Lyme disease season. An early beginning to the Lyme disease season was also associated with less cumulative precipitation and a lower mean saturation deficit before the start of the season.

Tick population dynamics and phenology are highly sensitive to temperature at multiple life stages.⁴⁴ The host-seeking behavior of the nymphal stage is most relevant for the transmission of B. burgdorferi to humans because nymphs are believed to be responsible for most human infections. Interstadial development rates in ixodid ticks typically increase with increasing temperature,^6–8,46,47 and the timing of nymphal host seeking is correlated with ambient temperatures.^6,43,48–50 The negative relationship between cumulative GDD through Week 20 and the week of the year when the Lyme disease season begins, indicating that higher cumulative GDD at Week 20 are associated with an earlier start to the season (or the positive relationship between the number of weeks to reach 300 GDD and the week when the Lyme disease season begins), is likely due in part to this positive effect of temperature on the activity of newly emerged nymphs in the spring. Cumulative GDD were a better predictor of seasonal timing than weekly minimum, mean, or maximum temperatures. Nymphal questing activity may track not just immediate environmental conditions, but temperatures earlier in the year as well. Newly emerged nymphs of some Ixodes species may undergo a behavioral diapause between emergence and host-seeking activity (questing) that is dependent on climatic conditions such as temperature.^9,51–54 In addition, larvae that feed later in the summer or fall may undergo developmental (morphogenetic) diapause and overwinter before molting.^9,52,55–57 In this case larval development and nymphal emergence would likely be subject to cumulative spring temperatures.^8,49 Tick development, survival, and activity levels are all potentially sensitive to moisture levels in addition to temperature. In the overall best-fit model (and three of the four regional models) a higher mean saturation deficit in the 5 weeks before the beginning of the Lyme disease season was associated with a delayed start to the season. Nymphal I. scapularis activity increases with ambient relative humidity,¹⁰ and the activity and density of other ixodid ticks is also negatively correlated with saturation deficit.^51,58 Ixodes scapularis nymphs also reach higher questing heights at higher relative humidity levels,¹¹ which may increase their likelihood of encountering humans. Higher saturation deficits may delay the beginning of the Lyme disease season because it decreases questing activity and decreases the likelihood of questing nymphs encountering humans. The cumulative precipitation from Week 8 to the beginning of the Lyme disease season also was associated with a later start to the season. Although spring or summer rainfall is positively correlated with ixodid tick densities in California,⁴³ this association is generally measured during the time of peak nymphal density rather than earlier in the year when nymphal activity begins and the first human Lyme disease cases are likely to occur. Heavy rainfall events may impede nymphal questing activity, which could delay the beginning of the Lyme disease season in humans.

In addition to meteorological effects on pathogen and vector biology, seasonal patterns in disease occurrence can also arise because of human activities that lead to an increased exposure to pathogens and their vectors.⁵⁹ It is likely that people will spend more time outdoors in areas where they may encounter questing ticks in warmer and drier weather. Therefore, the association between cumulative GDD, cumulative precipitation, and the beginning of the Lyme disease season may be partially driven by the influence of weather on human behavior in a way that affects the exposure of the human population to infected I. scapularis nymphs. However, the strength of the relationship between cumulative GDD and human behavior is likely to be weaker than the relationship between cumulative GDD and tick development rates because human activity levels are mostly associated with the current temperature rather than cumulative temperatures since the beginning of the year. Likewise, human activity is probably more strongly associated with the amount of current precipitation rather than cumulative precipitation from Week 8 through the beginning of the Lyme disease season. However, in the northern areas considered in our study where snowpack in some years can last until springtime the cumulative GDD and precipitation before the beginning of the Lyme disease season may have a more lasting effect on the amount of time people spend outdoors in areas where they are likely to encounter questing nymphs. In addition, cumulative temperatures and precipitation could influence other environmental factors such as seasonal flooding and plant phenology that may affect human activity levels.

The best-fit overall model performed relatively well in three of the four climatically defined regions examined in this study. All three meteorological parameters (cumulative GDD, cumulative precipitation, and mean saturation deficit) were statistically significant in the east, southern mid-Atlantic, and midwest regions, but only cumulative precipitation was statistically significant in the north region. The majority of the overall variation in the beginning of the Lyme disease season was caused by geographical differences between regions rather than interannual differences within a state or region. However, the continued significance of these meteorological variables at the within-region level suggests that there is an association between weather and the interannual variation in seasonality as well. With the exception of the north, cumulative GDD was consistently associated with an earlier start to the Lyme disease season and higher cumulative precipitation was consistently associated with a later beginning to the season. In the northern region (MA, ME, and NH) cumulative precipitation was still positively associated with the start of the Lyme disease season, but there was no relationship between temperature and the timing of seasonality. This lack of a relationship between temperature and the beginning of the Lyme disease season is somewhat surprising because Maine is the current northern limit of Lyme disease's geographic range in the United States, and the distribution of I. scapularis is believed to be limited by temperature.^60,61 Therefore, we might expect I. scapularis activity to be sensitive to climate variability in a region where mean temperatures are close to their lower temperature limit for survival and development. However, the interannual variation in cumulative GDD through Week 20 was lower in the north region than it was in the other three regions, therefore temperature might not have varied enough from year to year to influence the timing of the Lyme disease season in these northern states. The timing of the Lyme disease season in the north might also be associated with weather-independent human activity patterns.

The best-fit overall model, and all of the best-fit regional models, included several parameters (cumulative precipitation from Week 8 to the beginning of the Lyme disease season and the mean saturation deficit before the Lyme disease season) that can only be calculated once the Lyme disease season begins. Because of this constraint these models cannot be used to precisely forecast when the Lyme disease season will begin in advance. Despite this limitation, the strong correlation between cumulative GDD and the beginning of the Lyme disease season suggests that GDD calculations could be used to predict whether the Lyme disease season is likely to start earlier or later than usual. The strongest correlation was with the cumulative GDD through Week 20, which does not provide much lead time for forecasting, particularly because infection typically occurs a week or two before symptoms first appear, but the cumulative GDD as early as Week 10 was still correlated with the beginning of the season (R = 0.64) and could provide several weeks advance notice. Such information could be used to better time prevention efforts such as public awareness campaigns and acaricidal treatments, particularly since the peak of the Lyme season was also strongly associated with cumulative GDD. The correlation between cumulative GDD and the beginning of the season increased steadily from Week 10 (R = 0.64) to Week 20 (R = 0.74), providing a tradeoff between lead time and accuracy.

By analyzing the relationship between meteorological factors and the seasonality of Lyme disease occurrence in humans we have identified several variables associated with variations in when the Lyme disease season begins and peaks, as well as how long the season lasts, but not when the season ends. By identifying inflection points in the annual case curves from 1992 to 2007 we found that the beginning of the Lyme disease season varied by up to 10 weeks among the states where the disease is highly endemic and by up to 6 weeks within a state over this 16-year period. These methods could be used to calculate statistics for other infectious diseases with clear seasonal patterns. An analysis of the association between the variation in seasonality and meteorological variables, and other environmental and social factors, can be used to understand what factors drive disease occurrence as we have done here. Links between environmental factors and the timing of seasonal transmission can also be used to develop forecasting tools that inform disease prevention efforts. For infectious diseases that can cause large seasonal epidemics, such as influenza or dengue, these methods could also be used to identify factors that influence the timing and severity of peak disease occurrence, and the duration of the epidemic.