Mechanical Stability and Reversible Fracture of Vault Particles

Abstract

Vaults are the largest ribonucleoprotein particles found in eukaryotic cells, with an unclear cellular function and promising applications as vehicles for drug delivery. In this article, we examine the local stiffness of individual vaults and probe their structural stability with atomic force microscopy under physiological conditions. Our data show that the barrel, the central part of the vault, governs both the stiffness and mechanical strength of these particles. In addition, we induce single-protein fractures in the barrel shell and monitor their temporal evolution. Our high-resolution atomic force microscopy topographies show that these fractures occur along the contacts between two major vault proteins and disappear over time. This unprecedented systematic self-healing mechanism, which enables these particles to reversibly adapt to certain geometric constraints, might help vaults safely pass through the nuclear pore complex and potentiate their role as self-reparable nanocontainers.

Introduction

Vault particles are naturally designed nanoscale protein cages, widely found in eukaryotes. Since their discovery in 1986 (1), diverse hypotheses have been developed as to the possible functions of vaults, based on their unique capsular structure, their mobility, and their distinct subcellular localization. Most of these hypotheses implicate cargo transport, which suggests that they could act as a versatile regulatory platform for diverse cellular signal and transport processes (2).

The x-ray structure of rat liver vaults revealed that their shell is organized into two identical moieties, each consisting of 39 copies of the major vault protein (MVP) (Fig. 1 A) (3).

Figure 1.

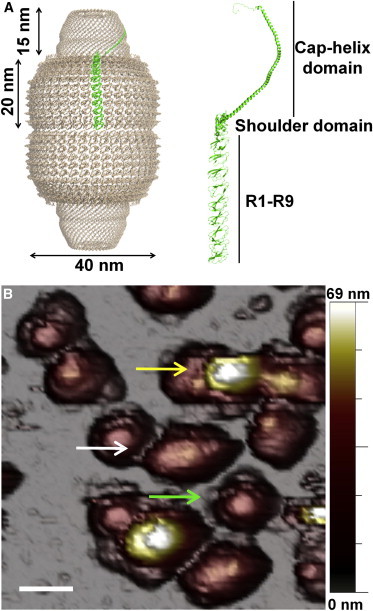
Vault structure and adsorption geometry. (A) Side view of a vault from x-ray data (3). The MVP is enlarged in the structure (green line). The MVP is composed of 12 domains, nine structural repeat domains at the N-terminus, an α/β shoulder domain, a cap-helix domain, and a cap-ring domain at the C-terminus. (B) General topography image of vaults in buffer conditions showing upright (yellow arrow) reclining (white arrow) and half-vault orientations (green arrow). Scale bar, 75 nm. To see this figure in color, go online.

The MVP monomer is organized in two well defined regions: the first half of the molecule folds into a series of small β-domains that assemble into a wide, thin-shelled barrel at the center of the particle, whereas the second half forms a long α-helix that assembles into the narrow cap at the C-terminal end. The N-terminal end of the MVP forms the particle’s waist and accounts for the noncovalent interface at the vault’s midsection. A combination of electrostatic and hydrophobic interactions governs the association of the two half-vault moieties (4). Natural vaults also enclose three minor components; two proteins, the vault poly-ADP-ribose polymerase (VPARP) and the telomerase-associated protein 1 (TEP1), together with several small noncoding RNA molecules (vRNA) (1,5,6). Vault-like particles, similar to purified endogenous vaults, are observed when rat MVP is expressed in insect cells, indicating that the MVP is sufficient to direct the formation of the vault shell (8). These vault-like particles, with overall dimensions of 40 × 40 × 70 nm³ and an average wall thickness of 1.5 nm, define an internal cavity (5 × 10⁴ nm³) that can store hundreds of molecules.

The peculiar structure and dynamics of the vault particles (9), their large size and natural occurrence in humans, together with the reported presence of unidentified cargos (2), have led to the idea that they could be exploited as natural nanocontainers for drug, nucleic acid, or protein delivery. In fact, in recent years, recombinant vaults have gone through significant engineering, including cell-surface receptor targeting and the encapsulation of a wide variety of molecules (10,11). However, using vaults as functional containers requires a deep knowledge of their structural stability. Interestingly, controlled deformation of individual particles has provided important insights into the mechanical stability of other macromolecular cages, such as viruses (12,13).

In this article, we study the mechanical properties of vaults using atomic force microscopy (AFM) under physiological conditions. We explore the stiffness of whole and half-vaults with single indentations and probe the stability of these particles by exerting cyclic load. Beyond the mechanical characterization of vault particles, our data monitor the first fracture/recuperation dynamics of a protein shell in which the particle repeatedly self-repairs over time.

Materials and Methods

Recombinant baculoviruses

Generation of a recombinant baculovirus (rBV) containing the full-length MVP was performed as follows. A DNA fragment containing the MVP sequence, flanked by NcoI and Kpnl restriction sites, was generated by polymerase chain reaction. The DNA fragment was digested with NcoI and KpnI and inserted into the multiple cloning site of the baculovirus transfer vector pFastBacHta (Invitrogen, Carlsbad, CA), previously digested with the same restriction enzymes. The resulting plasmid, pFB_MVP, was subjected to nucleotide sequencing to assess the correctness of the inserted MVP sequence and was then used to produce the corresponding rBV using the Bac-to-Bac system according to the manufacturer’s instructions (Invitrogen).

Production and purification of recombinant vaults

HighFive cells (Invitrogen) were infected with rBVs at a multiplicity of infection of 5 plaque-forming units/cell. Cells were harvested at 48 h postinfection, washed using phosphate-buffered saline and pelleted with a 5 min centrifugation at 3000 rpm. This pellet was resuspended in 6 mL of buffer A (75 mM NaCl, 50 mM Tris, pH 7.4, 1.5 mM MgCl₂, and 1 mM dithiothreitol) plus 1% NP-40 and protease inhibitors (protease inhibitor cocktail tablets, Roche, Basel, Switzerland) and maintained on ice for 30 min. The resuspended pellet was sonicated, and cellular debris was removed by centrifugation at 10,000 rpm for 30 min. The supernatant was applied to 4 mL of buffer A with 25% sucrose and centrifuged at 37,000 rpm (using a SW41Ti rotor) for 2.5 h. The resulting pellet was resuspended in 600 μL of buffer A and centrifuged for 1 min at 13,000 rpm. The supernatant was applied to a 25–50% sucrose gradient in buffer A and centrifuged for 45 min at 40,000 rpm. The gradient was fractionated and then analyzed by sodum dodecyl sulfate polyacrylamide gel electrophoresis and negative-stain electron microscopy. Finally, fractions enriched in recombinant vaults were concentrated to ∼5 mg/mL using a centrifugal filter device (Centricon YM-100, Millipore, Billerica, MA).

AFM

Measurements were performed with an AFM microscope (Nanotec Electrónica, Madrid, Spain) operating in Jumping mode plus (14). In this mode, the tip displaces laterally when it is far from the sample, and images are taken by performing force-versus-Z-piezo-displacement curves at all points. Most images were taken with a maximal force of ∼75 pN, which leads to average heights of 38 ± 2 nm and 35.5 ± 2 nm for reclining particles lying on the barrel and half-vaults, respectively. These values agree with the dimensions obtained by x-ray: 33.5 nm for half-vaults and 40 nm for reclining particles (3). Rectangular silicon-nitride cantilevers (RC800PSA, Olympus, Center Valley, PA) with a nominal spring constant of 0.05 N/m were used and calibrated by Sader’s method (15). The experiments were carried out under physiological conditions: one 20 μL drop of stock solution, consisting of vault particles under TMS buffer conditions, was incubated on a fresh highly ordered pyrolytic graphite surface (ZYA quality; NT-MDT, Tempe, AZ) and, after 30 min, washed with buffer until a volume of 60 μL was reached. The tip was also prewetted with a 20 μL drop of buffer.

To perform the nanoindentations, the Z-piezo was moved so that the top of the shell approached the cantilever tip at a loading rate of 60 nm/s. The bending of the cantilever, which indicated the force, was recorded simultaneously with a four-quadrant photodiode. These force-versus-Z-piezo displacement curves included the contribution of the cantilever and the particle. Therefore, we had to subtract the bending of the cantilever on the substrate to obtain the deformation of the particle. This procedure has been well established by the study of microtubules (16) and virus particles (17,18). Recently, a few reviews (12,13,19) have recapitulated the techniques and advances in this research field. The elastic constant of the particle was obtained from the slope of the initial linear part of the force-versus-indentation curve (FIC). The linear part of the indentation (regarding the elastic response of the shell) is sometimes preceded by a short-range nonlinear region due to electrostatic, van der Waals, and hydration forces (20,21). Therefore, we excluded this initial curvature when calculating the elastic constant of the particle. All the FICs were performed under identical experimental conditions, such as rate and kind of tip, to provide comparable parameters. Particles were imaged before and after curve sets of approximately five FICs. The values presented in Table 1 were obtained from 21 half-vaults and 13 reclining particles. The spring-constant value is the slope of the first curve performed on each particle. The breaking force, critical indentation, and energy were obtained by averaging 95 curves and 120 curves of 21 half-vaults and 13 reclining particles, respectively. This population size ranges within the typical number of curves found in the literature (16–18,22–25). To determine the energy supplied to the particle, we calculated the areas enclosed by the forward and backward curves.

Table 1.

Elastic constant, breaking force, and indentation at which shell ruptures

	K (N/m)	Fbreaking (pN)	Indentbreaking (nm)	Energy (kBT)	n
Half-vault	0.06 ± 0.03	165 ± 38	4 ± 2	302 ± 34	21
Reclining particle	0.03 ± 0.01	122 ± 83	3.9 ± 1.5	220 ± 34	13

The energy required for indentations at a given orientation is shown, as is the number of particles for each orientation. Values are given as the mean ± SD.

To check for any topographic change, we continued to scan with the AFM between FICs (Fig. S6 in the Supporting Material). To classify particles depending on their recovery times, we increased the statistics to raise the number of slow-recovery-time cases.

The experiments of mechanical fatigue consisted of consecutively imaging the particle at a constant force far below the breaking force of its structure (26). The imaging force was calculated as

$$\text{Imaging}\text{force }\left(\text{nN}\right)=K^{\text{cantilever}}\left(\raisebox{1ex}{$\text{nN}$}\!\left/ \!\raisebox{-1ex}{$\text{nm}$}\right.\right)\times \text{Calibration }\left(\frac{\text{nm}}{\text{V}}\right)\times \text{Set}\text{point }\left(\text{V}\right).$$

Force-versus-Z-piezo-displacement curves were performed on the substrate after each image to control the calibration of the system.

Finite-element model and tip-dilation model

Finite-element simulations were performed with FEMLAB 3.1 (Comsol, Zoetermeer, The Netherlands). The thick-shell model used in the simulation was designed to mimic the dimensions and geometry of the vault’s x-ray structure (assuming a wall thickness of 1.5 nm). The capsid wall was made of a homogenous material with a Poisson ratio of 0.3—similar to that used in other protein shells, such as viruses (12,13,22), and was meshed over 30,000 tetrahedral elements. To match the experimental curves with the simulation, the particle was indented with a 15-nm-radius sphere and Young’s modulus was varied until accordance between simulation and experiment was reached (16,18,24).

To create the model of a fractured vault, we used Sketchup (www.sketchup.com). The dilation process (27) was performed by implementing the algorithm provided by WSxM (28) with a 10-nm-diameter tip.

Results and Discussion

Surface attachment and AFM imaging

Once vaults are attached to a freshly cleaved highly ordered pyrolytic graphite surface, AFM imaging in jumping mode (14) reveals a variety of adsorption geometries. Fig. 1 B shows a general topography, where vaults present with three different orientations: as complete particles lying on either the barrel (reclining; white arrow) or the cap (yellow arrow), and as half-vaults adsorbed through the waist with the cap facing up (green arrow). Our study focuses on reclining particles and half-vaults, because the upright configuration is too unstable for experiments. AFM topographies reveal excellent agreement between the height of the particles and their nominal size (Fig. S1), thus excluding any effect of denaturation upon adsorption. AFM imaging at different feedback forces, a method used in previous studies with viruses (17,26), provides a first approach for testing the mechanical stability of vaults. Fig. 2 A presents a series of topographies in which a reclining particle and a half-vault are imaged under identical conditions.

Figure 2.

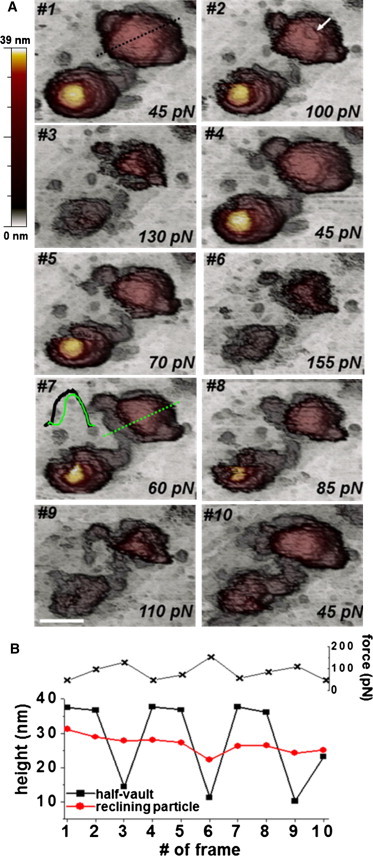
Dependence of vault stability on force imaging. (A) Sequential topographic images taken at ∼3 min intervals, each frame labeled with its corresponding imaging force. Scale bar, 50 nm. A comparison of the profiles (frame 7, inset) taken along the dotted lines of the topographies in frames 1 (dotted black line) and 7 (dotted green line) shows partial collapse of the structure. (B) Imaging force evolution (upper) and maximal height evolution of the half-vault (black) and the reclining particle (red). To see this figure in color, go online.

In this case, the imaging force is purposely changed from frame to frame (Fig. 2 B, black crosses), causing variations in the height of the structures. Topographies reveal that the reclining vault suffers some damage. For instance, in Fig. 2 A, a comparison between the topographies in frames 1 (black dotted line) and 7 (green dotted line) suggests partial collapse of the reclining structure at the barrel (frame 7, inset). In addition, the particle loses its height over time (Fig. 2 B, red circles). Despite these disruptions, however, in some frames we observe a partial recovery of the structure (Fig. 2, A and B, frames 4, 7, and 10). On the other hand, when the imaging force increases, the height of the half-vault structure is reduced abruptly from 36 nm to 15 nm (Fig. 2 B, black squares). Despite this large deformation, at lower imaging forces, the particle recovers its original height (Fig. 2, A and B). The ability to undergo such a large strain (∼60%) in a reversible manner, which was also reproducible for half-vault structures (Fig. S2), clearly demonstrates the remarkable structural stability of these particles under mechanical stress. In addition, the images show that the shell of the structure exhibits self-recovery capabilities on the local scale, as indicated by a fracture on the barrel structure that disappears over time (Fig. 2 A, frame 2, white arrow).

Stiffness and breaking force of individual particles

To investigate local phenomena rather than global deformations, we focused on performing individual nanoindentations on either a reclining particle or a half-vault (Fig. 3).

Figure 3.

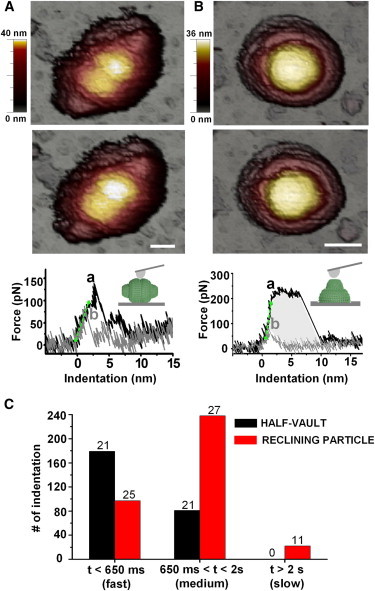
Indentation experiments on single vaults and histogram of the recovery time. (A and B) Images of a reclining particle (A) and a half-vault (B) before (upper) and after (middle) the FIC (lower). The forward curve (black) provides the elastic constant (slope of the initial linear part of the curve, green dashed line), the breaking force (maximum force reached, a), and the critical indentation (at a). The backward curve (gray) shows recovery during retraction of the tip. The same experiment performed on a half-vault. Shaded area in B represents the energy supplied to the vault during a FIC. Scale bar, 25 nm. (C) Histogram of the recovery time (RT) of both orientations. RT was classified as fast (RT < 650 ms), occurring during the retraction of the tip; medium (650 ms < RT < 2 s), occurring after the retraction of the tip but before the imaging of the particle; and slow (RT > 2 s), occurring during the imaging process. The histogram contains 260 FICs from 26 half-vaults (black) and 357 FICs from 28 reclining particles (red). Numbers of particles in the three RT ranges are shown above the bars. To see this figure in color, go online.

The single-indentation assay roughly consists of perpendicularly indenting an individual vault with the AFM tip. The tip is attached to a cantilever, whose bending is proportional to the force applied to the vault as it deforms (17). The resulting FIC provides information about the vault’s mechanical properties, such as stiffness (elastic constant) and breaking force (see Materials and Methods) (12,18,22). The slope of the linear part of the FIC after the mechanical contact between the tip and the sample (Fig. 3, A and B, lower) yields the elastic constant of the particle. The breaking force is defined as the maximum force reached before the drop (Fig. 3, A and B, lower, a). Our experiments provided average values for stiffness and breaking force of 0.03 ± 0.01 N/m and 122 ± 83 pN, respectively, for 13 reclining particles. These values increased to 0.06 ± 0.03 N/m and 165 ± 38 pN for 21 half-vaults (Table 1).

This result indicates that the stiffness value of half-vaults is double that of reclining particles. To check whether this result agrees with continuum mechanics, we constructed a finite-element model considering a shell with a geometry based on the x-ray structure of a vault (Fig. S3) (3). To reproduce the experimental curves with the simulation, the model was deformed with a sphere 15 nm in diameter, which mimics the apex of the AFM tip. The Young’s modulus of the vault was estimated by tuning the Young’s modulus of the model until the finite-element simulation coincided with the experimental data (see Materials and Methods). The procedure led to a value of 0.7 GPa, on the order of the Young’s modulus of other protein nanoshells (12).

Vault particles self-repair after rupture

The breaking force is a sign of particle damage, commonly ascribed to fracture of the structure induced by nanoindentation (29). To study these fractures, we focus on analyzing the forward and backward curves, because the area enclosed by them (i.e., Fig. 3 B, lower, shaded area) represents the energy supplied to the vault during a FIC (see Materials and Methods). The average energy provided to reclining particles and half-vaults was 220 ± 34 k_BT and 302 ± 34 k_BT, respectively (Table 1). In the forward curve, after a linear deformation (Fig. 3, A and B, lower), the structure of the vault fails, yielding to a steep drop in force. Experimentally, this feature would come from a permanent rupture of the structure (29–31), but here, the process seems to be reversible (32), as we observe a recovery of the force when the tip retracts (Fig. 3, A and B, lower, b). In fact, we use the point b to determine the recovery time (RT) during the FIC. The corresponding images of the particle before (Fig. 3, A and B, upper) and after (Fig. 3, A and B, middle) the FIC confirm that the vault structure remains intact. Interestingly, when we indented particles repeatedly, we found the same behavior (Fig. S4): all of the FICs show drops ascribed to ruptures, but the structure of the particle after the cyclic loading remains unaltered. This figure also suggests that the initial elastic behavior was restored after each fracture. In accordance with this, Fig. S5 shows that the average spring constant was maintained during at least the first indentation cycle (corresponding to five FICs).

Our results indicate that vault particles recover within a time frame on the order of 650 ms, which corresponds roughly to half the FIC time. Thus, the faster we image the failing structure, the greater the probability of monitoring any topographic change. To achieve this, we register the topographic evolution of the vault by switching off the y-scan and enabling only the x-scan (Fig. S6). Thus, we obtain a kymograph (Fig. S6, A and D, middle) that displays the height of the particle immediately after each indentation. In this way, we observed 22 events of reversible topographic damage in 11 different reclining particles, corresponding to RTs >2 s (the time span of a single FIC).

In addition, we found that some backward curves do not exhibit force recovery, even though the vault structure remains unaltered (Fig. S6 E, curves 1 and 7). We interpret these cases as corresponding to vaults that recuperate from failure after the tip is removed from the vault surface but do so before the particle is imaged, which corresponds to RTs between 650 ms and 2000 ms. To compare the recovery behavior of reclining particles and half-vaults, we classified FICs according to their RTs. We defined fast recovery as restoration of force during the backward curve (RT < 650 ms), medium recovery as when no restoration of force is observed but the subsequent topography shows an intact particle (650 ms < RT < 2 s), and slow recovery as when AFM imaging allows monitoring of the topography of the fractured vault (RT > 2 s). The histogram in Fig. 3 C, which classifies 617 FICs for 26 half-vaults and 28 reclining particles, shows that half-vaults recover their initial shape faster than do reclining particles. Indeed, 70% of the FICs on half-vaults (179 of 260) show a recuperation occurring before 650 ms, whereas only 22% of the FICs on reclining particles (97 of 357) do so.

The role that the bending and stretching energies play after the fracture could explain this difference in RT. Thin-shell theory predicts that more energy is needed to deform a spherical shell than to deform a cylindrical shell due to the ability of a cylinder to bend without much in-plane stretching (33). A vault particle can be considered as a spherocylinder whose stiffnesses in its spherical (k_sph) and cylindrical (k_cyl) parts are related by $k_{\text{sph}}/k_{\text{cyl}}\sim \sqrt{\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$h$}\right.}\sim 3.65$ (33), where R and h are the radius of the cylinder (R = 20 nm) and the wall thickness (h = 1.5 nm), respectively. By considering k_half-vaults and k_reclining as k_sph and k_cyl, respectively, our result, $k_{\text{sph}}/k_{\text{cyl}}\sim 2$, coincides with the trend predicted by the theory. Therefore, when the tip induces a fracture on the half-vault, the in-plane stress spreading over this structure (which is not present after the rupture of a reclining particle) may trigger a faster recovery.

Vault fractures occur along MVP-MVP contacts

Although continuum elastic theory provides an understanding of particle elasticity, the discrete protein structure of vault particles is required to investigate the fractures. Molecular model simulations (34) suggest that the abrupt changes in the indenting force (i.e., a in Fig. 3 A, lower) are due to the breakage of molecular bonds. Therefore, a correct interpretation of the fracture mechanism requires a revision of all inter- and intrasubunit noncovalent contacts. The building block of the vault particle is the MVP molecule. The x-ray structure of the entire vault reveals that the strongest MVP-MVP contacts are found between cap-helix domains, where hydrophobic interactions dominate the packing (29 of the 41 pairs of residues forming the interface between two adjacent helices are hydrophobic). The intermolecular interactions in the central barrel are weaker, mainly involving polar contacts (16 hydrogen bonds, 5 ionic bonds, and 10 hydrophobic contacts) (3,35,36). To roughly estimate the difference in interaction energy between these two regions we determined the noncovalent interactions of two consecutive MVP molecules using the program HBPLUS implemented in the package DIMPLOT (37,38). The energy values of −1.5 kcal/mol, −4.5 kcal/mol, and −40 kcal/mol, associated with hydrophobic interactions, hydrogen bonds, and ionic pairs, respectively, were taken from Brändén and Tooze (39). Using these values we find that the bonding energy between two α-helices is approximately four times higher than the bonding energy between two β-sheet domains. From an energetic point of view, this indicates that the fractures should appear in the barrel. In addition, our AFM experiment shows that the average energy supplied in a breakage-recovery cycle is 220 ± 34 k_BT for reclining particles and 302 ± 34 k_BT for half-vaults. These values are in the same order of magnitude, suggesting that the work needed to produce a fracture is similar for both orientations.

To study these fractures in more detail, we can also focus on the slow fracture-recovery cases (RT > 2 s), which lasted long enough to enable a complete AFM image of the damaged area before the recovery (Figs. 4 and S7). The AFM topographies in Fig. 4 A show the evolution of one reclining particle that recovered its initial shape within 90 s, the time required to take a complete AFM image. Fig. 4 A, middle, shows that the rupture was produced in the direction in which MVPs align. Profiles ε and γ in Fig. 4 B represent the evolution in height of the fractured area along the transverse and longitudinal directions respectively, of the vault. The black and green curves, which are the height profiles before and after the fracture, provide direct evidence of recuperation. Likewise, the red profiles depict the fractured zone: the ε-profile shows that the topographic outline is cut by a sharp fall, whereas the γ-profile reveals that after the increase in height the topography decreases monotonically. This result confirms that the transient breakage is produced in the barrel, and in addition, it allows us to study the pattern of fracture. The other slow-recovery cases (Fig. S7) also support the longitudinal fracture of the barrel, showing that the lines of rupture are aligned with the MVP-MVP contacts, independent of the orientation of the particle with respect to the scan direction. To interpret these data, we created a model that simulates the rupture (Fig. 4 D, upper). When the line of fracture is produced through the MVP-MVP contacts of the barrel, the ε- and γ-profiles of the geometrical tip-dilated model (27) (Fig. 4 D, lower) show excellent agreement with the experimental data (Fig. 4 B, blue lines).

Figure 4.

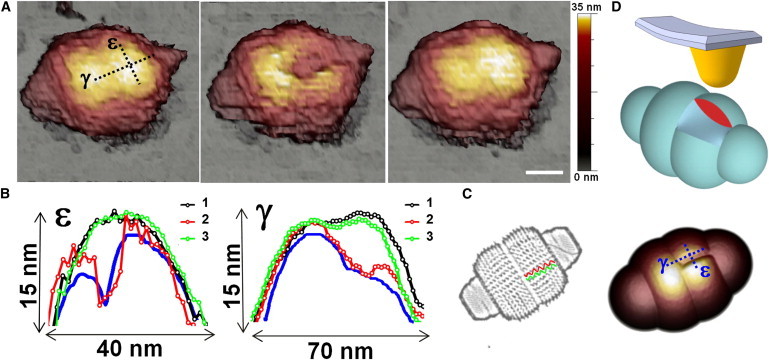
Reversible fracture. (A) Topographical images of a particle before fracturing (left), after fracturing (middle), and after recovery (right). Lines labeled ε and γ indicate the transverse and longitudinal directions, respectively. Scale bar, 35 nm. (B) Profiles of ε and γ (dotted black lines in A) before the fracture (black), after the fracture (red), and after the recovery (green). Blue lines are ε and γ profiles from the tip-dilation model in D. (C) Fracture is produced between the β-sheet domains of two neighboring MVPs (green and red lines). (D) Dilation model, showing a sketch of a fractured vault (upper) and a tip-dilation simulation (lower). To see this figure in color, go online.

Although the above analysis provides an overview of the pattern of fracture, the interpretation of single FICs is not trivial, as each case may depend on several uncontrolled factors, such as the shape and dimension of the tip or the relative tip-particle orientation. Despite this qualification, our data unequivocally indicate that the FICs show different features depending on the adsorption geometry (Fig. 5). For reclining particles, the force after the rupture exhibits several peaks (Fig. 5 A), whereas for half-vaults, the force exhibits a single peak (Fig. 5 B). This result suggests that direct contact between the tip and the barrel makes it possible to register the sequential separation of the β-sheet domains, which cannot be observed in half-vaults because the cap distributes the stress globally over the barrel. The pattern of the peaks for reclining particles suggests a sequential zipper-like breakage of bonds. Each of these peaks is likely caused by a fracture event, with the dissipated energy defined by the area under the curve (Fig. 5 C, inset, shaded area). This area represents the difference in work between deforming a particle with and without a breakage (16). For a rough calculation, we can estimate this area from the average distance and force of these steps (Δz = 1.3 ± 0.95 nm and 117 ± 50 pN). This result gives an average energy of ∼20 k_BT. We can compare this value to the strength of the noncovalent interactions that govern the assembly of the barrel domains, 2 k_BT for hydrophobic interactions and 8 k_BT for hydrogen bonds (39). Therefore, the energy of each peak could account for a few of these noncovalent interactions.

Figure 5.

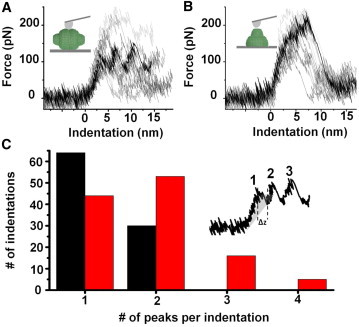
FIC patterns depend on vault orientation. (A and B) FICS for 21 indentations performed on 21 different reclining particles (A) and 13 indentations performed on 13 different half-vaults (B). (C) Histogram of the number of peaks counted in each indentation for 21 half-vaults (black) and 13 reclining particles (red). (Inset) Example of an indentation performed on a reclining particle, showing three peaks. The shadowed area indicates the work needed for a single fracture event. This area was calculated by the difference between the measured FIC and the backward extrapolation from the curve after the step. The obtained average energy of these steps was ∼20 k_BT. To see this figure in color, go online.

The barrel of the vault governs its structural strength

Consecutive AFM imaging at different forces provokes the disruption of some areas in the β-sheet region, whereas the α-helix domains of the cap remain unaltered (i.e., Fig. 2 A, frame 2). To determine whether this also happens under constant force, we performed fatigue experiments on half-vaults (26) (see Materials and Methods) and confirmed that the barrel was the region where the breakage first occurred (Figs. 6 and S8, and Movie S1).

Figure 6.

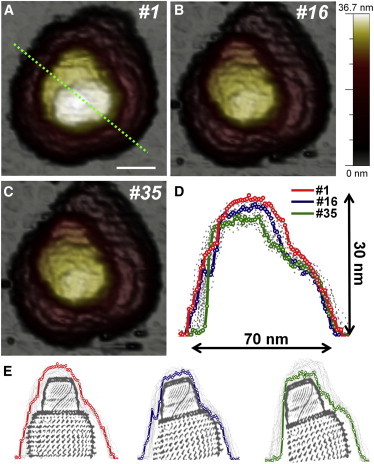
Mechanical fatigue of a half-vault. This particle was imaged along 37 frames at an imaging force of 65 pN (Movie S1). (A–C) Topographical images corresponding to frames 1, 16, and 35, respectively. Scale bar, 25 nm. (D) Evolution of the profile taken along the dotted line in frame 1. The profiles corresponding to frames 1, 16, and 35 are depicted in red, blue, and green, respectively. The rest of the profiles are depicted with dotted gray lines. (E) Sketch of the disruption suffered by the particle. To see this figure in color, go online.

Fig. 6 shows that, as a consequence of the disruption of the β-sheet region, the cap tilted and the particle lost its axial symmetry. Thus, the barrel structure is more prone than the cap to mechanical fatigue. It is tempting to relate this behavior to the lower interbonding energy of β-sheets (barrel) compared to that of α-helices (caps). Likewise, the intertwined and interwoven geometry of the α-helices, in contrast to the aligned orientation of the β-sheet domains, already suggests a greater mechanical stability in the cap region.

We also found that gentle variations in imaging force brought out striking differences in relative deformation between the two orientations. Whereas half-vaults underwent strains of ∼60%, reclining particles deformed by ∼10% (Figs. 2 and S2). The relatively small and continuous deformation observed in reclining particles may be caused by local bending and rearrangement of barrel proteins (41). In this case, the geometry of the system imposes a direct contact between the tip and the β-sheet domains. On the other hand, the large strain on half-vaults might be due to a global deformation. Half-vaults exhibited a quantized response in which, under mechanical stress, the height of the particle was reduced to 15 nm, which corresponds to the size of a cap alone (Fig. 1 A). Thus, an increase in the imaging stress on half-vaults provokes complete deformation of the barrels, whereas the caps maintain their shape—an idea that further supports the ability of vaults to open into flowerlike structures (42). All these data, together with the fact that we have only detected fractures on the barrel surface (Fig. S7), prove that the barrel is the structure that governs the mechanical strength of both adsorption geometries.

Biological implications and new insights into self-healing dynamics

Several studies have revealed that the exterior shell of the vault is a dynamic structure capable of breathing, so to speak, and transferring material from the environment to its interior (43). Although the precise function of vaults remains unclear, it is widely accepted that they act as cellular transporters (2). Our experiments unveil to our knowledge new dynamics of this nanostructure induced by mechanical stress. We demonstrate that the bonds between MVPs are able to self-repair simply by being in a liquid environment at room temperature. This feature indicates that these particles are highly adaptive to mechanical deformations, thus making them safe nanoplatforms capable of adapting to certain geometric constraints. In fact, these particles may be capable of translocating material through the nuclear pore complex (44,45), a gate with a functional diameter of 39 nm (46), below that of the vault (40 nm).

Vaults are promising drug delivery systems due to their biocompatibility and recent success in the engineering of targeted vaults with controllable release (47). Vault particles exhibit a highly regulated opening mechanism to efficiently incorporate and deliver a specific cargo. Thus, understanding vault dynamics is a necessary step toward comprehending their regulatory mechanism. Fracture recovery is likely related to the nature of the interdomain interactions, the thermal shaking of these broken inter-MVP bonds in a liquid milieu, and the geometry imposed by the vault. In this case, the interdomain unions of β-sheets (which are mainly due to ionic and hydrogen-bond interactions) are labile enough to allow particles to undergo reversible conformational changes at low energy inputs. In fact, the stress threshold that vaults must reach before breakage occurs is lower compared with those of other molecular shells: the force at which vaults rupture is at least five times lower than the breaking forces of other nanoshells with a similar Young’s modulus (17,22,29–31). On the other hand, vault particles seem optimized to self-repair after fracture. Although it has been suggested that these self-healing capabilities may be present in other protein cages (16,32,48), our experiments reveal a systematic fracture-recovery mechanism that has been topographically monitored for the first time, to our knowledge. Indeed, it seems that vaults may have evolved to facilitate low-energy conformational changes that reverse easily. The rare self-healing dynamics of the vault, apart from likely being related to their function inside the cell, could inspire nanomaterial science in the creation of engineered nanocontainers.

Conclusions

We have characterized the mechanical properties of individual vaults by performing indentations on reclining particles and half-vaults adsorbed at their waists. Our results demonstrate that vaults exhibit striking self-healing capabilities that enable them to quickly recover from fracture. Also, we found that this rupture consists of separating two neighboring MVPs in the barrel structure. We believe that these insights into vault dynamics will add valuable information to the current understanding of the role and function of these enigmatic particles and will lend support to the idea that they can be used as nanocontainers.

Supporting Material

Movie S1. Mechanical fatigue of a half-vault

This movie indicates the temporal evolution of Fig. 6.