Abstract
Because fibroblasts deposit the collagen matrix that determines the mechanical integrity of scar tissue, altering fibroblast invasion could alter wound healing outcomes. Anisotropic mechanical boundary conditions (restraint, stretch, or tension) could affect the rate of fibroblast invasion, but their importance relative to the prototypical drivers of fibroblast infiltration during wound healing—cell and chemokine concentration gradients—is unknown. We tested whether anisotropic mechanical boundary conditions affected the directionality and speed of fibroblasts migrating into a three-dimensional model wound, which could simultaneously expose fibroblasts to mechanical, structural, steric, and chemical guidance cues. We created fibrin-filled slits in fibroblast-populated collagen gels and applied uniaxial mechanical restraint along the short or long axis of the fibrin wounds. Anisotropic mechanical conditions increased the efficiency of fibroblast invasion by guiding fibroblasts without increasing their migration speed. The migration behavior could be modeled as a biased random walk, where the bias due to multiple guidance cues was accounted for in the shape of a displacement orientation probability distribution. Taken together, modeling and experiments suggested an effect of strain anisotropy, rather than strain-induced fiber alignment, on fibroblast invasion.
Introduction
Effective management of wound healing is an important clinical problem. In the United States alone, it is estimated that 37 million people per year suffer wounds from burns (1 million/year), automobile accidents (2 million/year), and surgical procedures (34 million/year) (1). Both delayed wound healing and prolonged wound healing can lead to adverse outcomes (2), such as disfigurement and impairment of limb or organ function (1). After myocardial infarction (1 million incidents per year in the United States), wound healing determines the risk of fatal complications such as infarct rupture and heart failure (3).
For roughly a century, mechanical boundary conditions (restraint, stretch, or tension) have been known to regulate wound healing (4), but mechanical effects are not yet sufficiently understood to inform effective management strategies (5). Release of isometric mechanical restraint applied to healing skin wounds has been shown to promote wound shrinkage, apoptosis of granulation tissue cells, and transition to mature scar (6,7). However, unloading of ruptured ligaments has been associated with abnormal organization of fibroblasts and collagen fibers in the scar and poor mechanical strength (8). After myocardial infarction, mechanically unloaded hearts had smaller scars with less fibrosis but prolonged inflammation and a disorganized collagen fiber structure (9). A moderate level of unloading of intestinal anastomoses was found to promote healing better than low or high unloading (10). Overall, mechanical tension is needed to support angiogenesis and extracellular matrix synthesis through proliferation of endothelial cells and fibroblasts and through differentiation of fibroblasts into myofibroblasts (11). Yet, excessive or abnormal scarring tends to occur in locations subjected to high levels of stretch, suggesting that mechanical environment can also promote pathological scar formation (11).
Although the role of mechanical tension in promoting proliferation, suppressing apoptosis, stimulating differentiation of fibroblasts into myofibroblasts, and upregulating matrix synthesis has been documented using both in vivo (6,7,11,12) and in vitro (13–17) wound models, few studies have focused on the effect of mechanical boundary conditions on fibroblast migration during wound healing. Because invading fibroblasts play a key role in replacing the provisional fibrin matrix of the wound with a collagen matrix that determines the mechanical integrity of the scar (18,19), altering fibroblast migration could alter wound healing outcomes. For example, a recent computational model predicted that delayed accumulation of myofibroblasts would cause wounds to expand, whereas prolonged survival of myofibroblasts would cause hypertrophic scarring (20).
Mechanical boundary conditions may regulate fibroblast migration in two ways. First, the speed of fibroblast migration has been shown to depend on substrate stiffness in two-dimensional (21) and three-dimensional (22) environments, and mechanical restraint, tension, or stretch can increase the apparent stiffness of the wound matrix (22). Second, anisotropic mechanical boundary conditions, such as uniaxial restraint, tension, or stretch, applied to cell-populated three-dimensional matrices have been shown to cause fibroblasts and other cells to preferentially align (23–28) and migrate (25,29) parallel to the axis of restraint, strain, or tension. Anisotropic mechanical boundary conditions could therefore have a twofold effect on the rate of fibroblast invasion 1), by increasing the apparent stiffness of the wound matrix, which could enable faster migration, and 2), by establishing an anisotropic strain or stiffness field sensed locally by fibroblasts, which could guide the trajectories of fibroblasts and consequently increase the efficiency of migration.
The importance of anisotropic mechanical boundary conditions relative to the prototypical drivers of fibroblast infiltration during wound healing is unknown. Fibroblast invasion is thought to be driven primarily by steric and chemical guidance cues. Because fibroblasts exhibit contact inhibition of locomotion (30), where collision of migrating cells causes reversal of front-rear polarity (31), the cell concentration gradient that develops as fibroblasts accumulate at the wound periphery will promote polarization and directional migration of fibroblasts away from the region of high cell concentration and into the wound (32). In addition, gradients of chemokines such as platelet-derived growth factor (PDGF), which are secreted by inflammatory cells that populate the wound site before fibroblast invasion, are considered strong drivers of directional migration of fibroblasts into wounds (19,33). Taken together, contact inhibition of locomotion and chemotaxis constitute an invasion guidance cue that directs fibroblast migration normal to the wound interface. It is unknown whether a mechanical guidance cue created by anisotropic mechanical boundary conditions can perturb the effect of this invasion cue.
We developed a wound healing model using a three-dimensional collagen-fibrin gel composite that would allow us to address questions about the interaction of guidance cues during wound healing in a controlled, readily observable setting. Our goal was to test the hypothesis that anisotropic mechanical boundary conditions increase the directionality and speed of migration of cardiac fibroblasts into a model fibrin wound. We also tested whether the response of fibroblasts to the anisotropic mechanical boundary conditions could be explained by strain-induced alignment of the wound matrix. Finally, we developed a computational approach for predicting the migration behavior of fibroblasts in response to the combinations of guidance cues encountered in our experimental wound healing model. We found that anisotropic mechanical boundary conditions can guide fibroblast migration during wound healing and represent a potential means not only of patterning the structure of the scar tissue, but also of accelerating the healing process.
Materials and Methods
Fibroblast-populated collagen gels were cast in square molds. An incision made in the center of each gel was filled with fibrin to simulate a wound. Uniaxial mechanical restraint was applied to the gels along the short or long axis of the fibrin wound. After two days of culture, cell nuclei were fluorescently imaged. The distribution of cells that migrated into the incision was fit to the diffusion equation to compute the apparent diffusion coefficient as a measure of the rate of infiltration of fibroblasts. Wound remodeling strains were measured from 0 to 2 days after creating the wounds as an indicator of the mechanical conditions within the wound. Fiber alignment within the fibrin wound matrix was quantified at 0 and 2 days after wounding to investigate the role fiber alignment may play in mediating any mechanical effect on fibroblast migration. Migration tracks of individual cells in the wound region were measured 1 day after wounding, and a computational model of fibroblast migration was used to infer what combination of guidance cues could explain the observed migration tracks.
Adult cardiac fibroblast isolation and culture
Cardiac fibroblasts were isolated and cultured using previously published methods (34). Briefly, ventricles were removed from Sprague-Dawley (Charles River, Wilmington, MA) rats (6 weeks old, weighing 180 g), minced into 1–3 mm pieces, and digested with Liberase Blendzyme 3 (Roche, Indianapolis, IN). Cells were recovered by centrifugation for 10 min at 400 × g, resuspended in cell culture medium (CCM) consisting of Dulbecco’s modified Eagle medium (DMEM, Sigma-Aldrich, St. Louis, MO) supplemented with 10% fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), 100 U/mL penicillin (Sigma-Aldrich, St. Louis, MO), 100 g/mL streptomyocin (Sigma-Aldrich, St. Louis, MO), and 2 ng/mL amphotericin B (Sigma-Aldrich, St. Louis, MO)), and transferred to cell culture flasks. After 4 h, the flasks were rinsed with phosphate-buffered saline (PBS, Sigma-Aldrich, St. Louis, MO) to remove nonadherent cells. Cardiac fibroblasts were maintained in an incubator at 37°C and 5% CO2. Cells were passaged 4 days after isolation, cultured for 2 more days, and harvested for use in experiments.
Fabrication of fibroblast-populated collagen-fibrin hydrogels
Fibroblast-populated collagen gels were created by mixing 0.2 M HEPES (Sigma-Aldrich, St. Louis, MO) (pH 9), 10× MEM (Sigma-Aldrich, St. Louis, MO), 3 mg/mL type I bovine collagen (PureCol, Advanced Biomatrix, San Diego, CA), and cells suspended in CCM at a ratio of 1:1:8:2 (34) to achieve final concentrations of 2 mg/mL collagen and 200,000 cells/mL. The collagen mixture was incubated with gentle agitation for 15 min, thoroughly mixed by pipetting, and 2.5 mL aliquots were distributed in a six-well plate that contained molds cut from porous polyethylene (Bel-Art, Wayne, NJ). Plastic rings were placed on top of the molds to prevent them from floating. After a 2 h incubation to polymerize the collagen solution, the gels were released from the bottoms of the wells, rinsed with PBS, and suspended in 2.5 mL CCM/well.
The porous polyethylene molds were discs 3.25 cm in diameter and 3 mm in thickness with a 1.5 × 1.5 cm square cut out of the center. The molds were pretreated with concentrated sulfuric acid (Sigma-Aldrich, St. Louis, MO) for 3 days to improve absorption of the collagen mixture, dialyzed for 3 days with deionized water, dried, and then sterilized in an autoclave (35). The six-well plates were precoated with bovine serum albumin (Sigma-Aldrich, St. Louis, MO) to prevent the gels from sticking to the polystyrene surface (34).
After incubation for 24 h, a fibrin wound was created in each collagen gel (Fig. 1 a). A 5 mm slit was cut in the center of the gel using a razor blade. The gel was rinsed with PBS and transferred to a new well, and 1 mL of a fibrinogen mixture was poured under and over the collagen gel to fill in the slit. The polyethylene mold was again locked in place with a plastic ring and the gel was incubated for 1 h to polymerize the fibrinogen mixture. The gel was then rinsed with PBS and suspended in 2.5 mL CCM supplemented with 100 ng/mL PDGF-BB, 100 ng/mL insulin-like growth factor-1, and 50 μg/mL ascorbic acid (Sigma-Aldrich, St. Louis, MO) to promote fibroblast migration and collagen secretion (36–38). Finally, a uniaxial mechanical boundary condition acting along either the short or long axis of the fibrin wound was imposed by cutting two opposing sides of the gel free from the polyethylene mold.
Figure 1.

Examples of the three-dimensional collagen-fibrin model wounds. (A) Fibroblast-populated collagen gels (CG) were cast in square polyethylene molds (M) and slits cut in the collagen gels were filled with fibrin gel (FG). Uniaxial mechanical restraint acted either along the short or long axis of the elliptical fibrin wounds (FE, free edge; RE, restrained edge). The images shown were taken 1 day after creating the fibrin wounds. The intensity histograms of these images were adjusted to improve contrast in grayscale. (B and C) Two days after creating the wounds, cell nuclei were stained with DAPI, the fibrin wounds were imaged, and cell coordinates (C, solid circles) and border coordinates were mapped (C, black curve). We quantified migration of fibroblasts across a gap of length L and width W (B, white box; C, dark circles). On each side of the wound, a coordinate system was defined with centroid at the wound edge and +x-direction toward the wound center (B).
The fibrinogen mixture was prepared by mixing 0.5 mL of 6 mg/mL fibrinogen, 0.5 mL of CCM, 1 μL of 1 M CaCl2, 1 μL of 100 μg/mL aminocaproic acid (Sigma-Aldrich, St. Louis, MO), and 2.5 μL of 100 U/mL thrombin (Sigma-Aldrich, St. Louis, MO) (38). Thrombin was not added until just before adding the mixture to the collagen gels. Some fibrin gels were prepared with 5 × 105 particles/mL of 10 μm latex microspheres to calculate the migration paths of cells relative to the surrounding matrix.
Microscopy and histology
The collagen-fibrin gels were cultured for two days. For the gels with microspheres embedded in the fibrin gel, after 1 day, the fibrin wounds were imaged on a light microscope with a 4× objective every hour for a total of 6 h. After 2 days, gels were fixed for 24 h in 4% paraformaldehyde (Sigma-Aldrich, St. Louis, MO), cell nuclei were stained with 4′,6-diamino-2-phenylindole (DAPI, Life Technologies, Carlsbad, CA), and the fibrin wounds were imaged at 4× on a fluorescence microscope. Some gels were processed for paraffin embedding, cut into 10 μm sections, and stained with eosin (Sigma-Aldrich, St. Louis, MO). Then fibrin fiber structures were imaged on a confocal microscope using a 60× objective with excitation at 543 nm and acquisition at 590 nm (Fig. S1 a in the Supporting Material) (39). We selected fields located along the short axis of the wound that were devoid of cells to avoid capturing any local, fibroblast-mediated remodeling of the wound matrix.
Quantification of cell migration characteristics
For the analysis of cell distributions after two days of migration, the border of the wound region was fit to an ellipse and the coordinates of the DAPI-stained cell nuclei were automatically acquired with a custom image processing algorithm implemented in Matlab that identified intensity peaks after background subtraction and noise filtering (Fig. 1, b and c). In a subset of images, coordinates of cell nuclei were measured manually to verify the accuracy of the automated approach. We restricted our analysis to cells that entered from the sides of the wound. The region of interest had length L that spanned the short axis of the wound and width W that spanned the middle third of the long axis of the wound. We calculated the cumulative number of cells (N) as a function of distance (x) from the edge of the wound to the center of the wound at t = 48 h after wounding. We averaged data from both sides of the wound into a single plot. Similar to the quantitative analysis of the linear under-agarose migration assay employed by Lauffenburger (40), we solved for an apparent diffusion coefficient (D) as a measure of the rate of fibroblast invasion by fitting each cumulative cell distribution to the solution of the diffusion equation for one-dimensional unsteady diffusion into a space with symmetric, constant concentration boundary conditions (Co).
| (1) |
For the analysis of cell migration tracks, coordinates of cells and microspheres were acquired manually from the time lapse images using ImageJ. Only cells within the center third of the long axis of the wound were analyzed. For each 1 h time interval and each tracked fibroblast, we computed the displacement of the fibroblast relative to the centroid of nearby microspheres (within a 500 μm radius). Migration tracks were calculated as the cumulative sum of these displacements over time. Mean-squared displacements (<d2>, <x2>, <y2>, straight-line distance from start point to end point) and mean-squared path lengths (<dp2>, <xp2>, <yp2>, cumulative distance from start point to end point through all intermediate points) were calculated using overlapping time intervals for the two-dimensional cell motions (d) and for the short (x) and long (y) axis components of the motions, as in the study by Dickinson et al. (41). The apparent orientation and apparent speed of each cell displacement were calculated as the angle of each displacement and as the magnitude of each displacement divided by the time step (1 h).
Quantification of fibrin wound deformation and matrix structure
To assess how the application of uniaxial mechanical restraint at the edges of the collagen gel affected the mechanical conditions within the fibrin wound, the short- and long-axis dimensions of the wound were measured at the beginning and end of the experiment, and remodeling strains were computed. We defined a metric of mechanical (or strain) anisotropy (ΔE) as the short-axis remodeling strain (ES) minus the long-axis remodeling strain (EL).
To test for fiber alignment within the wounds, we used Fiber3, an automated gradient detection algorithm, to measure the fiber orientation within subregions of each confocal image of the fibrin matrices (42) and then generated average fiber orientation histograms. We used the mean cosine of doubled fiber angles (<cos(2θ)>) as a metric of structural anisotropy, which has a range from −1 to 1, where positive values indicated fiber alignment along the short axis and negative values indicated fiber alignment along the long axis (34,41).
Computational model of fibroblast migration
We developed a computational model of fibroblast migration to infer environmental guidance cues from measurements of cell migration behavior. Guidance cues can be unidirectional or bidirectional. Unidirectional guidance cues, such as chemotactic or haptotactic gradients, cause cells to prefer a single direction of migration, whereas bidirectional guidance cues, such as uniaxial strain or aligned fibers, cause cells to prefer an axis of migration. We assumed these migration biases could be described with displacement orientation probability distributions. We used a single wrapped normal probability density function for a unidirectional guidance cue. We used the average of two identical wrapped normal probability density functions offset by 180° for a bidirectional guidance cue.
The wrapped normal distribution () is defined by a mean angle () and mean vector length (), which can vary from 0 to 1, where 0 indicates no alignment and 1 indicates perfect alignment (43). We used the mean angle and mean vector length to define vectors, which we called displacement probability vectors (), associated with each wrapped normal distribution.
| (2) |
| (3) |
We assumed that when a unidirectional and bidirectional guidance cue act simultaneously, the resultant displacement orientation distribution () can be determined by computing a weighted sum of the unidirectional displacement probability vector () with each of the bidirectional displacement probability vectors ( and ) using normalized weight factors ( and ), and then averaging the wrapped normal probability density functions associated with each of the resultant displacement probability vectors ( and ) (Fig. 2, a and b).
| (4) |
| (5) |
| (6) |
Similar to the approach of Codling et al. (44), we simulated fibroblast migration as a biased random walk. We chose a displacement frequency of and displacement magnitude of (adjusted as part of the optimization described below) and computed cell displacements for a sequence of orientations randomly sampled from a resultant displacement orientation distribution (). We simulated the migration of 50,000 fibroblasts and saved cell positions every hour for 5 h of simulated time (Fig. 2 c).
Figure 2.
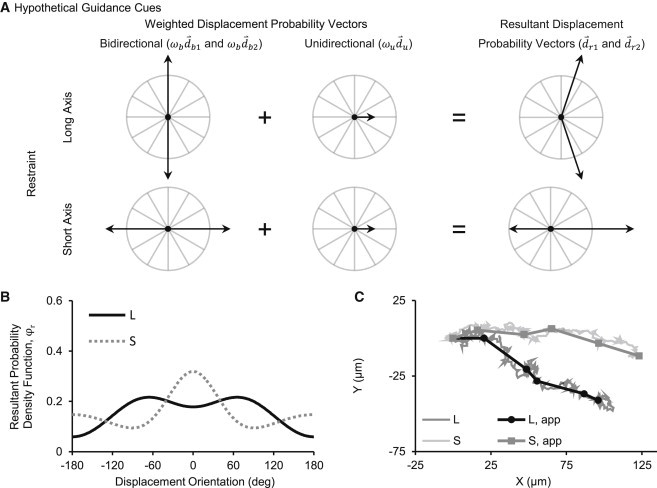
Computational model of fibroblast migration guided by environmental cues. (A) We computed resultant displacement probability vectors () as weighted sums of displacement probability vectors representing individual cues: a bidirectional cue (), due to mechanical or structural anisotropy, oriented along the axis of mechanical restraint; and a unidirectional invasion cue () oriented toward the center of the wound. (B) Then we calculated the associated resultant displacement orientation distribution () for long-axis restraint (L) and short axis restraint (S). (C) Finally, we simulated migration tracks by randomly sampling the distribution to determine the orientation of each incremental cell displacement. We generated apparent migration tracks (Lapp and Sapp) for comparison to our experimental data by saving the positions of the simulated cells after every hour of simulated time.
We considered the possible existence of two guidance cues: a bidirectional guidance cue, due to mechanical and/or structural anisotropy, oriented along the axis of mechanical restraint ( for long-axis restraint and for short-axis restraint); and a unidirectional invasion guidance cue, due to contact inhibition and/or chemotaxis, oriented toward the center of the wound (). Three free model parameters—the displacement magnitude () and the effective magnitudes of the bidirectional and unidirectional displacement probability vectors ( and )—were determined by fitting model results to experimental data. A multiparameter, multiobjective optimization problem was solved via exhaustive search to find the parameter values that minimized the weighted sum of 1), the error fitting the apparent orientation histogram, and 2), the error fitting the average apparent speed versus apparent orientation curve. We found that the optimization was insensitive to the weighting of the objectives and therefore averaged the optimal parameter values for objective weight factors ranging from 0.01 to 0.99.
Statistics
The unpaired two-tailed Student’s t-test was used to test whether the apparent diffusion coefficient (Dapp) differed significantly between the short-axis and long-axis restraint groups. The one-sample two-tailed student’s t-test was used to test whether mechanical anisotropy (ΔE) and structural anisotropy (<cos(2θ)>) differed significantly from a hypothetical value of zero.
Results
Mechanical environment within fibrin wounds
We restrained the collagen gels along either the short axis or long axis of the fibrin wounds to create different mechanical environments within the wounds, which we characterized by measuring wound remodeling strains between 0 and 2 days after creating the wounds. For short-axis restraint, the wounds stretched slightly along the short axis and compacted along the long axis (Table S1). The mechanical anisotropy was (), suggesting the presence of a mechanical guidance cue (Fig. 3 a). For long-axis restraint, the wounds compacted slightly and equally along both axes (Table S1). The mechanical anisotropy was (), suggesting the absence of a mechanical guidance cue (Fig. 3 a).
Figure 3.

Mechanical anisotropy, structural anisotropy, and rate of fibroblast infiltration. (A) Wound remodeling strains indicated that the wounds subjected to long-axis restraint compacted isotropically, whereas the wounds subjected to short-axis restraint stretched along their short axis and compacted along their long axis, and thus deformed anisotropically. N = 28 gels for short-axis restraint and 24 gels for long-axis restraint. (B) Wound fiber orientations indicated that fibrin fibers were weakly but significantly aligned along the axis of restraint for both groups. N = 4 gels for both groups. (C) Two days after creating the wounds, we calculated the cumulative number of cells (normalized by the concentration of cells in the collagen gel multiplied by the area of the observation window) as a function of distance (normalized by the short-axis length of the wound) from the edge to the center of the wound. More fibroblasts traveled farther into the fibrin wounds with short-axis restraint (S) than with long-axis restraint (L). We fit the diffusion equation to the cumulative distributions (L, fit and S, fit). (D) The apparent diffusion coefficients derived from the fits (Dapp) indicated that fibroblasts infiltrated the wounds along the short axis faster with short-axis restraint than with long-axis restraint. N = 28 gels for short-axis restraint and 24 gels for long-axis restraint.
Fiber alignment within fibrin wounds
We measured the strength of alignment of fibrin fibers in the wound matrix to test for structural guidance cues. Immediately after creating the wounds, fibrin fibers were slightly aligned along the long axis of the wound for both long-axis and short-axis restraint (Fig. S1 b). Two days after creating the wounds, fibrin fibers became slightly more aligned along the long axis of the wound for long-axis restraint, whereas fibrin fibers became slightly aligned along the short axis of the wound for short-axis restraint (Fig. S1 b and Table S1). For short-axis restraint, the structural anisotropy was (), suggesting the presence of a weak structural guidance cue (Fig. 3 b). For long-axis restraint, the structural anisotropy was (), suggesting the presence of a somewhat stronger structural guidance cue (Fig. 3 b).
Rate of infiltration of fibroblasts into fibrin wounds
We measured the cumulative distribution of fibroblasts along the short axis of the fibrin wounds to test whether the rate at which fibroblasts entered the wounds depended on the mechanical boundary conditions. More fibroblasts traveled farther into the wounds along the short axis when mechanical restraint acted along the short axis than when mechanical restraint acted along the long axis (Fig. 3 c). We obtained apparent diffusion coefficients from fits of the diffusion equation to the cumulative distributions (Table S1). The apparent diffusion coefficient, which indicated the rate of infiltration along the short axis, was 2.6-fold greater when mechanical restraint acted along the short axis than when mechanical restraint acted along the long axis () (Fig. 3 d).
Migration behavior of fibroblasts in fibrin wounds
We tracked the migration of individual fibroblasts in the fibrin wounds to determine whether a difference in the direction or speed of fibroblast migration could explain why the apparent infiltration rate differed between groups (Fig. 4, a and b). We parsed the migration tracks into apparent displacement vectors for each 1 h time interval and created scatterplots of apparent speed versus apparent orientation (Fig. S2, a and b). We calculated apparent orientation histograms, mean apparent speed versus apparent orientation curves, mean-squared displacement versus time curves, and mean-squared pathlength versus time curves to quantitatively summarize the migration behavior (Fig. 5). Fibroblasts migrated preferentially toward the center of the wound for both long-axis restraint and short-axis restraint (Fig. 5 a). However, fibroblast migration was oriented more strongly along the short axis of the wound with short-axis restraint than with long-axis restraint (Fig. 5 a). Apparent speeds were highest toward the center of the wound and of similar magnitude for both groups (Fig. 5 b).
Figure 4.
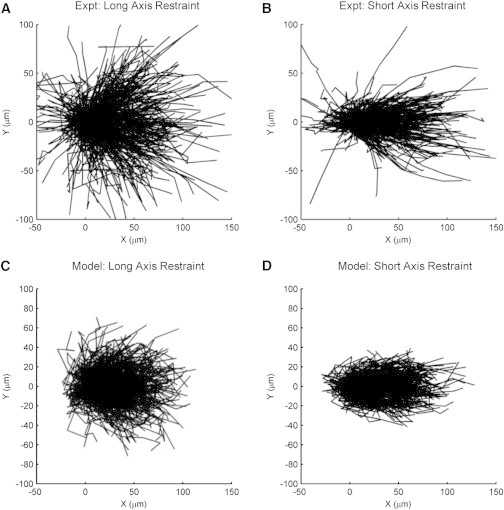
Fibroblast migration tracks measured after 1 day of wound infiltration. Migration tracks were measured in three gels per group, yielding a total of 568 cells tracked for long-axis restraint and 471 cells tracked for short-axis restraint. (A) For long-axis restraint, fibroblasts migrated preferentially toward the center of the wound (+x-direction). (B) For short-axis restraint, fibroblasts also migrated preferentially toward the center of the wound and migration tracks were aligned more strongly along the short axis (x axis). (C and D) The computational model reproduced the bulk of the fibroblast migration tracks for both mechanical conditions, except for the small subset of cells with highest net displacement.
Figure 5.
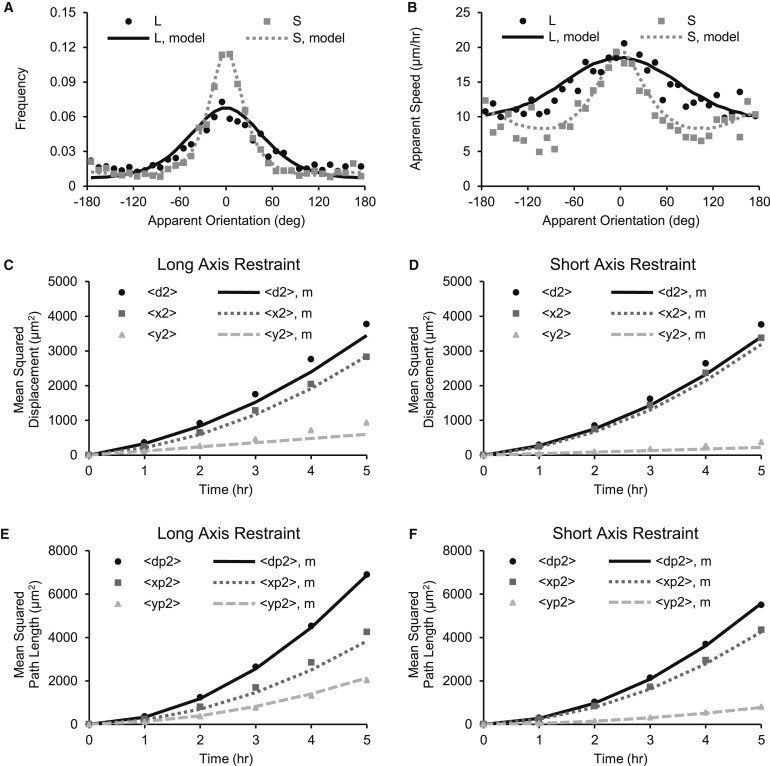
Quantitative summary of migration data. Markers indicate experimental data and curves indicate model data. (A) Fibroblast displacements were oriented more strongly along the short axis (0 and ±180°) with short-axis restraint (S) than with long-axis restraint (L). (B) Apparent speeds along the short axis were similar for short- and long-axis restraint, but apparent speeds along the long axis (−90° and 90°) were lower for short-axis restraint than for long axis restraint. (C–F) Mean-squared displacement curves were nonlinear but not as steep as the mean-squared path curves, indicating that migration lay between straight line motion and a random walk. The short-axis (x) bias was stronger with short-axis restraint than with long-axis restraint. The computational model of fibroblast migration reproduced all of the experimental data shown in these figures.
Computational model of fibroblast migration guided by environmental cues
We simulated fibroblast migration with a computational model to determine which guidance cues could explain the migration behavior we observed. We considered a bidirectional guidance cue oriented along the axis of restraint acting simultaneously with a unidirectional guidance cue oriented along the short axis toward the center of the wound. For long-axis restraint, the optimal fit to the migration data yielded a displacement magnitude of , and effective magnitudes of the displacement probability vectors of for the bidirectional (long-axis) guidance cue and for the unidirectional guidance cue (Table S2 and Fig. S3, a and b). For short-axis restraint, the optimization yielded dc = 1.7 μm, for the bidirectional (short-axis) guidance cue, and for the unidirectional guidance cue (Table S2, Fig. S3, a and b). These parameter values described a unimodal distribution of displacement orientations for long-axis restraint and an asymmetric, bimodal distribution for short-axis restraint (Fig. S3, c and d).
The computational model simultaneously reproduced the apparent orientation histogram, apparent speed versus apparent orientation curve, mean-squared displacement curves, and mean-squared pathlength curves for both long-axis restraint and short-axis restraint (Fig. 5). The model also reproduced the shape and scatter of the apparent speed versus apparent orientation data, except for the small subset of displacements with highest apparent speeds (Fig. S2, c and d). In a similar way, the model reproduced the fibroblast migration tracks, except for the small subset of cells with highest net displacements (Fig. 4, c and d).
Discussion
Mechanical regulation of fibroblast migration during wound healing
The rate of infiltration of fibroblasts along the short axis of the fibrin wounds was higher with short-axis restraint than with long-axis restraint. We considered two explanations of the higher rate of infiltration with short-axis restraint: mechanical and/or structural cues could have guided migration of fibroblasts preferentially along the short axis of the wounds (25,29,41), making invasion more efficient; or mechanical restraint could have increased the migration speed of fibroblasts along the short axis of the wounds (22). We measured apparent orientations and apparent speeds of migrating fibroblasts and found a strong guidance effect with short-axis restraint relative to long-axis restraint, but no greater speed of fibroblast migration along the short axis of the wounds. This suggested that mechanical environment, either directly or indirectly via structural cues, regulated the directionality of fibroblast migration, which affected the efficiency of invasion into the fibrin wounds.
Mechanical, structural, and invasion guidance cues in the fibrin wound model
Fibroblasts and other cells in three-dimensional matrices align (23–28) and migrate (25,29) parallel to the axis of greatest strain, restraint, or tension when exposed to anisotropic mechanical environments. For short-axis restraint, remodeling strains were anisotropic, suggesting the presence of a mechanical guidance cue oriented along the short axis of the wounds. For long-axis restraint, however, the strains were isotropic, suggesting the absence of a mechanical guidance cue. We hypothesize that the discrepancy between the applied long-axis restraint and observed isotropic remodeling strains was because most of the tension generated by fibroblasts in the surrounding collagen gel was parallel to, rather than in series with, the elliptical wound. This highlights the importance of obtaining local mechanical measurements for mechanobiological studies, even in seemingly simple culture systems.
Fibroblasts also orient along aligned structures such as fibers and microridges (41,45). Fibers in the fibrin wounds were significantly aligned along the axis of restraint, suggesting the presence of a structural guidance cue for both short- and long-axis restraint. Fiber alignment was stronger for long-axis restraint, suggesting that any migration bias due to fiber alignment should be stronger in this group. By measuring fiber alignment in regions devoid of cells, we quantified the global structural guidance cue in the fibrin wounds. However, fibroblasts can change the mechanical and structural properties of their local environment by depositing, degrading, and reorienting extracellular matrix fibers (18,24,25,46). Although the properties of the local environment are ultimately what cells sense, our interest in this study was assessing the roles of global guidance cues in regulating fibroblast migration during wound invasion. Essentially, we asked whether the global guidance cues that we measured (strain anisotropy and fibrin fiber alignment) gave rise to local guidance cues (potentially perturbed by fibroblast-mediated matrix remodeling) that were strong enough for us to observe effects on fibroblast migration.
Multiple factors can promote directed invasion of fibroblasts into fibrin wound matrices. Fibrin and fibronectin (covalently bound to fibrin during cross-linking) are haptotactic agents (47,48), and fibrin has binding sites for chemotactic agents, such as basic fibroblast growth factor and PDGF (49). Also, dense populations of fibroblasts may self-generate chemotactic gradients by internalizing and degrading growth factors (50–52). In addition, contact inhibition of locomotion can explain directional migration of fibroblasts from regions of high cell concentration to regions of low cell concentration (30–32,53). Regardless of the source of the guidance cue, directed invasion of dense populations of cells into cell-free zones has been observed repeatedly in two- (30) and three-dimensional cultures (22,54,55) and in vivo (53). We measured migration tracks of individual fibroblasts and discovered a unidirectional bias of fibroblast migration toward the center of the fibrin wounds for both long- and short-axis restraint. This suggested that an invasion guidance cue was present in our gels.
Inference of guidance cues biasing fibroblast migration
Our approach to inferring guidance cues was to 1), simulate the migration of cells in response to varying strengths of candidate cues; 2), compare the model simulations to experimental data; and 3), determine the cues and cue strengths that gave rise to migration behavior that agreed best with experimental observations. We found that we needed to compare distributions of apparent orientations and apparent speeds to evaluate the models. Population-averaged measurements, such as mean-squared displacement curves, were less useful because they could be matched by many different models. This difficulty was previously acknowledged by Simpson et al. (56), who argued that population-level measurements and models are sometimes too coarse to reveal the underlying features of cell migration (e.g., directed versus random), and instead, individual-based models should be used to interpret migration data. In a similar way, Coscoy et al. (57) demonstrated the need to examine distributions of multiple metrics obtained from migration tracks to determine their generating mechanism (e.g., diffusion, convection, noise) and advocated using simulations to compute these distributions for candidate mechanisms.
We considered the possibility that a bidirectional guidance cue oriented along the axis of restraint acted simultaneously with an invasion guidance cue oriented toward the center of the fibrin wound. According to the computational model, the influence of the bidirectional guidance cue was negligible for long-axis restraint but strong for short-axis restraint. This finding was consistent with our measurements of mechanical anisotropy, which suggested the presence of a mechanical guidance cue only for short-axis restraint, and inconsistent with our measurements of structural anisotropy, which suggested the presence of a structural guidance cue for both long- and short-axis restraint, where long-axis restraint had the stronger cue.
The finding that fibroblasts invading the fibrin wounds were insensitive to structural guidance cues was surprising, because aligned fiber matrices have been shown to bias fibroblast migration (41,58). However, in prior studies, competing guidance cues were not present. In our wound model, it is likely that the fiber alignment was too weak to perturb the response of the fibroblasts to the invasion guidance cue. Other studies have shown that competing guidance cues can overcome the influence of a structural cue. Rajnicek et al. (59) showed that a direct-current electric field applied over a nanogrooved substrate caused cells to migrate perpendicular to the grooves. In a similar way, Prodanov et al. (60) showed that cyclic uniaxial strain applied to a nanogrooved substrate caused cells to orient perpendicular to the grooves.
The finding that fibroblasts invading the fibrin wounds were sensitive to mechanical guidance cues was consistent with prior observations that mechanical environment strongly regulates fibroblast and collagen fiber alignment weeks into the healing process (4,61–63). In this work, we have further demonstrated that mechanical guidance cues can perturb the response of fibroblasts to invasion cues. Notably, anisotropic mechanical boundary conditions may increase the rate of fibroblast invasion, which may promote faster wound healing. This contrasts with the finding that cyclic equibiaxial stretch slowed migration of epithelial cells in scratch wound assays (64). Additional studies are needed to cover the full range of possible mechanical stimuli, such as static versus dynamic, isotropic versus anisotropic, and anisotropic at different angles.
Collagen-fibrin wound model
We developed a wound model using fiber matrices to approximate the three-dimensional environment that fibroblasts must navigate during wound healing in vivo. Differences in the morphology and migration of cells in three-dimensional constructs as compared to two-dimensional substrates have been well documented (46,65). We also mimicked a wound by actually cutting the collagen gels and by filling the defects with fibrin, which is a primary component of the provisional matrix formed after wounding in vivo (2,19,66).
Others have developed wound or woundlike models using three-dimensional matrices to study invasion of fibroblasts from cell-dense domains to cell-free domains (22,55,67–69). Notably, Grinnell and colleagues observed fibroblast invasion using nested collagen matrices, where a fibroblast-populated collagen gel was embedded in an acellular collagen gel (55). Their model was used to study how growth factors, density of the acellular collagen gel, and isotropic restraint of the acellular collagen gel regulate outward migration of fibroblasts (22,68).
An advantage of our model is the ability to control the mechanical boundary conditions acting on the tissue surrounding the wound, similar to what could be accomplished in vivo using sutures or adhesives. Also, we overcame the difficulty of tracking migration paths in the deformable matrices by using embedded microspheres as position reference markers, whereas others typically report population-level measures of cell invasion (55,67,69).
For further mechanobiological investigation, differently shaped molds could be used to alter the mechanical environment within the fibrin wounds, or the collagen-fibrin constructs could be integrated with devices used for static or dynamic stretching (70). Other guidance cues could be independently manipulated as well. For example, collagen or fibrin fibers could be prealigned by incubating the constructs in strong magnetic fields during polymerization (71), or chemokine gradients could be prescribed by embedding growth-factor-loaded microspheres in the gels (55).
Computational model of fibroblast migration guided by environmental cues
Our computational model is a potentially useful tool for predicting and interpreting migration behavior in response to combinations of guidance cues. The model required specification of only a displacement magnitude, displacement frequency, and displacement orientation probability distribution. We were able to infer these parameters by matching model results to experimentally measured distributions of apparent displacement orientations and speeds. We found that this model reproduced many detailed features of fibroblast migration and captured the biases of multiple simultaneous guidance cues. The model should be tested on additional data sets to determine the extent of its applicability.
Our approach was similar to, but more general than, the approach taken by Codling et al. (44), who used a single unimodal probability density function to capture the bias due to a generic unidirectional guidance cue, but did not compare the model to experimental data. Our model allows the circular probability density function to have more complicated shapes, as needed to capture the biases of combinations of unidirectional and bidirectional guidance cues. Furthermore, we quantitatively compared model results to experimental observations and demonstrated that our model can realistically simulate migration tracks. Notably, we did not include persistence in our model, and we did not allow migration speed to vary stochastically, which are features of the more common Ornstein-Uhlenbeck model of cell migration (72). We found that our simpler model matched the experimental data reasonably well and opted against introducing additional model complexity if not warranted by the data.
Others have developed models accounting for more than one guidance cue. Wagle and Tranquillo (73) derived a continuum equation for cell transport that included flux terms accounting for contact guidance and chemotaxis. McDougall et al. (74) calculated the direction of cell migration as a weighted sum of vectors accounting for persistence, contact guidance, and chemotaxis. Groh and Louis (75) modified the Ornstein-Uhlenbeck model of cell migration by adding force terms to the Langevin equation to account for contact guidance and chemotaxis, similar to the approach taken by Stokes et al. (72) to account for chemotaxis. Mousavi et al. (76) developed a force equilibrium equation where the viscous drag term is balanced by a stochastic force vector and a weighted sum of force vectors accounting for durotaxis, chemotaxis, thermotaxis, and electrotaxis. To our knowledge, these models have not been compared quantitatively to experimental data, which makes it difficult to assess their relative advantages and disadvantages.
One distinction, however, is that the influence of guidance cues on the direction of cell migration in our model is probabilistic. In contrast, the influence of guidance cues on the direction of cell migration in the other individual-based models is either entirely deterministic (74) or deterministic with superimposed random fluctuations (75,76). Interestingly, recently published work on signaling-vector analysis (77), which showed that the location of PI3K signaling correlated with the location of membrane protrusion and direction of cell migration, suggests that displacement orientation probabilities may actually reflect the activation pattern of intracellular proteins governing protrusive activity around the cell periphery. Consequently, although we captured the biases of guidance cues phenomenologically using wrapped normal probability density functions, the orientation probability density function could potentially be calculated from experimental data or computational models that describe the spatial regulation of cell protrusions by the extracellular environment. Stefanoni et al. (78) has taken a step in this direction by developing a model of durotaxis where displacement orientation probabilities were assumed to be proportional to the local stiffness felt by a cell pulling on its surroundings. In a similar way, De et al. (79) proposed that cell orientation is determined by intracellular machinery that effectively seeks to establish a strain or stress set point at the least energy cost, and therefore cell orientation depends on mechanical boundary conditions that determine the local resistance of the matrix to cell traction forces.
Conclusion
We tested whether anisotropic mechanical boundary conditions affected the directionality and speed of fibroblasts migrating into a three-dimensional model wound, which could simultaneously expose fibroblasts to mechanical, structural, steric, and chemical guidance cues. Mechanical environment was an important regulator of fibroblast migration in our wound model. Anisotropic remodeling strains were correlated with a directional bias of fibroblast migration that made infiltration of fibroblasts into the fibrin wounds more efficient. This bias was consistent with a direct effect of strain anisotropy on fibroblast migration and inconsistent with an effect of strain-induced fiber alignment. The mechanical guidance cue (strain anisotropy) did not increase the speed of fibroblast migration into the fibrin wounds. The migration behavior could be modeled as a biased random walk, where a combination of mechanical and invasion guidance cues biased the orientation probability distribution of cell displacements.
Acknowledgments
Funding for this work was provided by an American Heart Association Predoctoral Fellowship to A.D.R. and a National Institutes of Health grant (NHLBI RO1 HL-075639) to J.W.H.
The authors acknowledge technical assistance from Tracy Burcin.
Supporting Material
References
- 1.Aarabi S., Longaker M.T., Gurtner G.C. Hypertrophic scar formation following burns and trauma: new approaches to treatment. PLoS Med. 2007;4:e234. doi: 10.1371/journal.pmed.0040234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gurtner G.C., Werner S., Longaker M.T. Wound repair and regeneration. Nature. 2008;453:314–321. doi: 10.1038/nature07039. [DOI] [PubMed] [Google Scholar]
- 3.Holmes J.W., Borg T.K., Covell J.W. Structure and mechanics of healing myocardial infarcts. Annu. Rev. Biomed. Eng. 2005;7:223–253. doi: 10.1146/annurev.bioeng.7.060804.100453. [DOI] [PubMed] [Google Scholar]
- 4.Bunting C.H., Eades C.C. The effect of mechanical tension upon the polarity of growing fibroblasts. J. Exp. Med. 1926;44:147–149. doi: 10.1084/jem.44.2.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schouten H.J., Nieuwenhuis M.K., van Zuijlen P.P.M. A review on static splinting therapy to prevent burn scar contracture: do clinical and experimental data warrant its clinical application? Burns. 2012;38:19–25. doi: 10.1016/j.burns.2011.06.003. [DOI] [PubMed] [Google Scholar]
- 6.Carlson M.A., Longaker M.T., Thompson J.S. Wound splinting regulates granulation tissue survival. J. Surg. Res. 2003;110:304–309. doi: 10.1016/s0022-4804(02)00098-7. [DOI] [PubMed] [Google Scholar]
- 7.Gurtner G.C., Dauskardt R.H., Longaker M.T. Improving cutaneous scar formation by controlling the mechanical environment: large animal and phase I studies. Ann. Surg. 2011;254:217–225. doi: 10.1097/SLA.0b013e318220b159. [DOI] [PubMed] [Google Scholar]
- 8.Provenzano P.P., Martinez D.A., Vanderby R., Jr. Hindlimb unloading alters ligament healing. J. Appl. Physiol. 2003;94:314–324. doi: 10.1152/japplphysiol.00340.2002. [DOI] [PubMed] [Google Scholar]
- 9.Zhou X., Yun J.-L., Li Y.-M. Postinfarction healing dynamics in the mechanically unloaded rat left ventricle. Am. J. Physiol. Heart Circ. Physiol. 2011;300:H1863–H1874. doi: 10.1152/ajpheart.00830.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Waninger J., Kauffmann G.W., Farthmann E.H. Influence of the distance between interrupted sutures and the tension of sutures on the healing of experimental colonic anastomoses. Am. J. Surg. 1992;163:319–323. doi: 10.1016/0002-9610(92)90013-h. [DOI] [PubMed] [Google Scholar]
- 11.Agha R., Ogawa R., Orgill D.P. A review of the role of mechanical forces in cutaneous wound healing. J. Surg. Res. 2011;171:700–708. doi: 10.1016/j.jss.2011.07.007. [DOI] [PubMed] [Google Scholar]
- 12.Hinz B., Mastrangelo D., Gabbiani G. Mechanical tension controls granulation tissue contractile activity and myofibroblast differentiation. Am. J. Pathol. 2001;159:1009–1020. doi: 10.1016/S0002-9440(10)61776-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grinnell F., Zhu M., Abrams J.M. Release of mechanical tension triggers apoptosis of human fibroblasts in a model of regressing granulation tissue. Exp. Cell Res. 1999;248:608–619. doi: 10.1006/excr.1999.4440. [DOI] [PubMed] [Google Scholar]
- 14.Derderian C.A., Bastidas N., Gurtner G.C. Mechanical strain alters gene expression in an in vitro model of hypertrophic scarring. Ann. Plast. Surg. 2005;55:69–75. doi: 10.1097/01.sap.0000168160.86221.e9. discussion 75. [DOI] [PubMed] [Google Scholar]
- 15.Culbertson E.J., Xing L., Franz M.G. Loss of mechanical strain impairs abdominal wall fibroblast proliferation, orientation, and collagen contraction function. Surgery. 2011;150:410–417. doi: 10.1016/j.surg.2011.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Carver W., Nagpal M.L., Terracio L. Collagen expression in mechanically stimulated cardiac fibroblasts. Circ. Res. 1991;69:116–122. doi: 10.1161/01.res.69.1.116. [DOI] [PubMed] [Google Scholar]
- 17.Junker J.P.E., Kratz C., Kratz G. Mechanical tension stimulates the transdifferentiation of fibroblasts into myofibroblasts in human burn scars. Burns. 2008;34:942–946. doi: 10.1016/j.burns.2008.01.010. [DOI] [PubMed] [Google Scholar]
- 18.Gabbiani G. The myofibroblast in wound healing and fibrocontractive diseases. J. Pathol. 2003;200:500–503. doi: 10.1002/path.1427. [DOI] [PubMed] [Google Scholar]
- 19.Mutsaers S.E., Bishop J.E., Laurent G.J. Mechanisms of tissue repair: from wound healing to fibrosis. Int. J. Biochem. Cell Biol. 1997;29:5–17. doi: 10.1016/s1357-2725(96)00115-x. [DOI] [PubMed] [Google Scholar]
- 20.Murphy K.E., Hall C.L., Sean McElwain D.L. A two-compartment mechanochemical model of the roles of transforming growth factor β and tissue tension in dermal wound healing. J. Theor. Biol. 2011;272:145–159. doi: 10.1016/j.jtbi.2010.12.011. [DOI] [PubMed] [Google Scholar]
- 21.Pelham R.J., Jr., Wang Yl. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Miron-Mendoza M., Seemann J., Grinnell F. The differential regulation of cell motile activity through matrix stiffness and porosity in three dimensional collagen matrices. Biomaterials. 2010;31:6425–6435. doi: 10.1016/j.biomaterials.2010.04.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Matsumoto T., Sasaki J., Sohmura T. Three-dimensional cell and tissue patterning in a strained fibrin gel system. PLoS ONE. 2007;2:e1211. doi: 10.1371/journal.pone.0001211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee E.J., Holmes J.W., Costa K.D. Remodeling of engineered tissue anisotropy in response to altered loading conditions. Ann. Biomed. Eng. 2008;36:1322–1334. doi: 10.1007/s10439-008-9509-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pang Y., Wang X., Greisler H.P. Dynamic quantitative visualization of single cell alignment and migration and matrix remodeling in 3-D collagen hydrogels under mechanical force. Biomaterials. 2011;32:3776–3783. doi: 10.1016/j.biomaterials.2011.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Weidenhamer N.K., Tranquillo R.T. Influence of cyclic mechanical stretch and tissue constraints on cellular and collagen alignment in fibroblast-derived cell sheets. Tissue Eng. Part C Methods. 2013;19:386–395. doi: 10.1089/ten.tec.2012.0423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krishnan L., Underwood C.J., Weiss J.A. Effect of mechanical boundary conditions on orientation of angiogenic microvessels. Cardiovasc. Res. 2008;78:324–332. doi: 10.1093/cvr/cvn055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wagenseil J.E., Elson E.L., Okamoto R.J. Cell orientation influences the biaxial mechanical properties of fibroblast populated collagen vessels. Ann. Biomed. Eng. 2004;32:720–731. doi: 10.1023/b:abme.0000030237.20057.3e. [DOI] [PubMed] [Google Scholar]
- 29.Raeber G.P., Lutolf M.P., Hubbell J.A. Part II: Fibroblasts preferentially migrate in the direction of principal strain. Biomech. Model. Mechanobiol. 2008;7:215–225. doi: 10.1007/s10237-007-0090-1. [DOI] [PubMed] [Google Scholar]
- 30.Abercrombie M., Heaysman J.E. Observations on the social behaviour of cells in tissue culture. II. Monolayering of fibroblasts. Exp. Cell Res. 1954;6:293–306. doi: 10.1016/0014-4827(54)90176-7. [DOI] [PubMed] [Google Scholar]
- 31.Kadir S., Astin J.W., Nobes C.D. Microtubule remodelling is required for the front-rear polarity switch during contact inhibition of locomotion. J. Cell Sci. 2011;124:2642–2653. doi: 10.1242/jcs.087965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mayor R., Carmona-Fontaine C. Keeping in touch with contact inhibition of locomotion. Trends Cell Biol. 2010;20:319–328. doi: 10.1016/j.tcb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Barrientos S., Stojadinovic O., Tomic-Canic M. Growth factors and cytokines in wound healing. Wound Repair Regen. 2008;16:585–601. doi: 10.1111/j.1524-475X.2008.00410.x. [DOI] [PubMed] [Google Scholar]
- 34.Thomopoulos S., Fomovsky G.M., Holmes J.W. The development of structural and mechanical anisotropy in fibroblast populated collagen gels. J. Biomech. Eng. 2005;127:742–750. doi: 10.1115/1.1992525. [DOI] [PubMed] [Google Scholar]
- 35.Kolodney M.S., Wysolmerski R.B. Isometric contraction by fibroblasts and endothelial cells in tissue culture: a quantitative study. J. Cell Biol. 1992;117:73–82. doi: 10.1083/jcb.117.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Diaz-Araya G., Borg T.K., Carver W. IGF-1 modulation of rat cardiac fibroblast behavior and gene expression is age-dependent. Cell Commun. Adhes. 2003;10:155–165. [PubMed] [Google Scholar]
- 37.Shreiber D.I., Enever P.A.J., Tranquillo R.T. Effects of PDGF-BB on rat dermal fibroblast behavior in mechanically stressed and unstressed collagen and fibrin gels. Exp. Cell Res. 2001;266:155–166. doi: 10.1006/excr.2001.5208. [DOI] [PubMed] [Google Scholar]
- 38.Williams C., Johnson S.L., Tranquillo R.T. Cell sourcing and culture conditions for fibrin-based valve constructs. Tissue Eng. 2006;12:1489–1502. doi: 10.1089/ten.2006.12.1489. [DOI] [PubMed] [Google Scholar]
- 39.De Rossi A., Rocha L.B., Rossi M.A. Application of fluorescence microscopy on hematoxylin and eosin-stained sections of healthy and diseased teeth and supporting structures. J. Oral Pathol. Med. 2007;36:377–381. doi: 10.1111/j.1600-0714.2007.00542.x. [DOI] [PubMed] [Google Scholar]
- 40.Lauffenburger D., Rothman C., Zigmond S.H. Measurement of leukocyte motility and chemotaxis parameters with a linear under-agarose migration assay. J. Immunol. 1983;131:940–947. [PubMed] [Google Scholar]
- 41.Dickinson R.B., Guido S., Tranquillo R.T. Biased cell migration of fibroblasts exhibiting contact guidance in oriented collagen gels. Ann. Biomed. Eng. 1994;22:342–356. doi: 10.1007/BF02368241. [DOI] [PubMed] [Google Scholar]
- 42.Karlon W.J., Hsu P.P., Omens J.H. Measurement of orientation and distribution of cellular alignment and cytoskeletal organization. Ann. Biomed. Eng. 1999;27:712–720. doi: 10.1114/1.226. [DOI] [PubMed] [Google Scholar]
- 43.Mardia K.V., Jupp P.E. John Wiley & Sons; West Sussex, United Kingdom: 2000. Directional Statistics. [Google Scholar]
- 44.Codling E.A., Bearon R.N., Thorn G.J. Diffusion about the mean drift location in a biased random walk. Ecology. 2010;91:3106–3113. doi: 10.1890/09-1729.1. [DOI] [PubMed] [Google Scholar]
- 45.Loesberg W.A., te Riet J., Jansen J.A. The threshold at which substrate nanogroove dimensions may influence fibroblast alignment and adhesion. Biomaterials. 2007;28:3944–3951. doi: 10.1016/j.biomaterials.2007.05.030. [DOI] [PubMed] [Google Scholar]
- 46.Friedl P., Wolf K. Plasticity of cell migration: a multiscale tuning model. J. Cell Biol. 2010;188:11–19. doi: 10.1083/jcb.200909003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Naito M., Hayashi T., Kuzuya F. Fibrinogen is chemotactic for vascular smooth muscle cells. FEBS Lett. 1989;247:358–360. doi: 10.1016/0014-5793(89)81370-5. [DOI] [PubMed] [Google Scholar]
- 48.Thibault M.M., Hoemann C.D., Buschmann M.D. Fibronectin, vitronectin, and collagen I induce chemotaxis and haptotaxis of human and rabbit mesenchymal stem cells in a standardized transmembrane assay. Stem Cells Dev. 2007;16:489–502. doi: 10.1089/scd.2006.0100. [DOI] [PubMed] [Google Scholar]
- 49.Mosesson M.W., Siebenlist K.R., Meh D.A. The structure and biological features of fibrinogen and fibrin. Ann. N. Y. Acad. Sci. 2001;936:11–30. doi: 10.1111/j.1749-6632.2001.tb03491.x. [DOI] [PubMed] [Google Scholar]
- 50.Haugh J.M. Deterministic model of dermal wound invasion incorporating receptor-mediated signal transduction and spatial gradient sensing. Biophys. J. 2006;90:2297–2308. doi: 10.1529/biophysj.105.077610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Scherber C., Aranyosi A.J., Irimia D. Epithelial cell guidance by self-generated EGF gradients. Integr Biol (Camb) 2012;4:259–269. doi: 10.1039/c2ib00106c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.McLennan R., Dyson L., Kulesa P.M. Multiscale mechanisms of cell migration during development: theory and experiment. Development. 2012;139:2935–2944. doi: 10.1242/dev.081471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Carmona-Fontaine C., Matthews H.K., Mayor R. Contact inhibition of locomotion in vivo controls neural crest directional migration. Nature. 2008;456:957–961. doi: 10.1038/nature07441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Weiss P. Cellular dynamics. Rev. Mod. Phys. 1959;31:11–20. [Google Scholar]
- 55.Grinnell F., Rocha L.B., Jiang H. Nested collagen matrices: a new model to study migration of human fibroblast populations in three dimensions. Exp. Cell Res. 2006;312:86–94. doi: 10.1016/j.yexcr.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 56.Simpson M.J., Landman K.A., Hughes B.D. Distinguishing between directed and undirected cell motility within an invading cell population. Bull. Math. Biol. 2009;71:781–799. doi: 10.1007/s11538-008-9381-7. [DOI] [PubMed] [Google Scholar]
- 57.Coscoy S., Huguet E., Amblard F. Statistical analysis of sets of random walks: how to resolve their generating mechanism. Bull. Math. Biol. 2007;69:2467–2492. doi: 10.1007/s11538-007-9227-8. [DOI] [PubMed] [Google Scholar]
- 58.Liu Y., Ji Y., Rafailovich M.H. Effects of fiber orientation and diameter on the behavior of human dermal fibroblasts on electrospun PMMA scaffolds. J. Biomed. Mater. Res. A. 2009;90:1092–1106. doi: 10.1002/jbm.a.32165. [DOI] [PubMed] [Google Scholar]
- 59.Rajnicek A.M., Foubister L.E., McCaig C.D. Prioritising guidance cues: directional migration induced by substratum contours and electrical gradients is controlled by a ρ/cdc42 switch. Dev. Biol. 2007;312:448–460. doi: 10.1016/j.ydbio.2007.09.051. [DOI] [PubMed] [Google Scholar]
- 60.Prodanov L., te Riet J., Walboomers X.F. The interaction between nanoscale surface features and mechanical loading and its effect on osteoblast-like cells behavior. Biomaterials. 2010;31:7758–7765. doi: 10.1016/j.biomaterials.2010.06.050. [DOI] [PubMed] [Google Scholar]
- 61.Arem A.J., Madden J.W. Effects of stress on healing wounds: I. Intermittent noncyclical tension. J. Surg. Res. 1976;20:93–102. doi: 10.1016/0022-4804(76)90104-9. [DOI] [PubMed] [Google Scholar]
- 62.Fomovsky G.M., Rouillard A.D., Holmes J.W. Regional mechanics determine collagen fiber structure in healing myocardial infarcts. J. Mol. Cell. Cardiol. 2012;52:1083–1090. doi: 10.1016/j.yjmcc.2012.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rouillard A.D., Holmes J.W. Mechanical regulation of fibroblast migration and collagen remodelling in healing myocardial infarcts. J. Physiol. 2012;590:4585–4602. doi: 10.1113/jphysiol.2012.229484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Desai L.P., Chapman K.E., Waters C.M. Mechanical stretch decreases migration of alveolar epithelial cells through mechanisms involving Rac1 and Tiam1. Am. J. Physiol. Lung Cell. Mol. Physiol. 2008;295:L958–L965. doi: 10.1152/ajplung.90218.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Harunaga J.S., Yamada K.M. Cell-matrix adhesions in 3D. Matrix Biol. 2011;30:363–368. doi: 10.1016/j.matbio.2011.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Clark R.A.F. Fibrin and wound healing. Ann. N. Y. Acad. Sci. 2001;936:355–367. doi: 10.1111/j.1749-6632.2001.tb03522.x. [DOI] [PubMed] [Google Scholar]
- 67.O’Leary R., Wood E.J. A novel in vitro dermal wound-healing model incorporating a response to mechanical wounding and repopulation of a fibrin provisional matrix. In Vitro Cell. Dev. Biol. Anim. 2003;39:204–207. doi: 10.1290/1543-706X(2003)039<0204:ANIVDW>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 68.Miron-Mendoza M., Seemann J., Grinnell F. Collagen fibril flow and tissue translocation coupled to fibroblast migration in 3D collagen matrices. Mol. Biol. Cell. 2008;19:2051–2058. doi: 10.1091/mbc.E07-09-0930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Petroll W.M., Lakshman N., Ma L. Experimental models for investigating intra-stromal migration of corneal keratocytes, fibroblasts and myofibroblasts. J. Funct. Biomater. 2012;3:183–198. doi: 10.3390/jfb3010183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Huang L., Mathieu P.S., Helmke B.P. A stretching device for high-resolution live-cell imaging. Ann. Biomed. Eng. 2010;38:1728–1740. doi: 10.1007/s10439-010-9968-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Torbet J., Ronzière M.-C. Magnetic alignment of collagen during self-assembly. Biochem. J. 1984;219:1057–1059. doi: 10.1042/bj2191057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Stokes C.L., Lauffenburger D.A., Williams S.K. Migration of individual microvessel endothelial cells: stochastic model and parameter measurement. J. Cell Sci. 1991;99:419–430. doi: 10.1242/jcs.99.2.419. [DOI] [PubMed] [Google Scholar]
- 73.Wagle M.A., Tranquillo R.T. A self-consistent cell flux expression for simultaneous chemotaxis and contact guidance in tissues. J. Math. Biol. 2000;41:315–330. doi: 10.1007/s002850000040. [DOI] [PubMed] [Google Scholar]
- 74.McDougall S., Dallon J., Maini P. Fibroblast migration and collagen deposition during dermal wound healing: mathematical modelling and clinical implications. Philos Trans A Math Phys Eng Sci. 2006;364:1385–1405. doi: 10.1098/rsta.2006.1773. [DOI] [PubMed] [Google Scholar]
- 75.Groh A., Louis A.K. Stochastic modelling of biased cell migration and collagen matrix modification. J. Math. Biol. 2010;61:617–647. doi: 10.1007/s00285-009-0314-3. [DOI] [PubMed] [Google Scholar]
- 76.Mousavi S.J., Doweidar M.H., Doblaré M. 3D computational modelling of cell migration: a mechano-chemo-thermo-electrotaxis approach. J. Theor. Biol. 2013;329:64–73. doi: 10.1016/j.jtbi.2013.03.021. [DOI] [PubMed] [Google Scholar]
- 77.Melvin A.T., Welf E.S., Haugh J.M. In chemotaxing fibroblasts, both high-fidelity and weakly biased cell movements track the localization of PI3K signaling. Biophys. J. 2011;100:1893–1901. doi: 10.1016/j.bpj.2011.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Stefanoni F., Ventre M., Netti P.A. A numerical model for durotaxis. J. Theor. Biol. 2011;280:150–158. doi: 10.1016/j.jtbi.2011.04.001. [DOI] [PubMed] [Google Scholar]
- 79.De R., Zemel A., Safran S.A. Dynamics of cell orientation. Nat. Phys. 2007;3:655–659. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


