Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 7;4:4303. doi: 10.1038/srep04303

Temperature-Induced Coalescence of Colliding Binary Droplets on Superhydrophobic Surface

Nan Yi 1, Bin Huang 1, Lining Dong 1, Xiaojun Quan 1, Fangjun Hong 1, Peng Tao 1, Chengyi Song 1, Wen Shang 1,a, Tao Deng 1,b
PMCID: PMC3946014  PMID: 24603362

Abstract

This report investigates the impact of droplet temperature on the head-on collision of binary droplets on a superhydrophobic surface. Understanding droplet collision is critical to many fundamental processes and industrial applications. There are many factors, including collision speed, collision angle, and droplet composition, that influence the outcome of the collision between binary droplets. This work provides the first experimental study of the influence of droplet temperature on the collision of binary droplets. As the droplet temperature increases, the possibility increases for the two droplets to coalesce after collision. The findings in this study can be extended to collision of droplets under other conditions where control of the droplet temperature is feasible. Such findings will also be beneficial to applications that involve droplet collision, such as in ink-jet printing, steam turbines, engine ignition, and spraying cooling.

This paper studies the collision between binary droplets under different temperature settings on superhydrophobic surfaces. All previous studies of collision between binary droplets focused on droplets set at a fixed temperature1,2,3,4,5,6,7,8,9, and there is no report, to the best of our knowledge, of the temperature effect on the outcome of collision between droplets. Under appropriate collision conditions, the incoming droplet can rebound as it hits the stationary droplet on the superhyrodphobic surfaces10. This study shows that when there is an increase in temperature for both droplets or one of the droplets, there is increased possibility of coalescence after collision. The findings in this study introduce, for the first time, the temperature as an important parameter in studying and designing the interaction between liquid droplets.

Collision between liquid droplets is a common phenomenon that happens in many processes, such as rainfall11 and oil injection in engines12. Coalescence and separation are two common outcomes after droplet collision13. When binary droplets collide in the air, there is an air film at the interface of the two colliding droplets due to the present of air. The air film helps prevent the coalescence of the droplets and the breakage of the film will lead to coalescence13. Many prior studies of interaction between binary droplets are carried out under free flying condition at the atmospheric environment with a fixed temperature setting14. With varying velocities and impact angles, there are five distinct regions of collision under free flying condition15: 1.coalescence after minor deformation; 2.bouncing; 3.coalescence after substantial deformation; 4.coalescence followed by separation for near head-on collisions; 5.coalescence followed by separation for off-center collisions.

Recently there is increased research effort in studying collision of droplets on solid surfaces16,17,18,19,20,21,22,23,24,25,26 due to its critical role in many applications, such as ink-jet printing27, steam turbines28, and microfluidics29. Through both experimental work and theoretic modeling, Graham et al investigated the coalescence of two droplets on a solid surface with various wetting properties to study the dynamics of droplet coalescence with increased hydrophobicity30. Mertaniemi et al explored a droplet logic with rebounding droplet-droplet interaction on the superhydrophobic surface for future bio-computer10. Farhangi et al studied coalescence of a falling droplet with a stationary droplet on a superhydrophobic surface to characterize the kinetic energy needed for the detachment of the droplets from the surfaces31. Compared to the collision under free flying condition, the collision of binary droplets on solid surfaces has slightly different collision regions10,15. At low impacting velocities, as reported by Zhao et al32, the head-on collision of the binary liquid droplets on a solid surface can be categorized into four regions: coalescence, complete rebound, partial rebound after conglutination, and coalescence accompanied by conglutination. When the Weber number is relatively small, in the case of head-on collision, both coalescence and rebound will exist with the same collision condition32.

All the reported research of interaction between binary droplets, including studies under free flying condition or on a solid surface, involves binary droplets set at the fixed temperature, and most of time set at the room temperature (Figure 1(a)). This work studied the effect of the temperature in the collision of binary droplets on superhydrophobic surfaces, with both droplets heated (Figure 1(b)) or with a heated droplet impacting a cold stationary droplet on the superhydrophobic surfaces (Figure 1(c)). The finding in this work reveals that the rise in temperature of the droplets, either one or both droplets, increases the possibility of coalescence after the collision of the droplets. Such finding establishes the key role the temperature plays in droplets collision, and provides opportunities to design conditions for optimum droplet interactions or prevent the adverse effect of droplet coalescence.

Figure 1. Schematic of a collision between a falling droplet and a stationary droplet on a superhydrophobic surface.

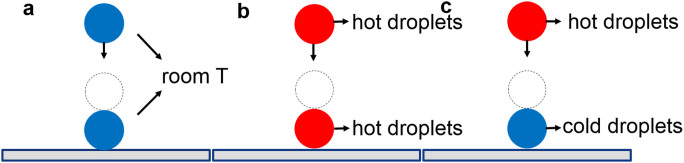
Figure 1

Open in a new tab

(a) Both droplets set at the room temperature; (b) Both droplets set at elevated temperature; (c) The two droplets set at different temperatures.

Results

The interaction of binary droplets was studied through the collision between a droplet released from a needle attached to a syringe and a stationary droplet sitting on top of the superhydrophobic silicon surfaces. Figure 2 shows the SEM image of the superhydrophobic silicon substrate and also the optical image of a stationary droplet placed on top of the substrate. The contact angle between the droplet and the substrate is close to ~154°.

Figure 2.

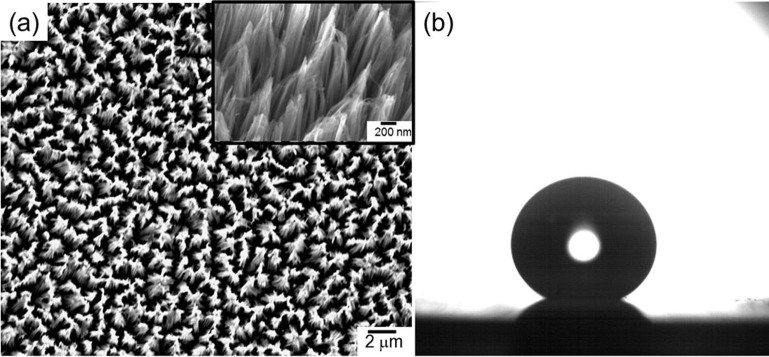
Figure 2

Open in a new tab

(a) Low and high magnification SEM images of the nanostructured silicon wafer surface; (b) Optical image of a stationary droplet placed on top of the substrate.

Weber Number (We) and impact parameter (B) were used to describe the collision process of the binary droplets. For identical droplets, We and B are defined as 2Rρv2/σ and l/2R, respectively. In the definition, R is the droplet radius, v is the relative velocity, l is the projected distance between the droplet centers in the direction normal to vector v, ρ is the density, and σ is the surface tension of the liquid. The impact parameter B represents the relative distance between the centers of the two droplets. When B = 1, the center distance equals to the sum of droplets radius and the collision is a grazing collision. When B = 0, it is a head-on collision. In this work, the influence of different releasing heights (5 mm to 30 mm), which have different Weber numbers, with head-on collision (B = 0) was studied. Table 1 summaries the distribution of coalescence states with the change of releasing height when both droplets were set at room temperature (25°C). The rebound state only occurred in a relatively narrow range of releasing height (10–15 mm) and mostly concentrated between 12 mm and 14 mm.

Table 1. The possibility of the coalescence states of head-on collision at different releasing height (B = 0, Tincoming = Tstationary = Troom = 25°C).

Height (mm) Percent of Coalescence(%)
5 100
10 92
12 68
13 34
14 72
15 94
30 100
Open in a new tab

At the releasing height of 5 mm, the droplets coalesced with small deformation as shown in Figure 3. With the low impacting velocity, the released droplet easily broke the air film between the droplets15 and formed a liquid bridge with the stationary droplet on the superhydrophobic substrate. The coalescence or separation of the binary droplets after collision was also determined by the strength of the liquid bridge4. In this case with releasing height at 5 mm, there was strong liquid bridge formation at about 5 ms and it contributed to the coalescence of the droplets.

Figure 3. Head-on collision of binary droplets with releasing height of 5 mm (B = 0; We = 0.48).

Figure 3

Open in a new tab

With the increase of releasing height, the possibility of rebound increased. When the releasing height was between 12 mm and 14 mm, a relatively large portion of rebound occurred. Figure 4 shows the high speed images of the droplets rebound at the releasing height of 13 mm. In this case, both droplets deformed elastically, and the impacting droplet did not break the air film. There was also no obvious formation of liquid bridge between the droplets15. The two droplets moved into different directions after the collision. At the releasing height of 13 mm, besides rebound, ~36% of collision also resulted in coalescence. In such cases, the two droplets did not merge together until the stationary droplet bounced off the superhydrophobic surface. When the impacting droplet rebounded, the stationary droplet also jumped up and caught the impacting droplet due to the formation of the liquid bridge. The coalescence occurred during the separation process instead of the collision process, similar to the coalescence of emulsion droplets33.

Figure 4. Head-on collision of binary droplets at releasing height of 13 mm (B = 0 We = 2.72).

Figure 4

Open in a new tab

As the releasing height increased further, Weber number also increased. With the relatively high Weber number, the kinetic energy of impacting droplet increased. The relatively high kinetic energy helped the impacting droplet break the air film. The liquid bridge was then formed and it facilitated the coalescence of the droplets13, as shown in Table 1.

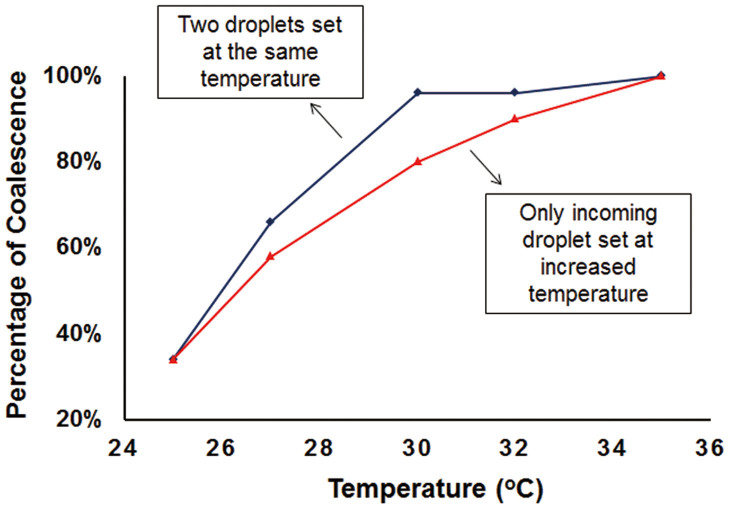
In studying the effect of temperature on the states of droplet collision, a releasing height of 13 mm (We = 2.72) was used due to the highest possibility of rebound state at that releasing height. The collision experiments were studied with two different temperature settings: (1) Both droplets were set at the same elevated temperatures; (2) Only the incoming droplet was set at the elevated temperatures, and the stationary droplets was set at 25°C.

As shown in Figure 5, the collision of the two droplets resulted in more coalescence than rebound with the increase of temperature for the incoming droplet only or for both droplets. Even a slight rise of temperature caused a large increase in the possibility of coalescence. When both droplets were heated, the percentage of coalescence was higher than that in the case when only incoming droplet was heated. Most collisions were in the coalescence state when both droplets were heated to 30°C, while there were ~20% of collisions resulted in the rebounding state when only the impacting droplet was heated to 30°C. If either the incoming droplet or both droplets were set at temperatures higher than 35°C, all collisions were in the coalescence state.

Figure 5. The increase in the possibility of coalescence with the increase of droplet temperature.

Figure 5

Open in a new tab

The increase in temperature not only resulted in the increased possibility of coalescence, it also shortened the time between the impact and the coalescence of droplets. Figure 6 compares the high speed video images of collisions with the change of the impacting droplet temperature. All collision happened with the same releasing height of 13 mm. When both droplets were set at room temperature, they merged at the time scale between 12 ms and 15 ms. As the temperature of the incoming droplet increased to 40°C, the droplets merged at the time scale between 6 ms to 9 ms. As the temperature of the incoming droplet increased to 50°C, the merge happened almost immediately, at the time scale between 0 ms and 3 ms.

Figure 6. Head-on collision of binary droplets with increased temperature of the incoming droplet at releasing height of 13 mm (Tstationary = Troom = 25°C, ΔT = Tincoming − Tstationary).

Figure 6

Open in a new tab

Discussion

There are several possible explanations for the observed coalescence of binary droplets set at elevated temperatures. One possible influencing factor is the surface tension. With the increase of the droplet temperature, there is a decrease of surface tension of the droplet, which results in the increase of the Weber number that may increase the possibility of coalescence. For the temperature range (25–35°C) studied in this work, however, there was little change of surface tension. The change of Weber number (from 2.72 to 2.92) was too small to influence the state of droplet collision. The second possible influencing factor is viscosity. During collision of the droplets, the droplets make contact and an air film will be trapped at the interface between the two droplets14. The increase of droplet temperature can decrease the viscosity of the droplet. Such decrease in viscosity encourages the formation of large contact area during collision and makes it easy for the impacting droplet to break the air film and form liquid bridge with the stationary droplet, which subsequently induces the coalescence. From the analysis of the high speed video images, however, there was no obvious increase of the contact areas as the droplet temperature increases.

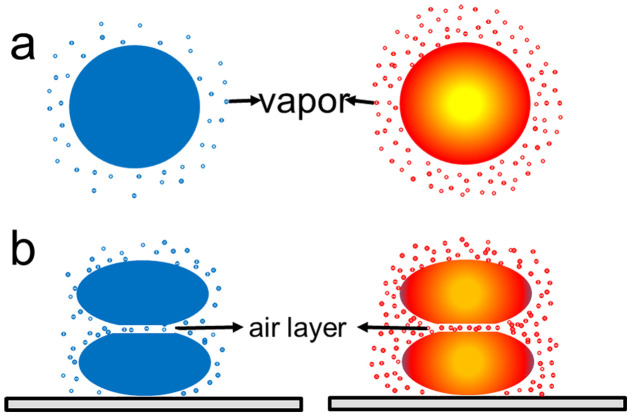
The third possible explanation centers on the impact of the water vapors around the droplets on the breakage of the air film at the interface between the droplets. As shown in Figure 7a, the rise of the temperature of the droplet will increase the vapor pressure, thus also the amount of vapor around the droplet34. Such increase of vapor molecules at the collision interface helps push out air at the interface and enables the breakage of the air film during collision. The increases of water molecules in the air film also facilitates the forming of liquid bridge during the contact and leads to the coalescence as shown in Figure 7b.

Figure 7. Schematic of the vapor effect to droplet collision.

Figure 7

Open in a new tab

(a): Water vapor around the cold droplet and hot droplet. (b) Air layer between the two droplets.

In this work, the influence of the droplet temperature on the head-on collision of binary droplet on superhydrophobic surface was studied. The droplet temperature played a key role in inducing the coalescence after the collision of binary droplets on superhdyrophobic surfaces. As the droplet temperature increased, the two droplets were more inclined to coalesce after collision. The study in this work demonstrated the importance of the droplet temperature on the outcome of collision of the binary droplets, and the findings can also be extended to collision of droplets under other conditions where the droplet temperature can be controlled.

Methods

Materials used

The chemicals used in the fabrication of superhydrophobic surfaces are as following: silver nitrate(99.8%, Aladdin, China); acetone(99.5%, Sinopharm Chemical Reagent Co. Ltd, China); ethanol(99.7%, Changshu Hong Sheng fine chemical Co. Ltd, China); sulphuric acid(98%, Sinopharm Chemical Reagent Co. Ltd, China); hydrogen peroxide(30%, Shanghai Ling Feng Chemical Reagent Co. Ltd, China);hydrofluoric acid(40%, Sinopharm Chemical Reagent Co. Ltd, China); ferric nitrate(98.5%, Sinopharm Chemical Reagent Co. Ltd, China). Perfluoro-1,1,2,2-tetrahydrooctyltrichlorosilane(97%, Alfa Aesar, US).

The silicon wafer was purchased from the Zhejiang Li Jing Photoelectric Technology Co. Ltd. The wafer is P type and its resistivity is in the range of 0.1 ~ 1 Ω·cm.

Generation of superhydrophobic surfaces

The superhydorphobic silicon substrate was generated through silver assisted etching35 followed by silanization with fluorosilane36. Following is the detailed process:

  1. The silicon wafer was cleaned with acetone, ethanol and deionized water; a mixture of H2SO4/H2O2 (v:v as 4:1) and diluted HF solution was used to remove the oxide.

  2. The cleaned wafer was dipped into the solution of 0.01 mol/L AgNO3 and 4.6 mol/L HF for 1 min at room temperature to deposit silver through electroless deposition.

  3. The wafer was transferred into the solution of 0.02 mol/L AgNO3, 0.135 mol/L Fe(NO3)3 and 4.6 mol/L HF for 1 hour at 50°C, washed with deionized water, and dried at room temperature.

  4. The nanostructured wafer was further treated with the fluorinated silane through vapor deposition.

Experimental setup

Figure 8 shows the experimental setup. The setup included a micropositioning system, an imaging acquisition equipment, a heating system and a droplet generator. The stationary droplet on the superhydrophobic substrate was aligned to the impacting droplet by the micropositioning stage. A heating stage (BILON-W-504S, Shanghai Bilon instrument Co. Ltd., China) was used to adjust the temperature of both the superhydrophobic substrate and the stationary droplet on the substrate. A syringe pump and a needle with inner-diameter ~0.3 mm were used to generate droplets with diameter ~2 mm. A heating system (DIYCH401, Shanghai Hua Jian Electric Heating Appliance Co. Ltd, China) was used to adjust the temperature of the needle between room temperature and 100°C with the temperature resolution of 1°C.

Figure 8. The setup for studying the collision of binary droplets on superhydrophobic surfaces.

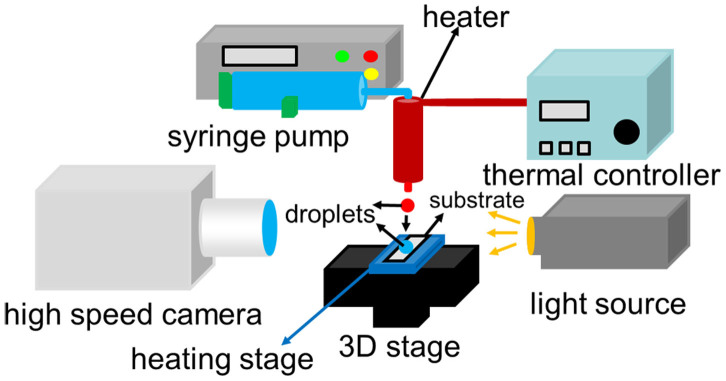
Figure 8

Open in a new tab

The superhydrophobic surface lies on a heating stage at the top of the 3D stage. Light source and high speed camera is aligned with the stationary droplet and incoming droplet is produced from the syringe pump and heated by the thermal controller.

Imaging hardware used in the setup included a high speed camera (X-Stream XS-4, IDT, US), a magnification zoom lens (XDS-0745, JANUS, China) that has 3× magnification, and an LED light source (C-F1230, Nikon, Japan). The camera can take images over 5,000 frames per second(fps) at full resolution of 512 × 512 pixels. The impact parameter and impact velocity were obtained through analysis of the high speed video images using the motion studio software from IDT.

The superhydrophobic substrate with stationary droplet on top was placed on the 3D micropositioning stage. Using the 3D stage, the stationary droplet was aligned carefully to enable the head-on collision between the two droplets. The releasing height between the tip of the needle and the substrate was in the range between 5 mm and 30 mm. All these experiments were conducted at room humidity (50%) to minimize the impact of humidity37,38. For every colliding condition, the experiments were repeated at minimum of 50 times to obtain the statistics of the collision states.

Author Contributions

W.S., T.D. and N.Y. conceived the idea and designed the experiments. N.Y., B.H. and L.D. conducted experiments. N.Y., T.D., W.S., X.Q., P.T., C.S. and F.H. helped data analysis and write the manuscript.

Acknowledgments

This work was supported by Natural Science Foundation of China (Grant No: 91333115), Natural Science Foundation of Shanghai (Grant No: 13ZR1421500), and the Zhi-Yuan Endowed fund from Shanghai Jiao Tong University. The authors also want to thank Mr. Zhenhui Wang and Mr. Wei Wang for their help and valuable discussions.

References

  1. Orme M. Experiments on droplet collisions, bounce, coalescence and disruption. Prog. Energy Combust. Sci. 23, 65–79 (1997). [Google Scholar]
  2. Eggers J., Lister J. R. & Stone H. A. Coalescence of liquid drops. J. Fluid Mech. 401, 293–310 (1999). [Google Scholar]
  3. Willis K. & Orme M. Binary droplet collisions in a vacuum environment: an experimental investigation of the role of viscosity. Exp. Fluids 34, 28–41 (2003). [Google Scholar]
  4. Gao T. C., Chen R. H., Pu J. Y. & Lin T. H. Collision between an ethanol drop and a water drop. Exp. Fluids 38, 731–738 (2005). [Google Scholar]
  5. Chen R. H. & Chen C. T. Collision between immiscible drops with large surface tension difference: diesel oil and water. Exp. Fluids 41, 453–461 (2006). [Google Scholar]
  6. Kim J. & Longmire E. K. Investigation of binary drop rebound and coalescence in liquids using dual-field PIV technique. Exp. Fluids 47, 263–278 (2009). [Google Scholar]
  7. Estrade J. P., Carentz H., Lavergne G. & Biscos Y. Experimental investigation of dynamic binary collision of ethanol droplets–a model for droplet coalescence and bouncing. Int. J. Heat Fluid Flow 20, 486–491 (1999). [Google Scholar]
  8. Pan K. L., Chou P. C. & Tseng Y. J. Binary droplet collision at high Weber number. Phys. Rev. E 80, 036301 (2009). [DOI] [PubMed] [Google Scholar]
  9. Liu D., Zhang P., Law C. K. & Guo Y. Collision dynamics and mixing of unequal-size droplets. Int. J. Heat Mass Transfer 57, 421–428 (2013). [Google Scholar]
  10. Mertaniemi H., Forchheimer R., Ikkala O. & Ras R. H. Rebounding Droplet-Droplet Collisions on Superhydrophobic Surfaces: from the Phenomenon to Droplet Logic. Adv. Mater. 24, 5738–5743 (2012). [DOI] [PubMed] [Google Scholar]
  11. Brazier-Smith P. R., Jennings S. G. & Latham J. Accelerated rates of rainfall. Nature 232, 112–113 (1971). [DOI] [PubMed] [Google Scholar]
  12. Nikolopoulos N., Nikas K. S. & Bergeles G. A numerical investigation of central binary collision of droplets. Comput. Fluids 38, 1191–1202 (2009). [Google Scholar]
  13. Ashgriz N. & Poo J. Y. Coalescence and separation in binary collisions of liquid drops. J. Fluid Mech. 221, 183–204 (1990). [Google Scholar]
  14. Brenn, G. & Ashgriz, N. (Ed.). Droplet Collision. Handbook of Atomization and Sprays: theory and applications. Springer U.S. 157–181 (2011). [Google Scholar]
  15. Qian J. & Law C. K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 331, 59–80 (1997). [Google Scholar]
  16. Richard D., Clanet C. & Quéré D. Surface phenomena: Contact time of a bouncing drop. Nature 417, 811–811 (2002). [DOI] [PubMed] [Google Scholar]
  17. Gunjal P. R., Ranade V. V. & Chaudhari R. V. Dynamics of drop impact on solid surface: Experiments and VOF simulations. AIChE J. 51, 59–78 (2005). [Google Scholar]
  18. Yarin A. L. Drop impact dynamics: splashing, spreading, receding, bouncing…. J. Annu. Rev. Fluid Mech. 38, 159–192 (2006). [Google Scholar]
  19. Zhang J. & Kwok D. Y. Contact line and contact angle dynamics in superhydrophobic channels. Langmuir 22, 4998–5004 (2006). [DOI] [PubMed] [Google Scholar]
  20. Wang Z., Lopez C., Hirsa A. & Koratkar N. Impact dynamics and rebound of water droplets on superhydrophobic carbon nanotube arrays. Appl. Phys. Lett. 91, 023105-023105-3 (2007). [Google Scholar]
  21. Kompinsky E. & Sher E. Experimental comparisons between droplet-droplet collision and single-droplet impacts on a solid surface. Atomization Sprays 19, 400–423 (2009). [Google Scholar]
  22. Li R., Ashgriz N., Chandra S., Andrews J. R. & Drappel S. Coalescence of two droplets impacting a solid surface. Exp. Fluids 48, 1025–1035 (2010). [Google Scholar]
  23. Li X., Ma X. & Lan Z. Dynamic Behavior of the Water Droplet Impact on a Textured Hydrophobic/Superhydrophobic Surface: The Effect of the Remaining Liquid Film Arising on the Pillars' Tops on the Contact Time. Langmuir 26, 4831–4838 (2010). [DOI] [PubMed] [Google Scholar]
  24. Hamlett C. A. E. et al. Transitions of water-drop impact behaviour on hydrophobic and hydrophilic particles. Eur. J. Soil. Sci. 64, 324–333 (2013). [Google Scholar]
  25. Hu H., Chen L., Huang S. & Song B. Rebound behaviors of droplets impacting on a superhydrophobic surface. Sci. China Ser. G 56, 960–965 (2013). [Google Scholar]
  26. Kompinsky E., Dolan G. & Sher E. Experimental study on the dynamics of binary fuel droplet impacts on a heated surface. Chem. Eng. Sci. 98, 186–194 (2013). [Google Scholar]
  27. Soltman D. & Subramanian V. Inkjet-printed line morphologies and temperature control of the coffee ring effect. Langmuir 24, 2224–2231 (2008). [DOI] [PubMed] [Google Scholar]
  28. Liu Z., Wu J., Zhen H. & Hu X. Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets. Energies 6, 204–219 (2013). [Google Scholar]
  29. Armani M., Chaudhary S., Probst R., Walker S. & Shapiro B. Control of microfluidic systems: two examples, results, and challenges. Int. J. Robust Nonlinear Control 15, 785–803 (2005). [Google Scholar]
  30. Graham P. J., Farhangi M. M. & Dolatabadi A. Dynamics of droplet coalescence in response to increasing hydrophobicity. Phys. Fluids 24, 112105-112105-20 (2012). [Google Scholar]
  31. Farhangi M. M., Graham P. J., Choudhury N. R. & Dolatabadi A. Induced Detachment of Coalescing Droplets on Superhydrophobic Surfaces. Langmuir 28, 1290–1303 (2012). [DOI] [PubMed] [Google Scholar]
  32. Wang F. C., Feng J. T. & Zhao Y. P. The head-on colliding process of binary liquid droplets at low velocity: High-speed photography experiments and modeling. J. Colloid Interface Sci. 326, 196–200 (2008). [DOI] [PubMed] [Google Scholar]
  33. Bremond N., Thiam A. R. & Bibette J. Decompressing emulsion droplets favors coalescence. Phys. Rev. Lett. 100, 024501 (2008). [DOI] [PubMed] [Google Scholar]
  34. Ranz W. E. & Marshall W. R. Evaporation from drops. Chem. Eng. Prog. 48, 141–146 (1952). [Google Scholar]
  35. Peng K., Wu Y., Fang H., Zhong X., Xu Y. & Zhu J. Uniform, Axial-Orientation Alignment of One-Dimensional Single-Crystal Silicon Nanostructure Arrays. Angew. Chem. Int. Ed. 44, 2737–2742 (2005). [DOI] [PubMed] [Google Scholar]
  36. Coffinier Y., Janel S., Addad A., Blossey R., Gengembre L., Payen E. & Boukherroub R. Preparation of superhydrophobic silicon oxide nanowire surfaces. Langmuir 23, 1608–1611 (2007). [DOI] [PubMed] [Google Scholar]
  37. Mockenhaupt B., Ensikat H. J., Spaeth M. & Barthlott W. Superhydrophobicity of biological and technical surfaces under moisture condensation: Stability in relation to surface structure. Langmuir 24, 13591–13597 (2008). [DOI] [PubMed] [Google Scholar]
  38. Yin L., Zhu L., Wang Q., Ding J. & Chen Q. Superhydrophobicity of natural and artificial surfaces under controlled condensation conditions. ACS Appl. Mat. Interfaces 3, 1254–1260 (2011). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES