Contour Tracking in Echocardiographic Sequences via Sparse Representation and Dictionary Learning

Abstract

This paper presents a dynamical appearance model based on sparse representation and dictionary learning for tracking both endocardial and epicardial contours of the left ventricle in echocardiographic sequences. Instead of learning offline spatiotemporal priors from databases, we exploit the inherent spatiotemporal coherence of individual data to constraint cardiac contour estimation. The contour tracker is initialized with a manual tracing of the first frame. It employs multiscale sparse representation of local image appearance and learns online multiscale appearance dictionaries in a boosting framework as the image sequence is segmented frame-by-frame sequentially. The weights of multiscale appearance dictionaries are optimized automatically. Our region-based level set segmentation integrates a spectrum of complementary multilevel information including intensity, multiscale local appearance, and dynamical shape prediction. The approach is validated on twenty-six 4D canine echocardiographic images acquired from both healthy and post-infarct canines. The segmentation results agree well with expert manual tracings. The ejection fraction estimates also show good agreement with manual results. Advantages of our approach are demonstrated by comparisons with a conventional pure intensity model, a registration-based contour tracker, and a state-of-the-art database-dependent offline dynamical shape model. We also demonstrate the feasibility of clinical application by applying the method to four 4D human data sets.

1. Introduction

Quantitative analysis of 4D echocardiographic images such as myocardial motion analysis (e.g., Tobon-Gomez et al. (2013); Craene et al. (2012); Compas et al. (2012); Yan et al. (2007); Ledesma-Carbayo et al. (2005); Hashimoto et al. (2003); Jacob et al. (2002); Papademetris et al. (2001); Kaluzynski et al. (2001); Shi et al. (1999)) provides important cardiac functional parameters (e.g., ejection fraction, wall thickening, and strain) for heart disease diagnosis and longitudinal therapy efficacy assessment. Segmentation of the left ventricular contours from echocardiographic sequences plays an essential role in such quantitative cardiac functional analysis. Due to gross intensity inhomogeneities, characteristic artifacts (e.g., attenuation, shadows, and signal dropout), and poor contrast between regions of interest, robust and accurate automatic segmentation of the left ventricle, especially the epicardial border, is very challenging in echocardiography.

The inherent spatiotemporal coherence of echocardiographic data provides useful constraints for echocardiographic segmentation and has motivated a spatiotemporal viewpoint of echocardiographic segmentation. The key observation is that the inherent spatiotemporal consistencies regarding image appearance (e.g., speckle pattern) and shape over the sequence can be exploited to guide cardiac border estimation. The spatiotemporal viewpoint is naturally supported by the fact that cardiologists also use a movie during clinical decision-making as the speckle pattern associated with deforming tissue can be observed in a movie whereas in a still frame the speckle pattern is not always useful (Noble and Boukerroui, 2006).

One intuitive way to perform spatiotemporal analysis is to extend spatial models, such as active contours (Kucera and Martin, 1997; Mikic et al., 1998; V. Chalana and Kim, 1996; Malas-siotis and Strintzis, 1999), Markov random fields (Dias and Leitão, 1996; Friedland and Adam, 1989; Herlin et al., 1994), and space-frequency (Angelini et al., 2001; Mulet-Parada and Noble, 2000), to the temporal domain and enforce temporal continuity of the cardiac border during the segmentation process. While these methods may render more consistent border estimates, they typically only impose a weak temporal constraint and mainly rely on low level image features, such as intensity, gradient, and local phase, to discriminate different regions or detect edges. It is well established that low level edge cue and region information are often not sufficient for a reliable and accurate segmentation of echocardiography (Noble and Boukerroui, 2006). Optical flow (Mikic et al., 1998) and Kalman filter (Jacob et al., 2002) have also been used to enforce temporal continuity.

Statistical models for learning offline shape, appearance, and motion priors from databases have received considerable attention in echocardiographic segmentation in recent years. Following the seminal work of Cootes et al. on statistical shape and appearance modeling (Cootes et al., 2001a,b), a number of spatiotemporal statistical models have been proposed for learning dynamical priors offline from databases. Bosch et al. (2002) proposed a 2D Active Appearance Motion Model (AAMM) which treats a 2D sequence as a single image to implicitly include motion information. Lorenzo-Valdés et al. (2004) proposed learning a spatiotemporal probabilistic atlas for cardiac MR segmentation. Dynamical shape models are proposed to explicitly learn cardiac dynamics. Examples include a second-order autoregressive model by Jacob et al. (2002), a second-order nonlinear model by Sun et al. (2005), a subject-specific dynamical model (SSDM) based on multilinear shape decomposition by Zhu et al. (2009), and a one-step forward prediction method based on motion manifold learning by Yang et al. (2008). While these statistical models have advantages in different aspects, an important common limitation stems from the assumption that different subjects have similar shape or motion patterns or their clinical images have similar appearance. This assumption may not hold for routine clinical images, especially for disease cases, due to natural subject-to-subject tissue property variations and operator-to-operator variation in acquisition (Noble and Boukerroui, 2006). The problem of forming a database that can handle a wide range of normal and abnormal heart images is still open. The dependence on databases places substantial constraints on the adaptability, deployment, and performance of these methods, especially in a physiological research setting.

Sparse representation is a rigorous mathematical framework for studying high-dimensional data and ways to uncover the structures of the data (Baraniuk et al., 2010). Recent advances in this area have not only caused a small revolution in the community of statistical signal processing (Baraniuk et al., 2010) but also led to several state-of-the-art results in computer vision applications such as face recognition (Wright et al., 2009), signal classification (Huang and Aviyente, 2006), texture classification, and edge detection (Mairal et al., 2008a; Peyré, 2009; Skretting and Husøy, 2006). Although images are naturally high dimensional, in many applications images belonging to the same class lie on or near a low dimensional subspace (Wright et al., 2010). Sparsity has proven to be a powerful prior for uncovering such degenerate structure. Based on this prior, the subspace of a class can be spanned in the sense of sparse representation by a dictionary of base vectors that can be learned from training examples. The dictionary naturally encodes the signal patterns of the class. It has been established that learned dictionaries outperform predefined ones in classification tasks, in particular for distorted data and compact representation (Rodriguez et al., 2007). Sparse representation has also recently been applied to medical image analysis settings such as shape prior modelling (Zhang et al., 2012a,b,c), nonrigid registration (Shi et al., 2012), and functional connectivity modelling (Wee et al., 2012).

In this paper, we present a dynamical appearance model (DAM) for echocardiographic contour tracking based on multiscale sparse representation and dictionary learning. Our approach exploits the inherent spatiotemporal coherence of individual echocardiographic data (as illustrated in Figure 1) for segmenting both endocardial and epicardial boundaries of the left ventricle. A schematic overview of the proposed approach is provided in Figure 2. The proposed segmentation method leverages a spectrum of complementary multilevel information including intensity, multiscale local appearance, and shape. We employ multiscale sparse representation of high-dimensional local image appearance and encode local appearance patterns with multiscale appearance dictionaries. We introduce an online multiscale appearance dictionary learning process interlaced with sequential segmentation. The local appearance of each frame is predicted by the DAM in the form of multiscale appearance dictionaries based on the appearance observed in the preceding frames. As the frames are segmented sequentially, the appearance dictionaries are dynamically updated to adapt to the latest segmented frame. The multiscale dictionary learning process is supervised in a boosting framework to seek optimal weighting of multiscale information and generate dictionaries that are both reconstructive and discriminative. Sparse coding with respect to the predictive dictionaries produces a local appearance discriminant that summarizes the multiscale discriminative local appearance information. We also include intensity and a dynamical shape prediction to complete the complementary information spectrum that we incorporate into a region-based level set segmentation formulation in a maximum a posteriori (MAP) framework.

Figure 1.

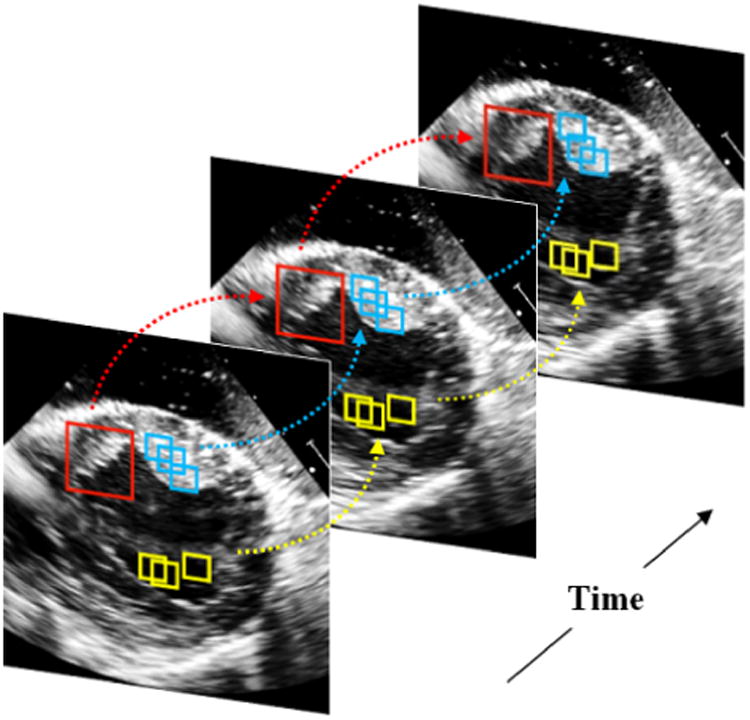
Spatio-temporal coherence of local image appearance at different scales. Local images in the same color present similar appearance. The arrows point out the temporal coherence of local image appearance.

Figure 2.

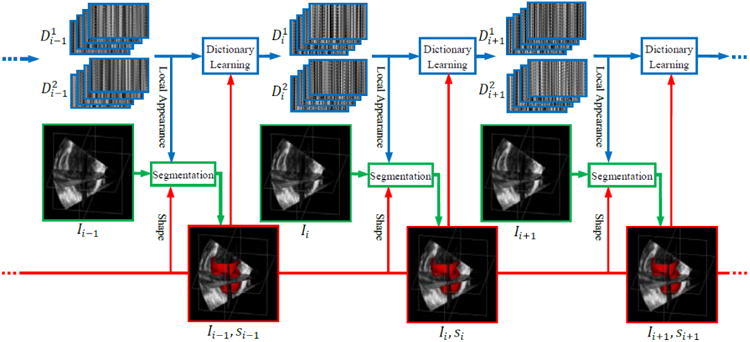
Dynamical dictionary updating interlaced with sequential segmentation. I_i is the image of frame i. s_i is the segmentation of frame i. $D_i^j$ represents multiscale appearance dictionaries for class j in frame i.

This paper is an extended version of the work that has been partially presented in our conference papers Huang et al. (2012a, b). In this paper, we elaborate our work with further details of theories, optimization, implementation, computational efficiency, and limitations that are either only summarized or not covered in our conference papers due to page limits. The other salient extensions are as follows. Instead of evaluating only the segmentation quality, we also apply our results to the estimation of ejection fraction which is more clinically relevant. In addition to comparison against pure intensity models, we also compare our method to a nonrigid-registration-based contour tracker that purely exploits temporal consistency. We present an in-depth analysis of parameter sensitivities to provide insights into parameter selection. We also extend the application of our method to 4D human data acquired from the apical long-axis window to investigate the feasibility of clinical application.

2. Materials and Methods

2.1. Local Image Appearance

The intensity of echocardiographic images involves substantial characteristic artifacts such as attenuation, speckle, shadows, and signal dropout due to the orientation dependence of acquisition (Noble and Boukerroui, 2006). Moreover, the contrast between regions of interest is poor and spatially varying. These characteristics make gray value insufficient for echocardiographic segmentation. A local image (i.e., a patch or block) centered at a spatial point, as shown in Figures 1 and 3, is a more reliable characterization of the point. Such local images present important local appearance information such as intensity patterns and anatomical structures to a degree depending on the scale. Finer scale local images (e.g., the smaller patches in Figure 1) characterize mainly local intensity patterns. Coarser scale local images (e.g., the larger patches in Figure 1) are dominated by anatomical patterns.

Figure 3.

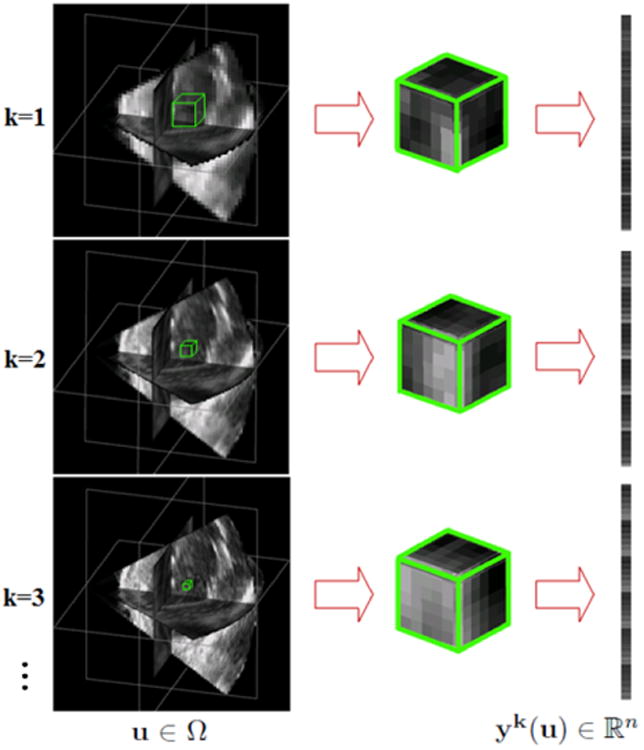
Construction of multiscale appearance vectors. From top to bottom, the images are ordered from coarse to fine resolutions and the physical sizes of the blocks vary from large to small. y^k(u) is an appearance vector for voxel u∈Ω at scale k.

In echocardiographic images, blood and different tissues present certain local appearance differences. The intra-class coherence and interclass difference are illustrated by the yellow and blue patches in Figure 1. Apart from these, the huge intra-class intensity inhomogeneity and appearance variations are usually the main challenges. The local images are naturally high dimensional, but those belonging to the same class still lie on or near a low dimensional subspace. Sparsity has proven to be a powerful prior for uncovering such degenerate structure. Sparse representation with over-complete dictionaries has sufficient expressiveness to represent the intra-class local appearance variations. The subspace of a class can be spanned in the sense of sparse representation by a dictionary of base vectors learned from training examples. The dictionary encodes the signal patterns of the class and summarizes intra-class coherence and variations. Furthermore, there is strong temporal coherence in echocardiographic images. That is, the appearance of a local region is relatively constant over the image sequence especially in two consecutive frames. Such spatiotemporal coherence of echocardiographic data as shown in Figure 1 provides a reliable spatiotemporal constraint for cardiac segmentation and forms the basis of our dynamical appearance model.

2.2. Multiscale Sparse Representation

Let Ω denote the 3D image domain. We describe the local appearance of each pixel u ∈ Ω in frame I_t with an appearance vector y_t(u) constructed by concatenating orderly the pixels within a block centered at u. A block having n pixels is written as a vector y_t(u) ∈ ℝⁿ. To leverage the complementary multiscale local appearance information, we describe the pixel u ∈ Ω with a series of appearance vectors ${\mathbf{y}}_t^k(\mathbf{u})\in {ℝ}^n$ at different appearance scales k = 1,…, S. We extract local images of different physical sizes from images smoothed to different degrees. The local images are subsampled to construct the appearance vectors. Figure 3 illustrates the construction of multiscale appearance vectors. More implementation details of multiscale representation are presented in section 2.5.

Under a sparse linear model, an appearance vector y ∈ ℝⁿ can be represented as a sparse linear combination of the atoms from an appearance dictionary D ∈ ℝ^n×K which is allowed to be over-complete (K > n). That is, y ≈ Dx, and ║x║₀ is small. The vector x containing very few nonzero entries is a sparse representation of y with respect to D. The appearance dictionary D can be learned from training examples. The atoms of the dictionary encode typical patterns of a specific appearance class, and the dictionary spans in the sense of sparse representation the subspace of that class. We approximate the coherence of an appearance class at a certain scale with a learned appearance dictionary. Given appearance vector y, dictionary D and a sparsity factor T, the sparse representation x can be solved by sparse coding:

$$\underset{\mathbf{x}}{min}{\Vert \mathbf{y}-\mathbf{D}\mathbf{x}\Vert }_2^2\mathrm{s}.\mathrm{t}.{\Vert \mathbf{x}\Vert }_0\le T.$$ (1)

Exact determination of sparsest representation has proven to be NP-hard (Davis et al., 1997). Approximate solutions are considered instead and several efficient pursuit algorithms have been proposed which include the matching pursuit (MP) (Mal-lat and Zhang, 1993) and the orthogonal matching pursuit (OMP) (Pati et al., 1993; Davis et al., 1994; Tropp, 2004) algorithms.

A cardiac shape s_t in I_t is embedded in a level set function Φ _t(u). We define ${\mathrm{\Phi }}_t^{+}(\mathbf{u})={\mathrm{\Phi }}_t(\mathbf{u})+{\psi }_1$ and ${\mathrm{\Phi }}_t^{-}(\mathbf{u})={\mathrm{\Phi }}_t(\mathbf{u})-{\psi }_2$, where ψ₁ and ψ₂ are constants. The estimation of shape s_t is equivalent to discriminating the two band regions ${\mathrm{\Omega }}_t^1=\{\mathbf{u}\in \mathrm{\Omega }:{\mathrm{\Phi }}_t^{-}(\mathbf{u})\ge 0\}$ and ${\mathrm{\Omega }}_t^2=\{\mathbf{u}\in \mathrm{\Omega }:{\mathrm{\Phi }}_t^{+}(\mathbf{u})>0,{\mathrm{\Phi }}_t(\mathbf{u})<0\}$ that are outside and inside the boundary. The two regions form two classes of local appearance. Given the knowledge of the preceding shape Φ _t-1, we define the region of interest at time t as ${\mathrm{\Omega }}_t^{\ast }=\{\mathbf{u}\in \mathrm{\Omega }:{\mathrm{\Phi }}_{t-1}^{+}(\mathbf{u})+{\zeta }_1\ge 0,{\mathrm{\Phi }}_{t-1}^{-}(\mathbf{u})-{\zeta }_2\le 0\}$. The constants ζ ₁ and ζ₂ are chosen to be large enough such that ${\mathrm{\Omega }}_t^1\cup {\mathrm{\Omega }}_t^2\in {\mathrm{\Omega }}_t^{\ast }$. Then we only need to discriminate the pixels $\mathbf{u}\in {\mathrm{\Omega }}_t^{\ast }$ to estimate s_t.

Suppose at a certain appearance scale, ${\mathbf{D}}_t^1,{\mathbf{D}}_t^2$ are two dictionaries adapted to appearance classes ${\mathrm{\Omega }}_t^1$ and ${\mathrm{\Omega }}_t^2$ respectively. They exclusively span in terms of sparse representation the sub-spaces of the corresponding classes. That is, they can be used to reconstruct typical appearance vectors from the corresponding classes. The reconstruction residue $R_t^c(\mathbf{u})$. of an appearance vector y_t(u) with respect to dictionary ${\mathbf{D}}_t^c$ is defined as

$$R_t^c(\mathbf{u})={\Vert {\mathbf{y}}_t(\mathbf{u})-{\mathbf{D}}_t^c{\widehat{\mathbf{x}}}_t^c(\mathbf{u})\Vert }_2,$$ (2)

$\forall \mathbf{u}\in {\mathrm{\Omega }}_t^{\ast }$, c ∈ {1,2} where ${\widehat{\mathbf{x}}}_t^c$, is the sparse representation of y_t with respect to ${\mathbf{D}}_t^c$. It is logical to expect that $R_t^1(\mathbf{u})>R_t^2(\mathbf{u})$ When $\mathbf{u}\in {\mathrm{\Omega }}_t^2$ and $R_t^1(\mathbf{u})<R_t^2(\mathbf{u})$ When $\mathbf{u}\in {\mathrm{\Omega }}_t^1$. This observation establishes the basis of sparse-representation-based discrimination and applies to all the local appearance scales.

Suppose J pairs of complementary dictionaries ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$, z = 1,…, J, are learned. Coding image I_t with the series of learned dictionaries produces a series of reconstruction residues ( ${\{R_t^1(\mathbf{u})\}}_z$ and ${\{R_t^2(\mathbf{u})\}}_z$) which form the multiscale discriminative appearance information. Combining the complementary multiscale information, we introduce a local appearance discriminant

$$A_t(\mathbf{u})=\frac{{\mathbf{1}}_{{\mathrm{\Omega }}_t^{\ast }}(\mathbf{u}){\sum }_{z=1}^J[(log\frac{1}{{\beta }_z}sgn({\{R_t^2(\mathbf{u})\}}_z)]}{{\sum }_{z=1}^{J}log\frac{1}{{\beta }_z}},$$ (3)

∀u ∈ Ω, where $1_{{\mathrm{\Omega }}_t^{\ast }}(\mathbf{u})=1$, $\forall \mathbf{u}\in {\mathrm{\Omega }}_t^{\ast }$, and $1_{{\mathrm{\Omega }}_t^{\ast }}(\mathbf{u})=0$ otherwise. β_z's are the weighting parameters of the J dictionary pairs that are optimized in the boosted dictionary learning process. This scalar indicates the likelihood that the point u is inside or outside the shape s_t.

2.3. Boosted Multiscale Dictionary Learning

Learning a dictionary D ∈ ℝ^n×K from a finite training set of signals Y = [y₁,…, y_M] ∈ ℝ^n×M is to solve a joint optimization problem with respect to the dictionary D and the sparse representation coefficients X = [x₁,…, x_M] ∈ ℝ^K×M:

$$\underset{\mathbf{D},\mathbf{X}}{min}{\Vert \mathbf{Y}-\mathbf{D}\mathbf{X}\Vert }_2^2\mathrm{s}.\mathrm{t}.\forall i,{\Vert {\mathbf{x}}_i\Vert }_0\le T.$$ (4)

Effective algorithms for solving the dictionary learning problem (4) include the K-SVD (Aharon et al., 2006), the MOD (Engan et al., 1999), and a stochastic algorithm (Mairal et al., 2009). The K-SVD has been widely used because of good convergence property. The main iteration of the K-SVD contains two stages: sparse coding and dictionary update. In the sparse coding stage, D is fixed and problem (1) is solved using the OMP to find sparse representations X. In the dictionary update stage, the atoms of the dictionary D are updated.

To obtain the appearance discriminant A_t defined in (3), the series of complementary appearance dictionary pairs ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$ and the corresponding weighting parameters β_z need to be learned. Leveraging the inherent spatiotemporal coherence of individual data, we introduce an online learning process to dynamically adapt multiscale dictionaries to the evolving appearance when the image sequence is segmented sequentially as illustrated in Figure 2. Three issues are important in this setting. First, the true distribution underlying the data Y is not known. A uniform distribution is usually assumed to place equal emphasis on all the training examples. Our observation is that there are harder and easier parts of the appearance space and more emphasis should be placed on the harder part to enforce the learned dictionaries to include the most discriminative patterns. The relative easier and harder parts can be different at different appearance scales. Second, the generic dictionary learning formulation (4) gets trapped in a local minimum and learns only the scale that corresponds to the size of local images (Mairal et al., 2008b). We decompose the multiscale information into a series of appearance dictionaries each of which is learned at a single scale. Third, the weighting of different appearance scales need to be optimized to achieve the best joint discriminative property of the multiscale dictionaries. To address these issues and strengthen the discriminative property of the learned appearance dictionaries, we propose a boosted multiscale appearance dictionary learning process supervised in an AdaBoost (Freund and Schapire, 1995) framework. The K-SVD dictionary learning algorithm is invoked to enforce the reconstructive property of the dictionaries. The boosting supervision strengthens the discriminative property and optimizes the weighting of multiscale information.

The proposed dictionary learning algorithm following the structure of the AdaBoost is detailed in Algorithm 1. Given training samples of appearance vectors belonging to two classes ${\{{\mathbf{Y}}_{t-1}^1\}}_k=\{{\mathbf{y}}_{t-1}^k(\mathbf{u}):\mathbf{u}\in {\mathrm{\Omega }}_{t-1}^1\}$ and ${\{{\mathbf{Y}}_{t-1}^2\}}_k=\{{\mathbf{y}}_{t-1}^k(\mathbf{u}):\mathbf{u}\in {\mathrm{\Omega }}_{t-1}^2\}$, k = 1,…, S, from the coarsest scale to the finest scale, it learns a series of J dictionary pairs ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$, z = 1,…, J and the corresponding weighting parameters β_z. Each dictionary pair is learned from a single appearance scale. The multiple scales are reused in cyclic order if J > S. Each pair of dictionaries are learned by the K-SVD algorithm, which is taken as a weak learning process making a weak hypothesis. J weak learners are employed to reach a strong hypothesis. Each weak learner faces a different distribution of the data that is updated based on the error made by the preceding weak learners, while the first weak learner makes the initial guess that the data obeys a uniform distribution. The appearance scale varies across the weak learners such that the error made at a certain scale can hopefully be corrected at the other scales. The weighting parameters of the multiscale information are optimized automatically through this boosting process. For t > 2, ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$ are well initialized with ${\{{\mathbf{D}}_{t-1}^1,{\mathbf{D}}_{t-1}^2\}}_z$ and updated with a smaller number of iterations than the initial learning process. ${\{{\mathbf{D}}_2^1,{\mathbf{D}}_2^2\}}_z$ are initialized with training examples. Figure 4 shows examples of the learned appearance dictionaries at different scales for the two local appearance classes inside and outside the endocardial border. The coarser scale dictionaries encode more high level anatomical patterns, while the finer scale dictionaries encode more low level speckle patterns.

Figure 4.

Examples of learned appearance dictionaries at different scales for the two local appearance classes inside and outside the endo-cardial border. The left (right) column from top to bottom represents three dictionaries from coarser scale to finer scale for the outside (inside) class. The dictionaries in the same row are at the same scale. The true physical size of the finer scale dictionary atoms is smaller than the coarser scale dictionary atoms.

Algorithm 1 Multiscale Appearance Dictionary Learning

Require: appearance vector samples ${\{{\mathbf{Y}}_{t-1}^1\}}_k={\{{\mathbf{y}}_{1,i}^k\}}_{i=1}^{M_1}$ and ${\{{\mathbf{Y}}_{t-1}^2\}}_k={\{{\mathbf{y}}_{2,j}^k\}}_{j=1}^{M_2}$, k = 1,…, S, initial dictionaries ${\{{\mathbf{D}}_{t-1}^1,{\mathbf{D}}_{t-1}^2\}}_z,z=1,\dots ,J$, and sparsity factor T.

${\mathbf{w}}_1^1={\{w_{1,i}^1\}}_{i=1}^{M_1}=\mathbf{1}$, ${\mathbf{w}}_2^1={\{w_{2,j}^1\}}_{j=1}^{M_2}=\mathbf{1}$.

for z = 1,…,J do k = S if z%S = 0; k = z%S, otherwise.

Resampling: Draw sample sets ${\stackrel{\sim }{\mathbf{Y}}}_1^z$ from ${\{{\mathbf{Y}}_{t-1}^1\}}_k$ and ${\stackrel{\sim }{\mathbf{Y}}}_2^z$ from ${\{{\mathbf{Y}}_{t-1}^2\}}_k$ based on distributions ${\mathbf{p}}_1^z={\{p_{1,i}^z\}}_{i=1}^{M_1}=\frac{{\mathbf{w}}_1^z}{{\sum }_{i=1}^{M_1}{w}_{1,i}^z}$ and ${\mathbf{p}}_2^z={\{p_{2,j}^z\}}_{j=1}^{M_2}=\frac{{\mathbf{w}}_2^z}{{\sum }_{j=2}^{M_2}{w}_{2,j}^z}$.

Dictionary Update: Apply the K-SVD to learn ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$ from ${\stackrel{\sim }{\mathbf{Y}}}_1^z$ and ${\stackrel{\sim }{\mathbf{Y}}}_2^z$: $\underset{{\{{\mathbf{D}}_t^c\}}_{z,}\mathbf{X}}{min}{\Vert {\stackrel{\sim }{\mathbf{Y}}}_c^z-{\{{\mathbf{D}}_t^c\}}_z\mathbf{X}\Vert }_2^2\mathrm{s}.\mathrm{t}.{\forall }_i,{\Vert {\mathbf{x}}_i\Vert }_0\le T;c\in \{1,2\}.$

Sparse Coding: $\forall \mathbf{y}\in {\{{\mathbf{Y}}_{t-1}^1,{\mathbf{Y}}_{t-1}^2\}}_k$, solve for the sparse representations with respect to ${\{{\mathbf{D}}_t^1\}}_z$ and ${\{{\mathbf{D}}_t^2\}}_z$ using the OMP, and get residues $R{(\mathbf{y},{\mathbf{D}}_t^1)}_z$ and $R{(\mathbf{y},{\mathbf{D}}_t^2)}_z$.

Classification: Make a hypothesis $h_z:\mathbf{y}\in {\{{\mathbf{Y}}_{t-1}^1,{\mathbf{Y}}_{t-1}^2\}}_k\to \{0,1\}:h_z(\mathbf{y})=\mathit{\text{Heaviside}}(R{(\mathbf{y},{\mathbf{D}}_t^2)}_z-R{(\mathbf{y},{\mathbf{D}}_t^1)}_z)$. Calculate the error of $h_z:{\in }_z=\sum _{i=1}^{M_1}{p}_{1,i}^z|h_z({\mathbf{y}}_{1,i}^k)-1|+\sum _{j=1}^{M_2}{p}_{2,j}^z{h}_z({\mathbf{y}}_{2,j}^k)$. Set βz = ∈z/(1 − ∈z).

Weight Update: $w_{1,i}^{z+1}=w_{1,i}^z{\beta }_z^{1-|h_z({\mathbf{y}}_{1,i}^k)-1|},w_{2,j}^{z+1}=w_{2,j}^z{\beta }_z^{1-h_z({\mathbf{y}}_{2,j}^k)}$

end for dictionary pairs ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_z$, weighting parameters βz, z = 1,…,J.

2.4. Left Ventricular Segmentation

The proposed method segments the echocardiographic sequence frame-by-frame sequentially and dynamically updates multiscale dictionaries on the fly as illustrated in Figure 2. Similar to the database-dependant offline dynamical shape models (Jacob et al., 2002; Sun et al., 2005; Zhu et al., 2009), we also assume a segmented first frame for initialization. It can be achieved by an automatic method with expert correction or pure manual segmentation. In this study, we initialize the process with a manual tracing of the first frame that is obtained using a 4D Surface Editor provided by the BioImage Suite software (Papademetris et al., 2005). In the surface editor, the user sets control points of 2D B-splineparameterized contours slice by slice. To reduce the propagation of errors, we utilize the periodicity property of cardiac dynamics to perform bi-directional segmentation similar to Zhu et al. (2010). Suppose {I₁,…, I_N} is the original sequence with end-diastolic (ED) frames I₁ and I_N, and end-systolic (ES) frame I_s. We simultaneously segment two subsequences: a forward subsequence {I₁, …, I_s} and a backward subsequence {I₁, I_N, …, I_s+1}. The endocardial and epicardial borders of the left ventricle are segmented separately but in the same way. Figure 5 illustrates the procedure of region-based level set segmentation of a current frame given the learned appearance dictionaries.

Figure 5.

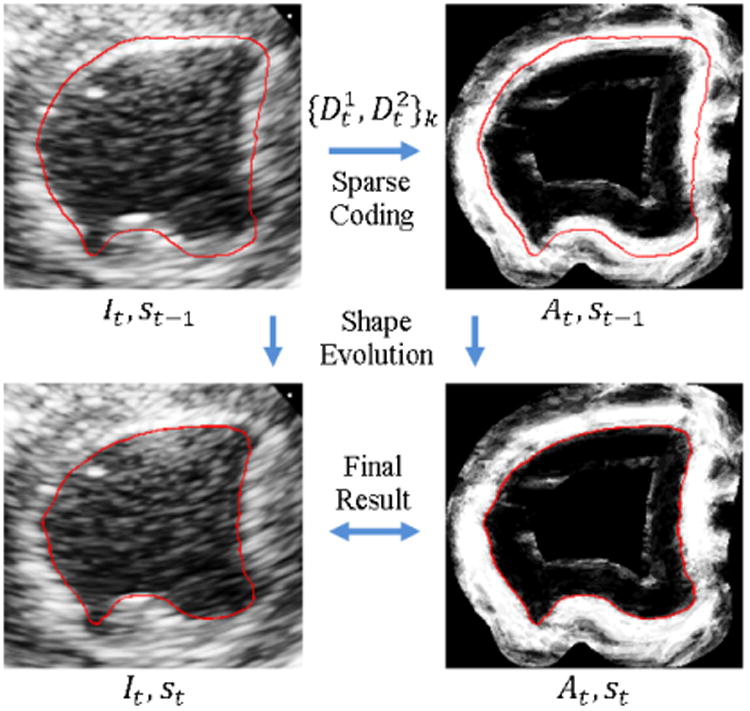
The procedure of region-based level set segmentation of a current frame given appearance dictionary prediction ${\{{\mathbf{D}}_t^1,{\mathbf{D}}_t^2\}}_k$. I_t is the image of frame t. s_t is the segmentation of frame t. A_t is the appearance discriminant.

2.4.1. MAP Estimation

We estimate the shape in frame I_t that is embedded in a level set function Φ _t given the knowledge of Φ̂_1:t-1 and I_1:t. We integrate a spectrum of complementary multilevel information including intensity I_t, multiscale local appearance discriminant A_t, and a dynamical shape prediction ${\mathrm{\Phi }}_t^{\ast }$. The level set function is estimated by maximizing the posterior probability:

$$\begin{array}{l}{\widehat{\mathrm{\Phi }}}_t=arg{max}_{{\mathrm{\Phi }}_t}p({\mathrm{\Phi }}_t|{\widehat{\mathrm{\Phi }}}_{1:t-1},I_{1:t-1},I_t)\\ =arg{max}_{{\mathrm{\Phi }}_t}p({\widehat{\mathrm{\Phi }}}_{1:t-1,}{I}_{1:t-1},I_t|{\mathrm{\Phi }}_t)p({\mathrm{\Phi }}_t)\\ \approx arg{max}_{{\mathrm{\Phi }}_t}p({\mathrm{\Phi }}_t^{\ast },A_t,I_t|{\mathrm{\Phi }}_t)p({\mathrm{\Phi }}_t)\\ \approx arg{max}_{{\mathrm{\Phi }}_t}p({\mathrm{\Phi }}_t^{\ast }|{\mathrm{\Phi }}_t)p(A_t|{\mathrm{\Phi }}_t)p(I_t|{\mathrm{\Phi }}_t)p({\mathrm{\Phi }}_t)\end{array}.$$ (5)

The shape regularization includes a temporal smoothness term $p({\mathrm{\Phi }}_t^{\ast }|{\mathrm{\Phi }}_t)$ and a spatial smoothness term p(Φ_t). Since Φ_t-1 and Φ_t-2 are both spatially and temporally close, we assume a constant evolution speed during [t − 2,t]. Within the band domain ${\mathrm{\Omega }}_t^1\cup {\mathrm{\Omega }}_t^2$ we introduce an approximate second order autoregressive shape prediction ${\mathrm{\Phi }}_t^{\ast }={\widehat{\mathrm{\Phi }}}_{t-1}+G({\widehat{\mathrm{\Phi }}}_{t-1}-{\widehat{\mathrm{\Phi }}}_{t-2})$ to regularize the shape estimation. Here G(*) denotes Gaussian smoothing operation used to preserve the smoothness of level set function. The temporal regularization is given by

$$p({\mathrm{\Phi }}_t^{\ast }|{\mathrm{\Phi }}_t)\propto exp\{-\gamma {\int }_{{\mathrm{\Omega }}_t^1\cup {\mathrm{\Omega }}_t^2}{({\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })}^{2}d\mathbf{u}\}.$$ (6)

The spatial regularization is the standard level set smoothness constraint on the arc-length of the propagating front

$$p({\mathrm{\Phi }}_t)\propto exp\{-{\int }_{\mathrm{\Omega }}\delta ({\mathrm{\Phi }}_t)|\nabla {\mathrm{\Phi }}_t|d\mathbf{u}\},$$ (7)

where δ(*) denotes a smooth Dirac function.

The discriminant A_t summarizing the multiscale local appearance is the most important information here. Based on its definition, it is reasonable to expect distinct A_t in ${\mathrm{\Omega }}_t^1$ and ${\mathrm{\Omega }}_t^2$ and the homogeneity of A_t within each region. Similar to the Chan-Vese model (Chan and Vese, 2001), the appearance discriminant likelihood is approximated with independent identical distributed (i.i.d.) Gaussian distributions inside and outside the boundary:

$$p(A_t|{\mathrm{\Phi }}_t)\propto {\prod }_{\mathbf{u}\in {\mathrm{\Omega }}_t^1}exp\{\frac{-{(A_t(\mathbf{u})-c_1)}^2}{2{\omega }_2^2}\}\times {\prod }_{\mathbf{u}\in {\mathrm{\Omega }}_t^2}exp\{\frac{-{(A_t(\mathbf{u})-c_2)}^2}{2{\omega }_2^2}\}.$$ (8)

The lowest level information is intensity which is helpful for estimating the endocardial border. We split the band domain ${\mathrm{\Omega }}_t^{\ast }$ into two band regions ${\stackrel{\sim }{\mathrm{\Omega }}}_t^1=\{\mathbf{u}\in \mathrm{\Omega }:{\mathrm{\Phi }}_{t-1}^{-}(\mathbf{u})-{\zeta }_2\le 0,{\mathrm{\Phi }}_t(\mathbf{u})\ge 0\}$ and ${\stackrel{\sim }{\mathrm{\Omega }}}_t^2=\{\mathbf{u}\in \mathrm{\Omega }:{\mathrm{\Phi }}_{t-1}^{+}(\mathbf{u})+{\zeta }_1\ge 0,{\mathrm{\Phi }}_t(\mathbf{u})<0\}$ that are inside and outside the boundary. The conventional i.i.d. Rayleigh distributions of I_t are assumed:

$$p(I_t|{\mathrm{\Phi }}_t)={\prod }_{\mathbf{u}\in {\stackrel{\sim }{\mathrm{\Omega }}}_t^1}\frac{I_t(\mathbf{u})}{{\sigma }_1^2}exp\{\frac{-I_t{(\mathbf{u})}^2}{2{\sigma }_1^2}\}\times {\prod }_{\mathbf{u}\in {\stackrel{\sim }{\mathrm{\Omega }}}_t^2}\frac{I_t(\mathbf{u})}{{\sigma }_2^2}exp\{\frac{-I_t{(\mathbf{u})}^2}{2{\sigma }_1^2}\}.$$ (9)

The Rayleigh model of speckle has proven a popular choice for ultrasound image segmentation (Noble and Boukerroui, 2006) and has been incorporated into the level set method of Sarti et al. (2005). This choice may not be optimal. There are several alternative models including K-distribution, Rice distribution, and Nakagami distribution. In this study, we focus more on the local appearance component which dominates the estimation problem. Since the intensity is not helpful for the epicardial discrimination in this setting, p(I_t|Φ_t) is dropped in the epicardial case.

2.4.2. Energy Functional

Combining (6), (7), (8), and (9), we introduce the overall segmentation energy functional:

$$\begin{array}{l}E(\mathrm{\Theta },{\mathrm{\Phi }}_t)\\ =-logp({\mathrm{\Phi }}_t|{\widehat{\mathrm{\Phi }}}_{1:t-1},I_{1:t-1},I_t)\\ \approx -logp[p({\mathrm{\Phi }}_t^{\ast }|{\mathrm{\Phi }}_t)p(A_t|{\mathrm{\Phi }}_t)p(I_t|{\mathrm{\Phi }}_t)p({\mathrm{\Phi }}_t)]\\ =v[{\int }_{{\stackrel{\sim }{\mathrm{\Omega }}}_t^1}\frac{I_t^2}{2{\sigma }_1^2}+log(\frac{{\sigma }_1^2}{I_t})d\mathbf{u}+{\int }_{{\stackrel{\sim }{\mathrm{\Omega }}}_t^2}\frac{I_t^2}{2{\sigma }_2^2}+log(\frac{{\sigma }_2^2}{I_t})d\mathbf{u}]\\ +K[{\int }_{{\mathrm{\Omega }}_t^1}{(A_t-c_1)}^{2}d\mathbf{u}+{\int }_{{\mathrm{\Omega }}_t^2}{(A_t-c_2)}^{2}d\mathbf{u}]\\ +\gamma {\int }_{{\mathrm{\Omega }}_t^1\cup {\mathrm{\Omega }}_t^2}{({\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })}^{2}d\mathbf{u}\\ +{\int }_{\mathrm{\Omega }}\delta ({\mathrm{\Phi }}_t)|\nabla {\mathrm{\Phi }}_t|d\mathbf{u}\end{array}$$ (10)

where Θ = [c₁, c₂, σ₁, σ₂] are parameters of the distributions of A_t and I_t. The parameters k, ν, and γ control the balance among the weights of A_t, ${\mathrm{\Phi }}_t^{\ast }$, and I_t. Using a regularized version (Chan and Vese, 2001) of the Heaviside function

$$H(x)=\frac{1}{2}(1+\frac{2}{x}arctan(\frac{x}{\varepsilon }))$$ (11)

and the one-dimensional Dirac measure

$$\delta (x)=\frac{d}{dx}H(x)=\frac{\varepsilon }{\pi ({\varepsilon }^2+x^2)},$$ (12)

we express the energy functional in the following way:

$$\begin{array}{l}E(\mathrm{\Theta },{\mathrm{\Phi }}_t)\\ =v{\int }_{\mathrm{\Omega }}[\frac{I_t^2}{2{\sigma }_1^2}+log(\frac{{\sigma }_2^2}{I_t})]H({\mathrm{\Phi }}_t)[1-H({\mathrm{\Phi }}_{t-1}^{-}-{\zeta }_2)]d\mathbf{u}\\ +v{\int }_{\mathrm{\Omega }}[\frac{I_t^2}{2{\sigma }_1^2}+log(\frac{{\sigma }_2^2}{I_t})][1-H({\mathrm{\Phi }}_t)]H({\mathrm{\Phi }}_{t-1}^{+}+{\zeta }_2)]d\mathbf{u}\\ +k{\int }_{\mathrm{\Omega }}{(A_t-c_1)}^{2}H({\mathrm{\Phi }}_t)[1-H({\mathrm{\Phi }}_t^{-})]d\mathbf{u}\\ +k{\int }_{\mathrm{\Omega }}{(A_t-c_2)}^2[1-H({\mathrm{\Phi }}_t)]H({\mathrm{\Phi }}_t^{+})d\mathbf{u}\\ +\gamma {\int }_{\mathrm{\Omega }}({{\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })}^{2}H({\mathrm{\Phi }}_t^{+})[1-H({\mathrm{\Phi }}_t^{-})]d\mathbf{u}\\ +{\int }_{\mathrm{\Omega }}\delta ({\mathrm{\Phi }}_t|\nabla {\mathrm{\Phi }}_t|d\mathbf{u}\end{array}.$$ (13)

2.4.3. Optimization

Keeping Φ_t fixed, we have the maximum likelihood estimate of Θ(Φ_t):

$$c_i({\mathrm{\Phi }}_t)=\frac{{\int }_{{\mathrm{\Omega }}_t^i}{A}_{t}d\mathbf{u}}{{\int }_{{\mathrm{\Omega }}_t^i}d\mathbf{u}},\forall i\in \{1,2\}$$ (14)

and

$${\sigma }_i{({\mathrm{\Phi }}_t)}^2\frac{{\int }_{{\stackrel{\sim }{\mathrm{\Omega }}}_t^i}{I}_t^{2}d\mathbf{u}}{2{\int }_{{\stackrel{\sim }{\mathrm{\Omega }}}_t^i}d\mathbf{u}},\forall i\in \{1,2\}.$$ (15)

To minimize the energy functional (13) with respect to Φ_t, we keep c_i fixed, substitute (15) for σ_i, and deduce the associated Euler-Lagrange equation. Parameterizing the descent direction by an artificial time τ > 0, we have the following evolution equation of Φ_t:

$$\begin{array}{l}\frac{\partial {\mathrm{\Phi }}_t}{\partial \tau }\\ =\delta ({\mathrm{\Phi }}_t)\nabla \cdot (\frac{\nabla {\mathrm{\Phi }}_t}{|\nabla {\mathrm{\Phi }}_t|})\\ -k\delta ({\mathrm{\Phi }}_t)[{(A_t-c_1)}^2][1-H({\mathrm{\Phi }}_t^{-})]\\ +k\delta ({\mathrm{\Phi }}_t^{-})[{(A_t-c_1)}^2]H({\mathrm{\Phi }}_t)\\ +k\delta ({\mathrm{\Phi }}_t)[{(A_t-c_2)}^2]H({\mathrm{\Phi }}_t^{+})\\ -k\delta ({\mathrm{\Phi }}_t^{+})[{(A_t-c_2)}^2][1-H({\mathrm{\Phi }}_t)]\\ +v\delta ({\mathrm{\Phi }}_t)[2log({\sigma }_1/{\sigma }_2)+I_t^2({\sigma }_2^2-{\sigma }_1^2)/2{\sigma }_1^2{\sigma }_2^2]\\ -2\gamma ({\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })\delta ({\mathrm{\Phi }}_t)H({\mathrm{\Phi }}_t^{+})[1-H({\mathrm{\Phi }}_t^{-})]\\ -\gamma {({\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })}^2\delta ({\mathrm{\Phi }}_t^{+})[1-H({\mathrm{\Phi }}_t^{-})]\\ +\gamma {({\mathrm{\Phi }}_t-{\mathrm{\Phi }}_t^{\ast })}^{2}H({\mathrm{\Phi }}_t^{+})\delta ({\mathrm{\Phi }}_t^{-}).\end{array}$$ (16)

With appropriate discretization and numerical approximations, our algorithm iteratively minimizes the energy functional (10) by taking the following steps:

1. Initialize ${\mathrm{\Phi }}_t^0$ With Φ̂_t-1, and set τ = 0;

2. Compute the maximum likelihood estimate of $\mathrm{\Theta }({\mathrm{\Phi }}_t^{\tau })$

3. Update ${\mathrm{\Phi }}_t^{\tau +1}$ using equation (16);

4. Reinitialize ${\mathrm{\Phi }}_t^{\tau +1}$ to a signed distance function after every few iterations;

5. Stop if ${\Vert {\mathrm{\Phi }}_t^{\tau +1}-{\mathrm{\Phi }}_t^{\tau }\Vert }_2<\xi$, otherwise set τ = τ + 1 and go to (b).

2.5. Implementation

We extract local images from smoothed images to approximate multiscale image decomposition. At each scale, the image is smoothed to a different degree and local images are extracted at a different physical size. From the coarsest appearance scale to the finest appearance scale, the physical size of the extracted local images decreases linearly from ∼ 15mm × 15mm × 5mm to ∼ 3mm × 3mm × 3mm. The local images are subsampled with 3D sampling grids. The grid spacing corresponds to the size of smoothing kernel and ranges from the original image voxel size at the finest scale to three times the original voxel size at the coarsest scale. For computational simplicity, we round the grid spacing to a multiple of the original voxel size and allow the appearance vector dimension to vary. The dimensions n of the appearance vectors range from 180 to 45. Larger n is typically better because more information is preserved. However, the larger n the higher the computational cost. Our current setting is reasonably accurate and robust but not too computationally expensive.

J determines the complexity of the learning model. Selection of J faces the overfitting-underfitting trade-off. Small J tends to underfit the data, while large J tends to overfit the data. Fortunately, the result is fairly constant over a wide range of J as shown in section 3.9. We use J = 10 weak learners to learn 10 pairs of dictionaries. For simplicity, we set the number of scales S = J. This selection is supported by the parameter sensitivity analysis in section 3.9. Another two important parameters for sparse coding and dictionary learning are the sparsity factor T and the dictionary size K. Fortunately, the results are fairly insensitive to these parameters as shown in Section 3.9. Larger K and T result in higher computational cost, we choose relatively small values K = 1.5n and T = 2.

Level sets represent only closed curves or surfaces, while the left ventricular border is open at the base. For the sake of easy manipulation of level set representation, we always segment up to a certain slice at the base end. Thus, the contours are fixed in the longitudinal direction at the base end. For images acquired from the parasternal window, the epicardial surface is often open at the apex. In this case, the apical end of the epicardial surface is also fixed in the longitudinal direction. The level set offset constantsΨ₁, Ψ₂, ζ_I, andζ₂ determine the sizes of band regions which should be large enough to accommodate the deformation between two consecutive frames while minimizing the computational cost. We find the following setting works well for both baseline and post-infarct images: Ψ₁ = 3mm, Ψ₂ = 2.5mm, ζ₁ = 1.8Ψ₁, and ζ₂ = 1.5Ψ₂ for endocardial segmentation and Ψ₁ = 2.5mm, Ψ₂ = 2.5mm, ζ₁ = 1.8Ψ₁, and ζ₂ = 1.5Ψ₂ for epicardial segmentation. At the level set segmentation stage, we normalize both I_t and A_t to [0,1]. The local appearance term A_t dominates the estimation. To choose the parameters, we drop the intensity and shape terms first by setting γ = 0 and ν = 0. Then we try different weights of the appearance term k and step sizes dτ. After dτ and k are determined, the weight of the shape term γ and the intensity weight v are gradually increased until the results start to worsen. We use the following parameter setting: dτ = 0.25, k = 3.3, γ = 0.01, and ν = 0.17. More details about parameter selection and parameter sensitivities are presented in Section 3.9.

3. Experiments and Results

3.1. Data

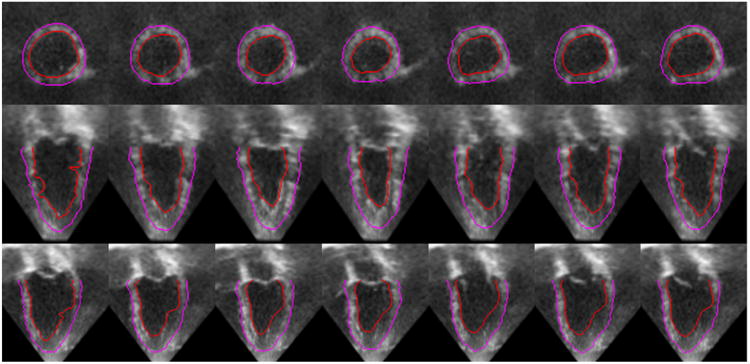
We validated our approach on 4D short-axis canine echocardiographic images acquired from the parasternal window. Twenty-six 4D B-mode images were acquired from both healthy and post-infarct animals using a Phillips iE33 ultrasound imaging system (Philips Health Care, Andover, MA) with a frame rate of about 40 Hz. All animal imaging studies were performed with approval of the Institutional Animal Care and Use Committee. Images were acquired in anesthetized open-chested animals with an X7-2 phased array transducer at 4.4 MHz suspended in a water bath over the heart. Acquisition time points included baseline and one hour and 6 weeks after surgical occlusion of the left anterior descending coronary artery. Each image sequence spanned a cardiac cycle and contained about 25 – 30 volumes. Typical image resolutions of the 3D volumes are ∼ 0.2 mm in the axial direction and ∼ 0.8 mm in the lateral and elevational directions. For the sake of easy manipulation of level set representation and computational efficiency, we down sampled the images to 0.5mm × 1mm × 1mm. Both endocardial and epicardial borders were segmented throughout the sequences. Figure 6 presents a representative example of our 3D segmentations in 3D, axial slice, coronal slice, and sagittal slice views. Figure 7 shows 3D endocardial and epicardial surfaces of sample frames from a representative 4D segmentation by our method.

Figure 6.

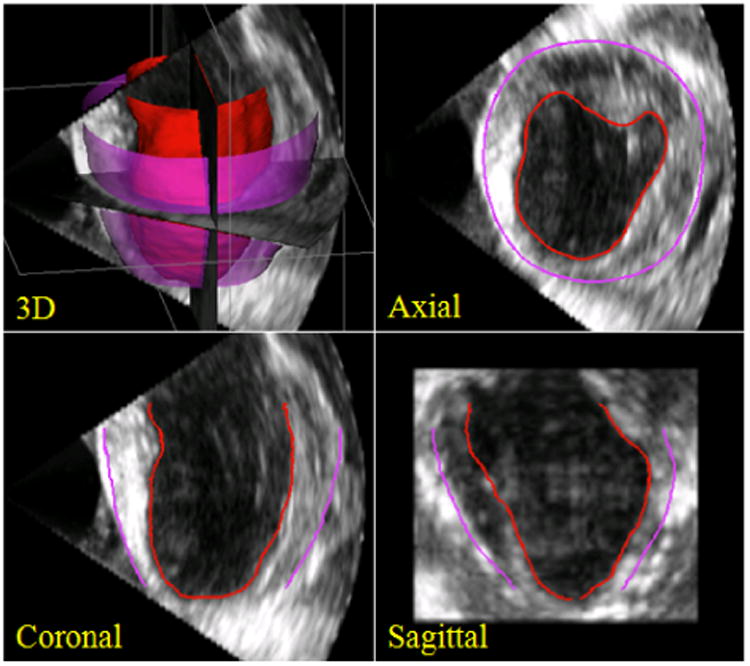
A typical example of 3D segmentations by our algorithm in 3D, axial slice, coronal slice, and sagittal sliceviews. Endocardial segmentations are in red and epicardial segmentations are in purple.

Figure 7.

3D endocardial (in red) and epicardial (in purple) surfaces of frames 1, 4, 7, 10, 13, 16, 19, 22, 25, and 28 of a representative canine echocardiographic sequence segmented using our approach.

3.2. Quantitative Evaluation

To assess the automatic segmentation quality, we randomly drew 100 volumes from the total ∼ 700 volumes for expert manual segmentation. Manual segmentation was carried out using the 4D Surface Editor of the BioImage Suite software (Papademetris et al., 2005). The final benchmark tracings were achieved by group consensus of two experts in cardiovascular physiology. Figure 8 presents sample axial, coronal, and sagittal slices of a 4D image overlaid with our automatic endocardial segmentation in red, automatic epicardial segmentation in purple, and the manual tracings in green. We used the following segmentation quality metrics: Hausdorff Distance (HD), Mean Absolute Distance (MAD), Dice coefficient (DICE), and Percentage of True Positives (PTP). Let A be a surface of automatic segmentation and B be the corresponding expert manual tracing. The HD for surfaces A and B is defined by

Figure 8.

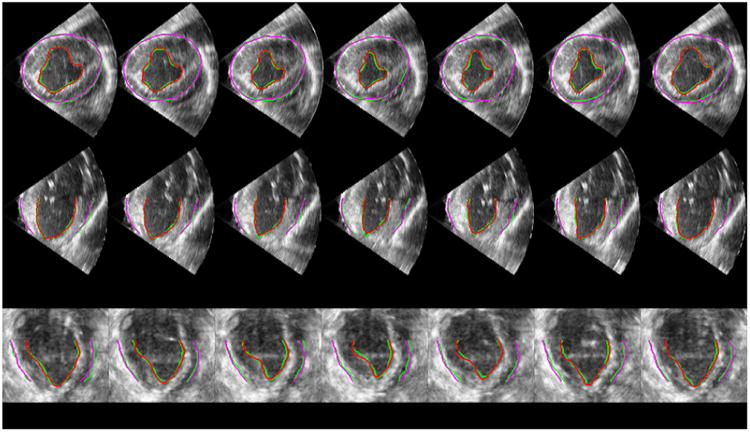
Sample axial (top row), coronal (middle row), and sagittal (bottom row) slices of a 4D image (a cardiac cycle) overlaid with our automatic segmentations (red and purple) and expert manual tracings (green). Each column represents a frame at a time point of the cardiac cycle. From left to right the frames are in chronological order with the two ends representing ED frames.

$$HD(A,B)=max\{\underset{\mathbf{a}\in A}{max}d(\mathbf{a},B),\underset{\mathbf{b}\in B}{max}(\mathbf{b},A)\},$$ (17)

where d(a, B) = min_b∈B ║b − a║₂. It measures the maximum distance between two surfaces. The MAD for surfaces A and B is defined by

$$MAD(A,B)=\frac{1}{2}\{\frac{1}{N_A}\sum _{\mathbf{a}\in A}d(\mathbf{a},B)+\frac{1}{N_B}\sum _{\mathbf{b}\in B}d(\mathbf{b},A)\}.$$ (18)

It measures the mean distance between two surfaces. Assume Ω_A and Ω_B are the regions enclosed by surfaces A and B. The Dice coefficient is given by

$$DICE(A,B)=\frac{2\text{Volume}({\mathrm{\Omega }}_A\cap {\mathrm{\Omega }}_B)}{\text{Volume}({\mathrm{\Omega }}_A)+\text{Volume}({\mathrm{\Omega }}_B)}.$$ (19)

It is a symmetric similarity index which is 0 for no overlap and 1 for perfect agreement. The PTP is defined by

$$PTP(A,B)=\frac{\text{Volume}({\mathrm{\Omega }}_A\cap {\mathrm{\Omega }}_B)}{\text{Volume}({\mathrm{\Omega }}_B)}.$$ (20)

It is 0 for no overlap. Larger PTP generally indicates better agreement but may also result from overestimation. It is not as good an overlap index as Dice coefficient, but it enables comparison with the reported results of previous methods that are presented in terms of PTP.

3.3. Comparison with Pure Intensity Models

Conventional pure intensity models for segmentation assume homogenous gray level distributions within each regions of interest. Rayleigh distribution is a classic intensity prior model for ultrasound data. When the dynamical appearance components are turned off, our approach reduces to a conventional region-based level set approach using a pure Rayleigh intensity model (Sarti et al., 2005). Pure intensity models are usually not sufficient for cardiac ultrasound segmentation. Adding prior terms (e.g., shape priors) can often lead to significantly improved results as shown by previous work (e.g., Jacob et al. (2002); Sun et al. (2005); Yang et al. (2008); Zhu et al. (2009). Comparison of our segmentation results with those of the Rayleigh model clearly shows the added value of the proposed DAM. Since the pure intensity model is generally sensitive to initial contours, we initialized the Rayleigh method with the first frame manual tracing for the segmentation of each frame.

In Figure 9, we compare typical examples of the segmentation results by our method and the Rayleigh model in different slice views. We observed that the Rayleigh method was easily trapped by misleading intensity information (i.e., intensity in homogeneities and characteristic artifacts) and generated erroneous border estimates, while our approach produced accurate segmentations agreeing well with the manual tracings. This demonstrates that our approach is robust to the gross intensity in homogeneities in echocardiographic images. In Figure 8, we compare our segmentations with the manual segmentations in three orthogonal slice views of a series of frames from a cardiac cycle. It shows that our estimates agree well with the manual tracings. Figures 7 and 8 qualitatively show the capability of our algorithm in estimating reliably 3D left ventricular endocardial and epicardial borders throughout the whole cardiac cycle. The Rayleigh method did not generate acceptable segmentation sequences in the experiment.

Figure 9.

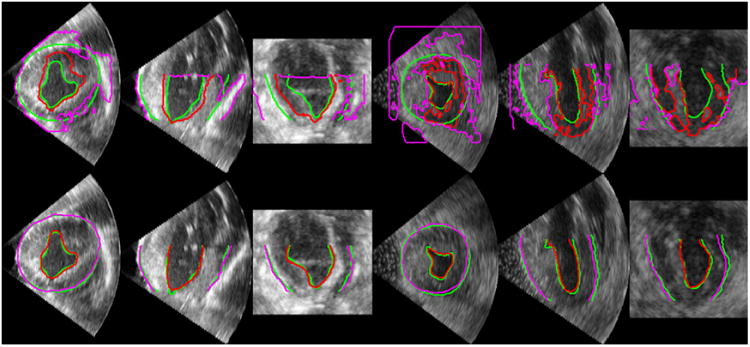
Comparisons of segmentation results by the Rayleigh model (top row) and our DAM (bottom row). Green: Manual segmentation. Red: Automatic endocardial segmentation. Purple: Automatic epicardial segmentation.

Tables 1 and 2 present the means and standard deviations of MAD, HD, DICE, and PTP achieved by our method and the Rayleigh model in segmenting endocardial and epicardial borders respectively. Our DAM significantly outperformed the Rayleigh model. It achieved much higher mean values of DICE and PTP, much lower mean values of MAD and HD, and significantly lower standard deviations of all the metrics than the pure intensity model. The quantitative results show the remarkable improvement of segmentation accuracy and robustness achieved by employing the DAM. These demonstrate that the individual spatiotemporal coherence captured by our multiscale sparse representation and dictionary learning procedure provides a strong constraint for left ventricular segmentation.

Table 1.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures for endocardial segmentation by the Rayleigh model and our DAM.

Method	DICE (%)	PTP (%)	MAD (mm)	HD (mm)
Rayleigh (Sarti et al., 2005)	74.9 ± 18.8	83.1 ± 16.3	2.01 ± 1.22	9.17 ± 3.37
Our DAM	93.6 ± 2.49	94.9 ± 2.34	0.57 ± 0.14	2.95 ± 0.62

Table 2.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures for epicardial segmentation by the Rayleigh model and our DAM.

Method	DICE (%)	PTP (%)	MAD (mm)	HD (mm)
Rayleigh (Sarti et al., 2005)	74.1 ± 17.4	82.5 ± 12.0	2.80 ± 1.55	16.9 ± 9.30
Our DAM	97.1 ± 0.93	97.6 ± 0.86	0.60 ± 0.19	3.03 ± 0.76

3.4. Comparison with Registration-based Trackers

The main classes of tracking methods in echocardiography that purely exploit the temporal consistency include optical flow (Mailloux et al., 1989; Mikic et al., 1998; Boukerroui et al., 2003), speckle tracking (Kaluzynski et al., 2001), and non-rigid registration (Ledesma-Carbayo et al., 2005; Elen et al., 2008; Myronenko et al., 2009). We compared our method with nonrigid-registration-based tracking. We performed multiscale nonrigid registration (free-form deformations (Rueckert et al., 1999)) of consecutive pairs of frames to track both endocardial and epicardial contours over the forward and backward subsequences as our algorithm did. An initial affine registration was followed by three levels of nonrigid registration. The sum of squared intensity difference (SSD) is used as the similarity measure. From coarse to fine, the spacings of the grids are 16× 16× 16 pixels, 8×8×8 pixels, and 4×4×4 pixels. We tried a series of different smoothness weights for nonrigid registration and got the best result when it was 1 × 10⁻⁵. The comparison here is based on this setting. For fair comparison, before computing the quality indices for the nonrigid-registration-based tracker, we cropped the longer one of the manual contour and the automatic contour at the base (for endocardial and epicardial borders) and the apex (for the epicardial border). This makes sure that the automatic contour and the manual contour correspond to the same portion of the left ventricular border.

We observed that our approach achieved more accurate segmentations. Figure 10 presents representative segmentation results of the ES frame by the two methods. Both methods had the worst results at ES due to accumulation of errors. Figure 10 shows that the registration-based tracking resulted in more errors at ES which indicates faster accumulation of errors. Tables 3 and 4 present the sample means and standard deviations of DICE, MAD, and HD and the computation time by nonrigid-registration-based tracking and our method. Our approach achieved higher mean value of DICE and lower mean values of MAD and HD for both endocardial and epicardial segmentation. In addition, our method achieved significantly lower standard deviations of all the metrics than the registration-based tracker in both cases. Both algorithms were implemented with a mixture of MATLAB and C++. We tested the two algorithms on a laptop with Intel quad-core 2.2 GHz CPU and 8 GB memory. The average computation time of our method was about 1 minute per frame. The average computation time of the registration-based tracker was about 10 minutes per frame. Our method was much faster than nonrigid-registration-based tracking. The results showed that our method outperformed the registration-based tracker in terms of accuracy, robustness and computational efficiency.

Figure 10.

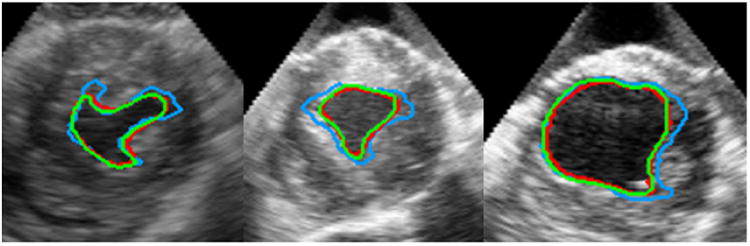
Comparisons of segmentation results by nonrigid registration and our DAM. Green: Manual segmentation. Red: Our DAM. Blue: Non-rigid registration.

Table 3.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures and computation time per frame for endocardial segmentation by nonrigid-registration-based tracking and our DAM.

Method	DICE (%)	MAD (mm)	HD (mm)	Computation Time (min)
Nonrigid Registration	89.3 ± 5.85	0.81 ± 0.28	4.55 ± 1.65	∼11
Our DAM	93.6 ± 2.49	0.57 ± 0.14	2.95 ± 0.62	∼1

Table 4.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures and computation time per frame for epicardial segmentation by nonrigid-registration-based tracking and our DAM.

Method	DICE (%)	MAD (mm)	HD (mm)	Computation Time (min)
Nonrigid Registration	94.0 ± 1.83	0.92 ± 0.38	6.59 ± 2.48	∼10
Our DAM	97.1 ± 0.93	0.60 ± 0.19	3.03 ± 0.76	∼1

3.5. Advantages of Multiscale Sparse Representation

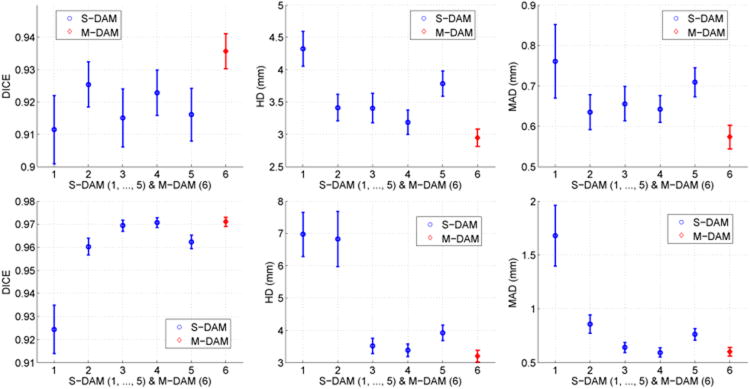
To study the advantages of multiscale sparse representation over single-scale sparse representation, we compared the proposed DAM in both cases of single-scale sparse representation (S-DAM) (Huang et al., 2012b) and multiscale sparse representation (M-DAM). The S-DAM was performed at 5 appearance scales ranging from fine scale ∼ 3mm × 3mm × 3mm to coarse scale ∼ 15mm × 15mm × 15mm. It learned dictionaries only at a single scale. The M-DAM utilized multiscale appearance information and learned dictionaries at multiple scales. The number of dictionary updating iterations and the number of boosting iterations are fixed for all the trials. The computational cost is equivalent for different trials. The segmentation results were evaluated with the metrics DICE, HD, and MAD. Their mean values were calculated and t-tests were performed to estimate 95% confidence intervals.

We observed that the use of M-DAM resulted in higher segmentation accuracy and less accumulation of errors compared to the S-DAM. Figure 11 shows segmentation examples where the advantages of M-DAM over S-DAM are visually clear. In these cases, the S-DAM made obvious errors either locally or globally that were effectively corrected by employing the M-DAM. This shows that the errors made at a certain scale can be corrected at other scales in the M-DAM framework. Figure 12 compares the mean values and 95% confidence intervals of DICE, HD, and MAD achieved by M-DAM and S-DAM in segmenting endocardial and epicardial borders. We observed that the performance of the S-DAM varied with the scale, which implies its sensitivity to the appearance scale. The appearance information at different scales has better discriminative power in different parts of the image domain. Using a single-scale sparse representation, we need to adjust the scale parameter carefully in order to get better results. The M-DAM achieved the best results in almost all the metrics (i.e., the highest DICE mean, the lowest HD mean, the lowest MAD mean, and the narrowest confidence intervals of all the metrics) for both endocardial and epicardial segmentations. These indicate significantly better segmentation robustness and accuracy, and thereby the advantages of multiscale sparse representation over single-scale sparse representation. By summarizing complementary multi-scale appearance information and optimizing the corresponding weights automatically, the M-DAM consistently produced more accurate segmentations without careful adjustment of the scale parameters.

Figure 11.

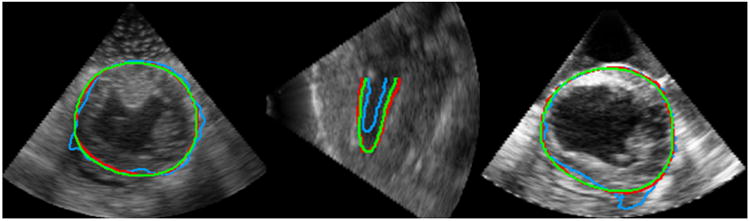
Comparisons of segmentation results by the S-DAM and the M-DAM. Green: Manual segmentation. Red: M-DAM. Blue: S-DAM.

Figure 12.

Means and 95% confidence intervals of DICE, HD, and MAD obtained by the S-DAM (blue, scales 1,…, 5) and the M-DAM (red, 6) for endocardial segmentation(top row) and epicardial segmentation (bottom row).

3.6. Comparison with Database-dependent Dynamical Models

In Tables 5 and 6, we compare the means and standard deviations of HD, MAD, and PTP achieved by our model and those reported in Zhu et al. (2009). The quality measure statistics obtained by our DAM are comparable with those by a state-of-the-art database-dependent offline dynamical shape model SSDM (Zhu et al., 2009). Our approach achieved a higher mean PTP and a lower mean MAD in segmenting epicardial borders. It also had a lower mean MAD for endocardial segmentation. SSDM obtained slightly higher PTP for endocardial segmentation and slightly lower HD for both cases. Our DAM achieved lower standard deviations of almost all the metrics. Here we present only a rough comparison of the two methods. It is difficult to fully compare the two methods, since the offline method depends on databases while our method does not. Different databases would produce different results for the offline method. Two methods rely on different sources of information (database vs. individual data) which are not mutually exclusive. This comparison suggests that the spatiotemporal constraint enforced through our online-learning-based DAM is comparable with the spatiotemporal constraint learned from a suitable database by the offline dynamical shape model SSDM.

Table 5.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures for endocardial segmentation by the SSDM and our DAM.

Method	PTP (%)	MAD (mm)	HD (mm)
SSDM (Zhu et al., 2009)	95.9 ± 1.24	1.41 ± 0.40	2.53 ± 0.75
Our DAM	94.9 ± 2.34	0.57 ± 0.14	2.95 ± 0.62

Table 6.

Sample means and standard deviations (expressed as Mean±SD) of the segmentation quality measures for epicardial segmentation by the SSDM and our DAM.

Method	PTP (%)	MAD (mm)	HD (mm)
SSDM (Zhu et al., 2009)	94.5 ± 1.74	1.74 ± 0.39	2.79 ± 0.97
Our DAM	97.6 ± 0.86	0.60 ± 0.19	3.03 ± 0.76

It is worth noticing that the DAM does not require more human interaction at the segmentation stage than the database-dependent offline dynamical models such as Jacob et al. (2002), Sun et al. (2005), and Zhu et al. (2009) which need manual tracings of the first or first few frames for initialization. Manual initialization is generally needed by conventional offline-statistical-model-based approaches in the case of echocardio-graphic segmentation, because aligning an unseen image to the reference space of the database can be very challenging and introduce substantial errors.

Since our DAM is database-free, it overcomes the limitations (e.g., generalization errors and costs) introduced by the use of databases. The DAM can be applied to a broader range of subjects including the cases (e.g., the post-infarct subjects in our study and children with congenital heart disease) where it is inappropriate to apply database-dependent a prior motion or shape knowledge. Our approach imposes a spatiotemporal constraint by learning directly from the individual data while offline dynamical models learn spatiotemporal constraints from databases. Our DAM complements offline database-dependent models and can be used to relax offline statistical models' dependence on the database quality.

3.7. Ejection Fraction Estimation

The ejection fraction is an important cardiac functional parameter and predictor of prognosis. We computed the left ventricular ejection fraction EF based on our endocardial segmentations. We detected ten landmarks distributed evenly at the base of the endocardial border based on local cross-correlation. We determined the longitudinal coordinate of the base by averaging the longitudinal coordinates of the ten points. Then we cropped the base of ES or ED whichever is too long based on the longitudinal coordinates. The ejection fraction is given by

$$EF=\frac{EDV-ESV}{EDV},$$ (21)

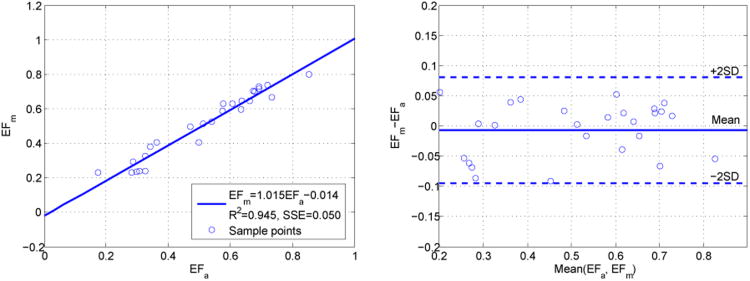
where EDV is the end-diastolic volume and ES V is the end-systolic volume. Figure 13 presents the linear regression analysis and Bland-Altman analysis comparing the ejection fraction measurements calculated from automatic segmentation (EF_a) and expert manual segmentation (EF_m). The linear fitting result was EF_m = 1.015EF_a − 0.014 with the coefficient of determination R² = 0.945 and the sum of squared errors SSE = 0.050. The mean difference between automatic and manual ejection fraction measurements (EF_m – EF_a) is −0.0064. The 95% limits of agreement (mean difference±2S D) are [0.0830, −0.0958]. The results showed good agreement between our automatic ejection fraction estimation and the ejection fraction measurement by expert manual tracing. Besides ejection fraction estimation, our segmentation results were fed to a combined shape tracking and speckle tracking framework to estimate myocardial strain where good correlation with the tagged MR benchmark was achieved. Further details have been reported in our conference paper compas et al. (2012)

Figure 13.

Linear regression analysis (left) and Bland-Altman analysis (right) showing the agreement between the ejection fraction measurements computed from automatic segmentations (EF_a) and manual segmentations (EF_m).

3.8. Applications to Human Data

We extended the application of our method to human data. We tested our method on four sequences of 3D human echocar-diographic images. The images were acquired from the apical long-axis view. Each sequencecontained about 15 frames and spanned a whole cardiac cycle. Typical resolutions of the 3D volume are ∼ 0.7 mm in the axial direction and ∼ 0.8 mm in the lateral and elevational directions. The segmentation results were qualitatively assessed by experts in cardiovascular physiology. The quality of our segmentation results on human data was similar to that on canine data. The estimated left ventricular borders agreed well with experts' interpretation of the images. Figure 14 shows the three orthogonal slice views of the segmentation results on a representative 4D human echocardiographic image. The manual initialization of the first frame and the automatic segmentations of the following frames are overlaid on the images. The figures qualitatively show the good accuracy of our algorithm on 4D human data. The estimated contours follow the deforming cardiac borders closely throughout the whole cardiac cycle. Comparisons between the automatic segmentations and the manual initialization show the accuracy of the automatic results is close to manual tracings. There were some irregularities in the manual surfaces due to the fact that contours were traced slice-by-slice. The automatic segmentations demonstrated better consistency compared to manual tracings. We also computed the ejection fraction of these human echocardiographic sequences. Table 7 presents the ejection fraction measurements computed from automatic and manual segmentations. The automatic estimates were close to the manual results. The EF result for human data was consistent with what we observed on canine data.

Figure 14.

Sample axial (top row), coronal (middle row), and sagittal (bottom row) slices of a 4D human echocardiographic image (a cardiac cycle) overlaid with segmentations. Each column represents a frame at a time point of the cardiac cycle. The contours in the first frame are manual tracings.

Table 7.

The ejection fraction measurements computed from automatic segmentations (EF_a) and manual segmentations (EF_m) for the four human echocardiographic sequences.

	Sequence 1	Sequence 2	Sequence 3	Sequence 4
EFa(%)	48.61	63.55	61.33	53.54
EFm(%)	51.58	64.94	68.16	50.31

3.9. Analysis of Parameter Sensitivities

In this section, we present a sensitivity analysis of the important parameters of our algorithm in the context of endocardial segmentation. To study contributions of the dynamical appearance components, we kept the weight of the intensity fixed and varied the weights of the appearance discriminant A_t and the shape prediction ${\mathrm{\Phi }}_t^{\ast }$ respectively. Figure 15 presents the effects of varying the weight κ of the appearance discriminant A_t. As expected, when the weight of the appearance discriminant increases gradually from a very low value, mean HD and mean MAD decrease significantly, mean DICE increases significantly, and the confidence intervals of the metrics narrow significantly. This demonstrates that the appearance discriminant contributes greatly to segmentation accuracy and robustness. This effect gradually diminishes before reaching the optimal weight. After the turning point, increasing the weight of A_t worsens the means and enlarges the confidence intervals at low rates due to the overweighting of the appearance discriminant. Figure 16 shows the effects of varying the weight γ of the shape prediction ${\mathrm{\Phi }}_t^{\ast }$. Varying γ results in much smaller changes of segmentation results compared to those of varying the appearance discriminant weight κ. However, there are noticeable improvements in mean values and confidence intervals of the metrics when γ increases from 0. The best results are achieved when γ∈ [6,12] × 10⁻³. The results show that the dynamical shape prediction contributes to improving the overall segmentation accuracy and robustness. The contribution of the shape prediction ${\mathrm{\Phi }}_t^{\ast }$ is smaller compared to the contribution of the appearance discriminant A_t.

Figure 15.

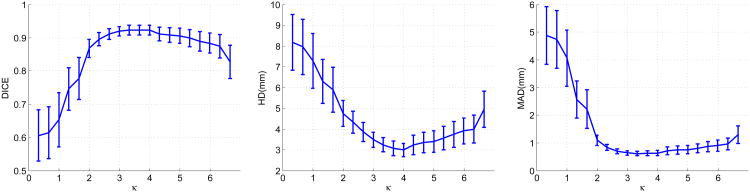
The effects of varying the weight κ of the appearance discriminant A_t. The curves represent mean values and the bars denote 95% confidence intervals.

Figure 16.

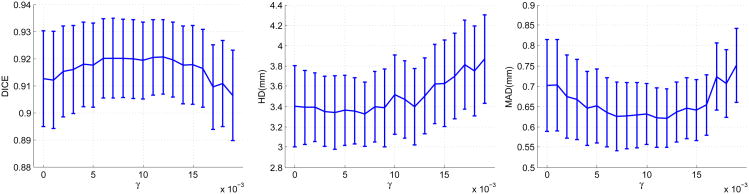
The effects of varying the weight γ of the shape prediction ${\mathrm{\Phi }}_t^{\ast }$. The curves represent mean values and the bars denote 95% confidence intervals.

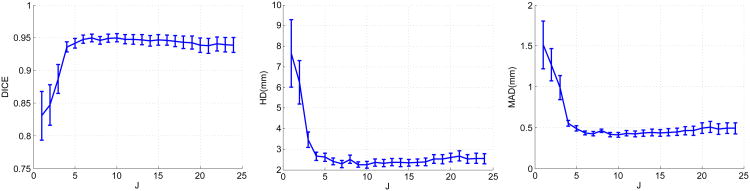
The most important parameters for sparse representation and dictionary learning are the sparsity factor T, the dictionary size K, the number of weak learners trained J, and the number of local appearance scales S. We varied each of these parameters separately while keeping the other parameters fixed to study how these parameters affect the segmentation results. Figure 17 shows the changes in means and 95% confidence intervals of the metrics as a result of varying the sparsity factor T. DICE increases while MAD and HD decrease as T increases from 1, which shows increasing the flexibility of sparse representation improves segmentation results. Above T = 4, the measures are rather stable when T varies. The change in the Dice coefficient within a wide range [4,16] of T is less than 1%. The change in MAD within this range is only ∼ 0.05 mm. The change in HD is ∼ 0.4 mm. The variations in the confidence intervals are minimal. These results demonstrate the method's robustness to the sparsity factor T.Figure 18 shows the effects of varying the dictionary size. Here, we redefine K as the ratio of the dictionary size to the dimension of the appearance vector n. As K increases from 0.5 (under-complete, K < 1) to 2 (over-complete, K > 1), DICE increases while MAD and HD decrease. These effects demonstrate that the increased expressiveness of the over-complete dictionaries results in better representation of the local appearance and thereby improves segmentation results compared to under-complete and complete dictionaries. Above K = 2, the measures are stable when K varies. We observed only minimal variations of the quality metrics DICE (< 1%), MAD (∼ 0.03 mm), and HD (∼ 0.3 mm), when we varied K within a wide range [1,6]. These results show that our method is robust to the dictionary size. Since the computational cost increases with the dictionary size, in practice, it is advisable to set K to a value in [1,3] for the sake of balancing accuracy and efficiency. Figure 19 presents the changes in means and 95% confidence intervals of the metrics resulting from varying the number of weak learners J while the number of appearance scales is fixed at 5. When J is small, the method underfit the data. As J increases from 1, DICE increases significantly while HD and MAD decrease significantly. This results from incorporation of more appearance scales and more weak learners. Beyond J = 6, the results are rather stable over a wide range of J as indicated by the flat curves. The best results are achieved around J = 10. Above J = 10, the dictionary learning process tends to overfit the training data and the error increases at a low rate. We also varied the number of appearance scales S while fixing the number of weak learners. Figure 20 presents its effects on the segmentation results. When S increases from 1 to 6, DICE increases gradually while HD and MAD decreases gradually. This shows the incorporation of more complementary appearance scales improves the results. The results do not present noticeable changes when S vary between [6,10], which means no additional constructive scales can be extracted. The analysis of parameter sensitivities shows that the method is rather robust to the major important parameters. There is no difficulty selecting a set of good parameters.

Figure 17.

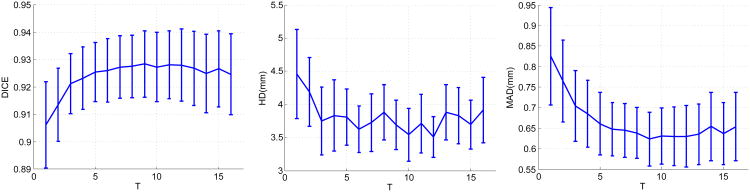
The effects of varying the sparsity factor T. The curves represent mean values and the bars denote 95% confidence intervals.

Figure 18.

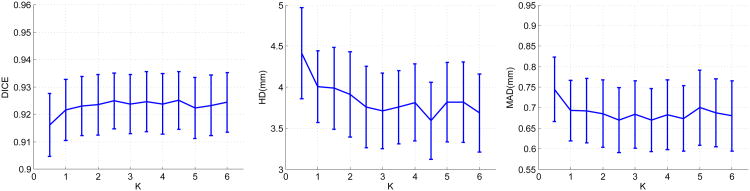
The effects o f varying the dictionary size. K denotes the ratio of the dictionary size to the dimension of the appearance vector n. The curves represent mean values and the bars denote 95% confidence intervals.

Figure 19.

The effects of varying the number of weak learners J while S = 5. The curves represent mean values and the bars denote 95% confidence intervals.

Figure 20.

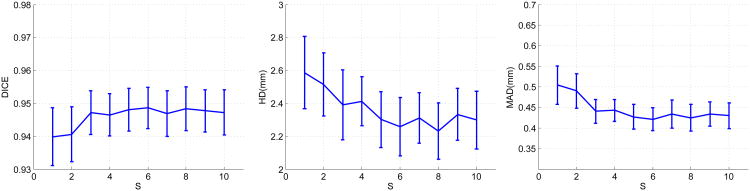
The effects of varying the sparsity factor T. The curves represent mean values and the bars denote 95% confidence intervals.

4. Discussion and Conclusions

We have proposed a dynamical appearance model that exploits the inherent spatiotemporal coherence of individual echocardiographic data for tracking both endocardial and epicardial boundaries of the left ventricle. It employs multiscale sparse representation of local image appearance and interlaces the sequential segmentation process with the dynamical multiscale appearance dictionary updating process supervised in a boosting framework. The multiscale appearance dictionaries are trained on the fly to be both reconstructive and discriminative and carry forward appearance information from preceding frames to following frames. The weights of multiscale local appearance information are optimized automatically. Our region-based level set segmentation formulation integrates a spectrum of complementary multilevel information including intensity, multiscale local appearance discriminant, and shape.

Our algorithm achieves segmentations that are close to manual tracings on both healthy and post-infarct data. Ejection fraction estimates computed from our segmentation results agree well with manual results. Our method results in significantly improved accuracy and robustness of left ventricular segmentation compared to conventional pure intensity models. This shows the individual spatiotemporal coherence is a strong constraint for echocardiographic segmentation and can be effectively utilized through multiscale sparse representation and dictionary learning. Our method also outperforms a nonrigid registration-based tracker in both segmentation accuracy and computational efficiency. We also show the advantages of multiscale sparse representation over single-scale sparse representation. Our approach achieves comparable results with those of a state-of-the-art database-dependent offline dynamical shape model SSDM. The spatiotemporal constraint imposed through our online-learning-based DAM is comparable with the spatiotemporal constraint learned from a suitable database by the offline SSDM. Our DAM is database-free and therefore more flexible and easier to be deployed, which is advantageous in physiological research. It can be applied to the cases where it is inappropriate to apply database-dependent a prior motion or shape knowledge. It complements conventional offline statistical models and can be used to relax the conventional offline model's dependence on the database quality.

While many prior studies on left ventricular functional analysis, either based on MR or ultrasound images, include the papillary muscle (PM) in the blood pool, we choose to exclude PMs from the blood pool in this study. The rationale is threefold. First, the border between the PM and the blood pool is much better defined than the border between the PM and the myocardium in echocardiography. Therefore the boundary of the blood pool can be more reliably segmented and tracked than the border between the PM and the myocardium. Second, the definition of EF excludes PMs from the blood pool. Even though previous work (Sievers et al., 2004) has found no statistically significant difference between EFs calculated by including or excluding PMs in the blood pool, there are studies showing that variable inclusion of papillary muscles can result in methodological variability whose impact is increased among patients with left ventricular hypertrophy (Janik et al., 2008; Han et al., 2008). Third, the segmentation result is an important input to our shape-tracking-based motion analysis framework (Papademetris et al., 2002) where curvature-based shape landmarks (such as due to PMs) and their temporal consistency play an important role.

The current framework has two limitations. Firstly, similar to many database-dependant offline dynamical shape models (e.g., Jacob et al. (2002); Sun et al. (2005); Zhu et al. (2009)), the current sequential segmentation process is initialized by a manual tracing of the first frame, which hasn't reduced the human interaction to a minimum. Integration of our model into previous automatic methods may reduce the amount of human interaction while improving the overall segmentation accuracy. This can be a future research direction, and this study mainly focuses on the benefit of our model. Secondly, the sequential process carries errors forward resulting in accumulation of errors. The segmentation accuracy decays from ED to ES, as shown in Figures 21 and 22. Fortunately, the decay rate is mild. The worst results that typically appear at ES are still fairly good, as shown by our good ejection fraction estimates. This limitation may be alleviated by employing more robust dictionary learning framework which can be a direction of future work (Huang et al., 2013). Integration of an offline learning stage may also help overcome this limitation.

Figure 21.

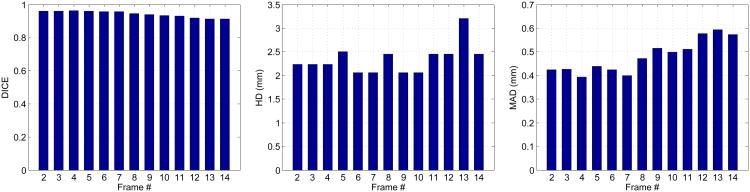
Endocardial segmentation quality measures at different frames of an example sequence from end-diastole to end-systole.

Figure 22.

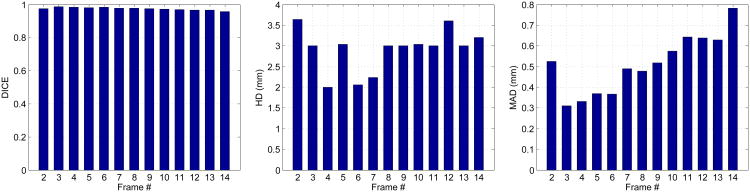
Epicardial segmentation quality measures at different frames of an example sequence from end-diastole to end-systole.

One limitation of the current study is that we have only one manual tracing result for each data set. Having multiple observers tracing the same data separately can provide a more comprehensive validation of the method. Another limitation is that we have tested the method only on a small set of human data. Future work will aim to overcome the current limitations and extend the application to other acquisition settings and other modalities. It is also of interest to develop an integrated online and offline learning framework to exploit their complementarities which may result in improvement of the overall segmentation performance.