Abstract
A cochlear implant (CI) presents band-pass-filtered acoustic envelope information by modulating current pulse train levels. Similarly, a vocoder presents envelope information by modulating an acoustic carrier. By studying how normal hearing (NH) listeners are able to understand degraded speech signals with a vocoder, the parameters that best simulate electric hearing and factors that might contribute to the NH-CI performance difference may be better understood. A vocoder with harmonic complex carriers (fundamental frequency, f0 = 100 Hz) was used to study the effect of carrier phase dispersion on speech envelopes and intelligibility. The starting phases of the harmonic components were randomly dispersed to varying degrees prior to carrier filtering and modulation. NH listeners were tested on recognition of a closed set of vocoded words in background noise. Two sets of synthesis filters simulated different amounts of current spread in CIs. Results showed that the speech vocoded with carriers whose starting phases were maximally dispersed was the most intelligible. Superior speech understanding may have been a result of the flattening of the dispersed-phase carrier’s intrinsic temporal envelopes produced by the large number of interacting components in the high-frequency channels. Cross-correlogram analyses of auditory nerve model simulations confirmed that randomly dispersing the carrier’s component starting phases resulted in better neural envelope representation. However, neural metrics extracted from these analyses were not found to accurately predict speech recognition scores for all vocoded speech conditions. It is possible that central speech understanding mechanisms are insensitive to the envelope-fine structure dichotomy exploited by vocoders.
Keywords: cochlear implant simulation, phase
INTRODUCTION
The ability to recognize speech in noise with cochlear implants (CIs) has not yet achieved parity with normal hearing (NH) (Friesen et al. 2001; Van Deun et al. 2010; Eskridge et al. 2012), likely a result of the poorer spectral and temporal resolution in electric hearing (Fu et al. 2004; Fu and Nogaki 2005). The channel vocoder has been used extensively to study aspects of speech understanding (Dudley 1939; Schroeder 1966; Shannon et al. 1995). Because vocoding principles are employed in CI processing (Loizou 2006), the vocoder has often been used to simulate electric hearing for NH listeners (Dorman et al. 1997; Fu et al. 1998; Nelson et al. 2003; Chen and Loizou 2011). By comparing how NH and CI listeners understand degraded speech signals, the vocoder parameters that best simulate electric hearing and factors that might contribute to the known gap in performance between NH and CI listeners are better understood. Like CIs, vocoders discard acoustic temporal fine structure (TFS) and present only passband envelope (ENV) information from the original waveform. These envelopes modulate the vocoder’s carrier. Although simple tones and filtered noise are the most commonly used carriers, Gaussian-enveloped tones (Lu et al. 2007) and harmonic complexes have also been used (Deeks and Carlyon 2004; Hervais-Adelman et al. 2011). It is unclear which vocoder carrier best approximates electric hearing, but different carriers result in different speech intelligibilities depending on the parameters chosen. Whitmal et al. (2007) found that sine vocoders, with flat intrinsic carrier envelopes and prominent sidebands, resulted in better modulation detection and speech understanding than noise vocoders. Using a lower envelope cutoff frequency, Hervais-Adelman et al. (2011) found that sine-vocoded speech was more difficult to understand than noise-vocoded speech, for a fixed modulation depth. These studies demonstrate that the carrier characteristics are important parameters affecting speech understanding with vocoders.
The present study tested speech recognition in noise for several different carriers. In addition, stimuli were generated using synthesis filters that simulated channel interaction caused by the spread of current in CI stimulation. The hypothesis that randomly dispersing the component starting phases of a harmonic complex carrier should flatten the carrier’s intrinsic envelopes and improve speech recognition was tested. Sine tone and noise carriers were tested in addition to the harmonic complex carriers.
Fidelity of neural encoding of envelope and TFS information as measured by neural cross-correlation coefficients has previously been shown to predict perceptual identification scores for vocoded speech in noise (Swaminathan and Heinz 2012). However, the assertion that the auditory system independently encodes envelope and TFS may be suspect (Shamma and Lorenzi 2013). Here, responses of an auditory nerve (AN) model (Zilany et al. 2009) to the vocoded and unprocessed stimuli were compared using shuffled cross-correlogram analyses (Joris 2003). Resulting neurometrics failed to predict psychoacoustic scores for all conditions, indicating that this analysis may not disentangle the differential effects of TFS and envelopes on vocoded speech intelligibility and that more central mechanisms may play a larger role in information extraction, in agreement with Shamma and Lorenzi (2013).
METHODS A: PSYCHOACOUSTICS
Stimuli
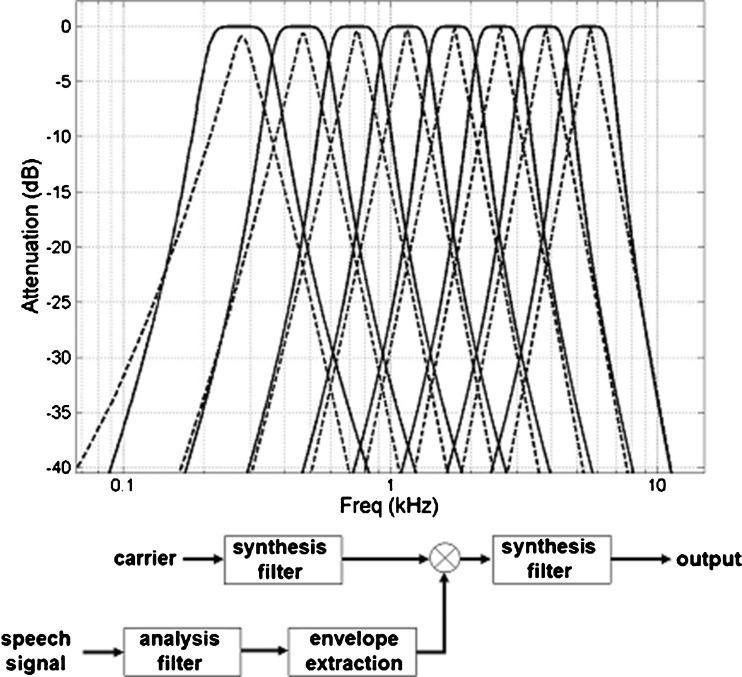
Fifty single-syllable, consonant-nucleus-consonant (CNC) words were vocoded using an eight-channel vocoder. Six vocoder carriers (sine tones, four different types of harmonic complexes with distinct starting phase distributions, and noise) were used to study the effects of carrier phase dispersion on speech understanding. The channel corner and center frequencies, calculated using Greenwood (1990) to simulate equal spacing on the cochlea, are presented in Table 1. In order to explore the detriment of simulated current spread, two sets of stimuli with different synthesis filters were generated and tested. Butterworth synthesis filters were used as a control for previously published data (Fu and Nogaki 2005), and simulated CI current spread synthesis filters (Bingabr and Espinoza-Varas 2008) were also tested. Synthesis filters are used to filter the carrier into separate channels prior to and following modulation, whereas analysis filters are used to divide the original speech signal into separate spectral channels. Magnitude responses for each set of filters (Butterworth and “current spread”) are plotted in Figure 1. Prior to vocoding, target words were mixed with a frozen token of ramped, steady-state, speech-shaped noise in order to produce stimuli with broadband signal-to-noise ratios (SNRs) of either 0 or −3 dB. The speech-shaped masker was synthesized through the inverse Fourier transform of the sum of all the CNCs’ magnitude spectra with a random phase spectrum. The target was imbedded in the masker approximately 1 s after the masker’s onset. Twelve hundred different stimuli were constructed in total (50 words × 2 SNRs × 2 synthesis filter types × 6 carrier types).
TABLE 1.
Filter corner and center frequencies (given in Hz) were chosen so as to simulate the equal physical spacing of electrodes on a cochlear implant
| f lower | f center | f upper |
|---|---|---|
| 202 | 281 | 359 |
| 359 | 473 | 587 |
| 587 | 752 | 917 |
| 917 | 1,156 | 1,395 |
| 1395 | 1,743 | 2,090 |
| 2090 | 2,593 | 3,097 |
| 3097 | 3,827 | 4,558 |
| 4558 | 5,617 | 6,677 |
FIG. 1.
Butterworth (solid line) and current spread (dashed line) filters’ (single-pass) magnitude responses. The Butterworth filters were used in analysis filtering for both stimuli sets and in synthesis filtering for one set of stimuli. The block diagram depicts application of analysis and synthesis filters.
In order to vocode the stimuli, the unprocessed words were band-pass-filtered into eight frequency-contiguous channels using third-order Butterworth analysis filters. Because these experiments studied the effects of phase, the filtering was performed using forward and reverse filtering, a zero phase-shift method which preserves phase relationships among components of different frequencies and results in an effective doubling of filter order. Carriers were also forward and reverse band-pass-filtered into eight channels using the appropriate synthesis filters (Fig. 1 shows the magnitude responses for a single pass). The signal envelope was extracted from each channel via full-wave rectification and low-pass filtering at 50 Hz, using a second-order low-pass Butterworth filter with forward and reverse filtering. Each channel’s envelope was then used to modulate the amplitude of the corresponding carrier channel. The envelope-modulated carrier channels were filtered again using their respective synthesis filters to attenuate any sidebands outside the original channel. Each vocoded stimulus was then constructed by summing its channels. Levels for each stimulus were adjusted to ensure that all stimuli had the same root-mean-square level. The sampling frequency was 48 kHz.
As mentioned above, two sets of synthesis filters were used (Fig. 1). The first set had identical parameters to those Butterworth filters that were used for analysis. These filters have flat magnitude responses in the pass band and overlap with the adjacent band at the half-amplitude (3-dB down) point. The second synthesis filter set was meant to better simulate the spatial dependence of current spread in CIs and consisted of 2,048-order finite impulse response (FIR) filters. These FIR filters were designed using the same center frequencies as the Butterworth filters and were calculated to produce current decay slopes of 3.75 dB/octave. Both of these synthesis filter sets exhibit the channel overlap that is characteristic of CI current spread, but the second set, the “current spread” filters, introduce additional dynamic range compression and exhibit localized peaks with steeply decaying skirts. Adjacent Butterworth filters magnitudes crossed at 3 dB of attenuation, and adjacent current spread filters magnitudes crossed at 11 dB of attenuation.
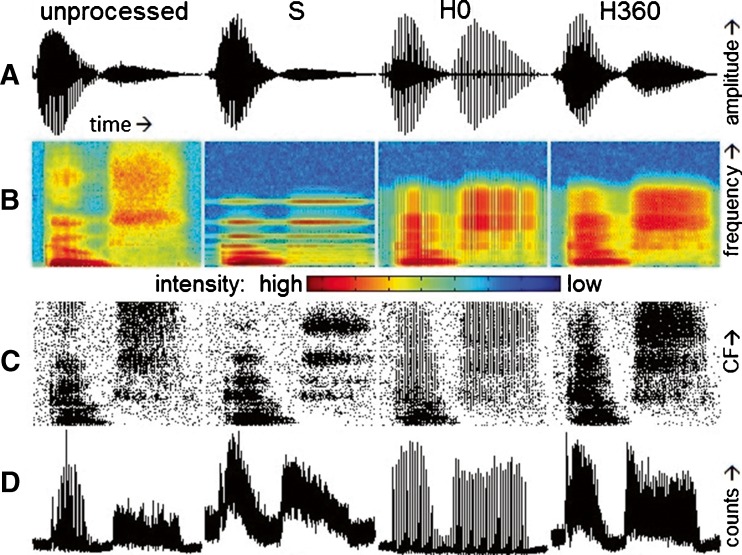
Given the prevalence of sine and noise vocoders in previous studies, sine tones with frequencies equal to the channel centers and band-pass-filtered white noise were used as “control” carriers for comparison with the harmonic complex carriers. The sine and noise vocoders will be denoted “S” and “N,” respectively. The harmonic complex carriers were complexes of 240 equally weighted, harmonically spaced sine tones with a fundamental frequency, f0, of 100 Hz. Each of the harmonic complex carriers had a different component starting phase distribution. The first harmonic complex carrier was in sine phase, i.e., the starting phase of each sine tone component was zero (“H0”). Thus, it resulted in a periodic, biphasic pulse train. The second harmonic complex carrier added a random value between 0 and π/2 to the starting phase of each component (“H90”). This processing resulted in a carrier waveform resembling a biphasic pulse train with low-amplitude noise between the pulses. The third harmonic complex carrier added a random value between 0 and 2π to the starting phase of each component (“H360”). While a single period of this carrier appears chaotic, it elicited a 100-Hz pitch percept due to the signal’s periodicity. These five carriers are summarized in Table 2. A fourth harmonic complex carrier based on the Schroeder-minus chirp (Schroeder 1970) was constructed and tested, but due to vocoder filtering, the desired temporal characteristics were lost. The resulting waveform and performance results were nearly identical to those of the H0 stimuli, and are not discussed further. Time domain plots and spectrograms of the unprocessed CNC “goose” in quiet and three vocoded tokens thereof are shown in the top two rows of Figure 2. These illustrations allow for qualitative feature comparison among vocoder outputs. Because of the similar appearances of stimuli for H0 and H90 carriers, the latter is not shown. Carrier N, whose output has a similar appearance as that for the carrier H360, is also not shown. The plot for the original (unprocessed) CNC shows a smooth envelope and regular fine structure corresponding to f0 voicing. Note the varying levels of broadband envelope similarity to the unprocessed signal among the vocoded samples as illustrated in the plots. The spectrogram for the original (unprocessed) CNC shows a clear onset burst, f0 voicing, and formants. Spectrograms for vocoded stimuli show the vocoder’s upper frequency limits and varying degrees of spectral and temporal resolution. The temporal energy troughs in the spectrogram for carrier H0 and the spectral energy troughs in the spectrogram for carrier S are also clearly visible. The vocoded tokens depicted in Figure 2 used Butterworth synthesis filters.
TABLE 2.
Vocoder carriers consisted of two commonly used control carriers (sine tones and white noise) and harmonic complexes with identical long-term magnitude spectra, only differing in component starting phase
| Carrier | Frequencies | Symbol | Phase of nth component |
|---|---|---|---|
| Sine | Filter center frequency | S | 0 ° |
| Noise | White noise | N | N/A |
| Harmonic complexes | 240 equally weighted sine harmonics with 100 Hz fundamental | H0 | 0 ° |
| H90 | Random 0–90 ° | ||
| H360 | Random 0–360 ° |
FIG. 2.
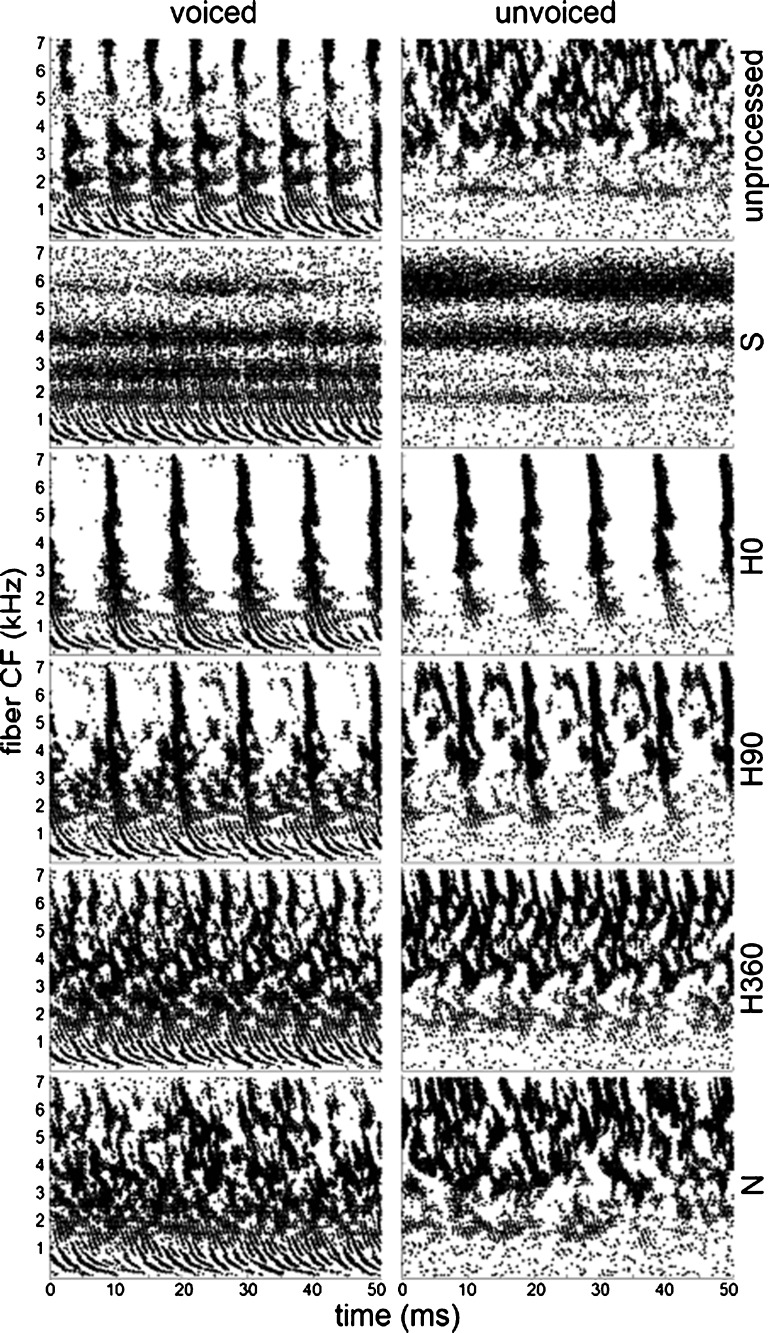
Plots of analyses of the CNC word “goose” in the absence of a masker allow for feature comparison among carriers, here all using Butterworth synthesis filters. Row A depicts time-domain waveforms, with intensity in arbitrary units on the vertical axis and time on the horizontal axis. Row B depicts spectrograms, with time on the horizontal axis, frequency from 0 to 10 kHz on the linear vertical axis, and intensity in arbitrary units encoded by color from blue (low) to red (high). Row C depicts modeled neural response PSTHs from 20 low-SR fibers per CF, with fiber CF ranging linearly from 0.1 to 7 kHz on the vertical axis, time on the horizontal axis, and a dot for each simulated action potential. Row D depicts summary PSTHs from 20 high-SR fibers, with counts on the vertical axis and time on the horizontal axis. The columns contain these depictions for unprocessed, S, H0, and H360—vocoded stimuli from left to right.
Procedure
Diotic, vocoded, closed-set speech recognition in noise was tested in NH listeners using a forced-choice task. Stimuli were presented via headphones (Sennheiser HD600) at an average level of 60 dB A in a double-walled sound-attenuating booth (IAC). Twenty-three NH listeners with thresholds less than 25 dB HL at all audiometric frequencies participated. Listeners consisted of 12 males and 11 females, aged 18–29, and they were paid for their participation. Informed consent was obtained, and procedures were approved by the University of Wisconsin Human Subjects Institutional Review Board. Thirteen listeners (seven males, six females) were tested on stimuli vocoded with the Butterworth synthesis filters, and ten other listeners (five males, five females) were tested on stimuli vocoded with the current spread synthesis filters.
During a brief familiarization period, participants listened to each of the 50 words at least once in quiet, with each presentation vocoded with a randomly chosen carrier. Listeners were therefore exposed to an average of fewer than ten CNC examples of each vocoder carrier prior to testing and were considered to be naïve rather than trained. Immediately following this exposure to vocoded speech in quiet, they listened to several of the stimuli (vocoder carrier again randomly chosen) with a background noise level of 0 dB SNR in order to acclimate to the timing of stimulus presentation within the background masker. Listeners were then tested on two blocks of 300 trials each (50 words × 6 vocoder carriers). The first block consisted of speech-in-noise stimuli with an SNR of 0 dB, and the second block consisted of stimuli with an SNR of −3 dB. Order of word and vocoder presentation was randomized for each subject, so the possible differential performance across carriers due to generalized learning (Hervais-Adelman et al. 2011) should be averaged across listeners. Testing for each block of trials lasted approximately 45 min, and blocks were separated by a break. During each trial, the listener identified the word among the 50 CNC word choices via a computer mouse and graphical user interface and was instructed to guess if unsure. Text representations of the words were arranged alphabetically in a 5 × 10 push-button matrix on the screen and were visible throughout stimulus presentation. The user was given unlimited time to decide on his or her chosen response. No correct-answer feedback was provided during testing.
METHODS B: PHENOMENOLOGICAL MODELING
A computational model of the cat AN fiber (Zilany and Bruce 2006, 2007; Zilany et al. 2009) was used to simulate responses to the vocoded and unprocessed stimuli. Shuffled cross-correlogram analyses (Joris 2003; Louage et al. 2004; Heinz and Swaminathan 2009; Swaminathan and Heinz 2012) of these simulated AN outputs were used to calculate “neural correlation coefficients,” metrics of how neural representations of envelopes and TFS of the unprocessed stimuli are preserved in the neural representations of the corresponding vocoded stimuli. These neural correlation coefficients were then entered as predictors for the psychoacoustic scores in several statistical models.
Simulated AN responses to each of the vocoded stimuli (“A”), the unprocessed stimuli (“B”), and inverted‐waveform versions thereof (“−A” and “−B”) were generated for fibers of low, medium, and high spontaneous rates (SRs) and of characteristic frequencies (CFs) of every natural number multiple of 100 Hz from 0.1 to 7 kHz. The stimuli were resampled to 100 kHz and mathematically converted to sound pressure level values; these input values are used by the model to generate simulated neuronal spike post-stimulus time histograms (PSTHs). Typically when conducting correlogram analyses, sound levels are chosen independently for each fiber in order to produce the best modulation levels. However, in order to simulate actual listening conditions, a single level was chosen (60 dB A) for each stimulus presentation to the model. Spikes were generated for 20 repetitions of a given stimulus, CF, and SR and were summed to create PSTHs with 50-μs bins. The following shuffled cross-correlograms (SCCs) were calculated between pairs of stimulus PSTHs for a given fiber CF and SR: SCCA/A, SCCA/−A, SCCB/B, SCCB/−B, SCCA/B, and SCCA/−B. The SCC is an all-order interval histogram between all non-identical single-repetition PSTH (henceforth “psthi”) pairs, so refractory effects within a single model neuron are ignored. Therefore, for autocorrelograms SCCA/A and SCCB/B, within-repetition intervals were subtracted from the all-pairwise interval calculation. The convolution required for the SCC calculation was performed in Fourier space, e.g., for SCCA/B and SCCA/A,
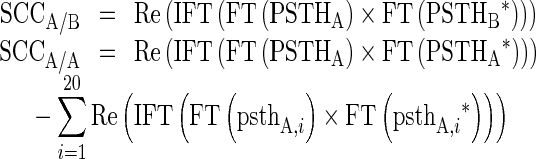 |
where * denotes complex conjugation, Re denotes taking the real part of the function, FT denotes the Fourier transform, IFT denotes the inverse Fourier transform, psthi denotes results from the ith simulation of 20, and PSTH denotes results from the sum of the 20 simulations.
The SCCA/B and SCCA/−B cross-correlograms are representations of the similarity of the AN model response to vocoded and unprocessed stimuli. Following normalization, “sumcors” and “difcors” were calculated from pair and inverted-pair SCCs:
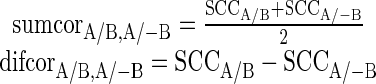 |
The sumcor emphasizes features common to the SCC of the vocoded and unprocessed signals and the SCC of the vocoded and inverted unprocessed signals. Therefore, since envelope is thought to be independent of stimulus polarity, the sumcor is a metric that represents envelope fidelity. Likewise, the difcor emphasizes features that are different between the two SCCs. Therefore, since TFS is thought to be dependent upon stimulus polarity, the difcor is a metric of TFS fidelity. The sumcor is low-pass filtered at the fiber’s CF in order to correct for “leakage” of TFS into the sumcor due to the nonlinearity of rectification present in neural responses (Heinz and Swaminathan 2009). For each stimulus and fiber SR, the maximum values of the sumcor were averaged across fibers of all CFs, while the maximum values of the difcor were averaged across fibers of CF below 3 kHz. In order to compare across different stimuli, these averages were normalized by calculating “neural correlation coefficients” for ENV and TFS:
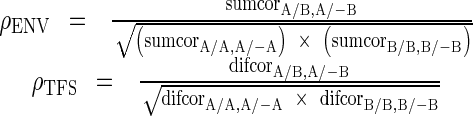 |
Each of the vocoded stimuli therefore had a ρENV and a ρTFS for each fiber SR. These neural correlation coefficients were then used as variables in linear regressions to predict psychoacoustic test scores. Additionally, ρ calculations were performed within stimuli, but across CF, in order to examine temporal pattern correlation across fibers of different CF (Swaminathan and Heinz 2011).
RESULTS A: PSYCHOACOUSTICS
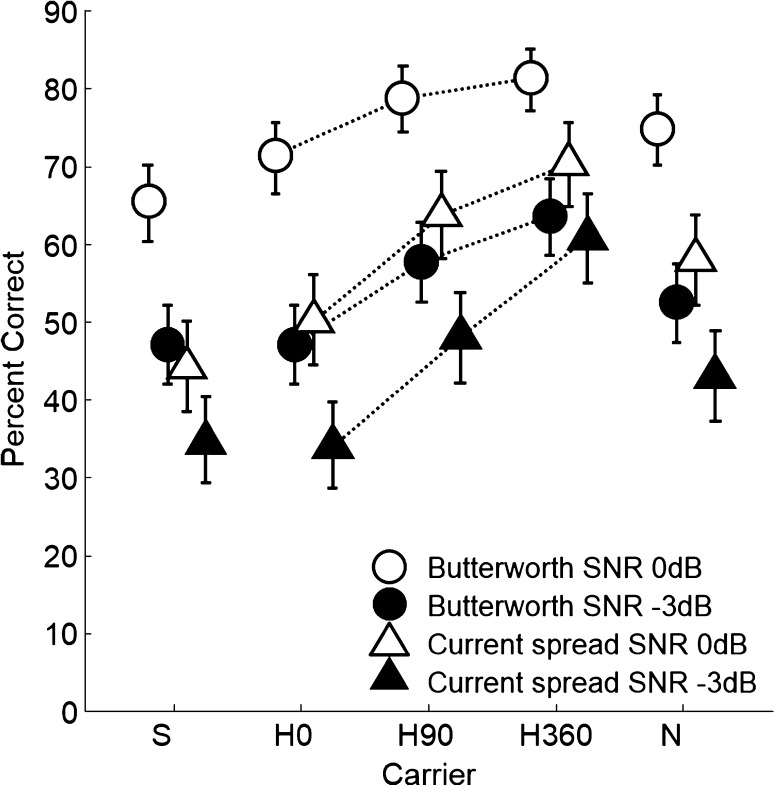
Performance was evaluated by comparing percent correct (%C) word recognition across conditions. Figure 3 shows the average %C for each synthesis filter type and SNR as a function of vocoder carrier. Dotted lines connect the data points for harmonic complex carriers H0, H90, and H360. Error bars show 99 % confidence intervals. In general, %C scores were higher with Butterworth synthesis filters and lower noise (0 dB SNR). For each SNR and synthesis filter combination, %C scores were the highest with the H360 carrier. In contrast, worst performance was observed with carriers S and H0. Finally, performance with the harmonic complex carrier improved monotonically with increasing component phase dispersion.
FIG. 3.
Psychoacoustic percent correct as a function of vocoder carrier for each of the combinations of synthesis filter and SNR, shown with 99 % confidence interval error bars. Dotted lines connect the points for harmonic complex carriers with different component starting phase dispersion (H0, H90, and H360).
Individual trial response data were analyzed with a binary logistic regression in order to determine which factors were best predictors of correct responses. The full-factorial regression included carrier, synthesis filter, and SNR as categorical variables. Results revealed significant effects of carrier, synthesis filter, and SNR (all p < 0.001), with Cox and Snell r2 = 0.075. A significant interaction was also found for synthesis filter type × SNR (p < 0.001) and synthesis filter type × carrier (p = 0.044). An analysis of variance was performed on averaged arcsine-transformed %C scores (Studebaker 1985) with carrier, synthesis filter, and SNR as factors. Results revealed significant main effects of carrier [F(5, 210) = 25.0, p < 0.001], synthesis filter [F(1, 210) = 77.0, p < 0.001], and SNR [F(1, 210) = 124.7, p < 0.001] and a significant interaction of synthesis filter and SNR [F(1, 210) = 7.2, p = 0.008]. Bonferroni-corrected post hoc analyses showed that overall performance with the H360 carrier was significantly higher than with all carriers (p < 0.001) except H90. Performance with the S carrier was worse than H360 (p < 0.001), H90 (p < 0.001), and N (p = 0.002) carriers. Performance with the H0 carrier was worse than with either the H360 or H90 carriers (p < 0.001). There was no significant effect of SNR for carriers S or H360, nor was there a significant effect of synthesis filter type for carriers H90 or H360.
RESULTS B: MODEL ANALYSES
Examples of PSTHs generated from the AN model for each CF and the results of summing these PSTHs across CF are shown in rows C and D of Figure 2, respectively. The model responses in row C follow the spectrotemporal patterns displayed in the corresponding waveforms and spectrograms (rows A and B). The summed PSTHs in row D reflect the broadband envelope characteristics of the time-domain signal.
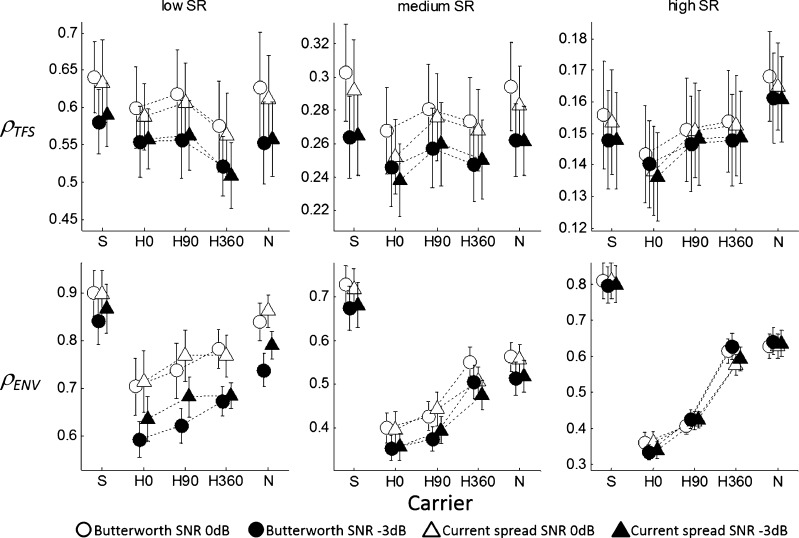
Envelope and TFS neural correlation coefficients (ρENV and ρTFS) were averaged across words for each SNR, synthesis filter, carrier, and fiber SR and are shown in Figure 4. As seen in the bottom row of Figure 4, averaged ρENV are positively correlated with increasing phase dispersion in the harmonic complex carriers for all fiber SRs. This reflects the trend of larger %C scores with more phase dispersion as seen in Figure 3. Averaged ρENV and ρTFS values are generally positively correlated with SNR, reflecting the trend of higher %C scores at the higher SNR and indicating neural envelope and TFS information is more disrupted by higher levels of noise. In contrast, the neural metrics failed to capture the performance degradation due to spectral modifications; averaged ρENV and ρTFS values do not generally follow performance based on synthesis filter type. The highest averaged ρENV and ρTFS values were obtained for the sine-vocoded stimuli, the stimuli with the flattest carrier envelopes. Interestingly, the sine vocoder also produced the lowest %C scores, but this may be a result of spectral rather than temporal degradations in the signal (i.e., spectral sparseness of eight single sine tones versus numerous tones in a harmonic complex or continuum of narrowband noises). Perhaps most striking about the neurometrics are the fairly high values of ρTFS. It is commonly assumed that the explicit exclusion of signals’ acoustic TFS during vocoding would result in neural patterns that contain TFS information that is unrelated to that of the original acoustic waveform. However, neural TFS is defined here as that part of the neural response pattern which changes due to signal inversion. Therefore, we must conclude that vocoding leaves some of the original signal’s neural TFS information intact, especially for low SR fibers. That is, the envelope representation by a vocoder preserves some aspects of the original signal that are phase-sensitive.
FIG. 4.
Neural correlation coefficients ρ for TFS (top row) and envelope (bottom row) computed between vocoded stimuli and the unprocessed tokens for modeled AN fibers of low SR (first column), medium SR (second column), and high SR (third column).
In order to explore the relationship between psychoacoustic performance and the effects of harmonic component phase dispersion in a simulated AN, the neural metrics were used to construct several statistical regression models. Three model classes were tested—A, B, and C. Within each model class, the predictive abilities of ρ values for each SR were tested independently and together, resulting in four models per class. These models were fit to performance with the harmonic carriers only, then used to predict performance with all carriers. The models’ abilities to predict performance with the harmonic complex carriers alone are also reported. Variable coefficients and statistics are shown in Table 3 (constant terms are omitted).
TABLE 3.
Statistical model variable coefficients, correlation coefficients, and significance values for tested models
| Model | Predictor | β | p | R 2 (all) | p | R 2 (HX) | p |
|---|---|---|---|---|---|---|---|
| A-low SR | ρ ENV | 1.64 | 0.009 | 0.003 | 0.808 | 0.510 | 0.009 |
| A-medium SR | ρ ENV | 1.54 | 0.009 | 0.003 | 0.820 | 0.508 | 0.009 |
| A-high SR | ρ ENV | 0.66 | 0.077 | 0.009 | 0.687 | 0.280 | 0.077 |
| A-all SRs | ρ ENV-LOW SR | 0.18 | 0.893 | 0.000 | 0.951 | 0.620 | 0.002 |
| ρ ENV-MED SR | 2.90 | 0.342 | |||||
| ρ ENV-HIGH SR | −0.92 | 0.493 | |||||
| B-low SR | ρ ENV | 1.65 | 0.024 | 0.003 | 0.815 | 0.510 | 0.009 |
| ρ TFS | −0.05 | 0.965 | |||||
| B-medium SR | ρ ENV | 0.98 | 0.012 | 0.046 | 0.363 | 0.846 | <0.001 |
| ρ TFS | 6.65 | 0.002 | |||||
| B-high SR | ρ ENV | −0.05 | 0.883 | 0.124 | 0.127 | 0.619 | 0.002 |
| ρ TFS | 19.89 | 0.020 | |||||
| B-all SRs | ρ ENV-LOW SR | −1.74 | 0.002 | 0.021 | 0.540 | 0.993 | <0.001 |
| ρ TFS-LOW SR | −1.60 | 0.159 | |||||
| ρ ENV-MED SR | 1.04 | 0.174 | |||||
| ρ TFS-MED SR | 25.41 | <0.001 | |||||
| ρ ENV-HIGH SR | 1.11 | 0.063 | |||||
| ρ TFS-HIGH SR | −35.81 | 0001 | |||||
| C-low SR | ρ ENV | −8.54 | 0.727 | 0.003 | 0.825 | 0.521 | 0.008 |
| ρ TFS | −12.78 | 0.676 | |||||
| ρ TFS × ρ ENV | 18.01 | 0.677 | |||||
| C-medium SR | ρ ENV | 6.74 | 0.306 | 0.081 | 0.224 | 0.861 | <0.001 |
| ρ TFS | 16.17 | 0.154 | |||||
| ρ TFS × ρ ENV | −22.26 | 0.376 | |||||
| C-high SR | ρ ENV | −6.21 | 0.613 | 0.094 | 0.190 | 0.631 | 0.002 |
| ρ TFS | 4.23 | 0.895 | |||||
| ρ TFS × ρ ENV | 41.20 | 0.616 | |||||
| C-all SRs | ρ ENV-LOW SR | −19.23 | 0.263 | 0.032 | 0.448 | 0.997 | <0.001 |
| ρ TFS-LOW SR | −21.84 | 0.275 | |||||
| ρ TFS × ρ ENV-LOW SR | 31.52 | 0.296 | |||||
| ρ ENV-MED SR | 29.87 | 0.274 | |||||
| ρ TFS-MED SR | 72.52 | 0.159 | |||||
| ρ TFS × ρ ENV-MED SR | −120.21 | 0.288 | |||||
| ρ ENV-HIGH SR | −39.72 | 0.316 | |||||
| ρ TFS-HIGH SR | −139.40 | 0.212 | |||||
| ρ TFS × ρ ENV-HIGH SR | 281.58 | 0.307 |
Models were built to predict performance data from neural correlation coefficients with harmonic carriers only. Correlation and significance are shown for prediction of performance with all carriers (“all”) and with harmonic carriers only (“HX”). Significant term coefficients are shown in bold
Model class A used the fidelity of envelope encoding (ρENV) as the only predictor, first for each fiber SR separately and then for fibers of all three SRs together:
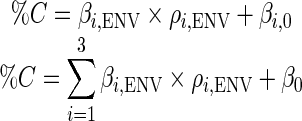 |
where the subscript i indexes the fiber SRs: low (i = 1), medium (i = 2), and high (i = 3). For low and medium SR fibers, positive and significant model coefficients were obtained, indicating that better envelope coding by low and medium SR fibers with dispersed-phase carriers correlates with improved speech recognition in noise. The all-SR model failed to produce any significant coefficients, and its ρENV coefficient was negative for high SR fibers, contradicting the presumption that agreement in neural representations of vocoded and unprocessed signals should be positively correlated with psychoacoustic performance.
Although the loss of all TFS information during vocoding is generally assumed, a phase-dependent response may persist. In order to assess the contributions of the fidelity of TFS encoding to speech understanding, model class B added ρTFS as a predictor:
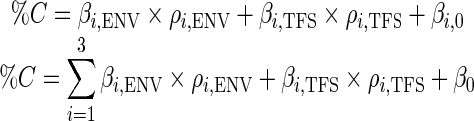 |
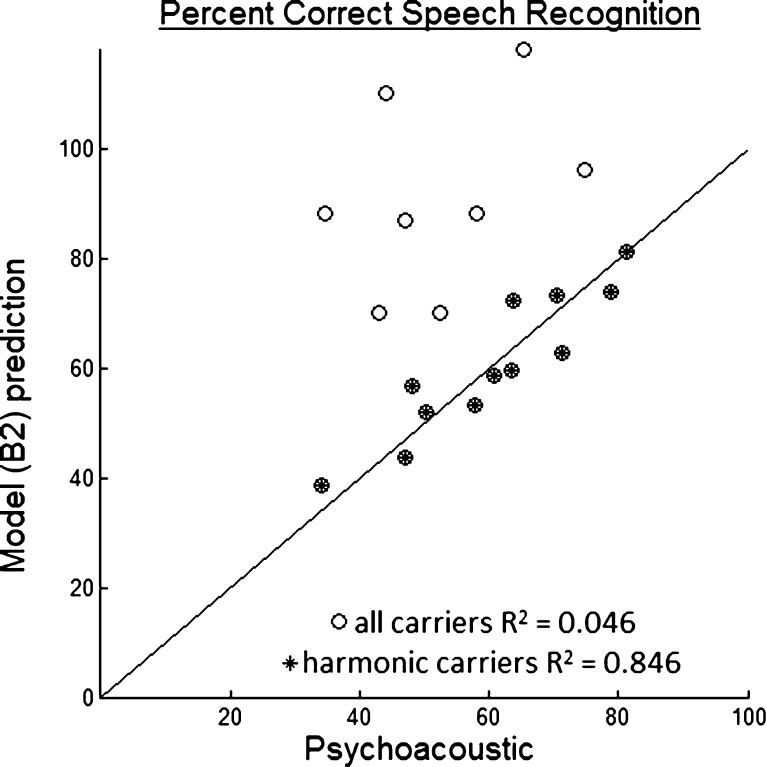
For low and medium SR fibers, model class B produced positive and significant term coefficients for ρENV. For medium and high SR fibers, positive and significant term coefficients were obtained for ρTFS. These findings support suggestions that low SR fibers may be better at encoding what we think of as envelope characteristics while high SR fibers may better encode TFS (e.g., Young and Sachs 1979). The predictions due to the medium-SR model of class B and psychoacoustic results are compared in Figure 5, where model prediction scores are shown as plotted point ordinates and psychoacoustic scores as the associated abscissae. As with the all-SR model of class A, the presence of negative coefficients in the all-SR model of class B indicates that this model is not strictly physiologically valid.
FIG. 5.
Measured and model-predicted percent correct speech recognition for each carrier, SNR, and synthesis filter type. The predicted scores with harmonic carriers, denoted by asterisks, lie along the measured-predicted diagonal, while the predicted scores with the sine and noise vocoders are much higher than psychoacoustic results. The model shown here, B2, used ρ TFS and ρ ENV predictors for medium-SR fibers only and had positive and significant term coefficients.
In order to further assess how the combined contributions of envelope and TFS fidelities influenced speech recognition, model class C added the interaction of ρENV and ρTFS as a predictor:
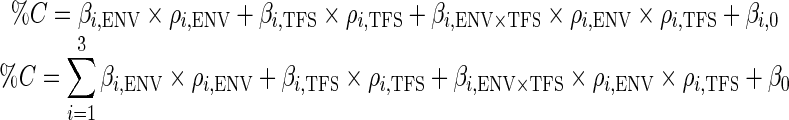 |
This is the type of model proposed in Swaminathan and Heinz (2012), although that study used only high SR fibers. No term coefficients were found to be significant with this model class.
As ρENV and ρTFS values, like %C, tended to vary systematically with harmonic carrier phase dispersion, nearly all models robustly predicted measured performance with the harmonic complex carriers. However, as illustrated in Figure 5, all models vastly over-predicted performance with the sine carrier and generally could not accurately predict performance with the noise carrier. The high ρENV values calculated for the sine vocoder indicate that it does indeed provide a flat carrier envelope for faithful signal representation, but it evidently has other characteristics that adversely affect speech understanding, such as sparse spectral representation.
We expected that the spectral profiles of the long-term AN activation patterns due to the harmonic carriers were identical due to the identity of their magnitude spectra. We also expected to observe differences among these patterns for sine, noise, and harmonic complex vocoded stimuli and for different synthesis filter types. However, there was not a large difference in spectral profiles between stimuli with Butterworth and current spread synthesis filters in CF/counts histograms, and most vocoded stimuli produced similar patterns that generally followed the corresponding unprocessed stimulus histograms. The sine-vocoded stimulus alone showed response peaks very near the channel center frequencies at CFs > 1 kHz, i.e., the carrier frequencies, which is to be expected. This exception of the sine vocoder may be a factor contributing to its poor corresponding psychoacoustic performance. Correlation analyses of vocoded and unprocessed spectral profiles revealed no consistent patterns. Clearly, the fidelity of long-term spectra as represented in the AN could be an important factor in determining vocoded speech recognition, but that conclusion is not supported here. In order to study the spectrotemporal dynamics of evolving neuronal activity, a next step might be to analyze short time-windowed SCCs and the evolution thereof throughout a speech-like signal.
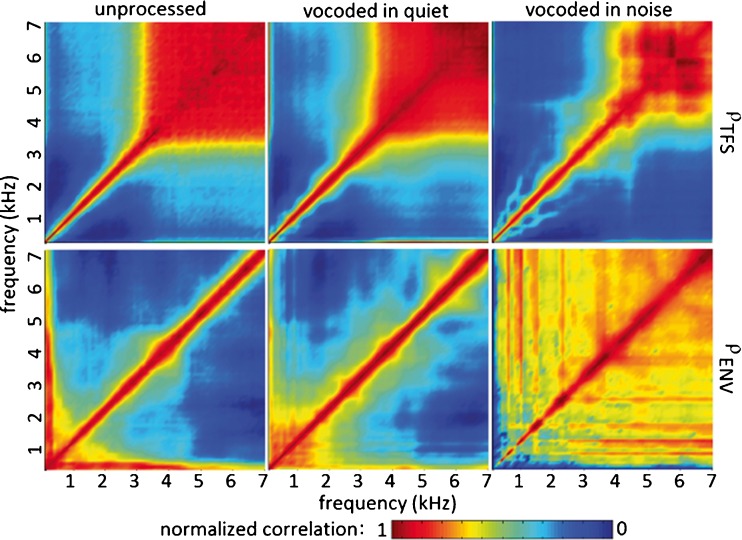
The nature of vocoders allows for speech signals to be represented by envelopes from a small number of channels. Prominent envelope fluctuations within an analysis band, perhaps generated in very localized spectral regions, are broadcast across the entire pass-band of the vocoder’s output channel. Hence, larger spectral regions of the auditory periphery are receiving coherent, smoothed, envelope information, and the loss of independent information may contribute to decreased intelligibility (Swaminathan and Heinz 2011). The across-fiber synchronous response to envelope and TFS is likely affected by vocoding and may reflect this loss of across-fiber information independence. In order to examine across-fiber envelope and TFS correlation, Figure 6 shows within-stimulus, across-CF ρENV and ρTFS (as opposed to the between unprocessed and vocoded, within same CF SCCs used above) for high SR fibers. These cross-correlations are averaged across all CNCs and conditions and thus only show the general effects of vocoding and masker addition. As expected, the peak correlation values appear along the diagonal. That is, correlations are the highest along the same CF, i.e., autocorrelation axis; in contrast, temporal firing patterns of fibers that have different CFs do not generally correlate. At CFs > 3 kHz, higher ρTFS values can be seen, due to the loss of phase locking; in this case, temporal response patterns of fibers that have different CFs are no longer mathematically orthogonal. This pattern is largely consistent regardless of whether one is observing unprocessed tokens, vocoded speech in quiet, or vocoded speech in noise. These patterns are as to be expected for broadband stimuli. For unprocessed and vocoded speech in quiet, ρENV is highest among fibers of closely neighboring CF. This trend is observed for all but the lowest CFs and means that fibers of remote CF are representing different envelopes. In contrast, for vocoded speech in noise, there is a high across-CF correlation of neural envelope representation at all CFs, indicating that redundant envelope information is carried by fibers of different CFs. The lack of unique envelope representations by different-CF fibers may be a characteristic limitation of vocoded speech in masking noise.
FIG. 6.
Across-fiber, within-stimulus neural correlation coefficients for TFS (first row) and envelope (second row). Columns show neural correlation coefficients calculated for all unprocessed stimuli, all vocoded stimuli in quiet, and all vocoded stimuli in noise from left to right. The horizontal and vertical axes depict modeled AN fiber CFs from 0.1 to 7 kHz, and color depicts the level of neural correlation from low (blue) to high (red).
DISCUSSION
This study examined the effect of carrier on closed-set vocoded speech recognition in noise. The carriers tested consisted of sine tones, band-pass-filtered white noise, and three harmonic complexes of f0 = 100 Hz with different amounts of random phase dispersion (none/0 °, 90 °, and 360 °). Results showed that randomly dispersed starting phases resulted in improved speech intelligibility. The proposed mechanism to explain this observed trend is the improved representation of envelopes with dispersed-phase harmonic complex carriers. However, this is not well explained by neural metrics calculated from simulated AN output patterns when taking into account the also-tested sine and noise carriers. In vocoding, the band-pass-filtered carrier is multiplied by a slowly varying envelope calculated from the original band-pass-filtered signal for a given channel. Therefore, the output envelopes reflect the temporal characteristics of envelopes of both the input signal and the unmodulated carrier. Although they have identical magnitude spectra, the H0 and H360 carriers have very different temporal envelopes. The H0 carrier is essentially a 100-Hz biphasic pulse train, while the H360 carrier is essentially periodic noise with a repetition rate of 100 Hz. By randomizing the phases of the harmonic components in the H360 carrier, these components add to create a carrier with a flatter temporal envelope that more fully represents the signal’s acoustic envelope. In low-frequency channels, the band-pass filtering renders all of the harmonic carriers very similar due to the low number of interacting harmonics within a channel. However, as the fourth channel (center frequency = 1,156 Hz) is approached, a sufficient number of harmonic components are added together such that differences emerge in the carrier envelope shapes. It is the higher number of harmonic components within a single channel that causes the temporal characteristics of the signals to resemble a pulse train and periodic noise for the H0 and H360 carriers, respectively. The vocoder outputs at these higher-frequency channels reflect these characteristics, which are comprised of a nearly continuous sampling of the signal envelope for carrier H360 and an envelope sampled every 10 ms for the H0 carrier. The relatively sparse envelope sampling by carrier H0 at this stage may be detrimental to speech perception even though the carrier meets the Nyquist criterion for the envelope, which was low-pass filtered at 50 Hz.
The hypothesis that temporally flatter carrier envelopes determined superior performance (e.g., Whitmal et al. 2007) posits that the acoustic information was best retained with carrier H360 due to its intrinsic temporal envelope characteristics. Examining stimuli vocoded with carriers H0 and H360 in rows B and C of Figure 2, we see that the spectral representations of the stimuli are similar and that the vocoded stimuli differ primarily in the time domain. The flat carrier hypothesis also accounts for the fairly high performance of the N carrier, whose envelopes are flatter for the higher-frequency, broader-band channels. However, it does not account for the high performance of carrier H90, whose temporal envelope is closer to H0 than to H360. Also, the flat carrier hypothesis does not account for the inferior performance of carrier S; with only one sine tone carrier per channel, this vocoder produced the flattest envelopes. We partially attribute the performance deficits associated with carrier S to spectral sparseness. Combined spectrotemporal effects may also be prominent factors affecting performance. It is known that stimuli with identical long-term spectra can evoke different perceptions if their temporal structures are different, and spectrotemporal patterns evoked by harmonic carriers depend largely on their phase spectra (Kohlrausch and Sander 1995; Carlyon 1996).
It is not clear from the present results how spectrotemporal pattern characteristics influence performance, but it may be instructive to inspect these patterns. Figure 7 shows the outputs of the AN model at CFs from 100 Hz to 7 kHz in 50 Hz increments for 50 ms voiced and unvoiced segments of the CNC “goose” in quiet (high SR fibers). Outputs with different carriers were compared in order to look for different spectrotemporal patterns of activation. Modeled AN fibers with CFs below ∼2 kHz exhibit phase locking, which is most evident when low-frequency information was present, i.e., during voiced speech. After accounting for the phase shift due to the basilar membrane traveling wave, these fibers responded largely in phase with their spectral neighbors (neighboring CFs). At higher frequencies, loss of phase locking was observed. Envelope sensitivity, as indicated by temporal bunching of fiber responses, appears to be present for CFs above ∼1 kHz. It is interesting to compare model responses for voiced versus unvoiced segments among the unprocessed and vocoded tokens. The response to unprocessed speech shows clear differences between voiced and unvoiced segments; the f0 is manifested by vertical striping and formant peaks are apparent in horizontal bands for the voiced segment, and a chaotically structured high-frequency response pattern is evident for the unvoiced segment. In contrast, the response patterns of the vocoded speech are more similar between segments. The main difference between patterns for voiced and unvoiced segments of vocoded speech is how much energy is allocated to each band. For example, the high-frequency activation patterns for carrier H90 are similar for voiced and unvoiced segments, but the amount of energy in those high-frequency bands is lower for the voiced segment. The availability of intermediate carrier envelope amplitudes to either be represented or absent in these patterns, in order to differentiate between voiced and unvoiced segments, may be a factor in the ability of a vocoder carrier to provide usable speech cues. As opposed to carriers H360 and H90, carriers S and H0 have no distinguishing temporal features which could be “turned on” as energy in a given band rises. Carrier N would have such “envelope depth” features, but they would not be consistent throughout the stimulus. However, this contrast was not investigated quantitatively. Carrier H0 resulted in a high temporal coincidence of fiber responses across CF, whereas carrier S resulted in asynchronous fiber responses across CF. The poor performance with both of these carriers indicates that temporal coincidence or asynchrony of responses of adjacent-CF fibers was not a common factor affecting performance.
FIG. 7.
Model outputs for high-SR fibers with CFs between 0.1 and 7 kHz at 50 Hz spacing, shown for voiced and unvoiced 50-ms segments of the CNC “goose” in quiet, for unprocessed and vocoded stimuli.
The dispersed-phase harmonic carriers resulted in better speech recognition scores than carriers S or N, yet carriers S and N resulted in higher neural correlation coefficients for envelope and TFS. It is clear that many of the temporal patterns present in the acoustics were reproduced by the AN model, suggesting additional variables are needed to explain psychoacoustic performance with these vocoders. For example, the significant spectral gaps in the sine vocoder’s representation of the signal could lead to a smaller number of fibers carrying that information and subsequent performance deficits. As for carrier N, since the H360 and N carriers both had relatively flat envelopes (as did carrier S), but also had the benefit of full-spectrum representation (which carrier S did not), the performance difference between H360 and N may be due to the repetitive nature of envelope fluctuations with H360, whereas carrier N’s envelope fluctuations are random.
Although the filter roll-off slopes for the Butterworth and current spread filters are roughly the same, the Butterworth filters have a flat gain in the passband, while the current spread filters are sharply peaked at the filter’s center frequency. This sharpness would result in amplitude modulations becoming more quickly attenuated as the sidebands move away from the filter center frequencies. Sine-vocoded speech relies heavily on sideband detection for recognition (Souza and Rosen 2009; Kates 2011), and this loss may be responsible for the lower recognition of speech vocoded with carrier S when implementing the current spread filters. Previous literature has shown better performance with the sine vocoder when high-frequency envelope fluctuations are retained (Dorman et al. 1997; Whitmal et al. 2007; Stone et al. 2008), so the observed performance deficits with carrier S may also be due to the low (50 Hz) cutoff frequency for envelope extraction used here.
It is difficult to directly translate the present study’s results to suggestions for CI processing. Electric hearing largely precludes the possibility of independently firing neighboring fibers because the current pulse phase-locks their firing (Moxon 1971; Kiang and Moxon 1972). In that respect, electric hearing seems to be much like listening with vocoder carrier H0, where fibers fire in unison, unanimously sampling and presenting the envelope at identical, discrete time points. While it has been tempting to seek to take advantage of the exquisite phase locking exhibited with electric stimulation for accurate presentation of temporal cues (van Hoesel and Tyler 2003), perhaps it is this very phenomenon which is disrupting information transfer. As illustrated by Shamma and Lorenzi (2013), internal spectrograms can be reconstituted from AN patterns by the application of a lateral inhibition network. Such mechanisms could have facilitated recovery of information not obvious in the AN patterns seen here. Auditory nerve activation without traveling wave delays, as occurs in electric hearing, might upset such patterns and disrupt the mechanisms that enhance internal spectrograms. However, accurate reproduction of the timing of AN activation due to traveling wave delays with electric stimulation would require extensive gains in spatial resolution relative to that with the devices commercially available today.
Acknowledgments
This study was supported by the NIH-NIDCD (5R01 DC003083, Litovsky; K99/R00 DC010206, Goupell) and also in part by a core grant to the Waisman Center from the NICHD (P30 HD03352). Computing resources of the University of Wisconsin’s Center for High Throughput Computing were used extensively for model calculations. The authors would like to thank the three anonymous reviewers and associate editor Robert Carlyon for invaluable comments and insights.
Contributor Information
Tyler H. Churchill, Phone: +1-415-2031716, Email: tchurchill@wisc.edu
Ruth Y. Litovsky, Phone: +1-608-262-5045, FAX: +1-608-263-2918, Email: Litovsky@waisman.wisc.edu
References
- Bingabr M, Espinoza-Varas B, Loizou PC. Simulating the effect of spread of excitation in cochlear implants. Hear Res. 2008;241:73–79. doi: 10.1016/j.heares.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlyon RP. Spread of excitation produced by maskers with damped and ramped envelopes. J Acoust Soc Am. 1996;99:3647–3655. doi: 10.1121/1.414963. [DOI] [Google Scholar]
- Chen F, Loizou PC. Predicting the intelligibility of vocoded speech. Ear Hear. 2011;32:331–338. doi: 10.1097/AUD.0b013e3181ff3515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deeks JM, Carlyon RP. Simulations of cochlear implant hearing using filtered harmonic complexes: implications for concurrent sound segregation. J Acoust Soc Am. 2004;115:1736–1746. doi: 10.1121/1.1675814. [DOI] [PubMed] [Google Scholar]
- Dorman MF, Loizou PC, Rainey D. Speech intelligibility as a function of the number of channels of stimulation for signal processors using sine-wave and noise-band outputs. J Acoust Soc Am. 1997;102:2403–2411. doi: 10.1121/1.419603. [DOI] [PubMed] [Google Scholar]
- Dudley H. Remaking speech. J Acoust Soc Am. 1939;11:169–177. doi: 10.1121/1.1916020. [DOI] [Google Scholar]
- Eskridge EN, Galvin JJ, Aronoff JM, Li T, Fu QJ. Speech perception with music maskers by cochlear implant users and normal hearing listeners. J Speech Lang Hear Res. 2012;55:800–810. doi: 10.1044/1092-4388(2011/11-0124). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friesen LM, Shannon RV, Baskent D, Wang X. Speech recognition in noise as a function of the number of spectral channels: comparison of acoustic hearing and cochlear implants. J Acoust Soc Am. 2001;110:1150–1163. doi: 10.1121/1.1381538. [DOI] [PubMed] [Google Scholar]
- Fu QJ, Nogaki G. Noise susceptibility of cochlear implant users: the role of spectral resolution and smearing. J Assoc Res Otolaryngol. 2005;6:19–27. doi: 10.1007/s10162-004-5024-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu QJ, Shannon RV, Wang X. Effects of noise and spectral resolution on vowel and consonant recognition: acoustic and electric hearing. J Acoust Soc Am. 1998;104:3586–3596. doi: 10.1121/1.423941. [DOI] [PubMed] [Google Scholar]
- Fu QJ, Chinchilla S, Galvin JJ. The role of spectral and temporal cues in voice gender discrimination by normal-hearing listeners and cochlear implant users. J Assoc Res Otolaryngol. 2004;5:253–260. doi: 10.1007/s10162-004-4046-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenwood DD. A cochlear frequency-position function for several species—29 years later. J Acoust Soc Am. 1990;87:2592–2605. doi: 10.1121/1.399052. [DOI] [PubMed] [Google Scholar]
- Heinz MG, Swaminathan J. Quantifying envelope and fine-structure coding in auditory nerve responses to chimaeric speech. J Assoc Res Otolaryngol. 2009;10:407–423. doi: 10.1007/s10162-009-0169-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hervais-Adelman AG, Davis MH, Johnsrude IS, Taylor KJ, Carlyon RP. Generalization of perceptual learning of vocoded speech. J Exp Psychol Hum Percept Perform. 2011;37:283–295. doi: 10.1037/a0020772. [DOI] [PubMed] [Google Scholar]
- Joris PX. Interaural time sensitivity dominated by cochlea-induced envelope patterns. J Neurosci. 2003;23:6345–6350. doi: 10.1523/JNEUROSCI.23-15-06345.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kates JM. Spectro-temporal envelope changes caused by temporal fine structure modification. J Acoust Soc Am. 2011;129:3981–3990. doi: 10.1121/1.3583552. [DOI] [PubMed] [Google Scholar]
- Kiang NY, Moxon EC. Physiological considerations in artificial stimulation of the inner ear. Ann Otol. 1972;81:714–730. doi: 10.1177/000348947208100513. [DOI] [PubMed] [Google Scholar]
- Kohlrausch A, Sander A. Phase effects in masking related to dispersion in the inner ear. J Acoust Soc Am. 1995;97:1817–1829. doi: 10.1121/1.413097. [DOI] [PubMed] [Google Scholar]
- Loizou PC (2006) Speech processing in vocoder-centric cochlear implants. In: A. Moller (ed) Cochlear and brainstem implants, vol 64. Karger, Basel, pp 109–143 [DOI] [PubMed]
- Louage DH, van der Heijden M, Joris PX. Temporal properties of responses to broadband noise in the auditory nerve. J Neurophysiol. 2004;91:2051–2065. doi: 10.1152/jn.00816.2003. [DOI] [PubMed] [Google Scholar]
- Lu T, Carroll J, Zeng FG (2007) On acoustic simulations of cochlear implants. Conference on Implantable Auditory Prostheses, Lake Tahoe, CA
- Moxon EC (1971) Neural and mechanical responses to electrical stimulation of the cat’s inner ear. Dissertation, Massachusetts Institute of Technology
- Nelson PB, Jin S-H, Carney AE, Nelson DA. Understanding speech in modulated interference: cochlear implant users and normal-hearing listeners. J Acoust Soc Am. 2003;113:961–968. doi: 10.1121/1.1531983. [DOI] [PubMed] [Google Scholar]
- Schroeder MR. Vocoders: analysis and synthesis. Proc IEEE. 1966;54:720–734. doi: 10.1109/PROC.1966.4841. [DOI] [Google Scholar]
- Schroeder MR (1970) Synthesis of low peak-factor signals and binary sequences with low autocorrelation. IEEE Trans Inf Theory 16:85–89
- Shamma S, Lorenzi C. On the balance of envelope and temporal fine structure in the encoding of speech in the early auditory system. J Acoust Soc Am. 2013;133:2818–2833. doi: 10.1121/1.4795783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon RV, Zeng F-G, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Souza P, Rosen S. Effects of envelope bandwidth on the intelligibility of sine- and noise-vocoded speech. J Acoust Soc Am. 2009;126:792–805. doi: 10.1121/1.3158835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone MA, Füllgrabe C, Moore BCJ. Benefit of high-rate envelope cues in vocoder processing: effect of number of channels and spectral region. J Acoust Soc Am. 2008;124:2272–2282. doi: 10.1121/1.2968678. [DOI] [PubMed] [Google Scholar]
- Studebaker GA. A “rationalized” arcsine transform. J Speech Hear Res. 1985;28:455–462. doi: 10.1044/jshr.2803.455. [DOI] [PubMed] [Google Scholar]
- Swaminathan J, Heinz MG. Predicted effects of sensorineural hearing loss on across-fiber envelope coding in the auditory nerve. J Acoust Soc Am. 2011;129:4001–4013. doi: 10.1121/1.3583502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swaminathan J, Heinz MG. Psychophysiological analyses demonstrate the importance of neural envelope coding for speech perception in noise. J Neurosci. 2012;32:1747–1756. doi: 10.1523/JNEUROSCI.4493-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Deun L, Van Wieringen A, Wouters J. Spatial hearing perception benefits in young children with normal hearing and cochlear implants. Ear Hear. 2010;31:702–713. doi: 10.1097/AUD.0b013e3181e40dfe. [DOI] [PubMed] [Google Scholar]
- van Hoesel RJM, Tyler RS. Speech perception, localization, and lateralization with bilateral cochlear implants. J Acoust Soc Am. 2003;113:1617–1630. doi: 10.1121/1.1539520. [DOI] [PubMed] [Google Scholar]
- Whitmal NA, Poissant SF, Freyman RL, Helfer KS. Speech intelligibility in cochlear implant simulations: effects of carrier type, interfering noise, and subject experience. J Acoust Soc Am. 2007;122:2376–2388. doi: 10.1121/1.2773993. [DOI] [PubMed] [Google Scholar]
- Young E, Sachs M. Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers. J Acoust Soc Am. 1979;66:1381–1403. doi: 10.1121/1.383532. [DOI] [PubMed] [Google Scholar]
- Zilany MS, Bruce IC (2006) Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery. J Acoust Soc Am 120:1446–1466 [DOI] [PubMed]
- Zilany MS, Bruce IC. Representation of the vowel /ε/ in normal and impaired auditory nerve fibers: model predictions of responses in cats. J Acoust Soc Am. 2007;122:402–417. doi: 10.1121/1.2735117. [DOI] [PubMed] [Google Scholar]
- Zilany MS, Bruce IC, Nelson PC, Carney LH. A phenomenological model of the synapse between the inner hair cell and auditory nerve: long-term adaptation with power-law dynamics. J Acoust Soc Am. 2009;126:2390–2412. doi: 10.1121/1.3238250. [DOI] [PMC free article] [PubMed] [Google Scholar]