Skip to main content
PMC home page
JARO: Journal of the Association for Research in Otolaryngology logoLink to JARO: Journal of the Association for Research in Otolaryngology
. 2014 Feb 7;15(2):175–186. doi: 10.1007/s10162-013-0439-3

Interindividual Variation of Sensitivity to Frequency Modulation: Its Relation with Click-Evoked and Distortion Product Otoacoustic Emissions

Sho Otsuka 1,2, Shigeto Furukawa 2, Shimpei Yamagishi 3, Koich Hirota 4, Makio Kashino 2,3,✉
PMCID: PMC3946142  PMID: 24504749

ABSTRACT

The frequency modulation detection limen (FMDL) with a low modulation rate has been used as a measure of the listener’s sensitivity to the temporal fine structure of a stimulus, which is represented by the pattern of neural phase locking at the auditory periphery. An alternative to the phase locking cue, the excitation pattern cue, has been suggested to contribute to frequency modulation (FM) detection. If the excitation pattern cue has a significant contribution to low-rate FM detection, the functionality of cochlear mechanics underlying the excitation pattern should be reflected in low-rate FMDLs. This study explored the relationship between cochlear mechanics and low-rate FMDLs by evaluating physiological measures of cochlear functions, namely distortion product otoacoustic emissions (DPOAEs) and click-evoked otoacoustic emissions (CEOAEs). DPOAEs and CEOAEs reflect nonlinear cochlear gain. CEOAEs have been considered also to reflect the degree of irregularity, such as spatial variations in number or geometry of outer hair cells, on the basilar membrane. The irregularity profile could affect the reliability of the phase locking cue, thereby influencing the FMDLs. The features extracted from DPOAEs and CEOAEs, when combined, could account for more than 30 % of the inter-listener variation of low-rate FMDLs. This implies that both cochlear gain and irregularity on the basilar membrane have some influence on sensitivity to low-rate FM: the loss of cochlear gain or broader tuning might influence the excitation pattern cue, and the irregularity on the basilar membrane might disturb the ability to use the phase locking cue.

Keywords: frequency modulation detection, otoacoustic emissions, ear canal reflectance, principal component analysis, multiple regression analysis

INTRODUCTION

Sensitivity to low-rate frequency modulation (FM) is assumed to mainly rely on the temporal fine structure (TFS) of a stimulus, which is represented by the pattern of neural phase locking at the auditory periphery (Moore and Sek 1995, 1996; Sek and Moore 1995). Given this assumption, the low-rate FM detection limen (FMDL) has been used to assess the ability to use phase locking information (Strelcyk and Dau 2009; Ruggles et al. 2011; Grose and Mamo 2012).

The shift of the excitation pattern that accompanies the frequency changes could also provide a cue for detecting FM: FM is converted to amplitude modulation (AM) by auditory filters tuned to frequencies flanking the stimulus carrier frequency and can be detected by monitoring an optimal point or the whole region of the excitation pattern (Zwicker 1965; Moore and Sek 1994). The roles of phase locking and excitation pattern cues for FM detection have been extensively discussed in the literature. Moore and colleagues measured FMDLs for various stimulus parameters and conditions, such as carrier frequency (fc) and modulation frequency (fm). They proposed that the relative contributions of excitation pattern and temporal cues to FM processing depend on fc and fm: For fc > 4,000 Hz, FM detection is thought to depend on the excitation pattern mechanism (Sek and Moore 1995). For lower fc, the excitation pattern mechanism is dominant at high fm (>10 Hz) and the temporal mechanism is dominant at very low fm (<5 Hz) (Moore and Sek 1995; Sek and Moore 1995). These ideas were tested by observing the effect of the superimposition of AM on FM detection (Moore and Sek 1996): If FM is detected by the excitation pattern mechanism, FM detection must be degraded by added AM. For lower fc, the increase in FMDL due to added AM becomes smaller as fm decreases. This result is consistent with the idea that low-rate FM for lower fc is detected by a temporal mechanism rather than the excitation pattern mechanism. Recently, Ernst and Moore (2010) suggested that even for low-rate FM, the excitation pattern mechanism has a strong influence on FMDLs at very low stimulus levels (e.g., 20 dB SL) due to sharper tuning of auditory filter or less precise phase locking at such levels. In summary, although low-rate FM detection mainly depends on the phase locking cue at moderate to high stimulus levels, the contribution of the excitation pattern cue cannot be eliminated. If the excitation pattern cue significantly contributes to low-rate FM detection, the functionality of cochlear mechanics underlying the excitation pattern should be reflected in the low-rate FMDLs. However, Strelcyk and Dau (2009) reported no significant correlation between low-rate FMDLs and psychophysical indicators of cochlear mechanics, such as audibility and frequency selectivity, in hearing-impaired listeners.

The present study explored the relationship between cochlear mechanics and low-rate FMDLs by evaluating physiological measures of cochlear function, namely, otoacoustic emissions (OAEs). OAEs are measured as small-amplitude acoustic signals in the ear canal. The function of the outer hair cells (OHCs) is assumed to be related to their generation (Probst et al. 1991), and OAEs have been used as a noninvasive tool for detecting impaired auditory function in humans (e.g., Probst et al. 1987). In particular, distortion product otoacoustic emissions (DPOAEs), which are evoked by a pair of tones, and click-evoked otoacoustic emissions (CEOAEs), which are evoked by a click, are commonly used for clinical applications and auditory research (Probst et al. 1991). DPOAEs are thought to arise from nonlinear distortion induced by the traveling wave (Dallos 1992) and CEOAEs are thought to arise via linear reflection by micromechanical impedance perturbations (Zweig and Shera 1995). Numerous studies have reported relationships between the OAE level and cochlear function: DPOAEs are reduced or absent in ears with hearing loss (e.g., Dorn et al. 2001), and CEOAEs are not observed in the audiometically impaired frequency range where hearing levels are higher than 20 dB (e.g., Lucertini et al. 1996). There is a correlation between the behavioral threshold and the DPOAE level (e.g., Dorn et al. 1999). A similarity between the input/output function of OAEs and psychophysically measured cochlear compression (e.g., Johannesen and Lopez-Poveda 2010) or loudness (Epstein et al. 2004) has been observed. These studies suggest that the CEOAE and DPOAE levels roughly reflect the amplitude of basilar membrane (BM) motion and that OAEs could be effective measures for differentiating the vibration characteristics of the BM from other factors, such as the function of inner hair cells or the auditory nerve.

The CEOAE level could also be used to evaluate the phase characteristics of BM motion: Hilger et al. (1995) suggested that the degree of mechanical irregularity along the BM partially determines the overall CEOAE level. This means that CEOAEs could allow us to access listeners’ irregularity profiles, which would not be revealed in audibility and frequency selectivity. The irregularity on the BM could influence the phase locking-based mechanism for detecting FM. Loeb et al. (1983), for example, proposed a hypothetical mechanism that encodes stimulus spectra by the distribution of cross-correlations between phase locking patterns that originate from two distinct points on the BM. This mechanism may underlie TFS-based FM detection. It is possible that a degree of irregularity on the BM could disrupt the frequency representation based on this mechanism, leading to the degradation of FM detection.

In the present study, we examined the extent to which the interindividual variation of FMDLs can be explained by the cochlear factors revealed in DPOAEs and CEOAEs. First, CEOAE and DPOAE spectra were compared between listeners with higher and lower FMDLs. Then, we used a principal component analysis (PCA) and multiple regression analysis to identify frequency characteristics of OAEs that are correlated to FMDLs and to examine the proportion of FMDL variance accounted for by the vibration characteristics of the BM, such as amplitude and irregularity.

METHODS

Participants

Twenty-nine volunteers (10 males and 19 females) aged 18–37 years (mean = 28, standard deviation = 5) participated in the study. All ears had normal pure tone audiometric thresholds (HL < 20 dB) from 0.25 to 8 kHz. FMDLs and OAEs were measured in the right ears. Twenty-seven participants showed a normal tympanogram; the peak-compensated static compliance was 0.3–2.0 ml and peak pressure was between -100 and +50 daPa. The static compliance of two participants was greater than 4.0 ml, and these two participants were not included in further analysis. The experiments were approved by the Ethics Committee of NTT Communication Science Laboratories.

Equipment

Stimuli were digitally synthesized with sampling rates of 96 kHz for the OAE measurements and 44.1 kHz for FMDL measurements and converted to analog signals using an Edirol UA-101 (24 bits). For the FMDL measurements, these converted signals were presented through Sennheiser HDA 200 headphones. For the OAE measurements, the analog signals were amplified by a headphone buffer and presented through Etymotic Research ER-2A earphones connected to an ER-10B low-noise microphone system. The two outputs from the ER-2A were calibrated using a DB2012 accessory (external ear simulator) of a Bruel and Kjaer Type 4257 ear simulator (IEC 711). Ear canal sound pressure was recorded using an Etymotic Research ER-10B low-noise microphone system inserted in each ear. All measurements were conducted in a double-wall sound-attenuating room.

Measurement of FMDLs

FMDLs were measured monaurally for carrier frequencies of 1, 1.5, and 2 kHz. For three participants, only the 1-kHz FMDL was measured. FM tones were generated using the following equation:

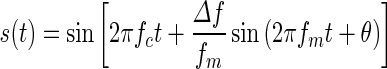graphic file with name M1.gif 1

where fc is the carrier frequency, Δf is the frequency excursion, and fm is the modulation rate. The phase θ was randomly changed for each presentation. fm was set at 2 Hz so that the TFS would be the dominant cue in the FM detection task (Moore and Sek 1996). The stimulus duration was 750 ms, including 20-ms raised-cosine ramps. The stimulus was presented at 55 dB sound pressure level (SPL). A two-interval two-alternative forced-choice (2I-2AFC) procedure and a two-down one-up transformed adaptive method were used to track 70.7 % (Levitt 1971) correct FM detection. The inter-stimulus interval was 500 ms. A measurement was terminated after 12 reversals, and the FMDL (in hertz) of the measurement was defined as the geometric mean of all Δf values of the reversal points following the fourth reversal. The step size was 20.5 for first four reversals and 20.25 for later reversals. The FMDL was estimated as the geometric mean over three measurements. Conditions were presented in random order. If the standard deviation (SD) of the logarithm (base 10) of the FMDLs for a given condition was greater than 0.2, two additional measurements were performed. The mean FMDL for each participant was estimated from all the measurements, except for measurements with extremely high FMDLs (>twice the mean FMDL of all the measurements for each participant), since these were probably due to a temporary loss of attention.

Measurement of DPOAEs

DPOAEs, the frequencies of which were 2f1–f2, were measured. The frequencies of the first and second primary tones (f1 and f2, respectively) had a constant ratio (f2/f1 = 1.2). The levels of the primary tones (L1 and L2) were chosen in accordance with the formula L1 = 0.4 L2 + 39 dB SPL, so as to maximize each of the 2f1–f2 DPOAEs (Kummer et al. 2000); L1 and L2 were set to 61 and 55 dB SPL, respectively. The duration of each stimulus was 300 ms, including 10-ms raised-cosine ramps. Each stimulus was presented ten times. The frequency response of each recorded waveform was computed by fast Fourier transformation (FFT) with an 8092 sample duration Hamming window. The level of the 2f1–f2 DPOAEs was defined as the value of the complex Fourier coefficient at the corresponding frequency. The noise level of each interval around 2f1–f2 was estimated by averaging the Fourier coefficients over the three nearest frequencies below and above 2f1–f2. Ten DPOAEs and noise waveforms were averaged, excluding responses with abnormal magnitudes (>0.01 Pa). DPOAEs were measured with f2 swept in the range from 0.5 to 2.5 kHz with a resolution of 90 Hz. The DPOAE and noise floor spectra were defined as the absolute values of the averaged 2f1–f2 DPOAE and noise as a function of f2. The confidence intervals of the DPOAE and the noise floor spectra for each participant were estimated by using a bootstrapping procedure: Ten waveforms were resampled from the ten recorded waveforms with replacement, and the average spectrum of the resampled waveforms was computed by the procedure described above. This procedure was repeated 1,000 times. By allowing replacement, some waveforms were selected multiple times and other waveforms were never selected. As a result, the smoothed spectrum calculated from each bootstrapped sample differed for each sample. Confidence intervals were defined as the 5th and 95th percentiles of the spectrum magnitudes at each frequency, based on the 1,000 bootstrapped samples. In DPOAE measurements, participants were seated comfortably and asked to remain as still as possible.

Measurement of CEOAEs

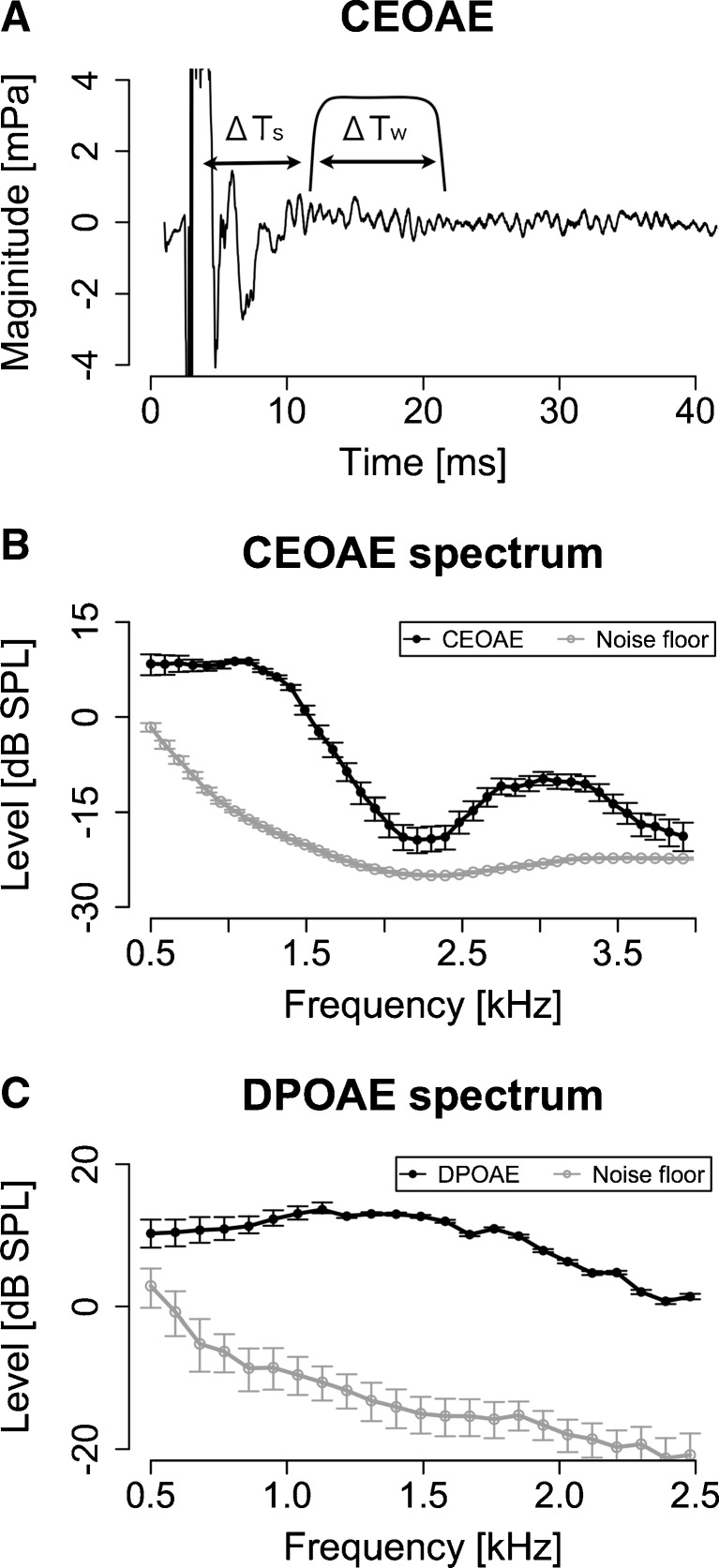
The stimulus sequence was presented in accordance with the double-evoked procedure (Keefe 1998), where most of the distortion artifacts of the loudspeakers can be removed and the nonlinear component of CEOAEs can be effectively extracted; three stimuli, S1, S2, and S12 (S12 means that S1 and S2 were presented at the same time), were each presented twice, resulting in a sequence comprising six clicks (S1, S1, S2, S2, S12, and S12). The peak equivalent sound pressure levels of S1 and S2 were 60 and 70 dB SPL, respectively. To eliminate contamination from nonlinear distortion of the system, S1 and S2 were presented from two different channels of the ER-2 earphone connected to the ER-10B low-noise microphone system. All clicks had a 100-μs duration and were presented at a rate of ten clicks per second. This stimulus sequence was presented 250 times. Although the stimuli were designed to allow extraction of the nonlinear component of the CEOAEs by using the double-evoked procedure (i.e., S1 + S2–S12; Keefe 1998), we decided, in the analyses, to focus on the linear component of the CEOAEs derived only from the responses to S2 by the linear windowing method (Kemp 1978; Kalluri and Shera 2007); a time window was set to eliminate short-latency ringing. This is because the linear component had a sufficiently large signal-to-noise ratio, while we could not derive sufficiently reliable nonlinear components.

CEOAE waveforms were computed by averaging adjacent response waveforms to S2. The corresponding noise waveforms were estimated as the difference between two adjacent response waveforms, and these noise waveforms were used only for the selection procedure, to reduce the effect of abrupt external noise. Two hundred low-noise CEOAEs and corresponding noise waveforms were selected from the 250 waveforms on the basis of the root mean-squared value of each noise waveform. The frequency responses of the 200 waveforms were computed by FFT with a time window with a 10.2-ms (1,028 samples) duration (ΔTw), including 2.5-ms raised-cosine ramps, starting at 7 ms (ΔTs) after the peak of each waveform (Fig. 2A). These windowed waveforms were padded with zeros to 9,600 samples so that the resolution of the FFT was 10 Hz (defined as Pm[k]: m = 1−200 and k = 1–4,799 (<Nyquist rate bin)). The CEOAE spectrum was defined as the absolute value of the averaged frequency responses. Noise energy of the kth frequency bin (|PN[k]|2) was defined by the following equation (Schairer et al. 2003):

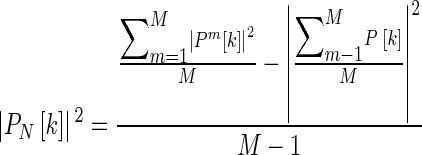graphic file with name M2.gif

where M is the repeated number, in this case 200. The CEOAE and noise floor spectra were smoothed by moving average with a 500-Hz-wide rectangular window. The CEOAE spectrum was resampled to have a 90-Hz resolution, and the frequency range was restricted to 0.5–4 kHz. Confidence intervals of the CEOAE and noise floor spectra for each participant were estimated by the bootstrapping procedure; 250 responses and corresponding noise waveforms were resampled from the recorded 250 waveforms with replacement. A smoothed spectrum was computed from these resampled waveforms by the procedure described above. This procedure was repeated 1,000 times. Confidence intervals were defined as the 5th and 95th percentiles of spectrum magnitudes at each frequency, based on the 1,000 bootstrapped samples. In CEOAE measurements, participants were seated comfortably and asked to remain as still as possible.

FIG. 2.

FIG. 2

Open in a new tab

The CEOAE and DPOAE spectra were measured with a sufficient signal-to-noise ratio. A A typical CEOAE waveform superimposed on the window used for the FFT. ΔT s was 7 ms and ΔT w was 10.7 ms (1,024 samples). B A typical CEOAE spectrum, which was derived from the window. C A typical DPOAE spectrum. Error bars show 95 % confidence intervals estimated by bootstrapping.

Measurement of ear canal reflectance

For 24 of the 29 participants, we evaluated middle ear function through ear canal reflectance. This was done to examine the extent to which the results could be accounted for by middle ear characteristics. Ear canal reflectance is the complex ratio between an incident wave and backward wave, which is reflected by impedance mismatch between the ear canal and eardrum. A smaller ear canal reflectance value means that more energy is transmitted to the middle ear, while a larger one means that more energy is reflected at the eardrum. The structure of the ear canal reflectance frequency response has been used for middle ear diagnoses (e.g., Feeney et al. 2003).

Ear canal reflectance was measured with the ear canal sealed with an ear tip attached to the ER-10B low-noise microphone system. The click for the measurements was calculated as a sinc function (sin(x)/x), using the following equation (Yates and Withnell 1999):

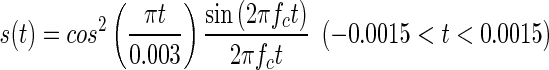graphic file with name M3.gif

where fc is the low-pass cutoff frequency, which was set at 10 kHz. The stimulus had a 3-ms duration and was presented at a rate of ten times per second. The peak equivalent sound pressure level of the click was 80 dB SPL. The clicks were presented 500 times. Measured waveforms were averaged across the recordings, excluding responses with abnormal magnitudes (>0.01 Pa) to remove artifacts such as coughs and respiration. The frequency response of the recorded sound was computed by an FFT based on a waveform sequence ranging from 0 to 84.3 ms (8,096 samples) after click onset. The frequency range was restricted to 0.25–4 kHz. Ear canal reflectance was computed using Thevenin’s equation (Keefe et al. 1992). If the low-frequency reflectance (below 500 Hz) was below 0.8, the probe tip was removed from the ear canal and reinserted to avoid a leaky probe fitting, which is generally accompanied by low reflectance values at low frequencies. The method described in Keefe et al. (1992) was used to calibrate the system. Calibration was conducted using a set of four brass tubes with an inner diameter of 8 mm and lengths ranging from 10 to 72 mm. The structure of the ear canal reflectance was analyzed by the same procedure as that used for DPOAE and CEOAE spectra (described below).

Statistical analysis

To explore features that characterize DPOAE and CEOAE spectra, we applied a PCA. The PCA was performed on vectors of OAE spectra, each vector representing one participant. The analyses were conducted separately for CEOAE and DPOAE spectra. Cross-correlations were used for computing relation matrices. We adopted the lowest number of principal components (PCs) that were required to account for 90 % of the variance.

A multiple regression analysis was applied to the extracted PCs (explaining variables) and FMDLs (explained variables) for each carrier frequency; three regression equations, for 1-, 1.5-, and 2-kHz FMDLs, were derived. In order to identify components that effectively accounted for FMDL variations, variable selections were made on the basis of leave-one-out cross-validation (LOOCV) (e.g., Lachenbruch and Mickey 1968), which estimates the model’s prediction accuracy for one unseen observation: A single observation was left out as a test observation, and the regression equation was derived from the remaining observations. Then, the squared prediction error for the test observation was computed. This procedure was iterated such that each observation was used once as a test datum, and the mean square error (MSE) of the predictions was calculated. The MSEs were calculated for all models generated by all possible combinations of explaining variables, and the combination showing the lowest MSE was selected. All statistical analyses were performed on the log10-scale FMLDs.

RESULTS

General characteristics of the measures

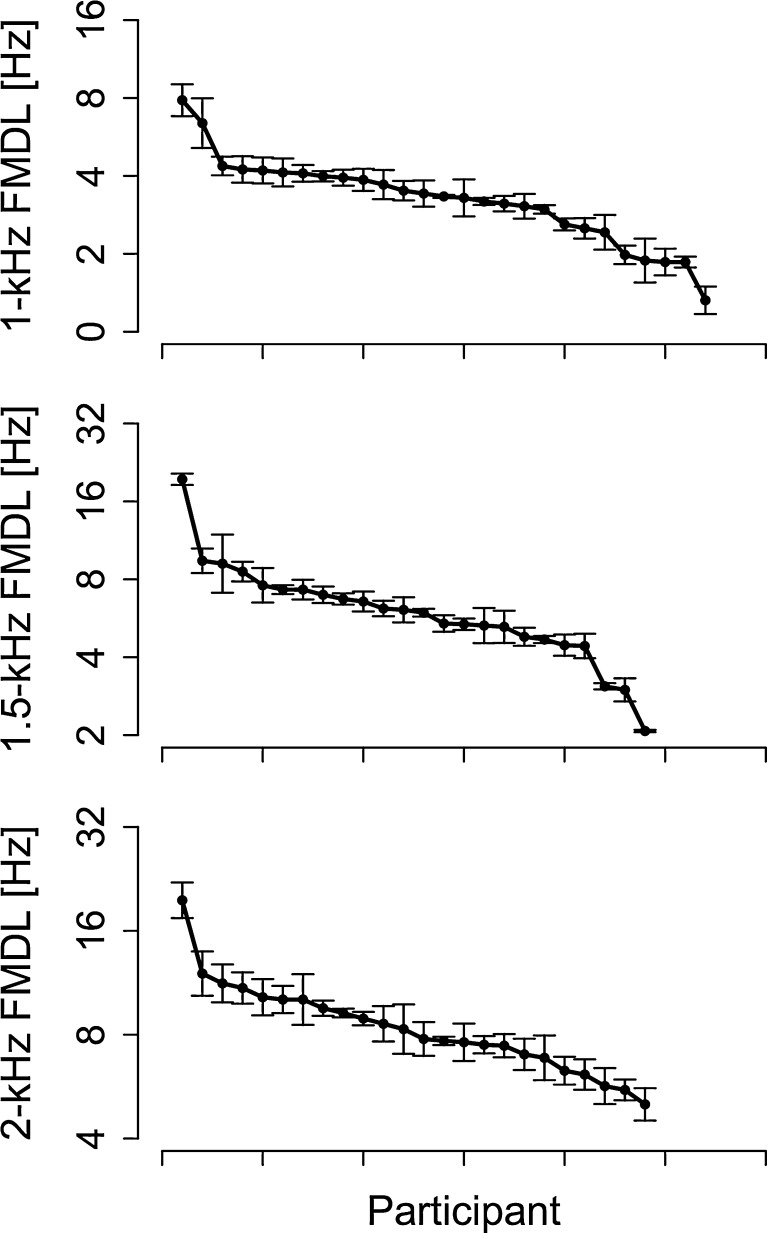
Individual FMDLs for 1-, 1.5-, and 2-kHz carrier frequencies are shown in Figure 1. FMDLs generally increased with increasing carrier frequency; mean FMDLs were 3.2 Hz (SD = 0.2) for the 1-kHz FMDL, 5.9 Hz (SD = 0.2) for the 1.5-kHz FMDL, and 8.3 Hz (SD = 0.1) for the 2-kHz FMDL (SDs were computed on a base-10 logarithmic scale). Significant correlations were found between the 1- and 1.5-kHz FMDL (Kendall’s τ22  = 0.48, p = 0.0012), between the 1- and 2-kHz FMDL (Kendall’s τ22  = 0.50, p < 0.001), and between the 1.5- and 2-kHz FMDL (Kendall’s τ22  = 0.60, p < 0.001). The ordering of the participants ranked by FMDL was roughly consistent across carrier frequencies.

FIG. 1.

FIG. 1

Open in a new tab

The intraindividual variation of FMDLs is relatively smaller than the interindividual variation. The individual FMDLs at 1, 1.5, and 2 kHz. FMDLs of each participant were sorted and arranged along the x-axis. The FMDLs were arranged for each carrier frequency, and the ordering of the participants is different for each carrier frequency. Error bars represent standard errors.

Typical OAE spectra are shown in Figure 2B. In the DPOAE spectrum, the noise floor was low relative to the DPOAE level (<−10 dB) except around 0.5 kHz (Fig. 2C). The CEOAE spectrum was significantly higher than the noise floor except around 4 kHz (Fig. 2B). The magnitudes of the CEOAE and DPOAE spectra tended to decrease with increasing frequency above 1 kHz. Similar tendencies were observed for other participants (Fig. 3).

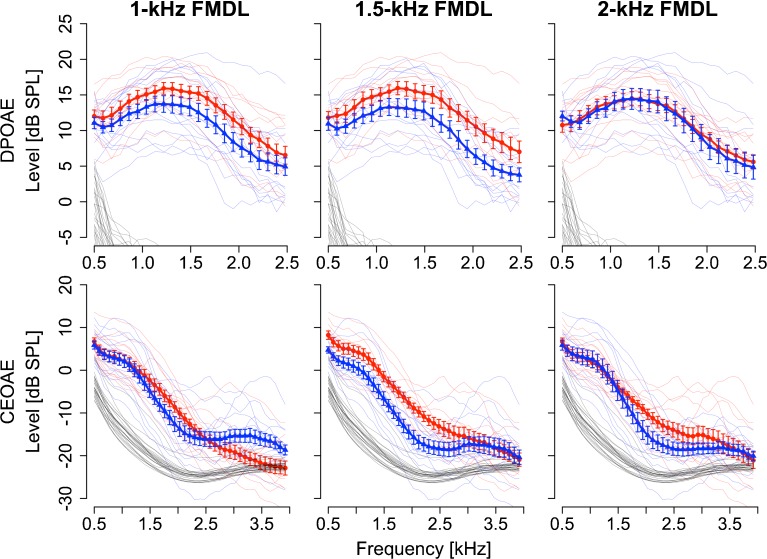
FIG. 3.

FIG. 3

Open in a new tab

Structural differences observed between the CEOAE spectra of the higher and lower FMDL groups. DPOAE spectra (first row) and CEOAE spectra (second row) for the higher FMDL group (blue triangles) and for the lower FMDL group (red circles). Comparisons of 1-, 1.5-, and 2-kHz FMDLs are shown from left to right. Error bars show the standard errors across listeners in each group. Individual data are plotted as thin lines. Noise floors are shown as black thin lines (noise floors not shown in DPOAE spectra ranging from −30 to −20 dB SPL).

Comparison between higher and lower FMDL groups

Participants were divided into two groups: those who had higher FMDLs than the average FMDL and those who had lower FMDLs than the average FMDL. The two groups were defined separately for each frequency (1, 1.5, and 2 kHz). The higher and lower FMDL groups comprised 15 and 12 participants for the 1-kHz FMDL, 13 and 11 participants for the 1.5-kHz FMDL, and 11 and 13 participants for the 2-kHzFMDL. DPOAE and CEOAE spectra for the two groups are shown in Figure 3. The two groups appeared to differ in that a clearer characteristic dip was observed at 2–3 kHz in the CEOAE spectra for the lower FMDL group and that the overall DPOAE level of the lower FMDL group was higher for the 1- and 1.5-kHz FMDLs.

For each carrier frequency in the FM detection task, a two-way split-plot analysis of variance was conducted for the CEOAE and DPOAE spectra, with participant group (the higher and lower FMDL groups) and frequency at which the CEOAEs or DPOAEs were measured as factors. For the CEOAE and for the 1.5-kHz carrier, there was a significant main effect of participant group (F1, 22 = 4.43, p = 0.047). No significant main effect was found in other analyses. Significant interactions of participant group and frequency were found in the following three cases: CEOAE for the 1-kHz carrier (F38, 950 = 5.8, p < 0.001), for the 1.5-kHz carrier (F38, 836 = 2.63, p < 0.001), and for the 2-kHz carrier (F38, 836 = 1.70, p = 0.0058). In order to specify frequency ranges that showed a significant effect of listener group, CEOAE spectra were divided into seven frequency regions in 500-Hz steps (centered at 770, 1,220, 1,760, 2,300, 2,750, 3,290, and 3,740 Hz) and the levels within the 500-Hz-wide band for each center frequency were averaged. These seven averaged levels were compared between the lower and higher FMDL groups for the 1-, 1.5-, and 2-kHz carriers. The significance level was corrected by the Bonferroni adjustment, in which the critical p value (=0.05) was divided by 21 (7 frequency regions × 3 carrier frequencies). Although no significant differences were found, marginally significant differences were found in the frequency region centered at 1,760 Hz (T22 = 3.1862, p = 0.0047 < 0.1/21) for the 1.5-kHz carrier.

Features of OAE spectra

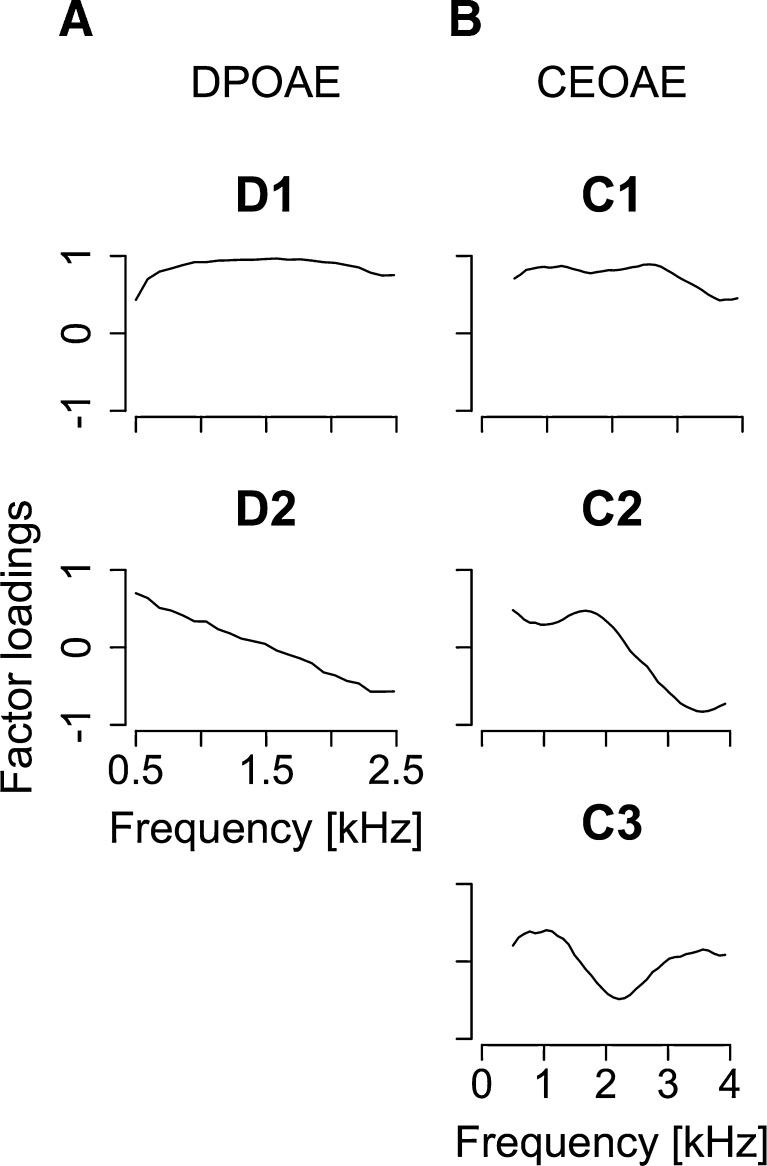
PCs extracted from DPOAE and CEOAE spectra are shown in Figure 4. The first and second PCs were selected for the DPOAE spectra (contributions of 76.2 % (D1) and 15.6 % (D2); cumulative contribution of 91.8 %). The first to third PCs were selected for the CEOAE spectra (contributions of 57.8 % (C1), 25.1 % (C2), and 7.54 % (C3); cumulative contribution of 90.4 %). High cumulative contributions (>90 %) ensured that these PCs could describe the main features of the OAE spectra. Generally, the first and second PCs captured the overall level of the responses and any tendency of the response to monotonically decrease with frequency, respectively. The third PC (C3) represented the dip around 2 kHz. Correlations among extracted PCs were relatively low (Pearson’s r < 0.5; summarized in Table 1), although significant correlations were found between D1 and C1 (Pearson’s r25 = 0.67, p < 0.001) and between D1 and C2 (Pearson’s r25 = 0.45, p = 0.018).

FIG. 4.

FIG. 4

Open in a new tab

A Factor loadings of first and second principal components (D1 and D2) extracted from DPOAE spectra. B Factor loadings of first to third principal components (C1, C2, and C3) extracted from CEOAE spectra. The cumulative contribution of R1–R4 was above 90 %.

TABLE 1.

Summary of correlation coefficients between extracted principal components. Boldface font indicates a significant correlation. OT means that two factors were orthogonal; these factors were derived from the same original variables in the PCA. Other orthogonal relations are not shown

C1 C2 C3
D1 0.67 ( p  < 0.001) 0.45 ( p  = 0.018) 0.12 (p = 0.55)
D2 −0.19 (p = 0.35) −0.11 (p = 0.57) 0.20 (p = 0.31)
C1 – OT OT
C2 OT – OT
Open in a new tab

Features that account for FMDL variation

Multiple regression analysis was employed to identify specific features of the OAE spectra that accounted for FMDL variation and to evaluate the proportion of the FMDL variance accounted for by those features. Based on the outcome of the LOOCV (see “Methods”), D1, C1, and C3 were selected for the 1-kHz FMDL (MSE was 0.023 on a log10 scale), D1 and C3 were selected for the 1.5-kHz FMDL (MSE was 0.028), and C3 was selected for the 2-kHz FMDL (MSE was 0.011). The regression equations derived from all the data are as follows:

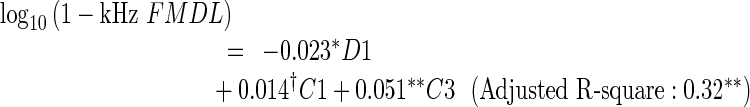graphic file with name M4.gif 2
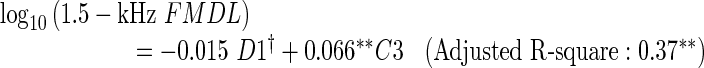graphic file with name M5.gif 3
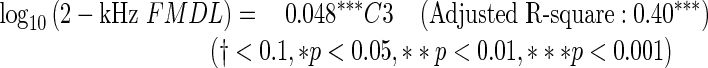graphic file with name M6.gif 4

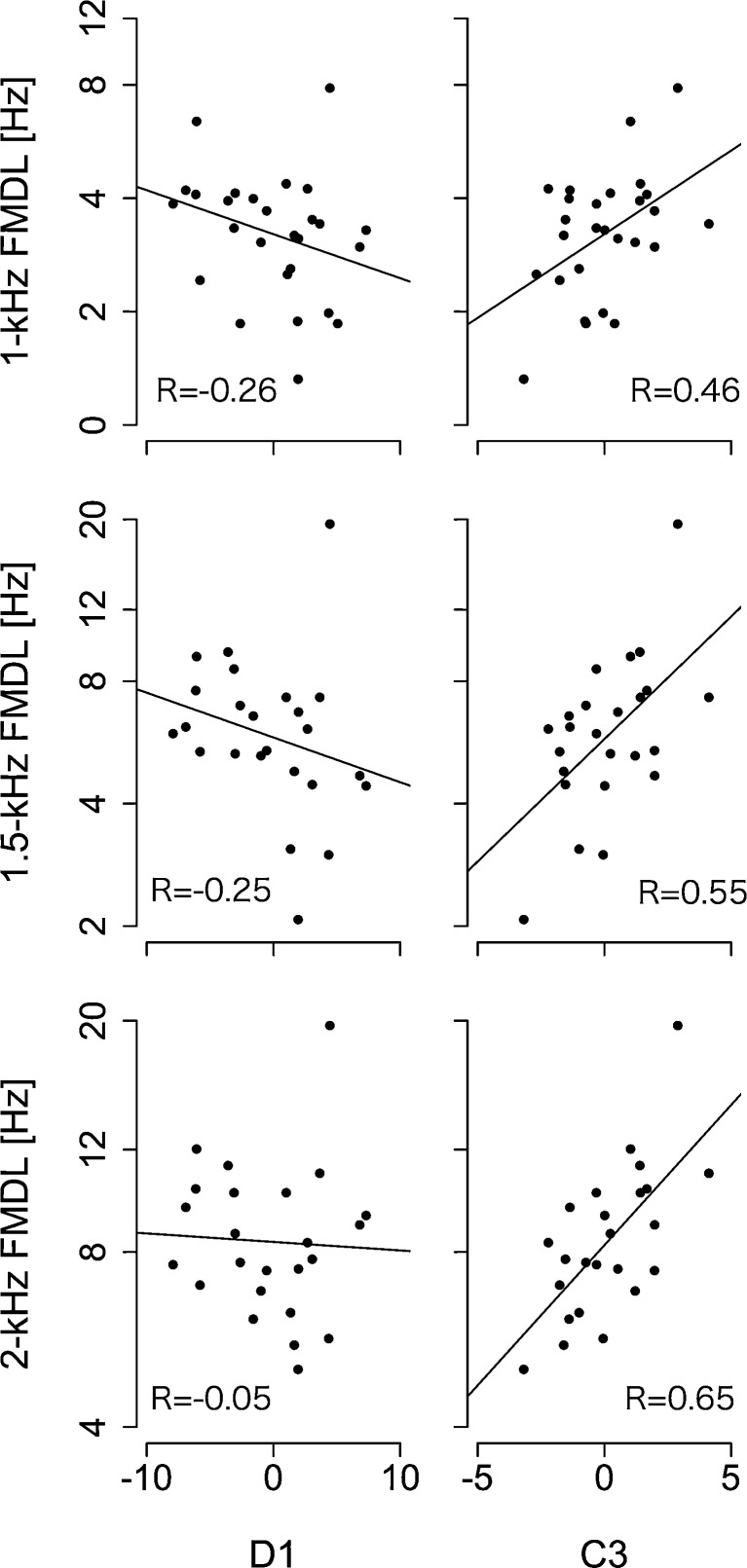
The results indicate that D1 (only for the 1-kHz FMDL) and C3 can account for the FMDL variation moderately well. The negative coefficient of D1 indicates that participants with relatively high DPOAE levels tended to show low FMDLs (i.e., high FM sensitivity). The positive coefficient of C3 indicates that participants with relatively large dips around 2 kHz in the CEOAE spectrum tended to show high FMDLs (i.e., poor FM sensitivity). These two factors could account for 32–40 % of the FMDL variation.

To ensure that the analyses were not influenced predominantly by the results for a few participants, Cook’s distance (Cook 1977) was computed for each participant. A large value of Cook’s distance indicates that the participant had a strong influence on the regression. Only participant 20 exhibited values above 0.5 in the regression for the 1.5- or 2-kHz FMDL. Regarding participant 20 as an outlier, we performed the same multiple regression analysis with LOOCV-based variable selection, discarding 20’s data. The resulting regression equations are as follows:

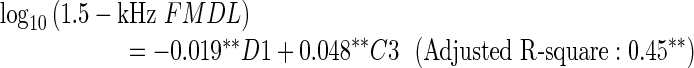graphic file with name M7.gif 5
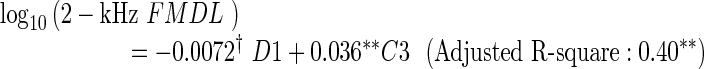graphic file with name M8.gif 6

(† < 0.1,* p < 0.05,** p < 0.01,*** p < 0.001).

The tendencies were unaltered by exclusion of participant 20, although the regression coefficients were slightly changed. While similar trends were observed for C3, the coefficient of D1 was significant in the regression for the 1.5-kHz FMDL and selected in the regression for the 2-kHz FMDL, additionally. Participant 20’s data appears to reduce the correlation of D1 with the 1.5- and 2-kHz FMDLs.

We conducted a simple linear regression analysis between the FMDLs and D1 or C3 including participant 20, and the results are summarized in Figure 5. A significant correlation was found between C3 and the 1-kHz FMDL (Pearson’s r25 = 0.46, p = 0.015), between C3 and the 1.5-kHz FMDL (Pearson’s r22 = 0.55, p = 0.005), and between C3 and the 2-kHz FMDL (Pearson’s r22 = 0.65, p < 0.001). No significant correlation was found between D1 and the 1-kHz FMDL (Pearson’s r25 = −0.26, p = 0.20), between D1 and the 1.5-kHz FMDL (Pearson’s r22 = −0.25, p = 0.23), and between D1 and the 2-kHz FMDL (Pearson’s r22 = −0.05, p = 0.82).

FIG. 5.

FIG. 5

Open in a new tab

C3 was significantly correlated with FMDLs. Correlations between D1 and FMDLs at each frequency (first column) and those between C3 and FMDLs at each frequency (second column). Regression lines were derived from linear least squares regression.

Relation with audiometry

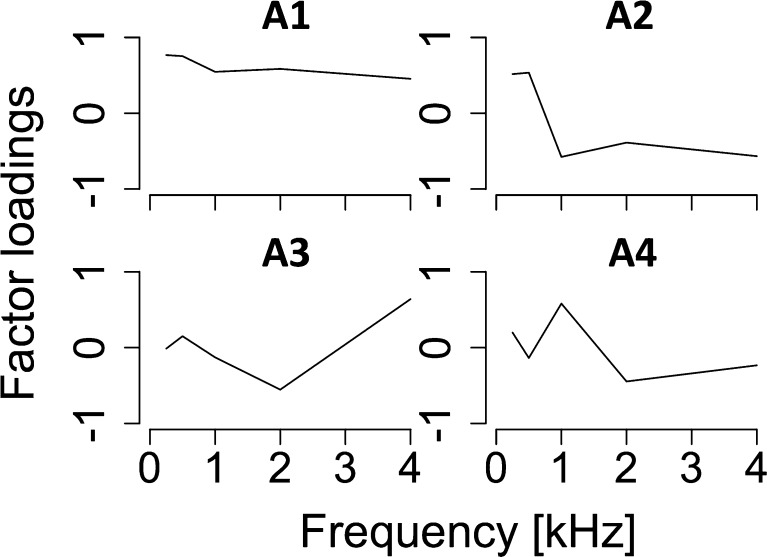
To analyze the relationship between audiometry and OAEs or FMDLs, a PCA was applied to the audiograms. The PCA was performed on vectors of audiometric thresholds at 0.25, 0.5, 1, 2, and 4 kHz, obtained from individual participants. The extracted PCs are shown in Figure 6: The first to fourth PCs were extracted (contributions of 40.0 % (A1), 27.1 % (A2), 15.1 % (A3), and 13.0 % (A4); cumulative contribution of 95.3 %). We did not find a statistically significant correlation between any pairs of audiometry-related components (A1–A4) and the FMDLs (|Pearson’s r22| < 0.37, p > 0.079). Although a significant correlation was found between C3 and A4 (Pearson’s r25 = 0.39, p = 0.042), no significant correlation was found between the other pairs of audiometry-related components and OAE-related components (|Pearson’s r25| < 0.34, p > 0.084).

FIG. 6.

FIG. 6

Open in a new tab

Factor loadings of first to fourth principal components (A1, A2, A3, and A4) extracted from the audiograms. The cumulative contribution of A1–A4 was above 90 %.

Ear canal reflectance cannot account for the structure of OAE Spectra

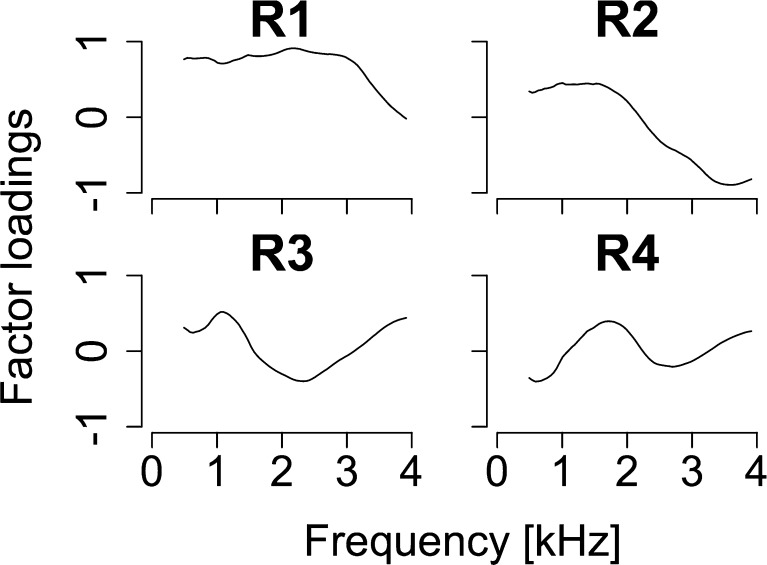
One might argue that the observed association between FMDLs and OAEs could be explained in terms of middle ear factors rather than cochlear ones. This argument is reasonable considering that both acoustic signals and OAEs are transmitted through the middle ear. To assess the role of the middle ear, we measured the ear canal reflectance as a measure representing middle ear function and compared it with the OAEs. We applied a PCA on the ear canal reflectance function. Extracted PCs from ear canal reflectance are summarized in Figure 7. The first to fourth PCs were selected for ear canal reflectance (contributions of 51.4 % (R1), 32.6 % (R2), 8.1 % (R3), and 5.32 % (R4); cumulative contribution of 94.3 %).

FIG. 7.

FIG. 7

Open in a new tab

Factor loadings of first to fourth principal components (R1, R2, R3 and R4) extracted from ear canal reflectance. The cumulative contribution of R1-R4 was above 90 %.

We did not find a statistically significant correlation between any pairs of middle ear-related components (R1–R4) and OAE-related components (C1–C3, D1–D2) (|Pearson’s r25| < 0.36, p > 0.064). These findings fail to support the argument that the observed association between FMDLs and OAEs could be explained by middle ear factors.

DISCUSSION

Comparison with previous studies

The FMDL in hertz tended to increase with increasing carrier frequency (Fig. 1). This tendency is consistent with previous studies (e.g., Strelcyk and Dau 2009; Moore and Sek 1996). DPOAEs were lowest at lower frequencies and reached a maximum around 1 kHz and gradually decreased with increasing frequency above 1 kHz (Fig. 2C). This tendency was also observed in previous studies (Sisto and Moleti 2005; Siegel and Hirohata 1994). The CEOAE level decreased from 1 to 4 kHz, as also observed in previous studies (Sisto et al. 2007; Keefe et al. 2011). However, the tendency for the CEOAE level to increase from 0.5 to 1 kHz, reported in previous studies, was not observed in the present study. This is probably due to the large noise floor around 0.5 kHz (black thin lines in Fig. 3, first row).

We found a significant positive correlation of two components, C1 and D1, which represent overall strengths of CEOAEs and DPOAEs, respectively. A correlation of CEOAE and DPOAE levels has been reported previously (e.g., Probst and Harris 1993). We found also a significant correlation between the tendency of the CEOAE spectra to decrease (C2) and D1. We are unaware of an earlier report of this correlation.

To our knowledge, the present study is the first to report a relationship between OAEs and FM detection performance. Our analyses incorporating PCA and multiple regression indicate that more than 30 % of FMDL variance can be accounted for by OAE features, specifically D1 (only for the 1-kHz carrier) and C3. This result suggests that the properties of cochlear mechanics affect FM processing.

Interpretation of the regression coefficients

The multiple regression analysis showed a negative correlation between D1 and FMDLs. As described earlier, this indicates an association between higher overall DPOAE levels and lower FMDLs (i.e., higher FM sensitivity). One interpretation of this result is that higher cochlear gain produced by OHCs results in better FM processing. This interpretation is consistent with earlier findings that hearing-impaired listeners, who tend to show decreased DPOAE levels (e.g., Dorn et al. 1999), exhibit deficits in FM detection tasks (Lacher-Fougere and Demany 1998; Moore and Skrodzka 2002; Strelcyk and Dau 2009). This interpretation, however, might appear to be inconsistent with the present study and the study of hearing-impaired listeners published by Strelcyk and Dau (2009), which showed no significant correlation between FMDLs and hearing level. Several studies reported a correlation between hearing level and DPOAE level (e.g., Dorn et al. 1999). This apparent inconsistency may be explained by a relatively weak contribution of OHC gain to FM detection. It should be recalled that the simple regression analysis between low-rate FMDLs and D1 showed no significant correlation (Fig. 5). It is possible that the BM nonlinearity responsible for the lateral suppression, not for amplification, is the major factor influencing FMDLs: Reduced lateral suppression would make the excitation pattern cue less effective, leading to poorer FM detection.

C3, which represents the characteristic dip at around 2 kHz, had a positive correlation with FMDLs. This indicates that participants who had a CEOAE spectrum with a deeper dip tended to show higher FMDLs, although this tendency was not clearly seen in Figure 3. Previous studies also observed such a characteristic dip in DPOAE spectra (Sisto and Moleti 2005; Kummer et al. 2000) and in CEOAE spectra (Sisto and Moleti 2005).

One can interpret the observed correlation between C3 and FMDL as indicating that the pattern of irregularity on the BM, which is assumed to generate CEOAEs, influences FM detection. Forward cochlear traveling waves are reflected by randomly distributed impedance perturbations due to irregularity such as spatial variations in OHC number or geometry (Wright 1984; Lonsbury-Martin et al. 1988) and one measured as CEOAEs in the ear canal. On the basis of experimental data, Hilger et al. (1995) suggested that the overall CEOAE level is partially determined by the amount of irregularity. Theoretically, the effect of the spatial profile of irregularity on the CEOAE level was suggested by coherent reflection theory (Zweig and Shera 1995), which is a prevailing theory for explaining the generation of OAEs. According to this theory, the energy of the reflected wave is enhanced when that the spatial frequency (fs) of the irregularity is equal to 2/λpeak, where λpeak is the wavelength of the traveling wave at its peak. In this condition, the reflected waves from the peak are combined in phase (i.e., coherently) and dominate CEOAEs because the magnitude at the peak is much higher than in the other regions. Given this argument, C3 might be accounted for by fluctuations in the amount of irregularity over spatial frequency: The amount of irregularity might be smallest around fs = 2/λpeak (2 kHz), where λpeak(2 kHz) is the wavelength of the traveling wave which is produced by a 2-kHz tone, and increases at lower and higher fs. As a result, the traveling wave which is produced by a 2-kHz tone would be reflected less effectively and the CEOAE spectrum would show a characteristic dip around 2 kHz, which is observed as C3. Since the wavelength changes along the traveling wave (i.e., longer in the tail region and shorter in the tip region), the strength of reflection varies along with the excitation pattern: The smaller reflections occur in the areas where wavelength is near λpeak(2 kHz) and the larger reflections occur in the areas where wavelength is lower and higher than λpeak(2 kHz). The inhomogeneous reflected waves might disturb the ability to use the phase locking cue. Loeb et al. 1983 proposed a temporal cue-based model where frequency discrimination is mediated by cross-correlations between the outputs from two distinct regions on the BM, and the relative phase of adjacent locations on the BM plays a key role. It is possible that inhomogeneous reflected waves as described above influence the relative phase on the BM, leading to a degradation of FM coding based on the phase locking cue. The excitation pattern could also be influenced, being made ragged by these inhomogeneous reflected waves, and the shift of the excitation pattern due to the superposition of FM might be less evident. As a result, FM detection based on the excitation pattern cue might also be degraded.

One might argue that the uneveness of cochlear gain could create C3 and influence FM processing. However, audiometry-related PCs (A1–A4) were not significantly correlated with FMDLs, although A4 was significantly correlated with C3. Thus, it is unlikely that uneven gain is responsible for C3 and FMDLs.

SUMMARY AND CONCLUSIONS

A PCA and multiple regression analysis showed that the overall DPOAE level and the depth of the characteristic dip in CEOAE spectra are significantly correlated with low-rate FMDLs. These factors can account for more than 30 % of inter-listener FMDL variance. These results imply that cochlear nonlinearity and irregularity on the BM have some influence on sensitivity to low-rate FM: Broader tuning due to the loss of cochlear nonlinearity could disrupt the excitation pattern cue, and the larger irregularity on the basilar membrane could make the phase locking cue less reliable. Overall, the present study demonstrated that nonneuronal peripheral factors, such as cochlear nonlinearity and irregularity, should be taken into account when a listener’s FM detection performance is interpreted.

ACKNOWLEDGMENTS

The authors thank Christopher Plack, the associate editor, Brian C. J. Moore, a reviewer, and one anonymous reviewer for their helpful comments on an earlier version of the manuscript.

Conflict of Interest

We declare that we have no conflict of interest.

Contributor Information

Sho Otsuka, Phone: +81-3-58416354, FAX: +81-3-58416354, Email: d117628@h.k.u-tokyo.ac.jp.

Shigeto Furukawa, Email: furukawa.shigeto@lab.ntt.co.jp.

Shimpei Yamagishi, Email: yamagishi@u.ip.titech.ac.jp.

Koich Hirota, Email: k-hirota@h.k.u-tokyo.ac.jp.

Makio Kashino, Email: kashino.makio@lab.ntt.co.jp.

REFERENCES

  1. Cook RD. Detection of influential observation in linear regression. Technometrics. 1977;19:15–18. doi: 10.2307/1268249. [DOI] [Google Scholar]
  2. Dallos P. The active cochlea. J Neurosci. 1992;12:4575–4585. doi: 10.1523/JNEUROSCI.12-12-04575.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Dorn PA, Piskorski P, Gorga MP, et al. Predicting audiometric status from distortion product otoacoustic emissions using multivariate analyses. Ear Hear. 1999;20:149–163. doi: 10.1097/00003446-199904000-00006. [DOI] [PubMed] [Google Scholar]
  4. Dorn PA, Konrad-Martin D, Neely ST, et al. Distortion product otoacoustic emission input/output functions in normal-hearing and hearing-impaired human ears. J Acoust Soc Am. 2001;110:3119–3131. doi: 10.1121/1.1417524. [DOI] [PubMed] [Google Scholar]
  5. Epstein M, Buus S, Florentine M. The effects of window delay, delinearization, and frequency on tone-burst otoacoustic emission input/output measurements. J Acoust Soc Am. 2004;116:1160–1167. doi: 10.1121/1.1768254. [DOI] [PubMed] [Google Scholar]
  6. Ernst SMA, Moore BCJ. Mechanisms underlying the detection of frequency modulation. J Acoust Soc Am. 2010;128:3642–3648. doi: 10.1121/1.3506350. [DOI] [PubMed] [Google Scholar]
  7. Feeney MP, Grant IL, Marryott LP. Wideband energy reflectance measurements in adults with middle-ear disorders. J Speech Lang Hear Res. 2003;46:901–911. doi: 10.1044/1092-4388(2003/070). [DOI] [PubMed] [Google Scholar]
  8. Grose JH, Mamo SK. Frequency modulation detection as a measure of temporal processing: age-related monaural and binaural effects. Hear Res. 2012;294:49–54. doi: 10.1016/j.heares.2012.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hilger AW, Furness DN, Wilson JP. The possible relationship between transient evoked otoacoustic emissions and organ of Corti irregularities in the guinea pig. Hear Res. 1995;84:1–11. doi: 10.1016/0378-5955(95)00007-Q. [DOI] [PubMed] [Google Scholar]
  10. Johannesen PT, Lopez-Poveda EA. Correspondence between behavioral and individually “optimized” otoacoustic emission estimates of human cochlear input/output curves. J Acoust Soc Am. 2010;127:3602–3613. doi: 10.1121/1.3377087. [DOI] [PubMed] [Google Scholar]
  11. Kalluri R, Shera CA. Near equivalence of human click-evoked and stimulus-frequency otoacoustic emissions. J Acoust Soc Am. 2007;121:2097–2110. doi: 10.1121/1.2435981. [DOI] [PubMed] [Google Scholar]
  12. Keefe DH. Double-evoked otoacoustic emissions. I. Measurement theory and nonlinear coherence. J Acoust Soc Am. 1998;103:3489–3498. doi: 10.1121/1.423057. [DOI] [PubMed] [Google Scholar]
  13. Keefe DH, Ling R, Bulen JC. Method to measure acoustic impedance and reflection coefficient. J Acoust Soc Am. 1992;91:470–485. doi: 10.1121/1.402733. [DOI] [PubMed] [Google Scholar]
  14. Keefe DH, Goodman SS, Ellison JC, et al. Detecting high-frequency hearing loss with click-evoked otoacoustic emissions. J Acoust Soc Am. 2011;129:245–261. doi: 10.1121/1.3514527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kemp DT. Stimulated acoustic emissions from within the human auditory system. J Acoust Soc Am. 1978;64:1386–1391. doi: 10.1121/1.382104. [DOI] [PubMed] [Google Scholar]
  16. Kummer P, Janssen T, Hulin P, Arnold W. Optimal L1–L2 primary tone level separation remains independent of test frequency in humans. Hear Res. 2000;146:47–56. doi: 10.1016/S0378-5955(00)00097-6. [DOI] [PubMed] [Google Scholar]
  17. Lachenbruch PA, Mickey MR. Estimation of error rates in discriminant analysis. Technometrics. 1968;10:1–11. doi: 10.1080/00401706.1968.10490530. [DOI] [Google Scholar]
  18. Lacher-Fougère S, Demany L. Modulation detection by normal and hearing-impaired listeners. Int J Audiol. 1998;37:109–121. doi: 10.3109/00206099809072965. [DOI] [PubMed] [Google Scholar]
  19. Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49:467–477. doi: 10.1121/1.1912375. [DOI] [PubMed] [Google Scholar]
  20. Loeb GE, White MW, Merzenich MM. Spatial cross-correlation. Biol Cybern. 1983;47:149–163. doi: 10.1007/BF00337005. [DOI] [PubMed] [Google Scholar]
  21. Lonsbury-Martin BL, Martin GK, Probst R, Coats AC. Spontaneous otoacoustic emissions in a nonhuman primate. II. Cochlear anatomy. Hear Res. 1988;33:69–93. doi: 10.1016/0378-5955(88)90021-4. [DOI] [PubMed] [Google Scholar]
  22. Lucertini M, Bergamaschi A, Urbani L. Transient evoked otoacoustic emissions in occupational medicine as an auditory screening test for employment. Br J Audiol. 1996;30:79–88. doi: 10.3109/03005369609077935. [DOI] [PubMed] [Google Scholar]
  23. Moore BCJ, Sek A. Effects of carrier frequency and background noise on the detection of mixed modulation. J Acoust Soc Am. 1994;96:741–751. doi: 10.1121/1.410312. [DOI] [PubMed] [Google Scholar]
  24. Moore BCJ, Sek A. Effects of carrier frequency, modulation rate, and modulation waveform on the detection of modulation and the discrimination of modulation type (amplitude modulation versus frequency modulation) J Acoust Soc Am. 1995;97:2468–2478. doi: 10.1121/1.411967. [DOI] [PubMed] [Google Scholar]
  25. Moore BCJ, Sek A. Detection of frequency modulation at low modulation rates: evidence for a mechanism based on phase locking. J Acoust Soc Am. 1996;100:2320–2331. doi: 10.1121/1.417941. [DOI] [PubMed] [Google Scholar]
  26. Moore BCJ, Skrodzka E. Detection of frequency modulation by hearing-impaired listeners: effects of carrier frequency, modulation rate, and added amplitude modulation. J Acoust Soc Am. 2002;111:327–335. doi: 10.1121/1.1424871. [DOI] [PubMed] [Google Scholar]
  27. Probst R, Harris FP (1993) A comparison of transiently evoked and distortion-product otoacoustic emissions in humans. In: Allum JHJ, Allum-Mecklenburg DJ, Probst R, Harris FP (eds) Prog. Brain Res. Elsevier Science Publishers B.V., Amsterdam, 91–99 [DOI] [PubMed]
  28. Probst R, Lonsbury-Martin BL, Martin GK, Coats AC. Otoacoustic emissions in ears with hearing loss. Am J Otolaryngol. 1987;8:73–81. doi: 10.1016/S0196-0709(87)80027-3. [DOI] [PubMed] [Google Scholar]
  29. Probst R, Lonsbury-Martin BL, Martin GK. A review of otoacoustic emissions. J Acoust Soc Am. 1991;89:2027–2067. doi: 10.1121/1.400897. [DOI] [PubMed] [Google Scholar]
  30. Ruggles D, Bharadwaj H, Shinn-Cunningham BG. Normal hearing is not enough to guarantee robust encoding of suprathreshold features important in everyday communication. Proc Natl Acad Sci. 2011;108:15516–15521. doi: 10.1073/pnas.1108912108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schairer KS, Fitzpatrick D, Keefe DH. Input-output functions for stimulus-frequency otoacoustic emissions in normal-hearing adult ears. J Acoust Soc Am. 2003;114:944–966. doi: 10.1121/1.1592799. [DOI] [PubMed] [Google Scholar]
  32. Sek A, Moore BCJ. Frequency discrimination as a function of frequency, measured in several ways. J Acoust Soc Am. 1995;97:2479–2486. doi: 10.1121/1.411968. [DOI] [PubMed] [Google Scholar]
  33. Siegel JH, Hirohata ET. Sound calibration and distortion product otoacoustic emissions at high frequencies. Hear Res. 1994;80:146–152. doi: 10.1016/0378-5955(94)90106-6. [DOI] [PubMed] [Google Scholar]
  34. Sisto R, Moleti A. On the large-scale spectral structure of otoacoustic emissions. J Acoust Soc Am. 2005;117:1234–1240. doi: 10.1121/1.1853208. [DOI] [PubMed] [Google Scholar]
  35. Sisto R, Moleti A, Shera CA. Cochlear reflectivity in transmission-line models and otoacoustic emission characteristic time delays. J Acoust Soc Am. 2007;122:3554–3561. doi: 10.1121/1.2799498. [DOI] [PubMed] [Google Scholar]
  36. Strelcyk O, Dau T. Relations between frequency selectivity, temporal fine-structure processing, and speech reception in impaired hearing. J Acoust Soc Am. 2009;125:3328–3345. doi: 10.1121/1.3097469. [DOI] [PubMed] [Google Scholar]
  37. Wright A. Dimensions of the cochlear stereocilia in man and the guinea pig. Hear Res. 1984;13:89–98. doi: 10.1016/0378-5955(84)90099-6. [DOI] [PubMed] [Google Scholar]
  38. Yates GK, Withnell RH. The role of intermodulation distortion in transient-evoked otoacoustic emissions. Hear Res. 1999;136:49–64. doi: 10.1016/S0378-5955(99)00108-2. [DOI] [PubMed] [Google Scholar]
  39. Zweig G, Shera CA. The origin of periodicity in the spectrum of evoked otoacoustic emissions. J Acoust Soc Am. 1995;98:2018–2047. doi: 10.1121/1.413320. [DOI] [PubMed] [Google Scholar]
  40. Zwicker E. Temporal effects in simultaneous masking by white-noise bursts. J Acoust Soc Am. 1965;37:653–663. doi: 10.1121/1.1909389. [DOI] [PubMed] [Google Scholar]

Articles from JARO: Journal of the Association for Research in Otolaryngology are provided here courtesy of Association for Research in Otolaryngology

RESOURCES