Modeling the Time-Varying and Level-Dependent Effects of the Medial Olivocochlear Reflex in Auditory Nerve Responses

Abstract

The medial olivocochlear reflex (MOCR) has been hypothesized to provide benefit for listening in noisy environments. This advantage can be attributed to a feedback mechanism that suppresses auditory nerve (AN) firing in continuous background noise, resulting in increased sensitivity to a tone or speech. MOC neurons synapse on outer hair cells (OHCs), and their activity effectively reduces cochlear gain. The computational model developed in this study implements the time-varying, characteristic frequency (CF) and level-dependent effects of the MOCR within the framework of a well-established model for normal and hearing-impaired AN responses. A second-order linear system was used to model the time-course of the MOCR using physiological data in humans. The stimulus-level-dependent parameters of the efferent pathway were estimated by fitting AN sensitivity derived from responses in decerebrate cats using a tone-in-noise paradigm. The resulting model uses a binaural, time-varying, CF-dependent, level-dependent OHC gain reduction for both ipsilateral and contralateral stimuli that improves detection of a tone in noise, similarly to recorded AN responses. The MOCR may be important for speech recognition in continuous background noise as well as for protection from acoustic trauma. Further study of this model and its efferent feedback loop may improve our understanding of the effects of sensorineural hearing loss in noisy situations, a condition in which hearing aids currently struggle to restore normal speech perception.

INTRODUCTION

The auditory system has the acute ability to encode communication sounds in quiet and across a wide range of background noise levels, despite the limited dynamic range of individual neurons. One mechanism that may help the auditory system to code sounds in varying background noise levels is dynamic range adaptation (Dean et al. 2005; Wen et al. 2009). Some dynamic range adaptation may be produced by the medial olivocochlear reflex (MOCR), which is mediated by a feedback loop from the level of the superior olivary complex to the outer hair cells (OHCs) (Guinan 2006). This feedback loop reduces the gain of the active process in the cochlea. It is a bilateral loop, so sound in one ear elicits both an ipsilateral and a contralateral MOCR (Gifford and Guinan 1987).

Several recent studies have incorporated aspects of the MOCR into auditory nerve (AN) models (Ferry and Meddis 2007; Messing et al. 2009; Brown et al. 2010; Chintanpalli et al. 2012). Typically, these have included only the ipsilateral MOCR. To accurately characterize the effects of the MOCR, it is important to determine the amount of gain reduction from both the ipsilateral and contralateral pathways of this bilateral reflex. The magnitude of the gain reduction produced by the MOCR has been measured at the level of the basilar membrane and AN in anesthetized animals by shocking the MOC efferents (Gifford and Guinan 1987; Murugasu and Russell 1996). From these and other data, the maximum MOCR strength for the ipsilateral, contralateral, and bilateral pathways has been estimated for anesthetized cat. Data on the relative strength of the ipsilateral and contralateral MOCR are also available from measurements of otoacoustic emissions (OAEs) (Liberman et al. 1996). However, these may not be directly interpreted as changes in cochlear gain due to the complicated nature of the multiple OAE-generating mechanisms (Shera and Guinan 1999). Furthermore, the amplitude changes seen in OAEs are smaller than those seen in CAPs measured in the same animals (Kawase et al. 1993; Puria et al. 1996).

Most models simulating aspects of the MOCR have primarily examined responses with efferents on or off. However, it is important to include a realistic simulation of the sluggish time-course of the MOCR. The time-course has typically been measured using various types of OAEs (e.g., Backus and Guinan 2006). Thus, unlike the gain reduction data, time-course estimates have been made not only in anesthetized animals but also in awake animals, including humans.

A recent study (Chintanpalli et al. 2012) used a well-established AN model based on cat data (Zilany and Bruce 2006, 2007) to demonstrate the feasibility of reducing OHC gain to simulate efferent effects in AN responses to a tone in noise. While it is difficult physiologically to avoid the ipsilateral efferent confound on estimates of contralateral efferent strength (Kawase et al. 1993), by fitting the AN model to the physiological data it was possible to estimate the amount of gain reduction from the ipsilateral and bilateral MOCR in static conditions. In the present study, this AN model was extended further by adjusting OHC gain as a function of time (based on the MOCR time-course), ipsilateral and contralateral stimulus levels, and center frequency (CF). Model parameters were derived by fitting the detection and discriminability data from AN fiber responses to tones in the presence of ipsilateral noise with and without continuous contralateral noise (Kawase et al. 1993). As in the physiological data, model responses demonstrated that contralateral noise can improve detection and discrimination of tones in the ipsilateral ear via OHC gain reduction that acts to reduce the noise response and, consequently, to increase the tone response. This dynamic level-dependent extension of the AN model allows the relevance of the MOCR in real-world conditions with temporally varying sounds to be evaluated, along with the relevance of the efferent system in cases of sensorineural hearing loss involving OHC damage.

METHODS

Overview of the efferent pathway

A well-established cat auditory nerve model (Zilany and Bruce 2006, 2007) was used to simulate AN synapse output and basilar membrane responses. This model has been thoroughly compared with physiological responses to a variety of stimuli including tones, speech, and noise (Carney 1993; Heinz et al. 2001; Zhang et al. 2001; Tan and Carney 2003, 2005; Zilany and Bruce 2006, 2007). The overall implementation of the AN model uses time-varying nonlinear filters that predict physiological responses from the cat auditory system including compression, suppression, and broadened tuning (for a review of other computational models, see Lopez-Poveda 2005). The use of a single control path to describe all of these nonlinearities means that hearing loss related to OHC dysfunction can be adjusted by the model parameter C_OHC (Heinz 2010). While this parameter was originally included to simulate the effects of hearing loss, decreasing OHC gain has previously been used to model the effect of the MOC efferent pathway (Ferry and Meddis 2007; Brown et al. 2010; Jennings et al. 2011; Chintanpalli et al. 2012). Thus, by varying the parameter C_OHC between 1 (full OHC gain) and 0 (no OHC gain), the differing strength of the MOCR can be simulated.

A schematic of the AN model is shown in Figure 1 and includes an efferent pathway that models the feedback of the MOCR with the output adjusting C_OHC at each time point of the model simulation [C_OHC(t)]. The amount of gain reduction indirectly depends on the input stimulus and the intermediate low-pass (LP) filter output OHC_LP in the OHC control pathway. The MOC feedback is stimulus dependent and varies with time, a significant improvement over the model introduced by Chintanpalli et al. (2012), where the MOC feedback was manually adjusted between discrete static values. Using the control path filter as the input to the efferent pathway assumes that the MOCR is driven by activity in a given afferent input channel. The tuning of the control path filter, a third-order gammatone filter (Zhang et al. 2001), is broader than that of the afferent C1 filter, similar to the observed broader tuning characteristics of efferent fibers (Liberman and Brown 1986; Lilaonitkul and Guinan 2009, 2012). The time-varying signal OHC_LP(t) is the input to the efferent pathway of the model, where it then is smoothed using an RMS filter (see “MOCR time-course”), converted to a decibel (dB) scale and then normalized in the level dependence (LD) block. Once the input signal has been normalized, the contributions of the ipsilateral and contralateral pathways are scaled and combined through addition.

FIG. 1.

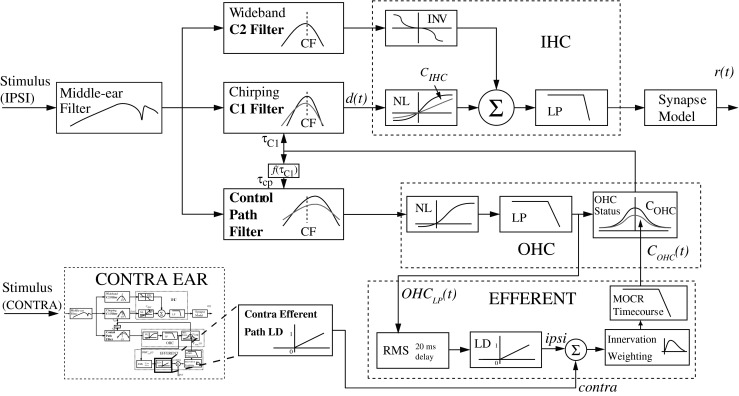
The auditory nerve model. The medial olivocochlear reflex (MOCR) was simulated by adjusting the model parameter C _OHC on a per sample basis to reduce outer hair cell (OHC) gain [C _OHC(t)]. The amount of gain reduction at each sample is based on the level of the LP output of the OHC block [OHC_LP(t)] of the model entering the pathway outlined in the EFFERENT block. The block labeled “Contra Efferent Path LD” indicates the corresponding level-dependence (LD) block in a second complete instance of the model corresponding to the contralateral ear. (Figure adapted from Zilany and Bruce 2007, with permission from the Journal of the Acoustical Society of America).

The contra LD block indicates the output of the efferent LD block from a second (contralateral) instance of the complete model. The two models are run simultaneously and are interconnected through these feedback lines. Initially, the ratio of ipsilateral to contralateral pathway contributions was fixed to 2:1 in dB based on the prevalence of physiological data (Guinan 2006); however, this was configured as an adjustable parameter in the model for reasons discussed below.

The next block of the efferent pathway models the change in efferent innervation along different locations in the cochlea by taking the summed binaural signal and multiplying by a scalar function of CF. The MOCR time-course block provides an exponential onset and decay using a second-order linear system, which has been shown to account for the level-independent nature of the MOCR time-course (Backus and Guinan 2006). Finally, the output of the time-course must be converted from a 0 to 1 scale (where 1 represents the maximum OHC gain in dB for this CF) to C_OHC(t), producing the desired threshold shift (Zilany and Bruce 2006, 2007).

Stimulus-level dependence of the efferent system

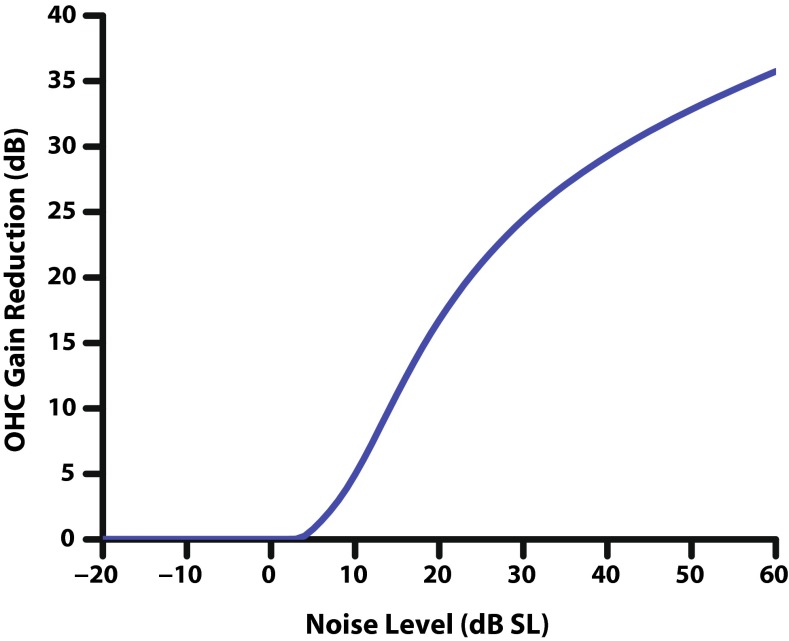
Since the strength of the MOCR is dependent on the stimulus level, the efferent pathway in the model should provide more gain reduction to the OHCs at higher sound levels. The level dependence (LD) block of the efferent pathway serves to define a threshold and increasing portion with variable slope for the gain reduction as a function of the input stimulus. By adjusting the two parameters of the LD block, threshold and slope, the amount of gain reduction in dB in the model can be controlled as a function of stimulus level in dB.

Although the output value of the LD function can exceed 1, the resulting sum after scaling the ipsilateral and contralateral pathways is capped at 1 (full OHC gain reduction). This restriction on the range of the function comes from the restriction on the range of C_OHC, ensuring that the output of the second-order system modeling the time-course will produce valid gain reduction values. This limit on the maximum efferent gain reduction strength (see Table 1) is included as an external model parameter to allow gain reduction to be less than the total amount of OHC gain for a given CF, i.e., to restrict the efferent system from completely suppressing the active process of the OHCs if desired. The function of the LD block in the model can be seen by plotting the output of the efferent pathway C_OHC(t) at an approximately steady state (0.75 s post-onset) as a function of stimulus level (Fig. 2). The saturation point of the efferent pathway is limited by OHC gain; we chose to set the maximum efferent gain reduction strength to 1 for all the results that follow.

TABLE 1.

Description of the parameters used in the AN model efferent pathway implementation. Parentheses indicate related physiologically relevant values. Referenced dB values are computed at 8 kHz, when relevant

Parameter	Description	Values
		Kawase et al. (1993) fit 15:1 ratio	2:1 ratio
MOCRthreshold	Gain reduction threshold (LD block)	−130.5 dB (5 dB SL)	−130.4 dB (5 dB SL)
MOCRslope	Slope of level dependence function (LD block)	0.0164 (0.637 dB/dB)	0.0162 0.637 dB/dB)
MOCRratio[0]	Ipsi pathway scaling parameter	0.4671 (15:1 in dB)	0.4464 (2:1 in dB)
MOCRratio[1]	Contra pathway scaling parameter	0.0551	0.2321
MOCRmax	Maximum OHC gain reduction	1 (55.4 dB max)	1 (55.4 dB max)
θ	Parameter in CF gamma function	6.83	6.83
k	Parameter in gamma function	1.79	1.79

FIG. 2.

Output of the efferent pathway of the model C _OHC(t) in dB reduction in OHC gain, as a function of ipsilateral noise level in dB SL at a CF of 8 kHz. The LD function of the efferent pathway produces two regions of efferent gain reduction: a threshold and an increasing portion. Not shown is a third saturation region at higher stimulus levels, which is produced by the limitation of the maximum OHC gain, or a lower limit that can be set in the model. Parameters for the LD block used in this figure can be found in Table 1.

The parameters of the LD function were determined by relating cat physiology to the model using signal detection theory (SDT) (Green and Swets 1966). This technique can be used effectively to relate physiological data to both measured data, such as auditory nerve data (Kawase et al. 1993), and simulated data, such as the AN model synapse output (Heinz et al. 2002). This approach predicts a perceptual sensitivity index, or d′ which is based on the stochastic nature of the neural spike rate as measured physiologically and from the AN model. The higher the value of d′ the more likely the signal is to be detected in the noise; a value near 1 typically represents the threshold (Green and Swets 1966). The distributions of the tone and noise were obtained by averaging the spike rates during the 50 ms of the tone and the noise immediately following the tone (Kawase et al. 1993; Chintanpalli et al. 2012). The sample mean of each distribution was estimated by the number of spikes in the physiological data over that time window. A correction factor of 0.5 was included for the variance since the spike count variability is known to be approximately half of a Poisson random process (Young and Barta 1986; Delgutte 1987). Eq. 1 shows the result of this approximation for the detection of a tone in noise, where subscript n indicates the noise region, subscript t indicates the tone + noise region, and r indicates the synapse output (in spikes per second) of the auditory nerve model:

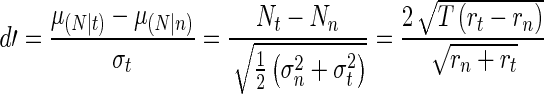1

Similarly to tone detection, d′ measures can also be used to estimate sensitivity of discrimination, for example, how well a 5-dB intensity increment in tone intensity can be discriminated in background noise. This metric was computed using the tone + noise region of the stimulus, where L in Eq. 2 is a given intensity level:

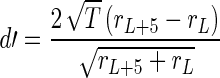2

An unconstrained nonlinear minimization was employed to determine parameters using fminsearch in MATLAB (based on the interior point algorithm). The objective function evaluated the sum of six normalized root-mean-square errors consisting of the d′ discrimination data from the Kawase et al. (1993) study (μ) corresponding to the model data (x) at three noise levels (10, 20, and 30 dB SL; parameter n) for both binaural and ipsilateral stimulation (parameter s, Eq. 3). This normalization of the mean squared error weights each condition and stimulus type equally in terms of its energy. Only the discriminability data was used for the model fitting due to the convenience that the discriminability curve starts and ends at approximately d′ = 0. This means that larger discrepancies in d′ at high tone intensities are not overemphasized when computing the mean squared error:

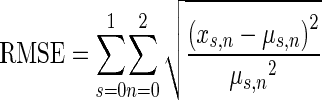3

Fitting the level dependence of the model was achieved with three parameters (see Table 1): LD threshold (MOCRthreshold), LD slope (MOCRslope), and ipsilateral scaling (MOCRratio[0]).

Innervation as a function of CF

The efferent innervation block in the model was implemented to reflect how innervation of OHCs by efferent fibers varies along the length of the cochlea. Liberman et al. (1990) reported that in the cat, efferent innervation of the cochlea is highest in the region of 4–10 kHz, and that electrical stimulation of the MOC revealed a similar trend in the strength of efferent response as a function of CF. To model this CF dependence of the MOCR, where x corresponds to the CF, a curve defining the gamma distribution function was employed to scale efferent strength, as shown in Eq. 4:

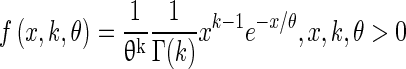4

The parameters θ and k were estimated using an unconstrained nonlinear minimization where the objective function consisted of the mean squared error between the model synapse output and the OCB stimulation effect from afferent AN fibers (Guinan and Gifford 1988; Liberman et al. 1990). It should be noted that the gamma function parameters were estimated independently of and prior to the level-dependent parameters of the model, since the level dependence is irrelevant when using the “shocks” setting of the model.

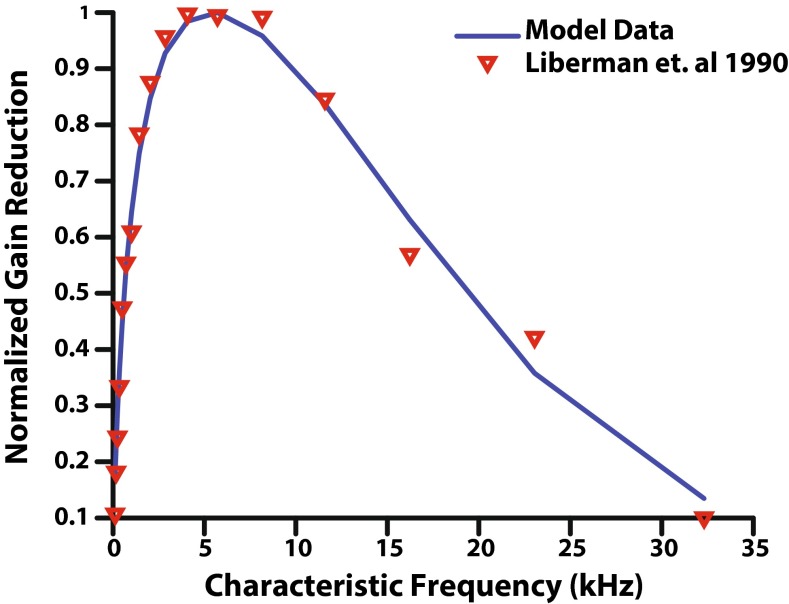
The result of adding the CF dependence block to the efferent pathway is shown in Figure 3. Model gain reduction based on synapse output was normalized by the maximum efferent gain reduction possible over all CFs resulting in gain reduction on a 0 to 1 scale (where the frequency with the maximum gain reduction has a value of 1), in order to match the data from the Liberman et al. (1990) study. These data served as validation of the AN model's efferent CF dependence. To achieve the best physiological accuracy, it is important that the synapse output of the model was used to fit to the electrical stimulation data rather than simply applying the function that fits the Liberman et al. (1990) data in the efferent innervation block.

FIG. 3.

Normalized gain reduction as a function of characteristic frequency. Physiological data (Liberman et al. 1990) obtained by shocking the MOC bundle in cats is reported as red inverted triangles on a 0 to 1 scale. Synapse output from the AN model with efferent feedback was normalized to a 0 to 1 scale to match the Liberman et al. (1990) data, and was generated using the “shocks” setting of the model.

MOCR time-course

In order to simulate the gain reduction effects due to the MOCR, it is necessary to model its build up and decay as a function of time. Otoacoustic emission data from Backus and Guinan (2006) demonstrate that the timing of the MOCR is largely unaffected by the level of the stimuli or by which ear was stimulated. Therefore, we took the approach of using a single linear model of the time-course and then determined the amount of gain reduction separately by fitting the model to physiological data. It was assumed based on these data that the same model can be used for ipsilateral and contralateral efferent feedback and that only the relative contribution of each pathway should need to be adjusted (Backus and Guinan 2006). A second-order linear system was used to model the time-course, with parameters based on measurements in humans using stimulus-frequency otoacoustic emissions (Backus and Guinan 2006, Appendix C). The system is specified by the two time constants of the system, τ₁ = 63 ms and τ₂ = 245 ms, and two scalars c₁ and c₂ (Eq. 5):

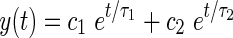5

A 20-ms delay was also introduced into the system, a result of the recursive RMS smoothing filter having a window length of twice that delay (Eq. 6). The time delay in the output corresponds to estimates of the onset and offset delay in humans through otoacoustic emission and behavioral data (Backus and Guinan 2006; Roverud and Strickland 2010; Jennings et al. 2011). The smoothing filter not only provides a delay in the actual system but also helps to make sure that the input to the LD function does not sharply alternate between sections of the piecewise function on a sample-by-sample basis.

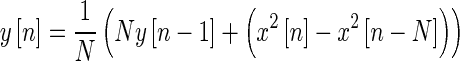6

Binaural contributions

The ipsilateral and contralateral pathways were first constrained to add with a 2:1 ratio in dB, based on existing physiological evidence from both efferent innervation of OHCs and maximum gain reduction possible as a result of electrical stimulation of the MOC bundle (Guinan and Gifford 1988). The strength of each pathway was also made a parameter in the model in a second implementation. This implementation of the model efferent pathway ensured that the ratio of binaural contributions remained fairly constant across CF, but the total amount of gain reduction in each pathway would vary with CF.

The efferent pathway also includes a binary vector parameter (for each ear) referred to as “shocks,” which introduces the possibility of simulating electrical stimulation by providing the maximum possible gain reduction for the ipsilateral, contralateral, or binaural channels. This is equivalent to setting the contribution of the specified efferent channel (ipsilateral, contralateral) to the maximum possible gain reduction or any other fixed level as specified by the binaural contribution parameters. The total gain reduction possible would also be affected by the blocks in the efferent model that followed the sum of the two pathways, including the limit on maximum efferent gain reduction and the CF dependence of efferent innervation.

Stimuli

The input to the model was an acoustic waveform with the output measured at either the level of the C1 filter for BM or at the level of the synapse output of a single fiber at the CF of the tone. The model simulated AN fibers with spontaneous rates (SRs) of 50 spikes/s (i.e., high SR) (Sachs and Abbas 1974; Liberman 1978) because for discriminability, only high-SR fiber data were presented by Kawase et al. (1993).

Stimuli were chosen to closely match those used by Kawase et al. (1993), with the bandwidth of the noise extending from 0.1 to 20 kHz. The tone was an 8-kHz sinusoid with a duration of 50 ms, including 3-ms cos² onset and offset ramps. This CF was chosen since it is known to elicit a large MOCR effect (see Fig. 3) and because it was used in a previous modeling study (Chintanpalli et al. 2012). Tones were generated from −20 to 110 dB SPL in 5 dB steps. The broadband noise had duration of 1 s with 5-ms cos² ramps. Kawase et al. (1993) used trains of tone bursts presented during continuous noise (turned on 5 s before the first tone burst). In the present study, a single tone burst was presented with an onset at a delay of 750 ms from the onset of the noise. The length of the preceding noise is a trade-off between computational time and allowing the MOCR to fully be activated by the noise (Kawase et al. 1993); the response to the noise alone was taken from a 50-ms time window after the tone (i.e., 800 ms from noise onset) (Kawase et al. 1993; Chintanpalli et al. 2012).

Noise levels in dB SL were calculated by first estimating a noise threshold for the model by averaging the rate-level functions of 50 (frozen) samples of noise at levels from 0 to 120 dB SPL. The threshold level corresponded to 10 % of the maximum synapse output on the rate level function (Chintanpalli et al. 2012). The tone levels were set in dB SL re: fiber threshold for the tone, as in the data reported by Kawase et al. (1993), so tone levels were calibrated to maximize the correlation between the d′ measured physiologically and predicted by the model.

RESULTS

Initial model fit

When first fitting the model, only three parameters described in the methods section (LD slope, LD threshold, and ipsilateral scaling) were used to fit physiological data, while the relative strength of the ipsilateral and contralateral pathways were fixed at a ratio of 2:1 based on anatomical and functional evidence. With this constraint in the model, a proper fit of the physiological data was achieved for ipsilateral stimulation (as shown in Fig. 4; optimal parameters shown in Table 1). The Kawase et al. (1993) data are plotted as symbols, where each panel corresponds to increasing levels of ipsilateral noise (10, 20, and 30 dB SL). The model simulation results are represented with lines. The physiological data used for the model fitting process are comprised of averages from many nerve fibers. While it is clear that the model data with ipsilateral noise only fit well to the physiology (Fig. 4, red triangles and solid lines), the model does not capture the data with ipsilateral and contralateral noise at high tone levels (blue circles and dashed lines).

FIG. 4.

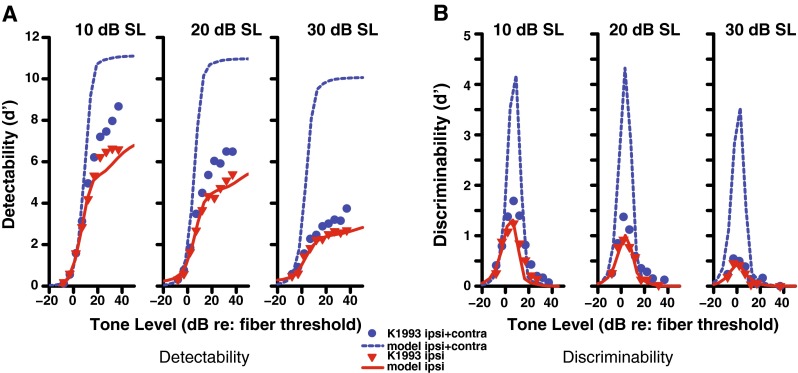
Detectability (A) and discriminability (B) of a tone in noise for a high-SR fiber with a CF of 8 kHz as a function of tone level. Physiological data (Kawase et al. 1993) are shown as symbols and model output as lines. The solid red line indicates stimulation with ipsilateral noise at the level (10–30 dB SL) indicated above each panel, while the dashed blue line indicates the same ipsilateral noise level and contralateral noise at a level of 50 dB SL. A ratio of 2:1 for the ipsilateral and contralateral contributions was used in these simulations.

Since the fit of the model was not optimal for the binaural system, alternatives to the design were tested. The model was implemented in several versions that varied the location in the efferent pathway where the binaural channels were combined (e.g., before or after the nonlinear function). None of the other attempted realizations of the model provided a better fit than shown in Figure 4. Because the 2:1 binaural ratio was only an estimate based mainly on anatomical and OAE measurements, the strength of both the ipsilateral and contralateral pathways were included as external model parameters that the user can change. Instead of restricting the ratio to be 2:1, we included the strength of both pathways in a separate nonlinear optimization. This allowed the model to better fit the physiological data (Fig. 5), with the end result being a much reduced contralateral strength and a ratio closer to 15:1 in terms of dB of OHC gain reduction (Table 1).

FIG. 5.

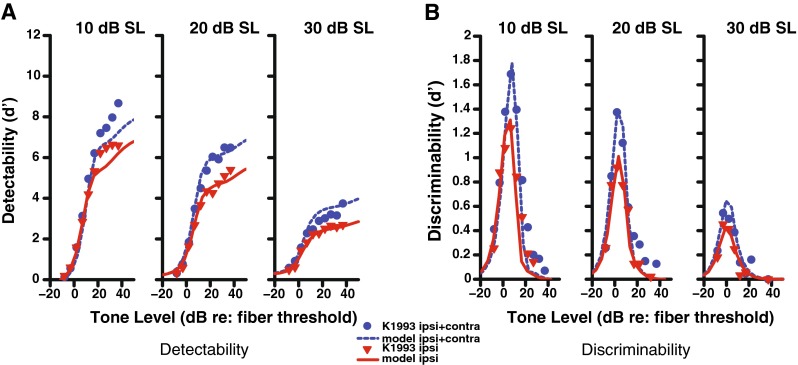
Detectability (A) and discriminability (B) of a tone in noise for a high-SR fiber with a CF of 8 kHz as a function of tone level. Physiological data (Kawase et al. 1993) are shown in symbols and model output as lines. The solid red line indicates stimulation with ipsilateral noise at the specified level 10–30 dB SL as indicated above each panel, while the dashed blue line indicates the same ipsilateral noise and contralateral noise at a level of 50 dB SL. The binaural ratio parameter was set as a free parameter in the nonlinear optimization (resulting in a ratio of approximately 15:1).

The limited strength of the contralateral pathway in the Kawase et. al data was surprisingly small and was not apparent before being modeled. One known weakness in this AN data is that the tone levels were presented sequentially in order of increasing level. As shown by Guinan and Stankovic (1996), using sequential levels can depress the response at high levels. As noted in Chintanpalli et al. (2012), this depression at high levels could lead to an underestimation of the amount of gain reduction by the MOCR. This could also lead to an overestimate of the ratio, since the added effect of the contralateral pathway might also be underestimated. Therefore, although the 15:1 ratio is not consistent with previous anatomical and functional estimates, there are potential reasons for this discrepancy when the model was fit to this tone-in-noise AN data set, as discussed further below.

Time-varying level-dependent effect of the MOCR

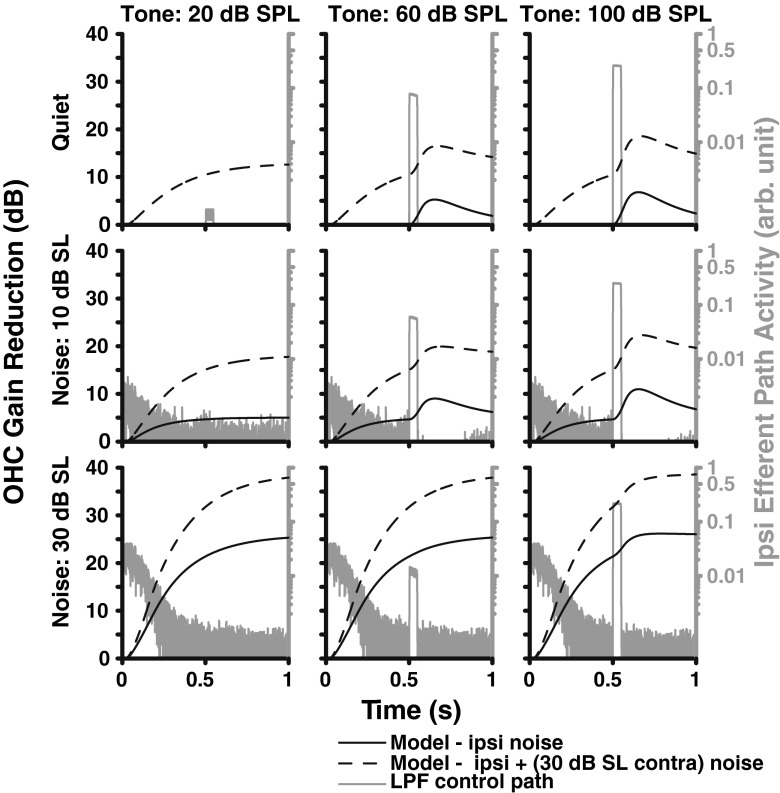
In order to visualize the time-course of the model, a tone-in-noise paradigm was used to demonstrate the effect of the efferent feedback as a function of time (Fig. 6). The response of the efferent pathway is displayed by plotting its input OHC_LP(t) (gray) and output C_OHC(t) (black). The top row includes no ipsilateral noise and a fixed level of contralateral noise. This condition makes it clear that a strong enough tone will evoke the ipsilateral MOCR (see the increase in activity following the tone in the middle and right panels), although it does not improve detectability in this case. Once ipsilateral noise is included, as in the second and third rows, the additional gain reduction from adding contralateral noise is differentially less. The efferent input OHC_LP(t) shows a decrease over time in the response to the noise amplitude as the MOCR strength increases, demonstrating that the efferent pathway has the effect of turning down the noise and improving the SNR between the tone and noise responses. At mid-noise levels (middle row), the efferent response evoked by the tone improves detectability by turning down the noise in the interval following the tone. Thus, even in this simple task, including the time-course of the MOCR is important. A binaural contribution ratio of 2:1 was used in these simulations, which can be seen in the asymptotic value in the bottom left panel (30 dB SL noise in both channels) where the ipsilateral gain reduction is twice the contralateral gain reduction.

FIG. 6.

Waveform corresponding to the amount of OHC gain reduction as a function of time for three noise (dB SL, rows) and tone levels (dB SPL, columns). These waveforms are presented for ipsilateral noise only (solid black line) and both ipsilateral noise and 30 dB SPL contralateral noise (dotted line). The input to the ipsilateral efferent block is also shown in gray, where the tone begins at 0.5 s. A binaural contribution ratio of 2:1 was used in these simulations, which can be seen in the asymptotic value in the bottom left panel (30 dB SL noise in both ears).

Effect of the MOCR on basilar membrane output

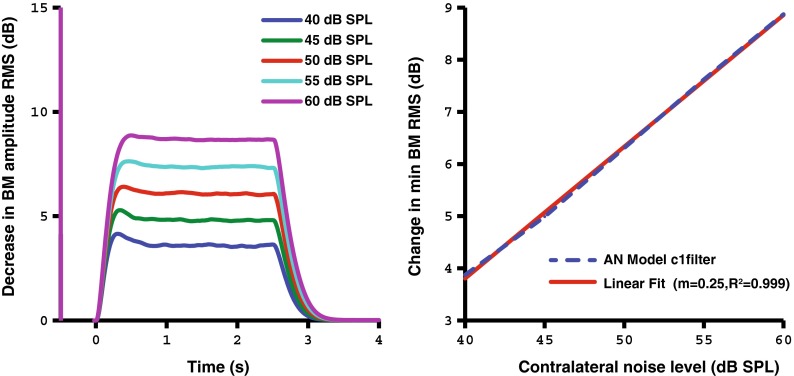
In addition to understanding how OHC gain changes as a function of stimulus level and time, we also sought to observe the direct output of the basilar membrane. Figure 7 shows how the RMS BM output of the AN model changes as a function of time and the contralateral stimulus level. The stimulus consists of an ipsilateral probe tone beginning at −0.5 s and a contralateral noise beginning at 0 s with a duration of 2.5 s. An exponential rise and decay can be observed in the BM change over time. The dB increase in BM RMS change is approximately proportional with the dB change in contralateral noise level. This trend follows similar estimates of this function in human SFOAE data, as expected from using a second-order linear system to model the MOCR time-course (Backus and Guinan 2006).

FIG. 7.

Time-varying C1 filter output of the AN model corresponding to the change in dB of the BM RMS amplitude in response to a contralateral noise of varying level (40–60 dB SPL, left panel). The right panel shows that the dB change in the RMS amplitude of the BM displacement is approximately proportional with the stimulus level in dB. The contralateral noise starts at 0 s with a duration of 2.5 s.

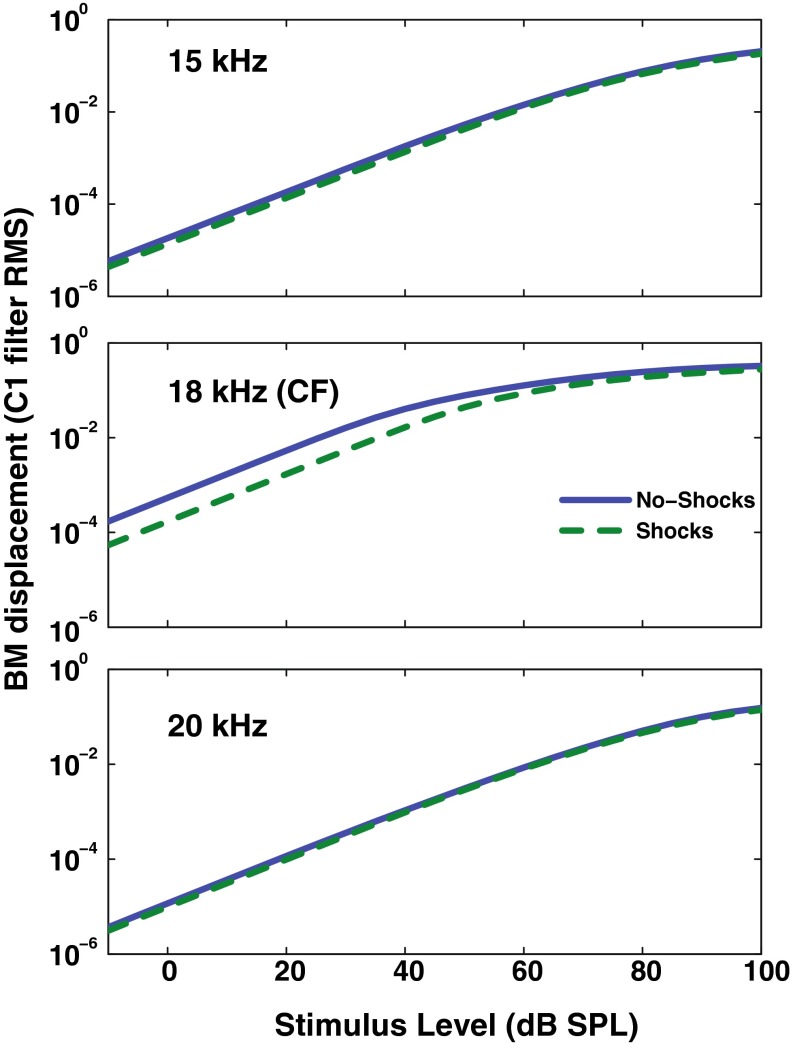
Predictions for the BM displacement with and without the efferent effect can be compared with animal data collected using electrical stimulation of the MOC bundle. With the AN model presented here, we can use the “shocks” setting for both the ipsilateral and contralateral ears and can simulate maximum OHC gain reduction. Figure 8 shows a “tuning” of the efferent feedback in the model, where the simulated MOC feedback only has an effect when a pure tone frequency is near the CF of 18 kHz. The model response differs from that of Cooper and Guinan (2006), which showed a differential effect of the efferent response above (larger) and below (smaller) CF.

FIG. 8.

Frequency dependence relative to CF of the C1 filter output as affected by the efferent block of the AN model when simulating electrical shocks to the MOC bundle (maximum efferent effect). Growth functions for simulated BM responses are shown for tones below (top), near (middle), and above (bottom) the CF with (dashed line) and without (solid line) the “shocks” setting enabled.

Rate-level functions across varying levels of OHC gain reduction

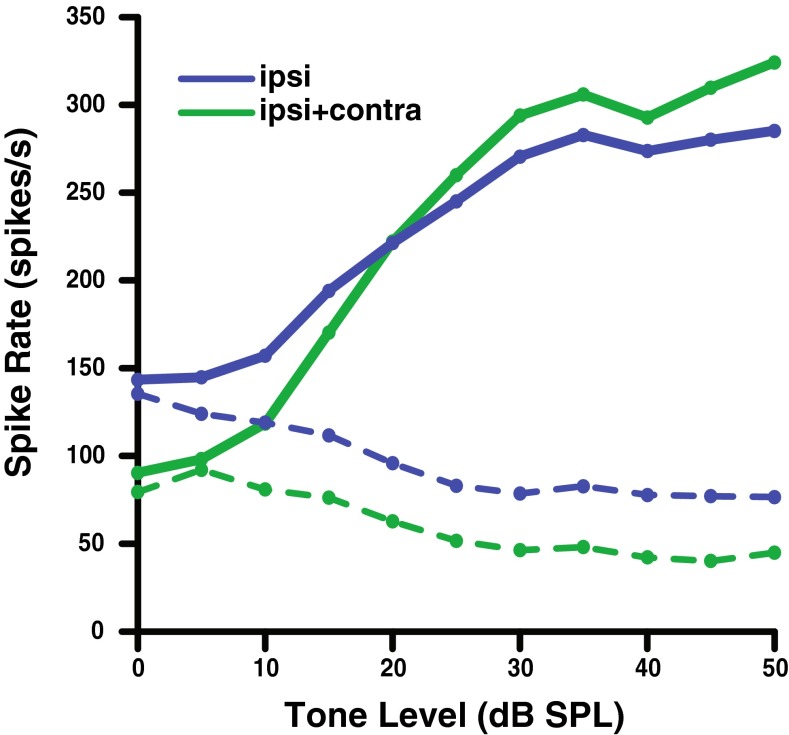
Figures 9 and 10 show AN fiber and model rate-level functions, respectively, for a single high-SR fiber with a CF of 8 kHz. The overall ipsilateral noise level was fixed at 10 dB SL and the contralateral noise at approximately 50 dB SL for all rate-level functions shown. Figure 9 shows AN data as measured under these conditions by Kawase et al. (1993), where blue lines were measured with ipsilateral noise and green lines with ipsilateral and contralateral noise. Each noise in the physiological study was presented for 5 s before the presentation of the first tone burst, thus not allowing the time-course of the MOCR to be evaluated. To illustrate the effect of the time-varying MOCR on tone responses, each panel in Figure 10 (AN model data) represents an increase in the duration of the noise prior to the onset of the tone. Solid lines represent the AN model response to the tone + noise condition, while the dotted lines represent the response to noise alone immediately following the tone. The strength of the efferent pathways used was that of the best fit to the Kawase et al. d′ data (15:1).

FIG. 9.

Effects of noise on recorded auditory nerve rate-level functions for a high-SR, 8-kHz CF fiber in the presence of an ipsilateral noise masker at 10 dB SL (blue), and both ipsilateral and contralateral noise (green). Dotted lines represent the response to noise alone, and solid lines represent the response to tone + noise. (Data redrawn from Kawase et al. 1993).

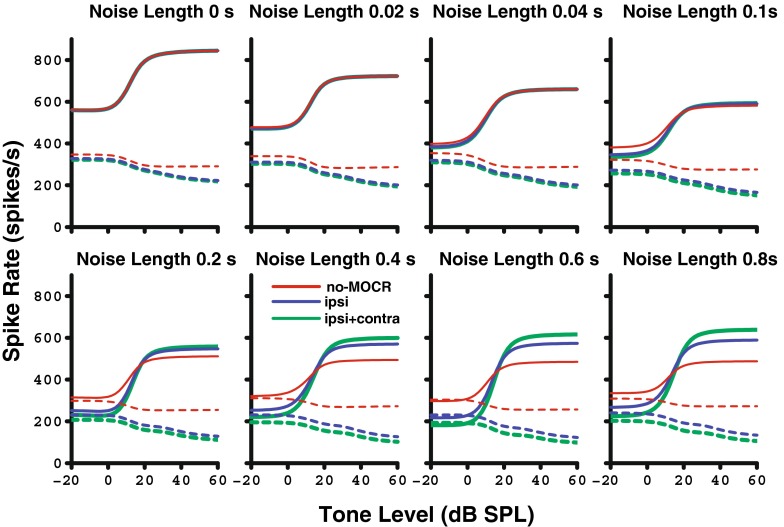
FIG. 10.

Rate-level functions as simulated with the auditory nerve model with (blue and green; best fit 15:1 binaural ratio) and without (red) efferent feedback. Each panel moving left to right shows increasing length of the 10-dB SL ipsilateral noise (with the duration preceding the tone ranging from 0 to 800 ms). Dotted lines represent the response in the noise-alone window immediately following the tone, while solid lines represent the response to tone + noise. The MOCR (blue and green) increases the separation between the firing rates of noise alone and tone + noise, which decompresses the rate-level functions and leads to improved detection and discriminability of the tone. Contralateral noise was presented at 50 dB SL for the ipsi + contra condition.

Looking first at the no-MOCR (red) functions, note that the tone responses decreased as the preceding noise durations increased due to neural adaptation in the tone + noise window. This affects the tone more than the noise, so the difference between the two decreases. The ipsilateral MOCR (blue) model caused both a decrease in the firing rate of the noise alone and an increase in the firing to the tone + noise condition as compared to the original model without the MOCR (red). Adding contralateral noise at 50 dB SL (green) further steepens the slope of the rate-level functions due to increased efferent OHC gain reduction. When comparing the model in a long noise duration condition (bottom right panel of Fig. 10) with the physiology (Fig. 9), the same overall trend of decompression of AN firing rate was observed. Because the model includes a control condition with no efferent feedback, the size of the ipsilateral efferent effect can be observed. Note that the size of the ipsilateral effect (blue compared to red) is substantially larger than the size of the contralateral effect (green compared to blue) due to the large optimal binaural ratio needed to fit the Kawase et al. (1993) AN fiber tone-in-noise data.

DISCUSSION

The current study simulates the MOCR by dynamically reducing OHC gain in the AN model and predicts the antimasking effects of both ipsilateral and contralateral noise on AN fibers as measured physiologically (Kawase et al. 1993). This model improves upon a previous model (Zilany and Bruce 2007; Chintanpalli et al. 2012), allowing for stimulus-dependent, time-varying control of the binaural efferent system. This model also includes the ability to simulate shocking the ipsilateral, contralateral, or bilateral MOC efferents as has been done in several physiological studies investigating the effect of efferent feedback (e.g., Gifford and Guinan 1987; Winslow and Sachs 1987). The resulting model fits the general trends of the time-varying, level-, and CF-dependent effects of the MOCR that occur in published physiological data.

Ratio of ipsilateral and contralateral MOCR gain reduction

Several studies have suggested that the relative strength of the ipsilateral and contralateral pathways should be approximately 2:1 as measured anatomically and physiologically in animals (e.g., Liberman et al. 1996). When forcing this constraint into the model, trends of the simulated data generally matched those of Kawase et al. (1993), but it was clear that the contribution of the model MOCR was too large when adding contralateral noise at low ipsilateral noise levels (Fig. 4). Referring to Figure 6 from Chintanpalli et al. (2012), which plots model detectability (d′) with various amounts of OHC gain reduction as well as the physiological AN data, it is clear that the difference in gain reduction between the no-MOCR model and the ipsi condition in the Kawase et al. (1993) data is far greater than twice the difference between ipsi and ipsi + contra conditions. This means that starting from the Zilany and Bruce (2007) model, a fixed 2:1 ratio in terms of dB gain reduction could not provide a proper fit for the Kawase et al. (1993) data set. Guinan and Gifford (1988) showed that electrical stimulation produced 20–25 dB of ipsilateral gain reduction and 8–10 dB of contralateral gain reduction. In contrast, comparisons between model predictions and physiological data in Figure 6 from Chintanpalli et al. (2012) suggest that for a 30-dB SL ipsilateral noise only a maximum of ~3 dB additional gain reduction is necessary to account for the effects of a 50-dB SL contralateral noise on tone-in-noise detectability, whereas up to 20 dB of gain reduction is needed to account for the ipsilateral ear detectability data.

Although the binaural ratio required to fit the AN tone-in-noise data from Kawase et al. (1993) is much larger than direct estimates based on anatomical and functional measures that generally fall between 2:1 and 1:1 (e.g., Liberman et al. 1996; Gifford and Guinan 1987; Lilaonitkul and Guinan 2009), there are other neural data that show surprisingly small contralateral effects. For example, May and Sachs (1992) showed that the background noise-induced effects on CF tone rate-level functions (both the horizontal shift and compression) measured in AN fibers from anesthetized cats were the same for binaural and ipsilateral noise stimulation, suggestive of a small contralateral effect. Although their conditions differed slightly from Kawase et al. (1993) in that equal ipsilateral and contralateral noise levels were used to simulate realistic binaural conditions, their data appear consistent with a smaller than expected contribution of contralateral noise, even when an intense 50-dB SL contralateral noise was used in the Kawase et al. (1993) study to demonstrate the presence of a contralateral effect on tone-in-noise detection.

Thus, it is possible that other factors beyond the ratio of anatomical connections may affect the functional binaural ratio for tasks involving complex stimuli, such as tones in noise. The data from Lilaonitkul and Guinan (2009) support this idea by demonstrating in human subjects that the binaural ratio can vary between 1:1 and 2:1 depending on whether broadband or narrowband noise was used to elicit MOCR activity. Thus, the idea of a fixed 2:1 binaural ratio that has evolved from anatomical and physiological studies in animals may be an oversimplification of the true ratio of functional OHC gain reduction from the ipsilateral and contralateral MOCR pathways, particularly for complex stimuli such as signals in noise for which the MOCR is often hypothesized to provide important perceptual benefits.

The specific discrepancy highlighted in the present modeling study may have resulted (at least in part) from the paradigm used to measure these AN data. One potential criticism of the Kawase et al. (1993) study is that the presentation paradigm included sequentially increasing tone levels. If the interstimulus interval was too small, the MOCR activated by the previous tone could affect that of the next stimulus (Guinan and Stankovic 1996). This would tend to depress the firing rates at higher levels, making detectability estimates plateau at a lower tone level. In the present study, the 2:1 ratio predicts higher discriminability than is seen in the neural data, consistent with this effect. Future modeling work could pass a series of stimuli as a single waveform input to the model using the exact presentation order from the Kawase et al. (1993) study to determine the effect of sequential presentation. Depending on the implementation of the model and computer system used, memory issues could be a limitation for extremely long stimulus lengths. However, it is uncertain if this effect would significantly change the binaural ratio since the tones are presented to the ipsilateral channel only.

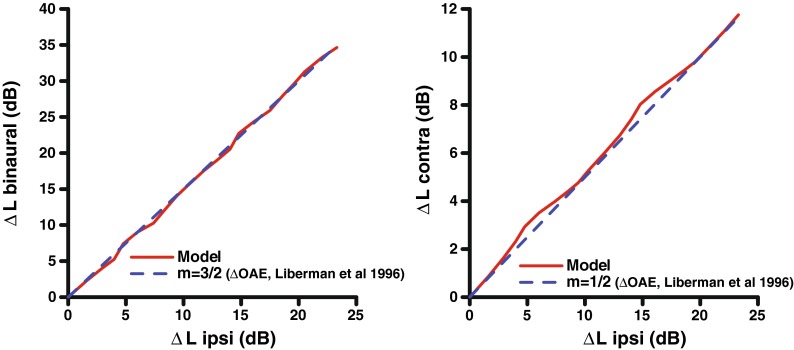
For both OAE and anatomical data, a direct relationship to the functional change in OHC gain in each pathway cannot be established directly. In addition, OAE paradigms often have to use nonoptimal stimuli to measure the effect of the ipsilateral efferent pathway. Typically, the amount of gain change would be commensurate with the shift in stimulus level (ΔL) needed to achieve the same input–output function. This level shift (ΔL) is a useful metric because the shift is measured from the linear response of the system, so the ΔL is equivalent to the amount of gain reduction in dB. The value of this shift ΔL was varied in the model by adjusting the maximum efferent gain reduction parameter in the system and using the “shocks” option. Figure 11 (right panel) compares the contralateral and ipsilateral rate-level function shifts from the AN model to the expected ratios based on cat OAE data (Liberman et al. 1996). Thus, it appears that our implementation of the scaling between the ipsilateral and contralateral pathways is appropriate to produce the desired ratio of ΔL shifts. However, the Liberman et al. data compare the change in OAE output in dB, not the shift in input stimulus level in dB for ipsilateral and contralateral stimulation. Thus, if BM compression were present, dB changes in output (e.g., OAEs) would not translate directly to dB changes in input (e.g., horizontal shifts in response-level curves). Another important difference may be that in the Liberman et al. (1996) study, the cats were anesthetized. Regardless of these discrepancies in the binaural ratio parameter, it is clear that the model accounts for the major time-varying, level-dependent, and CF-dependent trends that have been measured in physiological studies of the MOCR. Because of the uncertainty of the exact binaural ratio and that OAE evidence suggests that this ratio may differ across species (Guinan 2006), the efferent pathway binaural ratio was left as an adjustable parameter in the model to facilitate further testing, including the possibility of using “human” values.

FIG. 11.

Comparison of binaural, ipsilateral, and contralateral shifts in model rate-level functions for a range of efferent strength. A binaural ratio of 2:1 was used in the model to generate these data. The maximum amount of efferent gain reduction to the system was varied in the “shock” mode to induce a horizontal shift in the rate-level function. Also shown are the expected 3:2 and 2:1 ratios based on OAE data (dashed line) (Liberman et al. 1996).

Comparison with other models

This study is an extension of previous work with the AN model simulating the MOCR (Chintanpalli et al. 2012), where it was first demonstrated that the Kawase et al. (1993) data could be fit if the appropriate OHC gain reduction as a function of stimulus level was determined. The current study applied this concept and integrated it into a fully developed model, the first computational model incorporating binaural physiologically based time-dependent feedback at the level of the auditory nerve. We found that the level dependence of the model efferent pathway produces a similar trend as the optimal gain calculated by Chintanpalli et al. (2012), as evidenced by the fit to the Kawase et al. (1993) data. In the Chintanpalli et al. study, the optimal gain analysis (their Figs. 11 and 12) was based on maximizing the total dynamic range for discriminability based on the combination of responses from single high-SR, medium-SR, and low-SR fibers. The correspondence between that study and the results of the present study (Fig. 2) are useful, since the present study was limited to fitting the data from the high-SR fibers described in the Kawase et al. (1993) study. The values of optimal gain reduction in the Chintanpalli et al. study were nearly identical to the values in the present study for noise levels of 10 and 20 dB SL, growing nearly linearly. For higher noise levels, gain reduction values were also similar between the two studies, being slightly larger in the previous study up to a level of 40 dB (based on the 40-dB gain reduction cap used in that study). This level was chosen (somewhat arbitrarily in the previous study) as the cap to avoid including larger levels of gain reduction than were thought to be physiologically realistic. The gain reduction values in the current study continue to increase (Fig. 2) because the only limit used was the maximum OHC gain. A smaller limit on the maximum gain reduction can easily be imposed in the present model by setting the maximum efferent gain reduction parameter of the model (see Table 1). Such an approach was taken by Jennings et al. (2011) in modeling human behavioral results that may be related to MOCR feedback.

FIG. 12.

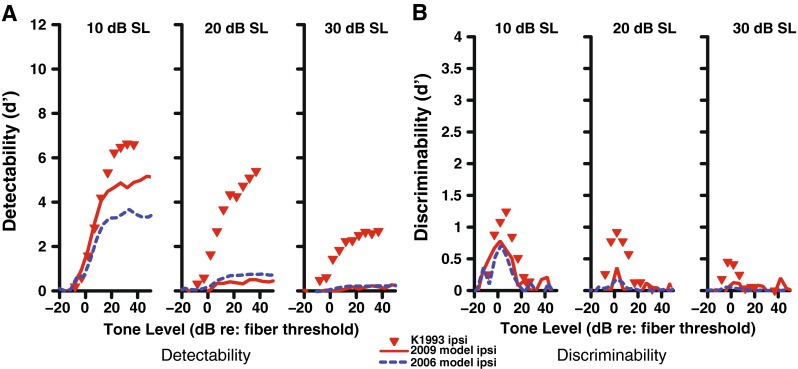
Detect ability (A) and discriminability (B) of a tone in noise for a high-SR fiber with a CF of 8 kHz as a function of tone level for the 2009 AN model with power-law adaptation (solid red line) (Zilany et al. 2009). Dotted blue lines indicate the original 2006 Zilany and Bruce model with no gain reduction, while physiological data (Kawase et al. 1993) are shown as red triangles. Stimulation with ipsilateral noise occurred at the specified level (10–30 dB SL) as indicated above each panel. The inability of the 2009 model to fit the data much better than the 2006 model without MOCR feedback suggests that power-law dynamics alone cannot account for AN tone-in-noise data and that OHC gain reduction to simulate the MOCR is needed.

Another study (Clark et al. 2012) that used the Meddis (2006) auditory nerve model also implemented a gain reduction that varies with time, but the physiological accuracy of their time-course was not clear. As part of our modeling effort, we tested using the low-pass filter used by Clark et al. (2012) as the time-course block at the beginning of our efferent pathway. There were several issues with this implementation, including that qualitatively the time-course of the efferent pathway output did not match that of Backus and Guinan (2006) after passing the output through any nonlinear function to impose level dependencies. Another issue addressed in the present model is that the level dependence and maximum amount of gain reduction possible by the system itself is both CF dependent and based on physiological data. In the Clark et al. (2012) study, the constraints on the CF dependence of the amount of gain reduction was not described. For example, their Figure 2 shows 40 dB of gain reduction at the relatively low center frequency of 500 Hz, which is not supported by physiological data (Guinan and Gifford 1988; Liberman et al. 1990).

Another important strength of the present model is that it is the first truly binaural auditory model where the efferent feedback is both crossed and uncrossed between ears. This is an important development given that a large portion of the physiological data measuring the MOCR uses contralateral stimuli; therefore, this work is critical for the modeling of physiological data that uses contralateral noise stimulation.

One possible drawback of our proposed AN model with efferent feedback is that it is based on the 2006–2007 Zilany and Bruce model and does not include the power-law dynamics that were implemented in a later version (Zilany et al. 2009). Since the MOCR is another form of adaptation to a longer duration stimulus, it could be argued that the power-law dynamics are all that are required to explain the efferent feedback. Although we did not implement the dynamic efferent pathway in the 2009 model, we compared the newer model with the physiological data obtained in the Kawase et al. (1993) study (Fig. 12). It is clear from this figure that the 2009 model does not fit the physiological tone-in-noise data, and moreover, the fit is not significantly better as compared to the 2006 model without any OHC gain reduction. Thus, it appears that OHC gain reduction (simulating the MOCR) is needed to account for the AN tone-in-noise detection and discrimination data.

CONCLUSION

The auditory nerve model with the new efferent pathway can enable further study of the complex nature of the MOCR within the peripheral auditory system, including the bilateral interaction for stimuli presented to both ears. The model accounts for the major time-varying, level-dependent, and CF-dependent trends in physiological studies of the MOCR. Furthermore, the model includes the ability to “shock” the system by statically applying the maximum efferent gain reduction in the system, which allows direct comparison to previous physiological studies that have used electrical stimulation to study the MOCR. These advances enable the modeling of many past and future experiments that quantify the MOCR, a system thought to be especially relevant for speech recognition in noisy situations as well as for protection from acoustic trauma. Further study of this model and its efferent feedback loop may also contribute to our understanding of the impact of sensorineural hearing loss on hearing in noise.