Deferred Feedback Sharply Dissociates Implicit and Explicit Category Learning

Abstract

The controversy over multiple category-learning systems is reminiscent of the controversy over multiple memory systems. Researchers continue to seek paradigms to sharply dissociate explicit category-learning processes (featuring verbalizeable category rules) from implicit category-learning processes (featuring learned stimulus-response associations that lie outside of declarative cognition). We contribute a new dissociative paradigm, adapting from comparative psychology the technique of deferred-rearranged reinforcement. Participants learned matched category tasks that had either a one-dimensional, rule-based solution or a multidimensional, information-integration solution. They received feedback only after each block of trials, with their positive outcomes grouped and their negative outcomes grouped. Deferred-rearranged reinforcement qualitatively eliminated implicit, information-integration category learning. It left intact explicit, rule-based category learning. Moreover, implicit category learners—facing deferred-rearranged reinforcement—turned by default and information-processing necessity to rule-based strategies that poorly suited their nominal category task. The results represent one of the strongest explicit-implicit dissociations yet seen in the categorization literature.

Introduction

Categorization is an essential cognitive function and a focus of cognitive research (e.g., Ashby & Maddox, 2010; Brooks, 1978; Feldman, 2000; Knowlton & Squire, 1993; Medin & Schaffer, 1978; Murphy, 2003; Nosofsky, 1987; Smith, Redford, & Haas, 2008). A lasting issue is whether one or multiple category-learning systems are necessary to account for the diverse categorization abilities of humans. A similar issue has been debated in the memory literature. In fact, these debates are related because proposed category-learning systems might map onto proposed memory systems (Ashby & O’Brien, 2005). Learning is a process of laying down memory traces, and there seems no reason why memory systems should not also learn categories. In that case, there may be as many category-learning systems as memory systems. Here we test for multiple category-learning systems using a distinctively new paradigm.

Categorization researchers have described tradeoffs that seem to support multiple systems. For example, different processes seem to dominate categorization at early versus late stages of category learning (Cook & Smith, 2006; Smith, Chapman, & Redford, 2010; Smith & Minda, 1998; Wasserman, Kiedinger, & Bhatt, 1988), when categories are small versus large (Blair & Homa, 2003; Homa, Sterling, & Trepel, 1981; Minda & Smith, 2001), and when the categorization rule is easy versus difficult to describe verbally (Ashby & Maddox, 2010). A growing consensus grants humans multiple categorization capacities (e.g., rule learning, prototype abstraction, etc.) that specialize in different aspects of learning and rely on different forms of memory (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Ell, 2001; Erickson & Kruschke, 1998; Homa et al., 1981; Maddox & Ashby, 2004; Rosseel, 2002; Smith & Minda, 1998; Smith et al., 2012). Even so, some researchers question multiple-system interpretations of some results (e.g., Nosofsky & Johansen, 2000) and others argue that all categorization phenomena can be explained using a unitary, exemplar-based process in which every previously seen exemplar from all relevant categories is accessed and compared to the current stimulus before a category judgment (e.g., Newell, Dunn, & Kalish, 2010; Nosofsky, Stanton, & Zaki, 2005). Our research helps resolve this issue.

Rule-based and Information-integration Categorization

Our empirical approach draws on the cognitive-neuroscience of categorization (Ashby & Ell, 2001; Maddox & Ashby, 2004; Ashby & Valentin, 2005). This area distinguishes an explicit categorization system that recruits declarative memory from an implicit system that recruits procedural memory. The explicit system learns by actively testing hypotheses using working memory and executive attention. It learns quickly, through sudden realizations of category rules that participants easily describe verbally. For example, people explicitly know a square’s defining characteristics. In contrast, the implicit system learns associatively through procedural-learning processes akin to conditioning. It learns slowly, relying on temporally contiguous reinforcement signals. Participants generally cannot describe their implicit categorization strategies. For example, people correctly categorize wolves and German Shepherds, but they do not easily explain how they do so.

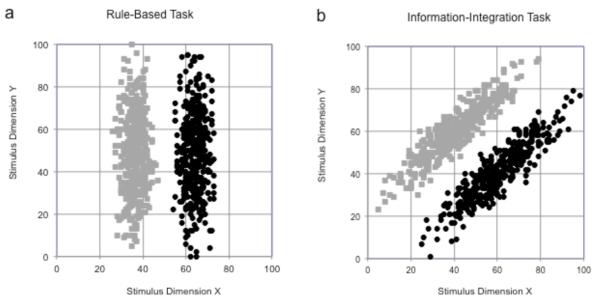
Much of the evidence for these systems comes from rule-based (RB) and information-integration (II) category-learning tasks (Figure 1). Each exemplar in these tasks is defined by its values on perceptually separable X and Y dimensions. For example, each stimulus might be a single line that varies across trials in length (Dimension X) and orientation (Dimension Y). In Figure 1, each gray and black symbol, respectively, denotes the dimensional values of a Category A or Category B member. Figure 1A shows possible stimuli for an RB task. Only X-axis variation carries valid category information, with low and high values on Dimension X defining Category A and B members, respectively. The participant must discover this rule from successive presentations of single category exemplars with feedback. This is an RB task because the solution is a one-dimensional rule. It is explicit because the solution is verbalizeable and discoverable through explicit hypothesis testing.

Figure 1.

A. A rule-based category structure illustrated, depicted within an abstract 100 × 100 stimulus space. The gray and black symbols, respectively, indicate Category A and B stimuli. B. An information-integration category structure, depicted in the same way.

In Figure 1B, Dimensions X and Y carry partially valid category information. To respond accurately, the participant must learn some principle of dimensional integration. This is an II task. One-dimensional rules are not optimal. A vertical or horizontal category boundary will not partition the categories sufficiently, causing errors. The cognitive system accomplishes this integration across dimensions, but it does so implicitly and procedurally. Humans cannot explain their II task solution verbally, especially when the stimulus dimensions are in different units (e.g., length and orientation).

The RB and II tasks are elegant mutual controls. They are matched for category size, within-category exemplar similarity, between-category exemplar separation, class discriminability (e.g., d’), and the proportion correct that is achievable by an ideal observer. Figure 1’s tasks are simply rotations of one another through stimulus space. Therefore, there is no objective, a priori difficulty difference between RB and II tasks. Smith et al. (2011) confirmed this equivalence by showing that pigeons (Columba livia) learn RB and II tasks equally well and at the same rate. Pigeons may learn at the same rate because they lack an explicit category-learning system that selectively advantages RB category learning. Humans generally learn RB tasks faster than II tasks, perhaps because they have that explicit system. If humans’ learning-rate difference arose because the II task is inherently difficult, then a less cognitively sophisticated species (pigeons) should be more challenged on the II task (relative to the RB task) than humans. That pigeons learn the tasks at the same rate is strong evidence that humans’ learning-rate difference arises because they learn the tasks differently, not because one task is difficult. In the same way, multiplication is faster than repeated addition, not because it is easier, but because it is a different process that unfolds differently.

Many dissociations have been demonstrated between RB and II category learning. For example, II learning is selectively impaired when reinforcement on categorization trials is delayed for several seconds (Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005), when learning is unsupervised (Ashby, Queller & Berretty, 1999), and when category knowledge is imparted observationally, not through trial-based reinforcement (Ashby, Maddox, & Bohil, 2002). II learning is apparently served by a cascade of temporally constrained events (perception, response selection, reinforcement—Maddox & Ashby, 2004).

In contrast, RB category learning may be more robust to reinforcement delays, unsupervised learning conditions, and so forth. RB learning may rely on hypotheses actively held in working memory. Other dissociations—for example, that RB learning is selectively hurt when working-memory resources are occupied by a concurrent task—support this idea (Waldron & Ashby, 2001). Consequently, RB learning potentially has great flexibility in application. Because its category knowledge is held in declarative consciousness, it can be applied or adjusted before, during, or after a trial and possibly even after the outcomes from several trials.

No single-system model and no simple difficulty hypothesis has been proposed that can account for even a few of the dissociations that have been reported between RB and II category learning. In contrast, the multiple-systems framework described here essentially predicts all of these dissociations a priori.

The evidence for multiple systems notwithstanding, the theoretical stakes are high, just as when the possibility of multiple memory systems emerged. Some categorization researchers apply a strict parsimony standard to defend a single-system account of categorization, and work continues to definitively evaluate the multiple-systems framework. Here, we introduce a new empirical dissociation that may qualitatively distinguish implicit and explicit categorization. The temporal constraints and flexibility of II and RB category learning, respectively, are crucial to the present test of the implicit-explicit framework in categorization.

A New Empirical Approach

Our paradigm incorporated a technique from recent cross-species studies (e.g., Smith, Beran, Redford, & Washburn, 2006). These researchers sought to prevent monkeys’ associative learning, keeping them from using trial-by-trial reinforcement to form stimulus-response linkages. The idea was to ask macaques to supply instead their own cognitive construal of a task. Yet researchers also had to include enough reinforcement to sustain animals’ participation.

The technique of deferred-rearranged reinforcement (hereafter, deferred reinforcement) met these requirements. Monkeys completed trial blocks with no feedback. At block’s end, they received together the reinforcements from all correct trials and then together the timeouts from all error trials. The processes of conditioning were defeated. Monkeys could not know which stimuli and responses they had gotten wrong or right. They could not learn stimulus-response pairs associatively. Smith et al. (2006) showed that this technique did make the task’s associative structure invisible for at least one macaque who clearly supplied his own cognitive construal instead.

Predictions

This technique is ideally suited for studying and possibly dissociating RB and II category learning. Deferred reinforcement should defeat the reinforcement-based processes underlying II learning. One prediction of our study was that II learning would collapse under deferred reinforcement.

In contrast, RB learners—by current theory—would have in mind their hypothesis and could evaluate its success at block’s end just as at trial’s end. A second prediction was that RB learning would flourish under deferred reinforcement.

Finally, by current theory, the explicit system emphasizes one-dimensional rules. If deferred reinforcement disabled II but not RB category learning, a third prediction was that II participants facing deferred reinforcement might turn—by information-processing necessity—to one-dimensional rules instead. Just like Smith et al.’s (2006) macaque, with the task’s associative structure made invisible, II participants would supply instead their own RB task construal because that was what they still could do.

The confirmation of these predictions would represent one of the clearest dissociations yet seen between RB and II category learning.

Method

Participants

University at Buffalo undergraduates —with normal or corrected-to-normal vision—participated for course credit. Participants’ data were excluded if they completed less than 300 trials (1 and 4 participants excluded, respectively, from the RB-Immediate and II-Immediate conditions) or if they showed significantly lower performance during their last 100 trials than during their first 100 trials (1, 2, 3, and 2 participants excluded, respectively, from the RB-Immediate, RB-Deferred, II-Immediate, and II-Deferred conditions). The final data set included 84 participants divided equally among the four conditions.

Stimuli

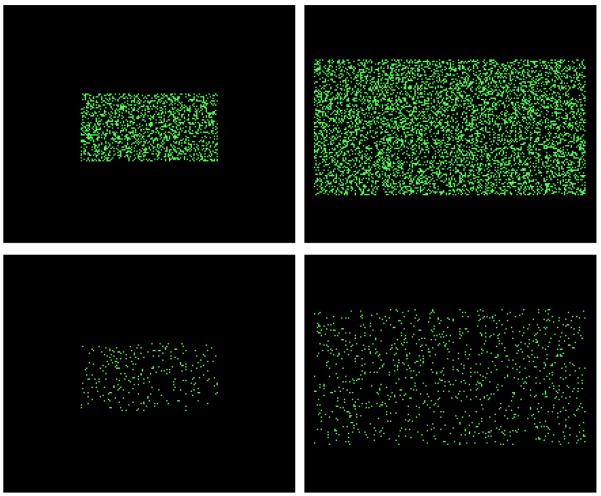
The stimuli were unframed rectangles containing green lit pixels, presented on a black background in the computer screen’s top center. Stimulus rectangles varied in size and pixel density. Both dimensions had 100 levels (Figure 2, caption). Figure 2 shows the stimuli in the four corners of the stimulus space.

Figure 2.

The 100 × 100 stimulus space illustrated. Rectangle size in screen pixels was calculated as 100+Level (width) and 50+Level/2 (height). Rectangles varied from 100 × 50 (Level 1) to 200 X100 (Level 100). Pixel density—that is, the proportion of total pixel positions that were illuminated—was calculated as .05 × 1.018^Level. Density varied from .0509 (Level 1) to .2977 (Level 100). Shown are Stimulus 1 1 (small-sparse), Stimulus 100 1 (big-sparse), Stimulus 1 100 (small-dense), and Stimulus 100 100 (big-dense). Stimuli were viewed from about 24 inches, presented on a 17-inch monitor (800 × 600 pixel resolution).

Category structures

Categories were defined by bivariate normal distributions along the stimulus dimensions as specified in Table 1. As each exemplar was selected as a coordinate pair in the 100×100 space, the abstract values were transformed into concrete size and density values. Each participant received their own sample of randomly selected category exemplars appropriate to their assigned task. To control for statistical outliers, exemplars were not presented if their Mahalanobis distance (e.g., Fukunaga, 1972) from the category mean exceeded 3.0. Figure 1 showed the category structures used here—a vertical RB task with size (Dimension X) relevant and a major-diagonal II task with size and density relevant.

Table 1. Distributional characteristics for the two category tasks.

Task	Category	MeanX	MeanY	VarX	VarY	CovarXY
RB	A	35.86	50.00	16.33	355.55	0
	B	64.14	50.00	16.33	355.55	0
II	A	40.00	60.00	185.94	185.94	169.61
	B	60.00	40.00	185.94	185.94	169.61

RB: rule-based; II: information-integration

Categorization trials

Below each to-be-categorized stimulus were the letters A (left) and B (right), with a central cursor (Figure S1, supplemental materials). Participants depressed the S or L on the keyboard to move the cursor across the screen until it reached the Category A or B icon, indicating that response. The keys corresponded spatially to the icons.

In the immediate-reinforcement condition, after a correct response, participants heard a whoop sound, earned a point, and saw their accumulated points (correct responses – incorrect responses). After an incorrect response, they heard a buzz sound, lost a point, received a 4 s timeout, and saw their accumulated points. The next trial followed.

In the deferred-reinforcement condition, participants completed six trials without feedback. After each response, the program simply gave the next trial. At block’s end, the participant received their positive outcomes grouped together (e.g., several whoops separated by .5 s for correct responses), then their negative outcomes grouped together (e.g., several buzzes separated by 4 s for incorrect responses). They were updated on their accumulated points. The next trial block followed.

Procedure

Participants were placed randomly into the RB or II task and the Immediate or Deferred condition. Trials continued until the 55-minute session ended or the participant completed 600 trials.

Formal modeling

We used a rule-based model to specify the vertical or horizontal line through the stimulus space that would best partition a participant’s Category A and B responses. We used an information-integration model to specify the slope and intercept of the (non-horizontal, non-vertical) line through stimulus space that would best partition the A and B responses. The best-fitting values for the parameters in the models were estimated using maximum-likelihood methods. We evaluated which model would have created with maximum likelihood the participant’s distribution of Category A and B responses in the stimulus space (details in Maddox & Ashby, 1993). The Bayesian Information Criterion (Schwarz, 1978) determined the best-fitting model (BIC = r lnN-2lnL, with r the number of free parameters, N the sample size, and L the model’s likelihood given the data).

Results

Accuracy-based analyses

The correct proportions for participants’ last 100 trials were entered into a two-way analysis of variance (ANOVA) with task type (RB, II) and reinforcement condition (immediate, deferred) as between-participant factors. 11 The crucial result was a significant interaction between task and condition, F (1, 80) = 4.03, p = .0481, η_p² = .0479, indicating that deferred reinforcement compromised II performance selectively.

RB-Immediate and RB-Deferred performance—.82 and .84 correct, respectively—were statistically indistinguishable, t (40) = −0.33, p = .744, Cohen’s d = −.10. There were 14 and 15 strong learners (terminal performance >= .80) in these conditions, respectively. Deferred reinforcement had no cost for RB category learning.

RB-Immediate and II-Immediate performance—.82 and .77 correct, respectively—were also indistinguishable, t (40) = 0.700, p = .488, Cohen’s d = .22. There were 14 and 11 strong learners in these conditions, respectively.

II-Immediate and II-Deferred performance—.77 and .64 correct, respectively—were distinguishable, t (40) = 3.76, p = .0005, Cohen’s d = 1.16. There were 11 and 0 strong learners in these conditions, respectively. Deferred reinforcement had a high cost for II category learning. We will see that the accuracy-based analyses sharply understated that cost.

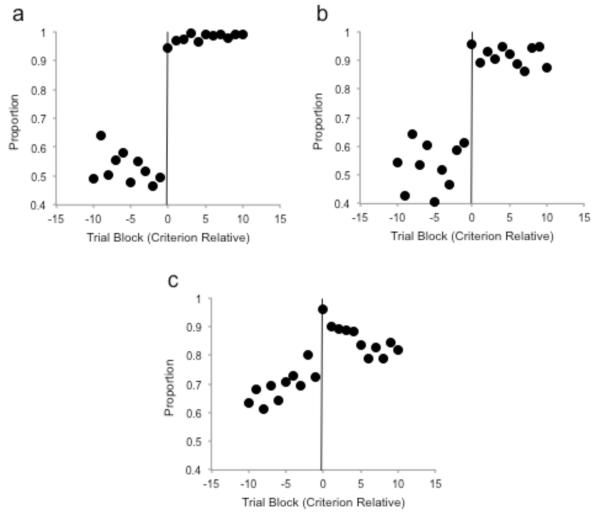
Figure 3A shows a backward learning curve for the RB-Deferred condition. We aligned the trial blocks at which the 15 strong learners reached a criterion (Block 0)—sustaining over 5 blocks .85 accuracy—to show the path by which they solved the RB task (Figure 3A, caption). RB performance transformed at Block 0 (.53 and .98 pre- and post-criterion)—from near-chance to near-ceiling performance. Figure 3A is perfectly intuitive if—and probably only if—one assumes the sudden discovery of a category rule. Figure 3A essentially defines the RB category-learning process that the literature has debated.

Figure 3.

A. A backward learning curve for RB-Deferred participants. In each 20-trial block, we scored all trials with X coordinate <= 40 or >=60. This let us accommodate variation in participants’ rule criterion near X=50, the true category breakpoint. Of these trials, we counted as correct A-Response trials with small X coordinates and B-Response trials with large X coordinates. We then found the participants (15) who met the criterion of reaching and sustaining .85 accuracy. We aligned their criterion runs (Block 0) to depict the path by which they solved the RB task. B. A backward learning curve for II-Deferred participants. In each 20-trial block, we scored all trials with Y coordinates >= 60 or <=40. Of these trials, we counted as correct A-Response trials with large Y coordinates and B-Response trials with small Y coordinates. We then found the participants (14) who met the criterion of reaching and sustaining .85 accuracy. We aligned their criterion runs (Block 0) to depict the path by which they chose an RB strategy in their nominal II task. C. A backward learning curve—assuming RB learning—for II-Immediate participants, constructed in the same way.

Figure 3B shows a backward learning curve for the II-Deferred participants but with a twist. That is, we assumed a Dimension Y, RB standard of correct and incorrect performance. We then found all the participants (14) who met the criterion of reaching and sustaining .85 accuracy defined in this rule-focused way (Figure 3B, caption). We aligned their criterion runs (Block 0) to depict the path by which these participants chose an RB strategy in their II task. These participants also jumped to rule use suddenly. This is a remarkable result because these participants were not RB reinforced. Their task was II. Their reinforcement contingency was II. Clearly, the reinforcement contingency was not controlling learning. Participants self-chose their RB strategy cognitively, facing the exigency of deferred reinforcement.

We repeated this analysis for the II-Immediate participants (Figure 3C). There was strong learning prior to Block 0 and only a small performance jump at criterion. Performance fell back down after the criterion blocks to a level continuous with that before criterion. The arrival at criterion was an artificial, statistical occurrence. The RB strategy was not evident in the II-Immediate condition (3C) but it emerged strongly in the II-Deferred condition (3B).

Model-based analyses

We modeled participants’ last 100 trials to ask whether they adopted appropriate decision strategies and whether deferred reinforcement disrupted those strategies or altered them in a theoretically meaningful way.

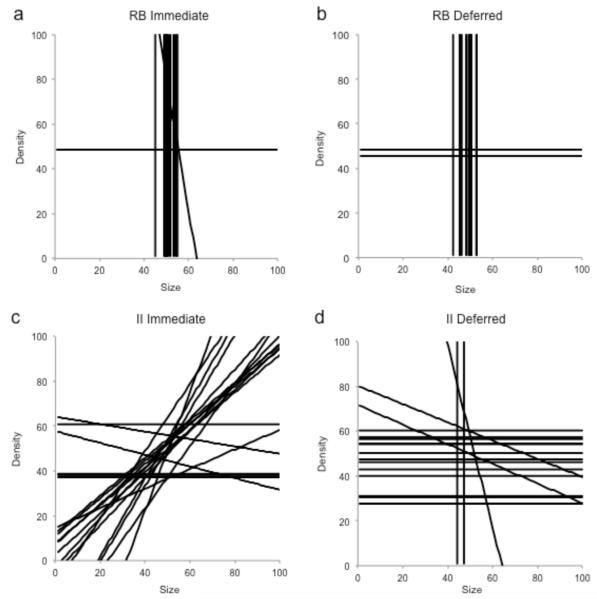
Figure 4A shows the modeling results for 15 RB-Immediate participants. (The poor performance of six other participants was not consistent with RB or II strategies—they were modeled to have a guessing strategy and no definite decision bound that could be drawn). The 15 decision bounds were mainly organized along the midline of the stimulus space’s X dimension. Many participants found the RB task’s adaptive solution—a one-dimensional size rule.

Figure 4.

A-DThe decision bounds that provided the best fits to the last 100 responses of participants in the rule-based (RB)-Immediate, RB-Deferred, information-integration (II)-Immediate, and II-Deferred conditions.

Figure 4B shows the modeling results for 17 RB-Deferred participants (4 participants modeled as guessers). The similarity to Figure 4A is clear-cut. Many of these participants also found the one-dimensional size rule. The model-based and accuracy-based analyses converged to show that that RB learning survived deferred reinforcement perfectly intact.

Figure 4C shows the modeling results for 19 II-Immediate participants. These decision bounds were generally organized along the stimulus space’s major diagonal. Many participants found a way to integrate the informational signals provided by the two stimulus dimensions toward making appropriate category decisions.

Figure 4D shows the modeling results for 18 II-Deferred participants. The dissimilarity from Figure 4C is striking. II category learning failed disastrously facing deferred reinforcement. There were no decision bounds tracing the stimulus space’s major diagonal. There was no appropriate information integration. Instead, participants defaulted to an RB strategy with decision bounds near the Y dimension’s midline. Possibly they defaulted to the only categorization process available under deferred reinforcement. They had to hold in mind a description of what they did over the whole trial block, so that the summary feedback—when it finally came—would be informative. Consistent with multiple-systems theory, this description took the form of a one-dimensional rule, not a principle for integrating information across dimensions. Figure 3B confirmed these participants’ process and point of rule discovery.

This result strengthens one’s interpretation of the accuracy-based analyses. The .64 accuracy achieved by II-deferred participants definitely does not signify 64% successful II learning. It signifies a heavy reliance on rules—that is, a reliance on the qualitatively wrong information-processing strategy for the II task. There wasn’t 64% II learning in this condition. There was 0% II learning under deferred reinforcement.

General Discussion

Summary

The controversy over multiple category-learning utilities is reminiscent of the debate over multiple memory systems. Categorization researchers continue to seek more sharply distinguishing paradigms. We contributed a new dissociative paradigm here by incorporating from comparative psychology the technique of deferred reinforcement.

We hypothesized that deferred reinforcement should disable associative learning and the II category learning that depends upon it. Deferred reinforcement eliminated II category learning. There may be no comparably strong demonstration in the literature.

We hypothesized that RB learners hold their category rule in working memory, still allowing its evaluation for adequacy at the end of the trial block when deferred reinforcement finally arrives. Confirming this hypothesis, RB learning was unscathed by deferred reinforcement.

The demonstration that II learning is fully dependent on trial-by-trial reinforcement, but RB learning is fully independent, supports the multiple-systems view by confirming the operation of qualitatively different category-learning processes in different tasks.

We hypothesized that—with II category learning disabled by deferred reinforcement—participants might fall back by necessity to RB strategies. They would need to maintain in working memory a description of their block-wide strategy so they could interpret the summary feedback when it arrived. According to multiple-systems theory, this working description would be a one-dimensional rule and not an information-integration principle. In fact, confirming multiple-systems theory in another way, II-Deferred participants clearly adopted one-dimensional category rules that did not suit their task’s II structure.

Dissociative Frameworks in Categorization

The confirmation of these three hypotheses represents one of the strongest RB-II dissociations yet seen.

One cannot attribute this dissociation to differential difficulty. We have discussed how RB and II tasks are controlled for every aspect of objective difficulty. Here the tasks were learned equivalently under immediate reinforcement, confirming that control. And, the result was not just that II learning worked more haltingly or with greater difficulty under deferred reinforcement. Instead, it did not engage at all—qualitatively—and the difficulty hypothesis cannot explain its complete absence. In addition, RB strategies showed a profoundly different learning trajectory from II strategies (Figure 3A). The difficulty hypothesis cannot explain that difference, either.

The difficulty hypothesis also raises more general concerns. If one defines difficulty by any objective standard, the tasks are matched for difficulty. If one defines difficulty by humans’ speed of learning and then uses difficulty to explain humans’ speed of learning, one is circular. If one explains humans’ speed of RB learning by an additional process or system that makes RB learning “easier,” one endorses multiple systems or processes. In the same way, one would not say that procedural learning—as compared to declarative memory—is preserved in amnesia because it is “easier.” There are more precise and theoretically illuminating things to say.

Nor can one claim that deferred reinforcement simply weakened the reinforcement signal by making it sporadic. Then, if RB and II learning depended on that signal equivalently, they would have been impaired equivalently. They were not. The demonstration that one learning process is reliant on trial-by-trial reinforcement, the other not, supports the multiple-systems view. Moreover, no possible explanation based in the strength of the reinforcement signal can explain why II-Deferred participants would have qualitatively shifted to RB processing. That shift is definitely not what the reinforcement signal was communicating, no matter its strength.

Another feature of the data disconfirms a single-system, exemplar-based explanation. The ability of exemplar models to capture learning trajectories in RB and II tasks has been debated (e.g., Ashby & Ell, 2002; Nosofsky & Kruschke, 2002). Exemplar models fit learning curves through gradual parameter changes. But the change shown in Figure 3A is qualitatively sudden, not gradual. Single-system models cannot fit this qualitative shift, or explain why there was no learning (i.e., no parameter changes) until Block 0, or explain why learning suddenly exploded at Block 0 (large parameter changes in one block). In contrast, all aspects of Figure 3A flow from assuming the sudden discovery of a category rule.

Our results do support the multiple-systems framework of categorization. Indeed, they instantiate perfectly the current theory of II learning. II category learning is presumably organized around a series of time-critical events that may surround the reinforcement-mediated strengthening of dopamine-related synapses (Ashby, Ennis, & Spiering, 2007). II learning cannot survive deferred reinforcement because the time-critical arrival of reinforcement is disrupted.

Our results also instantiate perfectly the current theory of RB learning. RB learning is presumably organized around rules actively held in working memory. RB learning survives deferred reinforcement because it does not depend on any temporal sequence of shaping or conditioning events. RB category knowledge is timeless in a sense because it is constantly available to consciousness. It is as fully applicable and updateable after a block of trials as after a single trial.

The present findings strengthen the fMRI evidence, the neuropsychological patient evidence, and other RB-II dissociative paradigms. Possibly the present data will bring the debate about RB, II, and multiple category-learning systems nearer to a consensual and collegial conclusion that would further the categorization literature’s theoretical development.

Adaptive Complementarity in Categorization

The multiple-systems framework in categorization points to an elegant division of cognitive labor that is insufficiently appreciated. Through II learning, cognition creates S-R bonds in a sense. Consequences (reinforcements) are the glue for associating adaptive behaviors to stimuli.

This system has considerable strengths. It produces stable behavior. It produces the behavior with the highest probability of reinforcement. It slowly, conservatively commits to behavioral solutions. It slowly, conservatively lets behavioral solutions go (through the class of extinction phenomena). It operates preattentionally, out of awareness, potentially granting it great phylogenetic breadth.

But this system has constraints. It depends on immediate reinforcement, time-critical event sequences, and persistent event repetition. Learning cannot occur off-line or with displacement in time or space from the task’s trials. New approaches cannot be chosen instantly at need. Old approaches cannot be replaced instantly at need.

RB learning is a perfect complement to II learning. It is not rigidly time locked. It does not depend on immediate reinforcement or event repetition. Learning can occur off-line and with displacement. Learning and unlearning can occur suddenly at need.

The Phylogenetic Depth of Adaptive Complementarity

The adaptiveness of these complementary categorization utilities raises a question of their phylogenetic depth that recent research has addressed. Smith et al. (2010) found that rhesus macaques (Macaca mulatta), like humans, sometimes learn RB tasks much faster than II tasks. Thus, nonhuman primates have some structural components of humans’ capacity for explicit categorization and glean some of the benefits of the RB category-learning system, though they may not have all the components of humans’ explicit system (e.g., full declarative awareness). Smith et al. (2012) generalized this finding to another large primate group, the New World monkeys.

In contrast, Smith et al. (2011) found that pigeons learned RB and II tasks to the same level at the same speed. In pigeons, the cognitive system may not have strongly committed to dimensional analysis and category rules. Pigeons may lack the explicit-implicit complementarity in categorization that primates possess. Pigeons’ performance could illuminate the ancestral vertebrate categorization system from which that of primates and humans emerged.

One sees from this discussion that the dissociative framework describing explicit and implicit systems of categorization continues to illuminate and enrich the cognitive and comparative literatures on categorization. It guides productive empirical research, generates testable predictions, and expresses important adaptive complementarities among the categorization utilities possessed by humans and some nonhuman species.