Bayesian Model Aggregation for Ensemble-Based Estimates of Protein pK_a Values

Abstract

This paper investigates an ensemble-based technique called Bayesian Model Averaging (BMA) to improve the performance of protein amino acid pK_a predictions. Structure-based pK_a calculations play an important role in the mechanistic interpretation of protein structure and are also used to determine a wide range of protein properties. A diverse set of methods currently exist for pK_a prediction, ranging from empirical statistical models to ab initio quantum mechanical approaches. However, each of these methods are based on a set of conceptual assumptions that can effect a model’s accuracy and generalizability for pK_a prediction in complicated biomolecular systems. We use BMA to combine eleven diverse prediction methods that each estimate pK_a values of amino acids in staphylococcal nuclease. These methods are based on work conducted for the pK_a Cooperative and the pK_a measurements are based on experimental work conducted by the García-Moreno lab. Our cross-validation study demonstrates that the aggregated estimate obtained from BMA outperforms all individual prediction methods with improvements ranging from 45-73% over other method classes. This study also compares BMA’s predictive performance to other ensemble-based techniques and demonstrates that BMA can outperform these approaches with improvements ranging from 27-60%. This work illustrates a new possible mechanism for improving the accuracy of pK_a prediction and lays the foundation for future work on aggregate models that balance computational cost with prediction accuracy.

1 Introduction

The calculation of pK_a values and titration behavior plays an important role in the analysis of biomolecular structure and function, including catalytic activity [19], ligand binding [59], and protein stability [6,9,46,71]. Accurate pK_a predictions, however, are challenging to calculate due to a variety of computational factors including appropriate treatment of electronic, solvation, and electrostatic effects [22,23,65] as well as adequate sampling of the biomolecular ensemble and response to titration state change [12,25,31,36,57,63,69,74]. A wide range of approaches have been developed for estimating the pK_a and titration behavior of proteins [1] and other biological molecules [60]. These approaches range from physics-based methods and simulations [3,37,63,68], to data-driven methods that are primarily based on statistical models [8, 44, 56]. To differentiate between these approaches, we will use the term method throughout this paper to indicate what many computational chemists would call a model for predicting pK_as, and we reserve the word model to indicate a statistical model. The topic of pK_a prediction has been thoroughly addressed in other articles [42].

Common across all pK_a methods is the uncertainty associated with selecting, specifying, and evaluating a set of processes, parameters, and mathematical systems in order to accurately estimate pK_a. This type of uncertainty, referred to as method selection uncertainty, is arguably the greatest source of error and risk associated with model-based estimation and can affect a wide range of scientific and mathematical disciplines [2, 15, 51]. One of the most powerful ways to address selection uncertainty is through ensemble-based estimates [5, 28, 45, 52]. In ensemble approaches, estimates from a collection of methods are combined (e.g., through a weighted average) to form a single aggregated estimate. The motivation behind ensemble-based approaches is based on two principles: 1) all methods in the ensemble possess some unique, useful information; and, 2) no single method is sufficient to fully account for all uncertainties. Proponents of ensemble-based approaches assert that the best method to use for estimation is a combination of all of the methods. The underlying premise behind this tenet is that the information and strengths of individual methods can be combined, and their corresponding weaknesses and biases can be overcome by the strength of the group [28, 47, 49, 55]. Ensemble-based estimates are therefore expected to be more reliable and potentially more accurate than individual methods, an expectation that has been upheld in numerous examples [5,28,41,45,48,52,55,61,73].

Recently, an informal “pK_a Cooperative” group has been established to explore the strengths and weaknesses of titration state prediction methods in the context of well-characterized experimental systems [42]. This paper uses the results of predictions from the Cooperative to investigate the utility of an ensemble-based approach called Bayesian Model Averaging (BMA) [28] to estimate pK_a values measured by the García-Moreno lab in staphylococcal nuclease [4, 6, 9, 10, 18, 26, 27, 31–35]. Although other statistical approaches have been used to train [40, 53] and analyze [8, 70] pK_a prediction algorithms, and BMA itself has been applied successfully for prediction tasks across many domains [41,48,61,72], this is the first application of the BMA approach to this problem domain.

2 Methods

2.1 Bayesian Model Averaging

For pK_a prediction, a basic BMA approach is to consider a set of prediction methods as a linear system [28, 47, 49]. Let y_i for i = 1, … , N be a series of pK_a observations, and let x_ij denote the i^th estimate obtained from the j^th prediction method for these observations.For example, given that y_i is the experimentally measured pK_a of Arg 313, each x_ij for j = 1, … , P would be a specific method’s estimate for this value. Given P prediction methods, the combination of all x_ij forms the numerical ensemble estimate matrix that, along with y_i, defines a linear regression model

$$y_i=\sum _{j=1}^P{x}_{\mathit{ij}}{\beta }_j+{∊}_i$$ (1)

Here, the parameter vector β_j defines the unknown relationship between the ensemble’s P constituents and ∊_i is the disturbance term that captures all factors (e.g., noise and measurement error) that influence the dependent variable y_i other than the regressors x_ij.

In evaluating Equation 1, the objective is to estimate the values β_j that will both fit the known pK_a data in y_i and facilitate the ability to make inferences on unknown pK_a values. Many different regression techniques can estimate β_j [7,30,38,50]; however, these techniques commonly generate estimates that vary in their ability to model and infer [13,21,28,47,49]. The risk and uncertainty associated with using one of these estimates over any other estimate (i.e., for statistical inference) is called statistical model uncertainty. Like method selection uncertainty, statistical model uncertainly is also a common source of error in predictive modeling [28,47–49,62].

BMA addresses the challenge of statistical model uncertainty by first evaluating all possible models that can be formed from the P prediction methods, and then combining each model’s estimates for β_j through a weighted average. This aggregation process generates an aggregate-based parameter vector, ${\beta }_j^{\mathrm{BMA}}$ (Equation 2) that can provide more accurate and reliable estimates than any ensemble method, and can also outperform other ensemble-based strategies (e.g., stepwise regression) [13,21,28,64].

Formally, there are k = 1, … , 2^P − 1 distinct combinations of the P methods, each with a corresponding statistical model, M^(k), and parameter vector, ${\beta }_j^{\left(k\right)}$. BMA combines each ${\beta }_j^{\left(k\right)}$, through a weighted average that weights each ${\beta }_j^{\left(k\right)}$ by the probability that its statistical model, M^(k), is the “true” model.

$${\beta }_j^{\mathrm{BMA}}=E[{\beta }_j\mid \mathrm{y}]=\sum _{k=1}^{2^P-1}E[{\beta }_j^{\left(k\right)}\mid \mathrm{y},M^{\left(k\right)}]\mathrm{Pr}(M^{\left(k\right)}\mid \mathrm{y})$$ (2)

In Equation 2, $E[{\beta }_j^{\left(k\right)}\mid \mathrm{y},M^{\left(k\right)}]$ is the expected value of the posterior distribution of ${\beta }_j^{\left(k\right)}$ that is weighted by the posterior probability Pr(M^(k)∣y) (i.e., the probability that M^(k) is the true statistical model given y_i). The expected posterior distribution of ${\beta }_j^{\left(k\right)}$ is approximated through the linear least squares solution of the given model M^(k) and pK_a response variable, y = [y₁, … , y_N]. The posterior probability term is estimated from information criteria [47]

$$\mathrm{Pr}(M^{\left(k\right)}\mid \mathrm{y})\propto \frac{e^{-\frac{1}{2}{B}^{\left(k\right)}}}{\sum _{l=1}^{2^P-1}{e}^{-\frac{1}{2}B\left(l\right)}}$$ (3)

where B^(k) is the Bayesian Information Criteria for model M^(k), and the information criteria itself is estimated [47]

$$B^{\left(k\right)}\approx N\log (1-R^{2\left(k\right)})+p^{\left(k\right)}\log N$$ (4)

Here R^2(k) is the R² correlation value for model M^(k), p^(k) is the number of methods used by the model (not including the intercept), and N is the number of pK_a values to be predicted. BMA’s aggregation thus weights each model’s expected parameter vector ${\beta }_j^{\left(k\right)}$ with the probability value that is based on that model’s ability to balance trade-offs between model complexity (i.e., the number of methods used) and goodness of fit. Models that use a larger number of methods, or that do not fit the observations well, are penalized and can be eliminated from the final aggregation process (i.e., their posterior probabilities are effectively 0). In this context, BMA combines the best models to provide an accurate estimate for the true parameter terms, β_j.

The resulting parameter vector, ${\beta }_j^{\mathrm{BMA}}$, obtained from Equation 2 helps to address model uncertainty by accounting for all systems of linear equations that can model the relationship between the measured pK_a values y_i and values x_ij predicted by each method j. More importantly, ${\beta }_j^{\mathrm{BMA}}$ can be used to estimate new pK_a values for unmeasured residues by combining new x_ij estimates.

2.2 pK_a data and prediction methods

We apply the BMA approach to a set of prediction methods that estimate 83 pK_a values for Lys, Asp, and Glu residues in staphylococcal nuclease mutants measured by the García-Moreno lab in a series of studies [4, 6, 9, 10, 26, 27, 31–35]. As this data is the largest set of systematic pK_a values available for any protein system, it provides an extremely valuable resource for the development of new computational methods for pK_a prediction.

The set of prediction methods for this data comes from a large-scale, collaborative exercise run by the pK_a Cooperative to assess and compare contemporary strategies for estimating pK_a values [42]. In this study, we have used only a subset of the methods demonstrated in the pK_a Cooperative tests and a subset of the original 83 “ground truth” experimental pK_a measurements. This restriction is due to the fact that most methods used in the pK_a Cooperative tests provided predictions for only a subset of the 83 residues and mutants characterized by the García-Moreno lab; most methods only provide estimates for half of the data. In order to include the maximum number of methods in the aggregation process, we only consider locations on the nuclease protein where all ensemble members provide a predicted estimate. As a result, our study is based on 36 measurements listed in Table I.

Table I.

This table lists the locations and experimental values for pK_a measurements on a series of mutant staphylococcus nuclease proteins used in our cross-validation study. References for each measurement are provided in the table:

Residue	D20d	E23c	E25c	K25b	K34b	K36b	E38c	E39c	E41c
pKa	4.0	7.1	7.5	6.3	7.1	7.2	6.8	8.2	6.5
Residue	D41d	D58d	K62b	D62d	E62c	D66d	E66a;c	E72c	K72b
pKa	4.0	6.8	8.1	8.7	7.7	8.1	8.5	7.3	8.6
Residue	D74d	E74c	D90d	E91c	K91b	E92c	E99c	D99d	D100d
pKa	8.3	7.8	7.5	7.1	9.0	9.0	8.4	8.5	6.9
Residue	E100c	K103b	K104b	D109d	D118d	E125c	D125d	D132d	E132c
pKa	7.6	8.2	7.7	7.5	7.0	9.1	7.6	7.0	7.0

^aDwyer et al., 2000 [18]

^bIsom et al., 2011 [31]

^cIsom et al., 2010 [32]

^dBertrand García-Moreno, personal communication, 2009.

The subset of pK_a Cooperative methods used in the BMA approach were chosen based on two criteria. First, we select those methods that predict the greatest number of common residues/mutants. Second, in the event that multiple method variants exist, we chose only a single variant to eliminate the number of highly correlated methods in the aggregate. We perform this second step to ensure that multicollinearity does not inflate the significance that certain methods have during model selection and averaging; such bias can create unstable estimates for ${\beta }_j^{\mathit{BMA}}$ that can reduce BMA’s predictive accuracy [11]. Table II summarizes the 11 methods that constitute our ensemble; each method predicts the 36 measurments in Table I. This table also lists each method’s approach for conformational sampling and its solvation model.

Table II.

This table lists the pK_a prediction methods used in our BMA approach. Sampling strategies include molecular dynamics (MD), Monte Carlo (MC), Rosetta structure refine ment (Rosetta), and static structure (Static). Solvation models include generalized Born (GB), Poisson-Boltzmann (PB), and empirical methods (Empirical).

Reference	Sampling strategy	Solvation model	Number of predictions made (out of 89 total)
“Null” model	—	—	89
Wallace J, et al, 2011 [63]	MD	GB	68
Warwicker J, 2011 [66]	Static	PB	83
Rostkowski M, et al, 2011 [53]	Static	Empirical	89
Milletti F, et al, 2009 [40]	Static	Empirical	74
Nielsen JE, et al, 2001 [43]	Static	PB	87
Witham S, et al, 2011 [69]	MD and MC	GB and PB	65
Word JM, et al, 2011 [70]	Static	PB	61
PDB2PKA [16, 43]	Static	PB	87
Song Y, 2011 [57]	MC and Rosetta	PB	69
Meyer T, et al, 2011 [39]	Static	PB	87

Four types of sampling strategies were used by the methods considered in this study: molecular dynamics (MD) simulations [63,69], Monte Carlo (MC) sampling [57,69], Rosetta model refinement [57], and static structures [39, 40, 43, 53, 66, 70]. Three basic types of implicit solvation models were used: generalized Born [17,58], Poisson-Boltzmann and related methods [14,20,29], and empirical approaches [40,53]. Finally, a “null” model consisting of model compound pK_a values (ASP = 3.8, GLU = 4.3, LYS = 10.5) is also included in the analysis. The results of these methods are shown in Figure 1.

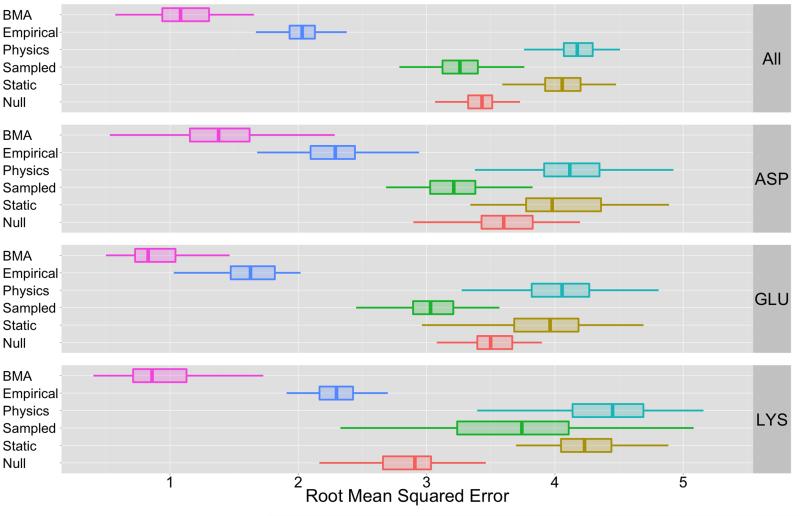
Figure 1.

This figure depicts a summary of root-mean-squared error for various conformational sampling and solvation methods (see Table II). The label “BMA” reflects performance for a BMA instance that uses all methods in Table II to construct β_BMA; we examine the performance effects of constraining the ensemble to specific methods (e.g., BMA based only on Static methods) in Figure 2 and Table VII. The “Sampled” set contains results from methods that use MD, MC, and Rosetta sampling methods; the “Static” set contains results from methods that did not use conformational sampling. The “Physics” set contains results from methods that use GB and PB solvation models; the “Empirical” set includes methods with empirical solvation models. From these results, we see that the BMA-based approach substantially outperforms all other classes of methods: BMA-based estimates reduce error by approximately 65% in comparison to methods that use conformational sampling, and by about 73% in comparison to the static-conformation and physics-based solvation methods. In comparison to BMA, empirical solvation methods provide the next-best estimates; these estimates are approximately 45% higher in error than BMA estimates. The mean RMSE values shown in this figure are listed in Table III. The statistical significance of BMA’s performance is based on p-values shown in Table VI.

2.3 Training and estimating with BMA

To train the BMA model, we began by randomly sampling (without replacement) 18 of the original 36 experimental pK_a measurements. Collectively, these sampled values form the observation vector y_i. The estimates from each of the 11 pK_a prediction methods in Table II for these measurements define the ensemble estimate matrix, x_ij. The observation vector and the ensemble estimate matrix form the linear system in Equation 1. Next, we estimated the ${\beta }_j^{\mathrm{BMA}}$ parameter from Equation 2 by assembling all k = 1, … , 2¹¹ − 1 = 2047 possible statistical models M^(k) and estimating each model’s posterior probability (Equation 3) based on its associated R^2(k) value and its number of independent parameters (Equation 4). The calculated parameters ${\beta }_j^{\mathrm{BMA}}$ are the weighted average of each statistical model’s ordinary least squares solution based on that model’s posterior probability. Finally, we use ${\beta }_j^{\mathrm{BMA}}$ to estimate the remaining 18 pK_a measurements that were not used to train the BMA model. This task is accomplished by combining the estimates of all methods in Table II for the validation data with ${\beta }_j^{\mathrm{BMA}}$ to produce an aggregate prediction.

3 Results and discussion

We exercised the training and estimation process in Section 2.3 repeatedly in a 100-fold cross-validation study to assess the performance of several prediction approaches. In each of the study’s 100 tests, we randomly selected (without replacement) 18 of the 36 experimental measurements as training data and used the remaining 18 measurements as validation data.Thus for a given test in our cross-validation study, we determined the root mean squared error (RMSE) of each prediction approach based on the validation data. The distribution of the RMSE for all 100 tests are reported for each predictive approach in our results (see Figures 1-3).

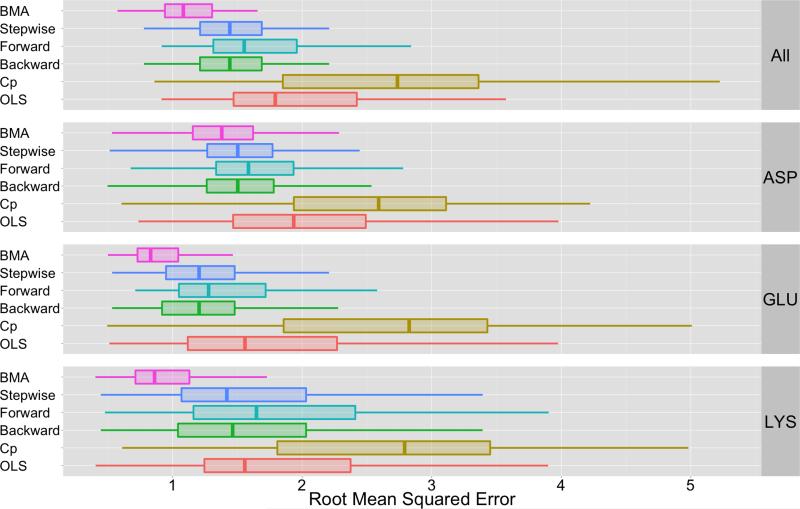
Figure 3.

This figure depicts a summary of root-mean-squared error for different ensemble approaches. The label “BMA” indicates that the BMA aggregate uses all methods from Table II to construct β_BMA. The other approaches are alternative ensemble techniques that are based on different strategies for model specification (see Section 3.3). The mean RMSE values shown in this figure are listed in Table V and the statistical significance of BMA’s performance is based on p-values shown in Table VIII. Based on data in Table VIII and Table V, BMA-based approach outperform all other ensemble techniques: BMA-based estimates reduce error by approximately 27% in comparison to Backward and Stepwise regression techniques and by 35% in comparison to Forward regression. In comparison to an ordinary least squares approach that uses all methods in II, BMA reduces error by approximately 46%. Finally, in comparison to C_p methods, BMA reduces error by approximately 60%.

Based on these RMSE distributions, we assessed the performance of BMA to a given prediction approach X through a Wilcoxon rank sum paired comparison test [67]. This non-parametric approach tests the hypothesis that the RMSE distributions of BMA and X are equal: H₀ : μ_BMA = μ_X. To control the familywise error rate of our tests (there were 56 paired tests in total), we applied a Bonferroni correction to determine a p-value threshold of $\alpha =\frac{0.05}{56}=9.0E-4$. Thus when comparing BMA to X, a Wilcoxon-generated p-value that is greater than 9.0E – 4 indicates we fail to reject H₀: the distributions are thus equal and we conclude that BMA and X are equivalent in their predictive accuracy. On the other hand, Wilcoxon-generated p-values that are less than 9.0E – 4 indicate we should reject H₀. In this latter case, we then compared the mean RMSE for BMA (Tables III, IV, and V) and the given technique to assess performance.

Table III.

This table lists the average root-mean-squared-error performance results from our 100-fold cross-validation study, ordered by the overall error obtained by the model or method. The table shows performance for BMA, the Null model, as well as performance of categories of pK_a prediction methods. The “Sampled” set contains results from methods which used MD, MC, and Rosetta sampling methods; the “Static” set contains results from methods which did not use conformational sampling. The “Physics” set contains results from meth ods which used GB and PB solvation models; the “Empirical” set includes methods with empirical solvation models. The ensemble of prediction methods is broken into two comparative groups based on conformational sampling strategy (e.g., MD, MC, and Rosetta sampling vs. static) and solvation model (GB and PB solvation methods vs. empirical methods). Additionally, cross-validation results are shown for all amino acids as well as for the individual amino acid types ASP, GLU, and LYS. The statistical significance of BMA’s performance is based on p-values shown in Table VI. Table VI indicates that BMA’s mean RMSE is statistically significant to all other methods. Based on this table’s mean RMSE scores, we see that the BMA-based approach outperforms all other ensemble techniques: BMA-based estimates reduce error by approximately 65% in comparison to methods that use conformational sampling, and by about 73% in comparison to the static-conformation and physics-based solvation methods. In comparison to BMA, empirical solvation methods provide the next-best estimates; these estimates are approximately 45% higher in error than BMA estimates.

Method class	All	ASP	GLU	LYS
BMA	1.155	1.376	0.924	1.023
Empirical solvation	2.031	2.264	1.609	2.280
Physics-based solvation	4.167	4.129	4.051	4.414
Sampled conformations	3.257	3.209	3.034	3.628
Static conformations	4.057	4.061	3.936	4.246
Null	3.420	3.598	3.516	2.861

Table IV.

This table lists the average root-mean-squared-error (RMSE) performance results from our 100-fold cross-validation study based on the distributions in Figure 2. The label “BMA” indicates that the BMA aggregate uses all methods from Table II to construct BMA. The “BMA-Empirical” and “BMA-Physics” labels indicate performance for BMA instances that are based on ensembles that only consider a subset of the total methods; e.g., the “BMA-Empirical” aggregation process only uses methods from the Empirical class to construct BMA. Likewise, “BMA-Static” and “BMA-Sampling” labels indicate performance for ensembles that are restricted by sampling strategies. The statistical significance of these mean RMSE values is based on p-values shown in Table VII. Table VII indicates the performance for all BMA instances is equivalent with the exception of two cases: the BMA-Physics ensemble when predicting LYS residues; and, BMA-Static when predicting ASP residues.

Aggregate	All	ASP	GLU	LYS
BMA	1.155	1.376	0.924	1.023
BMA-Empirical	1.127	1.443	0.867	0.845
BMA-Physics	1.164	1.318	0.959	1.111
BMA-Sampled	1.017	1.260	0.809	0.828
BMA-Static	1.175	1.496	0.944	0.830

Table V.

This table lists the average root-mean-squared-error performance results from our 100 X cross-validation study based on the distributions in Figure 3. The label “BMA” indicates that the BMA aggregate uses all methods from Table II to construct β_BMA. The other approaches are alternative ensemble techniques that are based on different strategies for model specification (see Section 3.3). The statistical significance of these mean RMSE is based on p-values shown in Table VIII. Table VIII indicates that BMA’s mean RMSE is statistically significant to all other methods. Based on this table’s mean RMSE scores, we see that the BMA-based approach outperforms all other ensemble techniques: BMA-based estimates reduce error by approximately 27% in comparison to Backward and Stepwise regression techniques and by 35% in comparison to Forward regression. In comparison to an ordinary least squares approach that uses all methods in II, BMA reduces error by approximately 46%. Finally, in comparison to C_p methods, BMA reduces error by approximately 60%.

Ensemble technique	All	ASP	GLU	LYS
BMA	1.155	1.376	0.924	1.023
Stepwise regression	1.564	1.541	1.298	1.766
Forward regression	1.740	1.680	1.436	2.044
Backward regression	1.565	1.543	1.295	1.768
Cp	2.839	2.756	2.851	2.858
Ordinary Least Squares (OLS)	2.089	2.219	1.865	1.983

We report the results of our study in three stages. Stage 1 compares the predictive results of BMA to predictions of different methods in Table II. Stage 2 assesses the robustness of BMA by evaluating BMA predictions that are based on different ensembles of methods from Table II. Stage 3 compares BMA’s performance to the performance of other aggregation approaches (e.g., Stepwise regression) to examine the benefits of addressing statistical model uncertainty.

3.1 Stage 1: Comparing BMA to the ensemble of pK_a methods

We have chosen to analyze the results by overlapping classes of methods (see Table II), rather than by individual method, for multiple reasons. First, we intend to confound the analysis of individual model performance out of respect for the authors of the methods who freely contributed their results to the pK_a Cooperative. The goal of the Cooperative is to encourage open conversation and exchange of ideas on improving biomolecular solvation models – not to rank or select “winners” from the pool of prediction methods. Second, the goal of this paper is to illustrate the potential benefits of model aggregation via BMA rather than analyze the performance of any single prediction method.

Table III and Figure 1 both provide an overview of the cross-validation pK_a prediction errors for BMA, the null model, and the various sampling and solvation methods. There are specific models in each of the categories (empirical, physics-based, static, and sampled) that will typically perform with errors < 2 pK_a units. For example, in Figure 1 we can see that for GLU the expected performance for all empirical models is < 2.

However, from these results, we see that the BMA-based approach substantially outperforms all other classes of methods for all amino acids: BMA-based estimates reduce error by approximately 65% in comparison to methods that use conformational sampling, and by about 73% in comparison to the static-conformation and physics-based solvation methods. In comparison to BMA, empirical solvation methods provide the next-best estimates; these estimates are approximately 45% higher in error than BMA estimates. The statistical significance of BMA’s performance is based on p-values shown in Table VI. Based on an α value of 9.0E – 4, this table indicates that we reject H₀ for all paired comparison tests. By comparing μ_BMA to other mean RMSE scores (see Table III), we concluded that BMA provides better performance than any method class in Figure 1.

Table VI.

This table contains p-values that indicate the statistical significance of BMA’s RMSE distribution compared to other methods in Figure 1. P-values are based on a Wilcoxon rank sum paired comparison test that detects if data populations for BMA and method X (e.g., Sampled or Static) are identical: Based on the 56 paired tests (Figures 1- 3) we determine a p-value threshold of α = 0.05/56 = 9.0×10⁻⁴; p-values less than 9.0×10⁻⁴ thus indicate that we reject the null hypothesis that the two distributions are identical. This table indicates that we reject this null hypothesis for all paired comparison tests and by comparing the mean BMA RMSE to other mean RMSE scores listed in Table III, As such, we conclude that BMA provides better performance than any method class in Figure 1. Repeated values in this table reflect floating point precision limits in the p-value calculation.

Method	All	ASP	GLU	LYS
Empirical	3.95×10−18	4.73×10−18	9.38×10−18	6.28×10−17
Physics	1.98×10−18	1.98×10−18	1.98×10−18	1.98×10−18
Sampled	1.98×10−18	1.98×10−18	1.98×10−18	2.17×10−18
Static	1.98×10−18	1.98×10−18	1.98×10−18	2.04×10−18
Null	1.98×10−18	2.04×10−18	1.98×10−18	8.09×10−18

3.2 Stage 2: Comparing different ensembles of methods for BMA

We applied BMA to five distinct ensembles, where each ensemble was based on a unique set of methods listed in Table II. We then compared the performance of each of these BMA instances to assess how changes in ensemble constituents affect BMA’s predictive accuracy. The first instance, labeled “BMA”, is based on an ensemble that includes all methods in Table II. This instance is the same BMA instance used in Section 3.1 and Section 3.3. The next four instances were based on a subset of the methods in Table II. Specifically, the instance labeled “BMA-Static” is based on an ensemble that only used methods that relied on static-conformations (see Table II, second column). Similarly, the instance labeled “BMA-Sample” utilized an ensemble that was defined by methods that only use conformational sampling. The last two instances, BMA-Physics and BMA-Empirical, were defined exclusively by methods that used physics-based or empirical solvation approaches respectively (see Table II, third column).

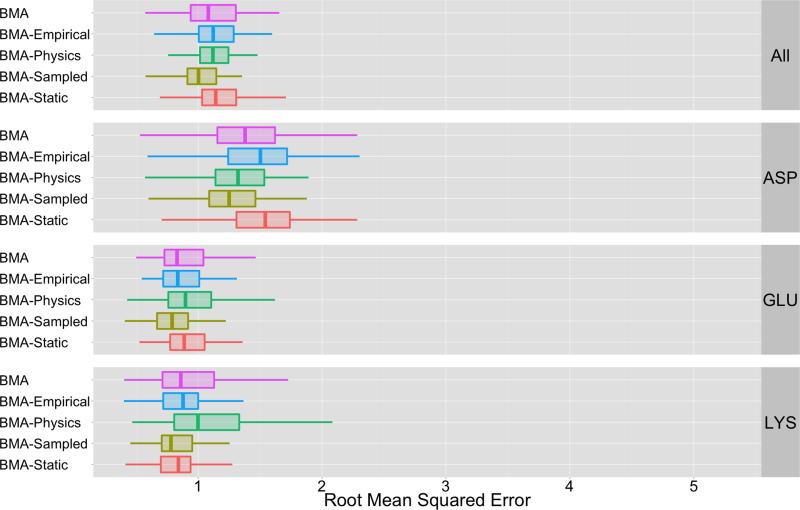
Figure 2 and Table IV summarize the cross-validation pK_a prediction errors for the various BMA instances. From the RMSE distributions in Figure 2, it is clear that all instances provide excellent predictive capability. The significance of the results in Figure 2 and Table IV are base on the p-values in Table VII. Based on an α value of 9.0E – 4, these p-values indicate that we accept H₀ for all comparison tests save two: the BMA-Physics ensemble when predicting LYS residues and the BMA-Static ensemble when predicting ASP residues. Thus for almost all cases, the performance of the BMA instances are equivalent. In the two exceptions where H₀ was rejected, the BMA instance based on the entire ensemble of methods reduced error by approximately 8% compared to the other instances. The results of these comparisons indicate that the BMA approach is robust and that BMA can overcome deficiencies observed in certain classes of methods (see Figure 1) to provide consistent predictive performance.

Figure 2.

This figure depicts a summary of root-mean-squared error for different BMA ensemble instances. The label “BMA” indicates that the BMA aggregate uses all methods from Table II to construct β_BMA. The “BMA-Empirical” and “BMA-Physics” labels indicate performance for BMA instances that are based on ensembles that only consider a subset of the total methods; e.g., the “BMA-Empirical” aggregation process only uses empirical methods to construct β_BMA. “BMA-Static” and “BMA-Sampling” labels indicate performance for ensembles that are restricted by sampling strategies. The mean RMSE values shown in this figure are listed in Table IV. The statistical significance of BMA’s performance is based on p-values shown in Table VII. Based on Table IV and Table VII, we conclude that the performance of all instances are equivalent with the exception of two cases (BMA-Physics predicting LYS and BMA-Static predicting ASP). In these two cases, BMA based on a full ensemble outperforms these instances by approximately 8%.

Table VII.

This table contains p-values that indicate the statistical significance of performance for BMA based on the different ensembles shown in Figure 2. P-values are based on a Wilcoxon rank sum paired comparison test as described in Table VI. This table indicates that we accept the null hypothesis that the methods using different ensemble subsets behave identically for all comparison tests save two (italicized for contrast): the BMA-Physics ensemble when predicting LYS residues; and, BMA-Static ensemble when predicting ASP residues. The predictive performance of BMA based on different ensembles is therefore equivalent in almost all cases. For these two cases where we reject the null hypothesis, we compare the mean RMSE of BMA to the mean RMSE of BMA-Physics and BMA-Static (Table IV) to identify that BMA reduces error by approximately 8% compared to these instances.

Aggregate	All	ASP	GLU	LYS
BMA-Empirical	1.19×10−1	1.00×10−3	4.92×10−1	9.58×10−1
BMA-Physics	5.83×10−2	9.90×10−1	9.38×10−3	1.19×10−4
BMA-Sampled	1.00	1.00	9.99×10−1	9.98×10−1
BMA-Static	2.20×10−3	7.32×10−6	8.08×10−3	9.90×10−1

3.3 Stage 3: Comparing BMA to other ensemble techniques

There are other approaches besides BMA that can combine an ensemble of methods to make an aggregate prediction. In our cross-validation study, we evaluated five common approaches for aggregating an ensemble and evaluated their predictive benefits in comparison to BMA. These methods included: forward regression, backward regression, step-wise regression, ordinary least squares (based on all methods in Table II), and Mallow’s Cp statistic. These techniques were chosen as they have all been used successfully for a variety of inference tasks [24, 54]. As all of these approaches constructed an estimate for β_i, training and predicting with these approaches was performed identically to how we trained and predicted with BMA (Section 2.3). As a result, we also followed the same procedure for comparing BMA’s predictive capability to these alternate ensemble-based prediction techniques.

Figure 3 and Table V provide an overview of the cross-validation pK_a prediction errors for the various ensemble-based prediction approaches and BMA (BMA used an ensemble that included all methods in Table II). The statistical significance of BMA’s performance in Figure 3 is based on p-values shown in Table VIII. Based on an α value of 9.0E–4, Table VIII indicates that we reject H₀ for all paired comparison tests. BMA’s RMSE distribution is therefore not equivalent to the RMSE distribution of any other ensemble-based technique

Table VIII.

This table contains p-values that indicate the statistical significance of BMA’s RMSE distribution compared to the other ensemble-based methods in Figure 3. P-values are based on Wilcoxon rank sum paired comparison test as described in Table VI. This table indicates that we reject the null hypothesis for all paired comparison tests and by comparing and conclude that BMA provides better performance than any ensemble approach in Figure 3.

Ensemble technique	All	ASP	GLU	LYS
Stepwise	3.85×10−15	1.29×10−4	7.25×10−17	5.78×10−14
Forward	9.94×10−17	4.10×10−9	6.57×10−18	2.41×10−16
Backward	3.85×10−15	1.12×10−4	8.37×10−17	6.76×10−14
Cp	1.96×10−17	2.41×10−16	1.50×10−17	1.86×10−16
Ordinary Least Squares (OLS)	1.19×10−17	1.19×10−13	3.32×10−17	4.12×10−14

As the distributions are not equal, we compared mean RMSE distributions of BMA to the other ensemble-based approaches in Figure 3 and Table V. From these mean RMSE, it is clear that the BMA-based approach outperforms all other ensemble-based prediction approaches: BMA-based estimates reduced error by approximately 27% in comparison to Backward and Stepwise regression techniques and by 35% in comparison to Forward regression. In comparison to an ordinary least squares approach that uses all the methods in Table II, BMA reduces error by approximately 46%. Finally, in comparison to Mallow’s C_p technique, BMA reduces error by approximately 60%.

4 Conclusions

This study demonstrates a proof-of-principle application of BMA to pK_a prediction using a single protein (staphylococcus nuclease) as a test case. While the performance of BMA is expected to generalize to a much broader set of pK_a prediction problems, the specific BMA model trained in this study is likely to be dependent on the staph nuclease system. In particular, the staph nuclease system has been engineered for stability and tolerates many internal titratable residues by shifting their pK_a values towards neutral titration states when covered with solvent. We note that this work is complementary to the hybrid methods developed by Witham et al. [69] which suggest the use of multiple or hybrid pK_a prediction methods based on the nature of the residue under consideration. For example, Witham et al. use structural features and the molecular environment to help select the best sampling and prediction method for a specific titratable residue. While our BMA approach is purely statistical in nature, the BMA method described here could also be trained to modify the aggregation process based on structural and environmental features (e.g., only look at ensembles of empirical methods for certain structural features and consider all methods for other structures). In future work we will look at penalizing computationally expensive methods that provide minimal accuracy benefits. Finally, we will explore larger datasets with a diverse set of bimolecular systems to provide a trained BMA pK_a prediction model using a variety of calculation methods.