Kinetic Isotope Effects as a Probe of Hydrogen Transfers to and from Common Enzymatic Cofactors

Abstract

Enzymes use a number of common cofactors as sources of hydrogen to drive biological processes, but the physics of the hydrogen transfers to and from these cofactors is not fully understood. Researchers study the mechanistically important contributions from quantum tunneling and enzyme dynamics and connect those processes to the catalytic power of enzymes that use these cofactors. Here we describe some progress that has been made in studying these reactions, particularly through the use of kinetic isotope effects (KIEs). We first discuss the general theoretical framework necessary to interpret experimental KIEs, and then describe practical uses for KIEs in the context of two case studies. The first example is alcohol dehydrogenase, which uses a nicotinamide cofactor to catalyze a hydride transfer, and the second example is thymidylate synthase, which uses a folate cofactor to catalyze both a hydride and a proton transfer.

1. Introduction

The chemical and physical mechanisms by which enzymes catalyze reactions receives considerable interest from chemists, owing to the many important intellectual and practical problems associated with enzymes. Enzymes catalyze a very diverse range of reactions, increasing rates by many orders of magnitude, but as of yet, there exists no thorough understanding of why they are so successful. Determining the mechanisms and sources of the catalytic power of enzymes would enable the development of useful biomimetic catalysts [1] and would facilitate the development of specific and potent drugs that affect enzymatic activity [2]. Though much mystery remains, some common themes have begun to emerge in recent years, especially among reactions involving the same (or similar) cofactors. Certain ubiquitous cofactors (e.g. nicotinamides, folates, flavins, etc.) play roles in very diverse reactions, but the physical mechanisms involved in these reactions are often strikingly similar. Here we seek to describe our current understanding of the physical mechanism of hydrogen transfer to and from some very well studied cofactors. One of the most useful experimental techniques for understanding H-transfers is the measurement of kinetic isotope effects (KIEs) and that will be the primary focus of this review. We note that from the perspective of the physical enzymologist, there is no distinction between a “cofactor” and a “substrate”: both molecules react during the reaction and the molecules’ overall roles in metabolic pathways are inconsequential to the physics of any given reaction. Thus, our discussion of the theory and interpretation of KIEs will be fairly general, but then we will highlight the use of KIEs in examples that involve H-transfers to and from ubiquitous cofactors: nicotinamide in alcohol dehydrogenase (ADH) and folate in thymidylate synthase (TSase).

2. Theory of KIEs

A KIE is the ratio of rates between two reactions that differ only in the isotopic composition of reactants (isotopologues):

$$KIE=\frac{k_{\mathit{\text{Light}}}}{k_{\mathit{\text{Heavy}}}}$$ [1]

Here, k_Light is the rate with the light isotope and k_Heavy is the rate with the heavy isotope. Isotopic substitution serves as a minimal perturbation to the reaction allowing an experiment to probe the nature of a reaction’s traversal across a potential energy surface (PES). To be clear, according to the Born-Oppenheimer approximation, the isotopic substitution does not affect a reaction’s electronic PES, so the kinetic changes that occur upon substitution reveal the nature of how a reaction proceeds from a reactant state to a transition state (TS). These kinetic changes result primarily from nuclear quantum effects including vibrational zero point energy (ZPE) and quantum mechanical tunneling. We have recently reviewed how both of these effects appear in measured KIEs, with an emphasis on why interpretations that ignore tunneling fail to explain H-transfers [3]. Here we will take it for granted that H-transfers involve a large degree of tunneling, which is the prevailing view among enzymologists [4–9], and focus on the interpretation of experiments in this context.

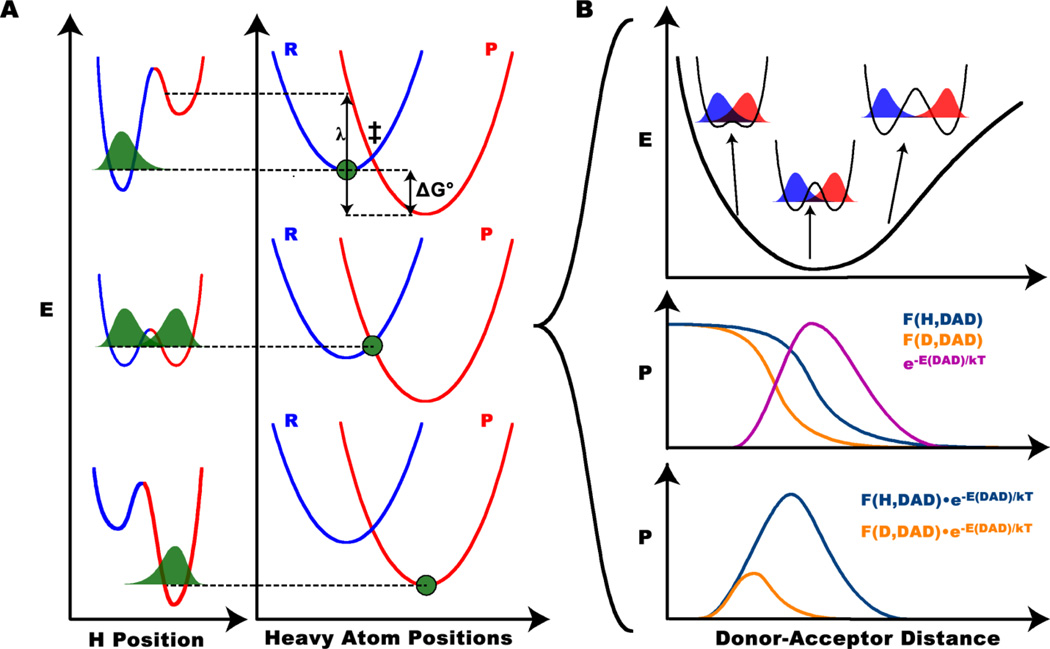
KIEs can be interpreted using Marcus-like models (Figure 1), which have also been referred to as environmentally coupled tunneling [10], vibrationally enhanced tunneling [11], and other names. Following the footsteps of Marcus theory of electron transfer [12], the key to this kind of model is that it makes a Born-Oppenheimer-like separation between the fast motion of the transferred H and the slow motion of the surrounding atoms, which includes the remainder of the substrates and the enzyme. Marcus-like models assume a mechanism of H-transfer where the surrounding atoms (the heavy atoms) rearrange from the ground state to a tunneling ready state (TRS), where the energy levels of the reactant well and the product well are degenerate (vibrational ground state or excited state), so efficient tunneling can occur. The TRS is the heavy atom configuration where the transferred particle is delocalized (i.e., in the process of tunneling) between donor and acceptor wells. This state is simply a delocalized transition state, which is typical to small particles transfer (e.g., electrons and protons), and thus involves longer DAD than the DAD at the pick of the energy barrier (i.e., the localized transition state). In Analogous to the dividing surface between reactants and products in traditional transition state theory, a system has a whole ensemble of TRSs. At each TRS, the efficiency of tunneling depends on the mass of the tunneling particle and the donor-acceptor distance (DAD). The rate (k) in this kind of model takes the functional form [6,10,13–17]

$$k=\frac{{\left|V\right|}^2}{h}\sqrt{\frac{\pi }{\lambda k_{B}T}}{e}^{\frac{{\left(\mathrm{\Delta }{G}^{\circ }+\lambda \right)}^2}{4k_{B}T\lambda }}{\int }_0^{\infty }F(m,DAD)e^{-E(DAD)/k_{B}T}dDAD$$ [2]

Figure 1.

Marcus-like model of H-tunneling. A) The three panels (top to bottom) represent three positions during the course of the reaction: reactant state, TRS, and product state. The reaction coordinate consists of heavy atom motion which is separated from the motion of the transferred particle via a Born-Oppenheimer-like approximation. In the reactant state (top), the ZPE of the transferred H is lower in the reactant well (blue) than the product well (red), so its wavefunction (green) is localized in the reactant well. When heavy atoms rearrange to a TRS (middle), the reactant well and product well are degenerate, so the H wavefunction is delocalized between the two and tunneling occurs. Upon further Heavy atom rearrangement (bottom), the transferred H can be trapped in the product well. B) At the TRS, fluctuations of the DAD affect the probability of tunneling. The top panel shows the PES along the DAD coordinate, highlighting the different levels of reactant-product wavefunction overlap at different DADs, which is proportional to the tunneling probability as a function of DAD. The middle panel shows the population distribution (magenta) corresponding to the PES in the top, along with the tunneling probability of H (purple) and D (orange) as a function of DAD. The bottom panel shows the product of the tunneling probability and population distribution shown in the middle panel, which gives the overall flux of reactive trajectories for each isotope as a function of DAD (the integrand of Eq. 2). Note that this model predicts that H-transfer occurs from a longer average DAD than D-transfer. Figure reproduced from ref [19] with permission from ACS.

The leading factors of this equation compute the rate of heavy atom rearrangement to reach a TRS based on the electronic coupling between reactants and products (V, the adiabaticity), the reorganization energy (λ), and the reaction driving force (ΔG°). The mass-sensitivity of these leading factors is generally negligible for 1° KIEs, so they cancel out when using this equation to model experimental KIEs [13].The integral yields the probability of tunneling to products once the system reaches the TRS and depends on the transmission probability, F(m,DAD), as a function of mass (m) and DAD, and a Boltzmann factor giving the probability of being at any given DAD. The transmission probability can be calculated assuming vibrationally diabatic transfer using either harmonic [14,17] or Morse potentials[18] to describe the H-wavefunctions, or, where a vibrationally adiabatic approach is necessary model calculations of relevant systems can be used to calculate the transmission probability [13].While the Boltzmann factor assumes a statistical distribution of states, the models would have very similar mathematical form if non-equilibrium dynamics were introduced, though currently, we are not aware of experimental findings that cannot be rationalized by a Boltzmann factor. Integrating the tunneling probability (weighted by the probability of being at each DAD) over all DADs gives the total tunneling probability. Since the thermal activation leading to the TRS in this model is insensitive to the mass of the 1° isotope (see below regarding 2° KIEs), but tunneling at the TRS is mass-sensitive, this model is useful for rationalizing experimental observations of temperature-dependent rates with temperature-independent or temperature dependent KIEs. So far, this versatile model can explain all the published data, whether enzymatic or not [6,13–15,17].

Based on this model, measurements of the temperature dependence of 1° KIEs probe the fast (fs-ps) enzyme and substrate dynamics that determine the structure of the TRS. Small, temperature independent KIEs indicate that the enzyme stabilizes a relatively rigid, narrowly distributed, well defined TRS where thermal activation of DAD fluctuation does not differently affect the tunneling probability of the different isotopes. If the KIEs are temperature dependent, the model suggests that the TRS has a broader distribution of DADs that changes with temperature, so tunneling of heavier isotopes is more probable at higher temperature, leading to decreased KIE at elevated temperature. We recently proposed that in some extreme cases of very steeply temperature dependent KIEs, one can conclude that the TRS exists as multiple distinct populations along the DAD coordinate [13]. This is not the only proposal of multiple populations to explain the temperature dependence of KIEs, [20] but nonetheless, this proposal has been met with some controversy [21,22]. Further work is necessary, of course, to examine this proposal, but the prediction provides a much-needed testable hypothesis for assessment of Marcus-like models. Recent advances in measuring single-molecule KIEs [22], for example, hold promise for testing this prediction. In the specific examples of ADH and TSase below, we will illustrate how to use the temperature dependence of 1° KIEs to understand the nature of those reactions.

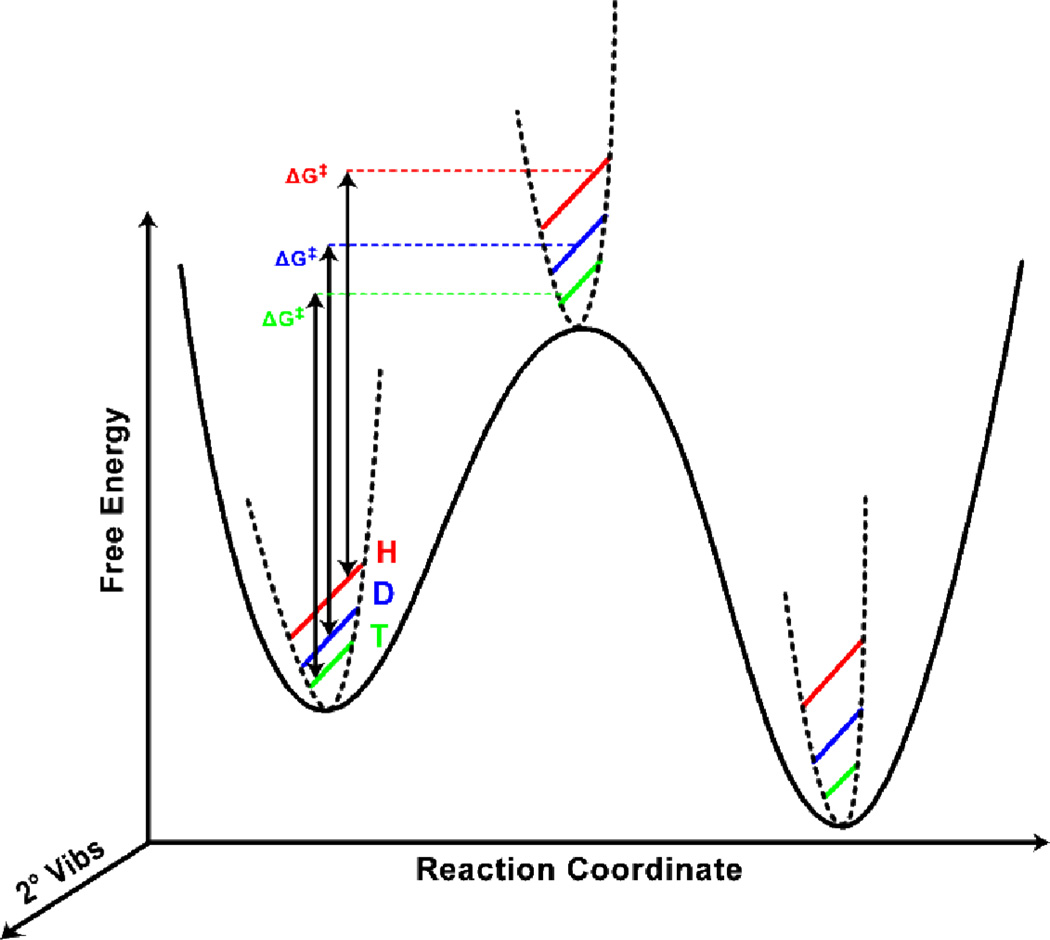
Secondary KIEs

Secondary (2°) KIEs are those KIEs where the isotopically labeled atom is not directly involved in bond cleavage or formation, as it would be for 1° KIEs. In the past, 2° KIEs were interpreted using semi-classical models [23] or models of “tunneling and 1°-2° coupled motion” [24–28]. We discuss tunneling and coupled motion below, in the context of ADH, but since those models do not address the temperature dependence of 1° KIEs, we hope to advocate for the use of Marcus-like models as a more general framework for interpreting 2° KIEs, as well as 1° KIEs. In both Marcus-like models and semi-classical models of KIEs [23,29] 2° KIEs arise from isotopic differences in ZPE that change along the reaction coordinate (Figure 2). In Marcus-like models, however, instead of assuming the reaction goes through a true transition state (i.e., a first-order saddle point on the electronic PES), one assumes that the TRS is the reaction’s bottleneck. Thus, the experimental 2° KIEs do not represent changes between a ground state and a TS, but changes between a ground state and a TRS. Mathematically, these KIEs appear in Eq. 2 as isotopic differences in the reorganization energy (λ) and the reaction driving force (ΔG°), which is proportional to the equilibrium isotope effect (EIE, the ratio of equilibrium constants for two isotopically substituted reactions). We note that in some cases, the motion of a 2° could be coupled to the tunneling mode and thus contribute to the mass-sensitivity of the integral in eq. 2.

Figure 2.

Changes of ZPE of 2° vibrations along the reaction coordinate, which lead to experimentally observable 2° KIEs. Although this model appears to be nearly identical to models of semiclassical KIEs, we emphasize that in Marcus-like models, the maximum point along the minimum energy path from reactants to products is not a saddle point on the electronic PES; it is a TRS, where the reactant and product surfaces are degenerate (cf. Fig. 1). The isotopically-sensitive phenomenological free energy of activation (ΔG^‡) shown here can be related to the variables in Eq. 2 (and Fig. 1) as described in the text. Figure reproduced from ref [30] with permission from Elsevier.

2° vibrational energy levels change during the course of reaction due to a variety of factors. ZPE can either decrease at the TRS, leading to a “normal” KIE (KIE>1), or the ZPE can decrease, yielding an “inverse” KIE (KIE<1). One can use the direction and magnitude of 2° KIEs to determine the structure of the TRS as follows. If isotopic substitution is at the α-position (α-2° KIEs), much of the change in ZPE results from rehybridization of the reacting donor or acceptor atom. For example, if, during the course of a reaction, a carbon atom changes from sp³- to sp²-hybridized, an H in the α-position gains a substantial amount of vibrational freedom during the reaction. This vibrational freedom corresponds to lower ZPE, resulting in a normal KIE. Note that for the opposite reaction, sp² to sp³, the 2° KIE is typically inverse, although tunneling makes that expectation less universal [31,32]. The extent to which the carbon is rehybridized at the TRS determines the magnitude of the 2° KIE. Traditionally, one could use the corresponding EIE as an upper bound for the KIE. If the carbon had completely rehybridized at the TRS, corresponding to a very late (product-like) TRS, one would observe a 2° KIE equal to the EIE. If, on the other hand, the TRS is very early (reactant-like), the hybridization (and ZPE) at the TRS will resemble the reactant state and the 2° KIE will be close to unity. Less common than α-2° KIEs, but perhaps equally useful, are β-2° KIEs, which refer to isotopic substitution two bonds away from the reactive center. β-2° KIEs report on charge accumulation at the TRS, as different isotopes differ in their abilities to participate in hyperconjugation [23].

This semi-classical interpretation was complicated when Cleland’s group observed 2° KIEs that exceeded the supposed limits of unity and the EIE [31]. While those findings originally led to the interpretation of tunneling and coupled motion, we have recently shown in the context of ADH [32] (and will discuss this in detail below) that by defining a TRS, instead of a TS, as the reaction’s bottleneck, the delocalization of the transferred particle at the TRS has the effect of inflating α-2° KIEs. That is, one can recover the observed inflated 2° KIEs without assuming any direct component of tunneling in the 2° atom. Therefore, to a large extent, one can use the same semi-classical principles of 2° KIEs to understand reactions that involve a large component of tunneling of the transferred atom. In the next section, we will discuss the details of using α-2° KIEs to understand ADH in the context of Marcus-like models.

Kinetic Complexity

Given the fact that the rate of substrate binding or product release often governs the overall turnover rate, extracting intrinsic KIEs (KIE_int, the KIE on the isotopically sensitive step) from the observed KIEs (KIE_obs) require a careful kinetic analysis [33]. Steps besides the chemical step of interest often mask the isotope effects on the chemical step, leading to KIE_obs<KIE_int —a phenomenon known as “kinetic complexity”. For instance, consider the following reaction mechanism:

The chemical step of interest in this mechanism is formation of enzyme-product complex, EP from enzyme-substrate complex, ES. The steps prior to the formation of ES complex or following the EP complex may reduce the KIEs depending on the “commitment to catalysis”. The interrelation between the KIE_obs and the KIE_int on the second order rate constant (V/K) can be given as follows [33,34]:

$${\text{KIE}}_{\text{obs}}=\frac{{\text{KIE}}_{\text{int}}+{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{r}}·\text{EIE}}{1+{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{r}}}$$ [3]

Here, C_f and C_r are forward and reverse commitments to catalysis on V/K, respectively. The forward commitment, C_f is the ratio of the forward rate constant for the isotopically sensitive step (k₃) to the net rate constant for the dissociation of the ES complex to E and S. Similarly, the reverse commitment, C_r is the ratio of the reverse rate constant for the isotopically sensitive step (zero in our simple example) to the net rate constant that breaks down the EP complex to E and P. For an irreversible reaction, like that above, Eq. 3 reduces to

$${\text{KIE}}_{\text{obs}}=\frac{{\text{KIE}}_{\text{int}}+{\mathrm{C}}_{\mathrm{f}}}{1+{\mathrm{C}}_{\mathrm{f}}}$$ [4]

In order to reduce commitments and better expose intrinsic KIEs, several kinetic tricks may be applied such as pre-steady-state measurements [35], changing pH or temperature [36], using alternative substrates [37], and mutagenesis [38]. Additionally, Northrop[34] developed a very useful method for finding intrinsic KIEs from observed KIEs using multiple isotope effects and the Swain-Schaad Exponent (SSE) [39]. The SSE is the relationship between KIEs using the three isotopes of hydrogen (H, D and T) and according to semi-classical theory, does not differ among different reactions:

$$SSE=\frac{\text{ln}\left(\frac{k_H}{k_T}\right)}{\text{ln}\left(\frac{k_H}{k_D}\right)}=1.4$$ [5]

Any of the three combinations of hydrogen KIEs can be used in the Northrop method, although the SSE has a different numerical value for the other two combinations [40]. For example, in case of H/T and H/D measurements, by combining Eqs. 4 and 5, along with some relatively simple algebraic manipulations, the Northrop method [34] uses the following equation to obtain KIE_int from measurements of two different KIE_obs [3]:

$$\frac{{\left(\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{D}}$}\right.\right)}_{\text{obs}}-1}{{\left(\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{T}}$}\right.\right)}_{\text{obs}}-1}=\frac{{\left(\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{D}}$}\right.\right)}_{\text{int}}-1}{{\left(\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{D}}$}\right.\right)}_{\text{int}}^1.4-1}$$ [6]

Thus, by measuring both and ${\left(\right[\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{D}}$}\right.\left)\right]}_{\mathit{\text{obs}}}\text{and}{\left(\right[\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{T}}$}\right.\left)\right]}_{\mathit{\text{obs}}}$, one can assess ${\left(\raisebox{1ex}{$k_{\mathrm{H}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{D}}$}\right.\right)}_{\text{int}}$. We note that the Northrop method assumes semi-classical values of the SSE, and it is interesting that both calculations [41] and experiments [40] demonstrated that these relations are holding for 1° KIEs even when tunneling is present (at least above 260 °K). This could be due to similar mass sensitivity to nuclear quantum effects at the grand state (e.g., ZPE) and at the transition state (e.g., tunneling). In what follows, we will discuss strong deviations from semi-classical behavior in secondary SSEs in ADH for the mixed labeling experiment, but no deviations have been reported for any measurement of pure SSE (in contrast to mixed SSE as discussed below). In the sections that follow, we will discuss two case studies: the nicotinamide in ADH and the folate in TSase. In ADH, the Northrop method has been largely unnecessary, but in many mutants of TSase, the Northrop method has been instrumental in extracting KIE_int.

3. Nicotinamide in Alcohol Dehydrogenase

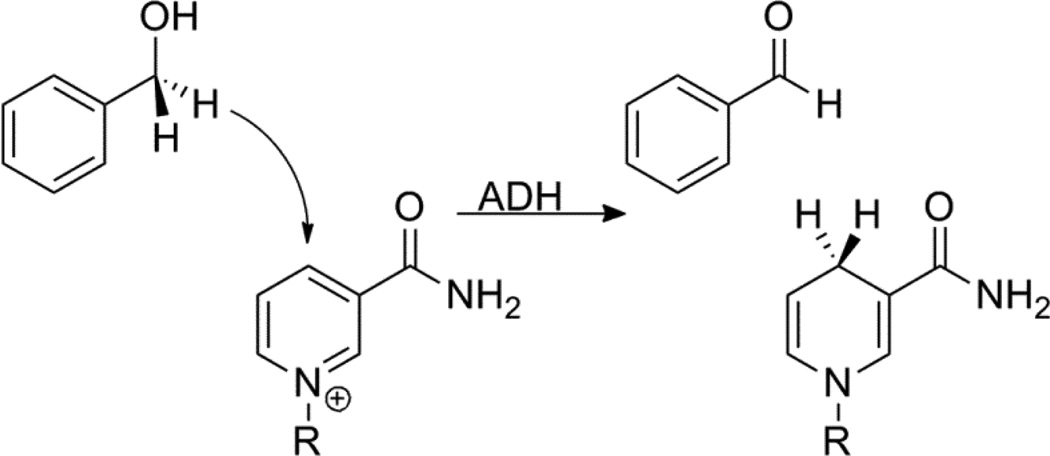
Nicotinamide cofactors such as nicotinamide adenine dinucleotide (NADH) or its 2’-phosphate analogue (NADPH) are ubiquitous in biology and ADH provides a very useful model system for studying the physical mechanism of nicotinamide-dependent hydride transfers. ADH catalyzes the oxidation of alcohol shown in scheme 1, and is a particularly useful model because in the yeast enzyme (yADH), the hydride transfer is completely exposed, so physical measurements are not hindered by kinetic complexity [37]. Furthermore, the reaction can proceed in both the forward and reverse directions using relatively similar conditions [37,42]. Much of the work on ADH has focused on using KIEs, especially 2° KIEs, to understand the nature of the TS and the roll of tunneling and dynamics in H-transfers. The surprising results of many of these KIE experiments, though, have been difficult to connect to a rigorous theoretical framework.

Scheme 1.

The hydride transfer catalyzed by ADH using benzyl alcohol as an alternative substrate. R= adenine diphosphate ribosyl.

Some of the first difficulties appeared when Klinman and coworkers compared 2° KIEs with Hammett substituent effects [37,42,43]. The α-2° KIE on alcohol oxidation was very close to the corresponding EIE, indicating a very late (product-like) TS, [43] whereas the substituent effects indicated just the opposite; the electronic structure of the TS was very reactant-like [37,42]. Clearly, this kind of blatant contradiction could not be rationalized by traditional semi-classical theories and was perhaps the first indication that those theories were missing a vital component to the mechanism of H-transfer.

Shortly after these experiments, Cleland and coworkers probed the reaction by measuring isotope effects on the cofactor and obtained some remarkable results [31,44]. Despite the fact that the relevant EIE was inverse, as expected for the sp² to sp³ transition of the cofactor in the backward reaction, the measured KIE was significantly normal. The authors proposed that this startling result indicated a component of 1°-2° coupled motion (Figure 3) in the reaction coordinate. Some theoretical calculations [24] verified the validity of that interpretation, but added to it the fact that the coupled reaction coordinate mode tunneled through the barrier. This theoretical model further predicted that tunneling and coupled motion would lead to a breakdown of the rule of the geometric mean (RGM). The RGM is a consequence of the semi-classical Bigeleisen model and states that there are no isotope effects on isotope effects [45,46]. After the theoretical model suggested that tunneling and coupled motion would lead to a breakdown, Cleland and coworkers tested the RGM in formate dehydrogenase, which also uses NAD⁺ as an oxidizing agent. The experiments found that indeed, the RGM failed to hold in this reaction, providing strong evidence for tunneling and coupled motion in nicotinamide-dependent H-transfers.

Figure 3.

Schematic of the model of tunneling and coupled motion. A) The reaction coordinate is composed of motion of 3 hydrogens (black): the transferred atom moving from donor to acceptor carbon (gray), and the 2° hydrogens swinging around as the donor and acceptor rehybridize. The red atom represents the oxygen of the alcohol/aldehyde. B) The coupled reaction coordinate mode shown in A tunnels through the barrier with an efficiency dependent upon the reactant (blue) and product (red) wavefunction overlap. Reproduced from reference [30] with permission from Elsevier.

Another important prediction [28] of the tunneling and coupled motion model was that the Swain-Schaad exponent (SSE) would be inflated from its semi-classical value [39]. As mentioned above, the SSE is the relationship between KIEs using different isotopes of hydrogen. Under the assumptions of the Bigeleisen model, including no tunneling and harmonic vibrational frequencies, the SSE does not depend on the reaction studied or the labeled position and a simple derivation shows that

$$SSE=\frac{\text{ln}(\frac{k_H}{k_T})}{\text{ln}(\frac{k_D}{k_T})}=3.3$$ [7]

Klinman and coworkers tested the SSE in yADH using what has come to be known as a mixed-labeling experiment [27]. In this experiment, the 2° H/T KIE is measured with H-transfer, but the 2° D/T KIE is measured with D-transfer, yielding a mixed-labeling SSE (mSSE), which should equal the standard SSE under semi-classical theory:

$$mSSE=\frac{\text{ln}\left(\frac{k_H^H}{k_T^H}\right)}{\text{ln}\left(\frac{k_D^D}{k_T^D}\right)}=3.3$$ [8]

Here $k_j^i$ is the rate with isotope i at the 1° position and isotope j at the 2° position. In ADH, conducting the experiment this way offers the advantage of a simpler synthetic procedure for the istopically labeled substrates. An unintended consequence of mixed-labeling experiments, though, is that any deviation from semi-classical behavior could be due either to a breakdown of the SSE or a breakdown of the RGM (or both). Nonetheless, when the mSSE in yADH was found to be greater than 10, it was seen as fairly conclusive evidence that the reaction occurred through tunneling and coupled motion. We note that certain calculations [47–49] that dispensed with some of the simplifying assumptions of the original SSE derivation suggested that the SSE or mSSE could be somewhat larger than 3.3 even without tunneling. Still, the large inflation found for yADH has served as indisputable evidence for a component of tunneling in the reaction.

Following these groundbreaking experiments on yADH, Klinman and coworkers began to examine how enzyme structure and dynamics contributed to the tunneling process in horse ADH (hADH) and a thermophilic ADH from Bacillus stearothermophilus (bsADH). In active site mutants of hADH where the H-transfer is rate-limiting, this enzyme, too, exhibits inflated mSSEs [38]. Furthermore, the extent of the inflation in the mSSE of various mutants, which was believed to indicate the extent of tunneling, corresponded with the DAD evident in the mutants’ crystal structures [50]. This finding suggested that enzymes may catalyze H-transfers by restricting the substrates to short DADs where efficient tunneling can occur.

Additional information on the dynamics of H-tunneling came from studies of bsADH that measured mSSEs, as well as 1° KIEs, over a large temperature range [51]. Within this enzyme’s physiological range (>30° C) the reaction exhibited temperature independent KIEs and inflated mSSEs, which are both indicative of a large component of tunneling. At lower temperatures, though, the mSSEs were less inflated and the 1° KIEs showed some temperature dependence. This revealed that within the enzyme’s physiological temperature range, it adopted a structure and dynamics that were well-suited to facilitate H-tunneling, but at lower temperatures, the enzyme went through a sort of phase transition to a conformation that was inadequate for catalyzing H-tunneling.

While the overall conclusions from this study still appear to hold, the consensus of the experimental community now is that tunneling makes a large contribution to reactivity in all H-transfers and at all temperatures accessible to enzymes [3,5,9]. From studies on other systems, there does not appear to be an obvious relationship between inflated mSSEs and the extent of H-tunneling [27,52]. Additionally, the model of tunneling and coupled motion that had been used to rationalize some of these data had great difficulty in explaining the temperature dependence of KIEs [3,5,53].

Thus, with Marcus-like models in mind, recent studies have re-examined some of the ideas behind tunneling and coupled motion. An analysis of all the data on inflated mSSEs from various ADHs found something surprising: the H/T KIE with H-transfer was relatively invariant (always equal to the EIE), but the D/T KIE with D-transfer varied significantly among different systems and it was this variability that led to the variation in mSSEs. In accordance with Marcus-like models, this suggested that the shorter DAD necessary for D-tunneling led to steric hindrance between the substrates, which hindered the rehybridization of the donor carbon and diminished the 2° KIE with D-transfer [54]. We recently tested this idea in yADH by measuring 2° KIEs on the reduction of benzaldehyde [32] and obtained results that echoed the KIEs measured on the cofactor [31]. Namely, despite the inverse EIE, [43] as expected for an sp² to sp³ transition, the measured KIE was slightly normal. Furthermore, the 2° H/T KIE was slightly deflated when measured with D at the 1° position. Using these new KIEs, as well as many previously measured KIEs, we were able to parameterize a model of the TRS for this reaction that reproduced all of the experimental 2° KIEs for yADH. Notably we found that a shorter DAD with D-transfer could reproduce the diminished KIEs with D-transfer, and the calculations further showed that Marcus-like models could reconcile the long-standing contradiction between the 2° KIEs and the Hammett substituent effects [32].

Additionally, we have just recently experimentally confirmed one of the principal predictions of this computational model [19]. The model predicted that if we measured both the H/T and D/T 2° KIEs with the same isotope at the 1° position, we would observe no deviation from the semi-classical SSE. Indeed, we found that the 2° H/T KIE was significantly deflated when D was at the 1° position and that the corresponding SSE was within the range predicted by some other models that do not have an explicit tunneling contribution [47–49]. Thus, this new interpretation of tunneling and coupled motion suggests that the inflated mSSE does not result from a direct component of tunneling on the 2° H, but instead results from the fact that the dynamics of nuclear tunneling force the system into different TRSs for H-transfer versus D-transfer.

Marcus-like models have also been useful in adding more detail to the interpretation of the temperature dependence of 1° KIEs in the thermophilic ADH. Our model [13] for fitting the temperature dependence of KIEs to a population distribution along the DAD coordinate showed that within the physiological temperature range, the TRS of this enzyme is confined to a very narrow DAD distribution at a relatively short DAD where tunneling is efficient, but that at lower temperatures, the enzyme fails to stabilize such a well-organized TRS. At lower temperatures, the system appears to exist predominantly with a population at a long DAD, where tunneling is inefficient, while there is a small population at DADs short enough that the ZPE of the transferred particle is above the barrier to transfer. A series of mutants of bsADH also showed this kind of phase transition outside of the enzyme’s physiological temperature range, but in the mutants, the temperature (in)dependence of the KIEs is reversed (i.e., KIEs are temperature dependent at physiological temperatures and temperature independent at lower temperatures) [55]. The implications of this flip in behavior for the mutants are difficult to understand. The interpretation of active site mutants of dihydrofolate reductase, for example, was far easier to rationalize; in that system, smaller active site side chains led to longer DADs and a broader distribution of DADs [13,56]. The presence of the phase transition in bsADH severely challenges our current level of understanding and more work is necessary to fully understand the dynamics of that system.

ADH, therefore, has taught us quite a bit about the nature of nicotinamide-dependent H-transfer, but certain aspects remain mysterious. Marcus-like models explain both the temperature dependence of KIEs, and the mSSEs in ADH, but we have not uncovered why ADH is unique in exhibiting inflated mSSEs. Very few other systems [57] have exhibited this behavior, despite the fact that tunneling is so vital to so many other systems. Are the 2° KIEs in ADH uniquely sensitive to the DAD or is the DAD in ADH uniquely sensitive to the transferred isotope? Other questions remain unanswered as to the nature of the phase transition in the thermophilic enzyme. How do the global dynamics of this enzyme affect the positioning of the substrates in the active site, and how do certain mutations alter the temperature range where these dynamics are optimal? ADH has served for many years as a model for understanding the physical mechanism of H-transfer to and from nicotinamide, but it clearly has not yet divulged all of its secrets.

4. Folate in Thymidylate Synthase

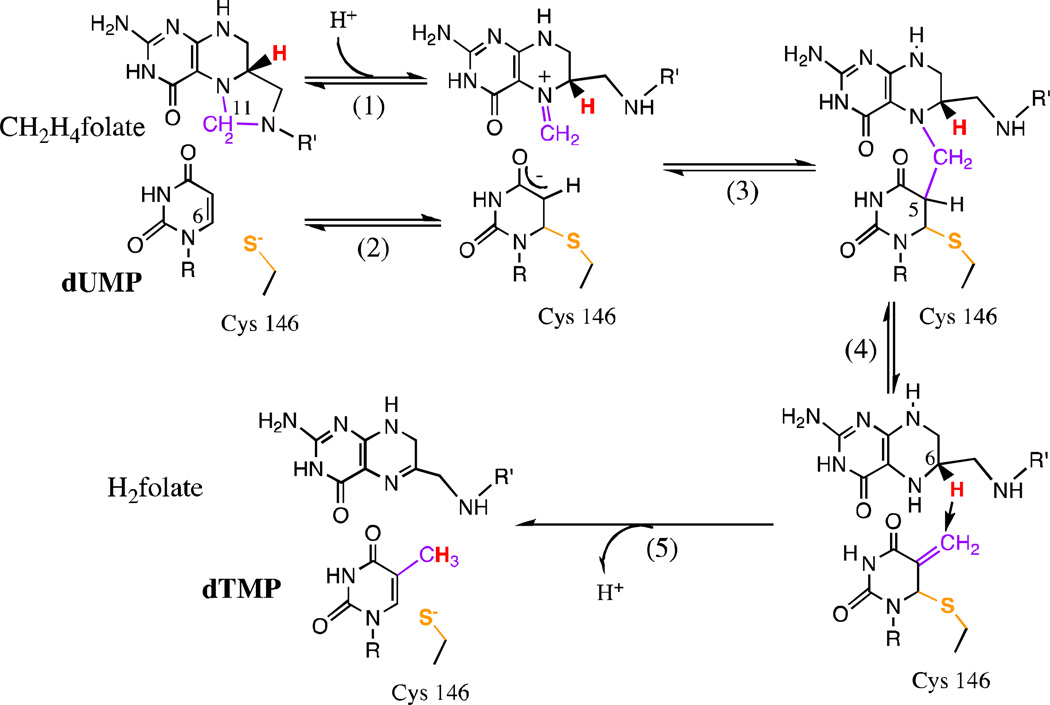
Thymidylate synthase (TSase) is a bisubstrate enzyme which catalyzes the de novo synthesis of 2’-deoxythymidine-5’-monophosphate (dTMP), a nucleotide indispensable for DNA biosynthesis [58]. TSase is unique among enzymes requiring folate cofactors in that N⁵,N¹⁰-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) serves as both a methylene donor and a reductant. The methylene group and the hydride are transferred from different sites of the folate to the substrate 2’-deoxyuridine-5’-monophosphate (dUMP), thus forming dTMP (Scheme 2). TSase is overexpressed in cancerous cells to facilitate faster cell growth, [59] which makes TSase a target for chemotherapeutic drugs, but common drugs such as antifolates and 5-fluorouracil often interfere with the metabolic processes of healthy cells, resulting in toxicity [60]. Careful investigation of the TSase mechanism may lead to the discovery of drugs that selectively target malignant tumor cells.

Scheme 2.

The proposed chemical mechanism of E.coli TSase. Reproduced from ref [30] with permission from Elsevier.

TSase catalyzes a complex cascade of chemical transformations (Scheme 2), including two different C-H bond activations: a fast and reversible proton transfer from C5 of dUMP (step 4 in Scheme 2) and an irreversible, rate-limiting hydride transfer from C6 of CH₂H₄folate (step 5 in Scheme 2). Numerous studies have probed the overall chemical mechanism of this reaction using steady-state and pre-steady-state kinetics, [58] α-2° KIEs [61,62] and crystallography [63,64] and we have recently reviewed much of this work [3]. Here we will focus primarily on some recent uses of 1° KIEs to explore the physical nature of the H-transfers and the role of protein dynamics in the C-H bond activations.

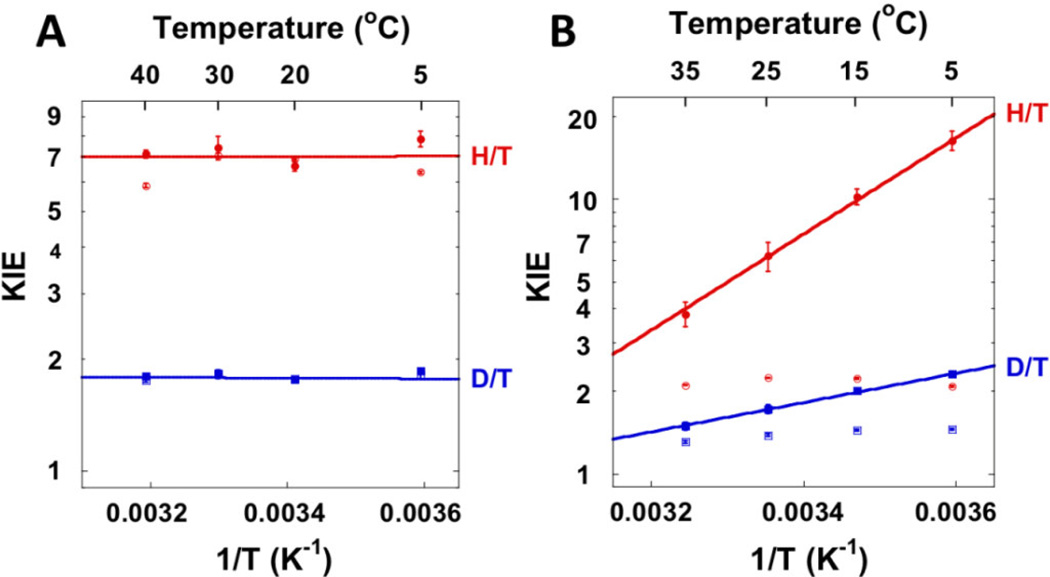
Spencer et al [62] reported that hydride transfer from the folate (step 4 of scheme 2) is rate limiting on both V and V/K. We measured 1° hydrogen KIEs on this step over a temperature range of 5–40°C and used the Northrop method to extract intrinsic KIEs [65]. The observed KIEs were equal to the intrinsic KIEs, confirming that the hydride transfer is rate-limiting on V/K. Steady-state initial velocity measurements showed that TSase requires a very small amount of activation energy (about 4.0 kcal/mol), suggesting a particularly well pre-organized ground state configuration for catalysis. The intrinsic KIEs were temperature independent (Figure 4), indicating a compact TRS and that the hydride tunnels from a narrow distribution of DADs that is unaffected by temperature.

Figure 4.

Temperature dependence of 1° KIEs on the hydride transfer (A) and the proton transfer (B) catalyzed by wt E.coli TSase. The empty and filled points are the observed and intrinsic KIEs, respectively. Reproduced from ref [67] with permission from ACS.

The proton transfer, on the other hand, is non-rate limiting and reversible, so kinetic complexity hinders the measurement of intrinsic KIEs [65]. Nonetheless, we applied kinetic tricks to bypass the commitments and measured the temperature dependence of intrinsic KIEs [66,67]. While the intrinsic KIEs on the hydride transfer were temperature-independent, the proton transfer presented a steep temperature dependence of KIEs, suggesting a broad distribution of DADs at the TRS (Fig. 4). Numerical fitting of these KIEs to a Marcus-like Model suggested that the proton transfer occurs from at least two populations with different DADs, unlike the single narrow population for the hydride transfer [13]. These observations demonstrate that the dynamics dictating the TRSs for the hydride and proton transfers are independent from one another, despite the fact that both transfers occur within the same active site. These findings lead to the conclusion that the temperature dependence of intrinsic KIEs probes the dynamics of a specific TRS; those dynamics cannot be linked to the overall flexibility of the enzyme.

Kinetic characterization of mutants is an excellent approach to investigate the role of specific protein motions in activating covalent bonds. Recently, for example, we mutated a residue (Y209W) [68] 8Å away from where the chemical transformation takes place and found substantial effects on the catalyzed chemistry. As in the wt, hydride transfer is completely rate-limiting in the mutant, but the mutation caused a 500-fold decrease in k_cat and more than a 4- and 15-fold decrease in Km for dUMP and CH₂H₄folate, respectively. The mutation increases the enthalpy of activation (ΔH^‡), while the entropy of activation (TΔS^‡) is unchanged, suggesting that changes in the active site caused by the distal mutation increase the protein’s energy barrier for reaching the TRS, thus decreasing the turnover rate. To identify how changes 8 Å away from the H-transfer propagate into the active site, we examined the structure and dynamics of the mutant by X-ray crystallography [69]. Even though the mutation significantly decreases the turnover rate, crystal structures of the mutant and wild-type are nearly perfectly superimposable, indicating no significant overall conformational changes. To investigate any dynamic effects of the mutation, we compared anisotropic B-factors of the wt and mutant, which indicate the amplitude and direction of atomic motions [69]. While residues 20–45 in the wild-type exhibit rigid body-like dynamics, the mutation disrupts those correlated vibrations. Although not apparent in the static crystal structure, the altered dynamics in Y209W appear to result in a partial opening of the active site that allows thiols in solution to compete for the exocyclic methylene intermediate prior to the hydride transfer (Scheme 2).

However, it appears that the fast (femtosecond to picosecond) dynamics at the TRS were hardly affected by the mutation, as the temperature dependence of intrinsic KIEs exhibited only minor changes. The lack of change in DAD distribution at the TRS is surprising in the context of the conclusions from the thiol trapping experiments that the active site is more open. The significant alteration of processes besides H-tunneling in Y209W suggest that the mutation perturbs motions at slow (ms-s) timescales. In this way, the observed disruptions in correlated vibrations in the crystal structure of the mutant appear to correspond to relatively slow dynamics, but more work is necessary to connect these dynamic changes to a specific step in the reaction. These findings add to a growing body of evidence that the dynamics of a distant residues can be involved in processes at the active site, which is apparent in other enzymes, such as DHFR [36], soybean lipoxygenase [70] and others [71].

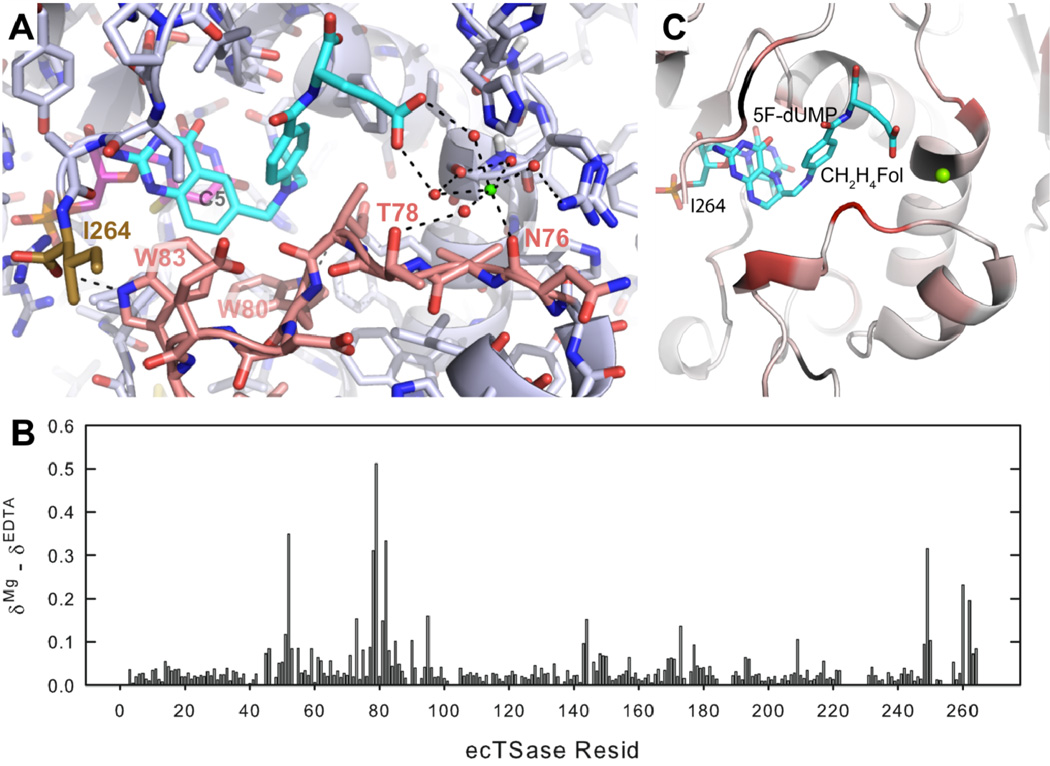
Another interesting phenomenon that highlights the role of long-range dynamic effects in enzymes is that Mg²⁺ enhances the catalytic activity of TSase. We have recently studied the ion’s mechanism of action through comprehensive kinetic, structural, and dynamics analyses [72]. Fluorescence assays, crystal structures, and NMR chemical shift changes show that Mg²⁺ loosely binds (K_d=3.7 mM) to the surface of TSase and forms a bridge between the glutamyl moiety of the folate cofactor and the enzyme through an H-bonding network. Though loosely bound to the surface of the protein and far away from the point of H-transfer (15 Å), Mg²⁺ binding leads to a 7-fold increase in turnover rate. NMR relaxation studies (Figure 5) demonstrate that the binding of Mg²⁺ to the surface of TSase rigidifies the overall protein structure on the ps-ns time scale. Mg²⁺ binding reduces the entropic barrier on k_cat by 1 kcal/mol while the enthalpy of activation remains unchanged. Since the hydride transfer is nearly completely rate limiting for k_cat both in the presence and absence of Mg²⁺ (as concluded from H/D non-competitive KIEs), these activation parameters are those of the hydride transfer step. The observed reduction in the entropic barrier for the hydride transfer can be correlated with the more rigid structure of the protein, as found by NMR. This ground state rigidity in a sense pre-pays the entropic cost of reaching the TRS. Mg²⁺ has little effect on intrinsic KIEs and their temperature dependence, so the ion does not appear to directly affect the structure and dynamics of the TRS, only the ground state. Our fluorescence studies show that Mg²⁺ binding increases the enzyme’s affinity for the cofactor, demonstrating that the linkage between the glutamyl moiety of the cofactor and the enzyme stabilizes the closed ternary complex. These findings once again highlight the importance of remote interactions and protein dynamics in accelerating rates which should be taken into account in designing drugs and biomimetic catalysts.

Figure 5.

(A) The binding site of Mg²⁺ (green) to the ecTSase complex with dUMP (magenta) and CB3717 (an antifolate, cyan) (PDB ID 4IW5). Note the distance between the Mg²⁺ and the point of H-transfer (C5 of dUMP). (B) Change in chemical shift of backbone amide upon Mg²⁺ binding to the ecTSase complex with 5F-dUMP and CH₂H₄folate. (C) Change in chemical shift of each residue shown from white (no change) to red (maximum change). Reproduced from ref [72] with permission from ACS.

TSase appears to use both structural and dynamic strategies to activate the C-H bonds of the folate cofactor. The enzyme distinguishes between a step where it uses compression to produce a narrow distribution of DADs for efficient tunneling (the hydride transfer) and one where it poses little constraint on the TRS (the proton transfer). Different steps in the catalytic cascade are susceptible to different strategies and future work will examine how different residues throughout the enzyme contribute to the interplay between entropy and enthalpy at the TRS.

5. Conclusions

Numerous enzymes require nicotinamide and/or folate cofactors to catalyze several key metabolic reactions. ADH (nicotinamide-dependent) and TSase (folate-dependent) serve as useful models for studying those classes of reactions, and for studying H-transfer in general. A combination of theoretical and experimental studies has extended our understanding of enzyme catalysis in last decades. Kinetic analyses such as KIEs and their temperature dependence have revealed several key features of how enzymes activate C-H bonds, especially in terms of enzyme dynamics and hydrogen tunneling. Additionally, Marcus-like models have begun to provide a semi-quantitative understanding of how enzymes attain an optimal distribution of H-donors in relation to H-acceptors to facilitate quantum mechanical tunneling [13,32]. Studies with TSase using mutations and alternate conditions have uncovered some aspects of how enzymes use dynamic effects on different timescales to achieve the acceleration necessary to meet metabolic demands.

While experiments such as measurements of the temperature dependence of KIEs improve our understanding of C-H bond activation and co-factor assisted enzyme mechanisms, we are still far from a point where we can de novo design an enzyme with equivalent catalytic power to natural enzymes [1]. Recent designs of new enzymes from basic principles only attained meager rate accelerations [73–75]. Such limitations may arise from an absence consideration of the dynamic motions and balance of flexibility vs. rigidity of the protein that contribute to catalysis in the new design. Given the potentially important catalytic role of such motions, taking advantage of them could also be useful in designing drugs that target rare but functionally important conformations to specifically and potently inhibit enzymes. In short, future studies aiming at understanding the role of enzyme dynamics and their functionality present an area of great challenges and promise from both intellectual and practical points of view.

Highlights.

• Kinetic isotope effects (KIEs) are interpreted by Marcus-like models of H-tunneling.

• KIEs’ temperature dependence reveals the nature of “Tunneling Ready States”.

• Enzymes’ kinetics and structures reveal the importance of dynamics in catalysis.