Effects of Hypoxanthine Substitution in Peptide Nucleic Acids Targeting KRAS2 Oncogenic mRNA Molecules: Theory and Experiment

Abstract

Genetic disorders can arise from single base substitutions in a single gene. A single base substitution for wild type guanine in the twelfth codon of KRAS2 mRNA occurs frequently to initiate lung, pancreatic, and colon cancer. We have observed single base mismatch specificity in radioimaging of mutant KRAS2 mRNA in tumors in mice by in vivo hybridization with radiolabeled peptide nucleic acid (PNA) dodecamers. We hypothesized that multi-mutant specificity could be achieved with a PNA dodecamer incorporating hypoxanthine, which can form Watson-Crick basepairs with adenine, cytosine, thymine, and uracil. Using molecular dynamics simulations and free energy calculations, we show that hypoxanthine substitutions in PNAs are tolerated in KRAS2 RNA-PNA duplexes where wild type guanine is replaced by mutant uracil or adenine in RNA. To validate our predictions, we synthesized PNA dodecamers with hypoxanthine, and then measured the thermal stability of RNA-PNA duplexes. Circular dichroism thermal melting results showed that hypoxanthine-containing PNAs are more stable in duplexes where hypoxanthine-adenine and hypoxanthine-uracil base pairs are formed than single mismatch duplexes or duplexes containing hypoxanthine-guanine opposition.

INTRODUCTION

Single base mutations in DNA occur frequently in nature, and variations in the genome can affect the development and progression of certain diseases. Mutations in specific genes can result in proteins with altered function ⁽¹⁾. An example of this phenomenon is oncogene activation in cancers ⁽²⁾. Nucleic acid probes that are designed to target oncogenes are usually only capable of recognizing one distinct sequence. In the case where several different single base substitutions occur in one location on a particular gene, single mismatches can lead to severe reduction in oligonucleotide targeting efficacy.

Peptide nucleic acids (PNA) are synthetic DNA/RNA analogs with a pseudo-peptide backbone, as opposed to the sugar-phosphodiester backbone found in DNA ⁽³⁾. PNA molecules can basepair with RNA and DNA, forming stable duplexes. Due to the lack of electrostatic repulsion within the neutral backbone of a PNA, PNA-DNA/RNA duplexes display higher thermal stability than RNA-RNA and DNA-DNA duplexes ⁽⁴⁾. As a result of their hybridization capabilities, PNAs have gained considerable interest as sense/anti-sense agents for treatment and diagnosis of genetic diseases ^{(5, 6)}.

An important feature of PNA-oligonucleotide complexes is the high degree of sequence specificity. Single mismatches can lead to a decrease in the thermal stability of the heteroduplex ⁽⁷⁾. This PNA feature could be used to develop agents targeting mutational hotspots for modulating gene expression in vivo or monitoring acquisition of mutations in a therapeutic approach ⁽⁷⁾. In that respect our laboratory has previously designed radionuclide-chelator-PNA dodecamer-peptide agents that radioimage oncogene mRNAs in tumors with single mismatch specificity ^(8–10).

A clinically relevant example of a single base substitution that leads to drastic pathological changes in gene expression is the KRAS2 oncogene ⁽¹¹⁾. The KRAS2 gene encodes a 21 kDa GTPase, K-Ras, which plays important roles in cell signaling. The twelfth amino acid in wild type K-Ras protein is a glycine, which enables a sharp bend in the K-Ras catalytic site. Mutations in the twelfth codon (GGU) of the KRAS2 mRNA, particularly single base substitutions, cause amino acid substitutions in the K-Ras protein that drive oncogenesis ⁽¹²⁾. Two common mutations in the KRAS2 mRNA twelfth codon involve substitution of the second guanine base for either an adenine or a thymine, giving rise to glycine to aspartate (G12D) or glycine to valine (G12V) mutations, respectively. We have previously distinguished these genetic variants in vivo by radioimaging with specific PNA dodecamers ^{(9, 10)}. Another mutation that frequently occurs in lung cancer, causing a glycine to cysteine mutation (G12C), is substitution of uracil for the first guanine ^{(13, 14)}.

An mRNA imaging agent that could recognize more than one pathogenic base mutation would increase the usefulness of the agent. Non-natural bases capable of hybridizing with more than one base would accomplish this goal ⁽¹⁵⁾. Hypoxanthine, a naturally occurring purine derivative, has been shown to form Watson-Crick hydrogen bonds with adenosine, cytosine, thymine and uracil, but only Hoogsteen base pairing with guanine ^{(16, 17)}.

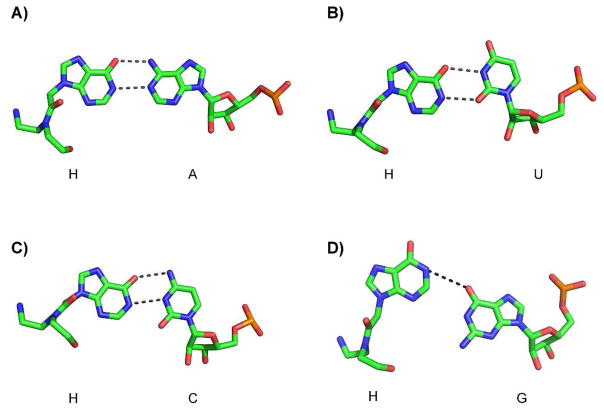
Hypoxanthine has similar chemical properties to guanine despite the lack of the N2 amino group, owing to its ability to form base pairs with multiple bases in a A-helix duplexes (Figure 1) ⁽¹⁸⁾. RNA-containing duplexes are constrained by the 2′-OH to form C3′-endo A-helices, while DNA duplexes prefer the C2′-endo B-helix ⁽¹⁹⁾. In some cases, hypoxanthine has been found to behave more like a G-analog rather than a universal base. By incorporating a hypoxanthine base in a PNA molecule, several base substitutions could be recognized with a single agent. The mutations in KRAS2 mRNA serve as an excellent model system to validate the specificity of hypoxanthine-containing PNAs to detect both the G12D and G12V variants.

Figure 1. Conformations of Watson-Crick base pair with hypoxanthine.

A) hypoxanthine-adenine pair, B) hypoxanthine-uracil pair, C) hypoxanthine-cytosine pair, and D) hypoxanthine-guanine pair. Dashed lines represent hydrogen bonds. Hydrogen atoms are omitted for clarity.

Earlier studies have focused on the synthesis of hypoxanthine-containing PNAs and their interaction with DNA targets ^(20–22). These studies showed a sequence-dependent duplex destabilization when hypoxanthine was incorporated. While T_m values generally decrease when hypoxanthine is substituted for a natural base, its decreased affinity for guanine can be utilized to select against guanine substitutions. In addition, the ability for hypoxanthine to basepair with U, or any other RNA base, has not been studied both computationally and experimentally.

Previous computational studies of hypoxanthine-containing PNA structures have been restricted to quantum mechanical calculations in a vacuum ⁽²¹⁾. Modeling of hypoxanthine-containing PNA structures compatible with molecular dynamics force fields in explicit aqueous solvent could provide insight to their structural, energetic and dynamic properties. To determine the effects on the stability of hypoxanthine-containing PNA dodecamers basepaired to KRAS2 mRNA targets, we performed molecular dynamics (MD) simulations of hypoxanthine-substituted PNAs in duplex with KRAS mRNA sequences. To correlate our simulations with experimental evidence, we synthesized the corresponding chelator-KRAS2 PNA-peptides, hybridized them to KRAS2 RNA icosamers (Table 1), and determined the duplex secondary structures and thermal stabilities by circular dichroism (CD) spectroscopy. We found that hypoxanthine substitutions lead to increased base opening and a slight loss of thermal stability. Nevertheless, a single hypoxanthine substitution was able to recognize both V12 and D12 mutant KRAS2 RNA sequences with similar affinity, in preference to wild type G12 KRAS2 RNA.

Table 1.

Chelator-AEEA-PNA-AEEA-peptide and KRAS2 RNA sequences

Label	Name	Sequence	m/zcalc	m/zmeas
pG12	KRAS2 G12 wildtype	N-SBTG2-DAP-AEEA-GCCACCAGCTCC-AEEA-D(Cys-Ser-Lys-Cys)-C	4326	4326
pD12	KRAS2 G12D mutant	N-SBTG2-DAP-AEEA-GCCATCAGCTCC-AEEA-D(Cys-Ser-Lys-Cys)-C	4341	4341
pV12	KRAS2 G12V mutant	N-SBTG2-DAP-AEEA-GCCAACAGCTCC-AEEA-D(Cys-Ser-Lys-Cys)-C	4350	4351
pDVA12	KRAS2 DVA12 wobble	N-SBTG2-DAP-AEEA-GCCAHCAGCTCC-AEEA-D(Cys-Ser-Lys-Cys)-C	4351	4352
mG12	KRAS2 G12 mRNA	5′-rAGUUGGAGCUGGUGGCGUAG-3′	N/A	N/A
mD12	KRAS2 D12 mRNA	5′-rAGUUGGAGCUGAUGGCGUAG-3′	N/A	N/A
mV12	KRAS2 V12 mRNA	5′-rAGUUGGAGCUGUUGGCGUAG-3′	N/A	N/A

Abbreviations: A: adenine; AEEA: aminoethoxyethoxyacetyl spacer; C: cytosine; DAP: diaminopropanoyl; G: guanine; H: hypoxanthine; SBTG: S-benzyl thioglycolyl N₂S₂ chelator; T: thymine; U: uracil; m/z: mass to charge ratio.

MATERIAL AND METHODS

Design of an empirical force field for PNA: the Sanders et al. force field

In order to develop an AMBER compatible force field for PNA we generated a new force field topology database (FFTopDB) following the building block procedure defined for standard amino acids ⁽²³⁾. Charge fitting was carried out using the standalone version of the RESP program (http://q4md-forcefieldtools.org/RED/resp/) following the two RESP stage fitting procedure⁽²⁴⁾. Quantum chemical calculations were performed by using N-acetyl-2-aminoethyl-glycine-N′-methylamide units with purine and pyrimidine bases linked to the backbone by methylene carbonyl bonds.

Six nucleoside bases were considered: adenine, cytosine, guanine, thymine, uracil and hypoxanthine. The charge derivation procedure was carried out automatically using the R.E.D. IV program available at the R.E.D. server ^{(25, 26)}. This web service allows for controlling the parameters that are necessary for geometric optimization and molecular electrostatic potential (MEP) calculations. The resulting charge values generated are compatible with the non-polarizable Cornell et al. force field ⁽²⁷⁾. Quantum chemistry computation was performed by using the Gaussian program 09 version A.01 ⁽²⁸⁾. 36 elementary building blocks were created and their geometries optimized using the 6-31G* basis set and the Hartree-Fock method ⁽²³⁾. Geometry optimization was performed using structural features extracted from a PNA-RNA hexamer duplex structure previously solved by NMR ⁽²⁹⁾. No PNA-RNA dodecamer duplex structure was available. MEP computations were carried out using the Connolly Surface algorithm and the HF/6-31G* level of theory to take into account the implicit polarization required in condensed phase molecular dynamics simulations using the additive Amber force field model ⁽²⁷⁾. For each building block one or two pairs of molecular orientations based on the rigid-body reorientation algorithm implemented in the R.E.D. program were considered in MEP computation leading to highly reproducible RESP charge values.

Setting specific intra-molecular and inter-molecular charge constraints between well characterized connecting groups during the RESP charge-fitting step generated a total of 18 molecular fragments. The central fragment of each PNA residue was obtained by imposing two intra-molecular charge constraints for zeroing sum of charges on the N-acetyl and N′-methylamide capping groups. The N-terminal fragment of the PNA residues was constructed by combining methylammonium and N-acetyl-2-aminoethyl-glycine-N′-methylamide derivatives in charge derivation. This fragment was generated by setting the two charge constraint values to zero during the fitting step: (i) an inter-molecular charge constraint between the methylammonium methyl group and the NH-acetyl group of each PNA unit, and (ii) an intra-molecular charge constraint for the PNA unit N′-methylamide group. The C-terminal fragment of the PNA residues was built following a similar procedure using acetate and N-acetyl-2-aminoethyl-glycine-N′-methylamide derivatives. This fragment was obtained by constraining the total charge of two groups of atoms to the zero value. One group involved in the acetate methyl group and the CO-N′-methylamide group of each PNA unit, and the other one the PNA unit N-acetyl group. As a result, the total charges of the central, N- and C-terminal fragments of the PNA units took integer values. Force field libraries for the molecular fragments were built by removing the atoms involved in the charge constraints from the molecules involved in charge derivation, and by adding a new atom connectivity between the methylammonium nitrogen group and the PNA C2′ carbon atom for the N-terminal fragment, and between the acetate carboxylate carbon and the PNA C5′ carbon atom for the C-terminal fragment. Atomic charges of the PNA backbone of the different building blocks were forced to be equivalent, leading to a highly consistent set of charges values within the FFTopDB.

Molecular Dynamics Simulations

System equilibration and production MD simulations were performed using the Amber 12 suite of programs ^{(30, 31)}. The LeaP module of AMBER12 was used to create parameter and topology files for the MD simulations using the ff99SB force field ^{(30, 31)}. RNA molecules were set to predicted protonation states at pH 7.0. Na⁺ and Cl⁻ counter-ions were added to each system to achieve neutrality and a salt concentration of 0.1 M. TIP3P water molecules were added with a minimum spacing of 30.0 Å (3.0 nm) from the box edges to the PNA-RNA molecules.

Energy minimization on each system was performed in a two-step process. First the solute atoms were restrained while the water and ion molecules were allowed to relax over 1000 steps. The entire system was then subjected to energy minimization using the steepest descent method for the first 1000 steps, followed by the full conjugate gradient method for an additional 24000 steps. Each molecular system was then heated to 300K for 100 ps followed by a 50 ps constant pressure simulation to adjust the density to 1 g/mL. An additional 500 ps simulation was run prior to production simulations to allow for further temperature and pressure equilibration.

Production runs were performed using a canonical ensemble (NVT) scheme. Langevin dynamics with a collision frequency of 2.0 were used for temperature regulation, ii) the SHAKE algorithm was used for all hydrogen atoms, and iii) the particle mesh Ewald method was employed to treat long-range electrostatics and van der Waals forces (cutoff of 8 Å) with an integration step of 2.0 fs. All Amber equilibration and production runs were performed using double precision ^{(31, 32)}. All production simulations were repeated in triplicate with random seeding for initial velocities and extended to 25 ns. Structural features were determined using the Curves+ software package ⁽³³⁾, while visualization of trajectories was performed in VMD ⁽³⁴⁾.

Accelerated Molecular Dynamics Simulations

Accelerated MD (aMD) is one method to increase the sampling of a molecular system to overcome the computational cost of long time scales. aMD modifies the system’s original potential energy surface (V(r)) by adding a boost potential (ΔV(r)) when V(r) falls below a certain threshold energy (E) ⁽³⁵⁾. The boost potential is defined as:

$$\mathrm{\Delta }V(r)=\{\begin{array}{ll}0,\hfill & V(r)\ge E\hfill \\ \frac{{(E-V(r))}^2}{\alpha +(E-V(r))},\hfill & V(r)<E\hfill \end{array}$$

where α modulates the depth and roughness of the energy basins on the modified potential. In order to enhance sampling of internal and diffusive degrees of freedom, a dual boosting potential was applied to the backbone torsion angles and the overall boost potential as

$$V(r)=V_o(r)+V_t(r)$$

$$V^{\ast }(r)=\{V_o(r)+[V_t(r)+\mathrm{\Delta }{V}_t(r)]\}+\mathrm{\Delta }{V}_T(r)$$

Where V_t(r) is the total potential of the torsional terms, ΔV_t(r) and ΔV_T(r) are the boost potentials applied to the torsional terms and the total potential energy, respectively. The parameters were set as follows: E_t = 1.2{〈ΔV_t(r)〉}, α_t= 0.20 kcal/mol.E_T=0.2 kcal/mol·number atoms plus the ensemble-averaged potential energy from the conventional MD simulations. α_T=0.2 kcal/mol·number atoms ^{(36, 37)}. aMD runs were performed for 50 ns.

MM-PBSA Calculations

The binding energies for each RNA-PNA duplex were calculated using the MM-PBSA method in Amber 11 ^{(38, 39)}. The MM-PBSA method calculates the binding free energy by the free energies of solvation for the complex (ΔG_duplex), PNA (ΔG_PNA) and RNA (ΔG_RNA):

$$\mathrm{\Delta }{G}_{\mathit{bind}}=\mathrm{\Delta }{G}_{\mathit{duplex}}-\mathrm{\Delta }{G}_{\mathit{PNA}}-\mathrm{\Delta }{G}_{\mathit{RNA}}$$

Each term is calculated by determining the enthalpic energy of the solute using molecular mechanics (E_MM), the polar solvation free energy (ΔG_solv), the nonpolar solvation free energy (ΔG_np) and the entropic contribution (ΔS):

$$\mathrm{\Delta }G=\langle E_{MM}\rangle +\langle \mathrm{\Delta }{G}_{\mathit{solv}}\rangle +\mathrm{\Delta }{G}_{np}-T\langle \mathrm{\Delta }S\rangle$$

The enthalpic term is taken as the average over the molecular mechanics force field terms for the solute. The solute vibrational entropy is estimated using either normal mode analysis or quasi-harmonic approximation. ΔG_solv is calculated using the Poisson Boltzmann (PB) equation. The nonpolar term (ΔG_np) is estimated from the solvent accessible surface area (SASA) ⁽⁴⁰⁾:

$$\mathrm{\Delta }{G}_{np}=\gamma \mathit{SASA}+\beta$$

Where γ is the surface tension, set to 0.0072 kcal/Ų. β is an offset value used to correct for the nonpolar contribution to the solvation free energy term ⁽⁴¹⁾. Free energy values were converted to theoretical melting temperatures using the following equation ⁽⁴²⁾:

$$\frac{1}{T_m}=\frac{R}{\mathrm{\Delta }H}ln[c_t]+\frac{\mathrm{\Delta }S-\mathit{Rln}[2]}{\mathrm{\Delta }H}$$

Where ΔH is calculated from the sum of the enthalpic terms in the MM-PBSA calculation, ΔS is the entropy value from normal mode analysis, R is the gas constant in kcal/mol·K and c_t is the concentration of each individual RNA/PNA strand in the CD experiments and has units of M.

For each RNA-PNA system, MM-PBSA calculations were performed using the last 8.0 ns of the simulation with 100 ps intervals. The entropy was determined using normal mode analysis using 50 frames over the 8.0 ns. All energy values represent 3 independent MD simulation runs for each RNA-PNA duplex. aMD MM-PBSA calculations were performed over the entire 50.0 ns simulation with 50 ps intervals. aMD entropy values were determined using the same method as for conventional MD (cMD) simulations. All calculations were performed with the MMPBSA.py.MPI module in Amber 11 with an ionic strength equal to 1.0 M. For MM-PBSA calculations the PB equation was solved numerically by the PBSA program included with in the AmberTools 12 module. The hydrophobic contribution was approximated by the LCPO method implemented within the Sander module ⁽⁴³⁾.

Synthesis of peptide nucleic acids with hypoxanthine substitutions

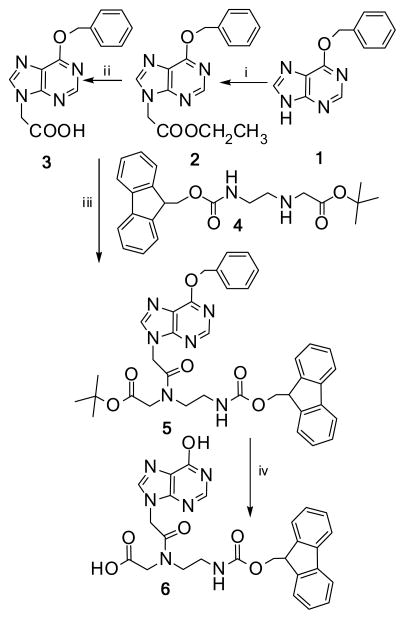
Synthesis of 2-(O⁶-benzyloxy-purin-9-yl) acetic acid, 3

As shown in Scheme 1, 6-benzyloxypurine, 1 (1 g, 4.42 mmol) and dry NaH (120 mg) were suspended slowly in dry DMF (dimethylformamide) (12 mL). The reaction mixture was stirred for 2 h at room temperature under argon. Subsequently, ethyl bromoacetate (525 mL) was added dropwise over a period of 3 h at room temperature under argon. After an additional 2 h of stirring, the solvent was removed by evaporation in vacuo. The mixture was dissolved in ethyl acetate (200 mL) and poured into a separating funnel. The organic layer was washed with brine (3×50 mL), followed by water (3×50 mL), dried over Na₂SO₄, and concentrated in vacuo. The crude product was purified by silica gel column chromatography using 2% MeOH in CH₂Cl₂ to obtain a white powder, ethyl-2-(O⁶-benzyloxy-purin-9-yl) acetate, 2 (980 mg, 71%). 500 mg of 2 was mixed with MeOH (10 mL) and cooled on ice to 0°C. Subsequently, aqueous 2 M NaOH (10 mL) was added to saponify the ethyl group, and the reaction was stirred for 30–40 min at 0°C. The solution was washed with cold CH₂Cl₂ (5 mL) or diethyl ether. The pH of solution was adjusted to 1 using aqueous 1 N HCl, resulting in precipitation of 2-(O⁶-benzyloxy-purin-9-yl) acetic acid, 3. The product was filtered, washed with water (2×30 mL), and dried to obtain a fluffy powder (418 mg, 92%): ¹H NMR (d₆-DMSO): δ 12.37 (s, 1H), 8.54 (s, 1H), 8.36 (s, 1H), 7.49–7.54 (m, 2H), 7.34–7.45 (m, 3H), 5.63 (s, 2H), 5.08 (s, 2H). MALDI TOF m/z calcd: 284.27; found: 285.09 (M+H⁺).

Scheme 1. Synthesis of hypoxanthine PNA monomer.

(i) NaH, DMF, rt, 2hr; ethy bromoacetate, rt, 5hr, 71%. (ii) 2M NaOH, 0°C, 40min, 92%. (iii) HATU, DMF, 1hr. (iv) DCM:TFA (2:1), rt, 30min; yield: 64% af ter HPLC purif ication.

Synthesis of N-(2-((fluorenylmethoxycarbonyl)aminoethyl)-N-(2-(6-(hydroxyl)-9H-purin-9-yl)acetyl) glycine (Fmoc-hypoxanthine-PNA monomer), 6

To an ice-cooled suspension of 2-(O⁶-benzyloxy-purin-9-yl) acetic acid, 3 (190 mg, 0.67 mmol) in dry DMF (8 mL), tert-butyl N-[2-(fluorenylmethoxycarbonyl) aminoethyl] glycinate, 4 (260 mg, 0.6 mmol) and N,N-Diisopropylethylamine (0.8 mL) were added. With stirring, the coupling agent HATU (O-(7-azabenzotriazol-1-yl)-N,N,N′,N′-tetramethyluronium hexafluorophosphate) (229 mg, 0.603 mmol) was added to yield tert-butyl N-[2-(fluorenylmethoxycarbonyl) aminoethyl]-N-[O⁶-benzyloxy-purin-9-yl) acetyl] glycine, 5. The reaction was stirred for 1 h at room temperature. The reaction mixture was poured into 50 mL NaHCO₃ solution (10% by mass) and extracted with ethyl acetate (3×100 mL). The combined organic extract was dried with Na₂SO₄, filtered, and the solvent was removed using a rotary evaporator. The residue was purified by silica gel column chromatography with a 2–10% gradient of MeOH in CH₂Cl₂. The tert-butyl and benzyl protecting groups were removed with CH₂Cl₂:CF₃CO₂H (3:1, v:v) at room temperature for 30 min. The reaction was monitored by thin layer chromatography. The final product N-(2-((fluorenylmethoxycarbonyl)aminoethyl)-N-(2-(6-(hydroxyl)-9H-purin-9-yl)acetyl) glycine, 6 was precipitated by adding to cold diethyl ether, followed by chromatography on an Alltech C₁₈ 22×250 mm column eluted with a gradient of 15–80% CH₃CN in water over 30 min to give the purified Fmoc-hypoxanthine-PNA monomer, 6 (222 mg, 64%): ¹H NMR (d₆-DMSO) δ 12.28 (s, 1H), 7.86–7.98 (m, 4H), 7.65–7.69 (d, J=9 Hz, 2H), 7.26–7.47 (m, 5H), 5.21 (s, 1H), 5.03 (s, 1H), 4.20–4.37 (m, 4H), 3.99 (s, 1H), 3.09–3.50 (m, 6H), 3.09–3.16 (m, 1H); MALDI TOF m/z calc: 516.51; found: 517.11(M+H⁺).

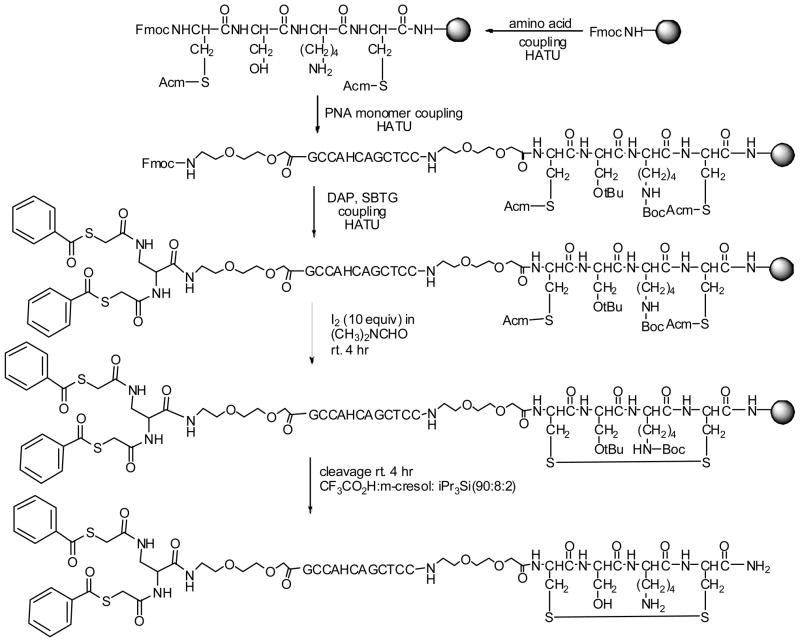
Synthesis of chelator-PNA-peptide sequences including hypoxanthine

The chelator-PNA-peptide chimeras in Table 1 were synthesized as shown in Scheme 2, purified, and characterized as described ⁽⁴⁴⁾. Automated Fmoc coupling of amino acids, spacers, PNA monomers, and chelators was carried out on a Protein Technologies PS3 synthesizer at the 10 μmol scale. The chimeras were purified to ≥95% homogeneity by reversed phase liquid chromatography at 50°C as described ⁽⁴⁴⁾. Molecular masses were determined by MALDI-TOF mass spectroscopy as described ⁽⁴⁴⁾.

Scheme 2.

Synthesis of SBTG2-KRAS2 G12DVA PNA-D(Cys-Ser-Lys-Cys).

Circular dichroism and thermal melting of PNA-RNA duplexes

CD spectra were obtained for PNA-RNA duplexes using a JASCO J-815 spectropolarimeter with Peltier temperature control. Spectra were recorded at 25°C over 320–200 nm wavelengths. Gel-purified RNA icosamers (Table 1) were purchased from Thermo Scientific (Dharmacon). Prior to measurement, samples were heated to 95° C for 10 min and then slowly cooled. All spectra were subjected to baseline correction. Final spectra were calculated as the average of 3 independent measurements. Stock RNA samples were suspended in H₂O and PNA molecules in 100 mM sodium acetate, pH 4.0. RNA-PNA solutions were diluted in 100 mM Na₂HPO₄, 1.0 M NaCl, 5 mM EDTA, pH 7.0, to reach a final concentration of 1μM:1μM. Thermal denaturation experiments were carried out by increasing the temperature from 25°C to 95°C at a rate of 1.0°C/min while monitoring the CD signal at 265 nm. T_m values were determined based on the assumption of a two-state model. Melting curves were normalized by subtracting baseline slopes ⁽⁴²⁾. The first derivative of the melting curves was computed with respect to the temperature (d /dT), and the maximum was used to determine the T_m. We have previously reported no perturbation of T_m due to peptide moieties on the PNAs ^{(45, 46)}.

RESULTS

Charge review and validation of the Sanders et al. force field for PNA

In order to study PNA molecules using MD simulations, we developed a new FFTopDB compatible with the Cornell et al. force field for nucleic acids and proteins. The R.E.D. program version IV provides the capabilities of charge derivation and force field library building for the entire set of PNA molecules with characterized molecular orientations and conformations ⁽²⁵⁾. The statistics module of R.E.D. IV was used to characterize and minimize the impact of the charge constraints used during the charge fitting step. A relative root mean square (RRMS) value of 0.041 between the MEP calculated by the quantum chemistry and that generated using the derived charges values obtained for the charge fitting step. A similar RRMS value was also obtained in the absence of intra-molecular change constraints, inter-molecular charge constraints and inter-molecular change equivalencing. Small RRMS values as well as small differences between the charge fitting steps carried out with and without charge constraints is one way to demonstrate the accuracy of the fitting step performed for the PNA force fields. The new FFTopDB has been submitted in the RESP and ESP charge database (R.E.DD.B.) and is available under the “F-93” R.E.DD.B. code at http://q4md-forcefieldtools.org/REDDB⁽⁴⁷⁾.

Comparison of average structures from experimental PNA-DNA/RNA and MD results

To study the stability of PNA-RNA duplexes containing mismatches and hypoxanthine substitutions, MD simulations were performed using RNA icosamer sequences of wild type and mutant KRAS2 sequences basepaired with PNA molecules (Supplementary Table 1). In order to access the accuracy of the Sanders et al. force field for PNA, we compared the overall helical parameters of 25 ns NVT simulations with experimental PNA-RNA duplex structures previously solved. PNA-RNA duplex helical parameters were found compatible with A-form RNA geometry (Supplementary Table 2).

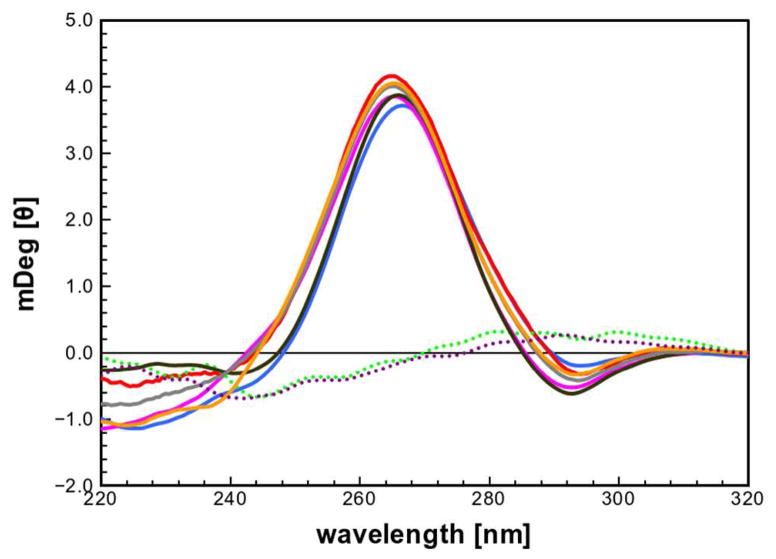
Analysis of the helical parameters revealed twist values in the range of 23–26° and average helical rise values of 2.4–2.7 Å. These values are slightly smaller than those found in fiber diffraction A-RNA helices containing adenosine-uracil and inosine-cytosine base pairs ⁽⁴⁸⁾. To validate our MD results, we synthesized PNA molecules with hypoxanthine substitutions and measured the helical content using CD spectroscopy. All PNA-RNA duplex spectra showed distinct features of A-like helices, particularly a negative absorbance band around 290 nm and a strong positive CD signal around 265 nm (Figure 2) ⁽⁴⁹⁾. The aminoethylglycine backbone of PNA molecules is highly dynamic relative to other nucleic acid backbones, and as a result a large conformational space is sampled while binding to a single stranded RNA. Average results of PNA backbone dihedral angles revealed that indeed the PNA backbone is highly flexible in the context of a complementary PNA-RNA duplex. MD results reported here agree with backbone properties of experimentally solved PNA-nucleotide complexes (Figure 3) ^{(29, 50, 51)}.

Figure 2. CD spectra of PNA-RNA duplexes.

Wavelength scans of 1 μM : 1 μM PNA-RNA duplexes in 100 mM Na₂HPO₄, 1.0 M NaCl, 5.0 mM EDTA, pH 7.0, were measured at 25°C. The pD12-mD12 is colored: pD12-mG12, blue; pV12-mV12, magenta; pDVA12-mD12, red; pDVA12-mG12, black; pDVA12-mV12, grey; pDVA12, orange; PNA alone, green dots; and pD12 alone, purple dots.

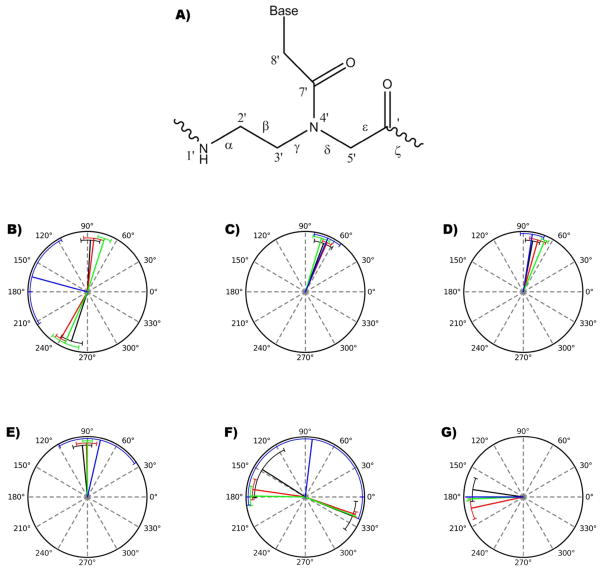
Figure 3. Backbone angles of PNA from MD simulations.

A) Lewis structure of a PNA monomer and the corresponding backbone angles. Average values were measured over 25.0 ns of simulation and compared to average values from available PNA-RNA/DNA structures. Polar plots for backbone angles were constructed, the black lines represents the angle measured from simulation, red a PNA-PNA duplex (PDB ID: 1PUP), green a PNA-DNA duplex (PDB ID: 1NR8) and blue a PNA-RNA duplex (PDB ID:176D). Circular plots represent the B) alpha, C) beta, D) gamma, E) delta, G) epsilon and F) zeta angle values. Error bars represent standard deviation of each base pair in a duplex.

Effects of hypoxanthine substitution on RNA-PNA base pairing

To compare the structure and dynamics of PNAs with hypoxanthine substitutions, we monitored the basepair parameters for each PNA-RNA duplex MD simulation. Several different helical parameters can be used to describe the different structural changes in nucleic acids and can be extended to PNA molecules in complex with single stranded RNA or DNA molecules ⁽³³⁾. We chose to focus our attention on the frequently mutated central base pairs of the twelfth codon. We placed a hypoxanthine at the corresponding fifth residue of the PNA dodecamer. Mismatches due to mD12 (GAU) and mV12 (GUU) KRAS2 RNA sequences should result in weak base pairing with a wild type pG12 PNA dodecamer. Hypoxanthine-containing PNAs were predicted to form stable base pairs with mD12 (adenine-hypoxanthine) and mV12 (uracil-hypoxanthine) RNAs, while mG12 (guanine-hypoxanthine) base pairing was predicted to be less stable. Shear, stretch and opening base pair parameters are a good measure of base pairing and spontaneous opening of base pairs.

Shear and stretch parameters are defined as the relative offset of the two base origins in the mean base pair plane ⁽³³⁾. Average shear values were calculated for the three base pairs corresponding to the twelfth codon and also for individual base pairs (position eight in the RNA sequence), where hypoxanthine substitution was incorporated (Table 3). Duplexes containing perfect matches (pD12-mD12, pV12-mV12 and pG12-mG12) had average shear values that ranged from −0.1 to 0.07 Å. Single mismatch shear values ranged from −4.0 to 2.2 Å. pDVA12-mD12, pDVA12-mV12 and pDVA12-mG12 had average shear values of 0.8, −2.4 and 1.8 Å, respectively.

Average stretch values measure the separation of Watson-Crick base pairs. These values ranged from −1.7 to 2.3 Å for all base pairs in the eight position of the RNA sequence. The largest stretch value occurred between the pDVA12 hypoxanthine base and the adenosine base of the mD12 RNA. This observation may reflect the poor base pairing capabilities of hypoxanthine (and inosine) with guanine as previously observed ⁽¹⁷⁾. The opening angle parameter, one of the primary measures of basepair opening, is defined as the angle between the two x-axes with respect to the average normal to the base plane. Positive opening values are indicative of opening towards the major groove, while negative values indicate opening in the direction of the minor groove. Large opening values towards the major grove were observed for hypoxanthine-guanine base pair of pDVA12-mG12 (53°) and the guanine-adenine base pair in pV12-mG12 (24°). This is in contrast to the other opening values for base pairs containing hypoxanthine: 11 and 3° for pDVA12-mD12 and pDVA12-mV12, respectively. This suggests that inability for the hypoxanthine-guanine base pair to form in the pDVA12-mG12 duplex resulting in substantial base opening accommodated by changes in the PNA backbone angles. Figure 4 shows that the lack of hypoxanthine-guanine base pairing results in a PNA base adjacent to the hypoxanthine being completely flipped out during the 25 ns of MD simulations. A hypoxanthine-adenine base pair, however, does not significantly affect the helical parameters or adjacent base pairs.

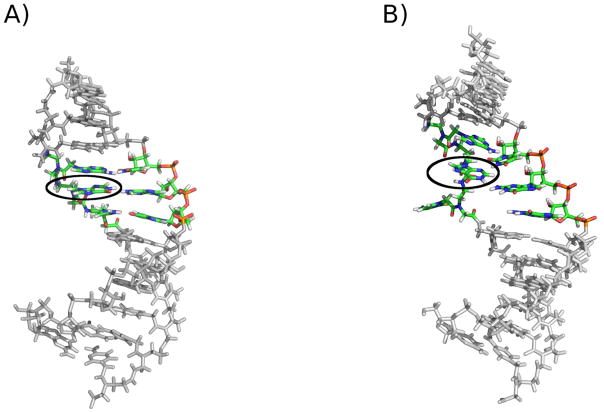
Figure 4. Hypoxanthine base pairing during MD simulations.

A) pDVA12-mD12 and B) pDVA12-mG12 duplexes. Shown are the structures of each duplex after 25.0 ns of MD simulation. The hypoxanthine base (circled) forms a Watson-Crick base pair (H-A) in A) while the H-G pair in B) causes distortions in the duplex leading to adjacent PNA base flipping.

Thermal measurements of RNA-PNA duplex stability

Next, the energetic effects of hypoxanthine substitutions in PNA-RNA duplexes were determined computationally and confirmed experimentally. The molecular mechanics-Poisson Boltzmann surface area method (MM-PBSA) was used to compute the free energy of various PNA-RNA duplexes from respective MD simulations. We used the normal mode approximation to calculate configurational entropy changes in each duplex. Typically nonlinear solvation methods overestimate the free energy values of biopolymer systems, restricting the possibility of calculating the absolute free energy change ⁽⁵²⁾. This overcompensation, however, does not prevent relative free energy values from being determined ⁽⁵³⁾. MM-PBSA calculations were performed on all the duplexes using the last 8.0 ns of each simulation (Supplementary Table 3).

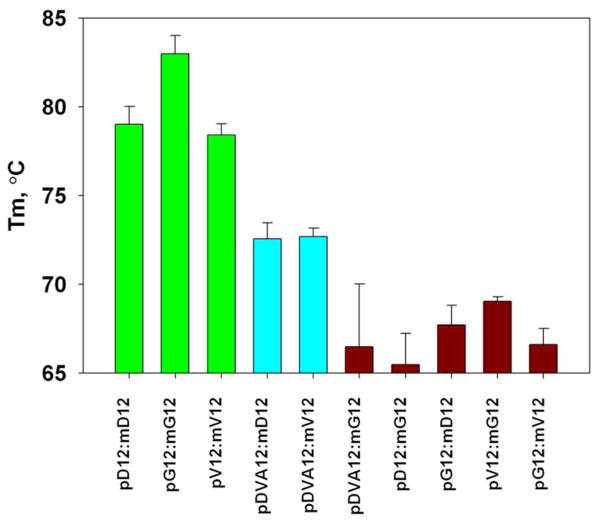
To test our hypothesis, we recorded CD melting curves at 265 nm, which revealed a decrease in stability of duplexes containing hypoxanthine relative to the corresponding complementary sequences without hypoxanthine (Table 2 and Figure 5). While all hypoxanthine substitutions displayed lower stabilities than complementary duplexes (group 1), the pDVA12-mD12 and pDVA12-V12 duplexes (group 2) were more stable than all the duplexes containing mismatches, or the pDVA12-mG12 duplex (group 3). The differences in the mean values among all ten duplexes are greater than would be expected by chance. Kruskal-Wallis One Way Analysis of Variance on Ranks revealed a statistically significant difference (p = <0.001). Finally, Holm-Sidak All Pairwise Multiple Comparison revealed statistically significant differences (p<0.001) among group 1, group 2, and group 3. The reduction of T_m of the pDVA12-mG12 duplex is comparable to the reduction of T_m for PNA-RNA duplexes containing a mismatch. This suggests that the hypoxanthine-guanine base pair reduces the duplex stability possibly by base flipping on the PNA molecule as observed in our MD simulations of pDVA12-mG12 duplexes.

Table 2.

Effects of hypoxanthine substitutions on average base and helical parameters.

Duplex (PNA-RNA)	Base pair at 8th position	Shear	Stretch	Opening	Tilt
pD12-mD12	T-A	−0.1 ± 0.01	0.034 ± 0.003	2.4 ± 0.2	−1.4 ± 0.2
pD12-mG12	T-G	2.2 ± 0.01	−0.3 ± 0.02	0.6 ± 0.3	1.3 ± 0.1
pG12-mG12	C-G	−0.06 ± 0.01	0.02 ± 0.004	0.8 ± 0.1	−2.1 ± 0.2
pG12-mD12	C-A	−2.7 ± 0.07	0.3 ± 0.04	6.9 ± 0.8	−4.8 ± 0.2
pG12-mV12	C-U	−4.0 ± 0.07	−1.7 ± 0.03	−2.9 ± 0.5	−10 ± 0.2
pV12-mV12	A-U	0.07 ± 0.01	0.02 ± 0.06	1.9 ± 0.2	−1.3 ± 0.2
pV12-mG12	A-G	−1.1 ± 0.1	0.1 ± 0.03	24 ± 1	−1.6 ± 0.2
pDVA12-mD12	H-A	0.8 ± 0.1	1.36 ± 0.03	11 ± 1	1.9 ± 0.2
pDVA12-mG12	H-G	1.8 ± 0.1	2.37 ± 0.1	53 ± 1	−2.6 ± 0.5
pDVA12-mV12	H-U	−2.4 ± 0.01	−0.2 ± 0.01	3.2 ± 0.3	−4.9 ± 0.2

Error values represent the standard error. A: adenine; C: cytosine; G: guanine; H: hypoxanthine; T: thymine; U: uracil.

Figure 5. Melting temperatures of RNA-DNA duplexes.

CD thermal ramps from 25°C to 95°C were monitored at the peak wavelength, 265 nm. T_ms calculated from first derivative peaks are shown with error bars corresponding to the standard deviation from 3 independent measurements. Holm-Sidak All Pairwise Multiple Comparison revealed statistically significant differences (p<0.001) among group 1, the complementary duplexes (green), group 2, the hypoxanthine-adenine and hypoxanthine-uracil duplexes (cyan), and group 3, hypoxanthine-guanine and mismatch duplexes (magenta).

In order to compare these two sets of results accurately, the theoretical melting temperatures were calculated from the MM-PBSA approach (Supplementary Table 3). However, computed T_m values had no correlation with experimentally measured values (r²=0.05) (Figure 6). This could be a result of the approximations made in the MM-PBSA method, the accuracy of our force field, or inefficient sampling of the free energy landscape. Enhanced sampling techniques can be employed to test the latter.

Figure 6. Correlation between predicted T_m values from MM-PBSA calculations and CD.

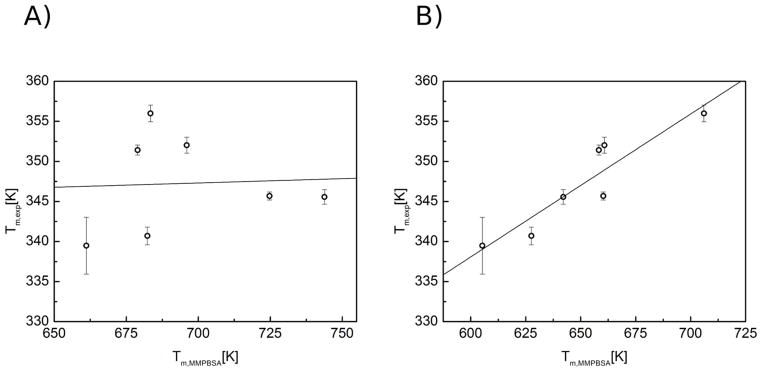
Predicted T_m values for PNA-RNA cMD (A) and aMD (B) simulations were compared with experimental T_m values from CD. The values were correlated for cMD (R² = 0.05) and aMD (R² = 0.84). Error bars represent standard deviation of 3 independent CD melting experiments.

aMD is one enhanced sampling method that does not require a priori knowledge of the ensemble or a biasing potential to force the system to a particular end-state. Instead, aMD applies a boost potential to the torsion angles and the overall potential energy surface thereby reducing the height of energy barriers. Theoretically aMD allows for the correct Boltzmann ensemble average to be recovered from the calculations performed on the modified potential energy surface. It has been shown that aMD simulations can reproduce the dynamics observed in millisecond conventional MD simulations for proteins ⁽³²⁾. To determine if the computed T_ms would be improved by increasing sampling efficiency during MD simulations, aMD simulations were performed for each RNA-PNA duplex by applying a boost potential to the torsional energy terms and the overall potential energy of the system.

50 ns simulations for each duplex were carried out. Post-processing by MM-PBSA was executed over the entire aMD run. A far better correlation between computed T_m values and those measured by CD (r²=0.84) was observed (Figure 6 and Supplementary Table 4). This level of agreement suggests that the inability to accurately predict relative T_m values for our PNA-RNA duplexes was the result of sampling inefficiency.

Helical and base pair values were also measured during the course of the aMD runs and the results are listed in Supplementary Table 5. The helical parameters for complementary sequences and hypoxanthine substitutions are similar to those observed in the conventional MD simulations. Mismatch and pDVA12-mG12 duplex helical parameters, however, were subject to higher variation relative to those obtained from conventional MD. Particularly, the base opening parameter increased for several mismatches (Supplementary Table 6).

Basepair opening may be affecting the MM-PBSA results. The energetic penalty for solvating the swung out base may explain the differences in free energy values calculated between conventional and aMD simulations. We did notice that there was increased base opening for pDVA12-mD12, but the energy value was not drastically reduced as the mismatch containing duplexes.

Discussion

Oligonucleotides capable of targeting single base substitutions could provide diagnostics or therapeutics for genomic alterations, particularly if the mutation of interest plays a role in disease development ^{(2, 54)}. Cancer genes provide powerful clinical examples of mutations that drive disease progression and homeostasis ⁽²⁾. Numerous studies have attempted to target genomic mutations using modified oligonucleotide therapies ^{(55, 56)}. PNAs are attractive to target genes for monitoring or treatment of disease due to their physicochemical properties and stability in vivo ⁽⁵⁷⁾. PNA molecules capable of recognizing specific single nucleotide polymorphisms in vivo are being developed to image and quantify oncogene expression ⁽⁵⁸⁾. The ability to discriminate at the base pair level could potentially increase the efficacy of PNA therapeutics.

In this study we designed, modeled, and synthesized PNAs containing a hypoxanthine monomer that correlates with the naturally occurring RNA nucleoside inosine. Hypoxanthine base has the ability to form Watson-Crick base pairs with multiple bases. The inosine nucleoside occurs naturally in the wobble position of the anticodon loop of tRNA molecules and plays roles in genomic degeneracy and mRNA-protein recognition. KRAS2 mRNA mutations play a major role in oncogenesis and tumor progression. Common mutations in this codon involve a substitution of a wild type guanine (G12) for adenine (D12) or uracil (V12) in the twelfth codon, causing aberrant protein function ^{(11, 12)}. We predicted that a short complementary PNA dodecamer with a hypoxanthine substitution at the mutant position would bind with higher affinity to the two mutations relative to the wild-type sequence.

Prior to synthesis of PNA molecules, we tested our hypothesis using molecular modeling techniques. Molecular MD simulations can be used to predict the dynamics of proteins and nucleic acids using first principles from physics ^{(59, 60)}. Given that PNA molecules are not standard biopolymers, a specific force field is required. To overcome this issue we performed quantum chemical calculations using the R.E.D. server to derive charge parameters for PNA molecules compatible with the Amber99SB force field. Several studies have previously reported AMBER force fields for PNA, but have either not incorporated hypoxanthine bases or used a low level of theory in MEP computation that is not fully compatible with the additive AMBER force field model ^(61–64).

Using MD simulations, we showed that the modeled PNA-RNA duplexes feature helical properties in agreement with experimentally determined A-RNA and A-DNA duplexes. To validate our results, we synthesized PNA molecules and performed CD spectroscopy to determine the secondary structural content of PNAs bound to KRAS2 RNA sequences. All complexes were capable of forming A-like helices in solution, which is in agreement with results obtained from MD simulations. We compared the backbone angles and found they are in good agreement with experimentally solved NMR and x-ray PNA-PNA/PNA-RNA duplex structures ^{(29, 50, 51)}.

Next, we sought to determine the structural and thermodynamic consequences of hypoxanthine incorporation in a PNA-RNA duplex. Given the base pairing preferences for hypoxanthine, we expected that our PNA incorporating a hypoxanthine would bind more tightly with the two KRAS2 mutant sequences relative to the wild type KRAS2 sequence. Results from MD simulations showed the hypoxanthine-guanine base pairing in the pDVA12-mG12 duplex resulted in distortions to the duplex by changes in the helical properties. Base pair opening is commonly observed phenomenon in DNA/RNA duplexes harboring mismatching bases ⁽⁶⁵⁾. We observed base pairing opening in pDVA12-mG12 duplexes during the course of a 25.0 ns simulation. This suggests that basepair opening occurs as a result of the inability of hypoxanthine-guanine to form a Watson-Crick base pair and that the opening occurs on the nanosecond timescale.

While MD simulations are capable measuring dynamics at the molecular scale, thermodynamic predictions are not as straightforward. Typically one has to apply a perturbation to the system and measure the potential of mean force to construct a free energy path to compute binding energies ⁽⁶⁶⁾. These methods can be computationally prohibitive due to the number of simulations necessary to obtain convergent free energy values. An efficient alternative is to use non-linear solvation energies to construct a free energy cycle from standard MD simulations. This method has been successfully applied in many cases to predict relative free energy values ⁽⁵²⁾. By applying the MM-PBSA method to our PNA-RNA MD simulations a set of relative free energy values can be obtained. To confirm our energetic predictions we performed thermal melts on PNA-RNA duplexes using CD. We then converted our theoretical free energy values to T_m(s) to compare with our experimental results. We found MM-PBSA failed to correlate with experimental values and could not accurately rank the duplex energies.

Obtaining accurate results using MM-PBSA/GBSA methods is often difficult due to approximations inherent in non-linear solvation models ⁽⁶⁷⁾. Another, less common problem is due to inefficient sampling of the thermodynamic ensemble for a particular system. Several theoretical methods exist to increase sampling or bias a system to sample a particular region of its free energy landscape ⁽⁶⁸⁾. aMD is an enhanced sampling method that has become attractive in recent years due to its ability to increase sampling time-scales several orders of magnitude over those accessible with standard MD simulations. Another unique feature is that it does not require any knowledge of the underlying free energy surface or reaction pathway, a limiting factor for several other methods ⁽⁶⁹⁾. In order to determine if the inaccuracies of our initial energetic predictions were a result of inefficient sampling, we applied aMD to our PNA-mRNA duplexes. After 50.0 ns of an aMD run, we calculated the helical parameters and compared them to the conventional MD results. Duplexes with complementary sequences retained similar helical properties to those observed in conventional MD. Duplexes containing mismatches, however, were subject to greater variation in base pairing parameters. This result was also observed for the pDVA12-mG12 duplex. This suggests the biasing potential was not causing local artificial distortions in the duplexes based on the similar helical parameters for matching sequences in both aMD and conventional MD.

Combining the MM-PBSA method with the aMD simulations also increased the correlation between theoretical and experimental T_m values. This led us to conclude that the decrease in thermal stability in duplexes containing mismatches is at least partially a result of base pairing flipping on the PNA. It also suggests that observed decreased in T_m for the pDVA12-mG12 duplex is due to the inability of H-G to form a Watson Crick base pair. This, in addition to overall higher melting temperatures for pDVA12-mD12 and pDVA12-mV12 duplexes, suggests that hypoxanthine substitutions would be able to discriminate between wild-type and the two mutant KRAS2 mRNA sequences. We recognize that our simulations are limited by the usage of fixed charged force field parameters and therefore not capable of reproducing accurate base stacking energies. Despite this, the high correlation between our experimental and computationally predicted melting temperatures leads us to conclude that our models are a good approximation and in-line with other computational studies of host-ligand binding energy studies ⁽⁷⁰⁾.

ABBREVIATIONS

A

adenine

AEEA

aminoethoxyethoxyacetyl spacer

C

cytosine

CD

circular dichroism

DAP

diaminopropanoyl

FFTopDB

force field topology database

G

guanine

H

hypoxanthine

MD

molecular dynamics

aMD

accelerated molecular dynamics

MEP

molecular electrostatic potential

MM-PBSA

molecular mechanics/ Poisson-Boltzmann surface area

NVT

number of particles, volume of system, temperature, of ensemble

PNA

peptide nucleic acid

SBTG

S-benzyl thioglycolyl N₂S₂ chelator

T

thymine

U

uracil