Abstract
There are numerous biological examples where genes associated with migratory ability of cells also confer the cells with an increased fitness even though these genes may not have any known effect on the cell mitosis rates. Here, we provide insight into these observations by analyzing the effects of cell migration, compression, and contact inhibition on the growth of tumor cell clusters using the Cellular Potts Model (CPM) in a monolayer geometry. This is a follow-up of a previous study (Thalhauser et al., Biol. Direct, 2010, 5:21) in which a Moran-type model was used to study the interaction of cell proliferation, migratory potential and death on the emergence of invasive phenotypes. Here, we extend the study to include the effects of cell size and shape. In particular, we investigate the interplay between cell motility and compressibility within the CPM and find that the CPM predicts that increased cell motility leads to smaller cells. This is an artifact in the CPM. An analysis of the CPM reveals an explicit inverse-relationship between the cell stiffness and motility parameters. We use this relationship to compensate for motility-induced changes in cell size in the CPM so that in the corrected CPM, cell size is independent of the cell motility. We find that subject to comparable levels of compression, clusters of motile cells grow faster than clusters of less motile cells, in qualitative agreement with biological observations and our previous study. Increasing compression tends to reduce growth rates. Contact inhibition penalizes clumped cells by halting their growth and gives motile cells an even greater advantage. Finally, our model predicts cell size distributions that are consistent with those observed in clusters of neuroblastoma cells cultured in low and high density conditions.
Keywords: Tumor growth, cell-cell interactions, cell fitness, computational method, Cellular Potts Model
1. Introduction
Tumorigenesis is a complex process in which cells acquire phenotypes that give them a competitive advantage (e.g., increased fitness) over untransformed cells. Most notably, these phenotypes include unrestricted proliferation and invasive potential, among other cancer hallmarks [38]. Tumor cells may acquire a high proliferation potential through alterations in the growth signaling pathway. For instance, mutations which permanently activate the growth-regulating Ras gene are found in about 20% of all human tumors [22]. A loss of function of the tumor suppressor gene p53, which is responsible for repairing DNA, regulating the cell cycle, and activating apoptosis, is also implicated in many tumors [47]. Such genetic mutations afford tumor cells a competitive advantage over surrounding tissues.
At the same time, genes associated with the migratory ability of cells have been found to increase cell fitness even though these genes do not directly affect cell mitosis rates. For example, while the cytoskeletal effector RhoC is not an oncogene (since RhoC does not transform normal cells), RhoC does inuence cell migration and tumorigenicity [19, 70]. Similarly, overexpression of the cytoskeletal adaptor molecule ABI-1 in breast cancer cell lines enhances cell migration and invasion potential [46], as does the integrin-associated focal adhesion kinase [14, 48].
We wish to understand what combinations of phenotypes give tumor cells enhanced fitness over untransformed cells. In this study, we focus on the individual and combined effects of cell motility, compression, and contact inhibition on tumor growth. In general, cells may move randomly, may move up gradients of chemical fields (chemotaxis), and may migrate along adhesion gradients (haptotaxis). At the sub-cellular level, polymerization and depolymerization of actin-derived cytoskeletal structures are most responsible for facilitating movement [5]. Compressive stress, resulting from proliferation of clusters of tumor cells in a confined geometry, may induce cytoskeletal modifications and the emergence of invasive phenotypes [12, 61, 74]. Motile tumor cells, which are thought to be precursors of metastatic activity [30], tend to be difficult to image and detect and are also more difficult to treat.
We also investigate contact inhibition, a phenomenon that restricts cell proliferation and motility of cells that are in contact with other cells [1]. The process of contact inhibition is well understood. Adherins junctions, or interactions between cells via receptors, play a significant role in signaling a cell to stop growth and movement. The transmembrane receptors nectins, cadherins, integrins and growth factor receptors have all been implicated in the signaling pathway of contact inhibition [68, 72]. A distinctive characteristic of cancer cells is partial or complete insensitivity to contact inhibition [29, 54] although some immortalized cancer cell lines remain sensitive to contact inhibition (e.g., neuroblastoma [13]). In this work, we explore how responsiveness to contact inhibition affects cluster growth and demonstrate the competitive advantage a loss of contact inhibition affords to tumor clusters.
To investigate the tumor behavior, we use a mathematical/computational model. Tumor models can be organized into three broad categories describing simulation dynamics: discrete, continuous, and hybrid. Each type has their benefits and drawbacks, with increased biological detail being associated with increased computational cost. See for example the reviews [7, 15, 20, 28, 50, 60]. Discrete simulations most easily incorporate biological laws and model cellular interactions, but this level of detail demands sub- stantial computational power. Continuous models are useful for simulating the growth dynamics at larger (tissue) scales, but are not able to distinguish among individual cells. Hybrid models [10, 20, 27, 45, 69], which combine features of both discrete and continuous models, are a promising approach but require more development before they can be broadly used.
In a recent study, Thalhauser et al. (2010) investigated the interactions of proliferation, migratory potential and cell death on the emergence of invasive phenotypes using spatial generalizations of the discrete, stochastic Moran process where the size and shape of the cells is not considered. In this study, migration is found to have a direct positive impact on the ability of a single mutant cell to invade a pre-existing colony and that a decrease in the proliferation potential can be compensated by an increase in the potential for cells to move. Here, we extend the study to include the effects of cell size and shape and cell-cell interactions such as adhesion and contact inhibition.
In this work, we focus on the growth of small cell clusters and we use the Glazier-Graner Hogeweg model (GGH), a discrete lattice-based modeling environment [17, 18, 35, 42, 66, 71]. This model, also known as the Cellular Potts Model (CPM), is very versatile and has been used to model, for example, gastrulation [49, 76], angiogenesis [4, 53, 57, 67], cell sorting [78], somite formation [41], intracellular dynamics [6], vasculogenesis [52, 65] and tumor growth [6, 9, 21, 33, 62, 75]. Continuum limits of the CPM have also been analyzed in the context of cell chemotaxis and solutions are well-described by Fokker-Planck equations for the cell probability density function [2, 3]. Very recently, the CPM has been extended to simulate individual cells migrating in fibrous extracellular matrix [63, 64]. Further, as part of a recent study of cell differentiation and migration, a thermodynamic analysis of the CPM was performed [39]. In [77], an analysis of the CPM at multiple time scales was conducted.
Through our investigation, we find that there is an interplay between cell motility and compressibility within the CPM. Interplay between cell characteristics and interactions has previously been noted as an important aspect of the CPM that requires further study [77]. In particular, the CPM predicts that increased cell motility leads to smaller cells. In fact, for sufficiently large cell motilities, cells may become unstable and actually vanish. This is an artifact in the CPM and we are not aware of any correlations between cell size and cell motility being observed experimentally. An analysis of the CPM enables us to derive an inverse-relationship between the cell stiffness and motility parameters that we use to compensate for motility-induced changes in cell size in the CPM so that in the corrected CPM, cell size is independent of the cell motility.
The remainder of the paper is organized as follows. In Sec 2, we present the CPM model. In Sec 3, results are presented and analyzed. Finally, in Sec 4, we draw conclusions and discuss further work.
2. The Model
2.1. The Cellular Potts Model
The CPM utilizes generalized cells mapped out on a uniform 2D-Cartesian grid. These generalized cells are specially-extended objects composed of a collection of grid cells (sometimes referred to as pixels) and can include both cells and extra-cellular matrix (referred to as “medium”). Each generalized cell is assigned an index, σ, and has cell type τ (σ). Here, we use two different generalized cell types: τ=1 (medium or ECM) and 2 (cell).
The simulation is stochastic and proceeds via a Monte Carlo method by repeating a basic operation, called an index-copy attempt. A grid cell, i⃗, is chosen at random from the simulation grid and attempts to copy its index σ(i⃗) onto a neighboring grid cell, i⃗neighbor. The simulation accepts this index-copy attempt with probability given by the Boltzmann acceptance function:
Here, ΔH is the difference in free energies of the proposed and initial configurations of the entire system. This difference in energy reflects the work done by forces acting by and upon cells [39]. The parameter Tm mimics the temperature and directly affects the probability of a successful copy attempt, e.g., a large Tm increases the rate of successful index-copy attempts. When the index-copy operation is repeated as many times as there are grid cells in the simulation grid, the simulation clock increments by one Monte Carlo step (MCS) and the process is repeated. Here, we present a brief description of the CPM and we refer the reader to references [18, 35, 42, 63, 71] for additional details.
The free energy in our model includes energies associated with cell-cell adhesion, volume constraints and motility:
| (2.1) |
The descriptions of the individual terms are included in the next subsections, followed by an explanation of other rules governing the simulation.
2.1.1. Adhesion
In the CPM, the adhesion energy between generalized cells is modeled as
| (2.2) |
where J is an interaction energy and δ is the Kronecker delta function. In the simulation consider the case that medium-medium (1,1) and tumor-tumor (2,2) interactions have the lowest energies while medium-tumor (1,2) or (2,1) interactions have the highest energy. Thus, medium-tumor interfaces have high relative energy and their length tends tend to be minimized. Here, we take J1,1 = 0, J1,2 = J2,1 = 12, J2,2 = 8.
The results primarily depend on the ratio of these energies to one another; the actual magnitude of these energies can in principle be related to the strength of cell-cell and cell-matrix receptor binding forces. If the coefficients are scaled upwards while keeping the ratio the same, the adhesion component of the Hamiltonian is weighted more heavily than the volume and motility energies. As we will discuss in Sec. 3.1, an interplay exists between all components of the energy, and changing the weight of one component requires the recalibration of the other two. Thus, if we scale the adhesion energy, we must scale the volume and motility energies, resulting in the total Hamiltonian, Htotal, being scaled as well. If we refer back to the Boltzmann acceptance function, scaling Htotal up by certain factor is equivalent to scaling the temperature coefficient, Tm, down by that same factor. Our simulations are robust to temperature variation, with no significant effect on cluster growth when Tm is changed from 4 to 100 (data not shown), although higher temperatures can potentially cause significant cell membrane fluctuations [35]. Thus, while adhesion certainly has a quantitative effect on the results, it does not affect qualitatively the results presented here provided all the energy components are rescaled. Consequently, since we are primarily interested in the interplay between cell motility and compressibility we do not vary the interaction coefficients in the adhesion energy in our studies here.
2.1.2. Volume
In the CPM, deviations of the volume υσ of a cell σ from a desired cell volume VT(σ, t) are penalized using the energy:
| (2.3) |
where λV is the cell stiffness (inverse compressibility). In the simulation VT varies for each cell depending what phase of the cell cycle the cell is in (see Sec. 2.2.1). Changes in volume energy can also be thought of as a measure of pressure a cell is experiencing from its surroundings [39].
2.1.3. Motility
Cell migration is modeled using an ExternalPotential plugin in CompuCell3D [71] to achieve random motion. Each cell is assigned a different random unit vector m⃗ that determines the direction of movement of the cell. In particular, we take m⃗ = (sin θ, cos θ), where θ is a uniformly distributed random variable in the interval [0, 2π). The energy associated with cell motility is modeled as
| (2.4) |
where s⃗ is the spin flip direction, which is the vector pointing from the current grid cell i⃗ to the neighboring grid cell i⃗neighbor where the index copy is attempted. Every 50 MCS, m⃗(σ), a new θ is chosen and the vector m⃗(σ) is updated. Note that this approach does not directly control cell movement. Rather, by altering λM, the probability of accepting index-copy attempts is changed, which in turn affects the average speed as well as direction of cells. Changes in the motility energy can be interpreted as the work done by forces exerted by a motile cell [39]. We have checked that this approach models cell motion via a random walk process. In particular, we observe that the mean squared displacement of a single cell increases linearly in time, with the rate of increase (the diffusivity) depending on λM, Tm, and the time interval for choosing θ. Increasing any of these parameters increases the effective diffusivity of the cell. In the Supplementary Material, we present characteristic results and effective cell diffusion coefficients obtained by changing λM.
Our approach mirrors that for chemotaxis in the CPM where the change in energy has been modeled as (e.g., [71]) , where c is the concentration of the chemical field. The coefficient λ is analogous to λM in Eq. (2.4). Both approaches function by biasing movement in certain directions via index-copy attempts.
2.2. Other rules governing cell behavior
2.2.1. Cell Cycle
Many models utilize a two-phase cell cycle: mitosis, the physical process of cell division, and interphase, the period between mitosis where cells double in volume [31, 32, 58]. Others are a bit more elaborate, with the cycle responding to external factors such as nutrient supply and available space [25, 59, 75] or an internal clock [43]. The cells in our model respond to both external and internal cues for progression through the cell cycle.
We focus on the four phases of the cell cycle that affect the volume of the cell: the G1, S, G2, and M phases. We do not model the quiescent phase G0. In the two gap phases, G1 and G2, cells increase their volume by producing macromolecules and organelles, preparing the cell for DNA replication and mitosis. This is modeled by increasing the target volume VT in time during these phases of the cycle. In the synthesis phase (S-phase), all cell growth is halted temporarily to simulate the stage of DNA synthesis. In the mitosis phase (M-phase), the cell, usually around 50 grid cells, divides into two daughter cells of equal volume along an randomly aligned axis.
In our model, procession from one stage to the next is regulated by both the cell volume υσ and a timer. We divide a complete cycle into 16 equally-timed stages, with the G1 and S phases persisting for 6 stages each and 4 stages total for G2 and M phases [43]. We scale these times to the model so that the G1, S, G2, and M phases last on average 94, 94, 37, and 25 MCS respectively, taking into account that the M phase is about a tenth of the cycle length. We also account for randomness in the cell cycle as follows. We take the length of each phase to be chosen from a uniform distribution bounded by a 25% deviation from the mean phase length. We note that this variation does not affect the results qualitatively. Also, in order for a cell in the simulation to pass from the G1 to S phase, we place a volumetric restriction, υσ ≥ 40, reflecting the effect of mechanical feedback (e.g., contact inhibition– see below) and compression on cell growth. Once the cell has passed the G1 phase, the cell is committed to mitosis and the rest of the phases follow based on the timing described above.
2.2.2. Contact Inhibition
Contact inhibition is a process by which cell growth and movement are halted due to contact with neighboring cells. Contact inhibition is exhibited by healthy tissue to prevent overgrowth, while a hallmark of tumor cells is the loss of contact inhibition. One approach is to model contact inhibition by mechanical stress [23, 32]. Another approach is a contact-dependent growth inhibition, meant to reflect signals cells receive through receptor proteins on the cell membrane. Our simulation implements both approaches. We model the stress effect by imposing a threshold minimum volume in order for a cell to proliferate (see the previous subsection). For contact-dependent growth inhibition, we posit that the more surface a cell shares with another, the less likely it is to grow. We aim to introduce contact inhibition in the simulation to model normal cell growth and compare that to the growth of tumor clusters.
We define the ratio rs to measure how much of the cell is in contact with other cells:
| (2.5) |
where sσ is the surface area of cell σ. The numerator signifies the area of cell membrane touching the medium and reflects the amount of space the cell has to move or grow. Thus, rs measures the percentage of the cell that is not surrounded by other cells. When rs = 1, this describes the situation of a single isolated cell while a cell with rs = 0 is completely surrounded by other cells. In other words, the parameter rs is a measurement of space availability.
In the model, if rs is less than a threshold parameter , then cell growth and motility are both arrested by holding VT constant and setting λM equal to 0. However, if , we follow the procedures described above for determining the cell volume and motility. The parameter controls the influence of contact inhibition such that when , the cells do not respond directly to contact with other cells.
2.3. Physical units and simulation set-up
A single cell in the simulation has a volume (area) of about υσ = 40 grid cells and cancer cells are about 20 µm in diameter. If these cells are circular in shape, the width of a grid cell would be about 2.8 µm. We can determine a temporal conversion by assuming that cells divide every 12 h [62]. In the simulation, a complete cell cycle is 250 MCS so 1 MCS is approximately 3 mins.
In our simulation, cells with λM = 100 travel at approximately 0.408 µm/min which is comparable to 0.326 µm/min recorded for cells on a collagen gel [37]. An isolated cell in the simulation undergoes a random walk, in which the direction of movement is changed at periodic intervals. The random variable of cell displacement after a given time interval is given by the probability distribution of a diffusion model. This model predicts that the mean square displacement < r2 > of the cell is proportional to the the time interval. In other words, < r2 >~ Dt, where D is the diffusion constant and t is the time elapsed. Indeed, we have verified that this relation holds in our simulations and have estimated the effective cell diffusion coefficient as a function of λM (see Supplementary Material).
Our simulations utilize a 500 × 500 rectangular grid corresponding to a physical domain roughly 1400 µm × 1400 µm in size. Such a grid can comfortably fit a cluster of 5000 cells. Initially, a single cell with size (area) 30 pixels is placed at the center of the grid. Simulations for each set of parameters were replicated 30 times and the average and standard error bars were calculated to generate the figures. A single simulation usually takes between 10–30 minutes to fill the entire grid on a 2.2 GHz Intel Core i7 Mac processor.
3. Results
3.1. Interplay between motility λM and stiffness λV on cell size and shape
We find that in the CPM, cell size depends on both λM and on λV. In particular, define the cell compression C(λV, λM) to denote the average compression a single cell experiences in the absence of all other factors except for motility and stiffness. More precisely,
| (3.1) |
where
| (3.2) |
is the compression of a single cell σ with motility λM and stiffness λV.
Table 2 presents a set of C-values generated by placing a single cell on a grid with periodic boundaries over the range 1 ≤ λV ≤ 10 and 0 ≤ λM ≤ 200. In order to isolate the effects of λV and λM, the cell is prohibited from proliferating as to not include cell-cell interactions. The C-value of the cell is recorded at every MCS for 10 runs of 10, 000 MCS each. The mean for each run is calculated and is used to determine the average values of C and the standard deviation.
Table 2.
Compression C-values, C(λV, λM) from Eq. (3.1). C = 1 denotes uncompressed cells. Data unavailable for λV = 1, λM > 60 because these cells are not stable and spontaneously vanish.
| λM = 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λV = 1.0 | 0.853 | 0.835 | 0.819 | 0.812 | 0.812 | 0.806 | 0.795 | – | – | – | – | – |
| 2.0 | 0.930 | 0.921 | 0.916 | 0.912 | 0.911 | 0.909 | 0.905 | 0.897 | 0.890 | 0.882 | 0.874 | 0.827 |
| 3.0 | 0.955 | 0.948 | 0.945 | 0.944 | 0.942 | 0.941 | 0.938 | 0.933 | 0.929 | 0.925 | 0.921 | 0.895 |
| 4.0 | 0.966 | 0.962 | 0.960 | 0.958 | 0.957 | 0.956 | 0.954 | 0.951 | 0.948 | 0.945 | 0.943 | 0.925 |
| 5.0 | 0.972 | 0.970 | 0.968 | 0.967 | 0.966 | 0.965 | 0.964 | 0.962 | 0.959 | 0.957 | 0.955 | 0.942 |
| 6.0 | 0.976 | 0.975 | 0.974 | 0.973 | 0.972 | 0.971 | 0.970 | 0.968 | 0.967 | 0.965 | 0.963 | 0.953 |
| 7.0 | 0.979 | 0.978 | 0.977 | 0.977 | 0.976 | 0.975 | 0.974 | 0.973 | 0.972 | 0.971 | 0.969 | 0.960 |
| 8.0 | 0.981 | 0.980 | 0.980 | 0.980 | 0.979 | 0.978 | 0.978 | 0.977 | 0.976 | 0.975 | 0.973 | 0.966 |
| 9.0 | 0.983 | 0.982 | 0.982 | 0.982 | 0.982 | 0.981 | 0.980 | 0.979 | 0.978 | 0.977 | 0.976 | 0.970 |
| 10.0 | 0.985 | 0.984 | 0.984 | 0.984 | 0.983 | 0.983 | 0.982 | 0.982 | 0.981 | 0.980 | 0.979 | 0.974 |
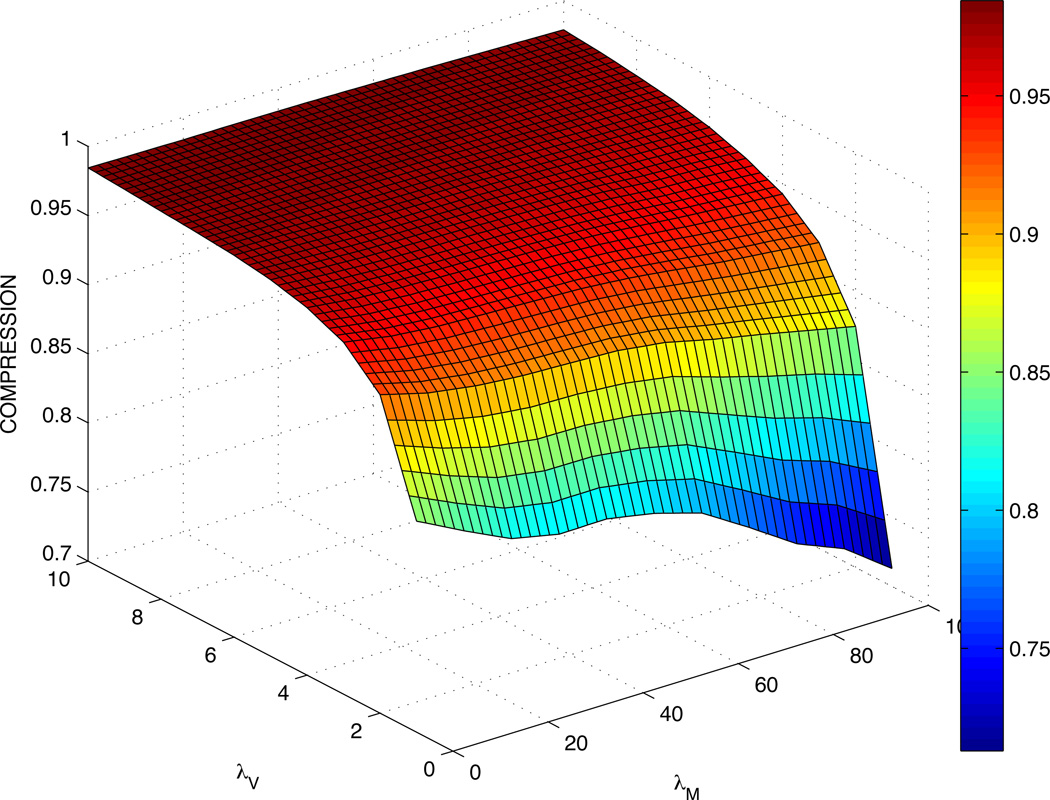
A 3D spline interpolant is used to predict values between the numbers obtained in Table 2. The corresponding plot of cell C-values is shown in Fig. 1. As expected, a large stiffness coefficient λV correlates with a C-value close to 1, as in this case cells tend to follow their target volumes closely. On the other hand, increasing the motility coefficient λM effectively decreases the C-values of cells. Some values for λV = 1 are not available at larger λM as the simulation becomes unstable and the cell often disappears because the volume constraint is so lax that its volume reaches 0.
Figure 1.
Compression C-values from Table 2 using a mesh created with cubic spline interpolation. Cells have smaller C-values for large λM and larger C-values for large λV.
An examination of Eq. (2.1) explains the interplay between motility λM and stiffness λV. Consider index copy attempts for which deviations between the actual and desired cell size would prevent the copy attempt from occurring. When the motility parameter λM is increased, the motility component of the energy becomes increasingly negative when s⃗ points in the opposite direction as m⃗. Thus, for sufficiently large λM, ΔH may become negative and the probability of the copy attempt can become equal to 1 even if the actual and desired cell volumes differ greatly. This is an artifact of the CPM as we are not aware of any correlations between cell size and cell motility being observed experimentally.
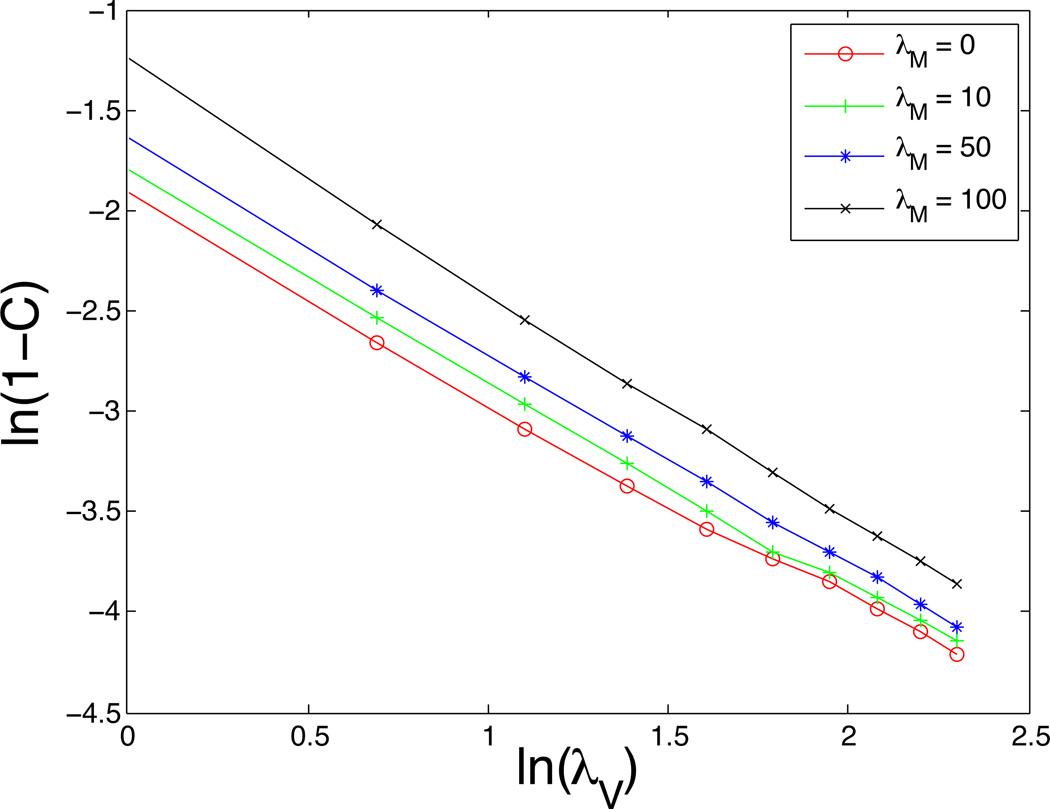
Using the C-values obtained in Table 2, we are able to determine a relationship between C and the parameters λV and λM. The data from Table 2 is plotted in Fig. 2 using log-log scale, which suggests an equation of the form:
| (3.3) |
where the values of the coefficient b and the exponent p are given in Table 3 for different motility coefficients λM. While there is some variability in b, the power p is quite close to 1. This inverse relationship between C and λV is reasonable because it suggests that λV should increase with λM in order to maintain the targeted cell size. This is consistent with the energy formulation since the energy contributions from motility and volume scale together. Equation (3.3) neatly reflects the results shown in Table 2 and so Equation (3.3) is used to calculate all further C-values taking values of p and b from data from Table 3. In particular, as described below, we consider cell cluster evolution using pairs of parameters (λV, λM) such that average compression C remains the same.
Figure 2.
A plot of ln(1 – C) vs. ln(λV) using the data in Table 2 suggests the relationship: with p ≈ 1.
Table 3.
The coefficient b and exponent p obtained by fitting the data in Table 2 with the form in Eq. (3.3).
| λM | Power (p) | Coefficient (b) |
|---|---|---|
| 0 | 0.980 | 0.140 |
| 10 | 1.017 | 0.161 |
| 20 | 1.051 | 0.177 |
| 30 | 1.062 | 0.185 |
| 40 | 1.051 | 0.186 |
| 50 | 1.051 | 0.191 |
| 60 | 1.057 | 0.201 |
| 70 | 1.087 | 0.223 |
| 80 | 1.106 | 0.244 |
| 90 | 1.114 | 0.259 |
| 100 | 1.130 | 0.280 |
| 200 | 1.160 | 0.380 |
At this point, we also check the shape of the cell as a function of λV and λM. We define the shape factor to quantify the shape of cell σ (keeping in mind that in the 2-dimensional field we have defined, the volume υσ, refers to the number of pixels in a cell, and surface area sσ refers to the cell perimeter). We have normalized the ratio so that the maximum possible value of Rσ is 1. This occurs when the cell takes on a square shape, leading to largest area for a given perimeter (in continuous space, a large Rσ would describe a circular cell). In this case, a square of side s would mean , so we normalize all values by dividing by 1/16 (i.e. k = 16). A small value of Rσ describes a cell with high surface area to volume ratio such as disk-like cells or cells with fingered boundaries. On the other hand, a large Rσ close to 1 describes a square-shaped cell. To study morphology, we simulate the behavior of a single, non-proliferating cell. Increasing the stiffness parameter λV causes υσ and sσ to rise, as one would expect since the cell is encouraged to be larger in size. However, while volume and surface area increase with stiffness, Rσ does not show any significant variation, as shown in Table 4. This implies that altering the stiffness parameter affects the size of cells but does not seem to influence their shape. However, when we increase cell motility λM, Rσ decreases, indicating a more elongated or figured cell shape for higher motilities.
Table 4.
Scaled values of for varying stiffness λV and motility λM parameters. All values are normalized by the theoretical maximum .
| λM = 0 | 10 | 20 | 30 | 40 | 50 | 100 | 200 | |
|---|---|---|---|---|---|---|---|---|
| λV = 1 | 0.7256 | 0.7091 | 0.6762 | 0.6413 | 0.6064 | 0.5683 | - | - |
| 2 | 0.7226 | 0.7086 | 0.6736 | 0.6373 | 0.6024 | 0.5722 | 0.4810 | 0.4531 |
| 3 | 0.7229 | 0.7072 | 0.6734 | 0.6387 | 0.6034 | 0.5629 | 0.4770 | 0.4442 |
| 4 | 0.7229 | 0.7070 | 0.6738 | 0.6390 | 0.6037 | 0.5720 | 0.4749 | 0.4368 |
| 5 | 0.7232 | 0.7070 | 0.6742 | 0.6386 | 0.6061 | 0.5747 | 0.4776 | 0.4280 |
3.2. The growth of cell clusters
3.2.1. The effect of cell compression
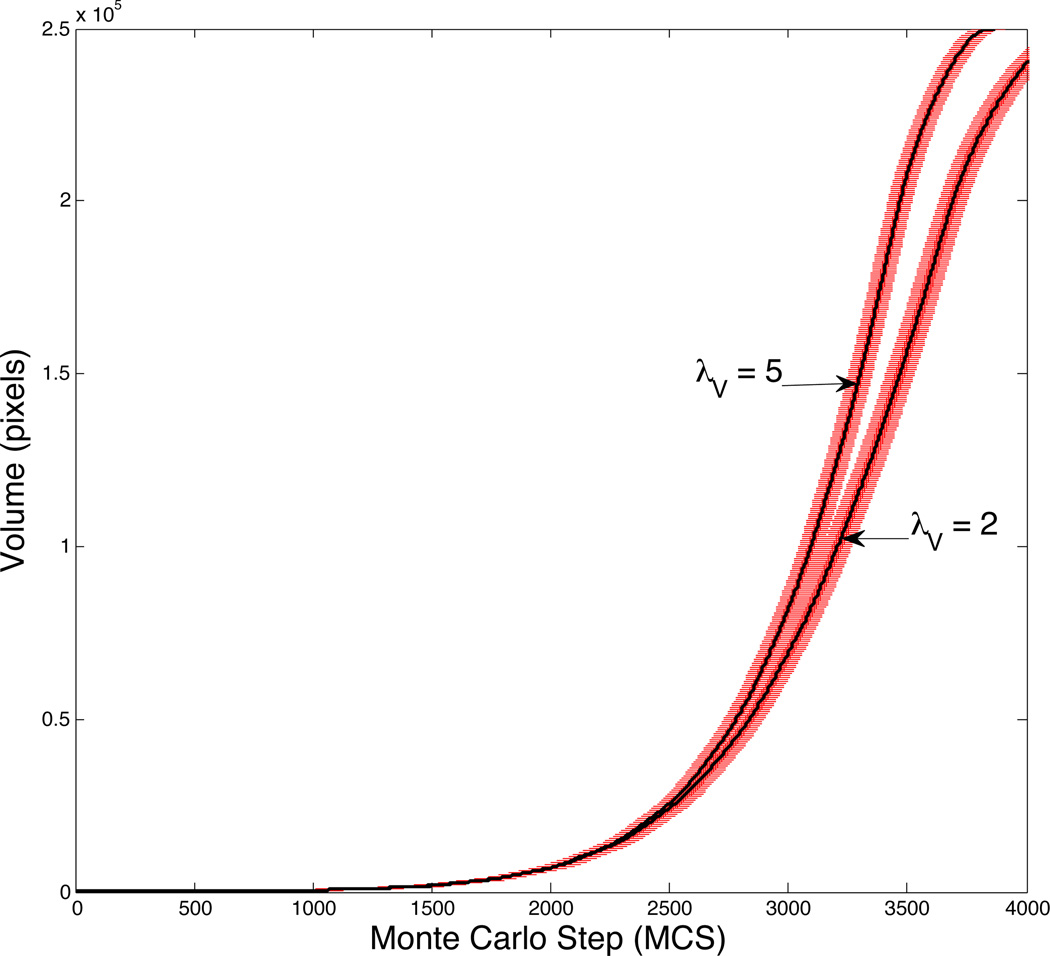
We next assess the effect of cell compressibility on the growth of cell clusters. We first do not factor in motility, setting the motility coefficient λM = 0. We also do not yet consider contact inhibition in this simulation and allow unimpeded growth in the G1 and G2 phases. Fig. 3 shows the volumes of the tumor cell clusters for two different cell stiffnesses, λV=2 and 5, with solid curves denoting the mean and the bars showing the standard deviation for results obtained by averaging over 10 runs. We see that cells with large λV grow more quickly than those with smaller λV. This faster growth is a result of a difference in both cell volume and number. Compression in the center of the tumor induces a deviation between their actual volumes and target volumes of the cells. In experiments, compressive stress, resulting from proliferation of clusters of tumor cells in a confined geometry, often results in cytoskeletal modifications and the emergence of invasive phenotypes [12, 61, 74]. In our simulations, cells with larger λV are more resistant to compression and are more likely to follow their growing target volumes. Our simulations show that, in addition to having a larger average cell size, tumors containing cells with large λV also contain more cells since cells with larger λV are better able to resist compression and therefore can undergo mitosis more readily than cells with smaller λV.
Figure 3.
Growth curves for λM and λV = 2 and 5, where the solid lines correspond to the mean volumes of the cell clusters and error bars denote the standard deviation for 10 realizations of the model.
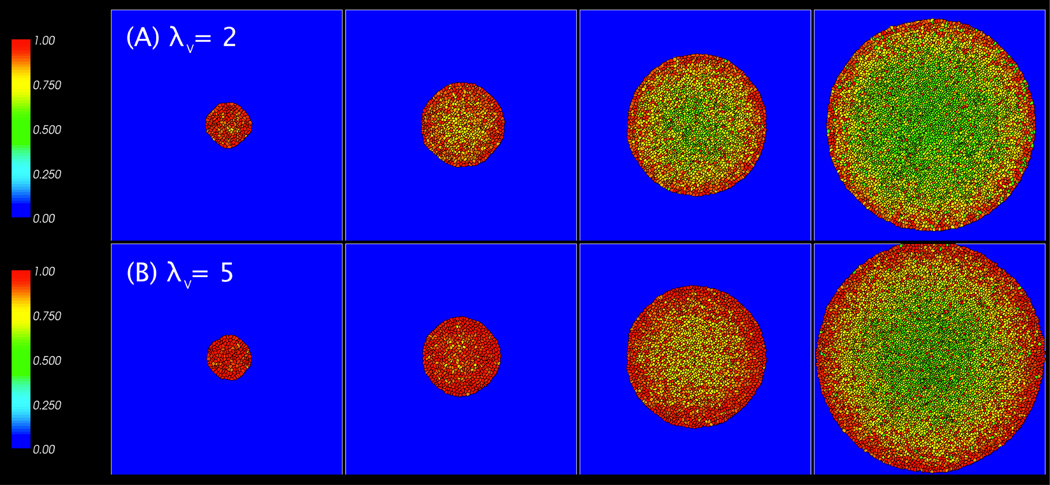
Fig. 4 illustrates typical compression patterns for tumor clusters with λV=2 and 5, where the cells are color-coded (see online version of the paper) based on the individual cell compression cσ defined earlier in Eq. (3.2). In each image, cells in the center tend to be compressed while cells near the tumor boundary are less compressed. This result is consistent with previous findings [16, 24, 31, 32, 51] which show that cells on the border of the monolayer experience much less pressure than those in the center. And, because the cells on the border experience less compression, their volumes tend to be larger. As the tumor increases in size at late times, cells on the tumor boundary hit the boundary of the computational domain and the simulation is stopped. Cells in contact with the computational boundary also show increased compression.
Figure 4.
Images of tumor cell clusters for λV = 2 (A) and 5 (B), with λM = 0 and at MCS = 2000 (8 days), 2500 (10 days), 3000 (12 days), and 3500 (14 days). Cells are colored by compression: cσ = υ σ=VT.
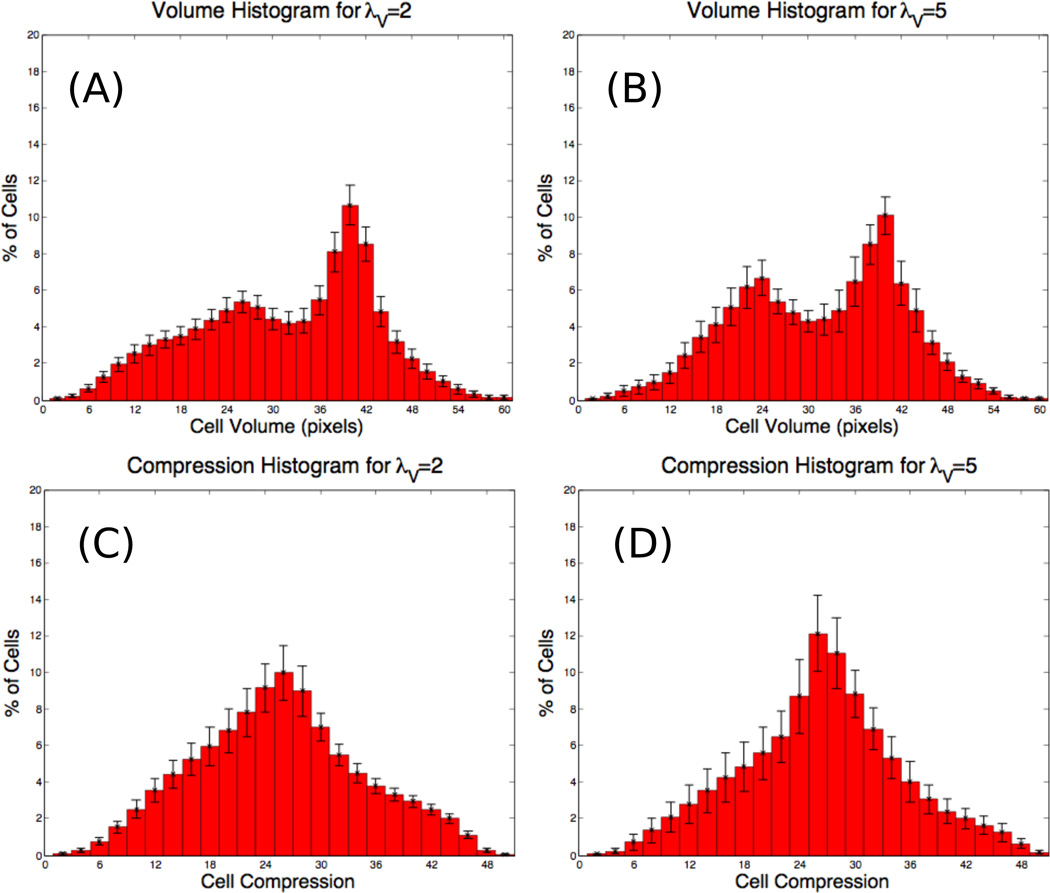
The distributions of the corresponding individual cell volumes are shown in Figs. 5(A) and (B) for λV = 2 and λV = 5, respectively. Comparing the two graphs, observe that the distribution for λV=5 is shifted slightly towards larger volumes and is narrower than that for λV=2. This is consistent with cells with larger λV being more resistant to compression. Indeed, comparing the compression ratios cσ for the two cases (Figs. 5(C) and (D)) clearly demonstrates that the cells with λV=5 are less compressed and follow the target volume more closely. In addition, we notice that there are two peaks in both the cell volume histograms (Figs. 5(A) and (B)), although the peaks are more pronounced for λV = 5. These peaks describe two distinct cell populations in a tumor cluster arising from different levels of compression experienced in the center and on the perimeter of the cluster. Bimodal distributions have also observed in neuroblastoma cell culture experiments (D. Stupack, personal communication).
Figure 5.
Histograms at MCS = 3500 (14 days) for (A) cell volume with λV = 2, (B) cell volume with λV = 5, (C) the compression cσ with λV = 2, (D) cσ with λV = 5.
3.2.2. The effect of cell motility
Next we analyze the effect of cell motility on cluster growth. Table 5 shows how the initial growth rate α (e.g., Ẋ ~ αX, where X is the total volume of the cluster) changes with stiffness λV and motility λM. We would expect from previous modeling work [73] that clusters containing highly motile cell lines would grow quickly since the motile cells are more diffusive and thus, less competitive for space to grow. Less motile cells are more likely to be in contact with one another and experience compression, whereas more freely moving cells are more likely to be contact with medium (ECM) and to be able to expand close to their target volume.
Table 5.
Initial growth rates (α) for λM = 0, 50, 100, 200 and λV = 1, 2, 3, 4, and 5. Data for λV = 1 are missing because cells are not stable for large λM and spontaneously vanish.
| λM = 0 | λM = 50 | λM = 100 | λM = 200 | |
|---|---|---|---|---|
| λV = 1 | 0.0011511 | 0.0011517 | – | – |
| 2 | 0.0011635 | 0.0011711 | 0.001169 | 0.0011771 |
| 3 | 0.0011687 | 0.0011721 | 0.0011748 | 0.0011835 |
| 4 | 0.0011739 | 0.0011726 | 0.0011774 | 0.0011844 |
| 5 | 0.0011874 | 0.0011794 | 0.0011795 | 0.0011887 |
Considering the individual columns in Table 5, we notice that λV correlates with faster growth, corroborating the results achieved in the previous section. The table also shows that increasing λM from 0 to 50 while keeping λV constant does not always lead to an increased initial growth rate, in contrast to the results obtained by Thalhauser et al. This is due to motility-induced cell compression as discussed earlier in Sec. 3.1.
Indeed, a comparison of simulations in which the C-values in Eq. (3.1) are fixed supports our hypothesis. Since C(λV, λM) = C(2, 0) = C(3.427, 100) = C(4.314, 200) = 0.93, cells in simulations with these parameters will experience the same overall compression. Once the motility-induced size changes of cells are corrected in the CPM, the remaining cell compression (e.g., changes in cell volume due to cell-cell interactions) is associated with the generation of solid pressure [39]. The corresponding initial growth rates α can be extrapolated from the entries in Table 5. We find that under these conditions, clusters containing motile cells have consistently larger initial growth rates as λM is increased, in agreement with previous work in which cell compressibility and surface contact inhibition were neglected [11, 16, 26, 40, 73]. This is further confirmed in Table 6 where the results obtained by fixing average compression values at C(2, 0), C(3, 0) and C(4, 0) are shown for λM = 0, 50, 100 and 200.
Table 6.
Initial growth rates (α) for λM = 0, 50, 100, 200 when the average compress-ibilities are matched to those values obtained from using C(λV, λM) = C(2, 0),C(3, 0); and C(4, 0).
| λM = 0 | λM = 50 | λM = 100 | λM = 200 | |
|---|---|---|---|---|
| C(2,0) = 0.930 | 0.0011635 | 0.0011718 | 0.0011761 | 0.0011850 |
| C(3,0) = 0.955 | 0.0011687 | 0.0011726 | 0.0011794 | 0.0011868 |
| C(4,0) = 0.966 | 0.0011739 | 0.0011793 | 0.0011833 | 0.0011875 |
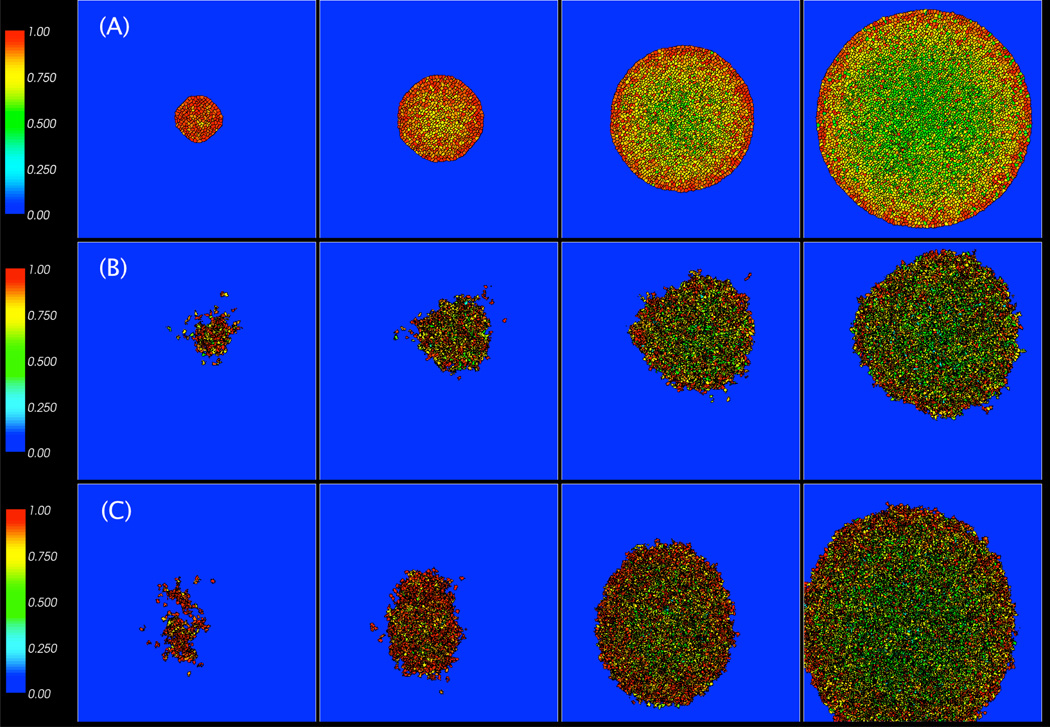
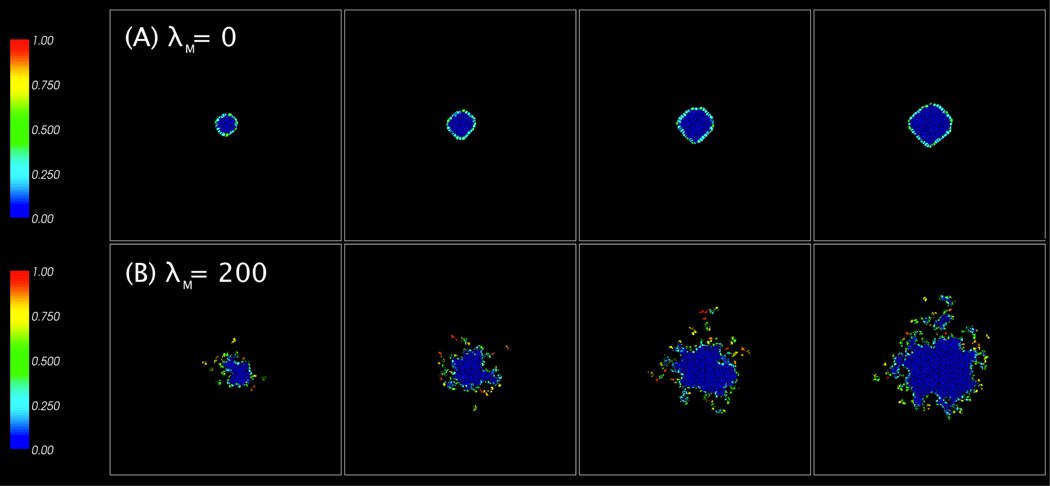
We study the compression patterns for these simulations and plot the results in Fig. 6. As expected, the darker, more compressed cells are generally in the centers of the tumors while the lighter, less compressed cells are on the periphery. These peripheral cells are larger and have more irregular shapes. The cluster of cells with (λV, λM) = (2, 200) in Fig. 6(B) is much smaller and the cells are more compressed than the other two cases since C(2, 200) = 0.827 < C(2, 0) = C(4.314, 200) = 0.93. Interestingly, the cluster with (λV, λM) = (4.314, 200) in Fig. 6(C) contains more compressed cells than the cluster with (λV, λM) = (2, 0) shown in Fig. 6(A). This is because the increased motility results in a larger cluster, which grows against the boundary of the computational domain. Note that the cluster itself is more irregularly shaped than that with λM = 0.
Figure 6.
Images of tumor cell clusters with (λV, λM) = (2, 0) in (A), (2, 200) in (B), and (4.314, 200) in (C) at MCS = 2000 (8 days), 2500 (10 days), 3000 (12 days), and 3500 (14 days).
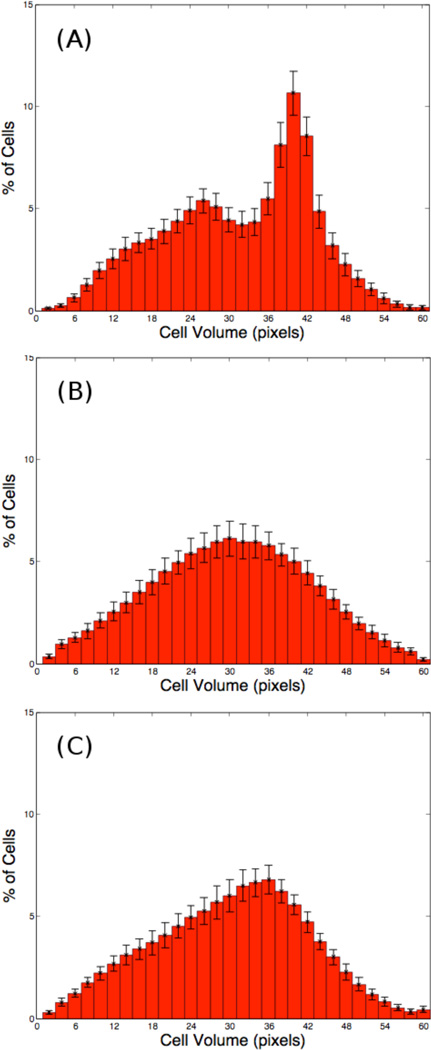
The corresponding cell volume distributions are shown in Fig. 7. When (λV, λM) = (2, 200) in Fig. 7(B), the cells have smaller sizes and the distribution is broader than those shown in Figs. 7(A) and (C), which correspond to (λV, λM) = (2, 0) and (λV, λM) = (4.314, 200) respectively. Observe that the distribution in (C) is narrower than that in (A) even though the majority of cells in (C) are smaller than those in (A).
Figure 7.
Histograms of cell volumes from the tumors clusters in Fig. 6 at MCS = 3500 (14 days) for (λV, λM) = (2, 0) in (A), (2, 200) in (B), and (4.314, 200) in (C).
3.2.3. The effect of contact inhibition
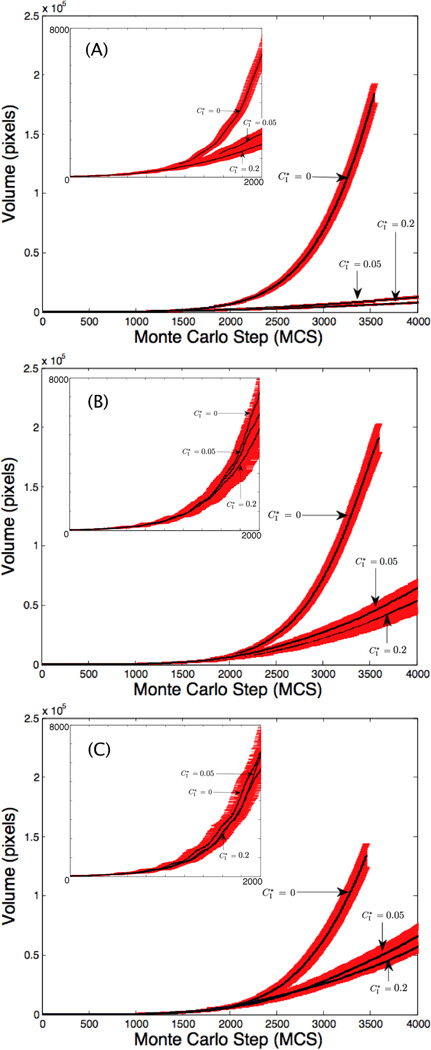
Finally, we assess the effect of contact inhibition on cell cluster growth. Figs. 8(A)–(C) show results for constant compression (C = 0.930) while the contact inhibition threshold and motilities are varied ( and λM = {0, 100, 200}). In all three figures, the larger compression threshold (e.g., stronger contact inhibition) correlates with slower cluster growth. A more restrictive contact inhibition parameter amplifies the effect that cell motility has on cluster growth rates. Cells in the center of the cluster are completely surrounded so their free-surface parameter is less than the threshold (), e.g., see Fig. 9, which shows cluster morphologies for with λM = 0 in (A) and λM = 200 in (B). Interior cells experience compression contact inhibition which prohibits them from reaching the υσ > 40 threshold for mitosis, as observed in other studies (e.g., [16, 31, 32, 51]). The results also confirm that increasing motility increases cluster growth rates, consistent with Sec. 3.2.2. When λM = 0 in (A), the clusters are compact and the number of cells at the periphery is highly constrained. When λM = 200 in (B), the cluster boundary is much more irregular due to increased cell motility and thus contains a larger number of cells. These boundary cells are then able to find space and proliferate leading to faster growth and enhancement of boundary irregularity. A difference in cluster growth rates is also observed in Figs. 8(A)–(C), with the λM = 100, 200 clusters growing much faster than λM = 0. There is little difference in rates between the λM = 100, 200 cases because the effect of motility on growth is saturated.
Figure 8.
Growth curves with , and 0.2 in each graph. In (A), λM = 0, in (B) λM = 100 and in (C) λM = 200. The insets feature the curves for the first 2000 MCS (8 days). The curves denote mean volumes and the error bars denote standard deviations for 30 realizations of the model. In all cases, the compression is fixed at C(λV, λM) = 0.93.
Figure 9.
Images of tumor cell clusters from Fig. 8 for , λV = 2, and λM = 0 in (A) and 200 in (B) at MCS =2000 (8 days), 2500 (10 days), 3000 (12 days), and 3500 (14 days). Cells are color coded based on the available area ratio rs.
This study of contact inhibition is particularly revealing for explaining why tumor clusters are more viable than healthy tissue. Normal tissue cells experience contact inhibition and a hallmark of tumor cells is the loss of contact inhibition, although a some immortalized cell lines remain sensitive to contact inhibition (e.g., neuroblastoma [13]). As the simulation data reveals, a complete loss of contact inhibition gives the rate of growth in tumor clusters a significant advantage over normal tissue.
3.3. Cell volume distribution study motivated by in vitro experiments
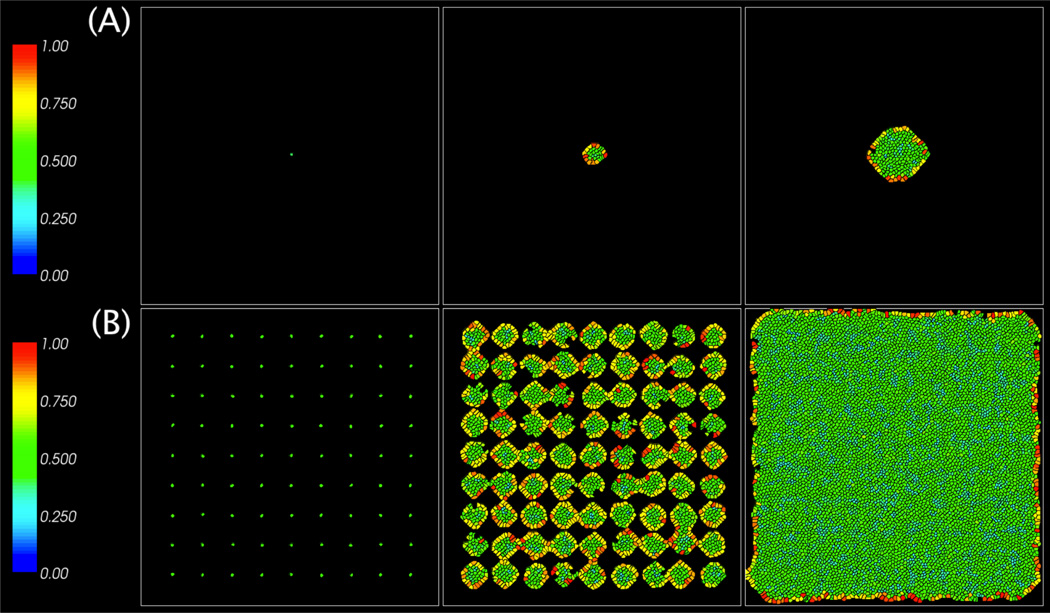
Unpublished experimental data provided to us by D. Stupack (personal communication) on the growth of in vitro clusters of neuroblastoma cells reveals interesting cell volume distribution patterns. The in vitro data shows that a bimodal cell volume distribution occurs in cell cultures that were plated in low densities. However, a unimodal cell volume distribution is observed in high density cultures. These observations served as motivation for the simulations described below.
We model the low density case by considering the growth of a single cluster of cells starting from a single initial cell. To model the high density case, cells were seeded close enough to each other such that the ensuing cell clusters strongly interact. The initial configurations and cluster evolutions are shown in Figs. 10(A) and (B), using the parameters: λM=0 and λV=2. A small contact inhibition threshold is used for both the low (A) and high (B) density cases, which is consistent with results for neuroblastoma [13]. A low motility condition was chosen as higher motility cells did not display the two peaks as observed in the experimental data (this is also consistent with the numerical results presented earlier in Figs. 7 (B) and (C) where the cell size distributions are unimodal when λM is large).
Figure 10.
Images of tumor cell clusters from the model at MCS=0, 1500 (6 days), and 3000 (12 days) for the cases shown in Fig. 11. (A): Low initial cell density (single cell); (B): High initial cell density (multiple cells spread evenly throughout the domain).
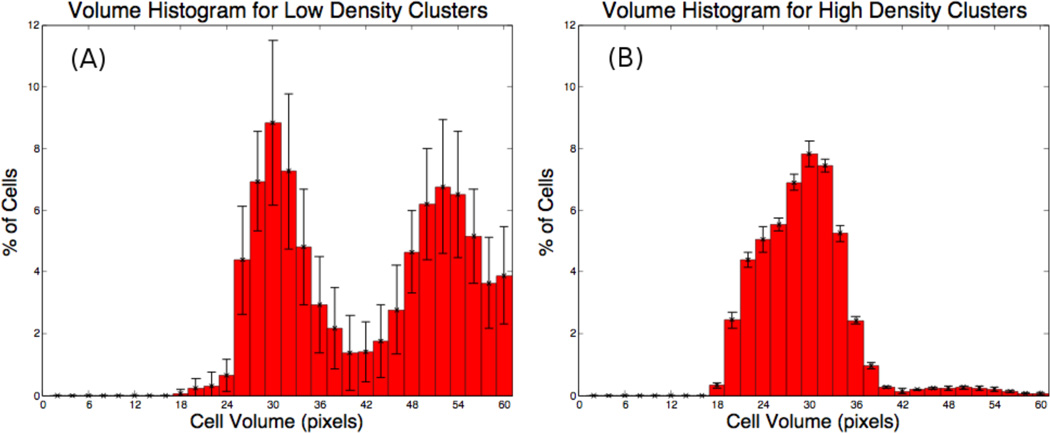
The cells in Fig. 10 are colored by compression cσ. Observe that in the low density case, the cells in the cluster interior are compressed while those on the boundary are less compressed. In the high density case, most of the cells are compressed while only a few on the boundary are less compressed. We plot the corresponding distributions of cell sizes in Figs. 11 (A) and (B). The cell size distributions are bimodal in the low density case (A) and unimodal in the high density case (B), consistent with experimental observations. The bimodal distribution in Fig. 11 appears to be amplified by contact inhibition (data not shown). Indeed, in the contact inhibited case, the central and peripheral cell populations are more distinct as inhibited cells will be stuck in the G1 phase. In the absence of contact inhibition, a bimodal distribution is still observed (e.g., Fig. 5), although the two peaks are not as distinct. Thus, the model predicts that contact inhibition enhances bimodality in the cell volume distribution.
Figure 11.
Volume histograms generated by the model simulating (A) low initial cell densities and (B) high initial cell densities. Note the bimodal distribution in (A) and the unimodal distribution in (B). See text for parameters.
4. Conclusion
In this work, we have used a Cellular-Potts modeling (CPM) approach to study the individual and combined effects of cell compression, motility, and contact inhibition. We explored an interplay between cell motility and compressibility within the CPM and found that increased cell motility leads to smaller cells. We could not find such a relationship in the biological literature and concluded that this is an artifact of the CPM. An analysis of the CPM showed that there is an explicit inverse-relationship between the cell stiffness and motility parameters. We used this relationship to compensate for motility-induced changes in cell size in the CPM so that in the corrected CPM, cell size is independent of the cell motility.
We found that tumor clusters grow larger and contain more cells when the cells are less compressible. These stiffer cells are able to follow their target volumes more closely than their more compressed counterparts, giving them larger volumes and allowing them to replicate more quickly. Interestingly, it has been reported that cancer cells are more compressible than normal cells [36], although normal cells proliferate at much lower rates. Experimentally, it is found that compressive stresses result in changes in cell size and shape, and may lead to the emergence of invasive phenotypes [12, 61, 74]. Further, the responses of normal and tumor cells to such stresses may also be different (e.g., [55]) and may also alter with treatment (e.g., [44]). These features can be incorporated in future models using the approach developed here.
The cluster sizes and cell numbers were also found to be increasing functions of cell motilities, consistent with previous modeling studies that do not consider cell size and shape (e.g., [8, 11, 25, 40, 73]) and biological observations where high motility rates have been linked to invasiveness, a key property of tumor cells (e.g., [14, 19, 34, 38, 48, 70]). Motility allows cells to find free space where they experience less compression and growth inhibition. Further, we have demonstrated that the effects of motility on cluster sizes were amplified under conditions of contact inhibition. In these situations, the cells can only proliferate, and move, if they have sufficient space, making it even more important for cells to find free space. Cells at the centers of tumor clusters were most affected.
Finally, we conducted a study of the effects of initial seeding densities on cell volume distributions. Our model predicts that when cells are seeded initially at low densities, contact inhibition results in the emergence of two distinct cell populations– a population of larger cells located at the cluster boundary and a population of smaller cells confined to the cluster interior. When the cells are seeded at high densities, most of the cells are compressed and the cluster population is dominated by compressed cells leading to a unimodal cell volume distribution. These results are qualitatively consistent with unpublished data.
As a next step, we plan to work with Dr. Stupack to perform quantitative comparisons of model and experimental results. Further, we plan to investigate cases in which the cells have varying motilities and to study the dynamics in mixtures of such cells, comparing the experimental results with model predictions. We also plan to further investigate the effect of cell shapes and surface areas, which also have the potential to inuence the results (e.g., [23, 24, 31, 56, 58]). For example, some cells may naturally have large surface area to volume ratios while other cells may have small ratios. In the CPM, this can be modeled by introducing an additional component to the energy that constrains the cell surface area (e.g., [71]).
Supplementary Material
Table 1.
List of model variables and parameters.
| Parameter | Description | Values (if applicable) |
|---|---|---|
| σ(i⃗) | Index of grid cell i⃗ | |
| τ(σ(i⃗)) | Cell type at grid cell i⃗ | 1 = medium (non-tumor cell); |
| 2 = tumor cell | ||
| Tm | Temperature of domain; | 4 |
| Jτ(σ(i⃗),τ(σ(j⃗)) | Adhesion energy | J1,1 = 0, J1,2 = J2,1 = 12, J2,2 = 8 |
| λV | Volume constraint magnitude | 2, 5 (Figs. 3–5); |
| 2, 4.3 (Figs. 6,7); | ||
| 2 (Figs. 8–11) | ||
| υσ | Volume of cell σ | |
| VT | Target volume | updated between 25–50 |
| sσ | Surface area of cell σ | |
| λM | Motility magnitude | 0 (Figs. 3–5,10,11); |
| 0, 200 (Figs. 6,7,9); | ||
| 0, 100, 200 (Figs. 8) | ||
| m⃗ | unit random vector describing the direction of movement | |
| I Contact Inhibition threshold | 0 (Figs. 3–7); | |
| 0, 0.05, 0.2 (Figs. 8,9); | ||
| 0.05 (Figs. 10,11) |
Acknowledgments
The authors gratefully acknowledge partial support from the National Science Foundation Division of Mathematical Sciences and the National Institutes of Health through grants P50GM76516 for a Center of Excellence in Systems Biology at the University of California, Irvine, and P30CA062203 for the Chao Comprehensive Cancer Center at the University of California, Irvine. The authors thank Dr. Maciek Swat of the Indiana University for providing technical support in the use of the CC3D simulation software, Dr. Dwayne Stupack of UC San Diego for providing unpublished experimental data, and Dr. Hermann Frieboes of U. Louisville for valuable discussions. Finally, we thank the reviewers whose questions and comments improved the paper.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Jonathan F. Li, Email: jonathanli@college.harvard.edu.
John Lowengrub, Email: lowengrb@math.uci.edu.
References
- 1.Abercrombie M. Contact inhibition and malignancy. Nature. 1979;281:259–262. doi: 10.1038/281259a0. [DOI] [PubMed] [Google Scholar]
- 2.Alber M, Lushnikov PM, Newman SA. Continuous macroscopic limit of a discrete stochastic model for interaction of living cells. Phys. Rev. Lett. 2007;99:168102. doi: 10.1103/PhysRevLett.99.168102. [DOI] [PubMed] [Google Scholar]
- 3.Alber M, Chen N, Glimm T, Lushnikov PM. Multiscale dynamics of biological cells with chemotactic interactions: from a discrete stochastic model to a continuous description. Phys. Rev. E. 2006;73:051901. doi: 10.1103/PhysRevE.73.051901. [DOI] [PubMed] [Google Scholar]
- 4.Ambrosi D, Gamba A, Serini G. Cell directional persistence and chemotaxis in vascular morphogenesis. B. Math Biol. 2005;67(1):195. doi: 10.1016/j.bulm.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 5.Ananthakrishnan R, Ehrlicher A. The forces behind cell movement. Int. J. Biol. Sci. 2007;3(5):303–317. doi: 10.7150/ijbs.3.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Andasari V, Roper RT, Swat MH, Chaplain MA. Integrating intra-cellular dynamics using CompuCell3D and bionetsolver: Applications to multiscale modelling of cancer cell growth and invasion. PLoS One. 2012;7(3):e33726. doi: 10.1371/journal.pone.0033726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Anderson ARA, Quaranta V. Integrative mathematical oncology. Nat. Rev. Cancer. 2008;8:227–234. doi: 10.1038/nrc2329. [DOI] [PubMed] [Google Scholar]
- 8.Basanta D, Hatzikirou H, Deutsch A. Studying the emergence of inva-siveness in tumours using game theory. Eur. Phys. J. Biol. 2008;63(3):393–397. [Google Scholar]
- 9.Bauer AL, Jackson TL, Jiang Y. A cell-based model exhibiting branching and anastomosis during tumor-induced angiogenesis. Biophys. J. 2007;92:3105–3121. doi: 10.1529/biophysj.106.101501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bearer EL, Lowengrub JS, Frieboes HB, Chuang Y, Jin F, Wise SM, Ferrari M, Agus DB, Cristini V. Multiparameter computational modeling of tumor invitation. Cancer Res. 2009;69(10):4493–4501. doi: 10.1158/0008-5472.CAN-08-3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Betteridge R, Owen MR, Bryne HM, Alarcon T, Maini PK. The impact of cell crowding and active cell movement on vascular tumour growth. Netw. Heterog. Media. 2006;1(4):515–535. [Google Scholar]
- 12.Boghaert E, Gleghorn JP, Lee KA, Gjorevski N, Radisky DC, Nelson CM. Host epithelial geometry regulates breast cancer cell invasiveness. P. Natl. Acad. Sci. USA. 2012;109(48):19632–19637. doi: 10.1073/pnas.1118872109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brodie C, Siriwardana G, Lucas J, Schleicher R, Terada N, Szepesi A, Gelfand E, Seligman P. Neuroblastoma sensitivity to growth inhibition by deferrioxamine: evidence for a block in G1 phase of the cell cycle. Canc. Res. 1993;53(17):3968–3975. [PubMed] [Google Scholar]
- 14.Burnton VG, Frame MC. Src and focal adhesion kinase as therapeutic targets in cancer. Curr. Opin. Pharmacol. 2008;8:427–432. doi: 10.1016/j.coph.2008.06.012. [DOI] [PubMed] [Google Scholar]
- 15.Byrne HM. Dissecting cancer through mathematics: from the cell to the animal model. Nat. Rev. Cancer. 2010;10:221–230. doi: 10.1038/nrc2808. [DOI] [PubMed] [Google Scholar]
- 16.Byrne HM, Drasdo D. Individual-based and continuum models of growing cell populations: a comparison. J. Math. Biol. 2008;58:657–687. doi: 10.1007/s00285-008-0212-0. [DOI] [PubMed] [Google Scholar]
- 17.Chen N, Glazier JA, Izaguirre JA, Alber MS. A parallel implementation of the Cellular Potts Model for simulation of cell-based morphogenesis. Comput. Phys. Commun. 2007;176:670–681. doi: 10.1016/j.cpc.2007.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cickovski T, Aras K, Swat M, Merks RM, Glimm T, Hentschel HG, Alber MS, Glazier JA, Newman SN, Izaguirre JA. From genes to organisms via the cell: a problem-solving environment for multicellular development. Comput. Sci. Eng. 2007 Jul-Aug;:50–60. doi: 10.1109/MCSE.2007.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Clark EA, Golub TR, Lander ES, Hynes RO. Genomic analysis of metastasis reveals an essential role for RhoC. Nature. 2000;406:532–535. doi: 10.1038/35020106. [DOI] [PubMed] [Google Scholar]
- 20.Cristini V, Lowengrub JS. Multiscale modeling of cancer: an integrated experimental and mathematical modeling approach. Cambridge University Press; 2010. [Google Scholar]
- 21.Dormann S, Deutsch A. Modeling of self-organized avascular tumor growth with a hybrid cellular automaton. In Silico Biol. 2002;2:1–14. [PubMed] [Google Scholar]
- 22.Downward J. Targeting RAS signaling pathways in cancer therapy. Nat. Rev. Cancer. 2003;3:11–22. doi: 10.1038/nrc969. [DOI] [PubMed] [Google Scholar]
- 23.Drasdo D, Forgacs G. Modeling the interplay of generic and genetic mechanisms in cleavage, blastulation, and gastrulation. Dev. Dynam. 2000;219:182–191. doi: 10.1002/1097-0177(200010)219:2<182::aid-dvdy1040>3.3.co;2-1. [DOI] [PubMed] [Google Scholar]
- 24.Drasdo D, Hohme S. A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys. Biol. 2005;2(3):133–147. doi: 10.1088/1478-3975/2/3/001. [DOI] [PubMed] [Google Scholar]
- 25.Enderling H, Hlatky L, Hahnfeldt P. Migration rules: tumors are conglomerates of self-metastases. Brit. J. Cancer. 2009;100:1917–1925. doi: 10.1038/sj.bjc.6605071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Enderling H, Anderson ARA, Chaplain MAJ, Beheshti A, Hlatky L, Hahnfeldt P. Paradoxical dependencies of tumor dormancy and progression on basic cell kinetics. Cancer Res. 2009;69:8814–8821. doi: 10.1158/0008-5472.CAN-09-2115. [DOI] [PubMed] [Google Scholar]
- 27.Frieboes HB, Chaplain MAJ, Thompson AM, Bearer EL, Lowengrub JS, Cristini V. Physical oncology: a bench-to-bedside quantitative and predictive approach. Cancer Res. 2010;71(2):298–302. doi: 10.1158/0008-5472.CAN-10-2676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Frieboes HB, Jin F, Chuang YL, Wise SM, Lowengrub JS, Cristini V. Three-dimensional multispecies nonlinear tumor growth-II: tumor invasion and angiogenesis. J. Theor. Biol. 2011;264:1254–1278. doi: 10.1016/j.jtbi.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Friedl P, Brocker EB. The biology of cell locomotion within three-dimensional extracellular matrix. Cell. Mol. Life Sci. 2000;57:41–46. doi: 10.1007/s000180050498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Friedl P, Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 31.Galle J, Loeffler M, Drasdo D. Modelling the effect of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell populations in vitro. Biophys. J. 2005;88:62–75. doi: 10.1529/biophysj.104.041459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Galle J, Hoffmann M, Aust G. From single cells to tissue architecture: a bottom-up approach to modelling the spatio-temporal organization of complex multi-cellular systems. J. Math. Biol. 2009;58:261–283. doi: 10.1007/s00285-008-0172-4. [DOI] [PubMed] [Google Scholar]
- 33.Ghaemi M, Shahrokhi A. Combination of the cellular potts model and lattice gas cellular automata for simulating the avascular cancer growth. Lect. Notes. Comput. Sc. 2006;4173:297–303. [Google Scholar]
- 34.Giese A, Bjerkvig R, Berens ME, Westphal M. Cost of migration: invasion of malignant gliomas and implications for treatment. J. Clin. Oncol. 2003;21(8):1624–1636. doi: 10.1200/JCO.2003.05.063. [DOI] [PubMed] [Google Scholar]
- 35.Glazier JA, Graner F. A simualtion of the differential adhesion driven rearrangement of biological cells. Phys. Rev. E. 1993;47(3):2128–2154. doi: 10.1103/physreve.47.2128. [DOI] [PubMed] [Google Scholar]
- 36.Guck J, Schinkinger S, Lincoln B, Wottawah F, Ebert S, Romeyke M, Lenz D, Erickson HM, Ananthakrishnan R, Mitchell D, Kas J, Ulvick S, Bilby C. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Bio-phys. J. 2005;88:3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haga H, Irahara C, Kobayashi R, Nakagaki T, Kawabata K. Collective movement of epithelial cells on a collagen gel substrate. Biophys. J. 2005;88:2250–2256. doi: 10.1529/biophysj.104.047654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hanahan D, Weinberg RA. The hallmarks of cancer: the next generation. Cell. 2011;144(5):646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 39.Harrison NC, Diez del Corral R, Vasiev B. Coordination of Cell Differentiation and Migration in Mathematical Models of Caudal Embryonic Axis Extension. PLoS ONE. 2011;6(7):e22700. doi: 10.1371/journal.pone.0022700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hatzikirou H, Basanta B, Simon M, Schaller C, Deutsch A. Go or grow: the key to the emergence of invasion in tumor progression? Math. Med. and Biol. 2010:1–17. doi: 10.1093/imammb/dqq011. [DOI] [PubMed] [Google Scholar]
- 41.Hester SD, Belmonte JM, Gens JS, Clendenon SG, Glazier JA. A multi-cell, multi-scale model of vertebrate segmentation and somite formation. PLoS Comput. Biol. 2011;7:e1002155. doi: 10.1371/journal.pcbi.1002155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Izaguirre JA, Chaturvedi R, Huang C, Cickovski T, Coffland J, Thomas G, Forgacs G, Alber M, Henstschel G, Newman SA, Glazier JA. CompuCell, a multi-model framework for simulation of morphogenesis. Bioinformatics. 2004;20:1129–1137. doi: 10.1093/bioinformatics/bth050. [DOI] [PubMed] [Google Scholar]
- 43.Jiang Y, Pjesivac-Grbovic J, Cantrell C, Freyer JP. A multiscale model for avascular tumor growth. Biophys. J. 2005;89:3884–3894. doi: 10.1529/biophysj.105.060640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kaffas AE, Bekah D, Rui M, Kumaradas JC, Kolios MC. Investigating longitudinal changes in the mechanical properties of MCF-7 cells exposed to paclitaxol using particle tracking microrheology. Phys. Med. Biol. 2013;58(4):923–936. doi: 10.1088/0031-9155/58/4/923. [DOI] [PubMed] [Google Scholar]
- 45.Kim Y, Othmer H. A hybrid model for tumor-stromal interactions in breast cancer. Bull. Math. Biol. 2013 doi: 10.1007/s11538-012-9787-0. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Larkins TL, Nowell M, Singh S, Sanford GL. Inhibition of cyclooxygenase-2 decreases breast cancer cell motility, invasion and matrix metalloproteinase expression. BMC Cancer. 2006;6:181. doi: 10.1186/1471-2407-6-181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lehmann BD, Pietenpol JA. Targeting mutant p53 in human tumors. J. Clin. Oncol. 2012;30(29):3648–3650. doi: 10.1200/JCO.2012.44.0412. [DOI] [PubMed] [Google Scholar]
- 48.Lim ST, Mikolon D, Stupack DG, Schlaepfer DD. FERM control of FAK function: Implications for cancer therapy. Cell Cycle. 2008;7:2306–2314. doi: 10.4161/cc.6367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Longo D, Peirce SM, Skalak TC, Davidson L, Marsden M, Dzamba B, DeSimone DW. Multicellular computer simulation of morphogenesis: blastocoel roof thinning and matrix assembly in xenopus laevis. Dev. Biol. 2004;271:210–222. doi: 10.1016/j.ydbio.2004.03.021. [DOI] [PubMed] [Google Scholar]
- 50.Lowengrub JS, Frieboes H, Jin F, Chuang Y, Li X, Macklin P, Wise S, Cristini V. Nonlinear modeling of cancer: bridging the gap between cells and tumors. Nonlinearity. 2010;23:R1–R91. doi: 10.1088/0951-7715/23/1/r01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mansury Y, Kimura M, Lobo J, Deisboeck TS. Emerging patterns in tumor systems: simulating the dynamics of multcellular clusters with an agent-based spatial agglomeration model. J. Theor. Biol. 2002;219:343–370. doi: 10.1006/jtbi.2002.3131. [DOI] [PubMed] [Google Scholar]
- 52.Merks RMH, Glazier JA. Dynamic mechanisms of blood vessel growth. Nonlinearity. 2006;19:C1–C10. doi: 10.1088/0951-7715/19/1/000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Merks RMH, Brodsky SV, Goligorsky MS, Newman SA, Glazier JA. Cell elongation is key to in silico replication of in vitro vas-culogenesis and subsequent remodeling. Dev. Biol. 2006;289:44–54. doi: 10.1016/j.ydbio.2005.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Miekus K, Czernik M, Sroka J, Czyz J, Madeja Z. Contact stimulation of prostate cancer cell migration: the role of gap junctional coupling and migration stimulated by heterotypic cell-to-cell contacts in determination of the metastatic phenotype of Dunning rat prostate cancer cells. Biol. Cell. 2005;97(12):893–903. doi: 10.1042/BC20040129. [DOI] [PubMed] [Google Scholar]
- 55.Murphy MF, Lilley F, Lalor MJ, Crosby SR, Madden G, John-son G, Burton DR. Evaluation of a nonlinear Hertzian-based model reveals prostate cancer cells respond differently to force than normal prostate cells. Microsc. Res. Techniq. 2013;76(1):36–41. doi: 10.1002/jemt.22132. [DOI] [PubMed] [Google Scholar]
- 56.Narang V, Wong SY, Leong SR, Abastado J, Gouaillard A. Comparing mathematical models of cell adhesion in tumors. Defense Sci. Res. Conf. Expo. 2011:1–4. [Google Scholar]
- 57.Peirce SM, van Gieson EJ, Skalak TC. Multicellular simulation predicts microvascular patterning and in silico tissue assembly. FASEB J. 2004;18:731–733. doi: 10.1096/fj.03-0933fje. [DOI] [PubMed] [Google Scholar]
- 58.Ramis-Conde I, Drasdo D, Anderson ARA, Chaplain MAJ. Modeling the inuence of the e-cadherin-beta-catenin pathway in cancer cell invasion: a multiscale approach. Biophys. J. 2008;95:155–165. doi: 10.1529/biophysj.107.114678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Rejniak KA. A single-cell approach in modeling the dynamics of tumor microregions. Math. Biosci. Eng. 2005;2:643–655. doi: 10.3934/mbe.2005.2.643. [DOI] [PubMed] [Google Scholar]
- 60.Rejniak KA, Anderson ARA. Hybrid models of tumor growth. Wiley Interdis. Rev. 2011;3:115–125. doi: 10.1002/wsbm.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ronan W, Deshpande VS, McMeeking RM, McGarry JP. Numerical investigation of the active role of the actin cytoskeleton in the compression resistance of cells. J. Mech. Behav. Biomed. 2012;14(C):143–157. doi: 10.1016/j.jmbbm.2012.05.016. [DOI] [PubMed] [Google Scholar]
- 62.Rubenstein BM, Kaufman LJ. The role of extracellular matrix in glioma invasion: a cellular potts model approach. Biophys. J. 2008;95:5661–5680. doi: 10.1529/biophysj.108.140624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Scianna M, Preziosi L. Cellular potts models: multiscale developments and biological applications. Chapman and Hall: CRC Press; 2013. [Google Scholar]
- 64.Scianna M, Preziosi L. Modeling the inuence of nucleus elasticity on cell invasion in fiber networks and microchannels. J. Theor. Biol. 2013;317:394–406. doi: 10.1016/j.jtbi.2012.11.003. [DOI] [PubMed] [Google Scholar]
- 65.Scianna M, Munaron L, Preziosi L. A multiscale hybrid approach for vasculogenesis and related potential blocking therapies. Prog. Biophys. Mol. Biol. 2011;106:450–462. doi: 10.1016/j.pbiomolbio.2011.01.004. [DOI] [PubMed] [Google Scholar]
- 66.Scianna M, Preziosi L, Wolf K. A cellular potts model simulating cell migration on and in matrix environments. Math. Biosci. Eng. 2013;10:235–251. doi: 10.3934/mbe.2013.10.235. [DOI] [PubMed] [Google Scholar]
- 67.Shrinifard A, Gens JS, Zaitlen BL, Poplawski NJ, Swat M, Glazier JA. 3D multicell simulation of tumor growth and angiogenesis. PLoS One. 2009;4:e7190. doi: 10.1371/journal.pone.0007190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.St. Croix B, Sheehan C, Rak JW, Florenes VA, Singerland JM, Kerbel RS. E-cadherin-dependent growth suppression is mediated by the cyclin-dependent kinase inhibitor p27Kip1. J. Cell. Biol. 1998;142:557–571. doi: 10.1083/jcb.142.2.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Stolarka M, Kim Y, Othmer H. Multiscale models of cell and tissue dynamics. Philos. T. Roy. Soc. A. 2009;367:3525–3553. doi: 10.1098/rsta.2009.0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Stoletov K, Motel V, Lester RD, Gonias SL, Klemke R. High-resolution imaging of the dynamic tumor cell-vascular interface in trans-parent zebrafish. Nature. 2007;104:17406–17411. doi: 10.1073/pnas.0703446104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Swat MH, Thomas GL, Belmonte JM, Shirinifard A, Hmeljak D, Glazier JA. Multiscale modeling of tissues using CompuCell3D. Method. Cell Biol. 2012;110:325–366. doi: 10.1016/B978-0-12-388403-9.00013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Takai Y, Miyoshi J, Ikeda W, Ogita H. Nectins and nectin-like molecules: roles in contact inhibition of cell movement and proliferation. Nat. Rev. Mol. Cell Biol. 2008;9:603–615. doi: 10.1038/nrm2457. [DOI] [PubMed] [Google Scholar]
- 73.Thalhauser CJ, Lowengrub JS, Stupack D, Komarova N. Selection in spatial stochastic models of cancer: migration as a key modulator of fitness. Biol. Dir. 2010;5:21–37. doi: 10.1186/1745-6150-5-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Tse JMJ, Cheng GG, Tyrrell JAJ, Wilcox-Adelman SAS, Boucher YY, Jain RKR, Munn LLL. Mechanical compression drives cancer cells toward invasive phenotype. PNAS. 2012;109(3):911–916. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Turner S, Sherratt JA. Intercellular adhesion and cancer invasion: a discrete simulation using the extended potts model. J. Theor. Biol. 2002;216(1):85–100. doi: 10.1006/jtbi.2001.2522. [DOI] [PubMed] [Google Scholar]
- 76.Vaslev B, Balter A, Chaplain MAJ, Glazier JA. Modeling gastrulation in the chick embryo: Formation of the primitive streak. PLoS One. 2010;5:e10571. doi: 10.1371/journal.pone.0010571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Voss-Bhme A. Multi-scale modeling in morphogenesis: a critical analysis of the cellular Potts model. PLoS ONE. 2012;7(9):e42852. doi: 10.1371/journal.pone.0042852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Zhang Y, Thomas GL, Swat M, Shirnifard A, Glazier JA. Computer simulations of cell sorting due to differential adhesion. PLoS One. 2011;6:e24999. doi: 10.1371/journal.pone.0024999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.