Compartmental models for apical efflux by P-glycoprotein. Part 1. Evaluation of model complexity

Abstract

Purpose

With the goal of quantifying P-gp transport kinetics, Part 1 of these manuscripts evaluates different compartmental models and Part 2 applies these models to kinetic data.

Methods

Models were developed to simulate the effect of apical efflux transporters on intracellular concentrations of six drugs. The effect of experimental variability on model predictions was evaluated. Several models were evaluated, and characteristics including membrane configuration, lipid content, and apical surface area (asa) were varied.

Results

Passive permeabilities from MDCK-MDR1 cells in the presence of cyclosporine gave lower model errors than from MDCK control cells. Consistent with the results in Part 2, model configuration had little impact on calculated model errors. The 5-compartment model was the simplest model that reproduced experimental lag times. Lipid content and asa had minimal effect on model errors, predicted lag times, and intracellular concentrations. Including endogenous basolateral uptake activity can decrease model errors. Models with and without explicit membrane barriers differed markedly in their predicted intracellular concentrations for basolateral drug exposure. Single point data resulted in clearances similar to time course data.

Conclusions

Compartmental models are useful to evaluate the impact of efflux transporters on intracellular concentrations. Whereas a 3-compartment model may be sufficient to predict the impact of transporters that efflux drugs from the cell, a 5-compartment model with explicit membranes may be required to predict intracellular concentrations when efflux occurs from the membrane. More complex models including additional compartments may be unnecessary.

Introduction

There is increasing recognition that free intracellular concentrations may be different from the free plasma concentrations when drugs are transporter substrates (1,2). Accurate estimation of unbound intracellular concentrations is necessary when predicting activities for intracellular processes including absorption, distribution, metabolism, and excretion (ADME), and pharmacological and toxicological targets (3). Ultimately, the relationship between unbound intracellular concentration and unbound plasma concentration (Kpu,u), must be determined in order to relate these activities to plasma drug levels (2,4–6). Regulatory guidances now include evaluation of transporter mediated drug-drug interactions (DDIs) from the perspective of both victim and perpetrator (7,8). Characterization of transporter activity and quantification of transporter kinetics are active areas of research, but standardization of experimental techniques and data interpretation continues to be challenging.

There are two kinds of experiments that are routinely conducted to characterize efflux transporter mediated processes. First, permeability is measured across cell monolayers in the A→B and B→A directions. These relatively straightforward experiments provide permeability and efflux estimates with sparse, often single point, data. Second, saturation experiments are conducted to determine kinetic parameters such as Km or Ki. These experiments require substantially larger datasets. In a previous report, we utilized single point data to develop and compare 3- and 5-compartmental (3C and 5C) models that estimate passive and efflux clearances, and predict intracellular concentration (9). In Part 1, we develop and evaluate additional models for bidirectional permeability by increasing model complexity. In Part 2, we apply these models to saturation data in order to predict kinetic parameters.

Free intracellular concentrations are difficult to determine experimentally, and modeling techniques may provide a means to estimate this important parameter (2). A number of modeling efforts have been used to describe combinations of permeability, transport, and metabolism, and these models inherently include predictions of intracellular concentrations (10). Compartmental approaches are commonly utilized to model uptake (5,11) and efflux transport (12,13), metabolism (11,14), and combinations of these processes. For example, Kalvass et al. use a three-compartment model with different efflux ratios to simulate passive permeability and transport (12). Bentz and coworkers solve for micro rate constants with multi-time-point permeability data (13). Menochet et al. utilize concentration-time profiles of parent and metabolites to simulate the combination of uptake and metabolism in hepatocytes (11). Different models require datasets of varying complexity depending on the number of parameters being estimated. The overall goal of this research is to develop models based on readily available in vitro data to predict intracellular concentrations in the presence of transporters.

P-glycoprotein (P-gp, ABCB1; MDR1) is an apical efflux transporter that appreciably affects the disposition of drugs. Differences in relative P-gp tissue expression as well as the orientation of the apical membrane determine the role of this transporter in drug distribution. For example, P-gp in brain endothelial cells effluxes drug from the apical membrane into the blood. This is a significant part of the blood-brain barrier, preventing many hydrophobic compounds from entering the brain. In the liver, the apical membrane forms the bile canaliculi, and P-gp effluxes molecules from the apical membrane into the bile. The orientation of the apical membrane relative to the blood (site of drug exposure) can influence the impact of P-gp on intracellular concentrations.

Increasing evidence suggests that P-gp effluxes drugs directly out of the apical membrane (15,16). Compartmental models that represent the cell as a single compartment can effectively simulate efflux transport out of the cytosol and uptake across the plasma membrane. Modeling efflux out of a membrane requires an explicit membrane compartment. We have previously shown that a 5-compartment model with explicit membrane compartments representing the apical and basolateral membranes can reproduce the impact of P-gp in brain and liver concentrations (9). In contrast to the 5-compartment model, the cellular environment is highly complex. Intracellular distribution encompasses partitioning into membranes and organelles (for example mitochondria and lysosomes), and may be influenced by cellular geometry and organization (for example membrane surface areas and transporter densities). In the studies reported in Part 1, we evaluate a number of compartmental configurations more complex than the 5-compartment model for their impact on predicted intracellular concentrations and model error. Characteristics evaluated include lipid content, the number, relative size, and configuration of explicit membrane compartments, and the apical-to-basolateral surface area ratio (asa). Models were developed with permeability data from six drugs in MDCK-MDR1 cells. The effects of experimental variability and model complexity on predictions and errors are discussed.

Materials and Methods

Chemicals and reagents

Reference compounds were supplied by Sigma-Aldrich (St. Louis, MO). Cell culture reagents were purchased from Invitrogen (Carlsbad, CA). Madin-Darby canine kidney cells (MDCK) were obtained from American Type Culture Collection (Manassas, VA). MDCK cells transfected with the MDR1 gene (MDCK-MDR1) were obtained from NIH (Bethesda, MD). Transwells (12-well, 11-mm diameter, 0.4-μm pores) were purchased from Corning Costar (Cambridge, MA).

Microsomal partitioning

Since the endoplasmic reticulum consists of unsorted membrane lipids (17), human liver microsomes were used as a model for membrane partitioning. Microsomal partitioning data was generated by equilibrium dialysis in a 96-well equilibrium dialyzer with a 5000MW cutoff as previously reported (18). Following dialysis, samples from each side of the plate was mixed with an equal amount of the opposite matrix and frozen. For analysis, standard LCMSMS conditions on an API4000 were used.

Cellular transport studies

MDCK-MDR1 cells were cultured and transport experiments were conducted as described previously (9,19). All cells were maintained in high glucose (4.5 g/L) DMEM supplemented with 10% FBS, 1% NEAA, 1% l-glutamine, penicillin (100 U/mL), streptomycin (100 g/mL) at 37 °C in a humidified incubator with 5% CO₂. All cells were seeded at a density of 60,000 cells/cm² onto collagen-coated, microporous, polycarbonate membranes in 12-well Transwell® plates. Cells were used between passages 10 and 14. The culture medium was changed 24 h after seeding to remove cell debris and dead cells; afterwards the medium was changed every other day for 6 days. The permeability assay buffer was Hanks’ balanced salts solution containing 10 mM hydroxyethylpiperazineethane sulfonic acid (HEPES) and 15 mM glucose at pH 7.4 (HBSSg buffer). The test compounds were prepared in HBSSg buffer to a final concentration of 5μM each.

Test compounds were dissolved in dimethyl sulfoxide (DMSO) and then diluted in Hanks’ balanced transport buffer (pH 7.4) (Mediatech, Herndon, VA). The amount of DMSO in the final transport solution was 1% (v/v). Experiments were conducted with or without the P-gp inhibitor cyclosporine A (CsA; 10 μM). The test compounds (5 μM final concentration) were dosed on either the apical side (A→B transport) or the basolateral side (B→A transport) and incubated in a humidified atmosphere at 37 °C with 5% CO₂. For single point experiments, samples were collected at the end of 90 minutes for experiments in each direction. All experiments were conducted in triplicate, and estimate means and standard deviations calculated. A total of 6 compounds were evaluated (Table S1). For permeability experiments, data is not accepted if recovery is less than 80%. Multiple time points were conducted to determine lag time. Conditions for the A→B experiments were repeated with sampling at 15, 30, 45, 60, 75 and 90 min. Target drug concentrations were analyzed by liquid chromatography-tandem mass spectrometry with previously described methods (9).

Modeling

The models were developed in a manner similar to that reported previously (9). Model assumptions include first order kinetics for all processes, equal passive clearances in the A→B and B→A directions, and no loss of drug to degradation or non-specific binding. Since back diffusion from the receiver compartment is included, sink conditions and steady-state are not assumed. Differential equations were developed as previously for the 3-, 4-, 5-, 6-, 7-, and 9-compartment models shown in Figures 1 and S1. Models with explicit membrane compartments used CL_i to represent the clearance of drug into the membrane and CL_o to represent the clearance of drug out of the membrane and into the apical, basolateral, or cellular compartments. When explicit membrane compartments were included in the model (all except the 3-compartment model), CL_o was equated to CL_i/Kp where Kp is the partition constant for the drug partitioning into microsomal membranes. For microsomes, it is assumed that 0.7 mL of lipid is available in a 1 mg microsomal protein/mL incubation (9). Various amounts of cellular lipid were included in the models (5–40%). When physiological volumes of plasma membrane lipid were used in a compartment (6Phys, 7Phys, and 9Phys), it was assumed that the plasma membranes contained 0.1% of cell volume. All other lipid volumes were divided evenly between the remaining lipid compartments in a model. For the 3C and 4C models where the plasma membrane has no explicit volume, CL_d was replaced with CL_i/2 (20). This allows explicit membrane and non-explicit membrane components to be used in the same model.

Figure 1. Compartmental models to predict the impact of transporters on intracellular concentrations.

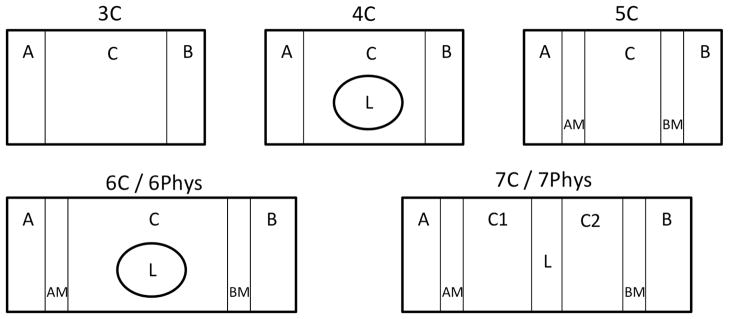
Models 3C-7C (models with mathematical volumes for plasma membrane), and 6Phys and 7Phys (models with physiologic volumes for plasma membrane) are depicted. Compartments are labeled as follows: A: apical; B: basolateral; C,C1,C2: intracellular; L: intracellular lipid; AM: apical membrane; BM: basolateral membrane.

Since it has been reported that in MDCK cells, the apical surface area is a fraction of the basolateral surface area (21), an apical surface area to basolateral surface area ratio (asa) was also varied in some of the calculations. For these calculations, asa was varied between 0.13 and 1. Since clearance is a permeability-surface area product, all clearances into or out of the apical membrane were multiplied by asa to simulate lower clearances with decreasing asa.

General steps for model development included:

1. Derive ordinary differential equations for the appropriate model (see Figures 1 and S1). Parameters that were varied include lipid compartment volumes, asa, and addition of a basolateral uptake transporter.

2. Set efflux clearance (CLae) = 0. Solve the differential equations for CLi in the A→B and B→A directions using receiver concentrations from either MDCK cells or MDCK-MDR1 cells + inhibitor.

3. Using the average CLi from step 2, solve the differential equations for CLae using the receiver concentrations from the MDCK-MDR1 cells.

4. Using the optimized clearance parameters from steps 2 and 3, simulate compartmental concentration -time profiles.

5. Calculate lag times by fitting the simulated receiver concentration-time data to the logistic function (equation 1). Lag times are obtained by extrapolation from the inflection point to the X-axis.

Models with Single Time Point Data

Differential equations for all models in Figure 1 were numerically simulated in Mathematica (Mathematica 8, Wolfram Research). For single point experimental data, initial donor and final receiver concentrations were used to optimize values for CL_i in the A→B and B→A directions using the FindFit optimizer in Mathematica. Single point data sets included either MDCK and MDCK-MDR1 values or MDCK-MDR1 data in the presence or absence of CsA. The CL_i values were obtained using either control MDCK cells or MDCK-MDR1 cells + CsA. The average A→B and B→A CL_i values were used as input parameters along with experimental MDCK-MDR1 efflux ratios to solve for efflux clearances. Since the efflux ratios are a ratio of A→B and B→A receiver concentrations, the system is over-determined and an error of the fit can be calculated from the predicted and observed receiver concentrations.

Lag times (t_lag) were calculated by fitting simulated receiver concentration data to a form of the logistic function (22) in Equation 1.

$$C_{\mathit{rec}}(t)=a\left(\frac{1}{1+e^{k(t_c-t)}}-\frac{1}{1+e^{k{t}_c}}\right)$$ Equation 1

In Equation 1, C_rec(t) is the receiver concentration as a function of time t, a is the asymptotic final concentration, k is the slope at the inflection point and t_c is the inflection point. The slope and inflection point were used to define the straight line and the lag time was calculated from the intersection of that line with the x-axis. This resulted in a consistent method to determine lag time from simulated data.

Models with Multiple Time Point Data

For time course data, the compartmental differential equations were fit simultaneously to the receiver concentration data (six time points collected in triplicate) to optimize a value for CL_i. In order to compare single and multiple time point fits, a CL_i value was also fit to the average of the 90-minute time points. Due to the variability in the experimental data, attempts to fit the logistics equation to experimental time course data were not meaningful. Instead, Equation 1 was fit to predicted data from the compartmental model and lag time was calculated as described above.

Miscellaneous Calculations

In order to investigate the possible impact of lysosomal trapping on permeability, pH partitioning equations (e.g. as described by Friden (6)) were used to simulate partitioning between the cytosol and a lysosomal compartment. Passive clearance into the lysosomal compartment was set as CL_i/2 (20). Lysosomal content was set to 10% of the cell volume. The impact of inclusion of a lysosomal compartment on errors, intracellular concentrations, and lag time was evaluated.

Error Analysis

Since passive membrane clearances were considered to be identical for all membranes, increasing model complexity by adding compartments does not result in additional optimizable parameters. Therefore, standard statistical methods to compare models such as AIC or BIC cannot be used. Since the apical efflux clearances were fit to the experimental efflux ratio, an objective model error could be calculated from the predicted and observed receiver concentrations (error = C_{receiver, obs}/C_{receiver, pred}).

In order to determine possible sources of model errors, we investigated the impact of altered receiver concentration on model error. First, simulated (error-free) receiver concentrations were generated with the 5C model. Next, receiver concentrations were varied in the presence and absence of CsA, for both the A→B and B→A directions. The only systematic change that resulted in non-random, positive errors was higher than expected permeability in MDCK-MDR1 (+ efflux) cells in the B→A direction. Therefore, we added a basolateral efflux transporter to the models and determined its impact on model error.

Results

Experimental variability affects model-predicted parameters

Table 1 lists the A→B and B→A receiver concentrations at 90 min, and efflux ratios (ER) for atorvastatin in MDCK-MDR1 cells with and without CsA. Data from three separate experiments are listed (atorvastatin1, atorvastatin2, and atorvastatin3). All three datasets were generated with standard protocols and procedures. Qualitatively, all three datasets suggest that atorvastatin has moderate-to-poor permeability and is a P-gp substrate. Atorvastatin3 data resulted in the lowest model error (data not shown), and was used for all subsequent studies. These results underscored the sensitivity of the model error to variability in experimental data. The data for all six compounds are given in Table S1 (Supplementary Material).

TABLE 1.

A→B and B→A receiver concentrations at 90 min and efflux ratios for atorvastatin in MDCK-MDR1 cells with or without CsA. Three sets of experiments are reported.

Drug	fum	Cell	C0	Cr,AB	Cr,BA	ER
			μM
Atorvastatin1	0.52	MDCK-MDR1	5	0.004	0.47	38
		MDCK-MDR1 + CsA	5	0.01	0.02	0.4
Atorvastatin2	0.52	MDCK-MDR1	0.5	0.001	0.05	12
		MDCK-MDR1 + CsA	0.5	0.005	0.01	0.9
Atorvastatin3	0.52	MDCK-MDR1	5	0.01	0.75	17
		MDCK-MDR1 + CsA	5	0.07	0.16	0.7

Notations are defined as follows: f_um: fraction of drug unbound in microsomes; C₀: drug concentration at time zero; C_r,AB: concentration in the receiver compartment upon apical drug exposure; C_r,BA: concentration in the receiver compartment upon basolateral drug exposure; ER: efflux ratio

Experimental variability was also evaluated by comparing experiments with different control cells. There are two possible controls for our MDCK-MDR1 cells – background MDCK cells and MDCK-MDR1 cells treated with the P-gp inhibitor CsA. Thus, datasets in MDCK-MDR1 ± CsA cells (Table S1) were compared with datasets from MDCK and MDCK-MDR1 cells (9). Using the 5-compartment model, errors were compared for six substrates at different lipid concentrations. The data for 10% and 40% lipid are given in Table 2. The average fold error for all six drugs at all lipid concentrations was 2-to 3-fold higher when background MDCK cells were used as controls (Table 2).

TABLE 2.

Fold error with the 5C model (asa = 1) in experiments with MDCK-MDR1 + CsA or MDCK cells. Errors at 10% and 40% lipid are listed.

Drug	Experiment
	MDCK-MDR1 + CsA	MDCK	MDCK-MDR1 + CsA	MDCK
	10% lipid		40% lipid
Atorvastatin	1.6	6.5	1.0	4.2
Loperamide	1.2	1.1	3.5	2.1
Labetalol	4.4	10.4	2.9	6.7
Pitavastatin	2.2	14.5	1.4	9.2
Minoxidil	2.4	2.8	2.1	2.5
Verapamil	1.0	1.5	1.5	1.1
Average fold-error	2.1	6.1	2.1	4.3

Model complexity and membrane compartments

The model errors for the various compartmental models are shown in Table 3. The errors were similar for each model and these errors alone are not sufficient to identify an optimal model. When efflux is out of the cytosol, the 3C model might be sufficient. However, the 5C model is the simplest model that allows efflux from the membrane. Although we have evaluated structural parameters (lipid content and fractional surface areas) for all models, for brevity, only the 5C model results will be presented. The predicted clearance values, lag times, and intracellular concentration ratios for the 5C model for asa = 1 and lipid content = 10% are listed in Table 4.

TABLE 3.

Comparison of model errors.

Model	Atorvastatin	Loperamide	Labetalol	Pitavastatin	Minoxidil	Verapamil	Avg Fold Error
3C	2	1.8	4.3	3.2	2	1	2.38
4C	1.2	0.8	2.8	1.9	1.8	0.7	1.43
5C	1.6	0.8	4.4	2.2	2.4	1	2.14
6C	1.8	0.9	4.6	2.5	2.4	1	2.23
6Phys	2.4	1.5	5.4	3.6	2.5	1.1	2.75
7C	2	1	5.4	2.9	2.7	1.1	2.52
7Phys	2.6	1.3	6	4.1	2.7	1.2	2.98
9C	2.3	1.1	6	3.4	2.8	1.2	2.80
9Phys	2.7	1.3	6.4	4.3	2.8	1.2	3.12

TABLE 4.

Estimates of clearances, lag time, and intracellular concentrations obtained with the 5C model. Parameter estimates are reported for asa = 1 and lipid content = 10%.

	CLi	CLae	tlag	Ccell,AB Ratio	Ccell,BA Ratio
	μl/min		min
Atorvastatin	2.7	0.033	43.1	9.66	1.28
Loperamide	32.1	0.681	16.5	43.84	1.91
Labetalol	1.7	0.105	33.4	20.35	1.43
Pitavastatin	3.5	0.030	45.3	10.21	1.08
Minoxidil	0.3	0.021	20.1	2.53	1.26
Verapamil	15.7	0.147	8.7	6.38	1.92

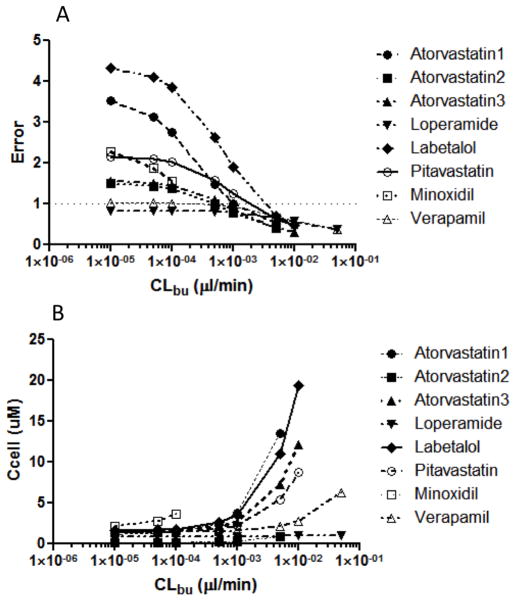
In a systematic evaluation of model errors, the only systematic change that replicated the observed non-random model errors was an increase in B→A permeability for the MDCK-MDR1 cells. This led us to add a basolateral uptake transporter to the 5C model with apical efflux. The effect of incorporating this uptake transporter on model error is shown in Figure 2A. Increasing the basolateral uptake clearance decreases the model error to a point. Figure 2B shows the impact of basolateral uptake clearance on intracellular concentration. Most of the error can be removed without a substantial change in predicted intracellular concentrations.

Figure 2. Impact of basolateral uptake transport on model error and predicted intracellular concentration.

All datasets in Tables 1 and S1 were used to build a 5C model with apical efflux as well as basolateral uptake. In the absence of basolateral uptake experimental data, a theoretical range of CL_bu was used to evaluate the impact of CL_bu on A) model error, and B) predicted intracellular concentration.

Effect of varying lipid content and asa on model parameters

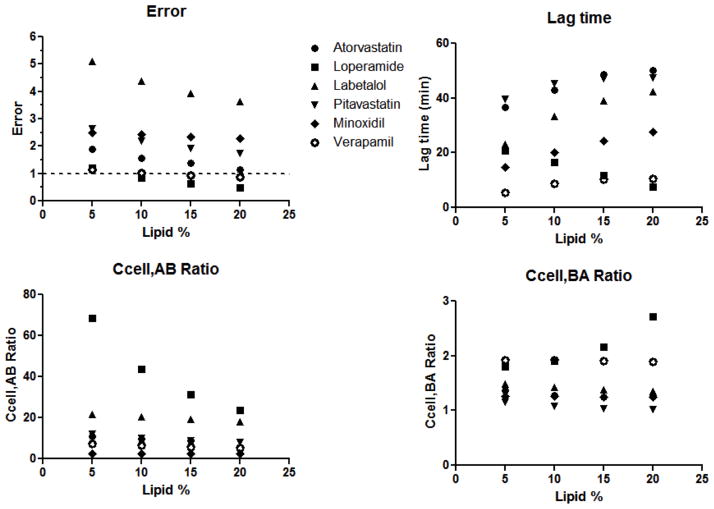
The effect of varying lipid content (5 – 20%) was evaluated for all models, and results for the 5C model (asa = 1) are reported in Figure 3 and Table S2. Similar trends were observed for all models. Model error decreased with increasing lipid content. Lag times increased with increasing lipid for all drugs, with the exception of loperamide. Loperamide has very a high partition constant and high permeability. Therefore the model converged to low lag time estimates at high lipid in order to achieve sufficiently high receiver concentrations. Intracellular concentration ratios in the A→B or B→A direction did not change markedly with varying lipid, again with the exception of loperamide. The C_cell,AB ratio of loperamide increased and C_cell,BA ratio decreased with increasing lipid. For all compounds, 10% lipid was used for subsequent model development.

Figure 3. Effect on lipid content on model predictions.

Lipid content was varied from 5 – 20% in the 5C model. Model errors, predicted lag times, C_cell,AB ratios and C_cell,BA ratios with varying lipid content are depicted for six compounds.

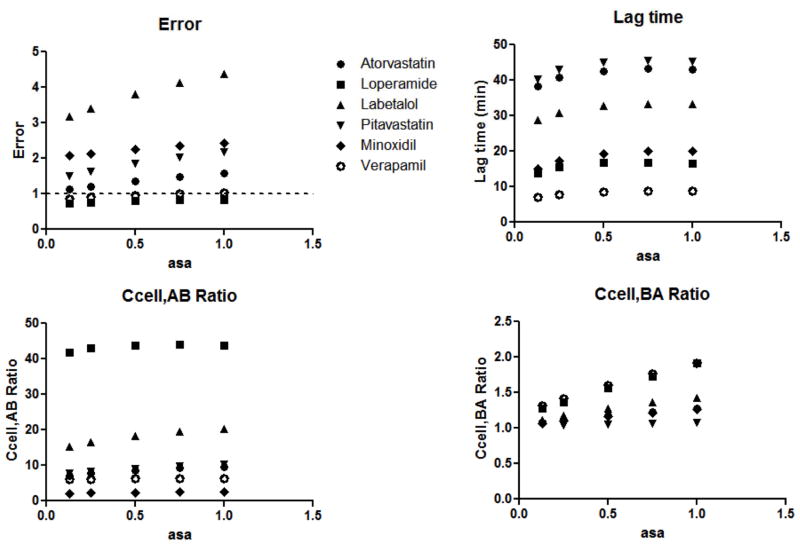
Next, the effect of varying asa (0.13 – 1) was evaluated for all models, and results for the 5C model (10% lipid) are reported in Figure 4 and Table S3. Similar trends were observed for all models. Varying asa did not have a marked effect on model error, lag time estimates, and intracellular concentration ratios. There was a trend of increasing error with increasing asa for some drugs (labetalol, pitavastatin, atorvastatin). This trend was also observed for C_cell,BA ratios for minoxidil and atorvastatin. Subsequently, asa = 1 was used for model development.

Figure 4. Effect of asa on model predictions.

Asa was varied from 0.13 – 1 in the 5C model. Model errors, predicted lag times, C_cell,AB ratios and C_cell,BA ratios with varying asa are depicted for six compounds.

Lag times are observed experimentally

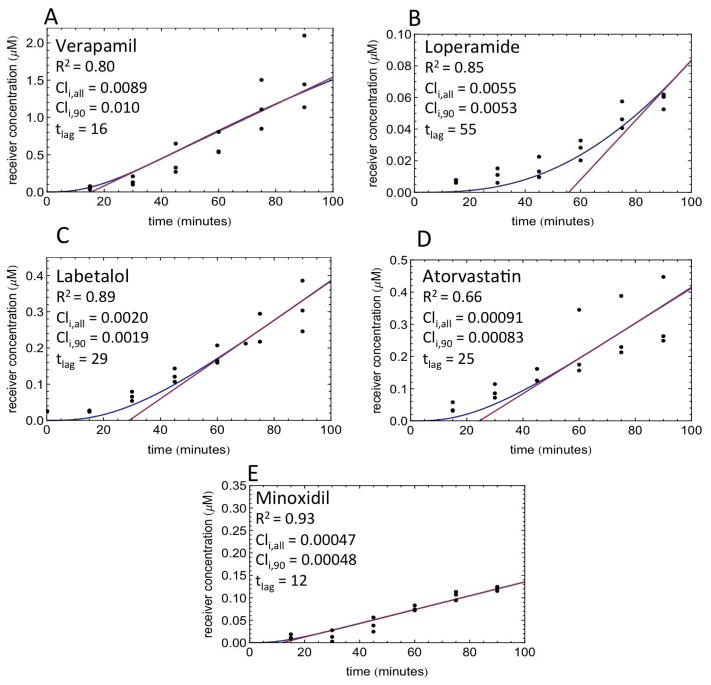
Lag times observed in MDCK-MDR1+CsA cells in the A→B direction for 5 compounds are depicted in Figure 5. The 5C model (10% lipid, asa = 1) was fit to the lag time data (Figure 5, blue line). CL_i estimates obtained with the entire concentration – time dataset (CL_i,all) compared well with CL_i estimates obtained with only the 90-min concentration data point (CL_i,90). Therefore, a time-course experiment may not be necessary in order to obtain cellular diffusion or active efflux clearance estimates. Lag times calculated with the logistic curve equation from the tangent at the inflection point of the curve (Figure 5, red line) are listed in Figure 5 for each drug. Due to experimental variability, it was necessary to fit Equation 1 to the model predicted data shown in Figure 5. This appears to work well for four of five drugs, but the calculated lag time appears to be overestimated for loperamide. It is clear from these data that lag times are observed experimentally for all compounds, and models built upon these datasets should capture the observed lag times.

Figure 5. Experimental lag times.

Receiver concentrations in direction as a function of time are depicted. Experiments were conducted in MDCK cells at 20μM drug concentration in triplicate, and data points are depicted as closed circles. Data were collected for A) verapamil, B) loperamide, C) labetalol, D) atorvastatin, and E) minoxidil. The 5C model-predicted concentration – time profile is depicted with a blue line. The tangent at the inflection point of the logistic curve to calculate lag time (t_lag) is depicted with a pink line. CL_i,all: CL_i predicted with the entire time course dataset; CL_i,90: CL_i predicted with the single point (90 min) data points.

Model predicted lag times are shown in Figure S2. It is noteworthy that the 3C and 4C models - models with no explicit apical or basolateral membrane compartment - did not predict a lag time for any drug. Of the remaining models, the 6Phys model predicted lower lag times compared to the other models. This is also expected since the 6Phys model differs from the 5–9C, 7Phys and-9Phys models in that it lacks a substantial barrier membrane compartment. Due to its low volume, the physiologic plasma membrane compartment reaches steady-state very quickly, resulting in low predicted lag times.

A→B versus B→A intracellular concentration differences are predicted with explicit membrane compartments

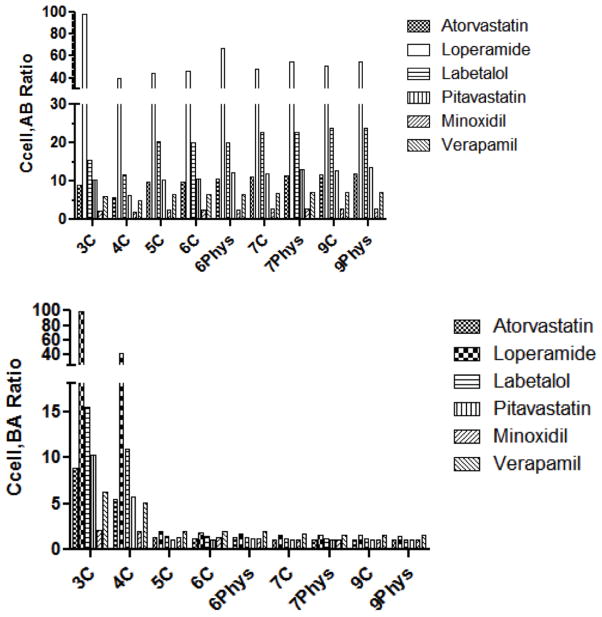
Intracellular concentration ratios (C_cell−efflux/C_cell+efflux) in the A→B and B→A directions (C_cell,AB and C_cell,BA respectively) are shown in Figure 6. Predicted C_cell,AB ratios were similar across models. On the other hand, very low C_cell,BA ratios were predicted by all models except 3C and 4C models. In other words, all models except the 3C and 4C models predict much higher decreases in intracellular concentration in the A→B than in the B→A direction. The 3C and 4C models predict large decreases in intracellular concentrations in both directions.

Figure 6. Comparison of intracellular concentration ratios among models.

C_cell,AB ratios and C_cell,BA ratios predicted from all compartmental models are depicted for six compounds.

Comparison of compartmental models

A total of 9 models were developed (Figure 1and Figure S1), as detailed under Methods. Estimates of clearance and intracellular concentrations, and errors are listed in Table S4. The 3C and 4C models – models with no explicit apical or basolateral membrane compartments – resulted in parameter estimates that were different from all other models for most drugs. Thus, CL_i estimates generally were up to an order of magnitude lower with the 3C and 4C model versus all other models. The estimates for CL_ae with the 3C and 4C models were several orders of magnitude higher compared to the other models. This is expected since the amount transported is [CL_ae * concentration] and the membrane concentrations are much higher than aqueous concentrations. With respect to intracellular concentrations, the C_cell,AB ratios were similar across all models. However, the C_cell,BA ratios were markedly higher with the 3C and 4C models compared to all other models. Finally, errors were comparable across all models (Tables 3 and S4). The inclusion of a lysosomal compartment (pH partitioning (6)) was evaluated but did not result in decreased errors, substantially different lag times, or intracellular concentrations (data not shown).

Discussion

The FDA and EMA guidances on transporters are evolving, and currently do not incorporate specific experimental assays into clear decision trees. This is expected given the diversity of available experimental in vitro systems and protocols, and undeveloped correlations with in vivo effects. Development of these correlations requires both an understanding of relevant concentrations and the kinetic parameters of the transporters of interest. While unbound extracellular concentrations can be measured, unbound intracellular concentrations cannot. The free drug hypothesis suggests that extracellular and intracellular unbound concentrations are equal for permeable compounds. This may not be true for uptake and efflux transporter substrates. Others and we have shown previously that compartment models can be used to predict intracellular concentrations. As discussed below, the present study evaluates the impact of experimental variability, model complexity, and model identifiability on in vitro analyses.

Experimental Variability

Experimental variability is a major factor when developing quantitative relationships for permeability data. The two factors that we have examined are experimental variability and inconsistencies between different cell-based models. For example the variability in the atorvastatin data in Table 1 shows that receiver concentrations can vary more than an order of magnitude on different days. The efflux ratios are more consistent, presumably since some of the variability cancels when ratios are calculated. Similar variability in permeability experiments has been reported in the literature. For example, the reported P_app values for verapamil in MDCK cells varies between 8 and 33 × 10⁻⁶ cm/sec (9,23).

Another factor contributing to variability is the use of different cell lines in the same experiment. Table 2 clearly shows that lower errors are obtained when addition of CsA to the MDCK-MDR1 cell line is used as a control. Others have suggested that different cell lines can have significant differences in permeability and/or transport (24). Differences in cell phenotype such as membrane composition, transporter expression, or tightness of cell junctions could contribute to experimental variability. For this reason, it is preferred to use inhibited cells (e.g. MDCK-MDR1+ CsA) versus background cells (e.g. MDCK) as a control for transporter experiments.

Model Complexity

In contrast to compartmental models, the actual path across a cell is complicated by membranes and organelles. An important component of this complexity that can be modeled is the partitioning of drugs into intracellular lipids. There are two ways we can represent intracellular membrane components. First, a membrane can form a barrier dividing the cellular compartment (e.g. 7C L in Fig. 1). In this case, the drug molecule must diffuse in and then out of the membrane compartment for passage across the cell. A second configuration is a lipid compartment within the cell for which an intracellular drug molecule can but need not diffuse through (e.g. 4C L and 6C L). When modeling the plasma membrane, lipid content can be divided evenly among all membrane compartments, or the plasma membrane compartments can be limited to physiological volumes - only 0.1% of the total cell volume (e.g. 6C or 6Phys respectively). Although we used the fraction unbound in microsomes to estimate membrane partitioning, other modeling efforts have incorporated Log P/Log D to predict Kp (20).

The data presented here suggests that adding model complexity (additional compartments, lysosomal partitioning, geometric changes) does not offer an advantage over the simpler 3C and 5C models. Only P-gp data are discussed here, but we expect similar results for other transporters. Thus, efflux out of the cytotosol and uptake from the extracellular fluid may be adequately modeled with the 3C model.

Error analysis suggests additional transporters

The model errors (Table 3) from the single time-point data arise from lack of consistency between control and efflux cells. Additional unaccounted differences (e.g. additional transporters besides apical efflux) may exist in the A→B and B→A directions. An analysis of the model errors revealed that observed errors (non-random, positive, and large) could only be reproduced with higher than expected permeability in MDCK-MDR1 (+ efflux) cells in the B→A direction. One possible origin of these errors is the presence of an endogenous basolateral uptake transporter that is inhibited by CsA. The presence of endogenous basolateral transporters in MDCK cells has been postulated previously (13,25). We can include a basolateral uptake transporter in our models and determine its impact on the model errors. Figure 2A shows the impact of basolateral uptake clearance (CL_bu) on the errors for the 5C model. As can be seen in this figure, large errors are dramatically reduced with increasing CL_bu. Similar results were obtained for the 7C model (data not shown). The observed decrease in errors is by no means proof of the existence of a basolateral transporter. Any process or property that increases the B→A permeability of the drugs would similarly decrease these errors.

As expected, inclusion of an uptake transporter can influence the intracellular concentration. As can be seen in Figure 2B, the predicted intracellular concentrations increase with increasing CL_bu. Poorly permeable compounds, e.g. labetalol, are more likely than highly permeable compounds, e.g. verapamil, to exhibit these increased concentrations. Comparing Figures 2A and 2B, it can be seen that most of the error is removed before large increases in intracellular concentrations are observed. The results in Figure 2 should be interpreted qualitatively. Errors could be due to factors other than basolateral uptake. Therefore mathematically minimizing errors by with CL_bu may not provide a true estimate of uptake. Experimental uptake data would be necessary to parameterize CL_bu and predict intracellular concentrations.

Impact of lipid content

With compartmental models, volumes such as lipid content need not be physiological, and can instead be mathematical (‘apparent’). These volumes are used to reproduce observed concentrations. In the present study, we have evaluated all our models at lipid contents ranging from 5% to 40% (Table S2). Data are shown for 5–20% lipid (Figure 3), because higher partitioning drugs such as loperamide cannot be correctly modeled at higher lipid content. Also, the physiological lipid content of cells is likely to be 5–10% of cell volume (26–28).

Impact of surface area ratios

In addition to membrane configuration and content, another consideration of the cell models is the relative surface area of the apical and basolateral membranes. It has been reported that the apical surface area of MDCK cells is 13% of the basolateral surface area (asa = 0.13 (21)). We therefore evaluated all models (at 10% lipid) at asa values ranging from 0.13 to 1.0 (Table S3). As seen in Figure 4, there is very little change in errors, lag time, and concentration ratios with changes in asa.

Model Identifiability

It is clear from the above discussions that the errors cannot definitively identify the best model. This not surprising since the mathematical equations of the models can be collapsed to identical forms (see Part 2). However, there are two observations for which some models diverge. First, a lag time is predicted for some but not all models. Second, although experimental receiver concentrations can be reproduced for all models, intracellular concentrations can vary dramatically as discussed below.

Lag time

Although there is variability in observed lag times between and within experiments (Figure 5), all compounds studied do show a lag time. These lag times are presumably due to both diffusional barriers and the need to equilibrate with intracellular membranes. As seen in Figure S2, the 3C and 4C models do not predict lag times. This is because these models have no membrane barriers. A molecule that crosses the first plasma membrane (with no explicit volume) is immediately available at the second plasma membrane. A lag time is predicted for the 6Phys model but the minimal volume of the membrane barrier allows rapid equilibration, and therefore, the lag times are minimal. On the other hand, all models with considerable membrane barrier volumes predict longer lag times.

It stands to reason that both poor permeability and high partitioning will increase lag times. Therefore it could be expected that physicochemical properties of drugs will be determinants of lag times. It is also possible that the complexities of cellular membranes contribute to delayed passage across cells. For example, the inner and outer leaflets of the plasma membrane have different compositions (29). Our current datasets are too sparse and too variable to model these complex relationships.

Intracellular concentrations

As stated earlier, predicting relevant concentrations of transporter substrates is critical for accurate in vitro - in vivo extrapolation. The impact of transporter activity on unbound intracellular concentrations can be evaluated with compartment models (6,11,30). For the models discussed here, models with explicit membranes predicted quantitative differences between the A→ B and B→A directions. As can be seen in Figure 6, the 3C and 4C models show substantial decreases in intracellular concentrations in the presence of active efflux for both A→ B and B→A directions. For all other models, active efflux results in minimal decreases in intracellular concentrations in the B→A direction. This is because the apical efflux is modeled out of the cell in the 3C and 4C models and out of the apical membrane in all other models. As discussed previously, decreasing the apical membrane concentration upon basolateral addition will result in at most a two-fold decrease in intracellular concentration (9).

The difference in apical and basolateral exposure becomes important when considering the impact of efflux transporters on tissue concentrations. A review of the numerous examples in the literature underlines the impact of P-gp expression on brain and liver exposure in mdr1 knockout mice (Table 5). The brain concentrations ratios (knockout to wild type) ranged from 1.3 to 73.6, with an average ratio of 19.2. In contrast, the liver exposure ratios ranged from 0.5 to 4.5 with an average of 1.7. While this is consistent with efflux out of the apical membrane, differences in transporter expression could also explain this data. An interesting exception is pitavastatin for which the predicted A→B intracellular concentration ratio is 10 whereas the experimental brain ratio is 1.3. These results are not surprising, since pitavastatin has been shown to be subject to both uptake and efflux transport in the rodent brain (31). This underscores the point that all transport activity must be accounted for, in order to have confidence in predicting intracellular concentrations (see Figure 2B).

TABLE 5.

Brain and liver concentration ratios in mdr1(−/−)/mdr1(+/+) mice, compared with ratios predicted from the 5C model.

Drug	Brain Conc. Ratio mdr1(−/−)/mdr1(+/+)	Predicted Ccell,AB ratio	Liver Conc. Ratio mdr1(−/−)/mdr1(+/+)	Predicted Ccell,BA ratio	Reference
Verapamil	9.5	6.4	1.1	1.9	(32)
Verapamil	7.7	6.4	n.d.	1.9	(33)
Loperamide	65	43	n.d.	1.9	(34)
Loperamide	31	43	n.d.	1.9	(33)
Loperamide	13.5	43	3.1	1.9	(35)
Pitavastatin	1.3	10	0.88	1.1	(36)
Digoxin	35.3	31	2.0	1.5	(37)
Morphine	1.7	n.d.	1.1	n.d.	(37)
Dexamethasone	2.5	n.d.	1.1	n.d.	(37)
CsA	17	n.d.	1.2	n.d.	(37)
Ondansetron	4.0	n.d.	0.9	n.d.	(35)
Vinblastine	22.4	n.d.	1.8	n.d.	(38)
Asimadoline	9.1	n.d.	1.1	n.d.	(39)
Nelfinavir	16.1	n.d.	3.0	n.d.	(40)
Selamectin	4.9	n.d.	0.5	n.d.	(41)
Ivermectin	59	n.d.	3.7	n.d.	(41)
Grepafloxacin	2.35	n.d.	0.88	n.d.	(42)
Tacrolimus	6.0	n.d.	1.7	n.d.	(43)
Apafant	73.6	n.d.	4.5	n.d.	(44)
SDZ PSC 833	2.1	n.d.	0.9	n.d.	(45)

n.d., not determined.

Summary

The major goal of this research effort is to provide models that can use in vitro data to predict in vivo intracellular concentrations in various tissues and in the presence of P-gp. Therefore, we have explored several models, with varying characteristics, including membrane configurations, lipid content, and membrane surface area ratios. When membranes are modeled explicitly, these characteristics have little effect on errors and predicted intracellular concentrations. Errors in these models may be primarily due to the presence of multiple transporters in the experimental system. Our results suggest that 1) a 3-compartment model may be sufficient when efflux occurs from the cell and capturing lag times is unnecessary; 2) a five-compartment model is sufficient to predict the impact of transport out of a membrane; 3) this model may be applicable to different cell types with different apical and basolateral surface areas and different lipid contents; and 4) these models can and should be expanded to include additional transporters as necessary. As our ability to identify and characterize individual transporters increases, these models can be expanded to predict complex cellular distribution.

Abbreviations

3C, 5C, 6C, 7C, 9C

3-, 5-, 6-, 7-, and 9-compartmental models respectively

6Phys, 7Phys, 9Phys

6-, 7-, and 9-comparment models with physiologic volumes of plasma membranes

A→B

apical to basolateral transport

ABCB1

ATP-binding cassette transporter B1

asa

apical-to-basolateral surface area ratio

B→A

basolateral to apical transport

C_{cell,AB ratio}

the ratio on predicted intracellular concentration in the A→B direction, without efflux transport to with efflux transport

C_{cell,BA ratio}

the ratio on predicted intracellular concentration in the B→A direction, without efflux transport to with efflux transport

CL_ae

active apical efflux clearance

CL_bu

active basolateral uptake clearance

CL_cib

clearance through a compound independent barrier

CL_d

passive diffusion clearance

CL_i

diffusion clearance into an explicit membrane compartment

CL_o

diffusion clearance out of an explicit membrane compartment

Kp

partition constant for the drug partitioning into microsomal membranes (Kp = CL_i/CL_o)

CsA

cyclosporine A

ER

efflux ratio

MDCK

Madin-Darby canine kidney cells

MDR1

multidrug resistance protein 1 gene

MDCK-MDR1

MDCK cells stably transfected with human MDR1

P_app

apparent permeability

P-gp

P-glycoprotein

t_lag

permeability lag time