Abstract
Magnetoencephalography (MEG) is an important non-invasive method for studying activity within the human brain. Source localization methods can be used to estimate spatiotemporal activity from MEG measurements with high temporal resolution, but the spatial resolution of these estimates is poor due to the ill-posed nature of the MEG inverse problem. Recent developments in source localization methodology have emphasized temporal as well as spatial constraints to improve source localization accuracy, but these methods can be computationally intense. Solutions emphasizing spatial sparsity hold tremendous promise, since the underlying neurophysiological processes generating MEG signals are often sparse in nature, whether in the form of focal sources, or distributed sources representing large-scale functional networks. Recent developments in the theory of compressed sensing (CS) provide a rigorous framework to estimate signals with sparse structure. In particular, a class of CS algorithms referred to as greedy pursuit algorithms can provide both high recovery accuracy and low computational complexity. Greedy pursuit algorithms are difficult to apply directly to the MEG inverse problem because of the high-dimensional structure of the MEG source space and the high spatial correlation in MEG measurements. In this paper, we develop a novel greedy pursuit algorithm for sparse MEG source localization that overcomes these fundamental problems. This algorithm, which we refer to as the Subspace Pursuit-based Iterative Greedy Hierarchical (SPIGH) inverse solution, exhibits very low computational complexity while achieving very high localization accuracy. We evaluate the performance of the proposed algorithm using comprehensive simulations, as well as the analysis of human MEG data during spontaneous brain activity and somatosensory stimuli. These studies reveal substantial performance gains provided by the SPIGH algorithm in terms of computational complexity, localization accuracy, and robustness.
Keywords: MEG, EEG, source localization, sparse representations, compressive sampling, greedy algorithms, evoked fields analysis
1. Introduction
Magnetoencephalography (MEG) is among the most popular non-invasive modalities of brain imaging, and provides measurements of the collective electromagnetic activity of neuronal populations with high temporal resolution on the order of milliseconds. Both techniques have applications in understanding the mechanisms of language, cognition, sensory function, and brain oscillations, as well as clinical applications such as localization of epileptic seizures.
Localizing active regions in the brain from MEG measurements requires solving the high-dimensional ill-posed neuromagnetic inverse problem: given measurements from a limited number of sensors (∼102 sensors) and a model for the observation process, the goal is to estimate spatiotemporal cortical activity over numerous sources (∼ 104 sources). The ill-posedness of this problem is due not only to the limited number of measurements compared to unknowns, but also due to the high spatial dependency between measurements. The ill-posed nature of the inverse problem limits the spatial resolution of MEG. In comparison, other imaging modalities such as functional magnetic resonance imaging (fMRI) or positron emission tomography (PET) have high spatial resolution, but poor temporal resolution.
In the past two decades, various inverse solutions have been proposed for MEG and Electroencephalography (EEG) source localization. The earliest proposals appearing in the literature aimed at regularized least squares solutions to the neuromagnetic inverse problem (Hämäläinen and Ilmoniemi, 1994; Pascual-Marqui et al., 1994; Gorodnitsky et al., 1995; Van Veen et al., 1997; Uutela et al., 1998). Later on, inverse solutions in the framework of Bayesian estimation were introduced, with the underlying assumption of temporal independence (Sato et al., 2004; Phillips et al., 2005; Mattout et al., 2006; Nummenmaa et al., 2007; Wipf and Nagarajan, 2009). In order to impose spatio-temporal smoothness on the inverse solution, subsequent algorithms in the Bayesian framework considered the design of spatio-temporal priors (Baillet and Garnero, 1997; Bolstad et al., 2009; Daunizeau et al., 2006; Daunizeau and Friston, 2007; Friston et al., 2008; Greensite, 2003; Limpiti et al., 2009; Trujillo-Barreto et al., 2008; Zumer et al., 2008) or employed linear state-space models (Galka et al., 2004; Yamashita et al., 2004; Long et al., 2011; Lamus et al., 2007). Despite their improved accuracy in source localization, many of these more recent solutions suffer from unwieldy computational complexity.
Sparse solutions to the MEG/EEG source localization problem have received renewed attention in recent years (Gorodnitsky et al., 1995; Durka et al., 2005; Vega-Hernández et al., 2008; Valdés-Sosa et al., 2009; Ou et al., 2009; Gramfort et al., 2011, 2012; Tian and Li, 2011; Tian et al., 2012). Although many of these methods are computationally demanding, they have been shown to enhance the accuracy of source localization. The sparsity constraints underlying these methods express the intuition that out of the ∼ 104 potential sources, only a small number are truly active. In many applications of MEG/EEG source localization, such as sensory or cognitive studies, the underlying cortical domains responsible for the processing are relatively focal and thus sparse. Processes that are spatially-distributed can also be sparse in some basis: for instance, resting-state fMRI dynamics are broadly distributed across cortex, yet appear to be organized within a small number of specific networks (Damoiseaux et al., 2006). Spatial sparsity is therefore not only a mathematically attractive constraint, but also one that is consistent with the neurophysiological processes underlying EEG and MEG.
The advent of compressed sensing (CS) theory has paved the way to establish a rigorous framework for efficient sampling and estimation of signals with underlying sparse structures (Donoho, 2006; Candès et al., 2006). CS methods have found applications in various disciplines such as communication systems, computational biology, geophysics, and medical imaging (see Bruckstein et al. (2009) for a survey of the CS results). The problem of recovering a sparse unknown signal given limited observations is combinatorial and NP-hard in nature (Bruckstein et al., 2009). Several solutions to this problem have been proposed, which can be categorized into optimization-based methods, greedy pursuit methods, and coding theoretic/Bayesian methods. These solution categories pertain to different regimes of sparseness as well as different ranges of computational complexity. Moreover, they all require certain notions of regularity in the measurement structure which must be satisfied in order to guarantee convergence and sparse recovery.
In this work, we develop an inverse solution to the MEG inverse problem in the context of CS theory that achieves both high localization accuracy and very low computational cost. This algorithm is based on a class of greedy pursuit algorithms known as Subspace Pursuit (Dai and Milenkovic, 2009) or Compressive Sampling Matching Pursuit (CoSaMP) (Needell and Tropp, 2009). These algorithms can achieve high recovery accuracy with low computational complexity, but are difficult to apply directly to the MEG inverse problem because of the high-dimensional structure of the MEG source space and the high spatial correlation in MEG measurements. We introduce novel algorithms that address both of these issues in a principled manner. Through comprehensive simulation studies and analysis of human MEG data, we demonstrate the utility of the proposed method, and its superior performance compared to existing methods.
2. Methods
2.1. The MEG observation model
The MEG data consists of a multidimensional time series recorded using an array of sensors located over the scalp. Let N denote the number of such sensors, and t = 1, … ,T denote the discrete time stamps corresponding to the sampling frequency fs. We denote by yi, t the magnetic measurement of the ith sensor at time t, for 1 ≤ i ≤ N and 1 ≤ t ≤ T. Let yt := [y1,t, y2,t, … , yN,t]′ denote the vector of measurements at time t. Finally, we denote the multidimensional observation time series in the interval [0, T] by the N × T matrix Y := [y1, y2, … , yT].
We pose the source localization problem over a distributed source model comprising dipoles with fixed locations and possibly variable orientations, representing the cortical activity. Let M be the total number of dipole sources distributed across the cortex, and let xi,t denote the amplitude of the ith dipole at time t. Denoting by Xt := [x1,t, x2,t, … , xM,t]′ the vector of dipole amplitudes at time t, the source space can be fully characterized by the M × T matrix X := [x1, x2, … , xT].
For a fixed configuration of dipoles, the observation matrix Y can be related to the source activity matrix X as follows:
| (1) |
where G ∈ ℝN×M is the lead field matrix and V := [v1, v2, … , vT] ∈ ℝN×T is the observation noise matrix. The lead field matrix G is a mapping from the source space to the sensor space and can be computed using a quasi-static approximation to the Maxwell's equations (Hämäläinen et al., 1993). The observation noise is assumed to be zero-mean Gaussian, with spatial covariance matrix C ∈ ℝN×N with no temporal correlation.
The MEG inverse problem corresponds to estimating X given Y, G and the statistics of V. The traditional source spaces used for MEG source localization have a dimension of M ∼ 103 – 105, whereas the number of sensors is typically N ∼ 102. Since M » N, the MEG inverse problem is highly ill-posed and hence requires constructing appropriate spatiotemporal priors in order to estimate X reliably.
2.2. The Minimum Norm Estimate
As outlined in the introduction, various source localization techniques have been developed since the invention of MEG. Arguably, the Minimum Norm Estimate (MNE) inverse solution is the most widely-used MEG source localization technique (Hämäläinen and Ilmoniemi, 1994). In what follows, we give a brief overview of the MNE and one of its recent variants.
The MNE inputs Y, G, C and a spatial prior covariance Q/λ2 ∈ ℝM×M on X with λ being a scaling factor, and solves for:
| (2) |
The role of the spatial prior covariance Q is to weight the penalization of the energy of the estimated sources across the source space (Hämäläinen and Ilmoniemi, 1994; Lamus et al., 2012). Moreover, the scaling factor λ can be viewed as a regularization parameter, controlling the Q-weighted ℓ2-norm of the estimate. The minimization is separable in time, and the estimate can be expressed in closed form as:
| (3) |
It is more convenient to compute the MNE estimate in a whitened model in favor of computational stability. The whitened model is obtained by the pre-multiplication of the observation model by C−1/2. Let Ỹ ≔ C−1/2Y and G̃ ≔ C−1/2G denote the whitened observation and lead field matrices, respectively. The spatial prior covariance Q can be chosen such that the SNR of the whitened model is of the order 1 (Hämäläinen, 2010), that is
| (4) |
This assumption implies that the SNR in the original observation model is of the order ∼ 1/λ2. The MNE inverse solution can be written in terms of the whitened parameters as:
| (5) |
Note that we have dropped the dependence of the solution on Q, λ and C due to the assumption of Eq. (4).
In the Bayesian framework, the cost function of MNE can be interpreted as the logarithm of the posterior density of X, given the observations Y and a Gaussian prior on X, corresponding to the following model:
| (6) |
Note that in the above formulation, the spatial prior covariance Q is considered data-independent. In order to adapt the covariance to the data, the Expectation-Maximization algorithm can be employed to iteratively update Q given an estimate of the sources. The resulting algorithm is denoted by sMAP–EM in Lamus et al. (2012), and will be referred to as MNE–EM hereafter in this paper.
2.3. Sparse MEG Source Localization
Since the advent of the compressive sampling theory, sparsity-based signal processing has become an active area of research in various disciplines such as communication systems, medical imaging, geophysical data analysis, and computational biology. The main questions addressed by sparsity-based signal processing are the following: 1) For a given signal, is there a domain in which the signal is sparse, or can be well-approximated by a sparse signal? 2) For a given sparse signal, how can one find a sparse representation? 3) What are efficient ways to measure/sample sparse signals? and 4) Given an efficient (compressive) sample of a sparse signal, how can one reconstruct it faithfully?
In order to develop a framework for sparse MEG source localization, one needs to carefully fit the above questions in the context of MEG. In order to address the first two questions, we focus our attention to a class of important applications of MEG source localization, which deal with spatially sparse sources of brain activity. Examples include evoked fields localization (Mäkelä et al., 1994; Hari et al., 2006) and seizure localization (Sutherling et al., 2004; Marks Jr, 2004). Therefore, a source space consisting of cortical patches of activity seems suitable for posing the sparse MEG source localization problem. We will discuss the construction of such a cortical patch decomposition model in the next section. The third question is not readily applicable to MEG source localization, since the observation mechanism (sensor locations, sampling rate, etc.) is dictated by the MEG devices and protocols. The problem of sparse MEG source localization can therefore be summarized as follows: given a time series of MEG measurements induced by sparse cortical patches of activity, is it possible to localize the sources efficiently (in space and time)?
In order to address the fourth question, we need to examine different classes of compressive sampling reconstruction algorithms. The existing algorithms can be categorized into three groups:
Optimization-based methods, such as ℓ1-norm minimization (Donoho and Elad, 2003; Candes and Tao, 2005) and the LASSO (Tibshirani, 1996). These algorithms are typically computationally demanding, but suitable for low to medium sparsity regimes and generic random-like measurement structures. For instance, the LASSO algorithm has a computational complexity of
 (M3 + NM2), where M and N denote the number of unknowns and observations, respectively (Genovese et al., 2012).
(M3 + NM2), where M and N denote the number of unknowns and observations, respectively (Genovese et al., 2012).Greedy pursuit algorithms, such as Orthogonal Matching Pursuit (OMP) (Mallat and Zhang, 1993; Tropp and Gilbert, 2007) and its variants, Subspace Pursuit (Dai and Milenkovic, 2009) and CoSaMP (Needell and Tropp, 2009). These algorithms are termed ’greedy’ because they simplify the combinatorial problem of sparse recovery by sequentially choosing a small subset of the source space which is highly correlated with the observations as the candidate inverse solution. Greedy algorithms enjoy a very low computational complexity, and are tailored for low sparsity regime and generic random-like measurement structures. For instance, the computational complexity of Subspace Pursuit and CoSaMP is
 (M log2M), where M denotes the number of unknowns (Needell and Tropp, 2009).
(M log2M), where M denotes the number of unknowns (Needell and Tropp, 2009).Coding theoretic (Akçakaya and Tarokh, 2008), Bayesian (Baron et al., 2010), and Group Testing approaches (Atia and Saligrama, 2012). This class of algorithms stand in-between the previous two categories in terms of computational complexity, but require very structured measurement designs. For instance, the computational complexity of the coding theoretic method developed by Akçakaya and Tarokh (2008) is
 (N2), where N denotes the number of observations (Akçakaya and Tarokh, 2008).
(N2), where N denotes the number of observations (Akçakaya and Tarokh, 2008).
In the context of MEG source localization, one is faced with a high-dimensional time series of observations, and therefore computational complexity is one of the main challenges. In addition, most of the MEG source localization applications deal with sparse sources of cortical activity. Therefore, the class of greedy pursuit algorithms seems to be an appropriate candidate for sparse MEG source localization. A notable greedy source localization technique for EEG was developed by Durka et al. (2005), in which the EEG data is first greedily decomposed into a set of Gabor atoms, and then localized using the LORETA inverse solution (Pascual-Marqui et al., 1994). However, in general, the measurement structure of MEG is very different than those required by the theory of compressive sampling, and therefore one needs to carefully modify these algorithms in order to adapt them for sparse MEG source localization.
2.4. Cortical Patch Decomposition
In order to build a densely sampled source space for MEG source localization, the cortical surfaces for each subject are reconstructed from MRI images, and each hemisphere is subsequently mapped onto a 3-sphere. Each 3-sphere is then approximated by the recursive subdivision of an icosahedron, resulting in a series of nested source spaces. Let S0 be the set of vertices corresponding to an icosahedron. The recursive subdivision results in the nested source spaces S1, S2, … ,S7 such that Si−1 ⊂ Si, for 1 ≤ i ≤ 7, and that the number of vertices in Si is given by Ki = 10 × 4i + 2 per hemisphere (Winkler et al., 2012). The densely sampled source space over both hemispheres is a decimated version of S7, which comprises ∼ 300, 000 vertices. For notational convenience, we denote the conventional densely sampled source space by S7.
Posing the MEG inverse problem in the source space S7 is superfluous given the limited number of sensors M ∼ 102, unless very accurate priors regarding the spatial configuration of the dipole sources are available to the estimator. In this regard, it is advantageous to coarsen the densely sampled source space in order to obtain an economical source space proportional in size to the sensor space. Building on previous work presented by Limpiti et al. (2006), we introduce a systematic way of coarsening the source space. In this coarsening technique, the Voronoi regions induced by the Euclidian norm from the source spaces S1, S2, and S3 over S7 are considered as the new coarsened source spaces. Each Voronoi region is denoted by a patch of cortical activity. We further reduce the order of the source space by only including the first few significant eigenmodes of each cortical patch in the forward model. The reduced order source space induced by the source space Si over S7 is denoted by
 i, for i = 1, 2, and 3. Figure 1 shows the lateral view of the left hemisphere decomposed into cortical patches at different levels of coarseness.
i, for i = 1, 2, and 3. Figure 1 shows the lateral view of the left hemisphere decomposed into cortical patches at different levels of coarseness.
Figure 1.
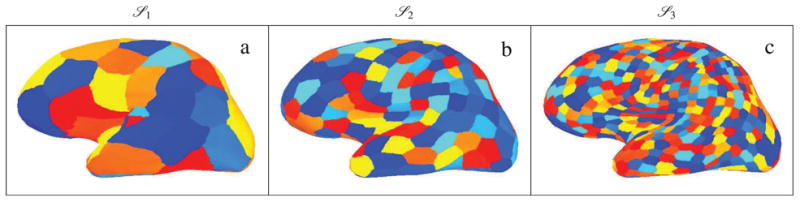
The cortical patch decomposition obtained by recursive subdivision of an icosahedron, (a)
 1, (b)
1, (b)
 2, and (c)
2, and (c)
 3.
3.
This procedure results in a significant reduction of the source space complexity, while maintaining a high representation accuracy. At the same time, the resulting source spaces provide a hierarchy of distributed bases for sparse representation of the cortical activity. For instance, consider the cortical patch decomposition model
 3, with 2 eigenmodes per patch. The dimension of this source space is 2|S3| = 4(10 × 43 + 2) = 2568, which is much smaller than the dimension of S7. On average, more than 90% of the energy of each patch can be recovered by only including two eigenmodes per patch in the resulting forward model. The details of the construction of these reduced-order source spaces, as well as their representation accuracy analysis, is presented in Appendix A. As it will be shown in the results section, our proposed inverse solution performs gracefully under the fixed representation error tolerance of the reduced-order source space models.
3, with 2 eigenmodes per patch. The dimension of this source space is 2|S3| = 4(10 × 43 + 2) = 2568, which is much smaller than the dimension of S7. On average, more than 90% of the energy of each patch can be recovered by only including two eigenmodes per patch in the resulting forward model. The details of the construction of these reduced-order source spaces, as well as their representation accuracy analysis, is presented in Appendix A. As it will be shown in the results section, our proposed inverse solution performs gracefully under the fixed representation error tolerance of the reduced-order source space models.
2.5. Overview of the Subspace Pursuit and CoSaMP algorithms for sparse recovery
The Subspace Pursuit (Dai and Milenkovic, 2009) and CoSaMP (Needell and Tropp, 2009) are two very similar algorithms for greedy compressive sampling. We give a brief overview of the Subspace Pursuit (SP) algorithm in what follows, and describe its similarities to and differences with CoSaMP.
We say that a vector x ∈ ℝM is s-sparse, if the support of x is of size s, that is,
| (7) |
Similarly, we say that a vector x ∈ ℝM is s-compressible, if the best s-term approximation of the signal in the ℓ1 sense contains most of the energy of the signal.
The SP algorithm is posed for a single observation model, given by:
| (8) |
where y ∈ ℝN is the observation vector, A ∈ ℝN×M is the measurement matrix, x ∈ ℝM is the unknown s-sparse (or s-compressible) vector, and n ∈ ℝN is the observation noise. We denote by A† the Moore-Penrose pseudo-inverse of A, and by A the column restriction of A to the index set given by
the column restriction of A to the index set given by
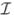 .
.
The SP algorithm inputs s, y and A, and is summarized as Algorithm 1. The main iteration of the SP algorithm consists of five steps. The first step identifies a candidate support for any component of the
|
|
| Algorithm 1 SP(y, A, s) |
|
|
Initialization: Let
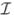 (0) be the index set corresponding to the s largest magnitude entries in the proxy vector p(0):=A′y, and let r(0) be the initial residual error given by
. (0) be the index set corresponding to the s largest magnitude entries in the proxy vector p(0):=A′y, and let r(0) be the initial residual error given by
. |
| Iteration: |
| 1: Identification and support merging: set ∪{s indices corresponding to the largest magnitude entries of the proxy p(ℓ):=A′r(ℓ−1)}. |
| 2: Estimation: set . |
3: Support trimming: set
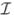 (ℓ) ={s indices corresponding to the largest magnitude entries of the estimate
}. (ℓ) ={s indices corresponding to the largest magnitude entries of the estimate
}. |
| 4: Residual update: set . |
5: Halting criterion: if
, let
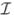 (ℓ)= (ℓ)=
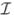 (ℓ−1), and quit the iteration. (ℓ−1), and quit the iteration. |
| Output: the final estimate . |
|
|
true vector which is possibly not identified yet, and merges the identified support with that of the current estimate. Given a generic residual error r, the candidate support set is identified through a ”proxy” given by p = A′r. If the columns of A are nearly orthonormal, one expects that the entries of the proxy p with high magnitudes provide a faithful representation of the unidentified components of the true vector (Dai and Milenkovic, 2009). The second step provides a restricted estimate of the true vector over the merged support. In the third step, the support of the estimate is trimmed down according to the input sparsity level s. The residual of the observation, containing any portion of the signal which is not possibly identified in the current estimate, is then updated given the trimmed support. Finally, the last step gives a halting criterion, which stops the exploration of the algorithm for further unidentified components of the true vector. The final estimate of the SP algorithm is a restricted least squares estimate over the final identified support of size s.
The CoSaMP algorithm differs with SP only in the first step of the iteration, where 2s indices are merged with the support of the current estimate. In the remainder of this manuscript, we jointly refer to these algorithms as SP/CoSaMP to maintain fairness of accreditation. Dai and Milenkovic (2009) and Needell and Tropp (2009) prove theoretical guarantees for stable recovery of s-sparse signals, as well as, s-compressible signals, given that the matrix A satisfies the Restricted Isometry Property (RIP). The RIP of order s requires that the singular values of any subset of the columns of A of size s are sufficiently close to 1. Dai and Milenkovic (2009) and Needell and Tropp (2009) show that if A satisfies the RIP of orders 3s and 4s, respectively, then stable recovery of the unknown signal x is guaranteed.
2.6. Adapting SP/CoSaMP for the MEG inverse problem
The SP/CoSaMP algorithms cannot readily be applied to the MEG inverse problem, due to the inherent structure of the MEG lead field which dramatically differs from the conventional measurement matrices employed for compressive sampling. Moreover, the MEG data is in the form of a time series, whereas the SP/CoSaMP algorithms are tailored for single observations. In the following subsections, we first construct the SP–MNE algorithm, a greedy algorithm in the tradition of SP/CoSaMP, which is suitably tailored for the MEG forward model. Next, we will use the SP–MNE algorithm as the core for an estimation procedure which moves across the hierarchy of cortical patch decomposition models and refines the spatial resolution of the inverse solution. The latter estimation procedure is denoted by the Subspace Pursuit-based Iterative Greedy Hierarchical (SPIGH) inverse solution.
2.6.1. SP–MNE: A Subspace Pursuit-based inverse solution for MEG
The MEG observation model differs with those of the SP/CoSaMP algorithms in two major aspects. First of all, it is in the form of a spatial time series, whereas for SP/CoSaMP, the observation model consists of a single time step. Secondly, the lead field matrix G is very structured with strong column correlations, and therefore does not satisfy the RIP requirements of SP/CoSaMP. The significance of RIP for the successful recovery of SP/CoSaMP algorithms is two-fold: on one hand, it guarantees that the proxy obtained in step 1 is a faithful representative of the undiscovered components of the signal, and on the other hand, it provides a sufficient degree of incoherence between the columns of A restricted to the support of the true vector x, which in turn leads to stable recovery of different components of x.
In order to adapt these algorithms for MEG source localization, we need to carefully account for these issues. In what follows, the lead field matrix G may correspond to the original densely sampled source space, or any of the cortical patch decomposition models. In the latter case, the superscripts are dropped for notational convenience.
1) Time series vs. single observations
The first issue can be handled in a straightforward fashion. Noting that the log-likelihood of the observation Y given X is of the form
| (9) |
all the operations carried out for a single time step can be generalized by mapping the absolute value operator | ⋅ | : ℝ ↦ ℝ to the operator in the whitened model. This choice ensures that the greedy algorithm selects sources with overall high activity during the observation interval, rather than selecting a new set of sources at each time instance.
2) Suitable proxy signal for greedy estimation
The first virtue of RIP for SP is that the proxy signal provides a faithful representative of the undiscovered components of the signal. However, the lead field matrix G does not satisfy the RIP requirements since the columns of G are highly correlated. Therefore, given a generic residual R in the whitened model, the proxy prescribed by the SP as P = G̃′R is not a faithful representative of the unidentified signal components. In fact, this proxy tends to favor superficial dipoles which have higher sensitivities. Moreover, since the proxy is computed repeatedly across iterations, any alternative proxy should be a low-complexity mapping from the sensor space to the source space that faithfully represents the unidentified signal components. These considerations lead us to choose the MNE mapping as a modified proxy, i.e.,
| (10) |
The MNE mapping corrects for the mismatch in the norms of the lead fields and is also quite low-cost to compute.
3) Enforcing incoherence during greedy pursuit
The second virtue of RIP for SP is the fact that the columns of A corresponding to the support of x form a nearly orthogonal basis. A closely related concept in compressive sampling is given by the mutual coherence of the columns of a given measurement matrix (Bruckstein et al., 2009). The mutual coherence of two columns Ai and Aj, for i ≠ j, is defined as
| (11) |
It can be shown that if μij ≤ μ, for all i and j, i ≠ j, and if μ is small enough, then the matrix A, with appropriate column normalization, satisfies the RIP of a desired order (Giryes and Elad, 2012). In the context of MEG, the columns of the lead field matrix G consist of the magnetic fields and gradients generated by a given cortical dipole at the locations of the MEG sensors. Therefore, two dipoles with similar orientations and locations may generate a very similar lead field and hence the mutual coherence of the columns of G can be unfortunately close to unity. Inspection of the mutual coherence of the columns of G with regard to the location of the corresponding dipoles reveals that on average, the farther two dipoles are, the less coherent their lead fields will be. Therefore, restricting the columns of G to a set with a bounded mutual coherence μ can be interpreted as a constraint on the target spatial resolution of the inverse problem. This observation motivates us to modify the identification step of the SP algorithm so that new components are merged to the current support only if the resulting set of lead fields has mutual coherence values sufficiently below 1.
Given the above modifications, a SP-based algorithm for MEG source localization is formally given as Algorithm 2. Note that one major difference between the SP–MNE algorithm and the SP algorithm corresponds to the initialization and identification steps, where the new components need to satisfy an incoherence criterion with respect to the current support. In Appendix C we present a fast routine to carry out this step.
|
|
| Algorithm 2 SP-MNE (Y, C, G, μ, s) |
|
|
Initialization: Let Ỹ = C-1/2Y and G̃ = C-1/2G. let
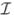 (0) be the index set corresponding to the s largest ℓ2-norm rows of the proxy matrix P(0) ≔ XMNE(Ỹ, G̃) greedily chosen such that the corresponding columns of G have a mutual coherence bounded by μ, and let R(0) be the initial residual error given by
. (0) be the index set corresponding to the s largest ℓ2-norm rows of the proxy matrix P(0) ≔ XMNE(Ỹ, G̃) greedily chosen such that the corresponding columns of G have a mutual coherence bounded by μ, and let R(0) be the initial residual error given by
. |
| Iteration: |
| 1: Identification and support merging: set ∪ {s indices corresponding to the largest ℓ2 norm rows of the proxy matrix P(ℓ)≔ XMNE(R(ℓ-1), G̃) greedily chosen such that the corresponding columns of G have a mutual coherence bounded by μ. |
| 2: Estimation: set . |
3: Support trimming: set
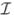 (ℓ)={s indices corresponding to the largest ℓ2-norm rows of the estimate Z(ℓ)}. (ℓ)={s indices corresponding to the largest ℓ2-norm rows of the estimate Z(ℓ)}. |
| 4: Residual update: set . |
5: Halting criterion: if
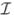 (ℓ) equals (ℓ) equals
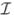 (k) for some k < ℓ, set (k) for some k < ℓ, set
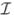 (ℓ) = (ℓ) =
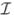 (k) and quit the iteration. (k) and quit the iteration. |
Output: the final estimate XˆSP-MNE(Y, C, G, μ, s) ≔ XMNE(Ỹ, G̃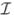 (ℓ)). (ℓ)). |
A useful variant of the SP–MNE algorithm can be obtained by substituting all instances of the MNE algorithm with the MNE–EM.
2.7. The SPIGH Algorithm
The SP–MNE algorithm can be combined with the hierarchy of cortical patch decompositions in order to construct a fast and efficient source localization algorithm. The key idea is to first obtain a preliminary estimate over a very coarse source space, in which the cortical activity is most likely highly sparse, e.g.
 1, and then move on to a finer source space, e.g.
1, and then move on to a finer source space, e.g.
 2, and compute the inverse solution over a neighborhood of the support of the estimate obtained over the coarser source space (
2, and compute the inverse solution over a neighborhood of the support of the estimate obtained over the coarser source space (
 1, in this case). In this manner, one can systematically refine the support of the estimate until reaching a desired resolution. Figure 2 shows a schematic depiction of this procedure. The resulting algorithm is denoted by the Subspace Pursuit-based Iterative Greedy Hierarchical (SPIGH) inverse solution and is formally summarized as Algorithm 3. The SPIGH algorithm inputs the observation matrix Y, the noise covariance C and the reduced-order lead fields
with the respective incoherence bounds
and sparsity levels
, and outputs the inverse solution over the source space S4.
1, in this case). In this manner, one can systematically refine the support of the estimate until reaching a desired resolution. Figure 2 shows a schematic depiction of this procedure. The resulting algorithm is denoted by the Subspace Pursuit-based Iterative Greedy Hierarchical (SPIGH) inverse solution and is formally summarized as Algorithm 3. The SPIGH algorithm inputs the observation matrix Y, the noise covariance C and the reduced-order lead fields
with the respective incoherence bounds
and sparsity levels
, and outputs the inverse solution over the source space S4.
Figure 2.
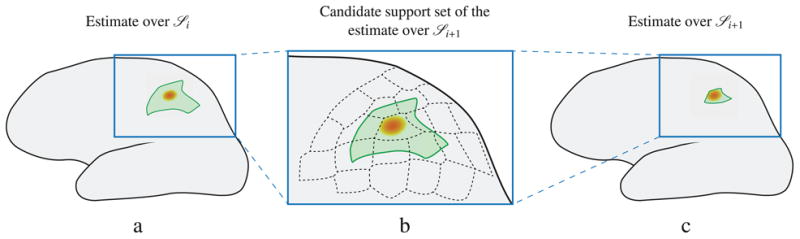
Schematic depiction of the systematic estimation refinement carried out by the SPIGH and SPIGH–EM algorithms across the hierarchy of source spaces. The orange patch shows the active region. a) the solid green closed curve shows the boundary of the estimate obtained by SP–MNE over the coarse source space
 i. b) the dashed black closed curves show the candidate support set for the estimate over
i. b) the dashed black closed curves show the candidate support set for the estimate over
 i+1, which consists of all the patches in
i+1, which consists of all the patches in
 i+1 contained in the estimate over
i+1 contained in the estimate over
 i and their nearest neighbors. c) the solid green closed curve shows the estimate obtained by SP–MNE over the finer source space
i and their nearest neighbors. c) the solid green closed curve shows the estimate obtained by SP–MNE over the finer source space
 i+1.
i+1.
Note that by iteratively refining the support of the signal, the SPIGH algorithm has the potential to decrease the mismatch between the source model and the true activity. Also, note that by replacing the MNE instances in the SP–MNE by the MNE–EM algorithm, a similar algorithm can be obtained, which we denote by SPIGH–EM. Apart from providing sparse solutions to the MEG inverse problem, a highly favorable virtue of the SPIGH inverse solution is its extremely low computational complexity. In Appendix B, we show that the computational complexity of SPIGH is comparable to that of MNE, in the low sparsity regime. Specific running times for our simulation studies are reported in Section 3, which confirm the very low complexity virtue of the SPIGH algorithm.
|
|
| Algorithm 3 SPIGH a |
|
|
Initialization: Let Ỹ = C−1/2Y and G̃ ≔ C−1/2G. Set
 1 := {1, 2, … , p1|S1|}, where p1 is the number of eigenmodes per patch in 1 := {1, 2, … , p1|S1|}, where p1 is the number of eigenmodes per patch in
 1. 1. |
| For i = 1, 2, · · · , 3 do: |
1: Estimate the cortical activity as
with the si-sparse support
 i ⊂ i ⊂
 i. i. |
2: Set
 i+1 = all the patches in i+1 = all the patches in
 i+1 overlapping i+1 overlapping
 i and their nearest neighbors in i and their nearest neighbors in  i+1, and go to step 1. i+1, and go to step 1. |
| End |
Output:
i.e., the final estimate is the MNE solution over the central dipoles given by the index set
 4. 4. |
2.8. Setting the parameters and initialization of SP–MNE and SPIGH
There are several parameters involved in the MNE, MNE–EM, SP–MNE and SPIGH algorithms, which need to be carefully chosen or estimated. We will discuss the choice of these parameters in this section. The estimation and regularization of the observation noise covariance and the selection of parameters for MNE also require some technical care; we describe these details in Appendix D.
The main parameters of the SP–MNE algorithm are s and μ. The sparsity level s can be chosen based on prior knowledge of the data under study. If no such knowledge is available, one can proceed with a traditional model selection procedure, by starting with s = 1 and increasing s until the change in the residual of the final estimates is no longer significant. By exhaustive simulation studies as well as analysis of real data sets, we have come up with a systematic heuristic for choosing the sparsity levels si. For the first iteration of SPIGH over
 1, we choose the sparsity level based on neurophysiological priors on the problem at hand. For instance, given the prior knowledge that the region of interest lies within the somatosensory cortex, the target sparsity level over the source space
1, we choose the sparsity level based on neurophysiological priors on the problem at hand. For instance, given the prior knowledge that the region of interest lies within the somatosensory cortex, the target sparsity level over the source space
 1 can be chosen to be s1 =4, since the somatosensory cortices of both hemispheres can be covered with 4 cortical patches in
1 can be chosen to be s1 =4, since the somatosensory cortices of both hemispheres can be covered with 4 cortical patches in
 1 (each with an average area of ∼24 cm2, with reference to a cortical surface with a normalized area of 1000 cm2). Next, for the subsequent source spaces
1 (each with an average area of ∼24 cm2, with reference to a cortical surface with a normalized area of 1000 cm2). Next, for the subsequent source spaces
 i+1, we choose the target sparsity to be twice the number of cortical patches identified by the SP–MNE algorithm over the previous source space
i+1, we choose the target sparsity to be twice the number of cortical patches identified by the SP–MNE algorithm over the previous source space
 i (note that the patch diameters double as one moves down to a finer source space). We will discuss specific instances of this heuristic, denoted by doubling heuristic hereafter, and its utility in Section 3.
i (note that the patch diameters double as one moves down to a finer source space). We will discuss specific instances of this heuristic, denoted by doubling heuristic hereafter, and its utility in Section 3.
The parameter μ can be chosen by inspection of the statistics of the coherence of the lead fields. It can be shown that on average, the farther two dipoles are, the smaller their mutual coherence would be. We selected a random ensemble of 100 dipoles for each source space, and computed the average mutual coherence of each dipole with its neighbors at a distance d. The maximum average mutual coherence was taken among the ensemble for each distance d. Then, we chose the value of the average mutual coherence corresponding to the average distance. This way, the final threshold μ can be viewed as the average worst-case mutual coherence of two randomly selected dipoles in the source space. Intuitively speaking, this choice of μ rejects the worst-case mutual coherence of two randomly selected dipoles. Nevertheless, the SPIGH algorithm seems to be robust to the choice of μ, as long as it is close to the average worst-case mutual coherence of the lead field matrix. We will discuss the specific numerical choices of μ obtained from realistic lead field matrices in the results section. In a nutshell, our empirical results show that μ ≈ 0.5 is a suitable choice, independent of the source space.
2.9. Recording and simulation setup
Data from MEG experiments were acquired inside an electromagnetically shielded room at the Martinos Center for Biomedical Imaging (Charlestown, MA, U. S. A.) using a dc-SQUID Neuromag Vectorview system (Elekta Neuromag, Helsinki, Finland). The 306-channel array consisting of 2 planar gradiometers and 1 magnetometer, at each of 102 sensor locations, was also employed in the simulation studies. For precise co-registration with the MRIs, 4 HPI coils were used to register the position of the subject's head relative to the SQUID sensors, and all anatomical landmarks and electrode locations were digitized using the 3-Space Isotrak 2 system. Studies were conducted with the approval of the Human Research Committee at the Massachusetts General Hospital.
Cortical surfaces were reconstructed from high-resolution MRIs and subsequently triangulated using the Freesurfer software. At each vertex in the densely sampled cortical mesh (∼300, 000 vertices), elementary dipoles were positioned with fixed orientations given by the local normal vectors over the surface. The MNE software package was used to compute the forward solutions using an MRI-derived single-compartment boundary-element model (BEM). All dipoles within 5mm of the inner-skull bounding surface were omitted from the lead field computations to avoid numerical inaccuracies that could potentially affect the dipole activity estimates.
We constructed three cortical patch decomposition models
 1,
1,
 2, and
2, and
 3, tiling both hemispheres with fixed geodesic radius and with average surface area of approximately 2380, 620, and 160 mm2, respectively, with reference to a cortical surface with a normalized area of 1000 cm2. As described in Appendix A, for the source spaces
3, tiling both hemispheres with fixed geodesic radius and with average surface area of approximately 2380, 620, and 160 mm2, respectively, with reference to a cortical surface with a normalized area of 1000 cm2. As described in Appendix A, for the source spaces
 1,
1,
 2, and
2, and
 3 we approximated each patch using p1 = 4, p2 = 3 and p3 = 2 eigenmodes, respectively. The value of the mutual coherence threshold μ for each source space was computed as described in Section 2.8.
3 we approximated each patch using p1 = 4, p2 = 3 and p3 = 2 eigenmodes, respectively. The value of the mutual coherence threshold μ for each source space was computed as described in Section 2.8.
For all the simulated patches of activity, the dipoles were spatially weighted across the active regions following an inverse parabolic trend with respect to the central dipole. In order to achieve a given SNR, we generated spatiotemporally white Gaussian noise with an element-wise variance of . For visualization purposes, estimates from all the somatosensory evoked fields data sets were smoothed using a moving average window of length 10 ms, chosen sufficiently small compared to the temporal variations in the underlying signals. Finally, the cortical color maps were created using the whole range of the estimated dipole amplitudes (in nAm), with bright yellow and bright blue corresponding to the maximum and minimum values, respectively.
3. Results
In order to evaluate the performance of the SPIGH algorithm in localizing both focal and spatially distributed activity across the human brain cortex, as compared to the MNE and MNE–EM algorithms, a number of realistic simulations and experimental data sets were employed. We first evaluate the response of the SPIGH algorithm to focal simulated patches of activity randomly chosen over the cortex, and examine its performance on a real data set of focal activity corresponding to spontaneous mu-rhythms. Then, using both simulated and real data corresponding to somatosensory evoked fields (SEFs) from right median nerve stimulation, we assess the algorithm's localization accuracy for spatially-distributed sources.
3.1. Localization of focal cortical activity: a simulation study
A total of 180 MEG recordings were simulated to evaluate the spatiotemporal performance of the MNE, MNE–EM, SPIGH and SPIGH–EM (a variant of SPIGH where the underlying MNE subroutines are replaced by MNE–EM) inverse solutions. Twenty cortical patches with an average radius of ∼ 7mm were randomly chosen over the entire cortical mantle. Ten Hertz sinusoidal waveforms (sampled at 200Hz over a period of 1s) with dipole moments in the range of 5–10 nAm were assigned to each discrete dipole location within the cortical patches. For each simulated patch of activity, MEG recordings were generated according to the observation model of Eq. (1), corresponding to SNR values in the range ∓12dB with 3dB spacings. A constant target sparsity level of , was used for the SPIGH and SPIGH–EM algorithms.
We propose two measures of localization performance for simulated focal activity denoted by localized energy ratio and localization resolution. The localized energy ratio is defined as the fraction of the energy of the estimate that lies within a 5mm margin of the true patch of activity (denoted hereafter by relaxed region of activity), measured in dB. The localization resolution is defined as the distance between the dipoles with maximum energy located within the true and estimated regions of activity.
Figure 3 shows the localized energy ratio as a function of SNR. On average, for an SNR of 6dB (typical for MEG source localization) approximately 74% and 50% of the energy of the SPIGH–EM and SPIGH estimates is allocated to the relaxed regions of activity, respectively. On the other hand, MNE–EM and MNE assign only about 27% and 5% of the estimated energy to the corresponding regions, respectively. Table 1 summarizes the average localization resolution and run time (using a 12–core Xeon workstation) of the four algorithms over the ensemble of simulated focal activity. On average, not only do the SPIGH–EM and SPIGH algorithms provide more than 50% of computational savings compared to MNE–EM and MNE, respectively, but they also yield a considerable increase in resolution.
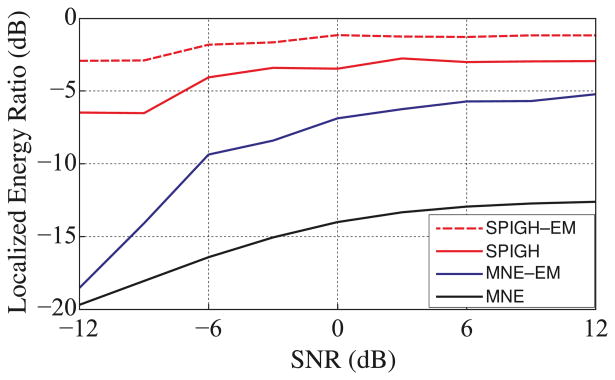
Figure 3.
The ensemble averaged localized energy ratio within a 5mm margin of the true activity (relaxed region) vs. SNR. The SPIGH–EM and SPIGH algorithms provide a 5–10 dB improvement in the localized energy ratio on average over MNE–EM and MNE, respectively. In particular, for SNR = 6dB, on average SPIGH–EM and SPIGH allocate 74% and 50% of the energy of the estimate to the relaxed region of activity, respectively, whereas MNE–EM and MNE on average allocate only about 27% and 5% of the energy to the corresponding regions, respectively.
Table 1.
Average localization resolution and run time of SPIGH–EM, SPIGH, MNE–EM, and MNE algorithms over the simulated ensemble for SNR = 6dB. The localization resolution is defined as the distance between the dipoles with maximum energy in the true and estimated regions of activity. The SPIGH–EM and SPIGH algorithms on average have ∼ 1 cm higher localization resolution than MNE–EM and MNE, respectively. Moreover, SPIGH–EM and SPIGH provide more than 50% of saving in computational complexity as compared to MNE–EM and MNE, respectively.
| SNR=6dB | Resolution (mm) (Mean ± Std.) |
Run time (s) (Mean ± Std.) |
|---|---|---|
| SPIGH–EM | 14 ± 13 | 62.210 ± 8.632 |
| SPIGH | 17 ± 11 | 0.174 ± 0.081 |
| MNE–EM | 23 ± 11 | 160.922 ± 0.242 |
| MNE | 24 ± 12 | 0.440 ± 0.014 |
A cortical snapshot of simulated and estimated dipole activity (for SNR = 6dB) from a patch located in the left occipital cortex is shown in Figure 4. Figures 4–a–1 and 4–a–2 show the spatial configuration and the magnetic field map of the simulated activity. Figures 4–b–1 through 4–b–3 show progression of the SPIGH–EM algorithm applied to the source spaces
 1 through
1 through
 3, respectively, and projected onto the source space S7. The inverse solutions provided by SPIGH–EM, MNE–EM, and MNE are depicted in Figures 4–c through 4–e, respectively. From the figure, one can clearly see that the SPIGH–EM algorithm is much more effective in localizing the power of the activity estimates. In particular, the MNE–EM and MNE inverse solutions underestimate the energy of the true activity by 2 and 3 orders of magnitude, respectively. For the given active region, the cortical map corresponding to the SPIGH algorithms highly resembles that of the SPIGH–EM algorithm, and is thus omitted for brevity. Note that the amplitudes of the intermediate estimates in Figures 4–b–1 through 4–b–3 are about two orders of magnitude smaller than those of the final SPIGH–EM estimate shown in Figure 4–c, due to the projection onto the densely sampled source space S7.
3, respectively, and projected onto the source space S7. The inverse solutions provided by SPIGH–EM, MNE–EM, and MNE are depicted in Figures 4–c through 4–e, respectively. From the figure, one can clearly see that the SPIGH–EM algorithm is much more effective in localizing the power of the activity estimates. In particular, the MNE–EM and MNE inverse solutions underestimate the energy of the true activity by 2 and 3 orders of magnitude, respectively. For the given active region, the cortical map corresponding to the SPIGH algorithms highly resembles that of the SPIGH–EM algorithm, and is thus omitted for brevity. Note that the amplitudes of the intermediate estimates in Figures 4–b–1 through 4–b–3 are about two orders of magnitude smaller than those of the final SPIGH–EM estimate shown in Figure 4–c, due to the projection onto the densely sampled source space S7.
Figure 4.
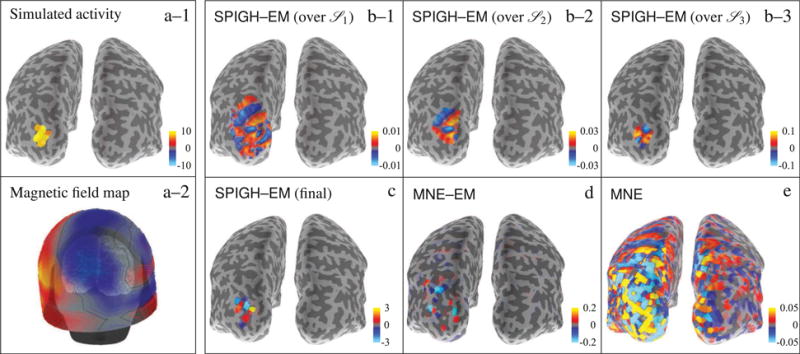
Cortical maps of different inverse solutions for a simulated patch of activity in the occipital cortex of the left hemisphere. The units of the color bars are in nAm. (a–1) simulated activity mapped to
 4, (a–2) magnetic field map over the MEG helmet, (b–1)–(b–3) SPIGH–EM estimates over
4, (a–2) magnetic field map over the MEG helmet, (b–1)–(b–3) SPIGH–EM estimates over
 1–
1–
 3, respectively, projected onto the densely sampled source space S7 (c) final SPIGH–EM estimate over S4, (d) MNE–EM estimate over S4, and (e) MNE estimate over S4. For this occipital patch of activity, the SPIGH estimate is identical to that of SPIGH–EM. We therefore omit the SPIGH estimate for brevity.
3, respectively, projected onto the densely sampled source space S7 (c) final SPIGH–EM estimate over S4, (d) MNE–EM estimate over S4, and (e) MNE estimate over S4. For this occipital patch of activity, the SPIGH estimate is identical to that of SPIGH–EM. We therefore omit the SPIGH estimate for brevity.
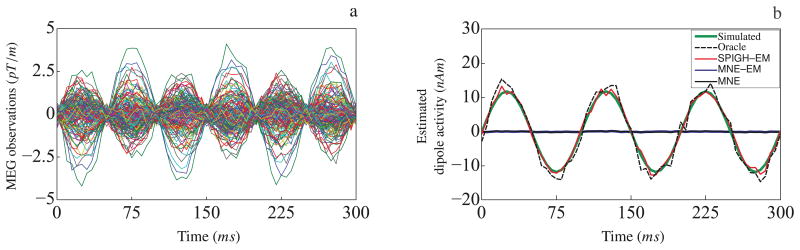
Finally, Figure 5 shows the temporal performance of the different inverse solutions for the same patch of simulated activity. Figure 5–a shows the first 300ms of the simulated MEG observations (gradiometer traces). Figure 5–b shows the corresponding time traces of the estimated dipole with the maximum energy for each inverse solution. We have included an Oracle estimate as a performance benchmark, which corresponds to the MNE–EM solution restricted to the true support of the simulated activity. As it can be observed from Figure 5–b, the SPIGH–EM solution closely resembles the time trace of the Oracle estimate, as well as the true simulated activity. MNE–EM and MNE, on the other hand, significantly underestimate the energy of the true activity. Once again, the SPIGH time traces are omitted for brevity, since they closely resemble those of SPIGH–EM.
Figure 5.
Temporal performance of different inverse solutions for a simulated patch of activity in the occipital cortex of the left hemisphere. (a) The first 300ms of the simulated MEG observation (gradiometer traces), (b) the corresponding time traces of the dipoles with the maximum energy for each estimate. The SPIGH–EM solution closely resembles the time trace of the Oracle estimate as well as the true activity, whereas MNE–EM and MNE significantly underestimate the energy of the simulated activity.
3.2. Localization of focal spontaneous brain activity: real data analysis
Next, we evaluate the performance of the SPIGH inverse solution on a real data set corresponding to spontaneous mu-rhythms recorded from a human subject. Magnetic brain activity was recorded during the following multi-condition experiment: (1) subject at rest with eyes closed, (2) at rest with eyes open, and (3) during sustained finger movement with eyes open. The recordings were digitized at 600Hz, minimally band-pass filtered in the range 0.1–200Hz, and finally down-sampled to 200Hz. The mu-rhythm represents activity close to 10 and 20Hz in the somatomotor cortex, and is known to reflect resting states characterized by lack of movement and somatosensory input (Long et al., 2011). The data was visually examined for segments with bursts of spontaneous activity, revealing strong periods of mu-rhythm during the resting conditions and suppressed activity during repeated finger motion. Accordingly, 1s of raw data with high-amplitude mu-oscillations was selected for source localization. MEG empty-room recordings were used to estimate the observation noise covariance (See Appendix D for the details of the noise covariance estimation and processing).
Empirically, we observed that the MNE–EM algorithm performs stably only when the noise covariance matrix is well-conditioned and close to diagonal. Given the noise covariance estimates depicted in Appendix D, one can clearly see that this condition holds true only for the subset of gradiometer channels, for the magnetometers are highly correlated in space. Consequently, we selected the subset of sensors corresponding to the gradiometers for source localization using the MNE–EM algorithm. Similarly, in order to avoid stability issues, we only applied the SPIGH algorithm to the real data, which does not require the MNE–EM algorithm.
The parameter μ for the SPIGH algorithm was chosen as μ ≈ 0.5. Based on prior knowledge of the focal nature of mu-rhythms and inspection of the topographical mapping of the MEG observations, we chose a target sparsity of s1 = 1 over the source space
 1, for we predicted that only one cortical patch in
1, for we predicted that only one cortical patch in
 1 with average area of ∼ 24 cm2 (with reference to a cortical surface with a normalized area of 1000 cm2) would sufficiently cover the active region on the left hemisphere (left somatomotor cortex). Using the doubling heuristic outlined in Section 2.8, the target sparsity levels of s2 = 2 and s3 = 4 where used in the subsequent source spaces,
1 with average area of ∼ 24 cm2 (with reference to a cortical surface with a normalized area of 1000 cm2) would sufficiently cover the active region on the left hemisphere (left somatomotor cortex). Using the doubling heuristic outlined in Section 2.8, the target sparsity levels of s2 = 2 and s3 = 4 where used in the subsequent source spaces,
 2 and
2 and
 3, respectively.
3, respectively.
Figure 6 shows the cortical maps of the inverse solutions given by SPIGH, MNE–EM, and MNE. The estimate given by SPIGH is highly focal to the left somatomotor cortex and matches functional regions identified in previous studies conducted using the same MEG recordings (Lamus et al., 2012), whereas the MNE–EM and MNE solutions are widely distributed. Moreover, the dipoles corresponding to the SPIGH estimate (within its full dynamic range) have one order of magnitude more energy than the corresponding MNE–EM and MNE dipoles, as predicted by our focal activity simulation studies.
Figure 6.
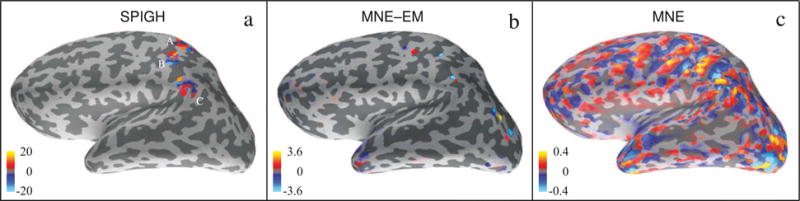
Cortical maps of different inverse solutions for spontaneous mu-rhythm activity. The units of the color bars are in nAm. (a) SPIGH, (b) MNE–EM, and (c) MNE.
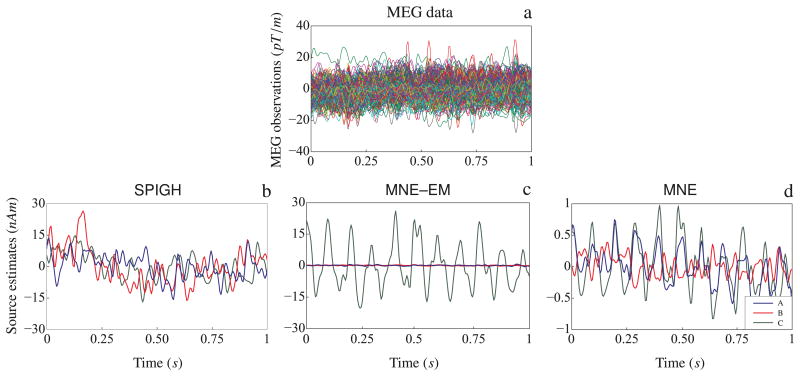
As shown in Figure 6–a, the SPIGH estimates in the source space S4 were finally clustered into 3 distinct groups (A, B, and C) via the k-means clustering algorithm. Figure 7–a shows the MEG observations employed for source localization (gradiometer traces). Figures 7–b through 7–d show the time traces of the dipoles with maximum amplitude in each of the identified clusters, for the SPIGH, MNE–EM and MNE estimates, respectively. The SPIGH estimates are one order of magnitude larger than the MNE estimates, which is consistent with our focal activity simulation study. MNE–EM, on the other hand, identifies one high amplitude dipole in one of the clusters, but significantly underestimates the activity in the other two.
Figure 7.
Time traces of the mu-rhythms identified by different inverse solutions. (a) MEG observations. For each of the clusters A, B and C shown in Figure 6–a, the time trace of the dipole with maximum amplitude is depicted for (b) SPIGH, (c) MNE–EM, and (d) MNE.
3.3. Localization of somatosensory evoked fields: a simulation study
In order to assess the performance of our proposed algorithm for the localization of spatially-distributed sources, we simulated an MEG experiment corresponding to SEFs from right median nerve stimulation. Cortical patches with an average radius of ∼14 mm were constructed over the following functional regions: contralateral primary somatosensory cortex (cS1), contralateral secondary somatosensory cortex (cS2), and ipsilateral secondary somatosensory cortex (iS2). Additionally, a smaller patch of radius ∼ 7 mm was formed over the posterior parietal cortex (PPC) of the left hemisphere. MEG measurements (250 ms with a sampling rate of 1kHz) with dipole moments in the range of 10–20 nAm were simulated across each of the four regions by combining a series of Gabor atoms of the form A exp (− (t − t0)2/2σ2), where A, t0 and σ2 stand for the amplitude, delay and width of each SEF component. The MEG observations were generated using an SNR of ∼7dB, with a diagonal observation noise covariance.
We only present the results for the SPIGH–EM algorithm, for under a near-diagonal noise covariance, replacing the MNE algorithm by MNE–EM in the SP–MNE routine yields an enhanced inverse solution. For the SPIGH–EM algorithm, the mutual coherence parameter μ is computed as described in Section 2.8, which gives a value of μ ≈ 0.5 for all the source spaces. The target sparsity level over the source space
 1 is chosen to be s1 =4, since the somatosensory cortices of both hemispheres can be covered with 4 cortical patches in
1 is chosen to be s1 =4, since the somatosensory cortices of both hemispheres can be covered with 4 cortical patches in
 1 (with an average area of ∼ 24 cm2 with reference to a cortical surface with a normalized area of 1000 cm2). The subsequent sparsity levels were chosen according to the doubling heuristic outlined in Section 2.8, and gives the values of s2 = 6 and s3 = 12.
1 (with an average area of ∼ 24 cm2 with reference to a cortical surface with a normalized area of 1000 cm2). The subsequent sparsity levels were chosen according to the doubling heuristic outlined in Section 2.8, and gives the values of s2 = 6 and s3 = 12.
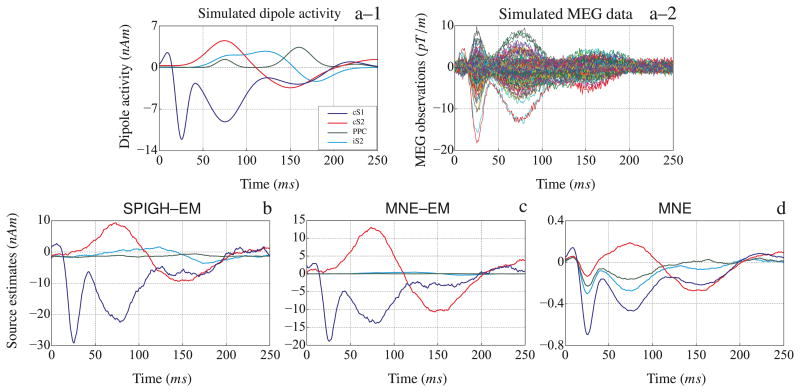
The cortical map of the estimates of the three inverse solutions is shown in Figure 8. Figure 8–a shows the cortical map of the simulated activity in each of the four cortical regions. The SPIGH–EM estimate is shown in Figure 8–b, which closely resembles the true simulated activity both in terms of spatial configuration and scale. Figures 8–c and 8–d show the spatial map of the estimates obtained by MNE–EM and MNE, respectively. Both algorithms underestimate the scale of the simulated activity, and blur the spatial localization of the four regions. In particular, the MNE–EM algorithm suppresses the activity in the iS2 cortex on the right hemisphere.
Figure 8.
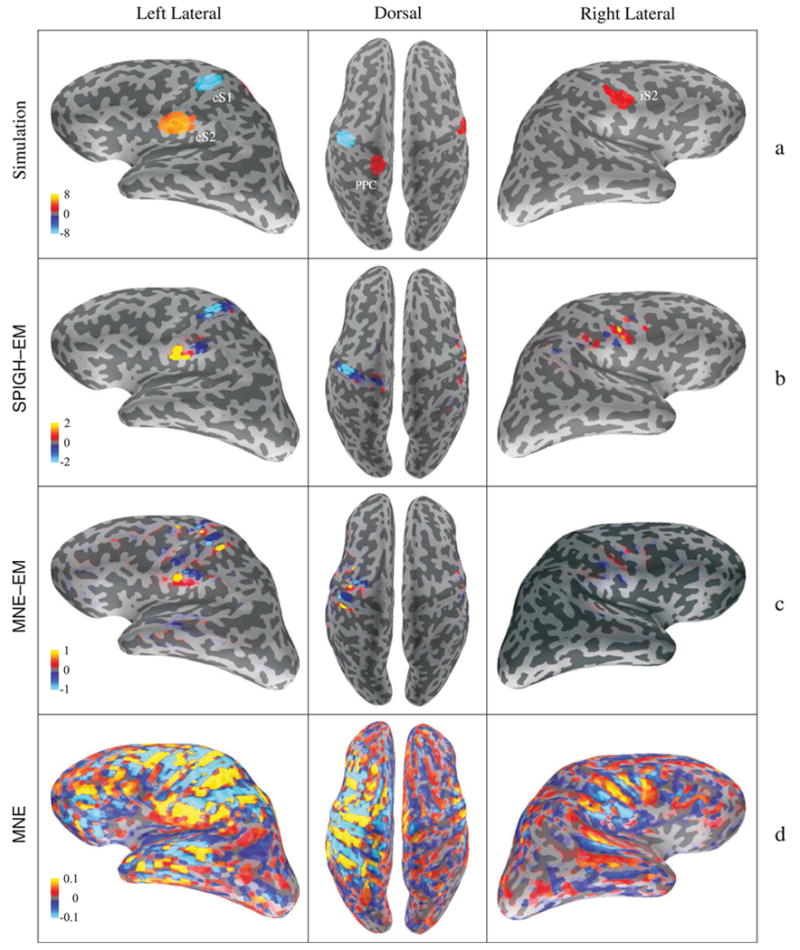
Cortical maps of the simulated and estimated somatosensory evoked fields. The units of all color bars are in nAm. The first, second and third columns correspond to the left lateral, dorsal, and right lateral views of the brain, respectively. (a) Simulated activity in the four cortical areas of cS1, cS2, PPC, and iS2. (b) SPIGH–EM estimates, (c) MNE–EM estimates, and (d) MNE estimates. The SPIGH estimate closely resembles the SPIGH–EM estimate, with similar and largely overlapping support and source values in the same range. We therefore omit the SPIGH estimate for brevity.
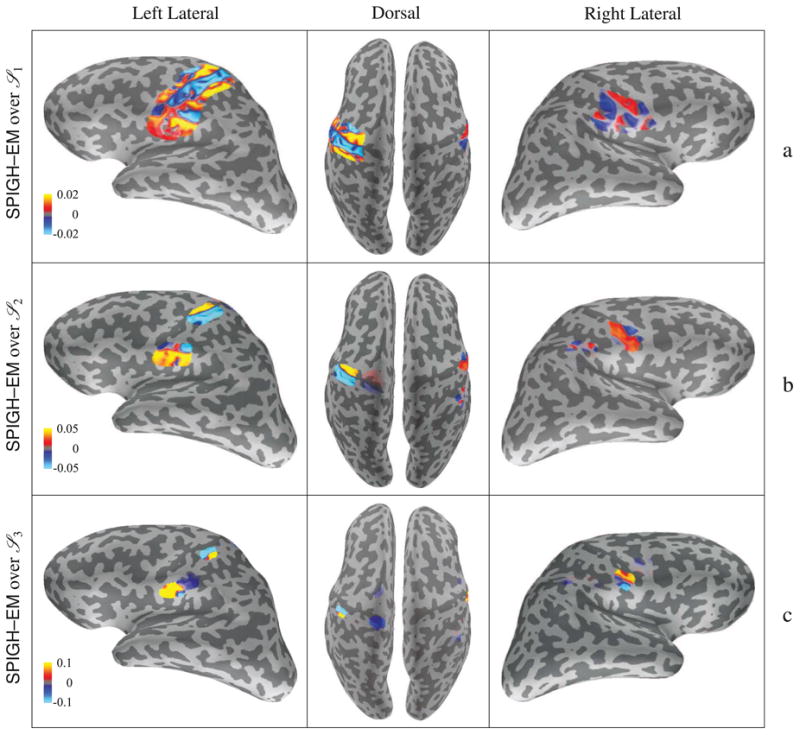
In Figures 9–a through 9–c, we show the progression of the SPIGH–EM estimates over the source spaces
 1 through
1 through
 3, respectively. As it can be seen in Figure 9–a, the estimate over the coarse source space
3, respectively. As it can be seen in Figure 9–a, the estimate over the coarse source space
 1 is able to spatially capture the location of the underlying activity. As the algorithm proceeds to finer source spaces
1 is able to spatially capture the location of the underlying activity. As the algorithm proceeds to finer source spaces
 2 (Figure 9–b) and
2 (Figure 9–b) and
 3 (Figure 9–c), the details of the spatial configuration of the estimate become closer to the simulated activity. Figure 9 also shows how the doubling heuristic for choosing the sparsity levels helps to increase the spatial resolution as the SPIGH–EM algorithm proceeds through finer source spaces.
3 (Figure 9–c), the details of the spatial configuration of the estimate become closer to the simulated activity. Figure 9 also shows how the doubling heuristic for choosing the sparsity levels helps to increase the spatial resolution as the SPIGH–EM algorithm proceeds through finer source spaces.
Figure 9.
Cortical map of the progression of the SPIGH–EM estimate over the source spaces (a)
 1, (b)
1, (b)
 2, and (c)
2, and (c)
 3, projected onto the densely sampled source space S7. The units of all the color bars are in nAm. As the SPIGH–EM algorithm proceeds through finer source spaces, the spatial resolution of the estimate increases. The SPIGH estimate follows a very similar progression, and hence is not shown for brevity.
3, projected onto the densely sampled source space S7. The units of all the color bars are in nAm. As the SPIGH–EM algorithm proceeds through finer source spaces, the spatial resolution of the estimate increases. The SPIGH estimate follows a very similar progression, and hence is not shown for brevity.
Figure 10–a–1 and 10–a–2 show the time traces of the dipoles with maximum energy in the active regions and the resulting MEG observations, respectively. Figures 10–b through 10–d show the time traces of the estimated dipoles with maximum energy within the relaxed regions around the simulated cortical patches for the SPIGH–EM, MNE–EM, and MNE algorithms, respectively. The SPIGH–EM algorithm recovers all four time traces within the scaling of the simulated activity. MNE–EM, however, only recovers two of the time traces within the original scales. Finally, the MNE algorithm underestimates the scale of the estimate by two orders of magnitude and the time traces estimated for the four different regions seem to be highly correlated.
Figure 10.
Source localization of the simulated somatosensory evoked fields from right median nerve stimulation. (a–1) Simulated dipoles with the maximum energy in contralateral primary somatosensory cortex (cS1), contralateral secondary somatosensory cortex (cS2), posterior parietal cortex (PPC), and ipsilateral secondary somatosensory cortex (iS2). (a–2) Simulated MEG observations (gradiometer traces) with an SNR of ∼ 7dB. The dipoles with the maximum energy within the relaxed regions around each of the four cortical areas, corresponding to the (b) SPIGH–EM, (c) MNE–EM, and (d) MNE estimates. The time traces in (b), (c) and (d) are smoothed with a rectangular window of duration 10 ms.
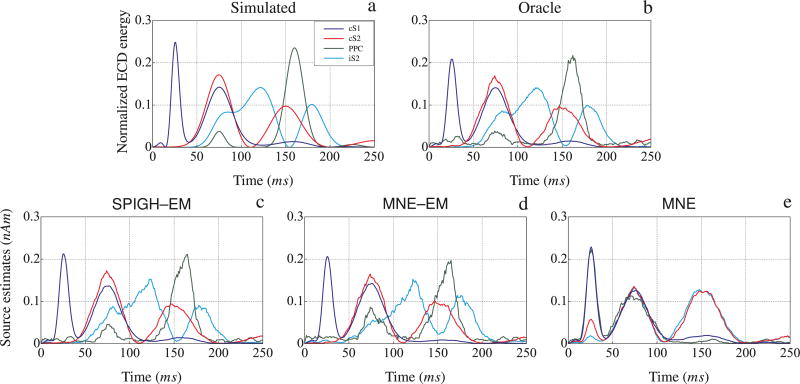
In addition to the above results, we evaluated the localization performance of the inverse solutions by computing the equivalent current dipole (ECD) energy within each of the four relaxed regions of activity. The ECD of a patch of activity is defined as the vector sum of all its dipoles. The energy of the ECD of each region is normalized to have a unit area under the curve. Figure 11 shows the ECD energy computed for the estimates of the SPIGH–EM, MNE–EM, and MNE algorithms, as well as those of the Oracle estimate and the true activity. In all four cortical regions, the ECD energies of the SPIGH–EM estimate, and to a lesser extent the MNE–EM, closely follow those of the Oracle estimate and true activity. The MNE algorithm, however, assigns a mixture of the underlying ECDs to the underlying cortical regions, and fails to capture the individual ECD energy waveforms.
Figure 11.
Normalized equivalent current dipole energy for the relaxed regions around cS1, cS2, iS2, and PPC vs. time, corresponding to the (a) simulated activity, (b) Oracle (MNE–EM restricted to the actual support of the activity), (c) SPIGH– EM, (d) MNE–EM, and (e) MNE estimates. The SPIGH–EM ECDs closely match those of the Oracle estimate, as well as the simulated activity. The traces are smoothed with a rectangular window of duration 10 ms.
Finally, it is worthy of mention that the computation time of the SPIGH–EM algorithm scales gracefully with the increased sparsity level, as compared to the focal simulation studies. In particular, the run-times of the MNE, MNE–EM, and SPIGH–EM algorithms on the SEF simulation were computed to be 0.456 s, 246.669 s, and 74.939 s, respectively. As expected, the SPIGH–EM algorithm is more than 3 times faster than its non-sparse counterpart.
3.4. Localization of somatosensory evoked fields: real data analysis
Next, we evaluate the performance of the different inverse solutions on a data set recorded from a human subject. Using an event-related design with random inter-stimulus intervals between 3–12s, the median nerve of the right wrist was electrically stimulated using current pulses slightly above the motor threshold and with 0.2 ms duration. The MEG recordings were acquired with a sampling rate of 1kHz and then band-pass filtered in the range 0.1–250Hz. A total of 17 epochs containing EOG signals with peak-to-peak amplitude below 150 μV were averaged offline with respect to stimulus onset.
The observation noise was estimated from raw data using 200 ms baseline segments prior to stimulus, and was then scaled by the effective number of averaged epochs (See Appendix D for details). As mentioned in Section 3.2, we selected the subset of sensors corresponding to the gradiometers for source localization using the MNE–EM algorithm. Moreover, in order to avoid stability issues, we only applied the SPIGH algorithm to the real data, which does not require the MNE–EM algorithm. The cortical maps of the different inverse solutions are shown in Figure 12. The SPIGH estimate (Figure 12–a) consists of focal clusters matching the known functional areas of cS1, cS2, iS2, and PPC, whereas the estimates given by MNE–EM (Figure 12–b) and MNE (Figure 12–c) are not clustered and smear the energy of their estimates over a large area of the cortex.
Figure 12.
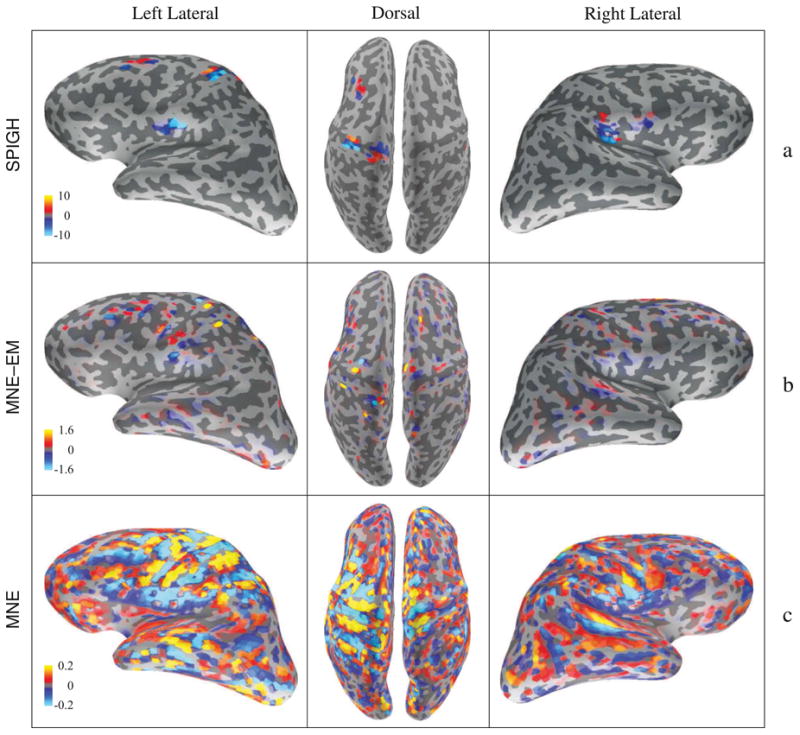
Cortical maps of the estimated somatosensory evoked fields. The units of all the color bars are in nAm. The first, second and third columns correspond to the left lateral, dorsal, and right lateral views of the brain. (a) SPIGH–EM estimates, (c) MNE–EM estimates, and (d) MNE estimates. The SPIGH estimates form focal clusters matching the known functional regions of cS1, cS2, iS2, and PPC.
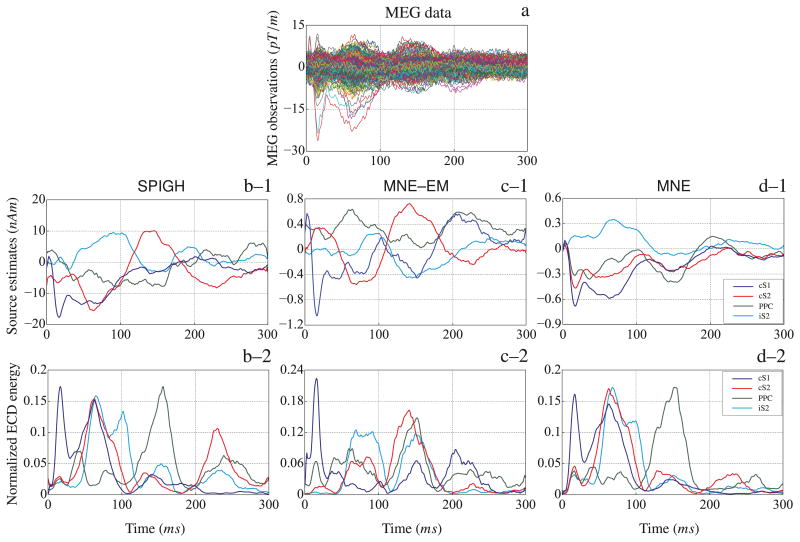
Figure 13–a shows the time traces of the MEG observations. We applied the SPIGH, MNE–EM, and MNE to localize the SEF sources. Using the k-means clustering algorithm, the SPIGH estimates were clustered into 4 groups matching the known cS1, cS2, iS2, and PPC functional areas. Figures 13–b–1 through 13–d–1 show the time traces of the dipoles with the maximum energy within the relaxed regions around the clusters identified by the SPIGH algorithm corresponding to the SPIGH, MNE–EM, and MNE estimates, respectively. The normalized ECD energies are shown in Figures 13–b–2 through 13–d–2, respectively. As it is implied from Figure 13, the SPIGH estimate has a higher energy than those of the MNE–EM and MNE. Moreover, the ECD energies corresponding to the SPIGH inverse solution seem fairly consistent with previous results, based on the same MEG recordings, presented in the source localization literature (Gramfort et al., 2011).
Figure 13.
Source localization of the somatosensory evoked fields from right median nerve stimulation. (a) MEG observations (gradiometer traces). The SPIGH estimate is clustered into four cortical areas using the k-means clustering algorithm, matching the known functional areas of cS1, cS2, iS2, and PPC. The dipoles with the maximum energy within each of the four cortical areas identified by the SPIGH algorithm are shown for the (b–1) SPIGH, (c–1) MNE–EM, and (d–1) MNE estimates. Similarly, the normalized ECD energy of the dipoles within the cortical areas identified by the SPIGH algorithm are shown for (b–1) SPIGH–EM, (c–1) MNE–EM, and (d–1) MNE estimates. The time traces in (b–1) through (d–2) are smoothed with a rectangular window of duration 10 ms.
Finally, as in the case of the SEF simulation study, the computational time of the SPIGH algorithm has a very favorable scaling with respect to the increased sparsity levels. The run-times of the MNE, MNE–EM (with only 204 gradiometers), and SPIGH were computed to be 0.368 s, 252.889 s, and 0.373 s, respectively. The SPIGH algorithm is more than 500 times faster than the MNE–EM algorithm, while being only 5 ms behind the MNE algorithm.
4. Discussion and Conclusion
In this work, we developed a greedy algorithm that iteratively solves the MEG inverse problem across a hierarchy of reduced-order source spaces and is highly effective in localizing the cortical activity throughout the cerebral cortex. The proposed algorithm, which he have named SPIGH, exhibits the low computational complexity inherent to sparse pursuit algorithms (Bruckstein et al., 2009), with computation time comparable to that of the widely-used MNE inverse solution. In addition, SPIGH provides a significant degree of flexibility in representing different configurations of sparse brain activity.
The novelty of our proposed hierarchical source space characterization is two-fold: on one hand, the nested source spaces allow a systematic refinement of the spatial resolution of the inverse solution, and on the other hand, they serve as a natural sparse representation basis for the cortical activity. Moreover, the proposed systematic refinement of spatial resolution through the hierarchical source space characterization fuses gracefully with the Subspace Pursuit algorithm, which is the estimation core of the SPIGH algorithm.
Although alternative models such as the equivalent current dipole model are present in the literature (Mosher et al., 1992; Uutela et al., 1998; Bertrand et al., 2001; Somersalo et al., 2003; Jun et al., 2005; Kiebel et al., 2008; Campi et al., 2008), they do not provide an accurate description of spatially distributed sources of cortical activity. The cortical patches and the corresponding basis functions that make up the cortical patch decomposition model are independent of the measured data and are solely based on the forward solution and on the topology of the cortical mantle. As depicted in Figure 1, the disjoint cortical patch lead fields clearly admit a low rank approximation across varying patch sizes. As a result, the reduced-order source spaces employed in this work have a cardinality proportional to the number of MEG sensors, and are up to ∼ 103 times more economical than the traditional densely-sampled source space. Hence, the reduced-order cortical patch decomposition model has a significant impact on reducing the ill-posed nature of the inverse problem, while only causing a negligible loss in the representation accuracy.
The SPIGH algorithm generalizes the applicability of a class of pursuit algorithms to sparse MEG source localization. Such a generalization is not straightforward due the intrinsically correlated measurement structure of MEG. Therefore, we have carefully modified the standard sparse pursuit algorithms by adopting and exploiting the structure of the MEG lead field matrix. To this end, we have restricted the greedy pursuit to sources which satisfy a degree of incoherence in the sensor space. An inevitable drawback of this modification is that the enforced incoherence in the sensor space translates to a limited spatial resolution in the source space. However, this limitation seems to stem from the fundamental biophysics of the MEG forward problem, namely, the tendency for scalp magnetic field observations to be spatially blurred even for very focal underlying sources. The resulting algorithm has a very low computational complexity, thanks to both the economical source space characterization and the greedy nature of the estimation framework. This makes the SPIGH algorithm appealing for large MEG data sets.
We have designed comprehensive simulation studies to evaluate the performance of the SPIGH algorithm in localizing focal sources of cortical activity. These studies reveal that our proposed algorithm enjoys, 1) significant robustness with respect to the SNR level, 2) high spatial resolution (∼ 1 cm), and 3) very low computational time. Application of the SPIGH algorithm to localizing focal spontaneous brain activity from real human data confirms the predictions of our simulation studies. In addition, we have designed a realistic simulation study for evaluating the performance of the proposed algorithm in localizing SEFs. In this case, the cortical activity comprises several distinct functional areas in the somatosensory cortices of both hemispheres. The SPIGH algorithm yields a highly accurate spatiotemporal localization of the underlying cortical activity comparable to an Oracle estimator (which has a priori information about the exact support of the cortical activity). Interestingly, the computation time of the SPIGH algorithm scales almost linearly with the number of active sources, and hence is comparable to that of the MNE inverse solution. Ultimately, we evaluate the performance of the SPIGH algorithm in localizing somatosensory evoked fields from median nerve stimulation recorded from a human subject. The solution provided by the SPIGH algorithm is consistent with previous results reported in the literature.
Another advantage of our proposed sparse MEG source localization technique applied to the localization of evoked fields is that the resulting inverse solution consists of fairly independent evoked field patterns. For instance, the estimate obtained by the widely-used MNE inverse solution in our somatosensory simulation study generates highly correlated evoked field waveforms (Figure 10–d), whereas the SPIGH algorithm is capable of discriminating the four distinct waveforms (Figure 10–b).
The promising performance of the proposed algorithm for MEG source localization makes it an appealing candidate for EEG applications, which is currently part of our work in progress. Finally, we have provided transparent prescriptions for setting the parameters of the proposed algorithm, as well as pre-processing of the MEG data, with the hope of facilitating the adoption of the SPIGH algorithm for MEG data analysis.
Highlights.
Cortical patch representation model with high accuracy and low complexity.
Adapting a well-established greedy pursuit algorithm to the MEG inverse problem.
Inverse solution with high localization accuracy and low computational complexity.
Performance evaluation through comprehensive and carefully designed simulations.
Performance evaluation using real human data (mu-rhythms and evoked fields).
Acknowledgments
This work was supported by National Institutes of Health (NIH) New Innovator Award DP2-OD006454 (to P.L.P.), R01-EB006385 (to E.N.B., M.S.H., and P.L.P.), and P41-RR014075-11 (to M.S.H.). We would like to thank Simona Temereanca for providing us with the mu-rhythm data used in this paper, and Alexandre Gramfort for constructive discussions regarding the SEFs experiment.
Appendix A. Cortical patch decomposition model
Consider the patches induced by the source space Si over S7. Let Ki denote the total number of patches induced by Si over S7, and let denote the set of patches. Hence, the observation model can be re-written as
| (A.1) |
where and denote the restriction of the lead field matrix G and the source activity matrix X to the vertices in the patch . Each matrix can be further approximated by its first few eigenmodes. That is, given the SVD of , the reduced-order approximation is given by
| (A.2) |
where pi is typically a small integer. Using the above approximation for all , one gets the reduced-order observation model
| (A.3) |
where
and
denotes the state space parameterization of the new model. We denote this reduced-order source space by
 i, and denote the corresponding observation model by the cortical patch decomposition model.
i, and denote the corresponding observation model by the cortical patch decomposition model.
The number of eigenmodes used for characterizing each patch establishes a tradeoff between the accuracy of representation and the ability to differentiate separate patches. While capturing the essential features of the spatial cortical activity the cortical patch decomposition model results in a considerable reduction in the state-space dimension. For instance, consider the cortical patch decomposition model
 3, represented by the lead field matrix G(3), with p3 = 2. The dimension of this source space is p3K3 = 2568, which is much smaller than the dimension of S7. Additionally, the cortical patch decomposition model minimizes the representation error on average over any generic spatial distribution of cortical patch activity (Limpiti et al., 2006).
3, represented by the lead field matrix G(3), with p3 = 2. The dimension of this source space is p3K3 = 2568, which is much smaller than the dimension of S7. Additionally, the cortical patch decomposition model minimizes the representation error on average over any generic spatial distribution of cortical patch activity (Limpiti et al., 2006).
It is possible to characterize the accuracy of such an approximation by inspecting the spectral properties of the reduced order model. Given the SVD of with singular values sorted in the descending order, the normalized mean representation accuracy (NMRA) for patch is given by:
| (A.4) |
which represents the fraction of the spectral energy of
captured by its largest pi eigenmodes (Limpiti et al., 2006). We choose the number of eigenmodes per patch for each source space to achieve an NMRA value of at least 90% for all the cortical patches. Figure A.14 shows the histograms of NMRA values computed for the cortical patch lead fields of source spaces
 1,
1,
 2, and
2, and
 3, with respective number of eigenmodes per patch given by p1 = 4, p2 = 3, and p3 = 2.
3, with respective number of eigenmodes per patch given by p1 = 4, p2 = 3, and p3 = 2.
Figure A.14.
Histograms of the normalized mean representation accuracy (NMRA) for the different source spaces
 1,
1,
 2, and
2, and
 3, with p1 = 4, p2 = 3, and p3 = 2 eigenmodes per patch, respectively. As the figure implies, for all source spaces more than 90% of the spectral energy of all the patches can be captured using the reduced-order approximations.
3, with p1 = 4, p2 = 3, and p3 = 2 eigenmodes per patch, respectively. As the figure implies, for all source spaces more than 90% of the spectral energy of all the patches can be captured using the reduced-order approximations.
Appendix B. Computational Complexity of the SPIGH algorithm
The computational complexity of the MNE inverse solution can be estimated in a straightforward fashion. Recall that G̃ ∈ ℝN×M and suppose that Q is diagonal. Then, the number of multiplications is given by M N2 + N3 + 2M N + N2 per time sample, which is
 (TMN2) overall, given that M > N. If N < M, for instance when the MNE solution is restricted to very few dipoles, the MNE solution can be computed with M2N + M3 + M N + M2 multiplications per time sample, which gives the total complexity of
(TMN2) overall, given that M > N. If N < M, for instance when the MNE solution is restricted to very few dipoles, the MNE solution can be computed with M2N + M3 + M N + M2 multiplications per time sample, which gives the total complexity of
 (TM2N).
(TM2N).
Next, we estimate the complexity of the SP–MNE algorithm. At each iteration, the identification and support merging requires
 (TM2N) + TM + 2s multiplications. The estimation requires
(TM2N) + TM + 2s multiplications. The estimation requires
 (Ts2N) multiplications. The trimming can be done using 2sT multiplications, and finally the residual update requires
(Ts2N) multiplications. The trimming can be done using 2sT multiplications, and finally the residual update requires
 (Ts2N) + TsN operations. Since s « M, the above multiplications are dominated by TM2N and hence the complexity of SP–MNE is
(Ts2N) + TsN operations. Since s « M, the above multiplications are dominated by TM2N and hence the complexity of SP–MNE is
 (TM2N) per iteration, which is comparable to that of MNE. Inspection of the convergence rate of the SPIGH algorithm suggests that a total of
(TM2N) per iteration, which is comparable to that of MNE. Inspection of the convergence rate of the SPIGH algorithm suggests that a total of
 (s) iterations suffice for the algorithm to meet the halting criterion. Therefore, the overall complexity of the SP–MNE is
(s) iterations suffice for the algorithm to meet the halting criterion. Therefore, the overall complexity of the SP–MNE is
 (TM2Ns), which is comparable to that of MNE when s « M.
(TM2Ns), which is comparable to that of MNE when s « M.
Since the SP–MNE algorithm is the core of the SPIGH algorithm, it is also straightforward to estimate the computational complexity of the latter. The computational complexity of SP–MNE applied on the source space
 1 is
1 is
 (Tp2|
(Tp2|
 1|2Ns1). For the subsequent source spaces
1|2Ns1). For the subsequent source spaces
 i, the computational complexity is
for i = 2, 3, since the estimate over
i, the computational complexity is
for i = 2, 3, since the estimate over
 i is of sparsity si and its cover in
i is of sparsity si and its cover in
 i+1 together with its nearest neighbors is not of cardinality greater than 16si+1 due to the geometry of the icosahedron subdivisions. Since typically si « |
i+1 together with its nearest neighbors is not of cardinality greater than 16si+1 due to the geometry of the icosahedron subdivisions. Since typically si « |
 1| = 84, for i = 1, 2, 3, and pi =
1| = 84, for i = 1, 2, 3, and pi =
 (1), the overall complexity of SPIGH can be estimated as
(1), the overall complexity of SPIGH can be estimated as
 (T|
(T|
 1|2N), which is comparable to that of the MNE algorithm applied to the
1|2N), which is comparable to that of the MNE algorithm applied to the
 1 source space. With a similar argument, it can be shown that the complexity of the SPIGH–EM algorithm is comparable to that of the MNE–EM algorithm applied to the
1 source space. With a similar argument, it can be shown that the complexity of the SPIGH–EM algorithm is comparable to that of the MNE–EM algorithm applied to the
 1 source space.
1 source space.
Appendix C. Greedy selection of the columns of the proxy matrix in the SP–MNE algorithm
In step 1 of the SP–MNE algorithm, one needs to identify s indices corresponding to the proxy matrix P(ℓ) with the largest ℓ2 norm, such that the corresponding columns of G have a mutual coherence bounded by μ. In order to check the mutual coherence of each two columns of G, one can compute the binary conflict matrix B(μ) off-line, where
| (C.1) |
Then, given a current support
 , the greedy procedure adds a new index j to
, the greedy procedure adds a new index j to
 such that
such that
| (C.2) |
That is, the new index j has the highest ℓ2 norm among all the possible indices which have at most a coherence of μ with the indices in the current support
 . This can be carried out by simply sorting
for all k satisfying
. Then, j is added to the current support
. This can be carried out by simply sorting
for all k satisfying
. Then, j is added to the current support
 and the greedy routine is repeated a total of s times. Note that for the SPIGH algorithm, the conflict matrix B(μ) can be computed off-line for all the lead fields
and the corresponding values of
.
and the greedy routine is repeated a total of s times. Note that for the SPIGH algorithm, the conflict matrix B(μ) can be computed off-line for all the lead fields
and the corresponding values of
.
Appendix D. Estimation and regularization of the observation noise covariance and setting the MNE parameters
The observation noise covariance matrix C can be estimated in various ways, depending on the application. A convenient way is to obtain the maximum likelihood estimate of C, given the empty room measurements (for spontaneous activity recordings) or pre-stimulus segments of data (for evoked fields recordings). In general, the noise covariance of MEG is ill-conditioned and requires regularization.
One way of remedying the ill-conditioned nature of the observation noise covariance is to apply diagonal loading to the estimate (Hämäläinen, 2010). Suppose that Ĉ denotes the maximum-likelihood estimate of the noise covariance matrix. Let ℳ and
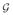 denote the sensor indices corresponding to the magnetometer and gradiometer MEG sensors, respectively. Then, one can load the diagonal entries of Ĉ as follows:
denote the sensor indices corresponding to the magnetometer and gradiometer MEG sensors, respectively. Then, one can load the diagonal entries of Ĉ as follows:
| (D.1) |
Where εm and εg are two small positive constants, and ei denote the ith Cartesian unit vector. The recommended values for εm and εg are in the interval [0, 1] (Hämäläinen, 2010).
Figure D.15–a shows the color map of the observation noise covariance for each MEG coil type corresponding to empty-room measurements of the device used in acquiring the spontaneous mu-rhythm data of Section 3.2. The covariance of the magnetometer noise contains undesirable off-diagonal components representing systematic device noise. Therefore, we performed offline denoising by applying the Signal-Space Projection operator to the data, which generally suppresses external disturbances by an order of magnitude or more (Tesche et al., 1995). Finally we diagonally loaded the estimated noise covariance with parameters εm = 1 and εg = 0.
Figure D.15.
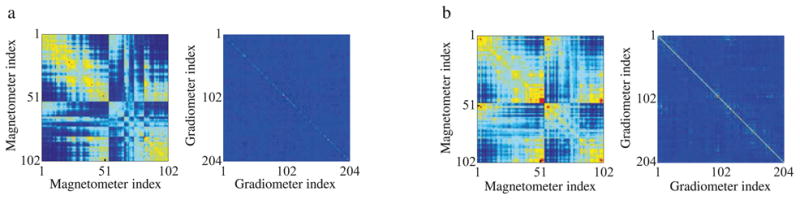
Color map of the observation noise covariances estimated from (a) empty-room recordings and (b) 200 ms pre-stimulus segments of the recorded epochs.
Similarly Figure D.15–b shows a color map of the estimated noise covariance for the magnetometers and gradiometers corresponding to the pre-stimulus segments of data from the somatosensory evoked field experiment of Section 3.4. Note that in particular, the spatial configuration of the magnetometer noise covariance is very different than that estimated from empty-room recordings (Figure D.15–a), and reflects the pre-stimulus background activity of the brain. The estimated noise covariance was diagonally loaded using the parameters εm =0.1 and εg =0.2
Recall that the source covariance matrix Q needs to satisfy Tr(G̃QG̃′) = N. Assuming that Q = qIM , the diagonal value q is given by q ≔ N/Tr(G̃G̃′). As for the whitening pre-multiplier C−1/2, we use the inverse of the Cholesky factor of C, which is given by the Cholesky decomposition C = LL′.
Footnotes
Note that when the doubling heuristic described in Section 2.8 is used, target sparsity levels s2 and s3 are not required as input, and can be recursively computed based on s1.
This work has been presented in part at the 2012 IEEE Engineering in Medicine and Biology Conference (Obregon-Henao et al., 2012).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akçakaya M, Tarokh V. A frame construction and a universal distortion bound for sparse representations. Signal Processing, IEEE Transactions on. 2008;56:2443–2450. [Google Scholar]
- Atia G, Saligrama V. Boolean compressed sensing and noisy group testing. Information Theory, IEEE Transactions on. 2012;58:1880–1901. [Google Scholar]
- Baillet S, Garnero L. A Bayesian approach to introducing anatomo-functional priors in the EEG/MEG inverse problem. Biomedical Engineering, IEEE Transactions on. 1997;44:374–385. doi: 10.1109/10.568913. [DOI] [PubMed] [Google Scholar]
- Baron D, Sarvotham S, Baraniuk R. Bayesian compressive sensing via belief propagation. Signal Processing, IEEE Transactions on. 2010;58:269–280. [Google Scholar]
- Bertrand C, Ohmi M, Suzuki R, Kado H. A probabilistic solution to the MEG inverse problem via MCMC methods: the reversible jump and parallel tempering algorithms. Biomedical Engineering, IEEE Transactions on. 2001;48:533–542. doi: 10.1109/10.918592. [DOI] [PubMed] [Google Scholar]
- Bolstad A, Van Veen BD, Nowak R. Space-time event sparse penalization for magneto-/electroencephalography. Neuroimage. 2009;46:1066–1081. doi: 10.1016/j.neuroimage.2009.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruckstein A, Donoho D, Elad M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM review. 2009;51:34–81. [Google Scholar]
- Campi C, Pascarella A, Sorrentino A, Piana M. A Rao-Blackwellized particle filter for magnetoencephalography. Inverse Probl. 2008;24:025023. [Google Scholar]
- Candè E, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. Information Theory, IEEE Transactions on. 2006;52:489–509. [Google Scholar]
- Candes E, Tao T. Decoding by linear programming. Information Theory, IEEE Transactions on. 2005;51:4203–4215. [Google Scholar]
- Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction. Information Theory, IEEE Transactions on. 2009;55:2230–2249. [Google Scholar]
- Damoiseaux J, Rombouts S, Barkhof F, Scheltens P, Stam C, Smith SM, Beckmann C. Consistent resting-state networks across healthy subjects. Proceedings of the National Academy of Sciences. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, Friston KJ. A mesostate-space model for EEG and MEG. Neuroimage. 2007;38:67–81. doi: 10.1016/j.neuroimage.2007.06.034. [DOI] [PubMed] [Google Scholar]
- Daunizeau J, Mattout J, Clonda D, Goulard B, Benali H, Lina JM. Bayesian spatio-temporal approach for EEG source reconstruction: Conciliating ECD and distributed models. Biomedical Engineering, IEEE Transactions on. 2006;53:503–516. doi: 10.1109/TBME.2005.869791. [DOI] [PubMed] [Google Scholar]
- Donoho D. Compressed sensing. Information Theory, IEEE Transactions on. 2006;52:1289–1306. [Google Scholar]
- Donoho D, Elad M. Optimally sparse representation in general (non-orthogonal) dictionaries via ℓ1 minimization. Proceedings of the National Academy of Sciences. 2003;100:2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durka PJ, Matysiak A, Martínez-Montes E, Valdés-Sosa P, Blinowska KJ. Multichannel matching pursuit and EEG inverse solutions. Journal of Neuroscience Methods. 2005;148:49–59. doi: 10.1016/j.jneumeth.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison LM, Daunizeau J, Kiebel SJ, Phillips C, Trujillo-Barreto NJ, Henson RN, Flandin G, Mattout J. Multiple sparse priors for the M/EEG inverse problem. Neuroimage. 2008;39:1104–1120. doi: 10.1016/j.neuroimage.2007.09.048. [DOI] [PubMed] [Google Scholar]
- Galka A, Yamashita O, Ozaki T, Biscay R, Valdés-Sosa PA. A solution to the dynamical inverse problem of EEG generation using spatiotemporal Kalman filtering. Neuroimage. 2004;23:435–453. doi: 10.1016/j.neuroimage.2004.02.022. [DOI] [PubMed] [Google Scholar]
- Genovese CR, Jin J, Wasserman L, Yao Z. A comparison of the Lasso and marginal regression. The Journal of Machine Learning Research. 2012;98888:2107–2143. [Google Scholar]
- Giryes R, Elad M. RIP-based near-oracle performance guarantees for SP, CoSaMP, and IHT. Signal Processing, IEEE Transactions on. 2012;60:1465–1468. [Google Scholar]
- Gorodnitsky IF, George JS, Rao BD. Neuromagnetic source imaging with FOCUSS: a recursive weighted minimum norm algorithm. Electroencephalogr Clin Neurophysiol. 1995;95:231–251. doi: 10.1016/0013-4694(95)00107-a. [DOI] [PubMed] [Google Scholar]
- Gramfort A, Kowalski M, Hämäläinen M. Mixed-norm estimates for the M/EEG inverse problem using accelerated gradient methods. Physics in Medicine and Biology. 2012;57:1937. doi: 10.1088/0031-9155/57/7/1937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramfort A, Strohmeier D, Haueisen J, Hamalainen M, Kowalski M. Information Processing in Medical Imaging. Springer; 2011. Functional brain imaging with m/eeg using structured sparsity in time-frequency dictionaries; pp. 600–611. [DOI] [PubMed] [Google Scholar]
- Greensite F. The temporal prior in bioelectromagnetic source imaging problems. Biomedical Engineering, IEEE Transactions on. 2003;50:1152–1159. doi: 10.1109/TBME.2003.817632. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS. MNE Software User's Guide. Massachusetts General Hospital; Charlestown, MA: 2010. [Google Scholar]
- Hämäläinen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography - theory, intrumentation, and applications to noninvasive studies of the working human brain. Rev Modern Phys. 1993;65:413–497. [Google Scholar]
- Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: Minimum norm estimates. Med Biol Eng Comput. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- Hari R, Karhu J, Hämäläinen M, Knuutila J, Salonen O, Sams M, Vilkman V. Functional organization of the human first and second somatosensory cortices: a neuromagnetic study. European Journal of Neuroscience. 2006;5:724–734. doi: 10.1111/j.1460-9568.1993.tb00536.x. [DOI] [PubMed] [Google Scholar]
- Jun SC, George JS, Paré-Blagoev J, Plis SM, Ranken DM, Schmidt DM, Wood CC. Spatiotemporal Bayesian inference dipole analysis for MEG neuroimaging data. Neuroimage. 2005;28:84–98. doi: 10.1016/j.neuroimage.2005.06.003. [DOI] [PubMed] [Google Scholar]
- Kiebel SJ, Daunizeau J, Phillips C, Friston KJ. Variational Bayesian inversion of the equivalent current dipole model in EEG/MEG. Neuroimage. 2008;39:728–741. doi: 10.1016/j.neuroimage.2007.09.005. [DOI] [PubMed] [Google Scholar]
- Lamus C, Hämäläinen MS, Temereanca S, Brown EN, Purdon PL. A spatiotemporal dynamic distributed solution to the MEG inverse problem. Neuroimage. 2012;63:894–909. doi: 10.1016/j.neuroimage.2011.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamus C, Long CJ, Hämäläinen MS, Brown EN, Purdon PL. Parameter estimation and dynamic source localization for the magnetoencephalography (MEG) inverse problem. 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Washington D.C., USA. 2007. pp. 1092–1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Limpiti T, Van Veen B, Wakai R. Cortical patch basis model for spatially extended neural activity. Biomedical Engineering, IEEE Transactions on. 2006;53:1740–1754. doi: 10.1109/TBME.2006.873743. [DOI] [PubMed] [Google Scholar]
- Limpiti T, Van Veen BD, Attias HT, Nagarajan SS. A spatiotemporal framework for estimating trial-to-trial amplitude variation in event-related MEG/EEG. Biomedical Engineering, IEEE Transactions on. 2009;56:633–645. doi: 10.1109/TBME.2008.2008423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long CJ, Purdon PL, Temereanca S, Desai NU, Hämäläinen MS, Brown EN. State-space solutions to the dynamic magnetoencephalography inverse problem using high performance computing. Ann Appl Stat. 2011;5:1207–1228. doi: 10.1214/11-AOAS483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäkelä J, Hämäläinen M, Hari R, McEvoy L. Whole-head mapping of middle-latency auditory evoked magnetic fields. Electroencephalography and Clinical Neurophysiology/Evoked Potentials Section. 1994;92:414–421. doi: 10.1016/0168-5597(94)90018-3. [DOI] [PubMed] [Google Scholar]
- Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries. Signal Processing, IEEE Transactions on. 1993;41:3397–3415. [Google Scholar]
- Marks W., Jr Utility of MEG in presurgical localization. Epilepsy Currents. 2004;4:208. doi: 10.1111/j.1535-7597.2004.04516.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattout J, Phillips C, Penny WD, Rugg MD, Friston KJ. MEG source localization under multiple constraints: An extended Bayesian framework. Neuroimage. 2006;30:753–767. doi: 10.1016/j.neuroimage.2005.10.037. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Lewis PS, Leahy RM. Multiple dipole modeling and localization from spatio-temporal MEG data. Biomedical Engineering, IEEE Transactions on. 1992;39:541–557. doi: 10.1109/10.141192. [DOI] [PubMed] [Google Scholar]
- Needell D, Tropp JA. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl Comp Harmonic Anal. 2009;26:301–321. [Google Scholar]
- Nummenmaa A, Auranen T, Hämäläinen MS, Jääskeläinen IP, Lampinen J, Sams M, Vehtari A. Hierarchical Bayesian estimates of distributed MEG sources: Theoretical aspects and comparison of variational and MCMC methods. Neuroimage. 2007;35:669–685. doi: 10.1016/j.neuroimage.2006.05.001. [DOI] [PubMed] [Google Scholar]
- Obregon-Henao G, Babadi B, Lamus C, Brown EN, Purdon PL. A fast iterative greedy algorithm for MEG source localization. Engineering in Medicine and Biology Society (EMBC), 2012 Annual International Conference of the IEEE, IEEE; 2012. pp. 6748–6751. [DOI] [PubMed] [Google Scholar]
- Ou W, Hämäläinen MS, Golland P. A distributed spatio-temporal EEG/MEG inverse solver. Neuroimage. 2009;44:932–946. doi: 10.1016/j.neuroimage.2008.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: A new method for localizing electrical activity in the brain. Int J Psychophysiol. 1994;18:49–65. doi: 10.1016/0167-8760(84)90014-x. [DOI] [PubMed] [Google Scholar]
- Phillips C, Mattout J, Rugg MD, Maquet P, Friston KJ. An empirical Bayesian solution to the source reconstruction problem in EEG. Neuroimage. 2005;24:997–1011. doi: 10.1016/j.neuroimage.2004.10.030. [DOI] [PubMed] [Google Scholar]
- Sato Ma, Yoshioka T, Kajihara S, Toyama K, Goda N, Doya K, Kawato M. Hierarchical Bayesian estimation for MEG inverse problem. Neuroimage. 2004;23:806–826. doi: 10.1016/j.neuroimage.2004.06.037. [DOI] [PubMed] [Google Scholar]
- Somersalo E, Voutilainen A, Kaipio JP. Non-stationary magnetoencephalography by Bayesian filtering of dipole models. Inverse Probl. 2003;19:1047–1063. [Google Scholar]
- Sutherling W, Crandall P, Engel J, Darcey T, Cahan L, Barth D. The magnetic field of complex partial seizures agrees with intracranial localizations. Annals of Neurology. 2004;21:548–558. doi: 10.1002/ana.410210605. [DOI] [PubMed] [Google Scholar]
- Tesche C, Uusitalo M, Ilmoniemi R, Huotilainen M, Kajola M, Salonen O. Signal-space projections of MEG data characterize both distributed and well-localized neuronal sources. Electroencephalography and clinical neurophysiology. 1995;95:189–200. doi: 10.1016/0013-4694(95)00064-6. [DOI] [PubMed] [Google Scholar]
- Tian T, Huang J, Shen H, Li Z. A two-way regularization method for MEG source reconstruction. The Annals of Applied Statistics. 2012;6:1021–1046. [Google Scholar]
- Tian T, Li Z. A spatio-temporal solution for the EEG/MEG inverse problem using group penalization methods. Statistics and its Interface. 2011;4:521–533. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B. 1996:267–288. Methodological. [Google Scholar]
- Tropp J, Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit. Information Theory, IEEE Transactions on. 2007;53:4655–4666. [Google Scholar]
- Trujillo-Barreto NJ, Aubert-Vázquez E, Penny WD. Bayesian M/EEG source reconstruction with spatio-temporal priors. Neuroimage. 2008;39:318–335. doi: 10.1016/j.neuroimage.2007.07.062. [DOI] [PubMed] [Google Scholar]
- Uutela K, Hämäläinen MS, Salmelin R. Global optimization in the localization of neuromagnetic sources. Biomedical Engineering, IEEE Transactions on. 1998;45:716–723. doi: 10.1109/10.678606. [DOI] [PubMed] [Google Scholar]
- Valdés-Sosa PA, Vega-Hernández M, Sánchez-Bornot JM, Martínez-Montes E, Bobes MA. EEG source imaging with spatio-temporal tomographic nonnegative independent component analysis. Human brain mapping. 2009;30:1898–1910. doi: 10.1002/hbm.20784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Veen BD, Van Drongelen W, Yuchtman M, Suzuki A. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. Biomedical Engineering, IEEE Transactions on. 1997;44:867–880. doi: 10.1109/10.623056. [DOI] [PubMed] [Google Scholar]
- Vega-Hernández M, Martínez-Montes E, Sánchez-Bornot JM, Lage-Castellanos A, Valdés-Sosa PA. Penalized least squares methods for solving the EEG inverse problem. Statistica Sinica. 2008;18:1535–1551. [Google Scholar]
- Winkler AM, Sabuncu MR, Yeo B, Fischl B, Greve DN, Kochunov P, Nichols TE, Blangero J, Glahn DC. Measuring and comparing brain cortical surface area and other areal quantities. Neuroimage. 2012;61:1428–1443. doi: 10.1016/j.neuroimage.2012.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wipf DP, Nagarajan SS. A unified Bayesian framework for MEG/EEG source imaging. Neuroimage. 2009;44:947–966. doi: 10.1016/j.neuroimage.2008.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita O, Galka A, Ozaki T, Biscay R, Valdés-Sosa PA. Recursive penalized least squares solution for dynamical inverse problems of EEG generation. Hum Brain Mapp. 2004;21:221–235. doi: 10.1002/hbm.20000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zumer JM, Attias HT, Sekihara K, Nagarajan SS. Probabilistic algorithms for MEG/EEG source reconstruction using temporal basis functions learned from data. Neuroimage. 2008;41:924–940. doi: 10.1016/j.neuroimage.2008.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]