Phase I Design for Completely or Partially Ordered Treatment Schedules

Abstract

The majority of methods for the design of Phase I trials in oncology are based upon a single course of therapy, yet in actual practice it may be the case that there is more than one treatment schedule for any given dose. Therefore, the probability of observing a dose-limiting toxicity (DLT) may depend upon both the total amount of the dose given, as well as the frequency with which it is administered. The objective of the study then becomes to find an acceptable combination of both dose and schedule. Past literature on designing these trials has entailed the assumption that toxicity increases monotonically with both dose and schedule. In this article, we relax this assumption for schedules and present a dose-schedule finding design that can be generalized to situations in which we know the ordering between all schedules and those in which we do not. We present simulation results that compare our method to other suggested dose-schedule finding methodology.

1. Background

It is sometimes the case in Phase I dose-finding studies in cancer that there exists more than one treatment schedule. The doses of a single agent can be expressed in multiple ways based on the frequency with which it is administered. For instance, whether a dose is given once a day for three days in a particular week or given once that week is likely to have an impact on the probability of observing dose-limiting toxicity (DLT) for that dose. Each of these “courses of therapy” can be considered a distinct combination of schedule and dose. For these trials, finding an acceptable dose and schedule becomes a two-dimensional dose-finding problem, where one dimension is the dose level of the agent and the other is the course of therapy. The goal becomes to find a dose-schedule combination with tolerable toxicity. Several methods have been suggested for finding an acceptable combination of dose and schedule. Braun, Yuan and Thall [1] proposed a method that determines a maximum-tolerated schedule in Phase I studies. This method allowed the schedule to vary, while fixing the dose. The proposal of Braun, Thall, Nguyen and de Lima [2], termed BTNL, simultaneously optimizes the dose and schedule of a cytotoxic agent. Li, Bekele, Ji and Cook [3] develop a dose-schedule finding algorithm based on a Bayesian hierarchical model that jointly models toxicity and efficacy.

A fundamental assumption of these methods is that the toxicity probabilities adhere to an order constraint both within and between schedules, i.e. the probability of toxicity for dose increases monotonically when the schedule is being held fixed, and vice versa. It is reasonable to assume that within schedule, the DLT probabilities increase as we increase dose and we refer to this as a complete order. However, the assumption that, for a given dose, the DLT probabilities can be completely ordered in terms of the different treatment schedules under consideration may not always be true. We provide an example in which the schedules are partially ordered in the following section. In this article, we present a dose-schedule finding design that eliminates this assumption and is able to handle the complexity of a lack of complete ordering information among the schedules.

In general, the problem of dose-schedule finding can be broadened to the more general framework of the problem of partial ordering in Phase I clinical trials. The partial order continual reassessment method (POCRM; [4]) was introduced for such problems, within the context of drug combination trials. Under the assumption of completely ordered schedules, the methods presented in this article are a novel application of POCRM to the problem of dose-schedule finding. When the assumption of completely ordered schedules is not reasonable, POCRM in its current form is not directly applicable to identifying acceptable dose-schedule combinations. Therefore, we relax this key assumption of the POCRM and propose a method for dose-schedule finding that has even less ordering information among the treatments available than trials of combined drugs. We demonstrate that we can concentrate DLT probability estimation within a reasonable subset of possible orders and rely on the near-optimal properties [5, 6] of the continual reassessment method (CRM; [7]) to generate efficient estimates of the MTD within these orders. We provide results comparing the performance of our proposed dose-schedule finding method to existing dose-schedule finding methodology (BTNL). The approach of Braun et al. [2] is to fully model the several aspects of the problem, which is more in tune with Bayesian thinking. Our approach, while it can make use of prior information, and, therefore have a Bayesian flavor, is more in the spirit of underparameterized “CRM-type” models. In the next section, we describe the problem of dose-schedule finding for both completely and partially ordered treatment schedules. In Section 3, we outline a proposed design for dose-finding under multiple schedules. In Section 4, we provide simulation results comparing the performance of the proposed design to existing dose-schedule methodology [2]. Finally, we conclude with some discussion.

2. Dose-schedule finding

2.1. Complete ordering among schedules

As an example of a dose-schedule finding problem, consider the Vidaza [8] trial described in Braun et al. [2] for the treatment of a blood cell disease, known as MDS, that often develops into acute myelogeneos leukemia (AML). The trial consists of four different schedules (A, B, C, D) and three doses (8, 16, and 24 mg/m²), resulting in the twelve (schedule, dose) combinations {(A, 8), (A, 16), (A, 24), (B, 8), …, (D, 24)}. For simplicity, we are going to label each of the twelve combinations, {d₁, …, d₁₂}, and we have a matrix of combinations of dose and schedule like that displayed in Table 1. A reasonable assumption to be made in these type of studies is that toxicity increases monotonically with dose within each schedule. In this case, we say that the DLT probabilities follow a complete order in that the relationship between all DLT probabilities for a certain schedule is completely known. For instance, denoting the probability of a DLT at combination d_i by π(d_i), in Schedule B, π(d₄) ≤ π(d₅) ≤ π(d₆). An assumption that is made in previous literature [2, 3] on dose-schedule finding is that the probability of toxicity for schedule increases monotonically when the dose is being held fixed. In this case we say that the DLT probabilities follow a complete order for a certain dose, and increases as the schedule moves from A to D. That is, Schedule D administers treatments more frequently than the other schedules and thus is considered more aggressive. This assumption is perfectly reasonable in the Vidaza [8] example due to the fact that the schedules are nested. In other words, administering the drug to patients in Schedule B amounts to repeating Schedule A twice, with a 25-day rest in between administrations. Essentially, using the term “schedule,” in this case is equivalent to saying that the drug is simply given more often. Therefore, for dose 8 mg/m², we assume π(d₁) ≤ π (d₄) ≤ π (d₇) ≤ π (d₁₀). This ordering information corresponds to completely knowing the relationship between DLT probabilities across all rows and up all columns of the matrix.

Table 1.

Combinations for 3 doses and 4 schedules

Schedule	Doses in mg/m2
	8	16	24
D	d10	d11	d12
C	d7	d8	d9
B	d4	d5	d6
A	d1	d2	d3

The ordering of combinations along the diagonals of the matrix is unknown. It may be clear that combination d₆ is more toxic than d₅, but we may not know the ordering between d₆ and d₈. Moving from d₆ to d₈ corresponds to decreasing the dosage of the agent from 16 mg/m² to 8 mg/m² but “increasing” the schedule of the treatment. Associated with each combination is a set of possible escalation treatments that can be specified prior to the beginning of the trial. For example, the possible escalation combinations for treatment d₁ are d₂ and d₄, meaning that if combination d₁ was tried and found to be sufficiently non-toxic, then escalation could proceed to previously untried d₂ or d₄. Taking into account the subset of combinations for which we know the toxicity order, we aim to formulate possible complete orders of the toxicity profile. Considering all possible complete orders is unreasonable in studies like the Vidaza [8] trial due to the large number of possibilities. One approach may be to reduce the problem to a complete order by imposing an implicit ordering on the combinations. If the ordering selected is correct, then operating characteristics of a chosen method are likely to be very good. If, however, the initial ordering is incorrect, we expect performance to be quite poor. Instead of imposing a single ordering, we could choose a small subset of orderings.

Our approach is to select a plausible subset of possible orderings, according to the known information among combinations. A reasonable approach taken by Wages and Conaway [9] for drug combination trials is to formulate possible orderings according to the rows, columns and diagonals of the matrix of combinations. Suppose, in general, we are going to consider a subset of M possible orderings indexed by m, m = 1, …, M. Let us begin by consider ordering the treatments across rows and up columns of the matrix. Therefore, two reasonable possibilities for the toxicity orderings are

1. Across rows [ m = 1]

   π(d₁) ≤ π(d₂) ≤ π(d₃) ≤ π(d₄) = π(d₅) ≤ π(d₆) ≤ π(d₇) ≤ π(d₈) ≤ π(d₉) ≤ π(d₁₀) ≤ π(d₁₁) ≤ π(d₁₂)

2. Up columns [ m = 2]

   π(d₁) ≤ π(d₄) ≤ π(d₇) ≤ π(d₁₀) ≤ π(d₂) ≤ π(d₅) ≤ π(d₈) ≤ π(d₁₁) ≤ π(d₃) ≤ π(d₆) ≤ π(d₉) ≤ π(d₁₂)

   There are many ways to arrange the treatments according to the diagonals of the matrix. For the sake of simplicity and in order to reduce the dimension of the problem as much as possible, we are going to restrict possible movements along diagonals to “up” movements and “down” movements. These two movements would result in the following two possible orderings of the DLT probabilities.

3. Up diagonals [ m = 3]

   π(d₁) ≤ π(d₂) ≤ π(d₄) ≤ π(d₃) ≤ π(d₅) ≤ π(d₇) ≤ π(d₆) ≤ π(d₈) ≤ π(d₁₀) ≤ π(d₉) ≤ π(d₁₁) ≤ π(d₁₂)

4. Down diagonals [ m = 4]

   π(d₁) ≤ π(d₄) ≤ π(d₂) ≤ π(d₇) ≤ π(d₅) ≤ π(d₃) ≤ π(d₁₀) ≤ π(d₈) ≤ π(d₆) ≤ π(d₁₁) ≤ π(d₉) ≤ π(d₁₂)

5. Alternating down-up diagonals [ m = 5]

   π(d₁) ≤ π(d₂) ≤ π(d₄) ≤ π(d₇) ≤ π(d₅) ≤ π(d₃) ≤ π(d₆) ≤ π(d₈) ≤ π(d₁₀) ≤ π(d₁₁) ≤ π(d₉) ≤ π(d₁₂)

6. Alternating up-down diagonals [ m = 6]

   π(d₁) ≤ π(d₄) ≤ π(d₂) ≤ π(d₃) ≤ π(d₅) ≤ π(d₇) ≤ π(d₁₀) ≤ π(d₈) ≤ π(d₆) ≤ π(d₉) ≤ π(d₁₁) ≤ π(d₁₂)

The dimension of the problem makes it difficult to practically consider much more information than what we have captured in these six orderings. We have provided a way of choosing a reasonable subset that is consistent with the partially known ordering information among combinations, and that is independent of the dimension of the matrix. The design outlined in this article can certainly accommodate other subset sizes, should we have more or less ordering information at our disposal. If, however, the only information we have is the assumption of a monotonicity across rows and up columns of the matrix, then we can use the methods outlined in Section 3 based on this “default” subset of six orderings and have confidence in its performance. Our simulation results will demonstrate that this practical manner of selecting orders produces strong operating characteristics in Phase I trials with multiple treatment schedules in terms of recommending acceptable dose-schedule combinations as the MTD, as well as allocating patients to combinations with acceptable toxicity.

2.2. Partial ordering among schedules

As previously stated, it is reasonable to assume that within schedules, the dose-toxicity ordering is completely known. However, the assumption that the DLT probabilities increase with schedule may not always be true. Therefore, a design that handles the complexity of knowing the ordering between some schedules and not knowing the ordering between others would be useful. This would enable us to relax the assumption of monotonicity across schedules, for a given dose, and propose a design that is more generalizable to the dose-schedule finding problem. An example of a Phase I trial with unknown ordering information between schedules, for a given dose, is that of Graux, Sonet, Maertens et al. [10]. In this trial, MSC1992371A, an oral inhibitor of aurora and other kinases, was administered under one of two different schedules. In Schedule A, patients received escalating doses of MSC1992371A on days 1–3 and days 8–10 of a 21-day cycle. In Schedule B, patients received escalating doses of the agent on days 1–6 of a 21-day cycle. The per administration dose, as well as the total amount of the drug given during the DLT assessment window, is the same for each schedule. In this case, it is difficult to completely ascertain the toxicity relationship between the two schedules for a given dose over the DLT assessment window, creating a partial order between Schedules A and B.

We continue to use the same structure (i.e. 3 doses × 4 schedules) as the Vidaza [8] example in Braun et al. [2], so that we can juxtapose simulation results for the case in which we have completely ordered schedules and the case in which we do not. As was previously pointed out, it is within reason to assume in this example that the probability of toxicity increases with both per administration dose and schedule. However, for illustrative purposes, suppose we assume that Schedule A is the least toxic schedule and Schedule D is the most toxic, but know nothing of the ordering between B and C. This would create the partial ordering called a loop ordering [11] displayed in Figure 1. By relaxing the assumption of completely ordered schedules in the Vidaza example, we want to see how much, if at all, performance diminishes by eliminating this assumption. We would expect some loss of performance for partially ordered schedules and the simulation results provide a measure of how much information is being lost as a result of not having a completely known schedule ordering. With this loop ordering, there are two possible complete orders associated with the partial ordering among schedules. It could be that (1) A ≤ B ≤ C ≤ D or (2) A ≤ C ≤ B ≤ D in terms of the order relationship between DLT probabilities. In Figure 2, these two possible arrangements are graphically displayed, with each sub-figure representing a monotonically increasing toxicity ordering across rows (between doses) and up columns (between schedules). Within each of these two ordering possibilities for the schedules, we have a complete ordering between doses and schedules as described in the previous section. Therefore, we can choose a reasonable subset of orderings for each schedule ordering possibility as described above and combine them into one subset of possible orderings. If we rely on the six orderings selected across rows, up columns, and up/down diagonals, then we would have a total of twelve orderings contained in the subset. The first six for Figure 2(a), are m = 1, …, m = 6 above and the remaining six, for Figure 2 (b), could be chosen in a similar fashion. Once we have chosen the subset of possible orderings with which to work, the methods of the following section can be implemented in order to find a schedule-dose combination with an acceptable rate of toxicity. If we have even less ordering information regarding the schedules at our disposal, the number of possible orderings to consider is compounded. Although the dimension of the problem increases, the methods outlined in this article are still applicable to partial orders other than a loop ordering. We have included simulation results for an example of a higher dimension problem in the Supplementary Material.

Figure 1.

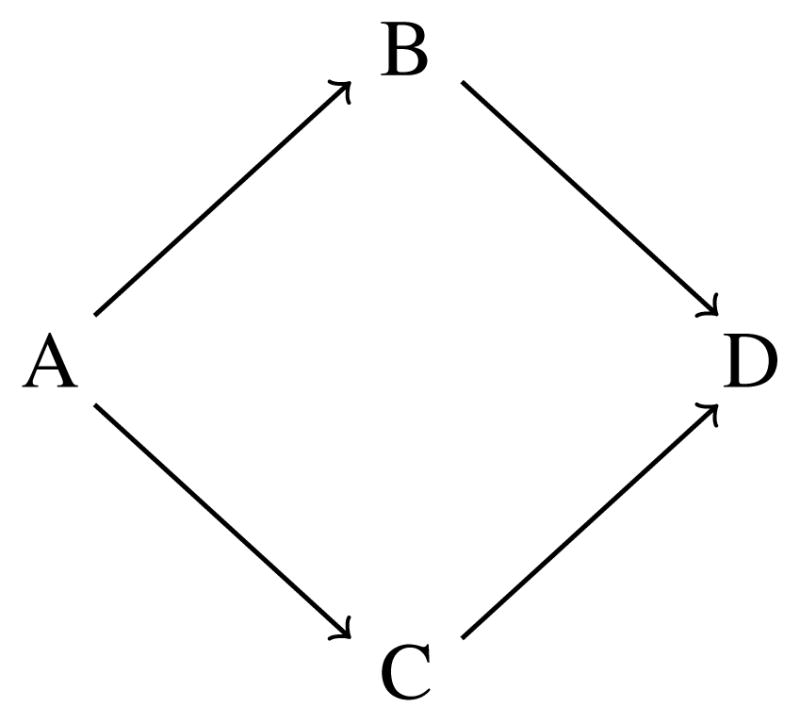
Example of a loop partial order

Figure 2.

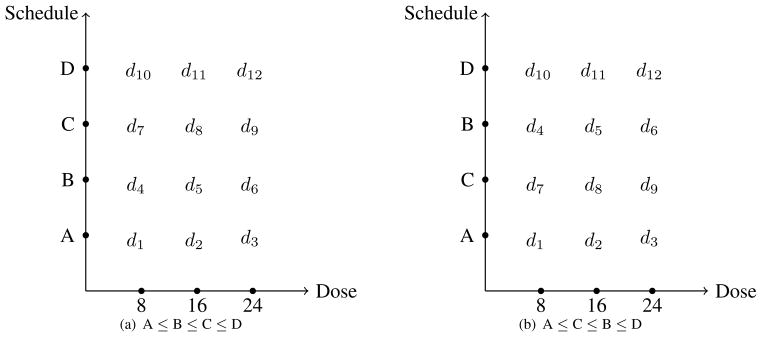
Possible arrangements of toxicity orderings between schedules. Toxicity increases as we move across rows and up columns of each sub-figure.

3. Trial design and conduct

3.1. First stage

Wages, Conaway and O’Quigley [12] made the case for using an initial escalation stage in drug combination trials and discussed the need for a variant of the traditional escalation schemes due to the fact that, in partially ordered trials, the most appropriate dose to which the trial should escalate could consist of more than one treatment combination. In the first stage, we make use of “zoning” the matrix of dose-schedule combinations according to the diagonals of the matrix in Table 1. The trial could begin in the zone Z₁ = {d₁} and the first cohort of patients be enrolled on this “lowest” combination. At the first observation of a toxicity in one of the patients, the first stage is closed and the second stage, which is model-based, is opened. As long as no toxicities occur, cohorts of patients are examined at each dose within the currently occupied zone, before escalating to the next highest zone. If d₁ was tried and deemed “safe”, the trial would escalate to zone Z₂ = {d₂, d₄}. If more than one dose is contained within a particular zone, we sample without replacement from the doses available within the zone. Therefore, the next cohort is enrolled on a dose that is chosen randomly from d₂ and d₄. The trial is not allowed to advance to zone Z₃ = {d₃, d₅, d₇} in the first stage until a cohort of patients has been observed at both all combinations in Z₂. This procedure continues until a toxicity is observed or all available zones have been exhausted. This procedure can certainly be modified for partially ordered schedules as displayed in Figure 2. For example, we could expand zone Z₂ to include d₇ as well, since we do not know the ordering between d₂, d₄, and d₇ with partially ordered schedules. These zones are simply a mechanism for getting the trial underway with a conservative initial escalation scheme. All of the simulation results presented below implement single patient cohorts in the initial stage. We have also run simulations using our methods with two-patient cohorts. In the latter case, the average sample size increased, but overall performance in terms of recommending acceptable dose-schedule combinations was relatively unchanged. Subsequent to a DLT being observed, the second stage of the trial begins.

3.2. Second stage

Once we have at least one toxic and one non-toxic response, the modeling stage begins. Suppose that we have formulated a subset of M possible orderings of DLT probabilities consistent with available ordering information among the dose-schedule combinations as described in the previous section. Consider a trial investigating k treatments labeled d₁, …, d_k similar to Table 1. For a particular ordering, m, we model the true DLT probability, π(d_i), at combination d_i using a class of models ψ_m(d_i, a), m = 1, …, M. A common model used in practice is the power model

$$\pi (d_i)\approx {\psi }_m(d_i,a)={\alpha }_{im}^a,i=1,\dots ,k;m=1,\dots ,M,$$ (1)

where α_1m, …, α_km represents the skeleton of the model and a ∈(0, ∞). Let us take account of any prior information regarding the probability of each ordering and allow M to be described by a set of prior probabilities p (m) = {p(1), …, p(M)}, where p (m) ≥ 0 and where Σ_m p (m) = 1. The treatment for the jth patient, X_j, is a random variable taking values x_j ∈ {d₁, …, d_k}. Let Y_j be a binary random variable, where 1 denotes the observation of a DLT for patient j. After inclusion of the first j patients into the trial, if the data are to be analyzed under ordering m, then the log-likelihood can be written as

$${\mathcal{L}}_{jm}(a)=\sum _{\ell =1}^j{y}_{\ell }log{\psi }_m(x_{\ell },a)+\sum _{\ell =1}^j(1-y_{\ell })log(1-{\psi }_m(x_{\ell },a)).$$ (2)

where any terms not involving the parameter a have been equated to zero. Under working model m, the maximum likelihood estimate of a is given by

$${\widehat{a}}_{jm}=arg\underset{a}{max}{\mathcal{L}}_{jm}(a).$$

We need some value for m so we weight each of the M candidate working models as we make progress. The updated probability of each ordering is then given by

$${\omega }_j(m)=\frac{exp\{{\mathcal{L}}_{jm}({\widehat{a}}_{jm})\}p(m)}{{\displaystyle \sum _{m=1}^M}exp\{{\mathcal{L}}_{jm}({\widehat{a}}_{jm})\}p(m)}.$$

Wages et al. [4, 12 ] propose an escalation method that selects the ordering with the largest probability ω_j(m). Therefore, we choose a single ordering, m^*, such that

$$m^{\ast }=arg\underset{m}{max}{\omega }_j(m),m=1,\dots ,M.$$

If there is a tie between two or more orderings, then m^* is chosen at random from among the tied orderings. Given m^*, the next patient is then allocated to the treatment x_j+1 = d_i such that

$$x_{j+1}=arg\underset{d_i}{min}\mid {\psi }_{m^{\ast }}(d_i,{\widehat{a}}_{{jm}^{\ast }})-\theta \mid ;i=1,\dots ,k$$

for some target DLT rate θ. For trials subject to partial orders, there may be more than one combination with DLT probability closest to the target. If there is a tie between two or more combinations, the patient will be randomized to one of the combinations with DLT probability closest to the target. The trial stops once enough information accumulates about the MTD.

3.3. Terminating the trial

In practice, investigators are likely to stop the trial if there are already many patients on the suggested treatment for the next patient. The stopping rule we use here is a practical one; the trial is stopped if more than a predetermined number, n_t, of patients are treated on a single treatment. In the first stage, the design will stop if escalation proceeds to the highest combination and n_t patients are treated with no DLT on the highest combination d₁₂. In this case, d₁₂ is declared the MTD. Also, in the first stage, if DLT is observed in the first enrolled patient on the lowest combination, then an additional patient is included at the lowest combination. If DLT is observed in both of the first two patients, then the trial is stopped for safety and no MTD combination is recommended. In the second stage, if the recommendation is to assign the next patient to a combination that already has n_t patients treated on the combination, the study is stopped and the recommended combination is declared the MTD. The simulations in the following section present results based on the stopping rule of n_t = 9 patients being already treated on a combination for the example discussed in Section 2. The design can certainly accommodate other rules. In general, making it so that the trial is “easier to stop” will result in smaller sample sizes and fewer toxicities per trial on average, but also in a smaller percentage of trials that recommended an “acceptable toxicity.” One of the goals of the simulation results is to demonstrate a strong performance by the design outlined in this section using a practical stopping rule such as the one described above.

4. Simulated results

We compared the performance of the proposed design with that of Braun et al [2] for finding acceptable dose-schedule combinations in Phase I clinical trials, as well as assessed its performance for smaller, more practical, sample sizes. In each set of 1,000 simulated trials, the target toxicity rate is θ = 0.30 and we incorporate a uniform prior distribution, p (m), on the orderings. The true toxicity probabilities for each of seven scenarios are provided in Table 2. As was noted in the previous section, the probability of DLT is modeled via the power parameter model with the skeleton values generated according to algorithm of Lee and Cheung [13] using the getprior function in R package dfcrm. (i.e. getprior(δ = 0.05, θ = 0.30, ν = 6, d = 12)). The location of these values were then adjusted to correspond to each of the possible orderings considered in the subset, creating M different skeletons of initial DLT probability estimates (see Table 4 of [12]). The primary objective of the trial is to recommend a single combination with a DLT rate closest to 0.30, keeping in mind there may be more than one. However, selecting combinations with DLT rates that are within a certain range of the target is still acceptable. Table 3 provides summary statistics for the performance of the designs. It reports the probability that each method selects an “acceptable” combination. These combinations were defined with respect to having true DLT probabilities within ±10% of the target rate and are indicated in bold-face type in Table 2. Table 3 also gives the mean sample size after 1000 runs (for trials not stopped after the first two patients), the percent of overall toxicity induced and the percent of trials stopped early for safety based on the stopping rules described above. The distribution of MTD dose-schedule combination selection and patient allocation across all combinations can be found in the Supplementary Material. Simulations were carried out using R statistical package and user-friendly R-code for implementing the proposed design can be downloaded at http://faculty.virginia.edu/model-based_dose-finding/.

Table 2.

Toxicity scenarios 1–7 for the dose-schedule combinations. Combinations with DLT probabilities between 0.20 and 0.40 are in boldface.

Schedule	Doses in mg/m2
	8	16	24	8	16	24
	Scenario 1			Scenario 2
D	0.22	0.26	0.30	0.31	0.45	0.62
C	0.16	0.18	0.23	0.18	0.32	0.54
B	0.09	0.12	0.18	0.09	0.21	0.40
A	0.05	0.07	0.11	0.03	0.14	0.28
	Scenario 3			Scenario 4
D	0.55	0.62	0.72	0.57	0.73	0.78
C	0.45	0.50	0.62	0.55	0.65	0.75
B	0.30	0.32	0.50	0.53	0.60	0.65
A	0.10	0.26	0.35	0.50	0.54	0.58
	Scenario 5			Scenario 6
D	0.30	0.48	0.70	0.50	0.60	0.75
C	0.14	0.32	0.55	0.30	0.50	0.60
B	0.12	0.30	0.48	0.12	0.30	0.50
A	0.10	0.28	0.45	0.03	0.15	0.30
	Scenario 7
D	0.10	0.60	0.70
C	0.05	0.50	0.60
B	0.03	0.30	0.55
A	0.01	0.10	0.50

Table 3.

Summary statistics for BTNL and four applications of the proposed method: (1) complete order schedules, no stopping rule, (2) partial order schedules, no stopping rule, (3) complete order schedules, stopping rule, and (4) partial order schedules, stopping rule. Acceptable combination is defined as any combination within ± 10% of the target.

	Scenario
	1	2	3	4	5	6	7
Probability of selecting an acceptable combination as MTD
BTNL	0.87	0.81	0.88	n/a	0.71	0.72	0.54
Proposed (complete, no stop)	0.73	0.86	0.87	n/a	0.81	0.85	0.70
Proposed (partial, no stop)	0.78	0.84	0.82	n/a	0.82	0.84	0.64
Proposed (complete, stop)	0.62	0.75	0.73	n/a	0.64	0.69	0.49
Proposed (partial, stop)	0.64	0.76	0.69	n/a	0.65	0.66	0.43
Probability of selecting no combination as MTD
BTNL	0.00	0.00	0.01	0.90	0.00	0.00	0.00
Proposed (complete, no stop)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Proposed (partial, no stop)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Proposed (complete, stop)	0.00	0.00	0.01	0.24	0.01	0.00	0.00
Proposed (partial, stop)	0.00	0.00	0.01	0.25	0.01	0.00	0.00
Mean number of patients enrolled
BTNL	60.0	60.0	59.5	28.7	60.0	60.0	60.0
Proposed (complete, no stop)	60.0	60.0	60.0	29.0	60.0	60.0	60.0
Proposed (partial, no stop)	60.0	60.0	60.0	29.0	60.0	60.0	60.0
Proposed (complete, stop)	25.6	24.6	22.4	14.5	23.4	24.3	24.3
Proposed (partial, stop)	26.1	25.7	23.3	15.2	24.3	25.5	25.6
Observed incidence of toxicity
BTNL	0.22	0.29	0.34	0.54	0.31	0.31	0.33
Proposed (complete, no stop)	0.21	0.28	0.32	0.50	0.31	0.31	0.33
Proposed (partial, no stop)	0.21	0.29	0.34	0.53	0.30	0.32	0.31
Proposed (complete, stop)	0.18	0.26	0.33	0.52	0.28	0.30	0.29
Proposed (partial, stop)	0.18	0.27	0.34	0.52	0.29	0.31	0.30

For 1000 runs, the maximum simulation standard error is approximately 0.016.

BTNL: Braun, Thall, Nguyen, de Lima method.

In Braun et al. [2], a mean of approximately 60 patients was enrolled in all scenarios, with the exception of Scenario 4 in which all combination are too toxic. In this scenario, a mean of 28.7 patients was enrolled before the trial stopped for safety. In order to provide a justifiable comparison to Braun et al. [2], we ran simulations that exhausted a predetermined sample size, rounded to the nearest integer of the mean sample sizes in Braun et al. (BTNL; [2]). In all simulated trials, the complete number of patients was exhausted and one of the available combinations was recommended at the conclusion of the trial. The goal of presenting these results is to show relative performance of the proposed design to BTNL when enrolling a comparable number of patients.

4.1. Comparison to Braun et al

In Scenario 1, BTNL outperforms the proposed method in terms of recommending an acceptable combination, selecting one of the four doses with DLT probabilities between 0.20 and 0.40 in 87% of simulated trials, while the proposed design for completely ordered schedules does this in 73% of the trials. The methods induce toxicity in a similar proportion of patients (0.22 vs. 0.20). In Scenario 2, our design yields a slightly higher selection percentage for acceptable combinations (86%) than the BTNL (81%) and, again, the methods induce toxicity in a comparable proportion of patients. The methods perform nearly identically in Scenario 3 in terms of selecting acceptable combinations as the MTD (88% vs. 87%).

In Scenario 4, there are no acceptable combinations and the BTNL stops the trial without selecting any combination 90% of the time. The proposed design does not include a stopping rule for this set of simulations, so a comparison in this scenario is difficult. The proposed method, carried out on a sample of 29 patients, chooses the lowest combination in 93% of simulated trials or one of its two diagonal neighbors in another 5%. It is also worth pointing out, approximately 90% of the patients were assigned to the lowest level or one of its two neighboring combinations. In Scenarios 5–7, the performance of the our design for both completely and partially ordered schedules demonstrates superior performance to the BTNL, selecting acceptable doses in approximately 10%, 13% and 16% more simulated trials, respectively. Overall, the simulation results indicate that, in terms of identifying acceptable combinations, the performance of the new method is competitive with that of existing dose-schedule finding methods. It is also important to notice that, even in the presence of partially ordered treatment schedules, the performance of the proposed method does not diminish significantly. In fact, the recommendation percentages for completely and partially ordered schedules are nearly identical in several scenarios, and the former outperforms the latter by merely 4 – 6% in other scenarios.

4.2. Inclusion of a stopping rule

We now examine the design proposed in this work when incorporating the stopping rules described in Section 3.3 for both completely and partially ordered schedules. It is clear from examining Table 3 that our design is performing well in terms of recommending acceptable combinations as well as treating patients at acceptable combinations, for both completely and partially ordered schedules, when the trials are stopped early. For instance, in Scenario 1, the proposed design selects one of the four doses with DLT probabilities between 0.20 and 0.40 in about 62% of simulated trials, while stopping the trial after a mean of approximately 26 patients. In Scenario 2, the proposed designs yield a selection percentage for acceptable combinations in approximately 75% trials and enrolls, on average, approximately 25 patients. In Scenario 3, our method with stopping rules recommends an acceptable combination in 73% of simulated trials while enrolling an average of only 22 patients per trial. The design appropriately stops trials in the presence of toxic combinations. In Scenario 4, all combinations are too toxic, so no combination is acceptable. On average, approximately 15 patients are enrolled before the trial stops about 24% of the time. The method also enrolled a majority of patients on the lowest combination d₁ or one of its two closest neighboring doses, d₂ or d₄, in a large percentage of trials (see Supplementary Material).

In Scenarios 5–7, both completely and partially ordered designs with stopping rules continue to demonstrate strong performance, selecting acceptable combinations in a high percentage of trials and allocating patients to acceptable combinations, while significantly cutting down on the typically large sample sizes seen in Phase I trials with many combinations. In Scenario 5, the method uses an average of 23 patients to recommend an acceptable combination as the MTD 64 – 65% of the time. In Scenario 6, with completely ordered schedules, our design selects acceptable combinations in 69% of simulated trials based on a mean of 24 patients, while with partially ordered schedules, it does this in 66% of trials based on approximately 26 patients. Finally, in Scenario 7, 49% of the time, an acceptable combination is recommended after enrolling 24 patients on average. This scenario contains the largest diminish in performance between complete and partial ordered schedules. Recommendation percentage drops 6% to 43% in partially order schedules from completely ordered. This should not be unexpected in that it is not reasonable to anticipate that a design with partially ordered schedules will perform as well as one with completely ordered schedules in every scenario. We should expect this loss of information to hinder performance in some cases. Overall, the simulation results indicate that the proposed method is a practical design for dose-finding under both completely and partially ordered treatment schedules. We can choose a small number of orderings, so as to reduce the dimension of the problem, and have confidence in the performance of the proposed design in terms of the criteria used to measure its performance in this section.

We also evaluated the performance of the proposed method under true toxicity scenarios that have DLT probabilities that are nonmonotonic in schedule. Table 4 provides the true probabilities under Scenarios 8–13, in which Schedule B is more toxic than Schedule C. These scenarios are Scenarios 1–3 and 5–7 of Table 2 with probabilities for Schedules B and C switched. We did not repeat Scenario 4, in which all combinations were overly toxic. Table 5 provides summary statistics for the performance of the “partial order schedules, stopping rule” application of the design to these scenarios. It is clear from examining Table 5 that the results are very close to those reported for partially ordered schedules / stopping rule in Table 3. This should not be unexpected since we have accounted for the uncertainty of actually knowing whether Schedule B is more toxic than Schedule C (orderings 1–6), or vice versa (orderings 7–12), by considering more orderings in the subset of possibilities. In other words, by taking account of the uncertainty of Schedule B or C being the more toxic treatment schedule, we have guarded against our method being reliant on this information, and thus achieve similar results in each case.

Table 4.

Toxicity scenarios 8–13 for the dose-schedule combinations. Combinations with DLT probabilities between 0.20 and 0.40 are in boldface.

Schedule	Doses in mg/m2
	8	16	24	8	16	24
	Scenario 8			Scenario 9
D	0.22	0.26	0.30	0.31	0.45	0.62
C	0.09	0.12	0.18	0.09	0.21	0.40
B	0.16	0.18	0.23	0.18	0.32	0.54
A	0.05	0.07	0.11	0.03	0.14	0.28
	Scenario 10			Scenario 11
D	0.55	0.62	0.72	0.30	0.48	0.70
C	0.30	0.32	0.50	0.12	0.30	0.48
B	0.45	0.50	0.62	0.14	0.32	0.55
A	0.10	0.26	0.35	0.10	0.28	0.45
	Scenario 12			Scenario 13
D	0.50	0.60	0.75	0.10	0.60	0.70
C	0.12	0.30	0.50	0.03	0.30	0.55
B	0.30	0.50	0.60	0.05	0.50	0.60
A	0.03	0.15	0.30	0.01	0.10	0.50

Table 5.

Summary statistics for “partial order schedules, stopping rule” application of the proposed method in Scenarios 8–13. Acceptable combination is defined as any combination within ± 10% of the target.

	Scenario
	8	9	10	11	12	13
Probability of selecting an acceptable combination as MTD	0.63	0.77	0.68	0.65	0.66	0.43
Probability of selecting no combination as MTD	0.00	0.00	0.02	0.01	0.00	0.00
Mean number of patients enrolled	25.9	25.4	23.3	24.5	25.4	25.8
Observed incidence of toxicity	0.18	0.27	0.34	0.29	0.32	0.30

5. Conclusion

In this article, we have proposed a new design for effectively estimating acceptable dose-schedule combinations in Phase I clinical trials involving multiple courses of study. In these trials, the toxicity order of all combinations is usually not fully known. Further, while we can assume a complete order for the doses under investigation within schedule, it may be that we cannot make this assumption for schedules within doses. Therefore, we have outlined a method that will handle this complexity by relaxing the assumption that toxicity always increases with schedule, and thus can accommodate partially ordered courses of therapy. The simulation results indicate that, in terms of identifying acceptable combinations, our method performs well in comparison to existing dose-schedule finding methods [2]. At the very least, the method gives the investigator an alternative to his or her design preference when presented with a Phase I trial with multiple treatment schedules. Further, the proposed method displays a strong performance for sample sizes that are smaller than have been typically reported in previous literature on dose-schedule finding.

If, for some reason, we happen to know the ordering of all combinations between all schedules, our method reduces to the CRM. The CRM has been shown to have near-optimal properties in trials of a single-agent, which can explain the strong performance of the our proposed design since we are essentially applying the CRM after having taken the extra step of choosing an ordering. Operating characteristics appear to be strong although more study, under a broader range of possible situations, may provide more insight into general behavior. We have tested our method in extensive simulation studies, of which only a small part are presented here. Because it is an extension of the well known CRM, it is believed that it will be more easily understood by clinicians and review boards. Overall, the strong showing of our method in extensive simulation studies gives us confidence in recommending it for practical use.