A unified GMDR method for detecting gene-gene interactions in family and unrelated samples with application to nicotine dependence

Abstract

Gene-gene and gene-environment interactions govern a substantial portion of the variation in complex traits and diseases. In convention, a set of either unrelated or family samples are used in detection of such interactions; even when both kinds of data are available, the unrelated and the family samples are analyzed separately, potentially leading to loss in statistical power. In this report, to detect gene-gene interactions we propose a generalized multifactor dimensionality reduction method that unifies analyses of nuclear families and unrelated subjects within the same statistical framework. We used principal components as genetic background controls against population stratification, and when sibling data are included, within family control were used to correct for potential spurious association at the tested loci. Through comprehensive simulations, we demonstrate that the proposed method can remarkably increase power by pooling unrelated and offspring’s samples together as compared to individual analysis strategies and the Fisher’s combining p-value method while it retains a controlled type I error rate in the presence of population structure. In application to a real dataset, we detected one significant tetragenic interaction among CHRNA4, CHRNB2, BDNF, and NTRK2 associated with nicotine dependence in the Study of Addiction: Genetics and Environment (SAGE) sample, suggesting the biological role of these genes in nicotine dependence development.

Introduction

Understanding how genetic mechanisms contribute to the formation of complex traits is one of the major challenges in genetics studies. Although the recent surge of genome-wide association studies (GWASs) has led to the discovery of many new loci that contribute to phenotypic variation, unraveling the so-called “missing heritability” (Manolio et al. 2009), may require more sophisticated strategies not limited to single-marker analysis. The ubiquitous existence of gene-gene (G×G) interaction is well documented, from the molecular interaction to statistical epistasis, and composes pivotal determinants in the formation of phenotypic outcomes. It is consequently anticipated that G×G interaction will help elucidate some of the missing heritability (Zuk et al. 2012).

Conventional single-marker methods that isolate interacting genes from their context likely obfuscate the interconnected networks and plausibly fail to model the complex gene networks that genuinely relate to a phenotypic outcome. Therefore methods in which association is tested by incorporating multiple genes have been proposed (see a recent review by Cordell (2009)). Among them, multifactor dimensionality reduction (MDR) method, originally for a case-control study, has sustained its popularity since it was proposed (Ritchie et al. 2001). Rather than modeling the interaction term per se as with regression methods, MDR seeks to capture a combination of loci of interest, a pattern that maximizes the phenotypic variation it explains. It treats the G×G interaction as a whole, coinciding to the very original epistasis described by Bateson and offering a solution that avoids decomposition as concerned in regression methods. As it projects the high-order interaction into one dimension, it theoretically overcomes the issue of high dimensionality, provided that the sample size is sufficient. Further development, such as generalized multifactor dimensionality reduction (GMDR), which integrated generalized linear model into MDR (Lou et al. 2007), and pedigree-based generalized multifactor dimensionality reduction (PGMDR) (Lou et al. 2008), allows MDR to be applied to both binary and continuous traits with adjustment for covariates whenever necessary and to pedigree data.

The family-based design and the population-based design (referred as unrelated-individual design) are among the most commonly used designs in genetic studies. Family-based association tests, such as transmission/disequilibrium test (Spielman et al. 1993), are well known for their robustness against population structure, such as population admixture and stratification. MDR has also been extended to family data (Chen et al. 2011; Lou et al. 2008; Martin et al. 2006). On the other hand, the power of family-based designs may decrease when the parental genotypes are uninformative. Although theoretically attractive, a family design is usually not as economically advantageous as an unrelated-individual design that is less laborious in sample collection. However, the genetic backgrounds of subjects in an unrelated-individual design can be quite different from each other, and if the population structure is not taken into account, false positive and false negative associations may arise and thus diminish the advantages of such designs. For unrelated subjects, methods have been proposed to infer genetic ancestry, such as genomic control (Devlin and Roeder 1999), structured association (Pritchard et al. 2000), and the principal components analysis (PCA) method (Price et al. 2006; Zhu et al. 2008) that provides a general solution for more complicated scenarios.

When data from both family-based and population-based studies are available, the ideal strategy is to combine the data, while eliminating the nuisance population structure that may inflate false positive and false negative rates. The consequently enlarged sample size will increase the chances of detecting gene-gene interactions. However, several practical issues arise in the application of this strategy. The major issues are how to correct for the population structure in founders of family samples and unrelated samples, and how to pool two kinds of samples together. A realized solution in association studies is to correct with a fixed effect model for the structure that can be inferred through a principal components analysis of unrelated individuals (Zhu et al. 2008).

Although the issues related to population structure and sample pooling have been well addressed in single-marker association studies, they remains unexplored in detection of interactions. The purpose of this study is to establish a general framework for detecting gene-gene interactions using unrelated and family samples. We proposed a unified nonparametric method, called unified generalized multifactor dimensionality reduction (UGMDR), which detects gene-gene interactions by incorporating both unrelated individuals and families. Simulations were conducted to demonstrate the benefit of the unified analysis to statistical power. A working example, from the Study of Addiction: Genetics and Environment (SAGE), was used to show the application of this method.

Materials and Methods

Correction for Population Structure in Family and Unrelated Samples

When the dataset consists of both unrelated and family samples, we need to correct for population structure and to construct appropriate statistics for combining GMDR analysis. We use unrelated samples including unrelated founders in families to infer ancestral composition of the whole sample and compute the SNP loading for unrelateds and children (see the supplementary method for details). And then we can adjust the phenotype of interest for eliminating effects of population structure by fitting a null generalized linear model (i.e., no effects of factors of interest), for example, a linear model Y = µ1 + PB + Zγ + εY = µ1 + PB + ε for a continuous phenotype, in which Y the vector for the phenotype, µ is the grand mean of the model, 1 is a vector of which all elements are 1, P is a N × L matrix representing the top L principal components for N individuals, B is a vector representing the effects of population structure, Z is the incidence matrix for the covariates such as age and gender, γ is the covariate effect vector, and ε is the vector of residuals. The population structure effects can be corrected by

$$\tilde{Y}=Y-\widehat{\mu }\mathbf{1}-\mathit{P}\widehat{\mathit{B}}-\mathit{Z}\widehat{\mathit{\gamma }}\widehat{Y}=Y-\widehat{\mu }\mathbf{1}-\mathit{P}\widehat{\mathit{B}}$$ (1)

Ỹ is the adjusted phenotypic value for both the principal components and the covariates. In their approach, Zhu et al (2008) suggested adjusting the genealogical effects both on the phenotypes and on the genetic markers, which is more theoretically attractive. In our approach that treats the markers as categorical variables, differing from the typical regression methods that treat genetic markers as quantitative or count variables (e.g., the number of alleles of interest in an additive model), we adjust only on the phenotypes but not on the genetic markers, as incorporating the principal components can substantially eliminate the confounding effects of other covariates. The resulting GMDR is valid in the sense of controlling correct type I error rates. As demonstrated in the simulations, the type I error rates were in good agreement with the given significance levels.

After adjusting for the principal components that account for the potential cryptic population structure, the phenotype and genotype will be independent under the null hypothesis. We use the adjusted phenotype to define an appropriate statistic and integrate with the multifactor data reduction strategy mentioned below. There are two kinds of data involved in the statistic: the sibs in nuclear families are genetically related, and parents of the nuclear families and the singletons are nominally unrelated. For unrelated subjects, the adjusted phenotype is used directly in the data reduction; for convenience of notation, we consider each unrelated individual as a family with only one member and denote statistic s_ij = ỹ_ij where j = 1. For sibs, to take the genetic dependence among the relatives into account, the within-family association statistic is used in the data reduction — the within-family association statistic can be computed via the conditioning algorithms under the null hypothesis, e.g., the within-family association statistic of the j^th individual in the i^th nuclear family with respect to a combination of loci L, ${\mathbf{s}}_{ij}^L={\tilde{y}}_{ij}{\mathbf{g}}_L({\mathbf{x}}_{ij})$ where g_L (x_ij) is a function contrasting the transmitted genotype at locus combination L to its reference distribution under the null hypothesis (Chen et al. 2011). For simplicity of notation, we discard the sign of locus combination in ${\mathbf{s}}_{ij}^L$ and g_L (x_ij) thereinafter. The principle behind the conditioning algorithm is as follows. Given a mating type (parental genotypes) or its minimal sufficient statistic, we have the reference genotypic distribution of offspring under the null hypothesis, denoted by G_M; different mating types have their respective genotypic distributions of offspring. Each of these genotypic distributions follows Mendel’s law only, and thus is independent of any phenotype. Nevertheless, the observed (or transmitted) genotypic distribution of offspring may differ conditional on the mating type and a trait of interest in the presence of genotype-phenotype association, denoted by G_M,T. The discrepancy between them will ascribe to the association of the combination of loci with the trait only, thus eventually eliminating the impact of locus-specific spurious association through comparison between G_M and G_{M, T}. Detailed numerical examples for conditional genotype distribution on nuclear families can be found in Rabinowitz and Laird (2000).

Multifactor-Reduction Algorithm

Our method is devised by integrating the statistic defined in the previous subsection (i.e., s_ij = ỹ_ij for unrelated subjects and s_ij = ỹ_ijg (x_ij) for siblings) into the GMDR framework, whose implementation of C-fold cross-validation (CV) is summarized as follows.

In step one, regardless of their familial or ethnic origins, individuals are assigned into C even or nearly even subdivisions. One of the subset is used as the testing set and the remaining one(s) as the training set. We set C = 10 throughout this report, but it can be other integers, such as C = 5 (Motsinger and Ritchie 2006).

In step two, a subset of γ factors are selected from all ω discrete factors of either genetic and/or environmental origin. A total of $\left(\begin{array}{c}\omega \\ \gamma \end{array}\right)$ distinct subsets can be chosen in this manner. Each such subset corresponds to a γ-dimensional finite grid, and each subject who is genotyped and assessed for the environmental exposures will fall into exactly one cell in this grid. The values of the statistic defined in the previous subsection are averaged over each cell. Each nonempty cell is labeled either high-risk if its average statistic value is not less than some threshold T, or low-risk otherwise. Without loss of generality, $T={\sum }_{i=1}^N{\sum }_{j=1}^{K_i}{\widehat{s}}_{ij}/N_T$, the mean of the sample, is used throughout the paragraphs below.

In step three, a multilocus model is formed by pooling high- and low-risk cells into two groups (i.e., high-risk and low-risk). The classification accuracy can be assessed by the averages of the statistic values in the high-risk group and the low-risk group, respectively.

In step four, the corresponding independent testing set (the set that is left out in steps two and three), is used to evaluate the testing accuracy for the model identified in step three. The testing accuracy is defined in the next subsection.

In step five, as there are C different pairs of training-testing sets, the above procedure is repeated for C rounds on the C training sets. The average testing accuracy over C testing sets can be calculated.

In step six, steps two to five are iterated for all other possible γ factor combinations, and the above procedure is repeated for $\left(\begin{array}{c}\omega \\ \gamma \end{array}\right)$ combinations.

Evaluation of p-value

In each round of cross-validation, testing accuracy (TA) is defined as:

$$\text{TA}=\frac{\text{TA}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}$$ (2)

where TP is True Positive, defined as having a high-risk value in the high-risk group, TN is True Negative, defined as having a low-risk value in the low-risk group, FP is False Positive defined as having a low-risk value in the high-risk group, and FN is False Negative defined as having a high-risk value in the low-risk group. For a training set, the rule of classification guarantees that classification accuracy is not less than 0.5; whereas TA may be lower than 0.5 due to statistical fluctuation. TA has an expected value of about 0.5 under the null hypothesis. Over C-fold cross-validation, the mean of TA, i.e., $\overline{TA}={\sum }_{i=1}^{C}T{A}_i$, is calculated and employed as the test statistic for evaluating G×G interaction.

In general, we use a permutation method to determine empirical p-value from the distribution of the permuted TAs under the null hypothesis. When the sample size is sufficiently large, as the result of the central limit theory, the p-value can be approximately assessed by the normal distribution of the C-fold mean of TA under the null hypothesis. An approximate Z score is $Z=\frac{\overline{\mathit{\text{TA}}}-E(\overline{\mathit{\text{TA}}})}{\sqrt{\text{var}(\overline{\mathit{\text{TA}}}})}$. The mean and standard deviation of TA could also be computed through permutations. It should be noticed that, there are two kinds of data involved in the test statistic. The sibs in nuclear families are genetically related, and parents of the nuclear families and the singletons are nominally unrelated. Although the genealogical effects of unrelated individuals can be adjusted through regression on the principal components, the family structure should be fully accounted for in building the test statistic. We use a hybrid strategy to evaluate the mean and empirical variance of the test statistic in permutations. As the genealogical effects of the unrelated individuals have already been adjusted, these singletons are exchangeable with each other in permutations, but the sibs are randomly shuffled only within the family because of the family structure effects. Permutations can be run for either the phenotype or the genotype at loci under consideration; both permutation schemes often yield nearly identical results. In this report, we permute phenotypes only.

Monte Carlo Simulations

Systematic simulations were performed to investigate the power in various scenarios. A recent admixed population with a similar ancestry to African-Americans was simulated for the scenarios considered. Four study designs with different sample size and ratio of families to singletons were adopted in the simulation study as tabulated in Table 1. Various disease models, relative risks and allele frequencies were considered in simulations (refer to the supplementary materials for details). To compare the proposed unified strategy with the separate analysis strategies, we computed the power of four methods: FAM for family-based method conditional on parental genotypes in which only sibs were used, CC for case-control method in which only case-control samples but no family samples were used, UN for method of unrelated individuals in which cases, controls and founders of families were used, and UI for the proposed unified method in which all cases, controls, founders of families and sibs are used. These first three methods are used as the reference methods for power comparison.

Table 1.

Design of the simulation experiments

Samples	Design I	Design II	Design III	Design IV
	200 families each with a discordant sibpair & 200 cases & 200 controls	200 families each with three siblings & 200 cases & 200 controls	200 families each with three siblings & 500 cases and 500 controls	320 families each with three siblings & 200 cases and 200 controls
Case-control	400	400	1000	400
Unrelated	800	800	1400	1040
Siblings	400	600	600	960
Total individuals	1200	1400	2000	2000

Notes: In Design I, neither parents were affected, whereas in Design II~IV at least one parent was affected.

UI was also compared with a benchmark method, the meta-analysis implemented with the Fisher’s combining p-value method for individual UN and FAM analyses (Fisher 1954). A Chi-square test statistic with four degrees of freedom was computed from the p-values of UN and FAM to determine the overall p-value and statistical power.

A Case Study

In this study, we managed to detect interactions among genes in the cohort for Study of Addiction: Genetics and Environment (SAGE). Majority of SAGE samples are unrelated, in addition to a few families, including, after quality control, a total of 3897 individuals from three subsamples: the Collaborative Study on the Genetics of Alcoholism (COGA) (1,178 individuals), the Collaborative Study on the Genetics of Nicotine Dependence (COGEND) (1,427 individuals) and the Family Study of Cocaine Dependence (FSCD) (1,292 individuals). Although many phenotypes were recorded, we were primarily interested in the genetic mechanism of nicotine dependence. SNPs in the nicotinic acetylcholine receptor (nAChR) α4 subunit (CHRNA4), the nicotinic acetylcholine receptor (nAChR) β2 subunit (CHRNB2), the neurotrophic tyrosine kinase receptor 2 (NTRK2, also known as the tyrosine kinase receptor gene, TrkB), and the brain-derived neurotrophic factor (BDNF) were selected to detect the G×G interaction among these genes.

The principal components analysis was run for the SAGE data to investigate the population mixture. The score statistics for nicotine dependence were computed in a logistic regression with adjustment for age, sex and the top five principal components. The unified method proposed in our study was used for three sub-samples individually and the whole sample. As a contrast, the meta-analysis was also conducted with the Fisher’s combining p-value method.

Results

Simulation Study

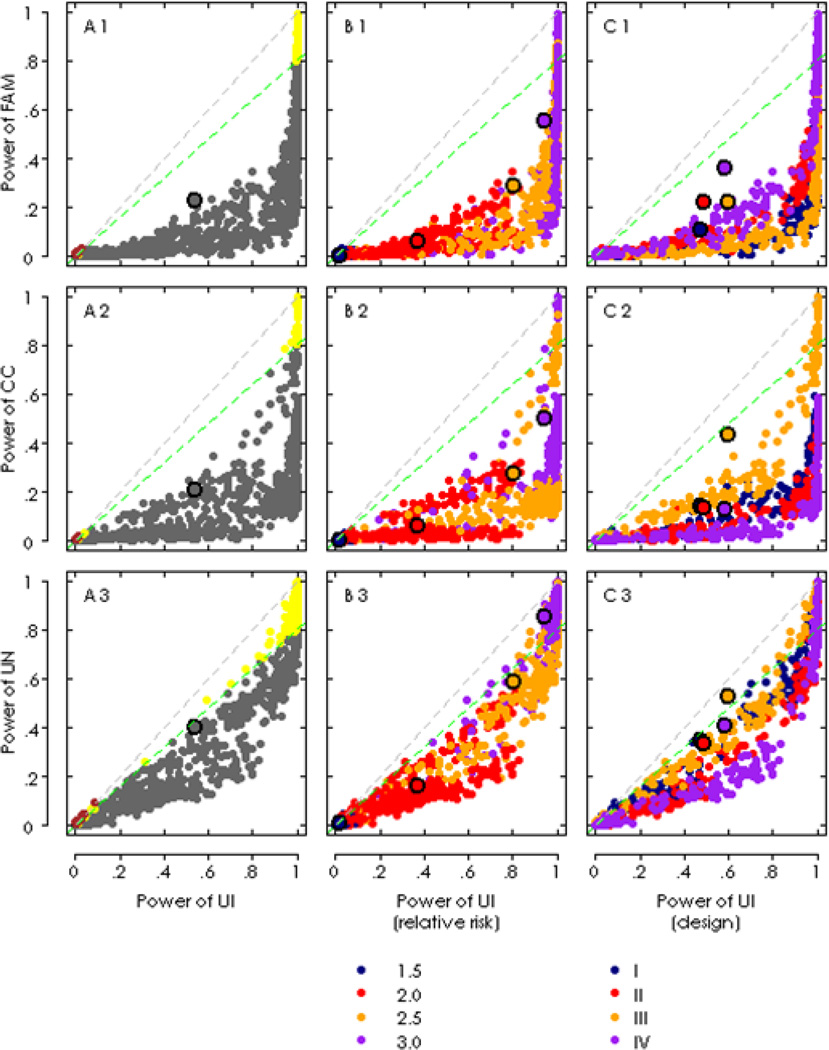
As the principal component method can precisely identify the ancestry of each individual (see the Supplementary result section and Supplementary Figures 1 and 2), we could use principal components to control population structure and get well controlled type I error rates (Supplementary Table 1). Simulations suggested UI in general outperformed the three reference methods in terms of power under various settings in the simulations (see Supplementary Table 2 for the impact of the power due to the simulated factors simulated). Figure 1 presents the power comparison of UI to the three reference methods. As shown in the first vertical panels (on the left side in Figure 1), the means of power over the 1200 scenarios, denoted by the black circles whose coordinates in the horizontal and the vertical axes were the mean of UI and that of a method compared in each panel, respectively, were about 0.55 for UI, 0.22 for FAM, 0.21 for CC, and 0.41 for UN. In other words, UI had a higher, at least 0.14, average power than the other methods (Also see Table 2 for details). The dots below the green lines indicate the power values of the other three methods that were less than 80% of UI, and most of those scenarios seemed to be of moderate statistical power values. And for those over the green lines, most were of powers close to 1 (few were close to zero), when relative risk was not less than 2.5 as indicated in panel B. In terms of power, the second best method was UN (Figure 1 A3), since around 35% scenarios reached 80% power of UI when relative risk not less than 2.5 under Designs III and IV. Very few scenarios, the dots highlighted in brown in the first vertical panels, the powers of UI appeared to be lower than the other three methods, but their values were extremely low. It seemed to be more likely attributed to sampling errors. Compared with other two reference methods, UN had the closest power to UI (Supplementary Figure 3) probably because UN can use more individuals than CC and FAM (Table 1). As UI can use all individuals in the simulated samples, whereas the other three methods could only use a part of them, it seemed well reasonable that UI outperformed other methods.

Figure 1.

Power comparison between the unified method and three reference methods given alpha=0.05. A The overall comparison of the power values. The gray points below the blue lines indicate the power values in their respective reference methods were less than 80% as much as the UI method, yellow points (yellow) larger than 80% but less than UI, the brown points greater than UI. The means of power were indicated with black circle, filled with gray, the horizontal value. B Comparison of the power with regard to the levels of relative risk. The means of power were indicated by the black circles, filled with their respective color of the level which they referred to. C Comparison of the power with regard to the study design. The means were represented the same as the panel B.

Table 2.

Power comparison for admixture population at alpha=0.05¹

Design Methods	I				II				III				IV
	FAM 2	CC 3	UN 4	UI 5	FAM	CC	UN	UI	FAM	CC	UN	UI	FAM	CC	UN	UI
RR=1.5
Checkerboard	.005	.003	.005	.017	.008	.003	.007	.026	.006	.012	.023	.047	.012	.003	.009	.037
Diagonal	.002	.003	.006	.013	.004	.001	.003	.013	.003	.008	.012	.027	.004	.001	.005	.016
Upper corner	.000	.001	.004	.008	.001	.001	.003	.008	.001	.006	.009	.015	.003	.002	.005	.016
RR=2.0
Checkerboard	.036	.023	.119	.324	.079	.025	.122	.405	.080	.249	.457	.719	.221	.028	.217	.693
Diagonal	.019	.024	.092	.210	.034	.019	.074	.261	.037	.161	.286	.477	.127	.026	.145	.486
Upper corner	.006	.016	.065	.120	.016	.015	.052	.152	.022	.133	.248	.376	.049	.013	.083	.274
RR=2.5
Checkerboard1	.203	.174	.613	.899	.389	.182	.602	.949	.410	.826	.956	.994	.787	.183	.783	.994
Diagonal	.082	.121	.431	.702	.227	.124	.404	.736	.268	.724	.899	.974	.505	.119	.569	.816
Upper corner	.043	.101	.357	.553	.084	.091	.259	.500	.125	.528	.693	.797	.315	.093	.453	.779
RR=3.0
Checkerboard	.460	.489	.932	.995	.764	.484	.933	.999	.790	.986	1.00	1.00	.973	.491	.987	1.00
Diagonal	.256	.375	.837	.970	.653	.398	.862	.991	.573	.917	.960	.980	.739	.308	.820	.962
Upper corner	.140	.323	.742	.863	.360	.275	.655	.849	.312	.672	.739	.801	.624	.262	.770	.909
Mean power	.104	.138	.350	.473	.218	.135	.331	.491	.219	.435	.524	.601	.363	.127	.404	.582

Notes:

¹Power = the proportion of true models significant at the given significance level in all simulations. Each power in this table is the mean of 25 scenarios, each of which was sampled on allele frequency between 0.05~0.95 and then replicated 500 times.

²FAM for family-based method

³CC for case-control method

⁴UN for unrelated individuals (unbalanced case-control)

⁵UI for unified method

We also examined the influences of different relative risks on power. Under each factor, simulations under each relative risk level were plotted as scattered points according to the means of power of UI (x-axis) and a reference method (y-axis) in each panel, providing a straight comparison. Then the distributions of the points filled with different color elucidated the pattern of power value under each method. As anticipated, the power increased with the relative risk. UI appeared to increase power substantially by 0.46 when the relative risk was increased in the interval of 2.0 (mean power=0.39) to 2.5 (mean power = 0.85), but increased by only 0.09 in the interval of 2.5 to 3.0. Similar trends were observed in the other three methods. When relative risk was as low as 1.5, neither UI nor a reference method demonstrated a practically appreciated statistical power regardless of the change of other factors.

The mean powers of UI were 0.45 and 0.53 for designs I and II, respectively, showing an improvement of ~0.08 caused by the addition of one offspring in each of the 200 nuclear families. After adding other 600 individuals to Design II, by either recruiting more unrelated samples in Design III or family samples in Design IV, the power increased to 0.606 and 0.607, respectively. This indicates that an increase in unrelated samples can give a power gain similar to an increase in nuclear families and, in practical application, we can adopt either of the two alternative recruitment schemes according to how easily the sample can be recruited.

The powers always increased corresponding to the magnitude of relative risk. The checkerboard models tended to have higher powers compared to the other two models. The general patterns are summarized in Figure 1. The corresponding patterns could be tied to their causes. For example, in Figure 1 B2, red points (RR=2.0) were clustered into two groups, and Table 1 indicates that it is the upper group that was arisen from increasing the case-control sample size by 600 individuals. When the alpha was decreased to 0.01, powers dropped off (Supplementary Table 3). But the averaged powers (in bold font) dropped less with UI compared to the reference methods. In Design IV, the mean powers of UI decreased from 0.607 down to 0.519 (by 14%), but for CC, from 0.138 down to 0.07 (by 49%).

Meta-analysis is used as a method to strengthen the signal from independent studies. Although FAM method using siblings only and the UN method using unrelated individuals can add up together to use the whole sample, their combined p-values, determined by the Fisher’s method, were not as powerful as our proposed unified method (Supplementary Table 4), consistent with the results from single-marker association studies (Macgregor 2008; Skol et al. 2007).

Real Data Analysis

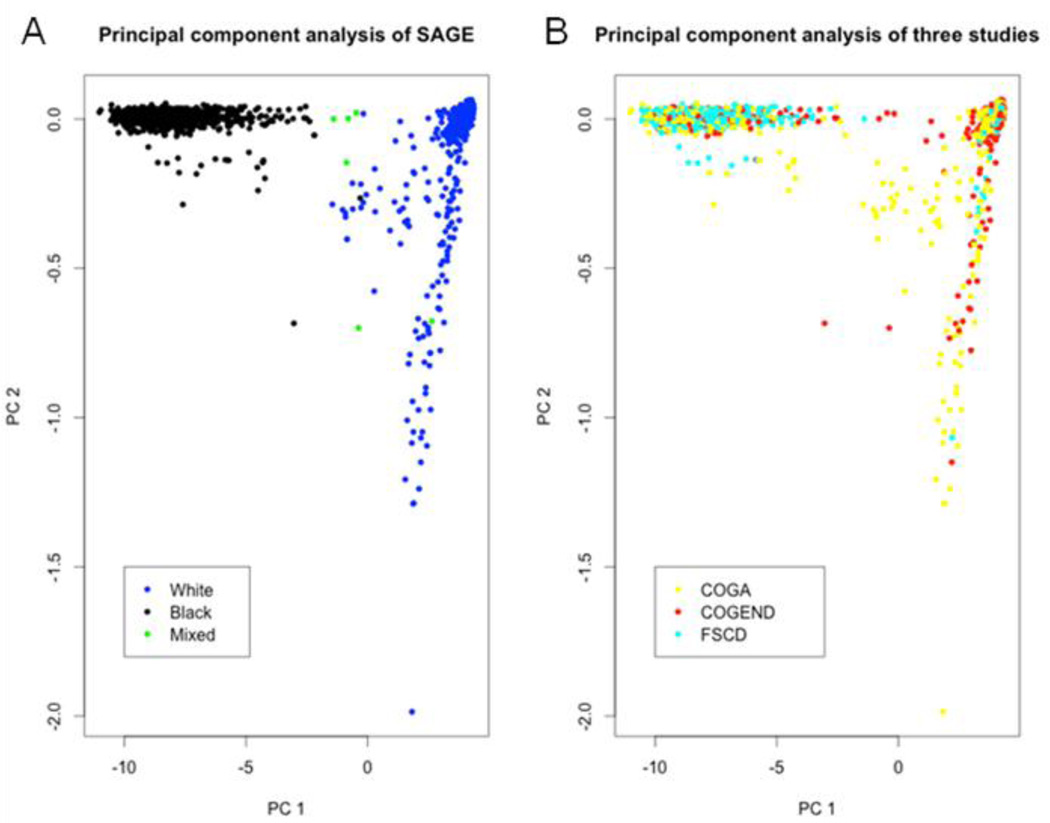
As illustrated in Figure 2A, there were black, white and mixed individuals in the SAGE cohort, and the admixed genetic background in fact was across each of the three subsamples in SAGE (Figure 2B). In this sense, SAGE made itself a suitable sample for demonstrating the unified GMDR methods.

Figure 2.

The principal components analysis for SAGE. As there were relatives in the SAGE sample, two-stage method, as described in our method, was used for building principal components. A) the genetic background of the SAGE sample were plotted into the first and the second PC axes. B) the genetic background for the three sub samples in SAGE in the first and the second PC spaces.

Recent studies revealed genetic associations with nicotine dependence of CHRNA4 (Feng et al. 2004; Li et al. 2005), NTRK2 and BDNF (Beuten et al. 2005). As indicated by biochemical studies, in the brain the α4β2-containing nAChR subtype makes up the majority of the high-affinity nicotine-binding sites and that under chronic nicotine exposure the genes for both subunits are upregulated. In our previous study, we also discovered the interaction among CHRNA4, CHRNB2, BDNF and NTRK2 underlying nicotine dependence (Li et al. 2008; Lou et al. 2007). Given the SNP information (dbSNP, Build 135), SAGE sample was mapped to 8 SNP markers in CHRNA4, 4 in CHRNB2, 25 in BNDF, and 130 in NTRK2, respectively, and in total it generated 104,000 (8×4×25×130) tetragenic interactions, one SNP from each of the four genes. The phenotype of interest was nicotine dependence, of which SAGE had 1,765 nicotine dependent individuals and 2,036 individuals not. The numbers of individuals that survived after quality control and also had the nicotine dependence phenotype are shown in Table 3 but the exact individuals used varied, due to missing genotypes or availability of other covariates, with each interaction model tested.

Table 3.

Interaction SNPs detected among CHRNA2, CHRNA4, BDNF and NTRK2

Model 1	Effective Individuals 2	Variance Contributed	Testing accuracy	p-value
rs1013402-rs1044394-rs2072660-rs6559840
SAGE	3786 (134)	0.0176	0.5468	6.46e-06
FSCD	1275 (121)	0.036	0.5428	5.81e-03
COGA	1089 (5)	0.0352	0.5156	1.35e-01
COGEND	1422 (6)	0.0125	0.4691	9.20e-01
META				2.48e-02

Notes:

¹In each model, from left to right, the SNPs are located in BDNF, CHRNA4, CHRNB2, and NTRK2, respectively.

²The used individual for detecting each tetragenic interaction model, and in the parenthesis were the number of siblings.

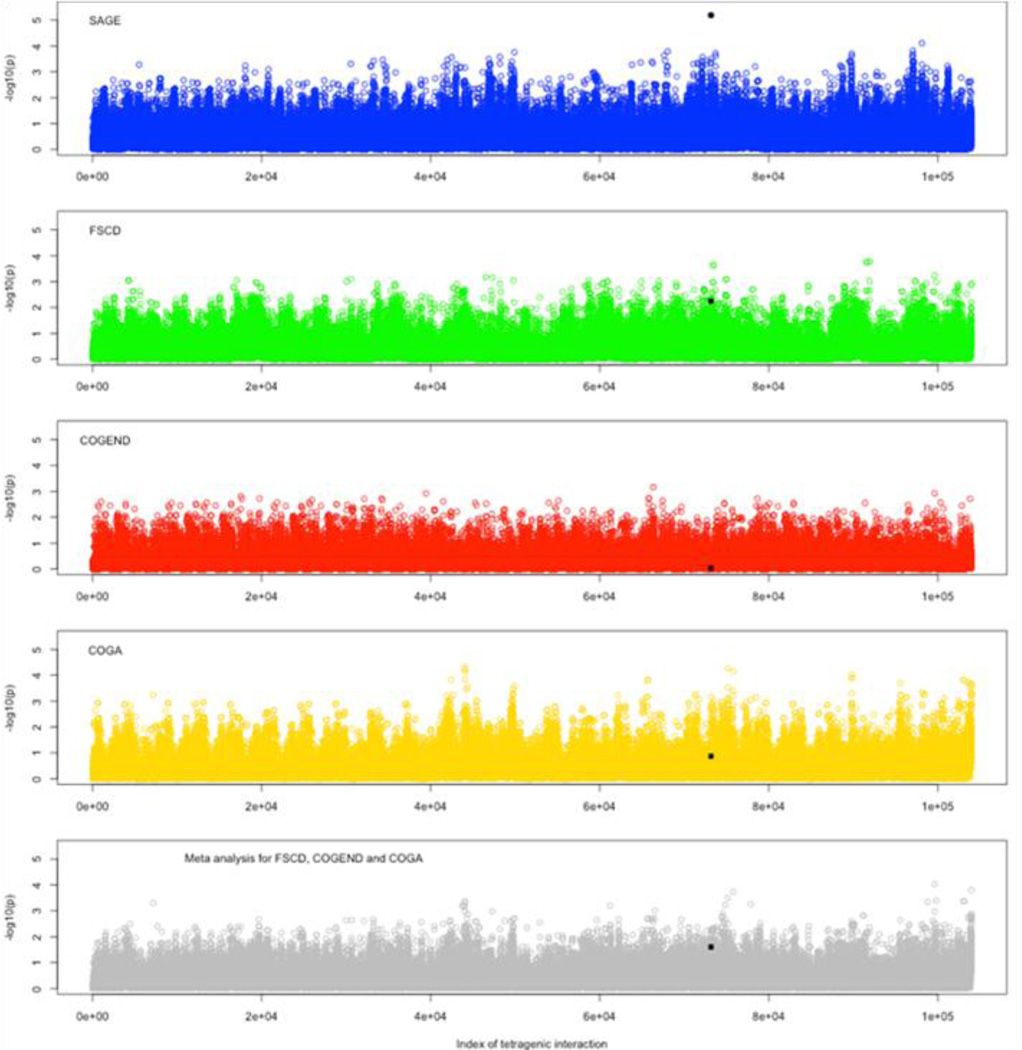
Using the unified method, we tested 104,000 tetragenic interaction models, which include one SNP marker from each gene. As expected, the distribution of the testing accuracy is a normal distribution (Supplementary Figure 4). Figure 3 shows Manhattan plots of the p-values from the analyses of the whole sample and three sub-samples, and the meta-analysis, respectively. The most significant tetragenic interaction model was rs1013402-rs1044394-rs2072660-rs6559840, having a p-value of 6.46e-06, which was detected in SAGE, whereas its p-values in the each of the subsamples and the meta-analysis for the three subsamples were less significant. It should also be noticed that because of the high linkage disequilibrium between SNPs within genes, the practical threshold of p-value would not be as conservative as the one given by Bonferroni correction. The p-value to declare significance remains an open question for the detected interactions. However, accounting for our previous discovery (Li et al. 2008; Lou et al. 2007), this p-value indicated that there was potential interaction of these four genes underlying nicotine dependence.

Figure 3.

Manhattan plots for tetragenic trans interactions. Manhatton plots for SAGE, FSCD, COGEND, COGA, and the meta analysis. The black square represented the interaction, rs1013402-rs1044394-rs2072660-rs6559840, which had the highest p-value in SAGE and in the three sub samples.

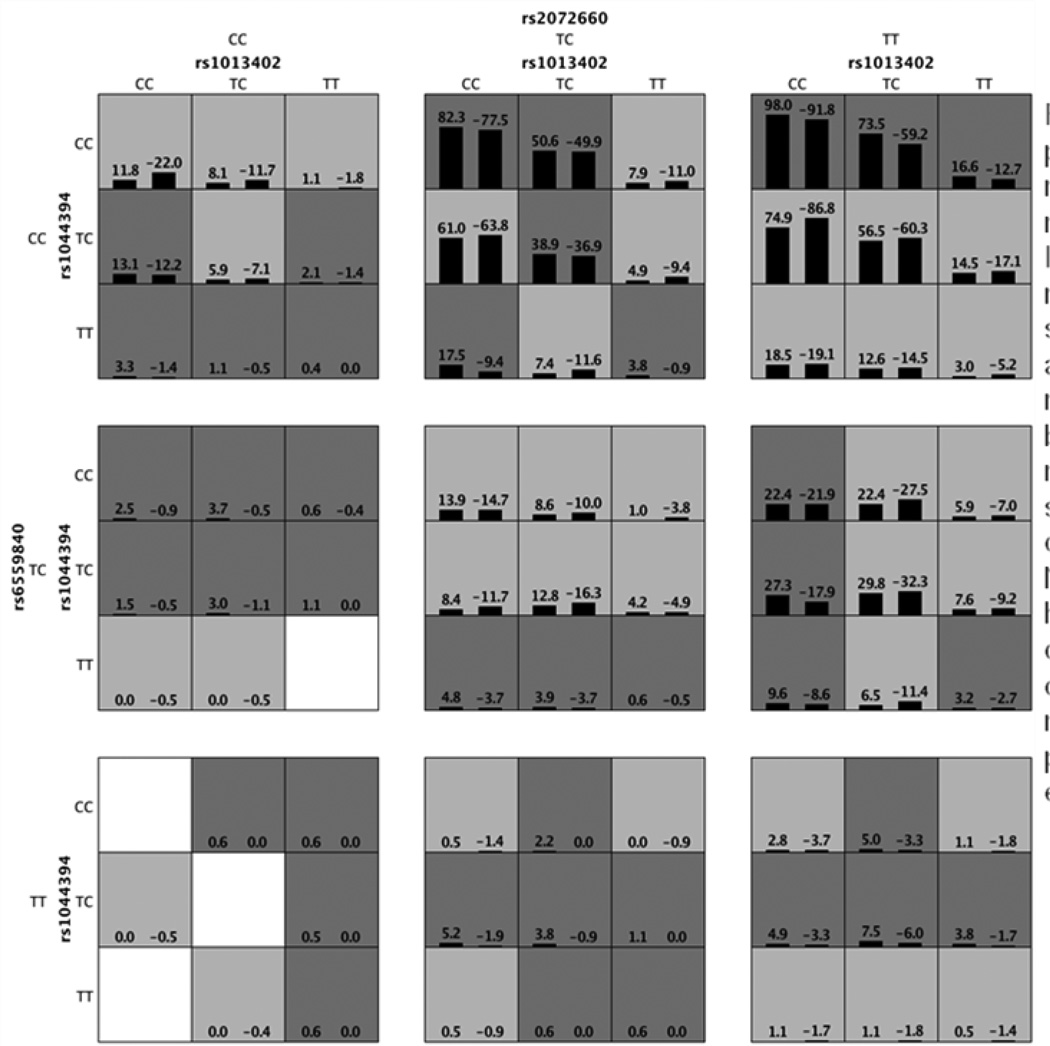
The high-risk and low-risk distribution of the identified multilocus models could be further illustrated (Figure 4). The patterns of high-risk and low-risk cells varied across each of the different multilocus dimensions, presenting evidence of epistasis. With increasing interaction loci, it is possible, given limited sample size, that merging empty genotypic cells might decrease robustness of a model. The biological mechanism, partially as revealed (Li et al. 2008), underlying the tetragenic model requires further investigation both through in silico analysis and laboratory verification in the future. However, it should be noticed that genetic heterogeneity on etiology has not been considered especially when across multiple cohorts of differential genetic admixture. It remains further investigation that the variation of the strength of the illustrated tetragenic signals in three cohorts reflects power issue or various genetic etiologies.

Figure 4.

The interaction pattern among rs1013402-rs1044394-rs2072660-rs6559840. In each cell, the left bar represents a positive score, and the right bar a negative score. High-risk cells are indicated by dark shading, low-risk cells by light shading, and empty cells by no shading. Note that the patterns of high-risk and low-risk cells differ across each of the different multilocus dimensions, presenting evidence of epistasis.

Discussion

Detecting G×G interaction underlying complex traits is getting increasing attention in genetic studies. Many theoretical and application studies have revealed the importance of interactions in the formation of phenotypic outcomes (Zuk et al. 2012). There is little doubt that interactions among genes play an important role in the genetic architecture of complex traits. In order to foster drug development and establish proper medical interventions, identifying G×G can be crucial. There are a couple of terms, such as statistical interaction, epistatic interaction, and additive interaction, commonly used in describing gene-gene interactions, as summarized in the literature (Wang et al. 2010). In our study, the interpretation of the interaction defined in this report is close to multilocus model or joint action of genes. Once interaction models of interest are identified using the method proposed, follow-up analysis might be applied depending on the purpose of the study. If statistical interaction is of interest, for example, main effects and interaction effects can be further estimated for a detected multilocus model. Given the method introduced in this report, after correction for population stratification, the unified GMDR can maximize the number of individuals available in the sample. As demonstrated in our simulations, the unified method had higher power in many of the scenarios simulated.

For the unified method proposed, the first step is to capture the genetic background of the sample. Currently, a couple of methods have been proposed (Price et al. 2010). PC coordinates can be inferred from the unrelated set of the sample (Zhu et al. 2008), such as used in our method, or inferred from another independent dataset. As demonstrated in our study, this method, either applied to an admixed population or a discrete population, can extract population structure in terms of ancestral origin very well and consequently control the type I error rate. The genetic interpretation of the first principal component was well connected to the averaged coalescent times between populations and Wright’s F_st statistics (McVean 2009), whereas the interpretation of admixed population, such as African Americans, requires careful modeling of the historical gene flow (Gravel 2012). Alternatively, mixed model approaches are also applied to control for population structure which may inflate the type I error rate (Wu et al. 2011). From the viewpoint of genetics, both methods used nearly the same genetic information. Using PCA tends to consider the effects due to genetic origin as fixed, whereas mixed model approaches treat them as random. So far, no conclusion is reached on which method is more appropriate in application. Although we demonstrated the advantage of improving statistical power after adjusting population structure by PCA, which are served as covariates in building the score statistic, the impact of including covariates may depend on other factors, such as prevalence of the disease. It should be noticed that decreasing power may occur under some scenarios (Pirinen et al. 2012). This topic deserves further investigation in relation to our method.

We assume there is no relatedness between the case-control individuals and the founders, who are used in estimating eigenvectors. In some cases particularly in the context of samples from isolated populations, cryptic relatedness may be problematic or there exists known relatedness. It is needed to incorporate the kinship coefficients or estimated kinship coefficients into the statistical model for eliminating relatedness effects (Bourgain et al. 2003; Choi et al. 2009). Furthermore, stringent quality control should be applied for excluding subjects with cryptic relatedness from GMDR analysis when it is an issue.

In the real data analysis, although our previous analysis (Lou et al. 2007) also detected tetragenic interaction analysis for nicotine dependence, but a case-control sample, with 382 subjects, was used at that time and as a result the p-value was not as significant as demonstrated in the present study. Classifying nicotine dependence into cases and controls also cause loss of information and consequently underestimate the genetic variance it explains. The real data analysis in this report showed more advantageous in power than our previous study. With our proposed method, it used a much bigger sample size, superior in statistical power after its population stratification had been corrected. As a typical complex trait, the genetic variants underlying the formation of nicotine dependence may be tiny in effect size but large in their total number. To reveal their genetic architecture, using single-marker based methods seem insufficient. As demonstrated in this report, as well as previous success cases, methods such as UGMDR may empower the discovery of the genetic determinants.

Limitations should be noticed for the proposed method. As it is currently designed for pooling unrelated sample with siblings from the nuclear families, complex pedigrees require more sophisticated calculation, such as attempt of controlling population structures with linear models or using flexible permutation strategies. In theory, the unified method can be extended to complex pedigrees but will increase the computational time exponentially with the generations included. The computational challenge and multiple testing problem also pose another hurdle in practice, especially for detecting high-order interactions for the whole genome data. More theoretical and computational work is required to address these challenges.