Fragment-based error estimation in biomolecular modeling

Abstract

Computer simulations are becoming an increasingly more important component of drug discovery. Computational models are now often able to reproduce and sometimes even predict outcomes of experiments. Still, potential energy models such as force fields contain significant amounts of bias and imprecision. We have shown how even small uncertainties in potential energy models can propagate to yield large errors, and have devised some general error-handling protocols for biomolecular modeling with imprecise energy functions. Herein we discuss those protocols within the contexts of protein–ligand binding and protein folding.

Introduction

Computer modeling of chemical processes has become an almost routine part of designing, directing, validating and sometimes predicting results of experiments in chemical, pharmaceutical and material sciences. The field has bridged a gap between theory and experiment that was previously difficult to traverse, especially for large biological systems. Computer models for biomolecular simulation have traditionally utilized simple potential energy functions that treat molecules as point charges bound by classical spring-like potentials and Lennard–Jones interactions [1]. Today, in the modern era of high-performance computing, the computational chemist’s toolbox is filled with hundreds of different theoretical models incorporating various physical effects with different approximations and parameters for different types of systems. Each model has its own set of advantages and disadvantages, and choosing the correct computational model for a particular problem has become an important initial step in chemical modeling.

To alleviate some of the difficulty in choosing an appropriate computational model, many reports have been published offering benchmark data for various models and methods on some subset of chemical space. Typically one selects the model with the lowest error (by RMS error or some other metric) for the relevant chemical system(s) and cites the benchmark work to give indication of probable error magnitudes. Unfortunately, computational chemistry has not made nearly as much use of statistical error concepts as have other fields like engineering or experimental biology [2]. Even so, some of the most successful algorithms in molecular modeling intrinsically benefit from error cancelation. Consensus scoring, wherein multiple scoring functions contribute to the overall score of the pose of a ligand in a binding site, typically leads to better predictions than individual scoring functions because uncertainties in the individual scores tend to cancel when averages are taken [3]. Another example is free energy perturbation where free energy differences are calculated by investigating the effects of alchemical mutations in a molecule [4,5]. Usually only a small number of molecular interactions are modified at a time, while the errors in the rest of the system largely cancel [6]. This can lead to reduced error in predictions as well.

If modelers were able to estimate their errors on-the-fly, they could correct for systematic errors and compare calculated values (e.g. conformational energies, binding affinities) using confidence intervals to give quantitative estimates of the reliability of their predictions. Recently we have been investigating methods for error estimation in biomolecular modeling [7–10]. In the following sections we will describe our approach, which includes on-the-fly systematic and random error estimation for proteins and protein–ligand complexes.

Fragment-based modeling

Large biomolecular systems can be considered as a set of many fragment interactions with each fragment contributing to the total potential energy of the system. For example, a small drug-like molecule could bind to a protein receptor in a pose consisting of a few distinct hydrogen bonds and several favorable van der Waals contacts (Figure 1) [11]. In the realm of proteins, a native protein fold is held together by many intramolecular interactions such as backbone–backbone hydrogen bonds and sidechain–sidechain interactions that stabilize the native structure enough to compensate for the loss of configurational entropy during the folding process [12,13]. Each of these component interactions has to be modeled accurately to make reliable in silico predictions [14].

Figure 1.

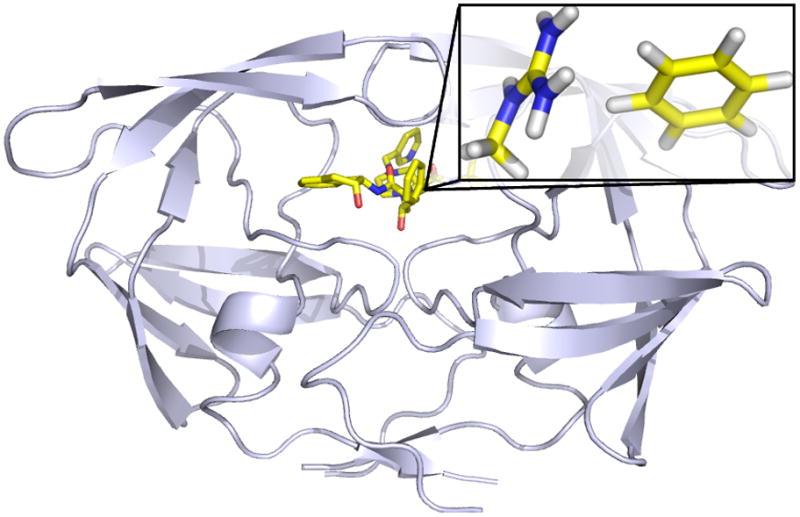
Structural model of an example protein–ligand complex (HIV-2 protease bound to indinavir). The binding pose can be decomposed into several distinct fragment interactions, such as hydrogen bonds and van der Waals contacts. An arginine–phenyl group interaction is highlighted here as an example. Each fragment-based interaction approximately contributes to the potential energy (not free energy) of the system independently. Therefore each fragment-based interaction approximately contributes error to the overall potential energy independently.

Additive energy models

To derive tractable error estimation formulas, we assume that fragment contributions to potential energy are independent and additive. This assumption is the basis of fragment-based drug design (FBDD) efforts as well as of most force field energy models. Theoretical support for the approximation can be seen in the work of Mark and van Gunsteren, who showed that energies and enthalpies can be represented by sums of fragment contributions if the global Hamiltonian is separable [15]. The same is not true for free energy or entropy, however. Empirical evidence from Baum et al. supports this claim [16]. Via isothermal titration calorimetry (ITC) assays of a series thrombin inhibitors, the authors showed that identical functional group modifications across the set of ligands yielded different effects on the free energy of binding (|ΔΔΔG| values of 0.5–0.7 kcal/mol), but the spread of changes in enthalpies of binding were very small (|ΔΔΔH| values of 0.02–0.07 kcal/mol). In other words, the change in free energy of binding as a result of the modification of a specific functional group in the ligand had a significant dependence on the remainder of the ligand, whereas the effects on enthalpies of binding were, by comparison, not very sensitive to the environment, suggesting that the enthalpic effects were approximately additive. Computational evidence can be seen in the study of many-body effects (here the ‘bodies’ are chemical fragments) in protein–ligand interaction energies by Ucisik et al., in which the interaction energy between a HIV-2 protease model and indinavir was computed (i) directly and (ii) as a truncated many-body expansion with different potential energy models [17]. Magnitudes of nonadditivity were measured by comparing the sums of two-body terms to the directly computed interaction energies. It was found that deviations from an additive model represented 0.1%, 0.9% and 14% of the total interaction energy for the M06-L/6-31G*, PM6-DH2 and HF/6-31G* models, respectively. Thus the additive model is a better approximation within some energy models than others, but in every case the two-body additive term is the dominant contributor to total protein–ligand interaction energies.

Error propagation

If we assume that each fragment interaction in a composite molecular system contributes to overall potential energies independently from the others (Equation 1), then Taylor series error propagation ends at first-order so that interaction energy errors propagate as either Equation 2 or Equation 3 depending on whether they are systematic or random [18].

$$\mathrm{\Delta }{E}_{int}^{\mathit{Total}}\approx \mathrm{\Delta }{E}_{int}^1+\mathrm{\Delta }{E}_{int}^2+\mathrm{\Delta }{E}_{int}^3+\cdots$$ [Equation 1]

$${\mathit{Error}}_{\mathit{Systematic}}={\mathit{Err}}_1+{\mathit{Err}}_2+{\mathit{Err}}_3\dots$$ [Equation 2]

$${\mathit{Error}}_{\mathit{Random}}=\sqrt{{\mathit{Err}}_1^2+{\mathit{Err}}_2^2+{\mathit{Err}}_3^2\dots }$$ [Equation 3]

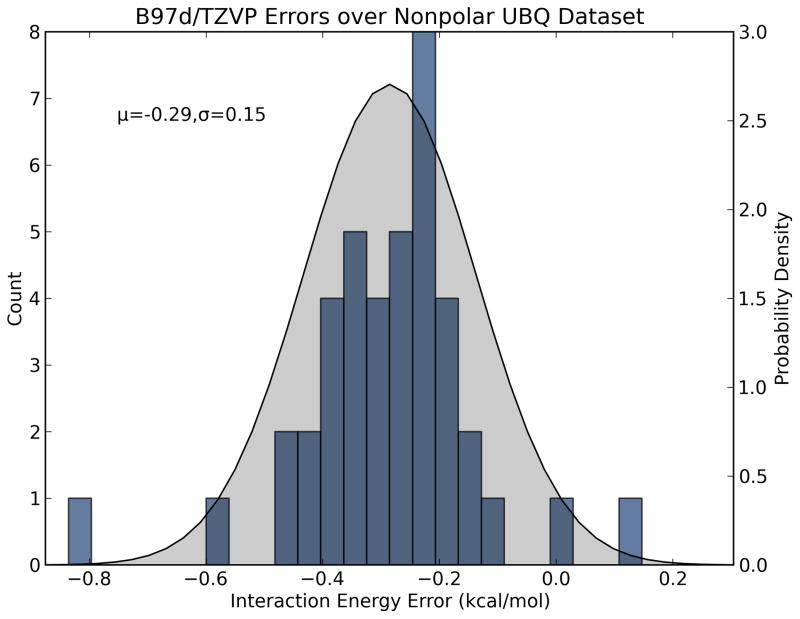
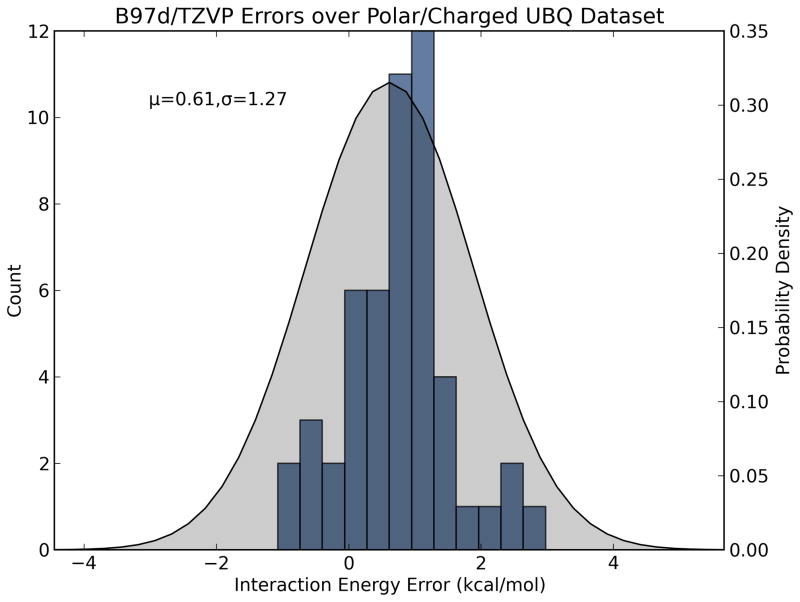
With these simple formulas in place, the challenge then becomes estimating each fragment-based error. This can be done in a statistical way by characterizing the performance of a given energy model on different classes of fragment interactions. That is, a large dataset of bimolecular fragment systems is generated and clustered by interaction class (e.g. polar, nonpolar, ionic, etc.), and the interaction energy of each complex is evaluated with a test energy function (e.g. AM1, GAFF). The absolute errors with respect to reference energy values [e.g. CCSD(T)/CBS] are plotted as a histogram (Figure 2). The data are then used to fit probability density functions (pdfs) describing the probable magnitudes of error for each type of interaction with the test method. We choose to model the error distributions with Gaussian pdfs, which contain two parameters: μ and σ² (Equation 4). Here μ represents systematic error (bias) per interaction and should be propagated according to Equation 2, whereas σ represents random error (imprecision) per interaction and should be propagated according to Equation 3. For example, from the distribution shown in Figure 2a we find that, for common interactions found in protein structures, B97-D/TZVP (a density functional method) tends to model nonpolar/van der Waals interactions very precisely with a slight offset (−0.29 ± 0.15 kcal/mol per interaction), but is less precise in modeling polar/charged interactions (0.61 ± 1.27 kcal/mol per interaction; Figure 2b).

Figure 2.

Histograms and probability density functions describing errors in absolute interaction energies of chemical fragments for B97-D and the TZVP basis set. (a) Nonpolar/van der Waals complexes (blue) are usually modeled with −0.29 ± 0.15 kcal/mol error whereas (b) polar/hydrogen bonding complexes (red) are modeled with 0.61 ± 1.27 kcal/mol error. These estimates can be propagated with Equations 5 and 6 to estimate the errors in modeling a large molecular system composed of many independent polar and nonpolar contacts.

$$P(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-{(x-\mu )}^2}{2{\sigma }^2}}$$ [Equation 4]

To estimate the total error in modeling a large system with B97-D/TZVP, we would first analyze the structure for the number of hydrogen bonds and van der Waals interactions, and then propagate the errors using the values of μ and σ² from the estimated pdf for B97-D/TZVP with Equations 5 and 6. Here N_i represents the number of detected interactions of class i, and the sum is over all interaction classes detected in the system. For example, in the crystal structure of ubiquitin (PDBID: 1UBQ) we detected 42 distinct van der Waals contacts and 50 hydrogen bonds. By using Equations 5 and 6 we estimate that B97-D/TZVP would model the energy of the protein with 18.32 ± 9.03 kcal/mol error. Thus the inaccuracy of the energy model yields a predicted shift in the energy of +18.32 kcal/mol, but this is easily corrected by subtracting it from the total calculated energy. The imprecision of the energy model yields an uncertainty in the energy estimate of ±9.03 kcal/mol. If the errors in the energy model behave according to the Gaussian pdf then it could be inferred that the ‘true’ energy or reference energy lies within this error bar with 1σ confidence.

$${\mathit{Error}}_{\mathit{Systematic}}=\sum _i{N}_i{\mu }_i$$ [Equation 5]

$${\mathit{Error}}_{\mathit{Random}}={\left(\sum _i{N}_i{\sigma }_i^2\right)}^{1/2}$$ [Equation 6]

Size dependence of potential energy error

The error propagation formulas in Equations 5 and 6 demonstrate how overall potential energy errors grow with increasing system size. Even with small fragment-based potential energy errors, overall propagated error can become prohibitively large for very large systems such as proteins. We hypothesized that current force fields have errors large enough to make it difficult to map out folding landscapes for large proteins accurately [9]. These landscapes are often thought of as being funnel shaped, where the native protein fold lies at the bottom of the free energy funnel. Potential function errors would have the effect of distorting these folding landscapes, leading to inaccurate predictions of protein folds.

Evidence for this distortion effect can be seen in the recent work of Shaw and coworkers, who have successfully simulated the folding of 12 small (≤80 amino acids) fast-folding proteins with long-timescale molecular dynamics [19]. In a following study, the group attempted to use similar methods to refine homology models of larger (63–192 amino acids) and slower-folding proteins [20]. It was observed that most of the native structures were unstable with modern force fields. Because simulations were initiated with the native and homology model structures, and these trajectories sampled overlapping regions of conformational space, incomplete sampling was ruled out as the source of failure. The authors then suggested (in line with our hypothesis) that these proteins have complicated free energy surfaces with competing minima, and that force field inaccuracies had led them to predict incorrect native structures.

The size dependence of potential function errors also gives some rationale to the success of alchemical free energy perturbation methods. With these methods, free energy differences between similar molecules are often estimated, and usually only a small number of chemical interactions are perturbed at a time. This means only a few molecular interactions are modified in the free energy estimation, while the rest are held constant. Only the modified interactions introduce errors in the estimate, and propagated error magnitudes are therefore usually very low.

Relationship between potential energy error and free energy

The determining factor of reaction rates and the spontaneity of biomolecular processes is the free energy, ΔG, which can be represented (Equation 7) as:

$$\mathrm{\Delta }G=\mathrm{\Delta }E+\mathrm{\Delta }{H}_{\mathit{corr}}-T\mathrm{\Delta }S+\mathrm{\Delta }{G}_{\mathit{sol}}$$ [Equation 7]

where we have deconstructed the total free energy change into the components of potential energy change ΔE, enthalpic corrections ΔH_corr, temperature T and entropy change ΔS, and the solvation free energy change ΔG_sol. The errors estimated with Equation 5 and Equation 6 apply to ΔE only, and thus we currently neglect errors from the ΔH_corr, ΔS and ΔG_sol terms. Because of this, we consider our total random error estimates to be lower limit random error estimates, because independent random errors grow monotonically with the addition of terms. By contrast, systematic errors in ΔE and the remaining terms can cancel or add depending on their signs. However, estimating the error in ΔS would be a formidable challenge, because accurate entropy estimations depend on accurate potential energy surfaces, which in turn depend on errors in ΔE. Thus the errors in ΔE and ΔS are correlated in a complicated way, and this is a relationship that has yet to be elucidated. There have been studies concerning the estimation of errors in ΔG_sol, and modern methods are able to predict solvation free energies to around 1 kcal/mol error for small neutral systems [21]. Unfortunately the propagation of solvation free energy errors can be difficult to predict owing to strong correlations between fragment contributions [22].

Owing to these complications, it might be preferable to use the equations of statistical mechanics directly by writing free energies and other variables in terms of partition functions (Equation 8). Such a formulation might be more favorable for error estimation, because these quantities depend only on the potential energies of each microstate sampled. In addition, the estimated errors in microstate energies can be propagated to estimate error bars in free energy directly (see below). Thus, by using direct integration methods like Equation 8, energy error estimates could be more easily interpretable.

$$F=-\mathit{RT}ln\lfloor \int e^{-\beta E(\mathbf{r})}d\mathbf{r}\rfloor$$ [Equation 8]

Practical concerns

This chemical fragment-based error propagation approach should be applicable to every large molecular system with mostly localized interactions, where fragment-additivity in potential energy is a good approximation. Nonadditivity is expected to be greater in delocalized systems such as metals or in water clusters, where nonadditivity effects have been reported to be up to 30% of total interaction energies [23]. Additional work is needed to develop methods to quantify and predict nonadditivity in biological systems. It could be possible to estimate uncertainties introduced by nonadditivity, and these uncertainties could be propagated along with estimates from the current model.

The effectiveness of the method also depends on the completeness and transferability of the error pdf database. We are now in the process of expanding our database in terms of size and range of interaction classes to improve our error predictions. For example, water–solute interaction errors should be accounted for in addition to protein–ligand interaction errors, but we have not yet generated error pdfs describing these interactions. The main bottleneck is, of course, performing the many high-level quantum chemical reference calculations. Once a large and diverse fragment interaction error database is completed, reliable error pdfs describing probable magnitudes of fragment-based errors can be generated. The resultant ability to estimate errors in large molecular systems can be performed very efficiently and can be used to estimate the amount of error present in computational models routinely.

An important note about our work thus far is that we use gas-phase ab initio interaction energies [typically CCSD(T)/CBS] as reference data. This presents a particular difficulty when comparing results with force fields that have been parameterized for liquid-phase simulations [24,25]. Here, a different type of modeling error arises when interactions are modeled that lie outside of the parameterization of the model [26]. For example, an atomistic water model trained to reproduce bulk properties like density or heat of vaporization would be expected to model average water–water interactions very well. However, the same model might poorly describe microscopic interactions with solute molecules, and each water–solute fragment interaction would contribute to the total potential energy error estimate. These types of modeling errors could still be predicted in principle, but would require a very different kind of reference dataset than we have generated.

Ensemble quantities

We now have machinery in place to estimate potential energy errors in static molecular structures, but single microstate energies are rarely useful for comparison with experiment. Rather, ensembles of structures contribute to thermodynamic observables such as free energy, and thus determination of their uncertainties is often more desirable. In our study of error propagation in statistical thermodynamic variables, we derived low-order error propagation formulas, compared them to Monte Carlo estimates of error propagation and discovered interesting error propagation behaviors [10].

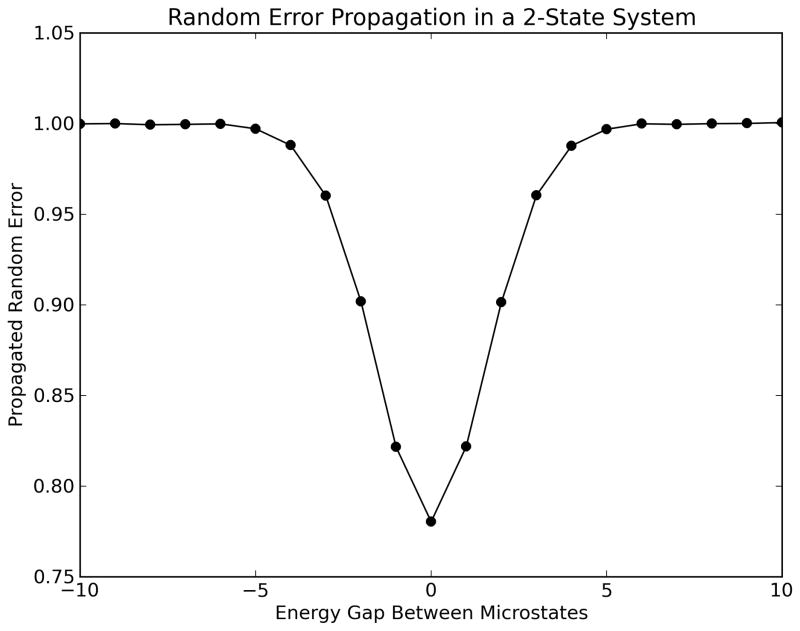
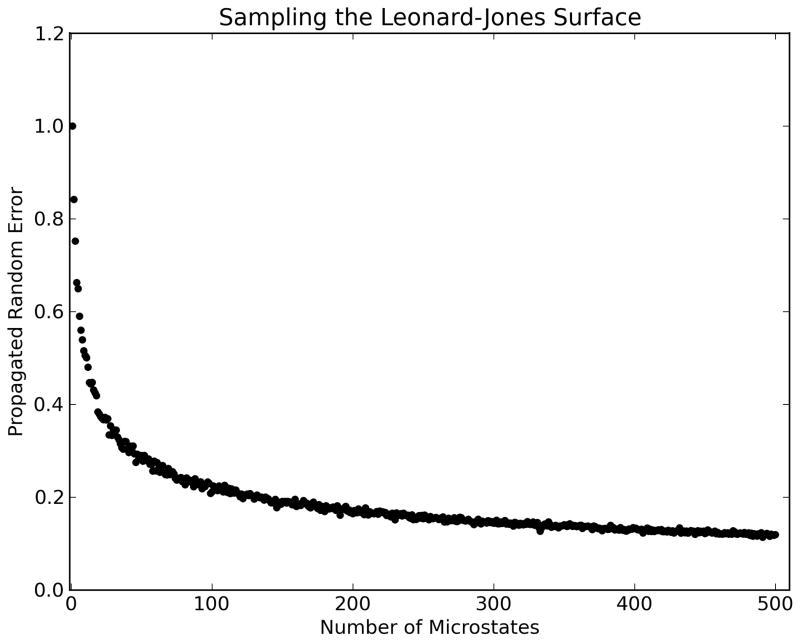
Assuming that microstate energies have independent systematic and random error components δE_i^Sys and δE_i^Rand, the first-order Taylor series error propagation formulas for observables in the discrete canonical ensemble are shown in Table 1. Of particular interest is our observation that random errors in free energy propagate as Pythagorean sums of Boltzmann-weighted microstate energy random errors. This has important implications for error reduction. As sums over P_i² (the squared Boltzmann weights or probabilities) decrease as microstates become more isoenergetic, propagated random error in free energy does as well. Figure 3a shows a hypothetical ensemble with two microstates at different energy gaps. Both microstates have uncertainties in their estimated energies of 1.0 kcal/mol, but at the isoenergetic point propagated random error decreases to below 0.8 kcal/mol. In addition, P_i decreases with the addition of microstates to the ensemble. Figure 3b shows this effect by sampling a Lennard–Jones surface, with randomly-selected states added incrementally to the ensemble each with 1.0 kcal/mol uncertainty. As 20–30 microstates are added, propagated random error decreases dramatically from the initial 1.0 kcal/mol to below 0.5 kcal/mol. The effect of additional sampling seems to diminish after this point, because propagated random error in free energy decreases more slowly toward zero as more microstates are added to the ensemble. These observations suggest that uncertainties arising from the use of imprecise energy functions can be minimized by incorporating local sampling of potential energy surfaces.

Table 1.

First-order formulas for propagation of independent microstate energy errors in the discrete canonical ensemble

Quantity	Formula	Systematic errors	Random errors
Free energy (A)	$-{\beta }^{-1}ln{\displaystyle \sum _i}{e}^{-\beta E_i}$	${\displaystyle \sum _i}{P}_i\delta E_i^{\mathit{Sys}}$	$\pm \sqrt{{\displaystyle \sum _i}{\left(P_i\delta E_i^{\mathit{Rand}}\right)}^2}$
Average energy (E)	${\displaystyle \sum _i}{P}_i{E}_i$	${\displaystyle \sum _i}|P_i(1-\beta E_i+\beta E)|\delta E_i^{\mathit{Sys}}$	$\pm \sqrt{{\displaystyle \sum _i}{\left(P_i(1-\beta E_i+\beta E)\delta E_i^{\mathit{Rand}}\right)}^2}$
Entropy (S)	$-k_b{\displaystyle \sum _i}{P}_{i}ln{P}_i$	${\displaystyle \sum _i}\left|\beta P_i\left[k_{b}ln(P_i)+S\right]\right|\delta E_i^{\mathit{Sys}}$	$\pm \sqrt{{\displaystyle \sum _i}{\left(\left(\beta P_i\left[k_{b}ln(P_i)+S\right]\right)\delta E_i^{\mathit{Rand}}\right)}^2}$

k_b is the Boltzmann constant, P_i is the normalized probability (Boltzmann weight) of state i and β = (k_bT)⁻¹ where T is the absolute temperature.

Figure 3.

Error propagation behaviors in free energy. Data was generated by Monte Carlo error analysis using microstates with assigned uncertainties of 1.0 kcal/mol. (a) Propagated uncertainties in free energy for a two-state system vs the potential energy difference between the two microstates. As the microstates become more isoenergetic, propagated random error decreases to a minimum. (b) Propagated uncertainty in free energy for sampling on an example Lennard–Jones surface. As more microstates are added to the ensemble, each with their own 1.0 kcal/mol uncertainty in energy, free energy random errors are decreased. Taken together, these data suggest that increased ‘local sampling’ of potential energy surfaces could be one strategy for reducing uncertainties in free energy estimation.

We also observed that low-order error propagation formulas are only useful when microstate energy errors are small. For very imprecise energy functions, Monte Carlo error propagation is recommended, in which random samples of microstate energy errors are drawn from appropriate distributions and free energy is computed many times to estimate a free energy distribution. The resulting free energy distribution can be used to estimate final uncertainties in free energy.

Based on our observations of error propagation behavior, we proposed a general error-handling methodology for comparing various states of a molecular system in terms of free energy. The first step is to (i) take independent configuration samples on a potential energy surface via Monte Carlo simulations or molecular dynamics snapshots separated by sufficiently long time intervals. The set of structures is then (ii) clustered into groups having similar structures and similar molecular contact counts (i.e. nearly the same numbers of hydrogen bonds, van der Waals contacts, etc.). The contact counts for the microstates are used along with the error pdf for the energy model to (iii) estimate systematic and random error magnitudes for each microstate energy. (iv) Systematic errors are removed, leaving only random error in each microstate energy. From here, (v) Monte Carlo error propagation is carried out to give a final free energy for the given state or cluster, along with its associated error bar. At this point, (vi) error-corrected free energy differences can be computed along with associated uncertainties at the desired confidence level.

Outlook and concluding remarks

As computational modeling of large chemical systems becomes more utilized, special care will need to be taken to account for the accumulation of modeling errors in potential energy functions. We have shown how these errors propagate with increasing system size and suggested one strategy to estimate and correct for them. We then showed that propagated errors in ensemble quantities can be reduced by incorporating local sampling of potential energy surfaces. This practice could be implemented to extend common endpoint methods and might improve their accuracy.

Our ability to estimate energy modeling errors relies on our database of interacting fragment complexes. A larger set of interacting chemical fragments from proteins and protein–ligand complexes classified by interaction type would enable more robust estimation of systematic and random errors. We are currently in the process of generating this database, which will be freely available via http://www.merzgroup.org and can be used for viewing error characteristics of common energy models, and downloading structures for training and testing new energy models against reference energies.

Highlights.

• Reliable simulations of biomolecules depend on the accuracy of potential functions

• Potential function errors propagate and increase with system size

• We propose a statistics-based method for estimating potential model uncertainties

• Conformational sampling naturally diminishes errors in free energy