Identifying the Default Mode Network Structure Using Dynamic Causal Modeling on Resting-state Functional Magnetic Resonance Imaging

Abstract

The default mode network is part of the brain structure that shows higher neural activity and energy consumption when one is at rest. The key regions in the default mode network are highly interconnected as conveyed by both the white matter fiber tracing and the synchrony of resting-state functional magnetic resonance imaging signals. However, the causal information flow within the default mode network is still poorly understood. The current study used the dynamic causal modeling on resting-state fMRI dataset to identify the network structure underlying the default mode network. The endogenous brain fluctuations were explicitly modeled by Fourier series at the low frequency band of 0.01–0.08 Hz, and those Fourier series were set as driving inputs of the DCM models. Model comparison procedures favored a model that the MPFC sends information to the PCC and the bilateral inferior parietal lobule sends information to both the PCC and MPFC. Further analyses provide evidence that the endogenous connectivity might be higher in the right hemisphere than in the left hemisphere. These data provided insight on the functions of each node in the DMN, and also validate the usage of DCM on resting-state fMRI data.

1 Introduction

The default mode network (DMN) is part of the brain structure that shows higher neural activity and energy consumption when one is at rest (Raichle et al., 2001). The DMN comprises the posterior cingulate cortex/precuneus (PCC), medial prefrontal cortex (MPFC), bilateral inferior parietal lobule (IPL), and other regions including inferior temporal gyrus. These key regions of the DMN are highly interconnected as conveyed by both white matter fiber tracing (van den Heuvel et al., 2008, 2009; Greicius et al., 2009) and functional synchrony of resting-state functional magnetic resonance imaging (fMRI) signals (Greicius et al., 2003; Biswal et al., 2010).

The DMN regions were also usually reported to be involve endogenous oriented tasks such as spontaneous cognition (Andrews-Hanna et al., 2010), memory retrieval, emotional process, and social cognition (Smith et al., 2008; Spreng et al., 2009; Laird et al., 2011). But the nodes within the DMN are functionally heterogeneous (Laird et al., 2009), and the exact functions of each node within DMN are still poorly understood. From a functional integration view, the function of a given region is better defined by the other regions to which it is connected. Studying how the information flows among the regions within the DMN can highlight the role of each region in the network (e.g. Menon & Uddin, 2010).

Effective connectivity which measures directional causal relationships is gaining more interest to understand brain functions. For fMRI study, effective connectivity is usually measured using Structural Equation Modeling (SEM, e.g. Bavelier et al., 2000), Granger Causality Analysis (GCA, e.g. Goebel et al., 2003), and Dynamic Causal Modeling (DCM, Friston et al., 2003). The SEM infers steady-state coupling between brain regions from the covariance structure of fMRI signals, but it ignores the temporal dynamics of the fMRI time series (Friston, 2011). The GCA uses vector autoregression models to measure the causal relationship of the fMRI time series. A few attempt have been made to investigated the directional influence among the DMN nodes using GCA (e.g. Jiao et al., 2011; Zhou et al., 2011), but their results are hardly consistent. One explanation for this may be due to the questional assumptions of GCA analysis of fMRI time series. For example, the temporal precedence assumptions of GCA are violated by regional differences in the latency of the hemodynamic response (Friston, 2011). In contrast, the DCM is originally proposed to deal with fMRI time series, which models the dynamic effective relationship at the neuronal level using differential equations. In addition, empirical evidence has shown the priority of DCM on modeling the neuronal coupling of fMRI data (David et al., 2008; Friston, 2008).

One challenge when using DCM to study resting-state network, however, is that the DCM model cannot be identifiable without any driving inputs (Stephan et al., 2010). Some attempts have been made to include stochastic terms in the model (Daunizeau et al., 2009; Moran et al., 2009), however both our spontaneous mental state and fMRI signals during the resting-state are not stochastic noises. The resting-state fMRI signals convey fluctuations in the low-frequency band typically within 0.01–0.08 Hz (Biswal et al., 1995; Cordes et al., 2001), and the low-frequency fluctuations (LFF) in the DMN and task-positive network are associated with alterations of internal and external oriented awareness (Vanhaudenhuyse et al., 2011). We argue that it is more appropriate to model the LFF explicitly instead of treating the LFF as stochastic noises.

In the present study, we adopt Fourier series components to model the fluctuation input within 0.01–0.08 Hz band of a resting-state signal. For a given periodic function f(x), the function can be approximated by the sum of a set of sine and cosine periodic functions:

$$f_{\mathit{LFF}}(x)=\frac{c_0}{2}+\sum _{n=1}^{\infty }[c_n^{cos}·cos(nx)+c_n^{sin}·sin(nx)]$$

Because the low frequency fluctuations are mainly within 0.01–0.08 Hz (Biswal et al., 1995; Cordes et al., 2001), we used the sinusoid functions in this range, with only 0.01, 0.02, 0.04, and 0.08 Hz. Note that the constant term is not of our interest, because the constant is not a part of fluctuation and a constant regressor is already in the general linear model of fMRI analysis. The inclusion of both sine and cosine functions makes sure that fluctuations in any phase within the low frequency band can be captured. This is the case that the LFF is not constrained across subjects. Therefore different subjects’ LFFs may convey different phases.

$$\begin{array}{l}{f}_{\mathit{LFF}}(x)\approx c_1^{cos}·cos(0.01·2\pi ·x)+c_1^{sin}·sin(0.01·2\pi ·x)\\ +c_2^{cos}·cos(0.02·2\pi ·x)+c_2^{sin}·sin(0.02·2\pi ·x)\\ +c_3^{cos}·cos(0.04·2\pi ·x)+c_3^{sin}·sin(0.04·2\pi ·x)\\ +c_4^{cos}·cos(0.08·2\pi ·x)+c_4^{sin}·sin(0.08·2\pi ·x)\end{array}$$

In addition to modeling the unknown endogenous inputs to the nodes of the default mode network, our Fourier basis set enables us to test for regions that responded to endogenous fluctuations using conventional (whole brain) SPM analyses. This is useful because it allows us to establish a construct validity in relation to the default mode as identified with independent component analysis (ICA). We hypothesized that the regions showing a significant response to fluctuating input would show similar spatial pattern as the ICA-defined default mode regions.

The neuronal model assumed by DCM can be written as the following ordinary differential Equation:

$$dz/dt=A·z+C·U$$

while

$$\begin{array}{l}C·U=c_1^{cos}·cos(0.01·2\pi ·x)+c_1^{sin}·sin(0.01·2\pi ·x)\\ +c_2^{cos}·cos(0.02·2\pi ·x)+c_2^{sin}·sin(0.02·2\pi ·x)\\ +c_3^{cos}·cos(0.04·2\pi ·x)+c_3^{sin}·sin(0.04·2\pi ·x)\\ +c_4^{cos}·cos(0.08·2\pi ·x)+c_4^{sin}·sin(0.08·2\pi ·x)\end{array}$$

Here, A corresponds to the average connectivity among regions, while the parameters in the matrix C couple the endogenous fluctuations above to N regional responses, denoted by z. It should be noted that one can include bilinear and nonlinear terms in the above model. In the present study, DCM models were systematically defined, which was comprised of four main regions of the DMN. The best DCM model was determined using the Bayesian model selection procedure (Stephan et al., 2009; Friston et al., 2011).

2 Methods

2.1 Subjects

The data set was derived from the 1000 functional connectomes project (http://fcon_1000.projects.nitrc.org/) (Biswal et al., 2010). Sixty four subjects’ MRI data from the Beijing_Zang dataset were used. The data set was divided into 3 parts with equal number of subjects. The current analyses only used the second part of this data set (n = 64). The mean age of these subjects was 21.2 years (range from 18 to 26 years). There were 21 males out of the 64 subjects.

2.2 Scanning parameters

The MRI data were acquired using a SIEMENS Trio 3-Tesla scanner from Beijing Normal University. Functional data were acquired using the following parameters: TR = 2s; volumes = 230); functional resolution was 3.125 × 3.125 × 3 mm with 64 × 64 × 36 voxels. The T1-weighted sagittal three-dimensional magnetization-prepared rapid gradient echo (MP-RAGE) sequence was acquired using the following imaging parameters: 128 slices, TR = 2530 ms, TE = 3.39 ms, slice thickness = 1.33 mm, flip angle = 7°, inversion time = 1100 ms, FOV = 256 × 256 mm².

2.3 Imaging data analysis

2.3.1 Preprocessing

The imaging data analyses were done using the SPM8 package (http://www.fil.ion.ucl.ac.uk/spm/) based on MATLAB. The first two images of each subject were discarded. Then all the functional images were motion corrected, and coregistered to subjects’ own high resolution anatomical image. The subjects’ anatomical images were normalized to the standard T1 template in the Montreal Neurological Institute (MNI) space as provided by SPM8. Then the normalization parameters of each subject were applied to the functional images to normalize all the functional images into the MNI space. Finally, all the functional images were spatially smoothed using a Gaussian kernel with 8 mm full width at half maximum (FWHM).

2.3.2 Spatial independent component analysis

Spatial ICA was used to identify the default mode network and to define the regions of interest (ROIs) for the DCM analysis. The Group ICA of fMRI Toolbox (GIFT) (http://icatb.sourceforge.net/) (Calhoun et al., 2001) was used to achieve these goals. 20 components were extracted, and the resulting component maps were visually inspected to identify the default mode network.

2.3.3 Modeling low frequency fluctuations

Eight box-car functions were included in the GLM model to capture the LFF signals. The cycle of the box-car functions were 100, 50, 25, and 12.5 s (representing 0.01, 0.02, 0.04, and 0.08 Hz, respectively), corresponding to binarized versions of the sinusoidal Fourier components used. The use of boxcar periodic functions, as opposed to sine periodic functions, was purely a pragmatic choice: SPM approximates inputs with a linear piece-wise function, specified in terms of onsets and durations. Therefore, the simplest way to specify a periodic function is to use a boxcar. In future work, we will consider different temporal basis functions (see discussion). There were two box-car functions for each frequency with 90 degree phase delay between the two (see Figure 1A). The box-car functions were not convolved with the hemodynamic response functions (HRF). Six head motion parameters were also added into the model to remove potential confounding variances caused by head motion. The GLM model also includes an implicit high pass filter of 1/100 Hz, to remove ultraslow fluctuations that were due to scanner drift. After estimation of the GLM model, a diagonal F-contrast of all the eight regressors was used to obtain the regions whose variance could be significantly accounted for by the inclusion of the binarized Fourier series regressors.

Figure 1.

Design matrix for capturing low frequency fluctuations. The first eight regressors represent four binaries Fourier pairs with 90 degree phase lag at the frequency of 0.01, 0.02, 0.04, and 0.08 Hz, respectively. The regressors nine through fourteen represent six head motion parameters. And the last regressor represents the constant term.

To validate the Fourier series approximation of low frequency fluctuation, group level analysis was conducted on the logarithmic transformed F-contrast images of each subject. The value of the logarithmic transformed F-contrast image represents the logarithmic variance of the LFF variables minus the logarithmic variance of residuals. Group-level one-sample t-test was conducted to identify the regions whose variance of LFF is consistently greater than the variance of residuals. Note that the variance of LFF and residuals are not necessarily equal. This means that the null distribution of our log transformed F-contrast images is not necessarily central. Thus the t-statistic of the one-sample t-test model reflects the relative sensitivity to the LFF as compared to noise rather than an absolute significance against zero.

2.3.4 Dynamic causal modeling

The DCM analyses were conducted using the DCM10 routine implemented in the SPM8. The ROIs of DCM analyses were defined according to the peak of the DMN independent component maps (green circles in Figure 2A). The regions included the medial prefrontal cortex (MPFC) (centered at 3, 54, −2), posterior cingulate cortex (PCC) (centered at 0, −52, 26), left inferior parietal lobule (LIPL) (centered at −50, −63, 32), and right IPL (RIPL) (centered at 48, −69, 35). For each subject, the volumes of interest were defined as spheres centered at those coordinates mentioned above with 8 mm radius. The first eigenvectors were extracted after removing the effect of head motion and low frequency drift.

Figure 2.

Default mode network maps obtained from the spatial ICA analysis (A), low-frequency fluctuation GLM analysis (B), and their overlaps (C). The four green spheres in panel A denote the four ROIs used in the DCM analysis. The ICA map was z transformed, and thresholded at z > 1.96. The LFF map was thresholded at p < 0.001 and cluster extend k > 11 (corresponding to cluster level FDR correction at p < 0.05). In panel C, the ICA map and LFF map were displayed in red and blue, respectively, and the overlap was displayed in violate.

The main purpose of the current DCM analysis was to investigate the endogenous effective connectivity. The modeled LFFs were set as driving input to all the four nodes, and different models were defined by varying only the endogenous connectivity parameters, A. To limit the number of possible models, it was assumed that the model was left right symmetrical. The models were specified in terms of three sets of connectivity as illustrated in Figure 3. Figure 3B illustrated three possible connections between the MPFC and PCC. Because these two regions are the main nodes of the DMN, there is no reason to construct a model without direct connections between these two regions. Figure 3C demonstrates possible connections between the bilateral IPL. Figure 3D illustrates possible relationship between the bilateral LPL and the two midline structures. Combinations of these three types of connections resulted in 3 × 2 × 5 = 30 models, all examined in this analysis.

Figure 3.

All possible connections among the four ROIs (A), and the strategy to define the model space (B–D). B) displays possible connection settings between the MPFC and PCC. C) displays possible connection settings between the bilateral IPL. And D) displayed possible connection settings between the bilateral IPL and the MPFC/PCC regions. Note that double arrow means reciprocal connections between two regions.

Bayesian model selection (BMS) (Stephan et al., 2009) was used to determine the best model after balancing the fit of data and the model complexity. Expected posterior model probabilities and exceedance probabilities were computed. BMS was first done on the three type of Families (Penny et al., 2010), and lastly, the BMS was also done on all the 30 models. Given the best model, the parameters from each subject were analyzed quantitatively using classical statistics to illustrate their size, in relation to inter-subject variability, using the standard summary statistic approach. One sample t-tests were conducted to examine whether these parameters have significantly nonzero values. In addition, repeated measure analyses of variance (ANOVA) were also conducted to examine the lateralization of these model parameters.

3 Results

3.1 Spatial ICA

The DMN independent component was identified by the spatial ICA analysis (Figure 2A). The four clusters included the medial prefrontal cortex (MPFC) (centered at 3, 54, −2), posterior cingulate cortex (PCC) (centered at 0, −52, 26), the left inferior parietal lobule (LIPL) (centered at −50, −63, 32), and right IPL (RIPL) (centered at 48, −69, 35). The peaks of the four clusters were used for further DCM analyses.

3.2 Effects of low frequency fluctuations

As illustrated in Figure 2B, at the between subject level, the regions showed consistent greater variance of LFF than variance of residuals resemble the DMN. Two main clusters were present. One cluster covers the regions including the posterior cingulate cortex, precuneus, and bilateral parietal regions; and the other cluster was comprised of regions including the medial prefrontal cortex, anterior cingulate cortex, and lateral frontal polar regions. By displaying the LFFs results together with the ICA DMN map, a clear overlap between the two maps of the four nodes of default mode network were observed (Figure 2C).

3.3 Dynamic causal modeling

Figure 4 shows the observed response and predicted response of the best model for an individual subject. It can be seen clearly that the LFFs can be captured by the DCM model. This also suggested that the current DCM analysis was not based on poor model fitting as currently criticized by Lohmann et al., (2012).

Figure 4.

Observed (in green) and predicted (in blue) response by the best model in the four ROIs for a single subject. AU, arbitrary unit.

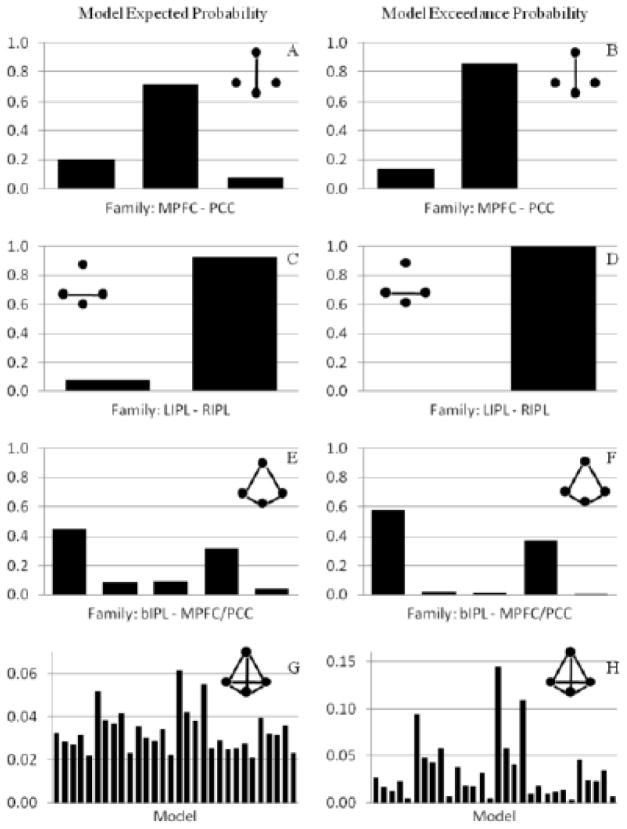
Bayesian model selections were first performed on three types of families, respectively (Figure 5). This form of family inference allows one to accommodate uncertainty about the architecture defined by other parameters and allows one to focus on specific questions about the existence and direction of particular connections within each of the three sets. The BMS of PCC - MPFC connectivity favored the backward connectivity from MPFC to PCC. Model exceedance probability for the MPFC to PCC family was 0.8576. The BMS of bilateral IPL connectivity favored the family with no direct connectivity. Model exceedance probability for the family was 0.9956. The BMS of bilateral IPL to MPFC/PCC families favored the model that bilateral IPL sent information to both the MPFC and PCC regions. Model exceedance probability for the family was 0.5819. Finally, the BMS procedure was done on all the 30 models. Not surprisingly, the overall model winner is the one which combined each winning family (shown in Figure 6). Model exceedance probability for the model was 0.1444.

Figure 5.

Expected probability (left) and exceedance probability (right) for the DCM model families and individual models in the Bayesian model selection. Panel A) and B) show the results of model comparison for the MPFC-PCC families. Panel C) and D) show the results of model comparison for the LIPL-RIPL families. Panel E) and F) show the results of model comparison for the bIPL-MPFC/PCC families. And the panel G) and H) show the results of model comparison for all the 30 models.

Figure 6.

The wining model and the group averaged endogenous connectivity parameters. The widths of the arrows represent the average connectivity strength. (*, p < 0.05 after Bonferroni correction )

The model parameters of the best model were fed into group level analysis. The mean connectivity strengths were displayed in Figure 6 and Table 1. The average connectivity from MPFC to PCC, from RIPL to MPFC, and from RIPL to PCC were all statistically significant after multiple comparison correction. However, the average connectivity from LIPL to MPFC and from LIPL to PCC were not significant. It can be seen that the effect sizes of the MFPC to PCC connectivity and the right hemisphere connectivity are in the medium to large range, whereas the effect size of the connectivity in the left hemisphere are only in the small to medium range. Accordingly, hemispheric differences were directly compared by using a 2 (from LIPL vs. from RIPL) × 2 (to MPFC vs. to PCC) repeated measure ANOVA (see Figure 7). There were no significant interaction between the forward/backward connectivity and hemisphere (F(1,62) = 1.917, MSE = 0.001, p = 0.171). Right IPL connectivity were greater than the left IPL connectivity to the MPFC/PCC (F(1,62) = 7.251, MSE = 0.011, p = 0.009). While, no differences were found between the connectivity to the MPFC and to the PCC (F(1,62) = 1.265, MSE = 0.009, p = 0.265).

Table 1.

Statistics for the endogenous connectivity parameters of the best DCM model.

Connection	Mean	SD	p
MPFC → PCC	0.0469 *	0.1064	7.95×10−4
LIPL → MPFC	−0.0012	0.1240	0.940
LIPL → PCC	0.0159	0.1014	0.215
RIPL → MPFC	0.0416 *	0.1146	5.10×10−3
RIPL → PCC	0.0487 *	0.0996	2.27×10−4

^*denotes statistical significance at p < 0.05 after Bonferroni correction.

Figure 7.

Evidences of left/right asymmetry of the endogenous connectivity parameters. Right IPL has greater average connectivity to the MPFC and PCC than the left IPL does. There are no differences between the connectivity to MPFC and to PCC, or their hemisphere interaction. The error bars represent standard error mean. (*, p < 0.05)

4 Discussion

By using the Fourier series to model low frequency fluctuations, the present study identified network structure underlying the DMN using the DCM on resting-state fMRI dataset. The best model suggested an information flow from the MPFC to PCC, and influence from bilateral IPL to the MPFC and PCC.

4.1 The default mode network

The MPFC and PCC are two main nodes of DMN, and are most robustly discovered in different approaches such as ICA and seed based correlations. The current results demonstrated a causal influence from the MPFC to PCC, but not vice versa. The influence from the MPFC to PCC is consistent with recent studies of resting-state fMRI using Granger causality analysis (Uddin et al., 2009; Jiao et al., 2011; Zhou et al., 2011), suggesting a robust causal influence from the MPFC to PCC. In the whole brain level, the PCC has recently been described as a structural core that links to major brain structures across the whole brain (Hagmann et al., 2008). Granger causality analysis of whole brain ROIs have suggested that the PCC is a robust driven hub, which receive information from the whole brain (Yan & He, 2011; Deshpande et al., 2011). Taken together, all evidences suggest a special role of PCC as a hub region that collect information from other DMN regions as well as across the whole brain.

The current study also found information flows from the bilateral IPL to the MPFC and PCC regions, suggesting a moderation role of the bilateral IPL in the DMN. However, this causal relationship is not consistent with recent findings using Granger causality (Jiao et al. 2011; Zhou et al. 2011). Zhou et al. (2011) found a causal influence from the LIPL to the MPFC, whereas Jiao et al. (2011) showed symmetrical causal influence from the MPFC to bilateral IPL and from bilateral IPL to PCC. This discrepancy may be due to subject sample variability or the different framework for measuring causality. We note that the current study has adopted a larger sample size of subjects than either of those two studies, and that the DCM framework has been demonstrated empirically to be a more valid method than the Granger causality to study network structure (David et al., 2008). Therefore, the driving role of bilateral IPL appears to be more acceptable given the current evidences, and this needs to be replicated in future studies.

Analyses on connectivity parameters illustrated higher connectivity from the right IPL to MPFC and PCC than from the left IPL. To the best of our knowledge, this is the first study to document connectivity asymmetry within the DMN. The IPL has been reported to show asymmetry both in term of structural organization (Eidelberg & Galaburda, 1984; Caspers et al., 2008), and of brain functions, including attention and planning (Robertson et al., 1988; Astafiev et al., 2003). Therefore, it is reasonable that the DMN subdivision of the IPL also menonstrate functional asymmetry. The role of the IPL asymmetry in the DMN needs to be further examined.

The current results and previous studies all show that the PCC is driven by all other regions in DMN and by other brain regions. Hence, one question may arise: how is the incoming information used, and how is the information transmitted? We hypothesize that the PCC information outflow may be relative to the interaction between networks. For example, the DMN regions show enhanced connectivity to visual regions to which the subject does not pay attention (Chadick & Gazzaley, 2011). This is in line with the theory that the DMN is a higher order cortical system that reciprocally exchange information with subordinate brain systems (Carhart-Harris & Friston, 2010). Thus, the functions of the DMN are better defined by the connectivity between the DMN and other task positive networks. Further studies are needed to systematically examine the connectivity between nodes in DMN and to nodes in task positive network in both resting-state context and specific tasks.

4.2 Methodological remarks

The current study has also demonstrated a method to capturing LFFs using the framework of GLM model, even though the phase of the LFF may vary across subjects. As illustrated in Figure 2B, the regions whose variance can be highly explained by the LFFs ensemble the default mode network. This is in line with previous observations that the regions in the default mode network have higher cerebral blood flow (Zou et al., 2009) and high amplitude of low frequency fluctuations (Zang et al., 2007). This method can be used to capture any periodical brain responses with unknown phases.

This report can be regarded as a proof of principle that deterministic dynamic causal models can be used to characterize intrinsic brain networks like the default node. The innovation here is to parameterize unknown endogenous fluctuating inputs in terms of a temporal basis set, here a “binarized” Fourier set. Clearly, this is a rather simple basis set that enforces a degree of periodicity in the modeled fluctuations. In future work, we will consider more realistic models using temporal basis functions, for example radial basis functions used in Riera et al., (2004) and Li et al., (2010). Practically, these are relatively easy to specify within SPM by parametrically modulating of a stream of short boxcar functions.

However, from the point of view of the present report, the fact that we were able to establish evidence for certain connection architectures, over others, shows that this approach to effective connectivity, in the absence of known inputs, is feasible and works even with a very simple model of fluctuations. Furthermore, because we used DCM10, our inference over models and parameters is rather conservative. This is because DCM10 uses non-informative priors on the precision of observation noise: more informative priors on signal to noise may reveal much stronger connections and possibly reveal reciprocal connections that were not evidenced in our data under the current model. We look forward to revisiting these data with more ambitious dynamic causal models in the future and addressing increasingly refined questions.

Highlights.

• The resting-state low-frequency fluctuations were modeled by Fourier series.

• The LFFs were set as driving input to the DCM models.

• The medial prefrontal cortex sends information to the posterior cingulate cortex.

• The bilateral inferior parietal lobule influence both the MPFC and PCC.

• Effective connectivity from the inferior parietal lobule were right lateralized.

Abbreviations

BMS

Bayesian Model Selection

DCM

Dynamic Causal Model

DMN

Default Mode Network

FDR

False Discovery Rate

fMRI

functional Magnetic Resonance Imaging

GCA

Granger Causality Analysis

GLM

General Linear Model

ICA

Independent Component Analysis

IPL

Inferior Parietal Lobule

LFF

Low-frequency Fluctuation

MNI

Montreal Neurological Institute

MPFC

Medial Prefrontal Cortex

PCC

Posterior Cingulate Cortex

ROI

Region of Interest

SEM

Structure Equation Model