A comparative analysis of spectral exponent estimation techniques for 1/f^β processes with applications to the analysis of stride interval time series

Abstract

Background

The time evolution and complex interactions of many nonlinear systems, such as in the human body, result in fractal types of parameter outcomes that exhibit self similarity over long time scales by a power law in the frequency spectrum S(f) = 1/f^β. The scaling exponent β is thus often interpreted as a “biomarker” of relative health and decline.

New Method

This paper presents a thorough comparative numerical analysis of fractal characterization techniques with specific consideration given to experimentally measured gait stride interval time series. The ideal fractal signals generated in the numerical analysis are constrained under varying lengths and biases indicative of a range of physiologically conceivable fractal signals. This analysis is to complement previous investigations of fractal characteristics in healthy and pathological gait stride interval time series, with which this study is compared.

Results

The results of our analysis showed that the averaged wavelet coefficient method consistently yielded the most accurate results. Comparison with Existing Methods: Class dependent methods proved to be unsuitable for physiological time series. Detrended fluctuation analysis as most prevailing method in the literature exhibited large estimation variances.

Conclusions

The comparative numerical analysis and experimental applications provide a thorough basis for determining an appropriate and robust method for measuring and comparing a physiologically meaningful biomarker, the spectral index β. In consideration of the constraints of application, we note the significant drawbacks of detrended fluctuation analysis and conclude that the averaged wavelet coefficient method can provide reasonable consistency and accuracy for characterizing these fractal time series.

1. Introduction

The human body is comprised of many physiological systems which interact in a nonlinear manner (Eke et al., 2000, 2002; Glass, 2001; Glenny et al., 1991; Goldberger and West, 1987; Huikuri et al., 1998, 2000; Ivanov et al., 1999). Accordingly, changes in functional outcomes in a given physiological system may be caused by trends in either one or many other systems (Eke et al., 2000, 2002; Peng et al., 1995b). Disease, aging, genetic disorders, and trauma can have significant effects on many physiological functional outcomes like gait (Hausdorff et al., 1999, 2000, 1997, 1995, 1996). The lo-comotor system consists of a group of components from the central nervous, musculoskeletal, and other physiological systems. Generally, locomotor system consists of the cerebellum, the motor cortex, and the basal ganglia, as well as visual, vestibular, and proprioceptive sensors (Hausdorff et al., 1995, 1996). This may be seen as a generalized control system. The cerebellum and basal ganglia receive information for processing, and sends control signals by the motor cortex. Current state information and feedback are provided by internal and external inputs from proprioceptive and sensory nerve and visual signals (Hausdorff et al., 1995, 1996; Eke et al., 2002). In a healthy subject, a stable walking pattern is maintained by the constant dynamic interaction between all of the components of the locomotor system.

Neurophysiological changes may alter the locomotor system’s ability to correctly modulate dynamic changes in the gait process (Hausdorff et al., 1997). For example, decreased nerve conduction velocity, loss of motor neurons, decreased proprioception, muscle strength, and central processing capabilities are notable declines due to advancing age (Hausdorff et al., 1997). Amyotrophic Lateral Sclerosis (ALS) is a neurodegenerative disease which severely affects the function of the motor neurons of the cerebral cortex, brain stem, and spinal cord (Hausdorff et al., 2000). Muscle weakness, increased fatigue and decreased endurance are characteristic of ALS (Sharma et al., 1995; Sharma and Miller, 1996). Parkinson’s Disease (PD) and Hunt-ington’s Disease (HD) are both neurodegenerative diseases which affect the basal ganglia (Hausdorff et al., 1997). PD and HD are marked by irregular of central motor control, the most apparent outcome of which is a chor-eiform or “dancing” like gait (Blin et al., 1990; Hausdorff et al., 1997). The common consequence among all of these disorders is increased stride interval time (Hausdorff et al., 1997). However, increased stride interval time alone is generally not indicative of any neurodegenerative disease, so the fluctuations of the stride interval must be considered to reveal any unique mechanisms of decline (Hausdorff et al., 1997, 2000). It is apparent that in general, such changes to components of the locomotor system from disease and aging result in abnormal gait. However, the identity and severity of the underlying mechanism(s) causing the functional decline are still unknown, and can be extremely difficult to identify and characterize due to the highly nonlinear and complex interactions of the constituent physiological systems (Hausdorff et al., 1997, 2000; Bassingthwaighte, 1988; Bassingthwaighte and Bever, 1991).

Stride interval time series, like many physiological processes, have been observed to possess complex statistical properties (Glenny et al., 1991; Goldberger and West, 1987; Ivanov et al., 1999; Hausdorff et al., 1997; Bassingthwaighte and Bever, 1991; Deligniéres et al., 2004; Kantelhardt et al., 2002; Peng et al., 1995a; Shlesinger, 1987). This phenomenon is due to the time evolution and complex interactions of many dynamical systems, imposed with random fluctuations, resulting in chaotic processes (Bak and Chen, 1991). The goal of fractal time series analysis is to establish a metric which can indicate this property and the nature of the statistics, correlation, and other unique properties of time evolving system parameters (Deligniéres et al., 2004; Mandelbrot, 1985; Mandelbrot and Van Ness, 1968; Delignieres and Torre, 2009; Delignieres et al., 2006). The fractal description of patterns, self similarity, and statistical properties at many time scales can reveal new meaningful information about the process (Delignieres and Torre, 2009; Delignieres et al., 2006). Thus, these techniques are very useful when evaluating physiological variables which are the outcome of complex dynamical system interaction.

The first primary aim of this paper is to clarify the interpretations of time series analyses for identifying the fractal properties of 1/f^β type scale invariant processes and highlight the inherent limitations of common methods. To validate the concept of fractal time series analysis, a number of established time, frequency, and time-scale domain estimation techniques are implemented and tested. The tests include the entire range of 1/f^β processes, with special consideration given to simulated signals most indicative of physiological processes. A matter which is often obfuscated in other studies of fractal analysis was the choice of a metric for the fractal characteristic. For consistency, the process parameter β, also referred to as the spectral index, was used as a metric for the fractal characteristic. The parameter β is convertible to other values commonly referred in the literature such as the fractal dimension D, the Hurst exponent H, and the scaling index α (Eke et al., 2002). β was chosen for use here for its ease in interpretation with respect to the power law spectrum of 1/f^β processes.

A second aim is to address the applications of these techniques to time series obtained in a physiological setting and their inherent constraints. A common limitation in acquiring physiological data, such as gait stride intervals, is the time series length (Eke et al., 2002; Delignieres et al., 2006; Bryce and Sprague, 2012). In many instances, the physical limitations of the test subject, equipment design, and other factors of the experimental setting limit the available length of acquired data. Accordingly, this paper will provide an evaluation of the algorithms with respect to short and long time series. It has also been recognized that the parameters of many physiological processes, such as stride interval time series, are by nature not zero mean (Hausdorff et al., 1999, 2000, 1997, 1995, 1996). To understand the effect of a time series with a nonzero mean, the estimation accuracy of each method was considered under three cases: (1) the normalized signal (2) the normalized signal with positive unit mean (3) a zero mean signal from the normalized signal minus its mean. Finally, to verify the efficacy of the methods in the physiological setting, each method will be applied to published gait stride interval time series. The spectral index is calculated for gait time series from subjects with PD, HD, ALS and healthy controls (Hausdorff et al., 2000, 1996). The calculated values provide a comparative basis with respect to other studies aiming to determine long range correlations and fractal behavior of gait stride interval time series (Hausdorff et al., 1995; Delignieres and Torre, 2009).

2. Power spectral densities of fractal process

It has been noted that the power spectral density is an informative perspective of fractal processes, which exhibits inverse power law scaling behavior by S(f) = 1/f^β. Processes of this type are henceforth referred to as 1/f^β processes (Eke et al., 2002; Delignieres and Torre, 2009; Shlesinger, 1987; Kasdin, 1995; Chen et al., 1997; Pilgram and Kaplan, 1998). Generally 1/f^β process can be classified as belonging to one of two classes, fractional Gaussian noise (fGn) or fractional Brownian motion (fBm) (Eke et al., 2002; Delignieres et al., 2006). For fGn class signals, the probability distribution of a segment of the signal is independent of the segment size and its temporal position in the signal (Eke et al., 2002). Thus, the correlation structure and any statistical descriptions of the process do not change over time, so the process is stationary (Delignieres and Torre, 2009). In an fBm signal, the probability distribution in a larger segment is equal to a distribution in a smaller segment when the distribution in the large segment is rescaled (Eke et al., 2002). Here, the inverse power law relationship is observed for the calculation of some statistical measure m on the segment of length n

$$\text{log}{m}_n=\text{log}p+H\text{log}n$$ (1)

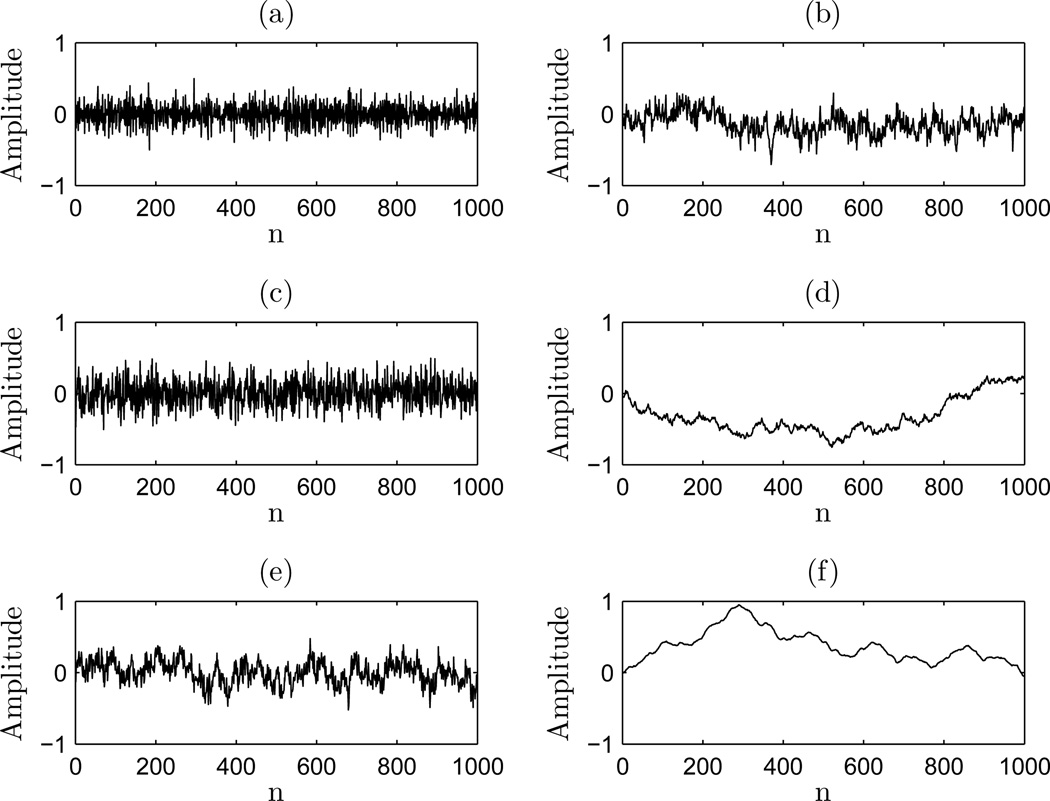
This implies the power law relationship where p is a proportionality factor and H is the Hurst exponent and H∃[0, 1] . The Hurst exponent is a commonly used metric for indicating the fractal nature of a fractional Gaussian noise or fractional Brownian motion process (Cannon et al., 1997; Davies and Harte, 1987; Crevecoeur et al., 2010). These processes have the property that the cumulative summation of an fGn signal results in a fBm signal (Eke et al., 2002). As a result, a given process is interconvertible from one class to the other by the integral or derivative (Eke et al., 2002; Shlesinger, 1987; Kasdin, 1995; Chen et al., 1997; Pilgram and Kaplan, 1998). This necessitates a unique Hurst exponent specific to each class of processes. These can be denoted H_fGn∃[0, 1] and H_fBm∃[0, 1] (Eke et al., 2002; Delignieres et al., 2006). H = 0.5 in each class is the special case, where H_fGn = 0.5 is white Gaussian noise (β = 0) and H_fBm = 0.5 is Brownian motion (β = 2) (Eke et al., 2002; Delignieres and Torre, 2009). White Gaussian noise is the characteristic process of the fractional Gaussian noise class of 1/f^β processes (Eke et al., 2002). The important property of white Gaussian noise is that energy is equally distributed for all frequencies. Thus, it has a flat power spectrum and β = 0. H_fGn < 0.5 is anti-correlated Gaussian noise, and H_fGn > 0.5 is correlated noise (Delignieres and Torre, 2009). Brownian motion is the characteristic process for the fBm class. These processes exhibit a 1/f^β power spectrum where β = 2 (Eke et al., 2002; Hausdorff et al., 2000). In this case, successive outcomes in the process are correlated, and the process exhibits non-stationary time evolution (Delignieres and Torre, 2009). H_fBm < 0.5 is anti-persistent Brownian motion, and H_fBm > 0.5 is persistent Brownian motion, where H_fBm = 0 is pink noise of 1/f¹ (Eke et al., 2002). Shown in Figure 1 (a) (c) and (e) are fGn signals of H = 0, 0.5, 1 and their corresponding (cumulatively summed) fBm signals Figure 1 (b) (d) and (f). This provides an overview of signals of each process class and their interconvertible relationship.

Figure 1.

Range of fGn and fBm class signals: (a) H_fGn = 0; (b) H_fBm = 0; (c) H_fGn = 0.5; (d) H_fBm = 0.5; (e) H_fGn = 1; and (f) H_fBm

In the case where β = 1, some correlation between timescales exists but is weak (Delignieres et al., 2006). In summary, a given process can be classified as belonging to one of these two distinct classes where β = 1 is the distinct boundary between each (Kasdin, 1995). The relationship between each class’s Hurst exponent and the power spectrum 1/f^β can be observed by the by the following relationships (Eke et al., 2002)

$$H_{\mathit{\text{fGn}}}=\frac{\beta +1}{2}$$ (2)

$$H_{\mathit{\text{fBm}}}=\frac{\beta -1}{2}$$ (3)

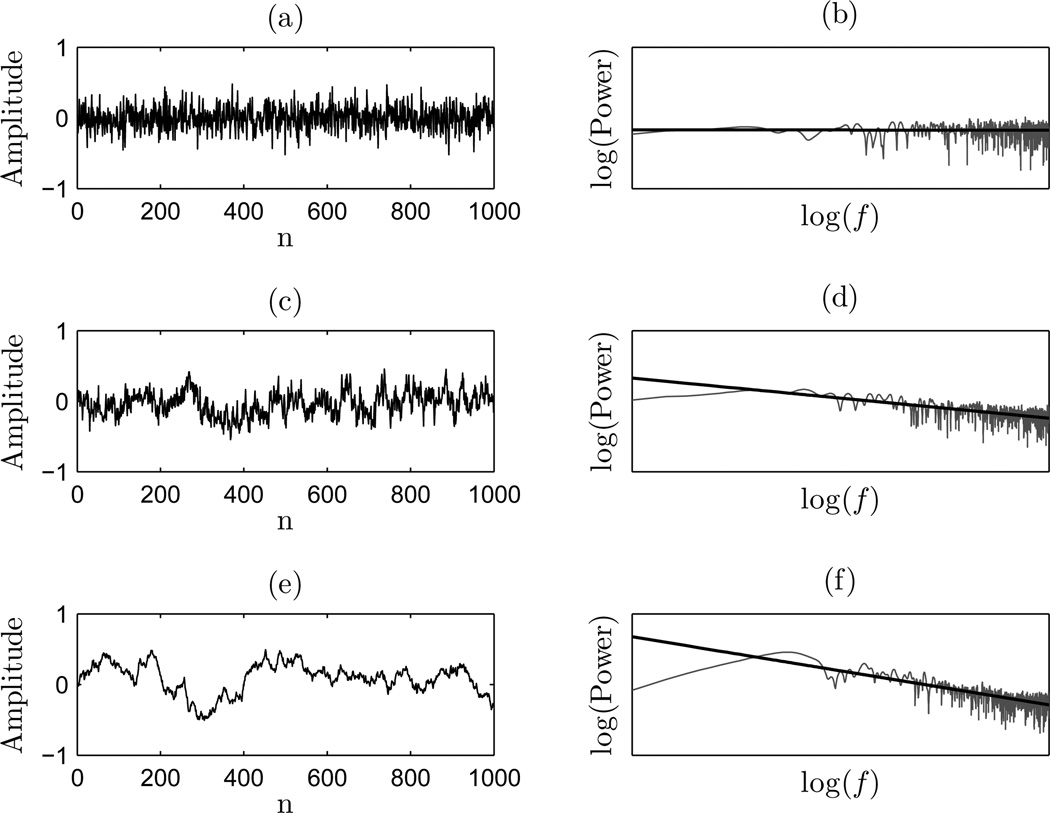
Thus, the range of all fGn and fBm processes for 0 < H < 1 correspond to −1 < β < 3, where the boundary between each class lies at β = 1 (Eke et al., 2002; Delignieres et al., 2006). Figure 2 gives an overview of an fGn Gaussian white noise (β = 0), pink noise (β = 1), and fBm Brownian motion or red noise (β = 2). Adjacent to each signal is its its log-log power spectrum, and the linear regression with slope indicating the corresponding β value.

Figure 2.

Sample time series and corresponding PSD with regression: (a) time series for β = 0; (b) PSD of β = 0 time series; (c) time series for β = 1; (d) PSD of β = 1 time series; (e) time series for β = 1; and (f) PSD of β = 2 time series.

Many well developed fractal estimation algorithms for finding the Hurst exponent are specific to each process class. The choice of a method to evaluate the fractal properties of a signal will accordingly be difficult in a setting where it is unclear which of the two classes the signal belongs. If such methods are inappropriately applied, the calculated class specific Hurst exponent will be incorrect. Consequently, its interpretation as a physiological biomarker will be ambiguous and potentially misleading. Awareness of this hazard is especially critical whenever the process lies at the boundary between fractional Gaussian noise and fractional Brownian motion. This case, when β = 1, a signal represents the type of fractal process most typically exhibited by physiological systems (Eke et al., 2002; Glass, 2001; Goldberger and West, 1987; Huikuri et al., 1998, 2000; Ivanov et al., 1999; Peng et al., 1995a; Sejdić and Lipsitz, 2013). As a result of this dichotomy, signal classification, the choice of a fractal characterization method, and the interpretation of its result becomes a critical yet inherently difficult procedure.

3. Algorithms for estimation of β values

For a 1/f^β process, β values can be estimated in time, frequency or time-frequency (time-scale) domains. Here, we overview several most prominent implementations in literature concerned with characterizing physiological phenomena.

3.1. Time Domain

This section overviews the three time domain fractal techniques implemented here. These are dispersional analysis, bridge detrended scaled window variance (bdSWV), and detrended fluctuation analysis (DFA).

3.1.1. Dispersional Analysis

For dispersional analysis, we refer to the proposal of this technique by Bassingthwaighte, et al (Bassingthwaighte, 1988; Bassingthwaighte and Bever, 1991; Bassingthwaighte and Raymond, 1995, 1994). This time domain based algorithm estimates the fractal characteristic by the variances of the mean of signal segments. Then, the standard deviation on various intervals is plotted versus the interval lengths on a log-log plot. A standard linear regression to this plot will have a slope indicating the fractional Gaussian noise Hurst exponent H_fGn, and the spectral index is found by β = 2H_fGn − 1 (Eke et al., 2002).

3.1.2. Scaled Window Variance

For evaluating processes by scaled window variance, we refer the method proposed by Cannon, et al (Eke et al., 2002; Delignieres et al., 2006; Cannon et al., 1997; Bassingthwaighte and Raymond, 1999). Similar to dispersional analysis, the variance is found on increasing sized intervals of the signal. This method introduced a modification to remove local trends on each interval. In this method, bridge detrending is implemented to remove the local trend. The data in each interval is detrended by subtracting the “bridge”, a line connecting the first and last points in the interval. Then, the standard deviation is calculated for each detrended interval. Finally, the standard deviation of each interval is plotted versus the interval size on a log-log plot.

A standard linear regression to this plot will have a slope indicating the fractional Brownian motion Hurst exponent H_fBm, and the spectral index is found by β = 2H_fBm + 1 (Eke et al., 2002).

3.1.3. Detrended Fluctuation Analysis

The approach for calculating the fractal index by detrended fluctuation analysis (DFA) is provided by Peng, et al (Peng et al., 1995b,a, 1994), and it has been thoroughly evaluated by others for many applications (Kantelhardt et al., 2002; Bryce and Sprague, 2012; Bardet and Kammoun, 2008; Caccia et al., 1997; Chen et al., 2002; Heneghan and McDarby, 2000; Hu et al., 2001; Kantelhardt et al., 2001; Schepers et al., 1992; Willson and Francis, 2003). DFA calculates the proposed “scaling exponent” α which is a useful to indicate the randomness of a time series over the boundary between fGn and fBm processes. The spectral index β is related to the DFA parameter α by (Eke et al., 2002)

$$\beta =2\alpha -1$$ (4)

Implemented here is general scheme where the smallest interval is restricted to $\lceil \frac{N}{100},10\rceil$ and the largest interval to $\lceil \frac{N}{10},20\rceil$

3.2. Frequency Domain

These techniques directly evaluate the power law scaling property of a fractal series’ power spectral density. There are many available methods for performing the spectral estimation required to evaluate a fractal process’s frequency domain 1/f^β power law (Pilgram and Kaplan, 1998; Heneghan and McDarby, 2000; Fougere, 1985). Here, the periodogram method and Eke’s ^lowPSD_we method are implemented (Eke et al., 2000, 2002; Delignieres et al., 2006). The periodogram method is used in calculating S(f), the square of the FFT after applying a Gaussian window. Eke improved on this method to more accurately characterize β for both signal classes. First, for the time series mean is subtracted, a parabolic window applied, and a bridge line connecting the first and last point of the signal is subtracted from the series. After calculating the power spectral density by the periodogram, all frequency estimates for f < 1/8f_max are omitted. Again, β is found by linear regression of the log-log power spectral density (Eke et al., 2002).

3.3. Time-Scale Domain

Proposed time-scale techniques by the wavelet transform are implemented (Eke et al., 2002; Audit et al., 2002; Jones et al., 1999; Simonsen et al., 1998; Veitch and Abry, 1999; Arneodo et al., 1996). The Average Wavelet Coefficient (AWC) method described by Simonsen and Hansen (Simonsen et al., 1998) is conveniently implemented for this function. For the continuous wavelet transform of signal where in this case a twelfth order Daubechies wavelet is used (Simonsen et al., 1998). The number of levels for the Mallat algorithm discrete wavelet transform is chosen with respect to the signal length, determined here as never lower than 2³ or greater than 2⁷ (Mallat, 1989). The result of the transformation provides the scale and transpose coefficients for the signal at the each of the prescribed levels. To find the averaged wavelet coefficient, the arithmetic mean with respect to the translation coefficient is calculated. The average coefficients versus the levels are plotted on a log-log plot. A standard linear regression to this plot will have a slope $H_{\mathit{\text{fBm}}}+\frac{1}{2}$, and the spectral index is found by β = 2H_fBm + 1 (Eke et al., 2002).

4. Evaluation of Algorithms

4.1. Discrete 1/f^β Process Generation

The first step in the analysis was the generation of a 1/f^β fractal process. Li, et al proposed a method to create a filter of fractional order for generating fBm fractal processes by stochastically fractional differential equations (Li, 2010; Li and Lim, 2006; Li and Chen, 2009). Kasdin extended this method for a generalized fractional filter inclusive of fGn and fBm signals, or 1/f^β processes (Kasdin, 1995). This method was implemented for this numerical analysis of 1/f^β processes. The transfer function of the fractional system that follows the power law of β is given by

$$h(n)=\frac{\mathrm{\Gamma }(\beta /2+n)}{n!\mathrm{\Gamma }(\beta /2)}$$ (5)

The realization of the process x(n) is found by the convolution operation

$$x(n)=w(n)\ast h(n)$$ (6)

where w(n) is randomly generated Gaussian white noise.

4.2. Numerical Analysis of Simulated Data Sets

The basis of this computational evaluation is the generation of 1/f^β power law processes. For completeness, β is calculated for all possible Hurst exponents in fGn and fBm classes for a total range −1 ≤ β ≤ 3. This is inclusive of fractional Gaussian noise and fractional Brownian motion processes for 0 < H < 1. However, the anti-correlated fGn (β < 0) and persistent fBm (β > 2) regime signals are not be a matter of serious consideration in regard to physiological processes. The methods are evaluated over a range of time series lengths in order to observe the relationship between signal length and calculation accuracy for each fractal method. Given the length limitations of previously recognized physiological data sets, time series lengths of 50, 100, 200, 400, 600, 800, 1,000, 2,500, 5,000, 7,500, and 10,000 points are considered. Given the stochastic nature of these processes, the procedure of signal generation and calculation is implemented in a Monte Carlo scheme, where each realization is repeated 1,000 times. In each iteration for a set signal length, the time series is normalized and evaluated by each of the methods. Next, and a unit mean offset is added, and this signal reevaluated by each method. Then the mean of the series is subtracted from the offset series, resulting in a zero mean signal, and reevaluated. These three cases are calculated for each signal length for 1,000 realizations, and the mean value of β from each estimation is calculated. This computational scheme is the basis of the theoretical qualification of the fractal characterization algorithms, with strong consideration of the two recognized constraints of signal length and mean. Over the range of β, processes of the given length are generated for [−1,3] incremented by 0.01.

4.3. Numerical Analysis of Stride Interval Data Sets

Lastly, the published data sets are re-examined. First considered are right foot gait stride interval time series from normal subjects, consistent with previous investigation by Hausdorff, et al in the study of long range correlations in stride interval fluctuations (Hausdorff et al., 1996) and reconsidered by Deligieneras (Delignieres and Torre, 2009). Each of 10 healthy adult subjects walked at a self selected slow, normal, and fast pace, providing 30 total time series. This study, henceforth referred to as Study I, implemented a power spectral analysis and DFA to find β and α respectively (Hausdorff et al., 1996) to qualify and compare each method for fractal dynamics in gait. The mean time series length for the ten healthy control subjects is 3,179 points. Given the signals’ significant length, these are considered to be a basis set for evaluating the algorithm performance under sufficiently long signal lengths. For consistency with the previous investigations, only the first 2,048 points are used for calculation.

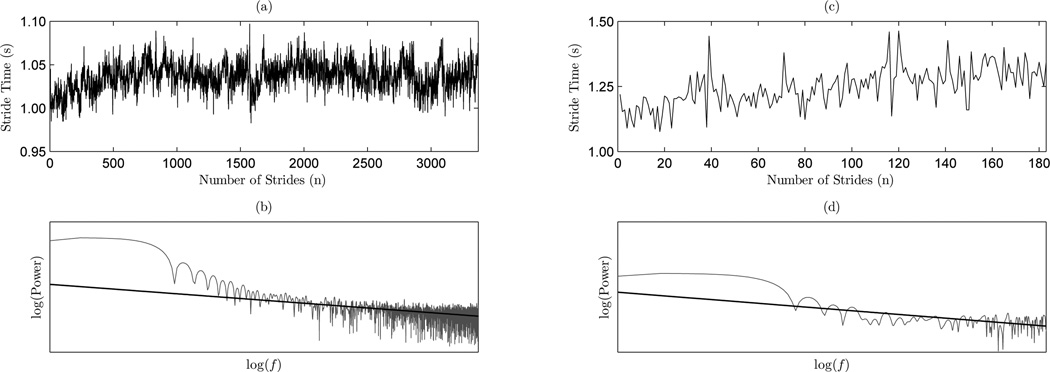
The second set comes from an investigation of gait dynamics in neurode-generative diseases. The data was obtained by Haussdorf, et al in investigations of healthy and pathological correlations in stride interval time series (Hausdorff et al., 2000, 1997, 1996). The signal lengths are considerably constrained due to the physical limitations of the subject. An example of healthy and pathological (ALS) time series provided by Studies I and II are shown in Figure 3 with their corresponding PSDs and regression lines.

Figure 3.

Sample stride interval time series and the corresponding PSDs: (a) Study I (healthy) time series; (b) PDS of Study I (healthy) sample time series; (c) Study II (ALS) time series; and (d) PSD of Study II (ALS) time series.

In the investigation henceforth referred to as Study II, α was calculated by DFA. To again retain consistency with the previous investigation, only the right foot stride interval time series is considered for calculation. Listed in Table 1 are the total number and mean length of time series for each of the cases of pathology and the control. The evaluation here is aimed to demonstrate the algorithm performance in the regime of short time series.

Table 1.

Number of time Series and mean length, Study II. ALS = Amyotrophic Lateral Sclerosis, HD = Huntington’s Disease, PD = Parkinson’s Disease, CO = Control.

	ALS	HD	PD	CO
Number of Series	13	20	15	16
Mean Length	196	242	184	255

For Study I, we fit a linear mixed model with estimated beta coefficient as the dependent variable; walking speed, calculation method and their interaction as fixed effects; and a participant random effect (Table 2). For Study II, we fit a similar model with participant group, calculation method and their interaction as fixed effects (Table 3). We used appropriately constructed means contrasts to obtain statistical significance of between-method comparisons of interest.

Table 2.

A comparative analysis of the algorithms for time series from Study I.

		β			α
		Slow	Normal	Fast	Slow	Normal	Fast
Study I	DFA	0.96± 0.13	0.80± 0.07	0.94± 0.09	0.98± 0.07	0.90± 0.04	0.97± 0.05
	PSD	1.01± 0.15	0.81± 0.09	0.94± 0.07	1.01± 0.08	0.91± 0.05	0.97± 0.04
Analysis	DFA	0.93± 0.13	0.77± 0.15	0.94± 0.17	0.97± 0.07	0.88± 0.08	0.97± 0.09
	lowPSDwe	0.73± 0.15	0.48± 0.09	0.62± 0.17	0.87± 0.08	0.74± 0.05	0.81± 0.09
	AWC	1.07±0.17	0.87±0.10	1.00± 0.18	1.03±0.09	0.94± 0.05	1.00± 0.09

Table 3.

A comparative analysis of the algorithms for time series from Study II.

		β				α
		ALS	HD	PD	CO	ALS	HD	PD	CO
Study II	DFA	0.48±0.13	0.20 ±0.07	0.64±0.11	0.82±0.09	0.74±0.07	0.60±0.04	0.82±0.06	0.91±0.05
Analysis	DFA	0.66±0.13	0.37±0.12	0.52±0.16	0.60 ±0.10	0.83±0.07	0.68±0.06	0.76±0.08	0.80±0.05
	lowPSDwe	0.56±0.08	0.26±0.09	0.39±0.11	0.49±0.05	0.78±0.04	0.63±0.05	0.70±0.06	0.74±0.03
	AWC	0.97±0.10	0.54±0.13	0.73±0.15	0.94±0.06	0.98±0.05	0.78±0.06	0.87±0.08	0.97±0.03

5. Results

Presented in this section are the results of the numerical analysis scheme. Secondly, the results from the evaluation of the published physiological data sets of long time series from healthy individuals and shorter time series of neurodegenerative disease subjects are examined. From the results of the numerical analysis, this paper seeks to indicate which of the estimators can most effectively evaluate fractal nature of the physiological time series under the various constraints. The importance of accurately measuring β of the physiological time series is also presented in this section, so the calculations of the physiological data are compared with previously published results.

5.1. Overall Theoretical Performance

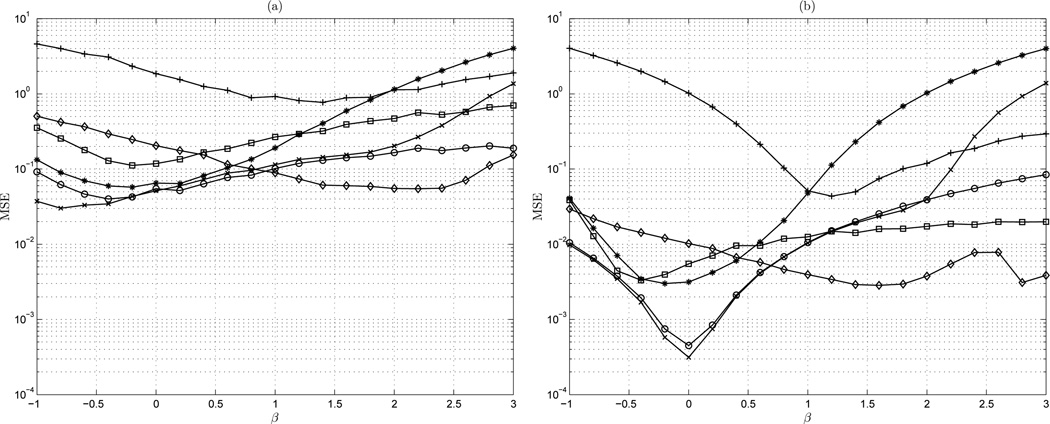
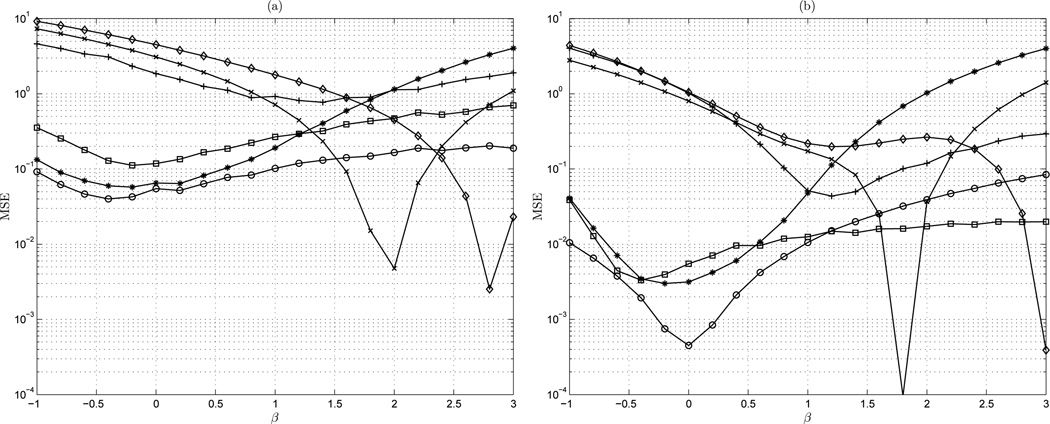
Considered first is the estimation accuracy of the algorithms for − 1 ≤ β ≤ 3. This presents the performance of the general scheme, which calculates the mean spectral index β of 1,000 random fractal signals of lengths varying from 50 to 10, 000 points. This is under a normalized condition. Shown are the mean-square error (MSE) of the estimators on the range −1 ≤ β ≤ 3 for signal lengths of of 100 and 10,000 points in Figure 4(a) and (b), respectively.

Figure 4.

MSE vs β: (a) n = 100 points; (b) n = 10,000 points. ◊ AWC; + bdSWV; □ DFA; * Disp; × PSD; ○ ^lowPSD_we

The results of the analysis indicate that some estimators are indeed not class independent. Figure 4(a) shows the MSE of the estimators on the range −1 ≤ β ≤ 3 for signal length of 100. For a short signal length, it is clear that bdSWV and dispersional analysis estimators are fBm and fGn class dependent, respectively. The bdSWV method exhibits very high MSE for the fGn class (β < 1) and dispersional analysis shows high MSE for all fBm class signals (β > 1). Similar error in the fGn class is noted for the AWC method, and the error decreases for β > 1. DFA exhibits relatively high MSE values for both fBm and fGn processes with a relatively flat profile on this range. However, DFA demonstrates slightly greater accuracy than AWC method for signals close to white Gaussian fGn signals. Both power spectral density methods, the periodogram (PSD) and the modified method ^lowPSD_we show quite consistent accuracy for all signal classes with a relatively flat MSE profile across the range of β. Interestingly, for short signal lengths, the basic periodogram (PSD) method is more accurate than the ^lowPSD_we method. However, the MSE of the PSD increases significantly for persistent fBm type signals (β > 2).

Considering the case of long time series length of 10,000 points given in Figure 4(b) it is clear that the bdSWV method has significantly high MSE for all fGn class signals (β < 1). Similarly, dispersional analysis demonstrates high MSE for all fBm class signals (β > 1). AWC shows relatively consistent MSE for both classes, though the MSE decreases as the signal type approaches Brownian motion (β = 2). There is though an observable MSE increase for persistent fBm signals. DFA similarly demonstrates class independent behavior, with lower MSE for fGn class signals. Again in the long signal length case, DFA indicates DFA exhibits a relatively consistent MSE in both the fGn and fBm class. Both power spectral density methods, the periodogram (PSD) and the modified method ^lowPSD_we demonstrate similar MSE, which is lowest for white Gaussian noise fGn processes. Higher MSE is observed for fBm class signals, though the error is not as high as in the class dependent dispersional and bdSWV methods. The modified PSD method shows higher accuracy than the standard periodogram for persistent fBm type signals (β > 2).

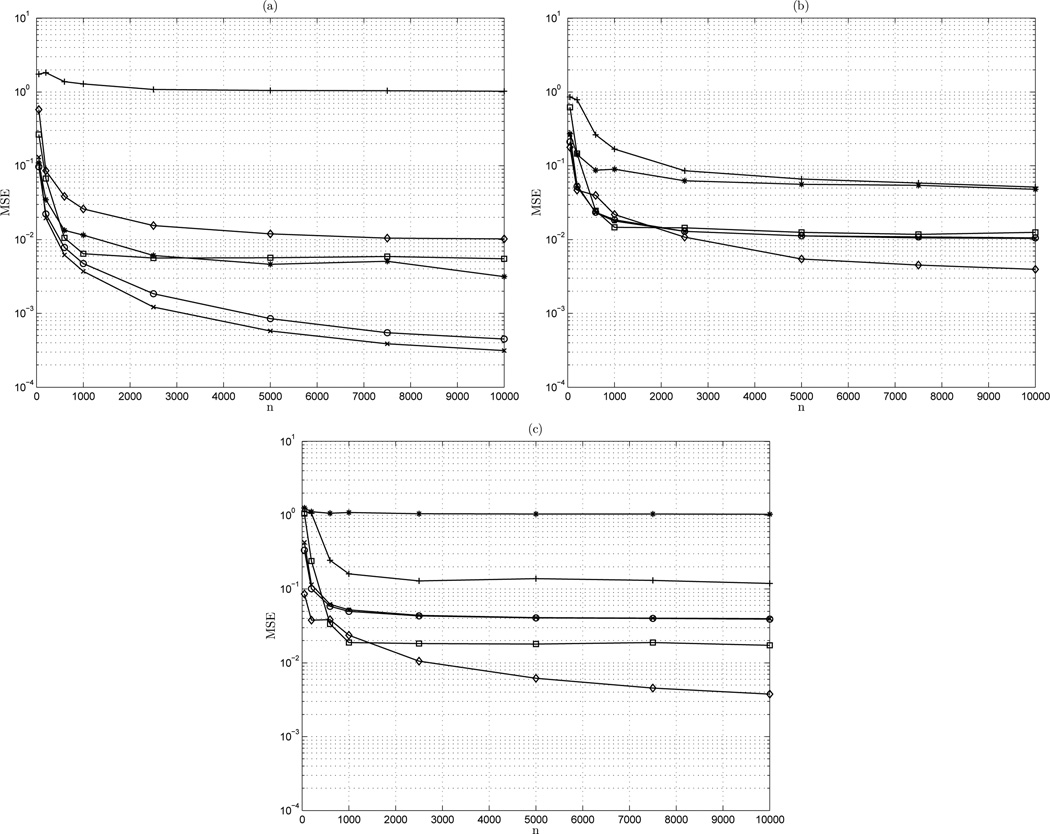
Given the clear relationship of the MSE and the signal length, examined next is the MSE value over a range of signal lengths. Each value is the 1,000 realization ensemble mean MSE for the given length. For conciseness, anti-correlated fGn (β = −1) and persistent fBm (β = 3) evaluations are excluded. Shown in Figure 5(a) is the mean-square error (MSE) of the estimators on the range 50 ≤ N ≤ 10,000 for white Gaussian noise fGn signals of β = 0.

Figure 5.

MSE vs n: (a) β = 0; (b) β = 1; (c) β = 2. ◊ AWC; + bdSWV; □ DFA; * Disp; × PSD; ○ ^lowPSD_we

For the white Gaussian noise case of fGn class signals β = 0, the MSE of the bdSWV method is high regardless of signal length. The MSE for dispersional analysis decreases as signal length increases, and at long signal length is among of the most accurate estimators for this signal class. Interestingly, DFA shows diminishing returns in accuracy beyond N = 1,000. AWC consistently shows increasing accuracy as signal length increases. For the white Gaussian case of fGn signals, the power spectral density methods again exhibit the lowest overall MSE which decreases for greater signal length.

The mean-square error of the estimators on the range 50 ≤ N ≤ 10, 000 is observed in the critical case of the boundary of fGn and fBm signals for 1/f^β processes of β = 1. Here, it is expected to see that regardless of signal length, both class dependent methods bdSWV and dispersional analysis exhibit crossover and a similar order of MSE. DFA shows initially high MSE that decreases as signal length increases, though again with quickly diminishing returns. The power spectral density methods show a similar profile. AWC again shows increasing accuracy as the length is increased. For shorter length signals cases, the MSE of AWC, DFA, and spectral methods are clustered closely together.

The third case consideration is the MSE versus length for Brownian motion fBm signals of β = 2. For the Brownian motion process indicative of the fBm class, the MSE of dispersional analysis is high regardless of signal length, indicating its class dependence. The MSE of bdSWV is lower than in the fGn class, though it is still significantly greater than other methods. DFA reaches its maximum accuracy at N = 1,000 points. AWC exhibits the sharpest drop off in error of all methods, and regardless of signal length has generally the lowest error for Brownian motion fBm class signals. The spectral methods show low MSE for very short time series, but quickly diminishing returns for signals greater than 1,000 points.

Considering the class dependence of the bdSWV and dispersional analysis methods, subsequent observations of the results will not consider findings for these methods. This is in the interest of determining a robust class independent estimator. Accordingly, ^lowPSD_we is considered class independent for its modifications which allow a more accurate estimation of fBm processes than the unmodified periodogram method. In conclusion, further elaborations on the MSE, mean error (ME), and standard deviation (SD) of techniques will consider DFA, ^lowPSD_we, and AWC.

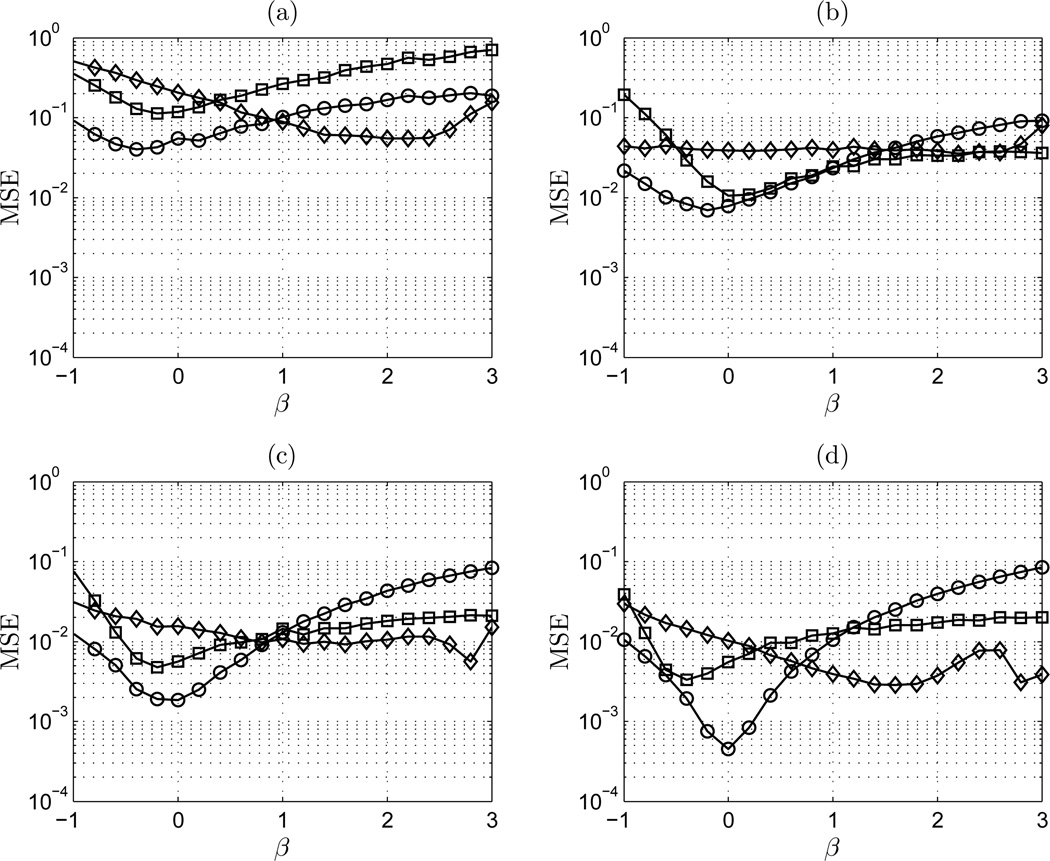
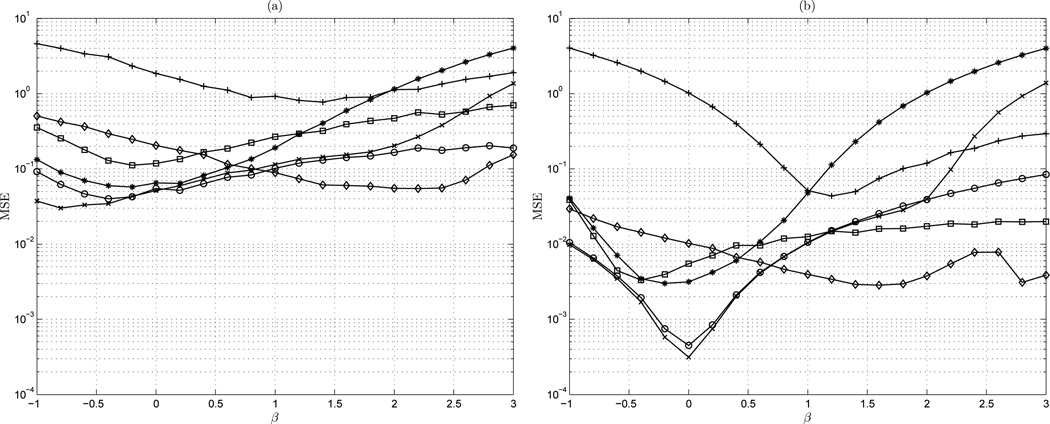
Figure 6 shows the mean-square error of the estimators DFA, ^lowPSD_we, and AWC on the range −1 ≤ β ≤ 3 for signal length of 100, 600, 2,500, and 10,000. For the two short series sets (N = 100, N = 600), all methods exhibit a relatively consistent profile of MSE over the entire range of β. For short time series, AWC is most accurate in the fBm class, and ^lowPSD_we is most accurate in the fGn class. DFA is generally less accurate than AWC and ^lowPSD_we. Though DFA may be more accurate than AWC at estimating a white Gaussian fGn process, the accuracy of ^lowPSD_we is still preferable. A similar observation can be made in longer time series of length 600, 2,500, and 10,000. DFA shows preferable performance to AWC near white Gaussian noise, and here the accuracy of ^lowPSD_we is always favorable. An important characteristic of AWC is its relatively flat MSE over the range of β for all signal lengths. A notable increase in MSE exists for ^lowPSD_we in the fBm class as the length is increased, due to the effects of more low frequency content in these signals.

Figure 6.

MSE vs β: (a) n = 100 points; (b) n = 600 points; (c) n = 2,500 points; and (d) n = 10,000 points. ◊ AWC; □ DFA; ○ ^lowPSD_we

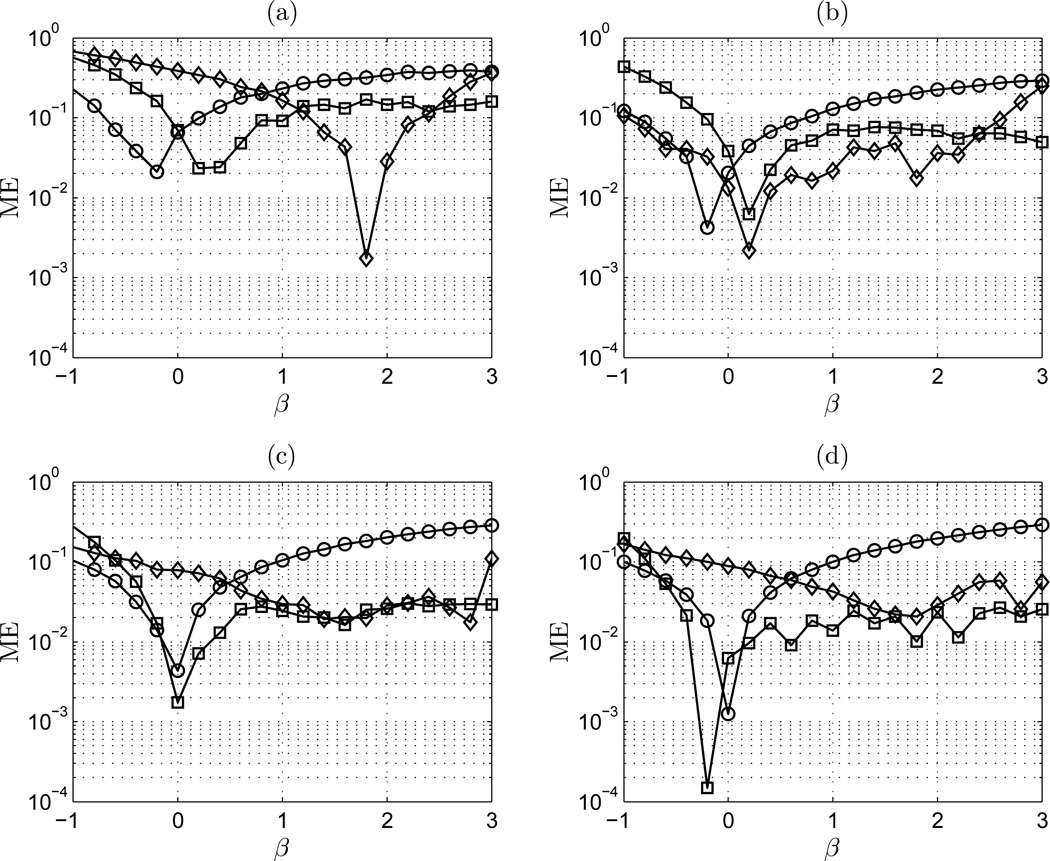
The definition of MSE necessarily combines the bias and variance into one value. To distinguish the individual effects of bias and variance in the notion of the estimators’ MSE on this range, the bias (mean error) and variance (standard deviation) will be examined separately in the following figures. Figure 7 shows the mean error (ME) of AWC, ^lowPSD_we, and DFA on the range −1 ≤ β ≤ 3 for signal lengths of 100, 600, 2,500, and 10,000.

Figure 7.

ME vs β. (a) n = 100 points; (b) n = 600 points; (c) n = 2,500 points; and (d) n = 10,000 points. ◊ AWC; □ DFA; ○ ^lowPSD_we

Figure 7 indicates that for short time series, the MSE of AWC is largely influenced by bias. This effect is diminished in the fBm regime. The mean error of DFA is lower than ^lowPSD_we and AWC for the fGn class. The MSE of DFA is consistently influenced by bias in the fBm range. ^lowPSD_we exhibits less overall fluctuation, and estimation bias increases with β. This is likely due to the influence of more low frequency components when evaluating the linear regression of the power spectral density. For subsequently longer signal lengths of 600, 2,500, and 10,000, the bias effects on the MSE of DFA and AWC are comparable beyond β = 0.

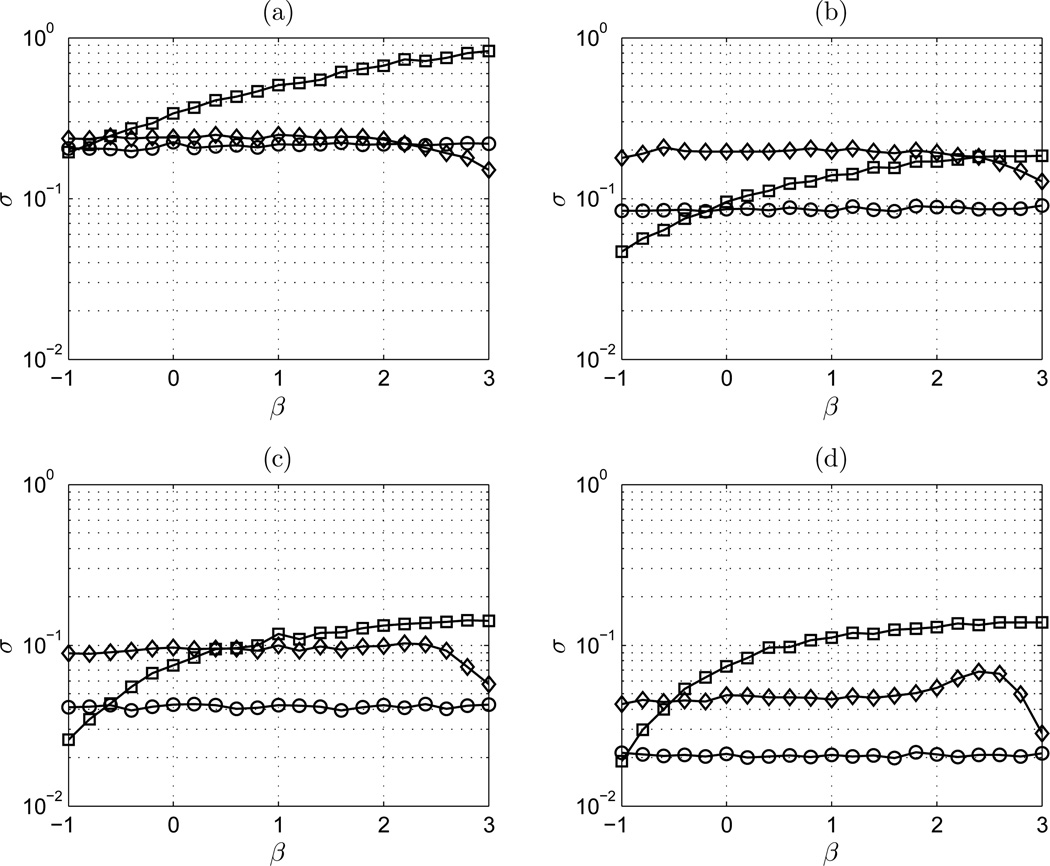
Figure 8 shows the standard deviation (σ) of DFA, ^lowPSD_we, and AWC on the range −1 ≤ β ≤ 3 for signal length of 100, 600, 2,500, and 10,000. For short signal length, the standard deviation of DFA is significant. The standard deviation of ^lowPSD_we and AWC are very consistent on the range of β. ^lowPSD_we shows the overall lowest standard deviation for both signal classes for all signal lengths. For longer signal lengths, the standard deviation profile of DFA is relatively unchanged. The profile of AWC is flat in each case, with increasing accuracy with signal length. DFA exhibits lower standard deviation than AWC for fGn class signals of length 600 and 2,500, though the accuracy of ^lowPSD_we is still preferential.

Figure 8.

σ vs β: (a) n = 100 points; (b) n = 600 points; (c) n = 2,500 points; and (d) n = 10,000 points. ◊ AWC; □ DFA; ○ ^lowPSD_we

5.2. Effects of Nonzero Mean

5.2.1. Added Unit Mean

Presented in this section are findings for realizations of the algorithms for the complete range −1 ≤ β ≤ 3 on an extension of the previously described scheme where a the signal is normalized and unit mean is added. Figure 9 (a) and (b) show the mean-square error of the estimators on the range −1 ≤ β ≤ 3 for biased signal length of 100 and 10,000, respectively.

Figure 9.

MSE vs β, added unit mean: (a) n = 100 points; (b) n = 10,000 points. ◊ AWC; + bdSWV; □ DFA; * Disp; × PSD; ○ ^lowPSD_we

Compared to the original normalized signal condition shown in Figure 9, the additional unit mean affects only the MSE of the frequency and time-scale domain methods. The adjustments introduced to the power spectral density method by ^lowPSD_we avoid the error effects of nonzero mean. It is critical to note that a significant DC component from a series mean will largely influence a low frequency range of the power spectral density, and subsequently the linear regression estimation for the spectral estimators. However, the constant unit mean has diminishing influence on increasingly non-stationary processes, and thus the effect is diminished as β increases. This observation is reflected in the findings of the dependence of the MSE on signal length with nonzero mean. Inaccuracy in the AWC method is significantly influenced in the fGn class, and error is still generally present for all fGn and fBm class signals. The nonzero mean has no effect on the time domain methods.

5.2.2. Removal of Mean

Finally observed is the estimation accuracy when the series mean is removed. These results are from the third extension of the numerical analysis scheme. From the second case where the signal is normalized and unit mean is added, the mean of the resulting signal is calculated and subtracted from the time series. Shown in Figure 10 (a) and (b) are the mean-square error of the estimators on the range −1 ≤ β ≤ 3 for a zero mean signal length of of 100 and 10,000, respectively.

Figure 10.

MSE vs β, zero mean: (a) n = 100 points; (b) n = 10,000 points. ◊ AWC; + bdSWV; □ DFA; * Disp; × PSD; ○ ^lowPSD_we

Figure 10 indicates that when the mean is removed by simply subtracting the mean value of the series, the estimation accuracy returns to the original profile. Thus, removing the series mean is valid to avoid errors in series estimation by methods which are sensitive. The original mean square error, mean error, and standard deviation profiles are realized when the series mean is removed and the series is reevaluated.

5.3. Gait Stride Interval Analysis

This section presents the results of the application of these techniques to experimentally measured gait stride interval time series. To keep the analysis concise, the methods implemented were those of the lowest MSE from each domain class. Thus, β was calculated by DFA, ^lowPSD_we, and AWC. For the AWC calculation, the preprocessing step of mean removal is performed. For a thorough evaluation of Study I, β is calculated and converted to α by the relationship $\alpha =\frac{\beta +1}{2}$. For clarity, these calculated values of β and α are presented separately in Table 2, showing the values (mean ± standard deviation) from the study and our calculations for DFA, ^lowPSD_we, and AWC. Furthermore, the calculated values were statistically different (p < 0.03) among the used approaches, except between AWC and DFA for fast and normal walks (p > 0.07).

Considered next are calculations for shorter time series of pathological gait conditions from Study II. Due to the physical limitations of the patients under investigation, the shortness of the time series length given in Table 1 is noted when considering the results of these calculations. Again, the spectral index β is calculated by DFA, ^lowPSD_we, and AWC and converted to the DFA scaling exponent α. The series mean has been removed for calculation by AWC. Table 3 shows the published and calculated values (mean ± standard error) of β and the corresponding of α for the calculations by DFA, ^lowPSD_we, and AWC methods. Furthermore, the AWC values were statistically different from the values calculated by DFA and ^lowPSD_we (p < 0.04) in all cases. However, the values calculated by DFA and ^lowPSD_we were not statistically different in any of the cases (p > 0.09).

6. Discussion

6.1. Simulated Signals

From the results of the theoretical evaluation of these techniques, distinct limitations and benefits of each of the methods can be observed. When determining an appropriate technique to evaluate the fractal nature of a process, it is critical to consider the time series length, any apparent mean, and in some cases the range on which the process’s spectral index might exist. It is therefore apparent from our analysis that making a conclusion about the fractal nature of short physiological time series can be quite tenuous. The nature of physiological data sets and their relationship to ideal 1/f^β profiles should be a significant consideration when drawing conclusions about the results of these analyses.

In the interest of determining class independent estimators, the dispersional and bdSWV methods are clearly not viable. Though developed for consideration of fGn and fBm class signals respectively, these methods can provide incorrect results for signals typical of physiological processes at β = 1. The recommendation to favor class independent methods is to effectively reduce the burden of determining the signal class before evaluation. DFA is a candidate, as it indicates no preferential performance in either class. Additionally, the evaluation is unaffected by a non-zero series mean. However, the results for DFA have significantly large mean-square error and standard deviation for short time series (Bryce and Sprague, 2012). It is apparent that DFA has little utility for short time series, and exhibits diminishing returns in accuracy for longer series, as other investigations have observed (Delignieres et al., 2006; Bryce and Sprague, 2012; Bardet and Kammoun, 2008).

A significant limitation of the frequency domain methods is the effect of low frequencies and DC on the accuracy of these methods. Indeed, a the critical property of fractal processes is that the power spectral density is not convergent for (ω = 0), and this presents some problems for analysis (Li, 2010). However, removing DC and low frequency content from the spectrum risks destroying low frequency information, and thus some scale invariant features of the process. Additionally, the significantly lower MSE observed in the spectral methods for white Gaussian fGn processes is likely an artifact of the time series generation by the same principle (Kasdin, 1995). Regardless, accurately estimating the properties of white Gaussian processes does not present any significant utility with respect to the interest of fractal characterization of physiological processes, where a simple autocorrelation analysis or Lilliefors test may suffice.

AWC has a more uniform performance for the range of fGn and fBm class signals. Though AWC was significantly affected by non-zero mean signals, this effect is corrected by the removal of the time series mean before evaluation. Unlike the modifications to spectral methods to eliminate ill-fitting due to DC or high frequency noise, this is a straightforward preprocessing step easily integrated with the main algorithm. This combination also provides intact frequency and scale dependent information of the series. DFA presents significant risk for short time series and provides no clear advantage in many instances, where ^lowPSD_we can likely provide a more accurate complement to AWC analysis. In general, given these two primary constraints of non-zero mean and short time series in gait stride interval signals, AWC can provide uniformly accurate characterization for short and long biased data series. Regardless, discretion of the desired precision and accuracy, illustrated by the mean error and standard deviation, is encouraged in all applications. Generally, the MSE of all estimators indicate that AWC is a generally robust method, consistent under many circumstances and favorable especially under conditions of physiological interest.

6.2. Stride Intervals Time Series

The analysis of the physiologically extracted time series provides perhaps the most significant indication of the applicability of these methods in a physiological setting. Table 2 shows the fractal characterizations for long time series of ten healthy adults walking at self selected paces. In these time series, the mean amplitude is 0.2025 and the mean of the series is 1.1481, indicative of the inherent non-zero mean offset. The effects of these signal characteristics are observed in our evaluation of these time series by DFA, ^lowPSD_we, and AWC. For the self selected slow, normal, and fast time series, the DFA and AWC methods evaluate a mean spectral index of 0.88 ± 0.15 and 0.98 ± 0.15 respectively. To validate this disparity, consider the results of the simulated time series for length of 100 and β = 1. The MSE of AWC is preferable in this instance, and is exemplified by observing the substantial standard deviation of DFA here. The underestimation of the spectral index here by ^lowPSD_we is noted. Considering physiologically eaningful conclusions from the pathological gait data is more difficult given the inherently short length of the time series. These evaluations given by Table 3 show the findings for short time series of ALS, Huntington’s Disease, Parkinson’s Disease, and control subjects. For all series, the mean time series length is 190 points. The mean amplitude is 0.2788 and the mean of the series is 1.0866, again showing a non-zero mean offset. For pathological gait time series, more stationary fGn type characteristics may be expected. Given the MSE for β on the range of [0,1] for length of 100, the accuracy of DFA, AWC, and ^lowPSD_we are generally comparable on the order of 10⁻¹. Table 3 still show disparity between each estimator, error largely affected by the time series length.

The drastic underestimation of the spectral index by the frequency do-main based method is observed in both studies. To avoid error in the es-timation introduced by noise, the ^lowPSD_we necessitates removal of high frequency components of 1/8 * f_max. The underestimation of the spectral index in the power spectrum indicates a greater effect of the high frequency content of the signal, so this adjustment did not quite nullify the effects of high frequency biasing. Though the MSE of AWC and DFA are similar, the AWC method is similarly biased but has much lower standard deviation. DFA on this range again presents significant standard deviation. This highlights the critical concern of the application of DFA to pathological time series of short length. It is therefore concluded here that the results provided by AWC are more tenable.

It is clear that DFA and spectral methods in many instances require extensive modification to properly assess the data. It is seen that necessity of such modifications as a potentially hazardous burden which could render results incorrect and obfuscate interpretations. Indeed, in the proposal of these methods for gait stride interval analysis by Haussdorf, the window sizes and fitting ranges for DFA and the frequency range for the spectral method linear regression required significant scrutiny to achieve a desired result (Hausdorff et al., 1996; Delignieres et al., 2006). In this case, the relationship between the scales of the significant physiological frequencies and noise frequencies can be inferred in a general sense. However, it is not always possible to make a clear distinction between noise and physiologically meaningful frequency content in all physiological and experimental settings. DFA similarly requires adjustment of the bounds of window size. This adjustment can significantly impacts the final calculation, and varies between applications depending on the amplitude of fluctuations in the chosen window. This would require specific specialization of this method for each application. The risks and burdens of specialization of these methods can be effectively reduced given the generally favorable performance AWC. It is noted that the only requirement to avoid errors in AWC is preprocessing the signal by subtracting the mean.

7. Conclusions

The objective of this study was to provide a comparative analysis of fractal characterization algorithms of 1/f^β time series with respect to physiological applications. Primarily, the numerical analysis allowed us to provide insight into the time series lengths and signal classes on which previously proposed algorithms returned acceptably accurate results. If fractal characteristics are of interest for some arbitrary physiological process, it is critical to choose a class independent algorithm with consistent accuracy and precision. When signal class is not given a priori or classification is not possible, the application of class dependent estimators is not feasible. The evaluation of these algorithms, bdSWV and dispersional analysis, has shown that the limited utility of these methods in this setting. However, these are still relatively valid evaluations if a signal class can be determined. Once a process can be classified as fGn or fBm by a more robust consistent and accurate estimator such as AWC, a class specific estimator may provide a useful complementary analysis. In contrast to the findings under simulation, the inherent nature of experimentally derived physiological signals present further challenges in evaluating fractal properties. The sensitivity of power spectral methods to a non-zero mean and high frequency were observed, and necessitate the task of distinguishing the range of physiologically meaningful frequencies from noise. Similarly, the potential errors influenced in DFA from large local fluctuations in small window sizes are noted. However, the application of a method requires the recognition of several key characteristics of pathological gait time series. First, the understood composition and function of the locomotor system insists that the statistical properties of the gait outcome can be analyzed to have fractal properties. It has been shown that aging and neurodegenerative diseases result in decreased central processing capabilities, proprioception, muscle strength and endurance, and significant dysfunction in motor neurons, the cerebral cortex, brain stem, and spinal cord. Accordingly, diminished function to any components of the locomotor system caused by aging or disease will affect these statistical outcomes and thus the fractal characteristic. Another key characteristic of pathological time series is the typically shortened length. In light of the results of the numerical analysis, the AWC method is recommended as a useful tool for measuring the fractal characteristic of time series. This is a useful tool which can more rapidly and accurately track functional changes in stride interval dynamics. Clinically, this translates to a biomarker of a potentially hidden pathology or decline due to disease or aging that can be quickly and reliably monitored and inform susbsequent therapeutic intervention. A final advantage of this application recognized by the comparative evaluation of these algorithms is the relief of the burden of specific adjustments for each application. This numerical and corresponding gait stride interval physiological analyses provide a justifiable basis for the applications of AWC to a variety signals of interest for a more informative indicator of the fractal nature of these processes.

• Many physiological systems can be modeled as fractal processes.

• We investigated various approaches for estimation of spectral behavior.

• The averaged wavelet coefficient method yielded the most accurate results.