Recent advances in computational methodology for simulation of mechanical circulatory assist devices

Abstract

Ventricular assist devices (VADs) provide mechanical circulatory support to offload the work of one or both ventricles during heart failure. They are used in the clinical setting as destination therapy, as bridge to transplant, or more recently as bridge to recovery to allow for myocardial remodeling. Recent developments in computational simulation allow for detailed assessment of VAD hemodynamics for device design and optimization for both children and adults. Here, we provide a focused review of the recent literature on finite element methods and optimization for VAD simulations. As VAD designs typically fall into two categories, pulsatile and continuous flow devices, we separately address computational challenges of both types of designs, and the interaction with the circulatory system with three representative case studies. In particular, we focus on recent advancements in finite element methodology that has increased the fidelity of VAD simulations. We outline key challenges, which extend to the incorporation of biological response such as thrombosis and hemolysis, as well as shape optimization methods and challenges in computational methodology.

1 Current devices and clinical application

Ventricular assist devices (VADs) provide full or partial mechanical circulatory support to one or both ventricles of the heart. They are used clinically in a range of adult and pediatric diseases, including congenital heart disease, cardiomyopathy, and post-infarction heart failure. They were first developed as a bridge to transplant to prolong life of critically ill patients awaiting organ availability. However, as designs have evolved to become smaller and even fully implantable, they can now be used as destination therapy, supporting one or both ventricles. More recently, there has also been success, most notably in pediatric patients, with use of VADs in bridge to recovery scenarios, allowing sufficient offloading for myocardial remodeling and recovery.¹

Heart failure (HF) is a major source of morbidity and mortality in the US, with more than 670,000 diagnoses predicted this year in the US.² HF is typically a progressive disease with a median survival of only 2 to 3 years after diagnosis.³ Patients with advanced HF have limited treatment options. While a small number may qualify for cardiac transplantation, this is limited by stringent selection criteria and lack of availability of donor hearts. Improvements in technology and patient outcomes, including development of smaller left ventricular assist devices (LVAD) suitable for use in a larger number of patients, have led to growth in the number of LVAD implants and the number of participating clinical centers. Estimates of the number of potential VAD recipients in the United States may be as high as 250,000–300,000.⁴

VAD technology has progressed significantly over the past two decades. Designs have evolved from pulsatile devices that mimicked the stroke volume of the human heart, to small implantable devices that deliver continuous flow. The 2001 Randomized Evaluation of Mechanical Assistance in the Treatment of Congestive Heart Failure (REMATCH) trial established the superiority of a pulsatile flow VAD to medical treatment of patients with advanced HF who were ineligible for cardiac transplantation.⁵ Due to the favorable outcomes demonstrated in REMATCH, the Food and Drug Administration (FDA) approved the use of the HeartMate XVE (Thoratec Corporation, Pleasanton, CA) for destination therapy in 2003.

Since that time, numerous alternative VAD designs have come on the market, and the use of VADs has expanded to include less critically ill patients, with improved selection leading to better outcomes.⁶ Notably, Thoratec's HeartMate II device, FDA approved for destination therapy in 2010, is now among the most predominant continuous flow devices on the market. It is implanted just below the diaphragm and connected to the aorta, leaving the circulatory system otherwise in tact. This device is smaller, quieter and more portable than most other devices, making it easier for patients to remain active. The HeartMate II LVAS Pivotal Study⁷ began in 2005 and evaluated the HeartMate II for two indications over an 18-month period: bridge to transplantation and destination therapy. Results showed that patients' designated NYHA heart failure class had significantly improved after six months of LVAD support compared to the pre-LVAD baseline, providing early evidence that continuous flow LVADs have advantages in terms of durability and reliability. In addition, the first HeartAssist5, a modern version of the DeBakey VAD weighing only 92 grams, was implanted at Heidelberg University Hospital in July 2009. Total artificial hearts, which replace both ventricles, have also come on the market, including Syncardias CardioWest device which was FDA approved in 2004, and AbioMed's AbioCor device, approved for humanitarian use in 2006.

Despite these advances, there are a number of ongoing clinical complications arising from VAD use. Bleeding is the most common early postoperative complication following implantation or explantation of LVADs, necessitating reoperation in up to 60% of recipients.⁸ With increased bleeding comes the need for blood transfusions, which can in turn increase the incidence of infection, pulmonary insufficiency, right heart failure, allosensitization, and viral transmission, some of which can prove fatal or preclude transplantation. Because VAD devices introduce non-biologic surfaces, predisposing the blood to clotting, there is generally a need for anticoagulation therapy, together with all of its inherent risks. Other problems include immunosuppression, clotting with resultant stroke, and bleeding secondary to anticoagulation. LVAD patients are also at elevated risk of developing von Willebrand disease, in which large multimers of von Willebrand factor are destroyed by mechanical stress, increasing the risk of bleeding.

In addition to the rising number of adults receiving VAD devices, use in children has also increased. Approximately one in 100 children are born with some form of congenital heart disease, and of those receiving surgery or catheter-based intervention, approximately 85% now survive into adulthood.⁹ Despite the advances in surgical and management methods, some of these patients will develop acute or chronic heart failure, requiring heart transplantation and/or mechanical support. It is estimated that approximately 10% of Fontan surgery patients will go on to experience early failure. With the number of available donor hearts for children fixed at a relatively constant value of ≈ 500 per year, compared to the nearly 1, 000, 000 people living with congenital heart disease in the US, there is a growing need for mechanical circulatory support for this population.¹⁰ Additionally, there is compelling clinical evidence that pediatric patients can heal with the help of mechanical circulatory support, supporting a bridge-to-recovery paradigm for VADs.¹¹

Currently, the only FDA approved VAD for infants and children is the Berlin Heart EXCOR device, a pneumatically driven pulsatile flow device, though adult congenital heart disease patients may be eligible for adult continuous flow devices. Over 800 pediatric patients worldwide have been supported with a Berlin Heart as a bridge to cardiac recovery or transplant.¹² While survival to transplantation is relatively high (63%–89%), complications are also common in patients supported with the EXCOR device, including thromboembolism (22%), bleeding requiring reoperation (29%), infection (67%), and adverse neurological events (69%).^13–16 Of these morbidities, the persistently high rate of stroke remains a particularly troubling complication associated with VAD support in children. A 2012 study compared the Berlin Heart to extracorporeal membrane oxygenation (ECMO) and concluded that a pediatric VAD available in several sizes as a bridge to heart transplantation (such as the Berlin Heart) was associated with a significantly higher rate of survival as compared with ECMO.¹⁷

2 Why VAD simulations?

With the increasing prevalence of VADs in clinical use, there is now focus on improving design performance to reduce co-morbidities, reducing device size, and allowing patients a more active lifestyle. Numerical simulations can be used to accelerate the design process and optimize current and future designs. In this paper, we present a focused review of selected recent advances in finite element simulation methodologies applied to VADs. Through three specific case studies, we illustrate the potential of simulations to accelerate the design process, optimize device designs, and improve performance. These three case studies, while by no means an exhaustive review of this highly dynamic field, are representative of three key areas of active research: pulsatile VADs, continuous flow VADs, and the interaction of VADs with circulatory physiology. For completeness, we also provide appropriate references to other major work in the field, and the reader is encouraged to refer to these for a broader view of recent developments.

Simulations offer a promising means to cheaply and efficiently test and optimize competing device prototypes, thereby reducing time to market, and identifying potential performance enhancements. Numerical analysis is an integral part of the design process in many industries (e.g., aerospace, automotive). At Boeing Corporation, for example, computational fluid dynamics (CFD) coupled to rigorous optimization algorithms are a crucial and cost saving part of the design chain for all major aircraft.¹⁸ Despite its demonstrated success in these large-scale applications, adoption of simulation tools has lagged behind in the medical device industry, though recently gaining favor. This is due in part to initial success with designs identified through trial and error and experimentation, as well as challenges associated with complicating factors of blood biochemistry, mechanobiology, and physiological response that make simulations challenging. While simulations have been applied more recently, particularly in the design of the HeartMate II and HeartAssist 5, there remains a need for increased adoption of simulation technology and formal design optimization algorithms.

In addition, the significant numerical challenges associated with VAD simulations can limit the applicability of commercial CFD solvers, often requiring specialized tool development. Design and simulation of artificial blood pumps present a number of unique challenges not encountered in more traditional industries. The micro-structural properties of blood affect both the choice of design objectives, such as minimizing blood damage and clotting, and also the possible need to account for non-Newtonian effects.¹⁹ Recent work aims to address the issue of objective functions which can be correlated with the accumulation of blood damage along flow pathlines, and the influence of constitutive model (Newtonian, generalized Newtonian, and viscoelastic) on the resulting optimal shapes. In this review paper, we illustrate selected finite element methodological advancements that overcome some of the challenges associated with VAD simulations through selected case studies, and discuss broader remaining challenges and future directions in modeling biological response, including hemolysis and thrombosis, and design optimization.

3 Preliminaries of finite element modeling methodology

Numerical modeling of blood flow in VADs relies on solving the Navier–Stokes equations of incompressible viscous flow. These equations enforce a point-wise balance of linear momentum and mass for the fluid, and thus allow solution of the unknown fluid velocities (vector quantity) and pressures (scalar quantity), both as functions of space and time. Analytical solutions of the Navier–Stokes equations exist only in a handful of cases, necessitating the use of computational fluid dynamics (CFD) for general VAD geometries to predict the hemodynamic phenomena of interest.

In CFD, the Navier–Stokes equations are solved approximately, generating a discrete solution for fluid velocity and pressure at every point in space in the computational domain and at each time of interest. Spatial discretization of the Navier–Stokes equations for applications having complex 3D geometries, such as VAD hemodynamics, is typically handled by means of a Finite Volume or a Finite Element Method (FEM). Finite element methods, which are a well-established computational methodology in the field of structural and solid mechanics, are a relatively new technology in fluid mechanics, and constitute an area of active research.²⁰ Among the many FEM approaches in fluid mechanics, the so-called Stabilized and Multiscale methods^21–23 as well as the more recent Residual-Based Variational Multiscale method,²⁴ and its moving-domain extension called the ALE-VMS method,^25,26 have reached the necessary level of maturity for general engineering CFD applications.

FEM is a function-based technology with a rich theoretical basis and systematic procedures for achieving higher-order solution accuracy for complex geometries. The weak or variational structure of FEM allows a natural imposition of non-standard inflow and outflow boundary conditions, robust handling of flows in moving spatial domains, including mechanical components in relative motion, and straightforward coupling with the governing equations of structural mechanics. These are some of the main simulation challenges for VADs, which we briefly discuss in what follows.

In application to flows with moving mechanical components, the Shear-Slip Mesh Update Method (SSMUM)^27,28 has been very instrumental. The idea behind the SSMUM was to restrict the mesh moving and remeshing to a thin layer of elements between the objects in relative motion. The mesh update at each time step can be accomplished by a “shear” deformation of the elements in this layer, followed by a “slip” in node connectivities. The slip in the node connectivities, to an extent, un-does the deformation of the elements and results in elements with better shapes than those that were shear-deformed. Because the remeshing consists of simply re-defining the node connectivities, both the projection errors and mesh generation cost are minimized. The SSMUM was implemented for objects in fast, rotational relative motion and applied to computation of flow past a rotating propeller²⁷ and flow around a helicopter with its rotor in motion.²⁸ In this review paper the SSMUM method is used in case study two, the simulation of the continuous-flow VAD.

As an alternative to SSMUM, a sliding interface technique has been proposed²⁹ for flows involving rotating and stationary components. Because no remeshing or reconnecting at the interface takes place in this method, the shared sliding cylindrical interface has nonmatching meshes on each side, and the enforcement of the kinematic and traction compatibility conditions at the sliding interface is done “weakly” using an appropriate modification of the governing equations of fluid mechanics at the discrete level. The sliding interface method was recently employed for wind-turbine “full machine” simulations^30,31 to handle the rotor-tower interaction, and is also suitable for continuous-flow VADs. Sliding interface finite volume methods have also been developed to simulate ducted propulsors for naval and turbo machinery applications.³²

To model pulsatile VADs, dynamic interaction of air, blood, and a thin membrane separating the two fluids needs to be considered. Coupled fluid-structure interaction (FSI) simulations at full scale are essential for realistic and accurate modeling of pulsatile VADs. This is because the motion and deformation of the thin membrane depends on the flow in the device blood and air chambers, and the flow patterns, in turn, depend on the motion and deformation of the membrane. As a result, the fluid and structural mechanics equations need to be solved simultaneously, with appropriate kinematic and traction coupling at their interface. The computational challenges for FSI of pulsatile VADs include large, buckling motions of a very thin membrane, the need for periodic remeshing of the fluid mechanics domain (due to the large motions of the membrane, which induce very large changes in the blood and air flow domain geometry during the cycle), and the necessity to employ tightly coupled FSI solution strategies due to the very strong added structural mass effect present in the problem. The state-of-the-art in FSI modeling and simulation is able to address these challenges (see a recent book on FSI³³ and references therein), however, there is currently no readily available, off-the-shelf commercial software where these techniques are implemented and that may be robustly deployed for this class of problems.

To model the structural mechanics of the flexible membrane, in recent work³⁴ the authors employed a rotation-free Kirchho–Love shell formulation^35,36 discretized using Isogeometric Analysis (IGA)^37,38 based on Non-Uniform Rational B-Splines (NURBS).³⁹ IGA-based thin shell formulations possess several accuracy and efficiency benefits that are discussed at length in recent work,^40,41 and, as such, present a good alternative to more standard FEM approaches.

Finally, as the devices supporting blood circulation, VADs are connected with the rest of the cardiovascular system, and the two subsystems are coupled. In modeling of VADs, the influence of the circulatory system on the VAD hemodynamics is taken into account by the use of the appropriate pump inlet and outlet boundary conditions. These constitute a significant source of uncertainty in the modeling, and are an area of extensive ongoing research in the cardiovascular simulation community. At the pump inlet a time-dependent blood flow rate is typically prescribed, while at the outlet one typically applies resistance or RCR-type boundary conditions,^42–44 which explicitly relate the flow rate and pressure at a given outlet face. Coupling with a lumped parameter model of the circulatory system is also an option that has been employed extensively in patient specific models of pediatric cardiology and coronary flows.^45–47 In the case of pulsatile VADs, on the blood chamber side, the roles of inlet and outlet boundaries are reversed when the pump switches from the fill to the eject stage. When the flow reverses through the outlet boundary, it is essential to “stabilize” the fluid mechanics formulation using an outflow stabilization technique first proposed by Bazilevs et al.,⁴⁸ and found to be minimally invasive in subsequent work.⁴⁹

4 Experimental Validation

Validation via in vitro experiments continues to play a crucial role in simulation method development and evolution of pump designs. Experimental studies comparing and characterizing flow in continuous flow VADs have been performed to identify key performance criteria and map the flow fields under different operating conditions.^50–52 Pulsatile VADs have also been extensively evaluated using particle image velocimetry under a range of operating conditions, and under conditions representative of device weaning and end-diastolic delay.^53–55 The need for further validation of blood pump components was illustrated by disparities in results reported in the recent FDA challenge to assess CFD performance, with sub-satisfactory agreement compared to experimental results.^56,57 Future validation efforts are needed to demonstrate the reliability of CFD and FSI to accurately characterize the flow field, but also for predictions of blood damage and platelet activation, as described below.

5 Case study 1: A Pediatric Pulsatile VAD

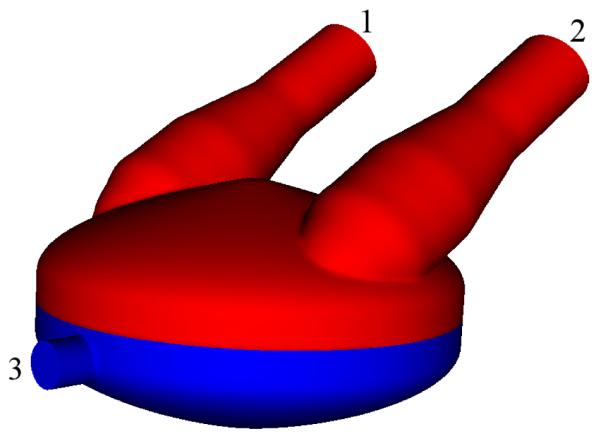
The results in this section are taken from the original reference³⁴ where we carried out a simulation of a generic pulsatile VAD. Geometric parameters, such as width, height, and angles of the entrance and exit arms are consistent with current designs, and are meant to be a generic representation of current commercially available devices such as the Berlin Heart. The computational domain of the VAD is shown in Figure 1.

Figure 1.

The PVAD computational domain, with the blood domain in light color, and the air domain in dark color. The inlet and outlet face of the blood chamber are labeled 1 and 2, respectively. The air-side inlet/outlet face is labeled 3.

A stroke volume of 73 mL and an ejection fraction of 68% were chosen for this device. A beat frequency of 80 bpm is used for a pump output of 5.8 L/min. Each pump cycle may be broken up into two components, the fill stage and the ejection stage, lasting 0.45 s and 0.3 s, respectively. During the pump cycle we prescribe the time-dependent flow rate at the air chamber inlet that is consistent with the above data, which is within the typical physiologic range for adult-sized models. In the blood chamber, we alternate boundary conditions at the inlet and outlet between the Neumann and Dirichlet condition as necessary. We do not directly compute the valve motion in the simulation. At the outlet we impose two conditions. During the fill stage we impose a zero-velocity (i.e., no flow) boundary condition. During the ejection phase, however, we impose a resistance boundary condition

$$p=C_{r}q+p_0,$$

where q is the volumetric flow rate on the outlet face, C_r is a prescribed resistance value, p₀ is the distal pressure, and p is the pressure at the outlet face. For the simulation we choose p₀ to be 65 mmHg, which enforces a minimum pressure of 65 mmHg during ejection. The resistance value is set to C_r = 183 g/(s cm⁴), which gives a maximum systolic pressure of 108 mmHg. The inlet face uses the same boundary conditions, but, obviously, with opposite phase.

Both air and blood are treated as incompressible, Newtonian fluids. The blood density and dynamic viscosity are set to 1 g/cm³ and 0.04 poise, respectively. The air density and dynamic viscosity are set to 1.205 × 10⁻³ g/cm³ and 2 × 10⁻⁴ poise, respectively. Given the VAD geometry, fluid properties, and flow rates employed, the peak Reynolds number is about 10,000 in the blood chamber, and 7,000 in the air chamber. These values are based on the inlet/outlet branch diameters and flow speeds. Note that the VAD blood chamber Reynolds number, which is higher than that in the large blood vessels of the human cardiovascular system (e.g., the thoracic aorta), is in the turbulent range. The membrane is a flexible thin sheet, commonly made of polyurethane. We use membrane material properties consistent with those of the Penn State VAD, the LionHeart.⁵⁸ The LionHeart membrane has a thickness of 0.38 mm, density of 1.1 g/cm³, and Young's modulus of 550 MPa.⁵⁸ In our simulation, we use a thinner membrane of 0.25 mm, which is reflective of the smaller device used for the pediatric population, as was provided in private communication.⁵⁴

The VAD simulation was carried out for two time cycles. All the data presented is gathered from the second time cycle, and the time t = 0 in all figures refers to the beginning of the second cycle. Figures 2–4 show snapshots of the computed blood flow speed and membrane deformation. The simulation captures a very complex membrane motion, with many folds, clearly seen in Figures 3 and 4. The deformed membrane surface is notably smooth, with no sharp kinks on the mesh edges, which is due to the underlying smoothness of the NURBS discretization. This buckling motion is smoother than is typically attained using more traditional methods. Since the structural kinematics is used to drive the fluid mechanics mesh deformation, the smoother buckling motion ensures that the fluid mechanics mesh at the fluid-structure interface remains smooth.

Figure 2.

Flow speed (cm/s) in the deformed blood chamber configuration at t = 0.15 s.

Figure 4.

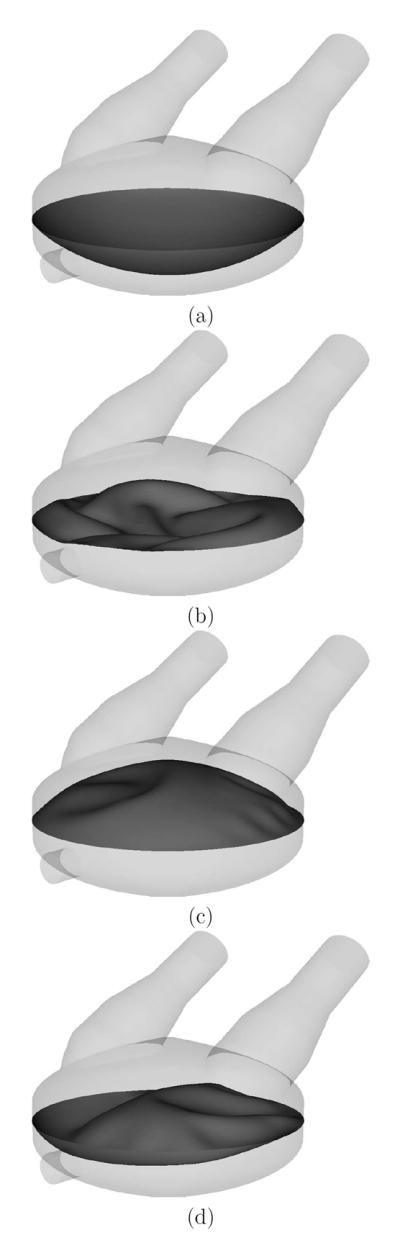
The membrane deformed configuration at time (a) t = 0 s, (b) t = 0.15 s, (c) t = 0.3 s, and (d) t = 0.525 s.

Figure 3.

Top view of the membrane deformed configuration at t = 0.15 s. Despite the complex deformation pattern, the wrinkles on the membrane surface are smooth.

During the fill stage, the inlet jet impinges on the chamber wall, and flows along the wall creating a strong vortex. The vortex is destroyed early in the eject phase, as seen in Figure 5. This strong vortex is a chief source of the wall shear stress and flow stagnation in the center of the device, and may play an important role in thrombus formation. Strong rotating flow during filling was also observed experimentally in prior work⁵⁴ and will be of interest in the future validation efforts.

Figure 5.

Blood flow speed (cm/s) at 0.5 cm above the plane separating the blood and air chambers. In-plane vectors shown during (a) expel stage (t = 0.14 s) and (b) fill stage (t = 0.665 s).

There are a number of other recent studies on development and optimization of pediatric VAD technology. Mechanical circulatory support based on an impeller pump design has been proposed for single ventricle congenital heart patients by Rodefeld and colleagues in several recent studies combining high fidelity large eddy simulation modeling with in vitro testing with compelling results.^59–61 Additional promising work in design and optimization of pediatric ventricular assist devices includes simulation and optimization of a miniature maglev device. This work incorporates inverse modeling for optimization, geometry parameterization, blood damage models, and the commercial CFD package Star-CD into a fully automated framework.^62,63 Other groups have investigated design of axial flow pumps for circulatory support in single ventricle patients in both simulation and in vitro models.⁶⁴ Significant in vitro and animal testing has been reported for the Penn State Pediatric pulsatile device.^65,66 A number of groups have simulated the blood damage and flow patterns in artificial valves, which are an essential component of VAD performance.^67,68 A recent report summarizes the family of devices developed under a recent NIH program for development of pediatric circulatory support devices.⁶⁹

6 Case study 2: An adult continuous flow VAD

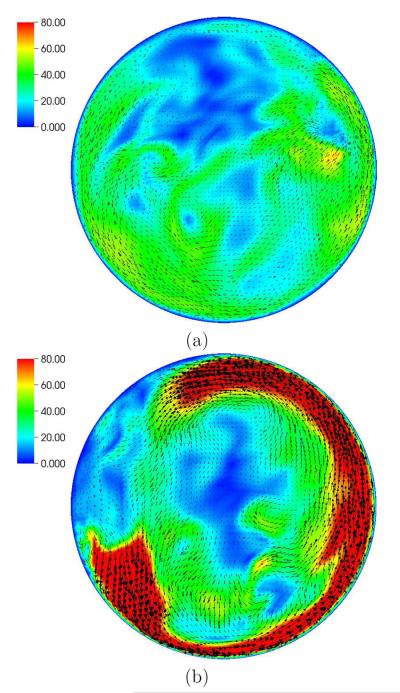
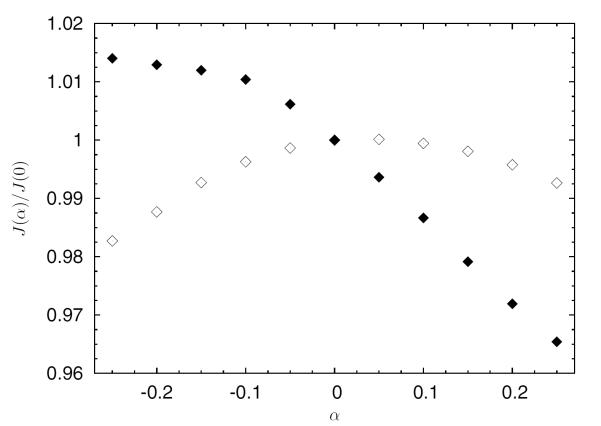
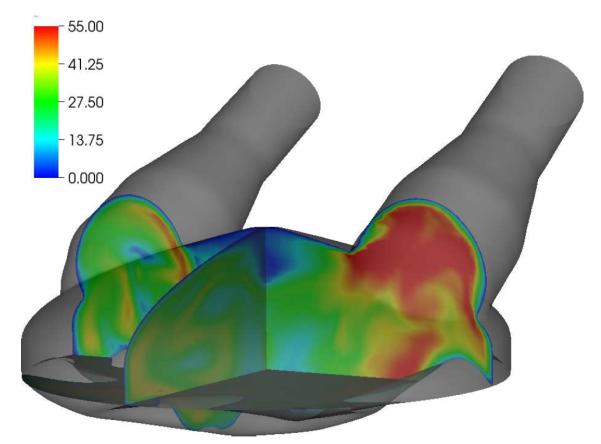
Simulations of continuous flow devices present a different set of challenges due to their rotating components and complex geometry. In this example, an axial left-ventricular assist device similar to the current DeBakey LVAD from MicroMed Cardiovascular of Houston, Texas is examined for possible shape modifications in order to increase its hemocompatibility.⁷⁰ In Figure 6, part of the already discretized surface mesh of the pumping chamber of the device is shown, with the surface mesh elements shaded according to the displacements allowed during the optimization process. The white elements are not deformable, and surround the impeller and upstream regions of the device. Green (light grey) surface elements belong to the diffuser portion of the pump and move as a rigid body along the device axis, controlled by a single shape parameter. Blue (dark grey) surface elements are deformed to accommodate the axial displacements of the diffuser. The Open Flipper toolkit⁷¹ is used to deform the elements in a manner consistent with the original CAD geometry. Figure 7 shows the dependence of two objective functions, one evaluating the integral of shear rate over the flow volume (empty markers) which is related to blood damage, and one measuring the pressure head across the pump (solid markers) which is related to pump hydraulic performance. The optimal shape parameter will depend on the relative weighting of these two quantities. Figure 8 shows the distribution of the scalar shear rate measure for two values of the shape parameter. A trust-region optimization scheme is used effectively in this case to find the optimal parameter values.

Figure 6.

Model of a DeBakey left ventricular assist device. Selection of the handle region (green) and the modeling region (blue) in Open Flipper in order to modify the gap width between impeller and diffuser.

Figure 7.

Modification of the gap width between impeller and diffuser and resulting objective function values for shear (empty markers) and pressure head (solid markers). Values are normalized by the respective value for the initial design.

Figure 8.

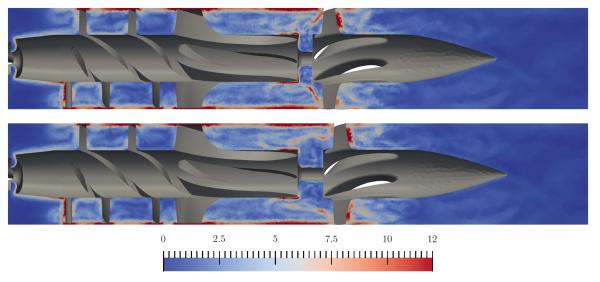
Shear rate [10³ s⁻¹] for slices through the DeBakey geometry at t = 88 ms. Two designs are compared: reducing the initial gap width by 0.25 din (top) and increasing the gap width by 0.25 din (bottom).

The above case study illustrates the role of custom finite element algorithms to performing design parameterization studies on VAD geometries. However, there have been a number of other key advances in the simulation of continuous flow devices and total artificial hearts that should be noted. Bluestein and colleagues performed extensive analysis of the Syncardia total artificial heart, which is a pulsatile device intended for adult use. Their study included platelet reactivity studies and FSI modeling of both the membrane and valves using the commercial software ADINA.⁷² Centrifugal and rotary pumps have been evaluated in CFD simulations by several groups, primarily using commercial software to characterize the flow fields and stress environment.^73,74,74 A key area of research related to continuous flow VADs is characterization of hemolysis and thrombotic risk, as discussed in 8.1 and 8.2.

7 Case study 3: VAD circulatory system interaction

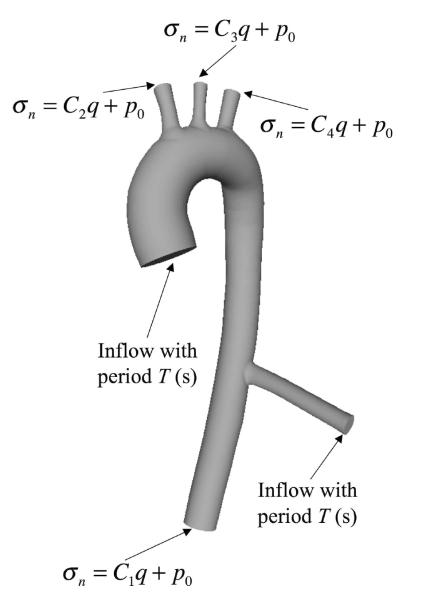
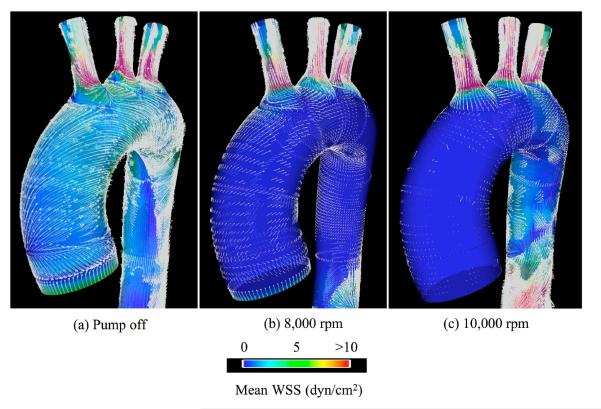
In addition to simulations of internal hemodynamics in VAD designs, CFD also offers the capability to simulate vascular hemodynamic conditions following device implantation. Bazilevs et al.⁴⁸ reported an FSI simulation of a patient-specific model of the aorta, from the aortic valve to the descending thoracic aorta, and including the effect of the Jarvik 2000 LVAD implanted in a descending configuration modeled as an additional, rigid branch vessel with prescribed inflow boundary conditions (see Figure 9). The simulation was done using NURBS-based IGA both for the blood flow and 3D solid vessel wall. The effect of the LVAD on hemodynamics is complex and demands a locally 3D model of the flow in the aortic valve and aorta, which is evidenced in Figure 10. Three pump settings are considered: 1. Healthy heart and the pump is off; 2. Medium pump setting, where the pump is supplying nearly 50% of the flow; 3. High pump setting, where the pump is supplying nearly 100% of the flow. Figure 11 shows the mean WSS vectors focusing on the aortic arch. In the healthy case, the vectors follow the helical pattern, which is consistent with the behavior of the blood velocity in this case. For the pump-assisted simulations, the magnitude of the WSS is much lower in the arch, and, furthermore, for the highest pump setting, the WSS vectors point in the direction that is opposite to the conventionally assumed direction. The flow was also found to be more or less completely stagnant in the arch for the highest pump setting. Flow stagnation in the aortic arch is the likely source of blood clot formation in this location. Moreover, exposure of the vascular wall to a relatively low WSS may increase intercellular permeability and consequently increase the vulnerability of these regions of the vessel to atherosclerosis.

Figure 9.

Flow in a patient-specific thoracic aorta with LVAD. Boundary conditions for the fluid mechanics domain. C_a, a = 1, 2, 3, 4, are the resistance constants, σ_n is the normal component of the traction vector, q is the volumetric flow rate, and p₀ is responsible for setting the physiological pressure level in the blood vessels. The LVAD branch is attached on the right side of the vessel, modeling the LVAD implantation in a descending configuration.

Figure 10.

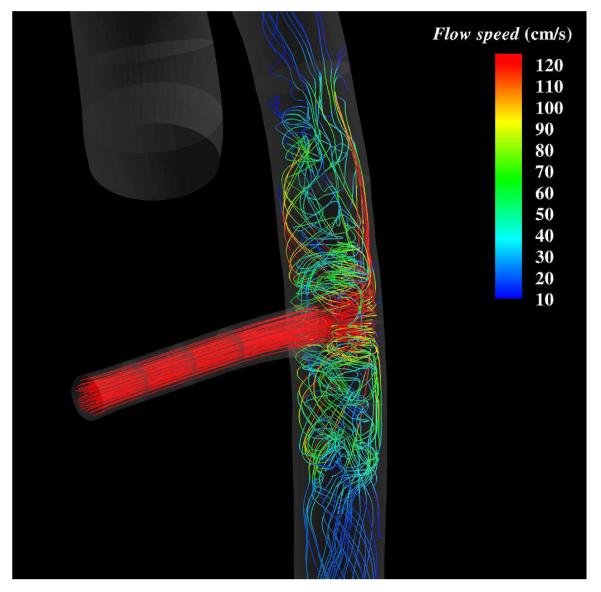
Flow in a patient-specific thoracic aorta with LVAD. Flow streamlines at peak systole in the LVAD attachment region. LVAD is operating at the highest setting.

Figure 11.

Flow in a patient-specific thoracic aorta with LVAD. Mean WSS vectors and the magnitude of the mean WSS.

Several other groups have also examined the interaction between VADs and circulatory physiology. Notably, a recent study aimed to optimize LVAD placement for reduced stroke risk. By adjusting the angle of the cannula during implantation, the risk of emboli migration was quantified probabilistically, and was found to significantly reduce with an optimal choice of angles.⁷⁵ Lumped parameter modeling was used to compare the impact of continuous vs. pulsatile flow in a model of mechanical circulatory support and physiology. Influences of control strategies was assessed with regard to physiologic interaction. It was shown that pulsatile flow resulted in increased cardiac index and coronary flow, and decreased ventricular stroke work and heart rate, with better systemic and coronary perfusion.⁷⁶

8 Blood damage and thromboembolic risk

Blood damage and stroke risk are perhaps the two biggest challenges arising in the clinical use of VADs. These two adverse phenomena are discussed in the following subsections.

8.1 Quantifying the risk of hemolysis

Hemolysis in VADs refers to the release of hemoglobin from the red blood cells (RBC) into the plasma. Above a critical level, free hemoglobin is toxic for the kidneys and can lead to multiple organ failure. Hemolysis can occur when RBCs are deformed and fragmented by shear stress;⁷⁷ however, the relation between macroscopic flow characteristics, such as shear stress, and microscopic RBC response, such as pore formation or fragmentation, is complicated and not yet fully understood.

Artificial flow devices in particular are capable of producing non-physiological levels of shear stress. Based on experimental data obtained in a Couette viscometer by Wurzinger et al.,⁷⁸ Giersiepen et al.⁷⁹ developed a correlation for steady-shear hemolysis. Previous works attempted to relate the three-dimensional flow effects to steady-shear loading through a single scalar parameter; for example, Bludszuweit proposed a representative stress parameter derived from the six components of the deviatoric stress tensor.⁸⁰ Models of this kind assume an instantaneous one-to-one relationship between local stress and RBC deformation; therefore, they can be referred to as “stress-based”.

Several authors have pointed out the importance of considering the loading history of the cells.^81,82 When integrating the Giersiepen relation along pathlines, because of its nonlinear dependence in time, this is not taken into account. Two approaches to overcome this deficiency are the definition of a linear damage fraction⁸³ and the introduction of a virtual time step.⁸⁴

Another concern in the long term use of VADs is that RBCs are repeatedly exposed to mechanical straining. The aging of RBCs was incorporated into a scalar damage accumulation model by Yeleswarapu et al.⁸² This model requires a damage function, which is unknown in complex flow situations. To compute the damage of blood cells passing through the device more than once, Goubergrits and Affeld define a mean exposure time and mean shear-stress.⁸⁴ A viscoelastic model with two time scales of hemolysis has been proposed recently by Arwatz and Smits.⁸⁵ Several of those stress-based models have been evaluated regarding their blood damage prediction accuracy in comparison to experimental data in a benchmark approach by Gu and Smith.⁸⁶

Most of the blood damage models found in the literature rely on a stress-based approach. As an alternative to the direct conversion of the stress tensor, a strain-based method was proposed;⁸⁷ using analogies to droplets exposed to shearing, a comparative shear stress is derived based on the deformation of RBCs in the flow. The deformation of a single RBC is tracked by solving an evolution equation for a symmetric, positive definite morphology tensor. The eigenvectors of the tensor represent the half-axes of the droplet. The evolution equation was adopted from Maffettone and Minale;⁸⁸ details on its enhancement can be found in Arora et al.⁸⁷

Stress-based models are known to over-estimate hemolysis; in contrast, the strain-based approach produced hemolysis values that were in good agreement with experimental data.^87,89 To further improve the understanding of blood damage in medical devices and to ease the analysis of large, transient simulation data, we have incorporated the strain-based hemolysis model into a virtual environment.⁹⁰ The environment helps to visualize and identify critical regions inside the device; RBCs are depicted as icons with a transparent hull and regions of high hemolysis are highlighted by the release of marker particles. The static overview of one or more pathlines is used as a metaphor to conveniently navigate through the transient data set.

In the context of shape optimization, it is common practice to define the objective function as a volume integral of quantities directly related to shear stress. As can be expected from the over-prediction seen in stress-based measures, these integrals do not reflect hemolysis adequately. Several modifications, e.g., velocity-weighted variants, of the integrand were tested but results were not satisfactory. Garon and Farinas⁹¹ replaced the pathline-based computation of hemolysis based on the Giersepen-Wurzinger correlation with a volume-based integration, making it more suitable for shape optimization tasks, and later included a damage fraction model.⁸³ A volume-based approach has been recently also combined with the RBC morphology tensor computation.⁹² Efforts to validate the existing models with targeted experiments have been also intensifying.^93–96

8.2 Quantifying the risk of thrombosis

Another concern in LVAD design, arguably more important than hemolysis in short-term applications, is the quantification of the risk of platelet activation, aggregation and subsequent biochemical process of thrombus formation. Pathologic flow patterns occurring in VADs chronically activate platelets and trigger thrombus formation. In high-speed rotary VADs, platelets are exposed to shear stresses up to 8,000 dyne/cm² and extremely high shear stress rates for short durations^97,98 This exposure may be sufficient to activate platelets and sensitize them to increased susceptibility in response to subsequent non-pathological shear stress exposure.⁹⁹ The optimization of VAD thrombogenic performance requires the development of flow-induced platelet activation and biometrical thrombosis cascade models that can be integrated into numerical simulations as part of the design process.

Due to limitations of computational power, discrete (i.e. individual cell tracking) approaches to modeling thrombosis are generally restricted to the study of fundamental platelet mechanisms at very small time and length scales; see, e.g., Filipovic et al.¹⁰⁰ A few groups have developed cellular-level and multi scale models incorporating individual platelets and hemodynamics, however many of these have dealt with endothelial, i.e. surface-mediated, injury response, rather than shear-induced thrombosis relevant to VADs. We briefly summarize selected models from both categories, and the reader is referred to additional detailed reviews focused on the biochemical and multi scale models of thrombus formation.^101,102

Strong et al.¹⁰³ undertook one of the first numerical studies of platelet thrombus growth due to advection and diffusion in combination with a surface-reaction rate. Although that model was a single-species model based on significant simplifications, it was helpful in qualitatively describing the relative effects of advection, diffusion and surface reaction on platelet adhesion to polymer materials. Additionally, methods of platelet diffusivity estimation and computation of free and covered surface portions were introduced and later used by Sorensen et al.¹⁰⁴ and others. Sorensen et al.¹⁰⁵ proposed to model the distributions of platelets and agonists by an advection-diffusion-reaction (ADR) equation system. Platelet adhesion to surfaces was modeled via constant shear-independent reaction rates, but aggregate formation and influence of platelets on the flow was not included. On the other hand Sorensen's model did take into account chemical platelet activation not only via the platelet-released agonist ADP, but also via synthesis of thromboxane A2 from activated platelets and platelet-phospholipid-mediated thrombin generation. Two further equations describing the concentrations of prothrombin and the thrombin-inhibiting substance ATIII are related to the coagulation cascade. In this manner Sorensen did not model the complete complex cascade but only its last steps where prothrombin is converted into thrombin. Good agreement was obtained for two-dimensional test cases with simple geometries. For application to a three-dimensional test case of a tubular expansion, the agreement with experimental data was less favorable¹⁰⁶ and it was concluded that more complete equations to model the transport mechanism would be needed.

Subsequent studies attempted to model the cascade process in greater detail. Fogelson and Guy¹⁰⁷ introduced a mathematical model with elastic links for describing adhesion of platelets to the injured wall and binding between activated platelets. Furthermore, many investigators used simplified models for the study of platelet reactions under various flow conditions, including works by Affeld et al.,^108,109 David et al.¹¹⁰ and Longest and Kleinstreuer.¹¹¹ Anand et al.¹¹² developed a viscoelastic thrombus model including both rheological properties of the thrombus and multiple biochemical reactions leading to growth and detachment of mural thrombi. However, none of these early models had yet incorporated the effect of the growing thrombus on the flow field.

Development of multi scale models incorporating both hemodynamics and biochemistry of the thrombosis cascade has primarily focused on injury-mediated mechanisms. Of note,the group of Alber and colleagues developed a discrete cellular potts model (CPM) in which individual platelets as well as other blood cells are represented as extended objects with fluctuating volumes and boundaries.^101,113,114 In this framework, convection and diffusion components of the PDEs for chemical concentrations within blood flow are solved. Then, ODEs representing the coagulation reactions on the surface membrane of each activated platelet are solved together with the PDE reaction terms to simulate biochemical reactions. These simulations describe the spatial structure of the developing thrombus both in time and space. Fogelson and colleagues have also developed coupled multi scale models coupling the immersed boundary method with biochemistry models and flow simulation. At the cellular level, the immersed boundary method models individual platelet behavior including platelet activation by chemical activators and subcellular level platelet-platelet adhesion and dissociation. A microscopic submodel is employed, consisting of a convection diffusion reaction equation describing dynamics of the platelet secreted activator (e.g., ADP or thrombin) in the fluid. This model can then be combined with more sophisticated coagulation submodels which separate coagulation reactions into those occurring on platelet membrane surfaces and those in the solution phase. The submodel describes a finite number of binding sites for coagulation zymogens and enzymes on the platelet surface, which regulates coagulation reactions.

Of greater relevance to VADs, in which thrombosis is primarily shear-mediated, the majority of existing works use a continuum approach due to the complexity of VAD geometry and cost of CFD simulations. Continuum models treat blood as a continuous homogeneous medium, with the flow described by a form of the Navier-Stokes equations. The solution for the blood flow represents the advective term of advection-diffusion and advection-diffusion-reaction equation systems. Early models were based on empirical correlations using power law relationships for shear stress during certain exposure times to measure propensity for mechanical platelet activation. However, these models do not account for relevant dynamic phenomena, such as loading rate dependence and platelet sensitization to high stress conditions, which characterize the dynamic flow conditions in VADs.

Platelet damage due to shear stress activation is a well known contributor to thrombotic risk. A more comprehensive phenomenological model for cumulative platelet damage was developed by Bluestein and colleagues to express platelet activation state (PAS). Optimal model parameter selection was performed using a genetic algorithm to match experimental data from a hemodynamic shearing device.¹¹⁵ Recent models from this group have also incorporated activation and sensitization of platelets due to dynamic stress history.¹¹⁶

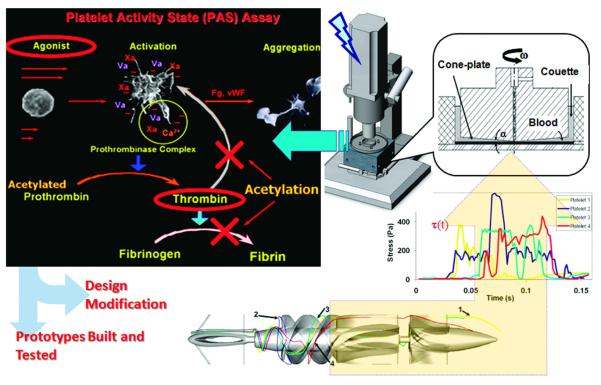
The concept of device thrombogenicity emulation (DTE), combining in silico numerical studies with in vitro measurements, was also introduced more recently by Bluestein and colleagues, and is summarized in Figure 12.¹¹⁷ This framework aims to a) overcome limitations of CFD methods that consider shear stress alone without consideration of biochemical reactions, b) address the lack of resolution of platelet-scale flow features, and c) to account for stress loading histories. The aim of DTE is to offer a design loop with multiple integrated steps as follows. First, one performs device optimization in computational simulations with FSI, and extracts from these simulations the relevant stress loading histories experienced by individual platelets, modeled by particle tracking. Second, these histories are emulated in vitro and the resulting platelet activity is measured experimentally in a hemodynamic shearing device. The design loop is iterated to reduce device thrombogenicity, which can then be verified in physical design prototypes. The DTE framework was demonstrated in a proof of concept study with a rotary blood pump VAD in a recent study.¹¹⁷ The DTE framework uniquely bridges between simulated platelet stress histories and experimentally measured platelet activation.

Figure 12.

Schematic of the Device Thrombogenicity Emulation (DTE) framework. (bottom-left) Representative platelet trajectories in the flow field of a ventricular assist device (debakey VAD); (bottom-right) Emulation of stress-loading history of typical platelet trajectories in the hemodynamic shearing device (HSD); (top-right) Computer-controlled HSD where platelets are exposed to uniform shear stress; (top-left) Principle of the modified prothrombinase assay used to measure the activity state of platelets sampled from the HSD. Courtesy of Danny Bluestein, reprinted with permission from PloSOne¹¹⁷

9 Design and optimization

Combining the above advancements in finite element methodology with established hemolysis or thrombosis-based cost functions, one can set the stage for optimization of device designs that may mitigate adverse hemodynamic conditions and device thrombogenicity. When choosing an optimization method, the primary distinction is between gradient-based and derivative-free methods. Factors contributing to this choice include the availability of cost function gradients, computational cost of the function evaluations, the level of noise and discontinuities in the function, complexity of implementation, the number of design parameters, convergence properties, efficiency and scalability. In cardiovascular shape optimization, each cost function evaluation requires a time-dependent, three-dimensional solution of the Navier-Stokes equations. These problems are computationally expensive to evaluate, often requiring post processing steps.

A general optimization problem may be formulated with linear bound constraints as follows,

$$\begin{array}{cc}\hfill \mathrm{minimize}\hfill & \hfill J\left(\mathbf{x}\right)\hfill \\ \hfill \text{subject to}\hfill & \hfill \mathbf{x}\in \Omega ,\hfill \end{array}$$ (1)

where $J:{\mathbb{R}}^n\to \mathbb{R}$ is the cost function, and x is the vector of design parameters. The parameter space is defined by $\Omega =\{\mathbf{x}\in {\mathbb{R}}^n\mid \mathbf{l}\le \mathbf{x}\le \mathbf{u}\}$, where $\mathbf{l}\in {\mathbb{R}}^n$ is a vector of lower bounds on x and $\mathbf{u}\in {\mathbb{R}}^n$ is a vector of upper bounds on x. In a cardiovascular shape optimization problem, the function J(x) depends on the solution of the Navier-Stokes equations, and the cost function value is computed in a post processing step.

In spite of these challenges, there has been important progress in applying gradient-based optimization methods to cardiovascular problems, mostly with 2D geometries and/or steady flow. Non-Newtonian e ects in shape optimization have been examined by.^118,119 Optimization of blood pump components has been carried out by Antaki and others,^120,121 and Quarteroni and others have applied optimization to shape design for arterial bypasses.^122–125 However, applying gradient methods in a fully time-dependent setting using unstructured solvers, complex geometries and constraints and in the presence of FSI, which are common in cardiovascular flow problems, remains a challenge.

Methodologies for gradient and derivative-free optimization have been developed and applied to cardiovascular simulations. Recent advances in derivative-free methods will easily translate to VAD design in future work, as the function evaluations can be treated as a black box with no restriction on cost function definition.

Derivative-free optimization methods can offer a promising alternative to gradient based methods. The surrogate management framework (SMF)^126,127 is a derivative-free pattern search optimization method that relies on surrogates for increased efficiency. Previous work successfully applied SMF to the constrained optimization of an airfoil trailing-edge for suppression of vortex shedding noise in laminar flow^128,129 and for the suppression of broadband noise in turbulent flow.¹³⁰ In addition, the application of derivative-approximating trust region methods to steady flow fluid mechanics problems has been explored by Lehnhäauser and Schäafer.¹³¹

The main idea behind the SMF method is to increase efficiency by using a surrogate function to “stand in” for an expensive function evaluation, while also benefiting from the convergence properties of pattern search methods. In contrast to genetic algorithms, this class of pattern search methods are among the only derivative-free methods with established convergence theory.^132–134 Advantages of SMF are its non-intrusive nature, ease of implementation, efficiency, and parallel structure.

The SMF algorithm typically consists of a SEARCH step, employing a Kriging surrogate function for improved efficiency, together with a POLL step to guarantee convergence to a local minimum.^135,136 The exploratory SEARCH step uses the surrogate to select points which are likely to improve the cost function, but is not strictly required for convergence. Convergence is guaranteed by the POLL step, in which points neighboring the current best point on the mesh are evaluated in a positive spanning set of directions to check if the current best point is a mesh local optimizer. Recent work has extended the SMF method to incorporate uncertainties in design variables and model parameters.^137,138

These methods have been successfully applied in the cardiovascular setting to optimize idealized geometries, including an end-to-side anastomosis, and vessel bifurcation.¹³⁹ Sankaran et al. demonstrated a shift in optimal bypass graft anastomosis angles and radius when incorporating uncertainties to perform robust optimization. The SMF method has also been applied in constrained shape optimization of a novel Y-graft conduit design for surgical palliation in single ventricle congenital heart patients.^140,141 These methods should be leveraged for VAD optimization, accounting for uncertainties and constraints, in future work. For example, they could be non-intrusively combined with the DTE framework described above to optimize for thrombogenicity reduction in a combined simulation and in vitro set up.

10 Outlook and future challenges

We have reviewed recent significant advancements in both methodology and approach to finite element simulation of VAD hemodynamics. We provided three case studies illustrating advances in finite element methodology for modeling both pulsatile and continuous flow devices for use in adults and children. In addition, we outlined recent developments in models to quantify risk of hemolysis and thrombosis, which are the major source of morbidity and mortality associated with VADs. The use of high-fidelity numerical simulations will enable accelerated identification of new designs in future work, ultimately leading to reduced thrombogenicity and improved patient outcomes. We refer the reader to several other review articles that provide further perspective on advances in thrombogenicity, experimental testing, and remaining challenges in the field.^{102,142–144}

Despite recent progress, challenges remain to increase the relevance and utility of VAD simulations in the device design process and in the clinic. First, complete modeling of blood biochemistry remains computationally intractable due to high computational cost. There is therefore a need for continued development and validation of reduced order models to measure the risks of thrombosis and hemolysis. Second, there is a need for integration of the advanced simulation and formal optimization methods outlined above to accelerate the design process in the presence of constraints and uncertainties. As the optimization process identifies new designs, the need will also arise for rapid prototyping of simulation-derived designs for experimental testing. Third, as simulation methods mature, there is an increased need for validation of simulated risk of thrombosis and hemolysis against clinical data in VAD patients and animal models. Finally, one cannot ignore the underlying physiology of the patient, and VAD models should be coupled to lumped parameter network models of circulatory physiology to elucidate the interplay between the device and physiologic conditions. This is particularly compelling in pediatric cardiology due to the complex physiology and unusual anatomy in congenital heart disease patients.