Locking the Active Conformation of c-Src Kinase through the Phosphorylation of the Activation Loop

Abstract

Molecular dynamics umbrella sampling simulations are used to compare the relative stability of the active conformation of the catalytic domain of c-Src kinase while the tyrosine 416 in the activation loop (A-loop) is either unphosphorylated or phosphorylated. When the A-loop is unphosphorylated, there is considerable flexiblity of the kinase. While the active conformation of the kinase is not forbidden and can be visited transiently, it is not the predominant state. This is consistent with the view that c-Src displays some catalytic activity even when the A-loop is unphosphorylated. In contrast, phosphorylation of the A-loop contributes to stabilize several structural features that are critical for catalysis, such as the hydrophobic regulatory spine, the HRD motif, and the electrostatic switch. In summary, the free energy landscape calculations demonstrate that phosphorylation of tyrosine 416 in the A-loop essentially “locks” the kinase into its catalytically competent conformation.

INTRODUCTION

The family of Src-related non-receptor tyrosine kinases includes nine highly conserved proteins (Src, Yes, Fyn, Lyn, Lck, Blk, Hck, Fgr, and Yrk) with similar regulatory mechanisms ^{1; 2}. In their active state, these enzymes catalyze the transfer of γ-phosphate of an adenosine triphosphate (ATP) molecule covalently onto a tyrosine residue in substrate proteins and peptides ³. Members of the Src-family are crucial to cellular signaling pathways regulating cell growth, proliferation, metabolism, differentiation and migration ^{1; 2; 4; 5; 6; 7; 8}. Therefore, the activity of Src family kinases (SFKs) is highly regulated in order to maintain normal cellular signal transductions. Mutations at certain residues could make SFKs constitutively active, leading to a number of diseases, particularly cancers. For example, SFKs contribute directly to colon tumor growth and treatment with herbimycin A demonstrates a reduction in c-Src activity and colon tumor growth ⁹. For this reason, SFKs represent attractive drug targets for curing certain types of cancers ^{10; 11; 12; 13}.

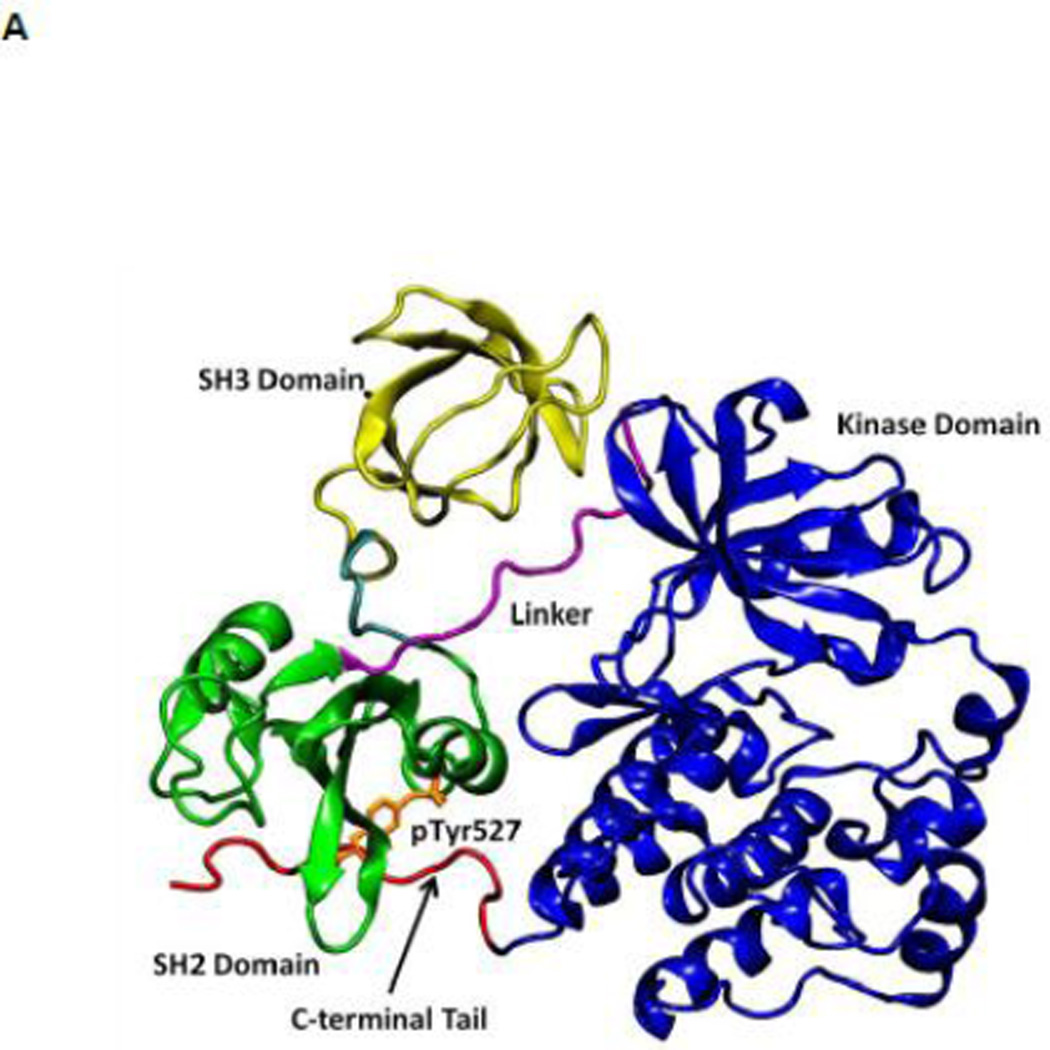
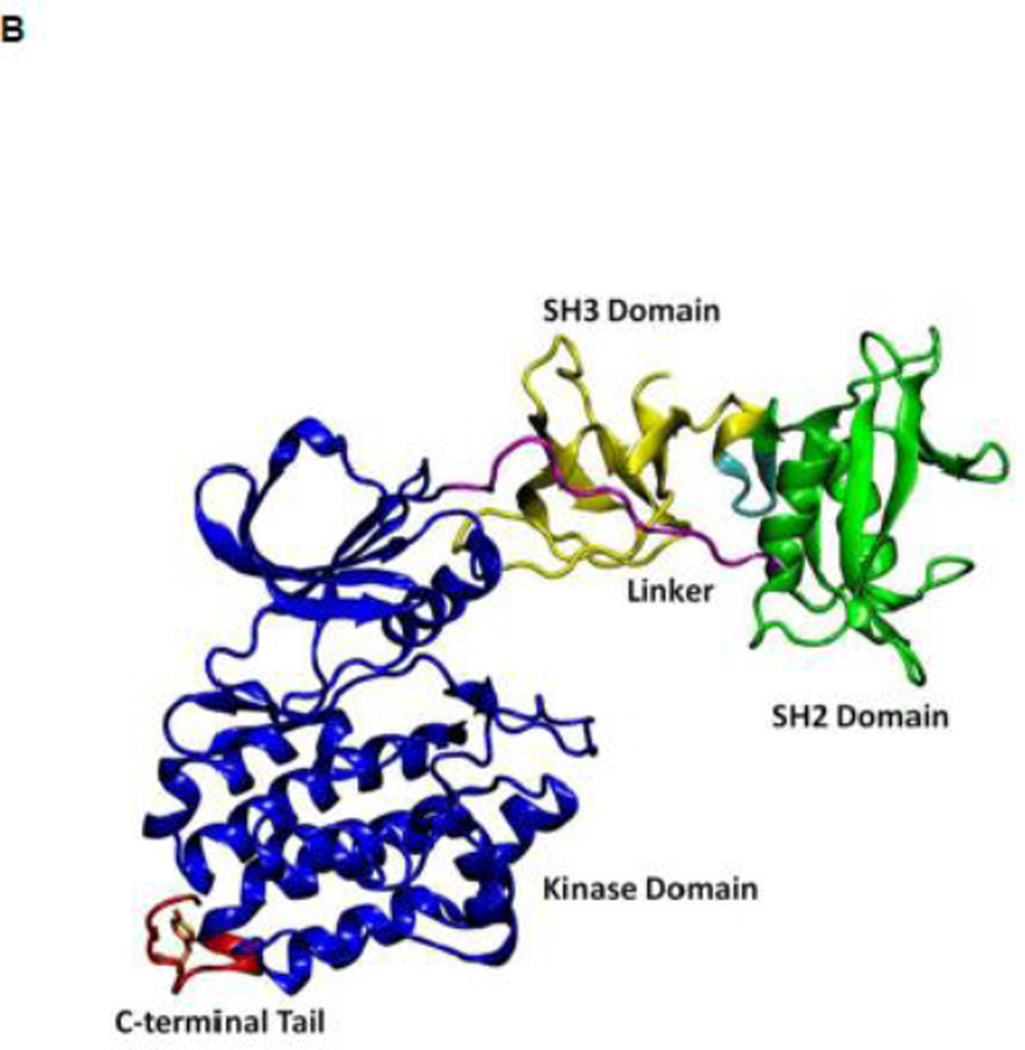
All SFKs share a common architectural scaffold comprising an N-terminal myristoylation site, a Src-homology 3 (SH3) and Src-homology 2 (SH2) regulatory domains, followed by a catalytic domain (kinase domain). The activity of SFKs is regulated through allosteric conformational transitions in multiple domains and the phosphorylation of two distant tyrosine residues ¹. The inactive state (down-regulated state) of SFKs adopts an auto-inhibitory conformation, which is illustrated in Figure 1A using the representative structure of c-Src kinase ¹⁴. Y416 located in the A-loop (residues 404 to 424) controlling access to the enzymatic active site is unphosphorylated, while Y527 near the kinase C-terminal binding to the SH2 domain is phosphorylated (chicken c-Src numbering is used throughout this paper). In the inactive configuration, the A-loop is closed and partially folded, preventing substrate from entering active site. Moreover, the αC helix (residues 304 to 318) is rotated outward and E310 in the αC helix is making a salt-bridge with R409 (in the A-loop). Furthermore, SH3 and SH2 domains are assembled on the backside of the kinases and SH2 domain binds to phosphorylated Y527 (pY527) and the SH3 domain binds to the linker connecting the SH2 and kinase domains. The binding of pY527 to SH2 domain clamps the SH3-SH2 tandem in the auto-inhibitory conformation. Disruption of either SH2-pY527 or SH3-linker interaction disassembles the auto-inhibitory conformations and eventually leads to the activation of Src kinases ^{1; 15} A representative structure of the full-length active conformation of the SFKs is shown in Figure 1B.

Figure 1.

(A) Auto-inhibited conformation of c-Src kinase. From N-terminus to C-terminus, this figure shows SH3 domain (in yellow), a connector between SH2 and SH3 domains (in cyan), SH2 domain (in green), linker region which connects SH2 and kinase domains (in purple), the kinase domain (in blue), and the C-terminal tail which contains Y527 (in red). In the auto-inhibited conformation, SH3 domain binds linker, SH2 domain binds phosphorylated Y527. (B) Reassembled active-like conformation of c-Src kinase. The same color code used previously is adopted here. In the reassembled active-like conformation, SH3 domain unbinds the linker, SH2 domain unbinds Y527, and Y527 is not phosphorylated. (C) Sequence of the construct that is used in the simulations. Important residues and motifs that will be analyzed are colored.

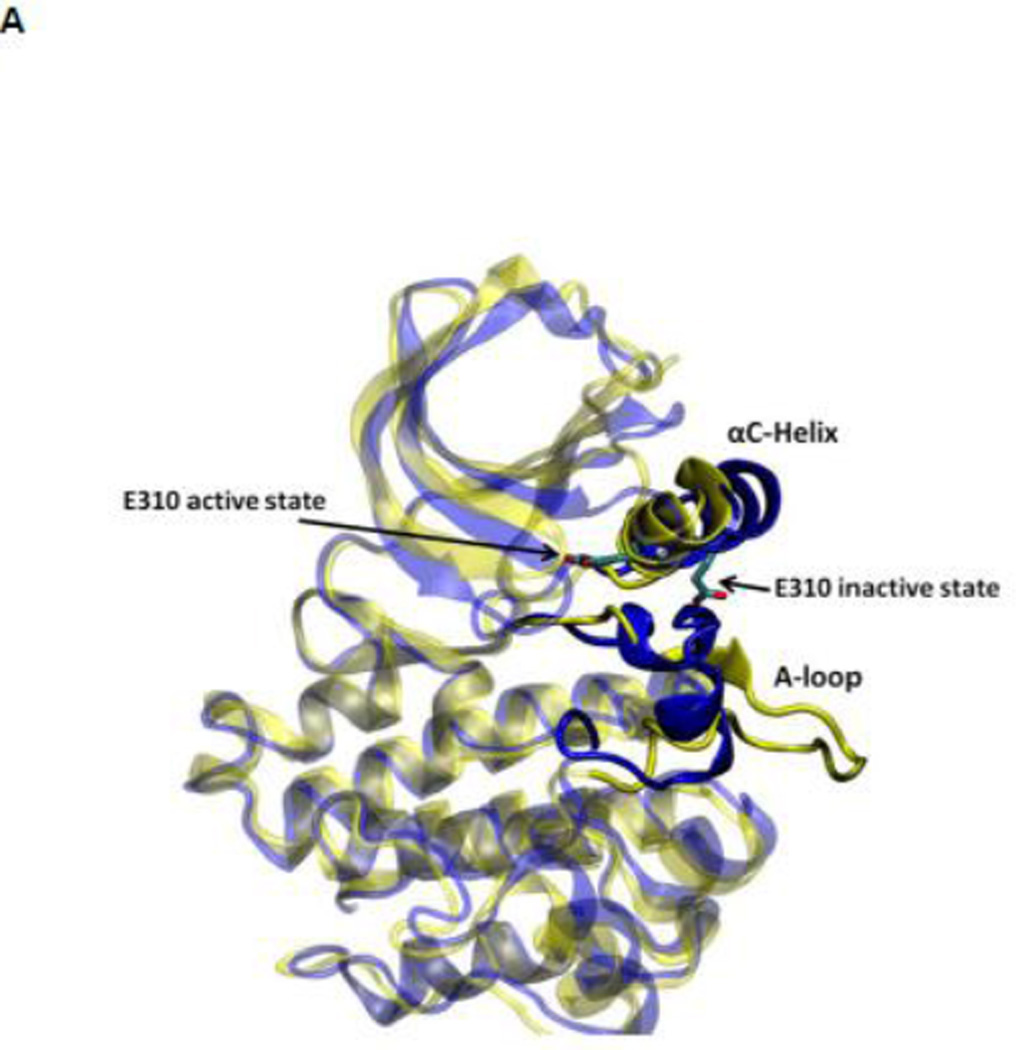
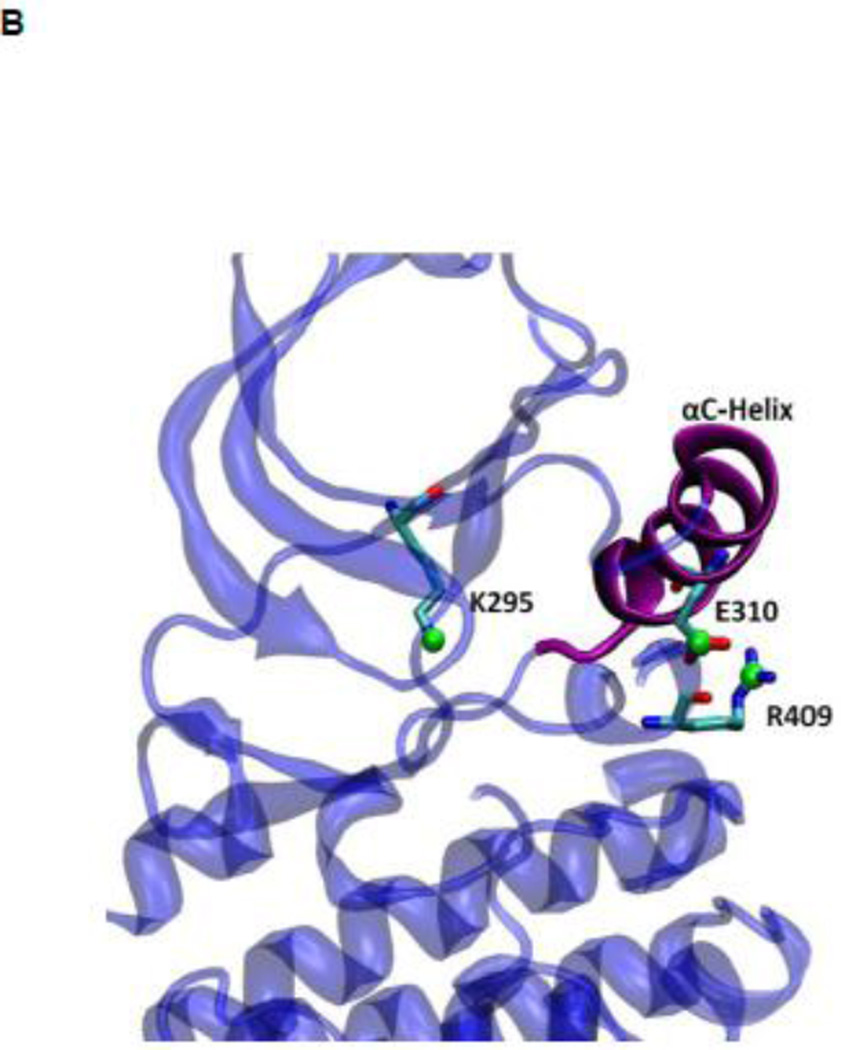
During the activation process, the kinase domain undergoes important conformational changes involving primarily the αC helix and the A-loop (where Y416 is located). In the activated c-Src kinase domain, the αC helix is rotated inward and E310 makes a salt-bridge with K295, salt link believed to be critical for catalysis. The A-loop in the active state becomes extended away from the active site, allowing the binding of substrate and exposing the A-loop to trans-phosphorylation. Figure 2A illustrates the kinase domain of c-Src kinase in its inactive (PDB code 2SRC ¹⁴) and active-like (PDB code 1Y57 ¹⁶) configuration respectively. Additional structural features critical in the activation of Src kinases include the formation of two “hydrophobic spines” ^{8; 17; 18; 19}: a regulatory spine (R-spine) and a catalytic spine (C-spine). The spines, formed by conserved, noncontiguous and interacting amino acids in active kinases, can be dynamically formed and broken, switching the kinase activity on and off. Rotation of the αC helix from inward to outward in the activation/deactivation process breaks the R-spine. An additional conformational change involving a phenylalanine part of the R-spine leads to a different inactivated state ²⁰.

Figure 2.

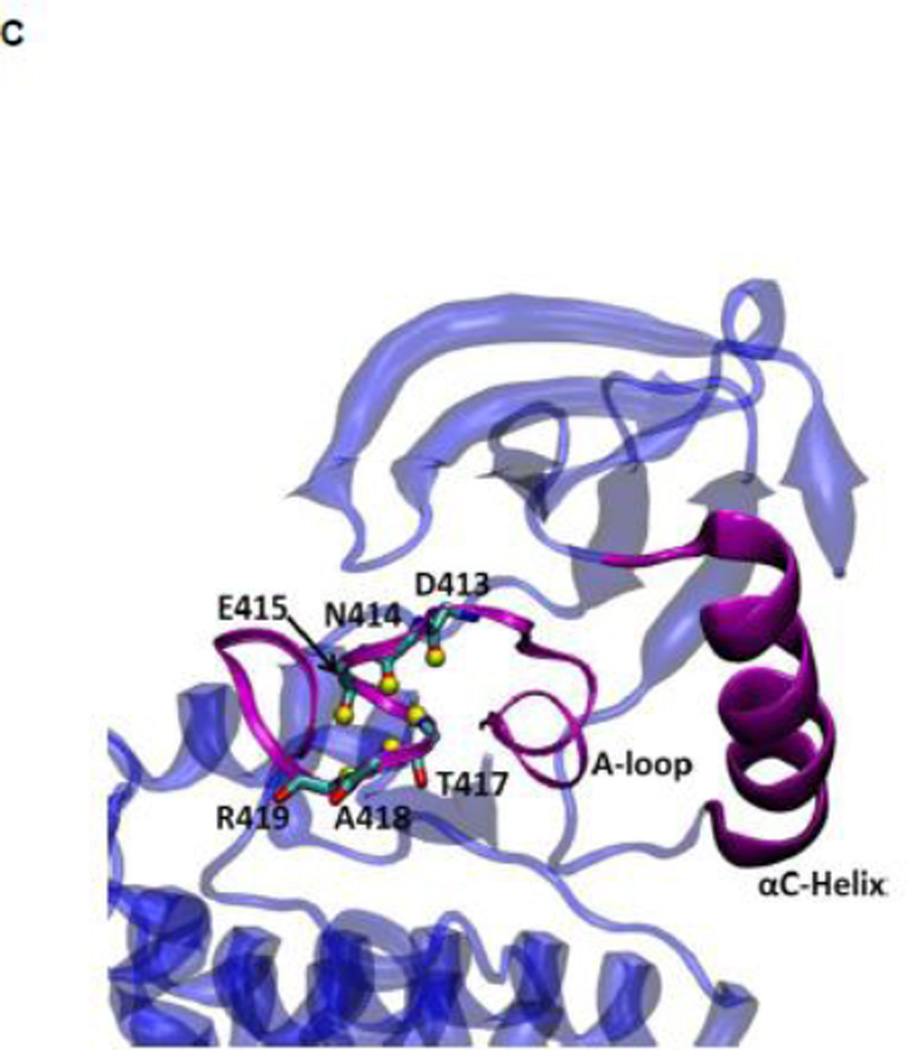
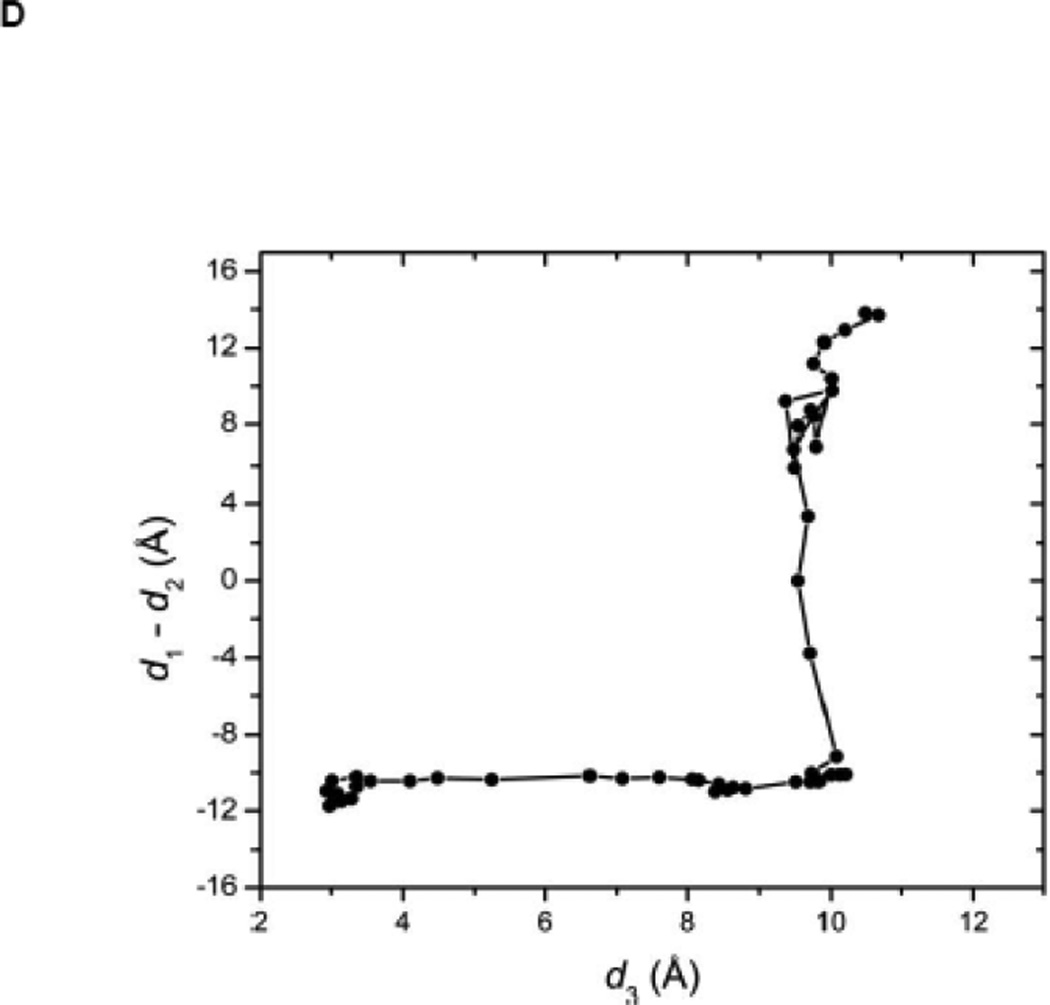
(A) Kinase domain in inactive (colored in blue) and active-like (color in yellow) conformation. The E310 in the αC helix is shown to demonstrate the movement of the αC helix. E310 is pointing outward in the inactive conformation, whereas it’s pointing inward in the active-like conformation. The A-loop is partially folded in the inactive kinase, but it becomes fully extended in the active-like conformation. (B): Selection of atoms that defines the motion of the αC-Helix. Atoms which are colored in green characterize the break/formation of salt bridges. d₁ is the distance between E310 Cδ atom and R409 Cζ atom. d₂ is the distance between E310 Cδ atom and K295 Nζ atom. The αC-Helix is this plot is colored in magenta. (C) Selection of atoms that defines the motion of the A-loop. Atoms in the A-loop which are colored in yellow form hydrogen bonds in inactive conformation. They are used to characterize the extension of the A-loop. Both the A-loop and the αC-Helix are colored in magenta in this plot. (D) Projection of the smoothed string onto order parameter space.

While phosphorylation of the conserved tyrosine residue in the A-loop is the factor most commonly associated with a fully active kinase, exemplified by the X-ray structure of active Lck ²¹, the situation is actually more complex. In fact, SFKs can still perform their catalytic function with unphosphorylated A-loop ²². Furthermore, a crystallographic X-ray structure of full-length c-Src shows that it can adopt an active-like conformation ¹⁶, similar to that of fully active Lck ²¹—even though the conserved tyrosine in the A-loop remains unphosphorylated. One implication is that several conformations must be permitted, in which the A-loop can extend away from the active site to expose unphosphorylated Y416. As a consequence, it is likely that Y416 could become the substrate of another active Src kinase, in a trans-phosphorylation process. This is consistent with the biphasic enzyme activity observed after mixing unphosphorylated Hck kinase, peptide substrate and ATP, and by experiments with point mutations on Y416 ²³. Experiments studying the catalytic activity of the wild-type and Y416A mutation ²² as well as investigation of X-ray structure of Hck ²⁴ have suggested that phosphorylation of the A-loop might serve to stabilize the A-loop in a position favorable for substrate binding ⁷. Phosphorylation of the A-loop is also demonstrated to increase the accessibility of regulatory domain for binding exogenous ligands ²⁵. However, how phosphorylation of the A-loop stabilizes the active conformation and how it affects the activation process is not clear. Answering these questions is critical for our understanding of the regulation of c-Src kinase.

Molecular dynamics (MD) simulations based on atomic models may help answer these questions by providing energetic, kinetic and structural information that is not easily accessible from experiments. Earlier studies focused on the role of the linker connecting the SH2 and kinase domains ^{26; 27; 28}. Significant portion of computer modeling has investigated the conformational transition pathway in the isolated kinase domain as well. The conformational transition in the Src kinase domain also serves as an natural target for simulation methods such as targeted MD ^{23; 29}, string method ^{30; 31}, Markov models ^{32; 33; 34; 35} and maximum flux transition path method ³⁶. Umbrella sampling (US) calculations have also been carried out by Banavali and Roux ³⁷ to study the A-loop opening. Markov analysis of structural clusters obtained from unrestrained MD simulations of Hck kinase has suggested the existence of two intermediate conformations in addition to the canonical active and inactive conformations of the kinase domain ^{35; 38}. The Markov analysis also demonstrated that the A-loop opens up first in the activation, followed by the switch of salt-bridges. This observation suggested that Hck kinase domain moves in a concerted fashion during activation. A similar concerted motion has been found in a study of c-Src kinase domain by string method calculations as well ³⁹. Since the A-loop is open in the intermediate conformations and Y416 is at least transiently accessible to be phosphorylated, the phosphorylation of Y416 does not necessarily have to wait until the entire kinase domain adopts an active-like conformation. Therefore, a direct study concerning transition pathway with Y416 phosphorylated is needed to elucidate the effect of phosphorylation of the A-loop.

In the present study, we examine the conformational flexibility of the kinase domain of c-Src with the unphosphorylated and phosphorylated A-loop using MD simulations and potential of mean force calculations ⁴⁰. The potential of mean forces (PMFs) yielded from US calculations could answer the critical question of how much phosphorylation of the A-loop stabilizes the kinase domain in its active state. Analysis of the pair-wise interaction energies of key residues upon phosphorylation would also explain whether phosphorylation on the A-loop just affects the A-loop and how does it affect those residues. In order to facilitate the convergence of umbrella sampling and reduce the computational cost, we have integrated string method which generates transition pathways and a self-learning adaptive scheme into our umbrella sampling calculations when investigating large conformational transitions like this. Our calculations demonstrate that phosphorylation of the A-loop changes the conformational equilibrium of c-Src kinase domain. It considerably stabilizes the active conformation, locking the kinase domain in the active state during the activation process. The calculations also suggest that phosphorylation on the A-loop will also stabilize regions and interactions in c-Src that are key to catalysis.

RESULTS and DISCUSSION

Free energy landscape and stability of the active conformation

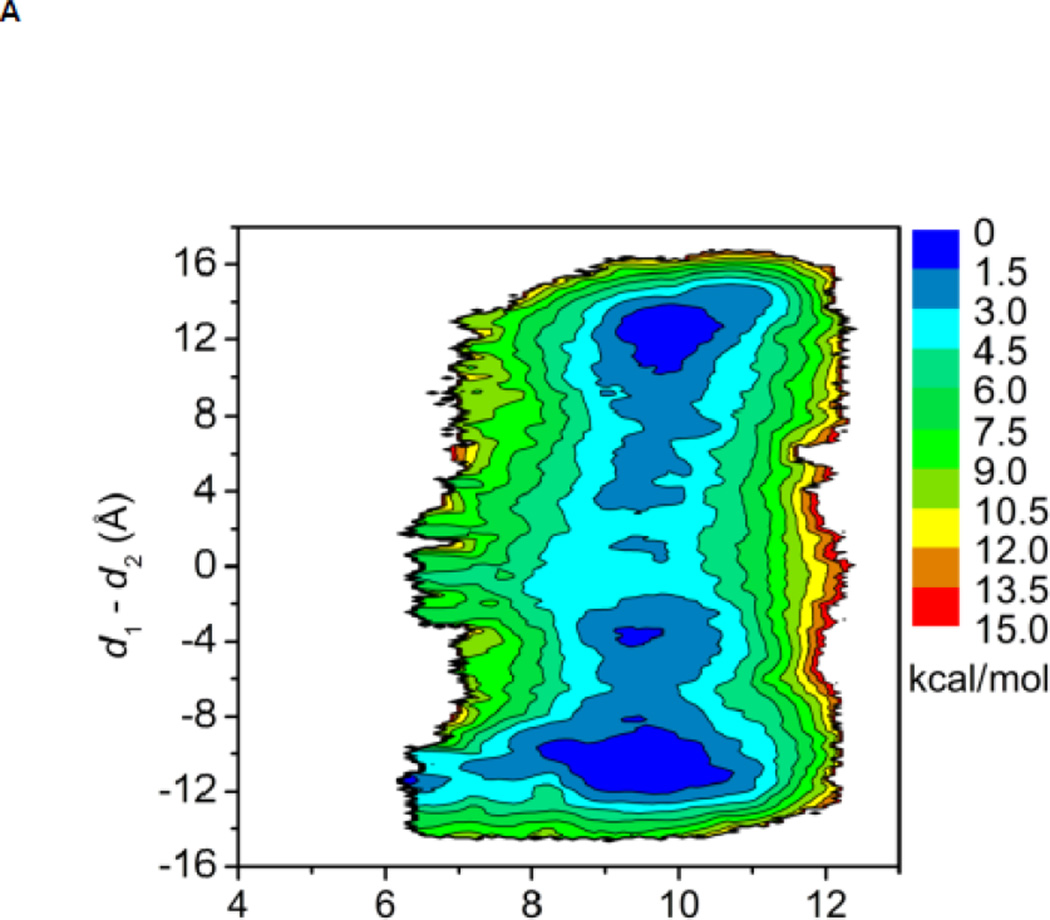
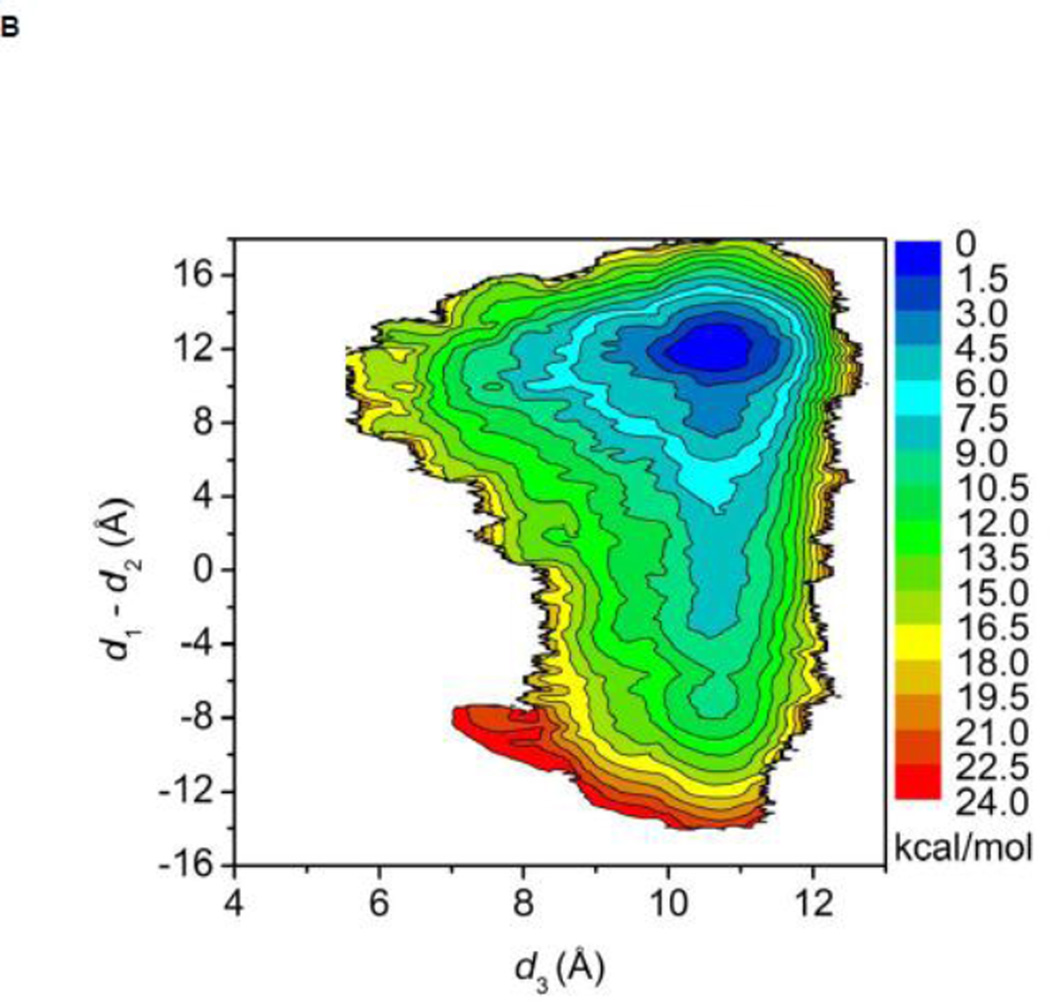
The free energy landscapes of the kinase domain of c-Src when Y416 in the A-loop is either unphosphorylated or phosphorylated are shown in Figure 3A and B, respectively. In both cases, the calculation is quantifying the conformational flexibility of the isolated kinase domain in the overall neighborhood of the active-like 1Y57 X-ray structure. When the A-loop is not phosphorylated, a broad range of conformations is allowed. As a consequence, while occurrences of an active-like conformation are not forbidden, the kinase domain does not exclusively remain in a catalytically competent state. The free energy basin in the top part of the map (at “9.5, 12.0”) corresponds to the 1Y57 active-like conformation in which the αC helix is rotated inward and the A-loop is extended. The second basin at the bottom of the map (at “9.5, −12.0”) corresponds to an intermediate state that has been previously observed in several simulations of the Src family kinases ^{35; 38; 39}. In this conformation, the αC helix is rotated outward, as in the inactive state, but the A-loop is extended and more open, as in the active state. The free energy surface suggests that the kinase domain of c-Src could temporarily maintain an open and extended conformation for the A-loop regardless of the αC helix rotation. Hence, a plausible hypothesis is that even rare visits to this state would be sufficient to allow Y416 to become trans-phosphorylated by another kinase during a bimolecular encounter, thereby stabilizing the kinase domain into its active state. Consistent with this view, the free energy landscape in Figure 3B shows that only a narrow region is allowed with pY416, indicating that the kinase domain is now locked into a catalytically competent state which then becomes essentially the only allowed conformation. To the best of our knowledge, this is the first US calculation of c-Src with its A-loop phosphorylated. Therefore, special attention is paid to monitor the convergence of the free energy landscape. An additional 40 ns of MD sampling was carried out for each of the 620 umbrella windows. The free energy landscape that is displayed in Figure 3B is essentially unchanged when comparing with the landscape that is obtained from the US simulation with 50 ns per window. Hence, the free energy landscape shown in Figure 3B appears to be well converged. The steep free energy well observed in Figure 3B perhaps explains why members of the Src family crystallized with the A-loop phosphorylated have only been observed to adopt the active conformation. The sharp rise in free energy suggests that the kinase with its phosphorylated A-loop is unlikely to return to a conformation with the catalytically inactive outward-rotated αC helix. The range of accessible conformation of catalytic domain is drastically reduced by the phosphorylation of the A-loop, and the latter is stabilized in a configuration that is favorable for substrate binding. The free energy landscape in Figure 3B suggests that a kinase would rapidly adopt the active conformation if its A-loop was phosphorylated while the kinase is in the intermediate state corresponding to the bottom well of Figure 3A. These observations are consistent with the experimental observation that the kinase domain displays some catalytic activity in the unphosphorylated form and its catalytic activity is greatly enhanced while its A-loop is phosphorylated ²².

Figure 3.

Free energy landscapes of c-Src kinase domain activation when the A-loop becomes open. (A) Y416 is unphosphorylated. (B) Y416 is phosphorylated. When Y416 is not phosphorylated, a multi-state equilibrium exists and the c-Src kinase domain is not locked in either state. Phosphorylation of the A-loop alters the landscape considerably and locks the kinase domain in the active conformation. As a consequence of locking the active conformation by phosphorylation of the A-loop, the population of catalytically capable species is increased, causing an elevated catalytic activity.

The overall stability of the active conformation 1Y57* was also assessed by monitoring the fluctuation of the root-mean-square deviation (RMSD) of the Cα atoms relative to the active-like conformation and relative to wt-3DQW* during the 20 ns of MD equilibration process (see Figure S1). After 20 ns of equilibration, the RMSD reaches a plateau at ~2Å. The end structure from the equilibration process of 1Y57* and wt-3DQW* are displayed together in Figure S2A to show their structural similarity. Unrestrained MD simulations of the 1Y57* (phosphorylated active conformation) and of the wt-3DQW* kinase drift toward the center of the free energy basin (see Figure S3), consistent with the overall free energy landscape obtained from the US calculations. Further examination is performed by comparing the local structural similarities between the active conformation 1Y57* and wt-3DQW*. The conformation of the active site, activation segment (residue 404 to 432), and the hydrophobic regulatory spine are compared in Figure S2B to S2D. The active site and regulatory spine in 1Y57* are in good agreement with wt-3DQW*. However, the activation segment opens wider in 1Y57* than that in wt-3DQW*. An inspection of the A-loop suggests that electrostatic interactions may be at the origin of these differences. In 1Y57*, the electrostatic interactions among oppositely charged R409, R419 and E412, pY416 rearrange the side chains of those residues and require larger space to accompany this rearrangement compared with wt-3DQW*. However, the D404-F405-G406 (DFG) motif (at the N-terminus of activation segment) that coordinates the magnesium ions, and the APE motif (at the C-terminus of activation segment) that is important for substrate binding, are both very consistent in 1Y57* and wt-3DQW*. It is of particular interest to evaluate the effect of A-loop phosphorylation on catalytically important structural features. Those include the hydrophobic regulatory spine (R-spine), the HRD motif in the catalytic loop ^{17; 18}, and the electrostatic network ^{29; 35}. These are examined in the following.

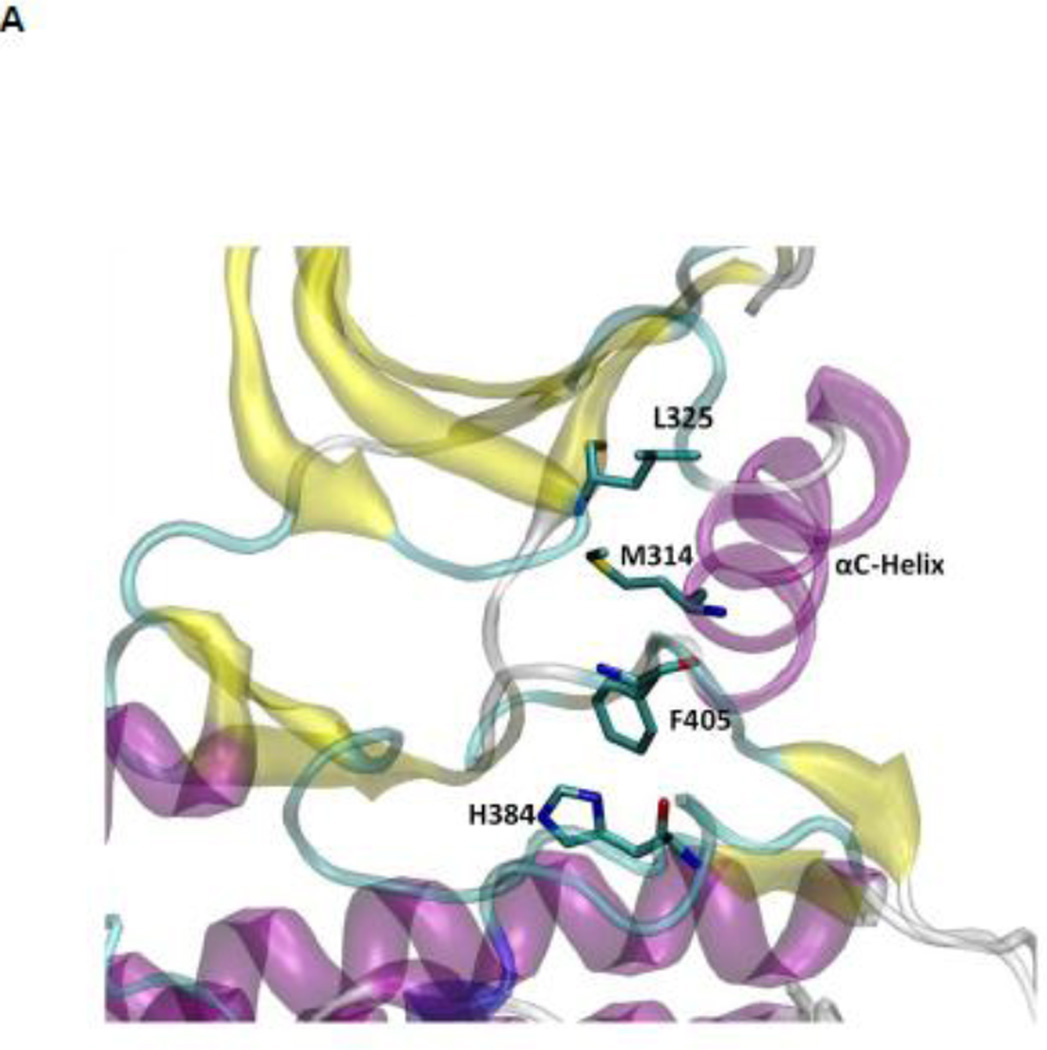
The hydrophobic regulatory spine (R-spine)

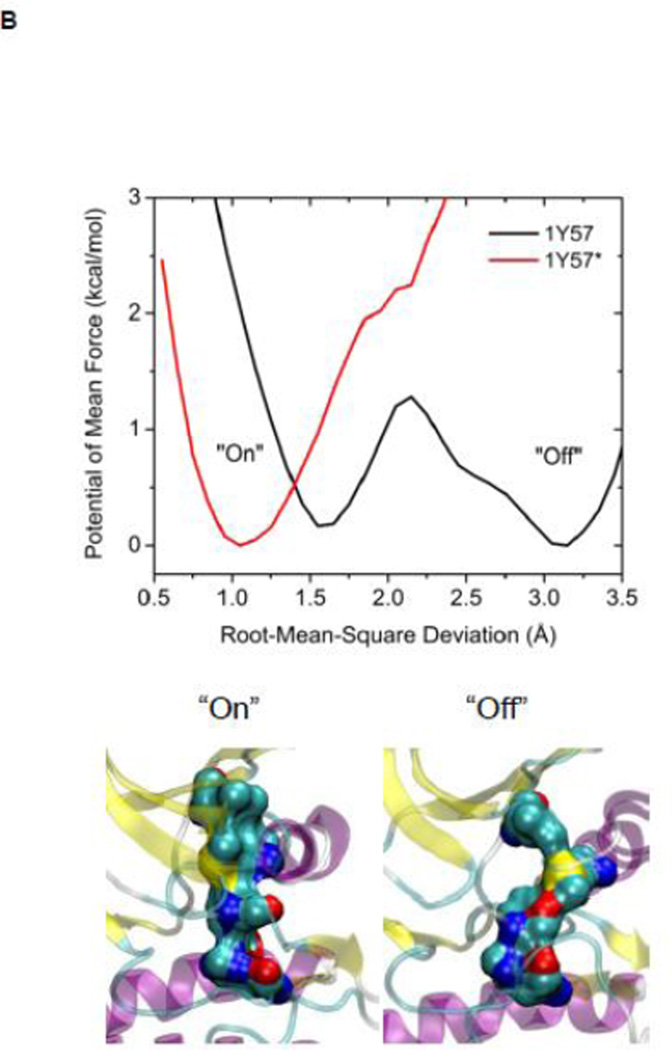
The R-spine consists of four residues extending from the N-lobe to the C-lobe (see Figure 4A): L325, M314, F405, and H384 ²⁰. It is a critical element of an active catalytically-competent kinase ^{17; 18; 19}. The R spine links the two lobes of kinase domain and couples with A-loop. Among those four residues, M314 comes from the αC helix, F405 from the DFG motif, and H384 from the HRD motif. The outward rotation of the αC helix corresponding to the inactive state breaks the salt-bridges of the electrostatic switch as well as the R-spine. All active kinases have the DFG motif in the “in” conformation. A different inactive state occurs when the DFG motif is in the “out” conformation, which also correlates with a disruption of the structural integrity of the regulatory spine. The R-spine is formed even when the kinase domain adopts the active-like conformation with unphosphorylated A-loop (the stable state at the top of Figure 3A). However, its stability is greatly increased (essentially locked) when the A-loop becomes phosphorylated. Figure 4B, showing the 1D PMFs as a function of the RMSD of the R-spine relative to 1Y57* conformation, demonstrate the free energy profile of the stability of the R-spine before and after the A-loop is phosphorylated. The conformation of the R-spine in 1Y57* is very similar to that in 1Y57 so choosing one as the reference frame to define the RMSD is adequate. Both 1D-PMFs were calculated on the basis of the existing umbrella windows (no additional US calculation were needed to obtain those PMFs). As shown in Figure 4B, two stable conformations of the R-spine are possible when the A-loop is not phosphorylated. The conformation centered around 1.6 Å of RMSD relative to 1Y57* corresponds to a state in which the R-spine is formed (“on” conformation in Figure 4B), while the other one is associated with the broken form of the spine (“off” conformation in Figure 4B). When the A-loop is not phosphorylated, even the active “on” conformation of the R-spine differs slightly from the conformation enhanced by 1Y57*. The free energy well corresponding to the “on” form of the R-spine exists for 1Y57, but with a slightly larger RMSD. The free energy difference between those two stable conformations (“on” minus “off”) is ~0.35 kcal/mol from integrating the Boltzman factor of the PMF shown in Figure 4B. This suggests that the R-spine is not locked into a single catalytically-competent configuration when the A-loop is open and unphosphorylated. However, it is important to keep in mind that the US calculation considered only the set of simulation windows in the overall neighborhood of the active state with an open A-loop. Specifically, these simulations do not include the down-regulated inactive state with a closed unphosphorylated A-loop. As this conformation is very stable, the catalytically competent form of the R-spine of the unphosphorylated kinase would appear considerably more unfavorable than that suggested by the 1D-PMF shown in Figure 4B if all the possible states of the kinase were taken into account. The sign of the free energy difference indicates that the non-catalytic competent form of the R-spine is slightly more favorable. In contrast, phosphorylation of the A-loop abolishes the broad flexibility of the R-spine, locking it in its catalytic competent “on” state. Similar results are also obtained using a new order parameter to monitor the flexibility of the R-spine and are displayed in Figure S4. However, the flexibility of the R-spine demonstrated in Figure 4B, especially the small free energy difference, is a consequence of the fact that the A-loop in the 1Y57 active-like system is already open (the US simulations windows were chosen to lie in the neighborhood of the active state and the inactive state was not explicitly included). If the down-regulated inactive state was included in the simulation of the unphophorylated kinase, the closed conformation of the A-loop would dominate, and as a result, the “off” state of the R-spine would be greatly favored. In this context, the net effect of phosphorylation would appear as a dramatic shift of the conformational equilibrium from the “off” state to the “on” state.

Figure 4.

(A) A structural view of the R-spine in the active state. (B) 1D-PMFs as a function of the RMSD of the regulatory spine (R-spine) relative to 1Y57* conformation. All heavy atoms in the R-spine are used in the calculation of RMSD. When the A-loop is open and unphosphorylated, the 1D PMFs indicate that the R-spine is flexible and is easy to break, as shown by the double free energy well in the PMF. Phosphorylation of the A-loop under these conditions locks the spine in the active conformation, which then appears as a single free energy basin in the PMF. Region that is to the left of 2.15 Å of RMSD is defined as the R-spine formed, while the rest is defined as the R-spine broken. Two representative structures are also illustrated.

To provide details of the effect of phosphorylation on each component of the R-spine, the interaction energies between a residue in the R-spine and the rest of the system (protein, ATP, magnesium ions, water) are calculated for the active 1Y57* and active-like 1Y57 conformations, ΔE_{unphos → phos} ≡ E(1Y57*) - E(1Y57). The effect of phosphorylation for a given residue is ascribed to ΔE_{unphos → phos}. By definition, a positive (negative) ΔE_{unphos → phos} implies that the phosphorylated state is destablized (stabilized) by this interaction. The sum of ΔE_{unphos → phos} values is −0.6, −2.1, −1.1, and −8.8 kcal/mol for L325, M314, F405 and H384, respectively. Phosphorylation of the A-loop stabilizes all four residues of the R-spine. This phenomenon could explain the free energy basin corresponding to the “on” form of the R-spine shifts to the left when the A-loop is phosphorylated. Figure S5 display the ΔE_{unphos → phos} as a function of residue index for all four residues. Among all the ΔE_{unphos → phos} values, those from L325 and M314 are relatively small in scales, as shown in Figure S5. This is consistent with the long distance from either L325 or M314 to Y416. However, the accumulation of small negative ΔE values contributes to the second largest favorable factor for M314. For F405, two ΔE_{unphos → phos} values contribute oppositely to the sum most. The ΔE_{unphos → phos} with E310 is 6.6 kcal/mol, while the ΔE_{unphos → phos} with water is −8.2 kcal/mol. A more detailed analysis of the destabilizing interaction between F405 and E310 is given in Figure S6. The large change in interaction energy between F405 and E310, due to the A-loop changing phosphorylation state, indicates that the R-spine (and the DFG-motif because F405 is shared in both regions) links the αC helix and P-site on the A-loop. The most prominent stabilizing effect upon phosphorylation of the A-loop is reflected by H384. It mainly comes through the interaction with water molecules surround it. It’s worth pointing out that interaction with water molecules also changes significantly for Y416 when it’s phosphorylated. Considering the closeness among Y416, F405 and H384, solvent may play a role in correlating the phosphorylation site (P-site) on the A-loop with the R-spine.

The HRD motif

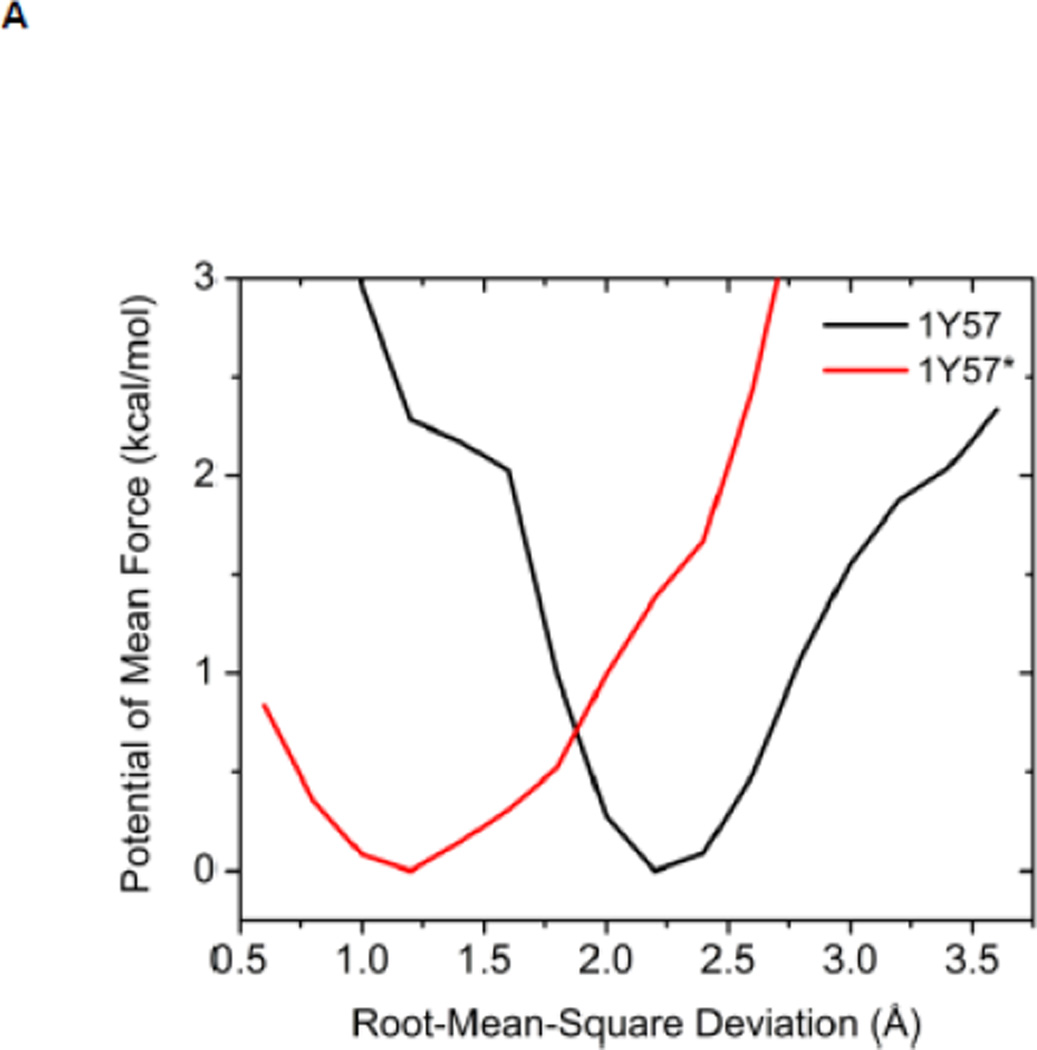
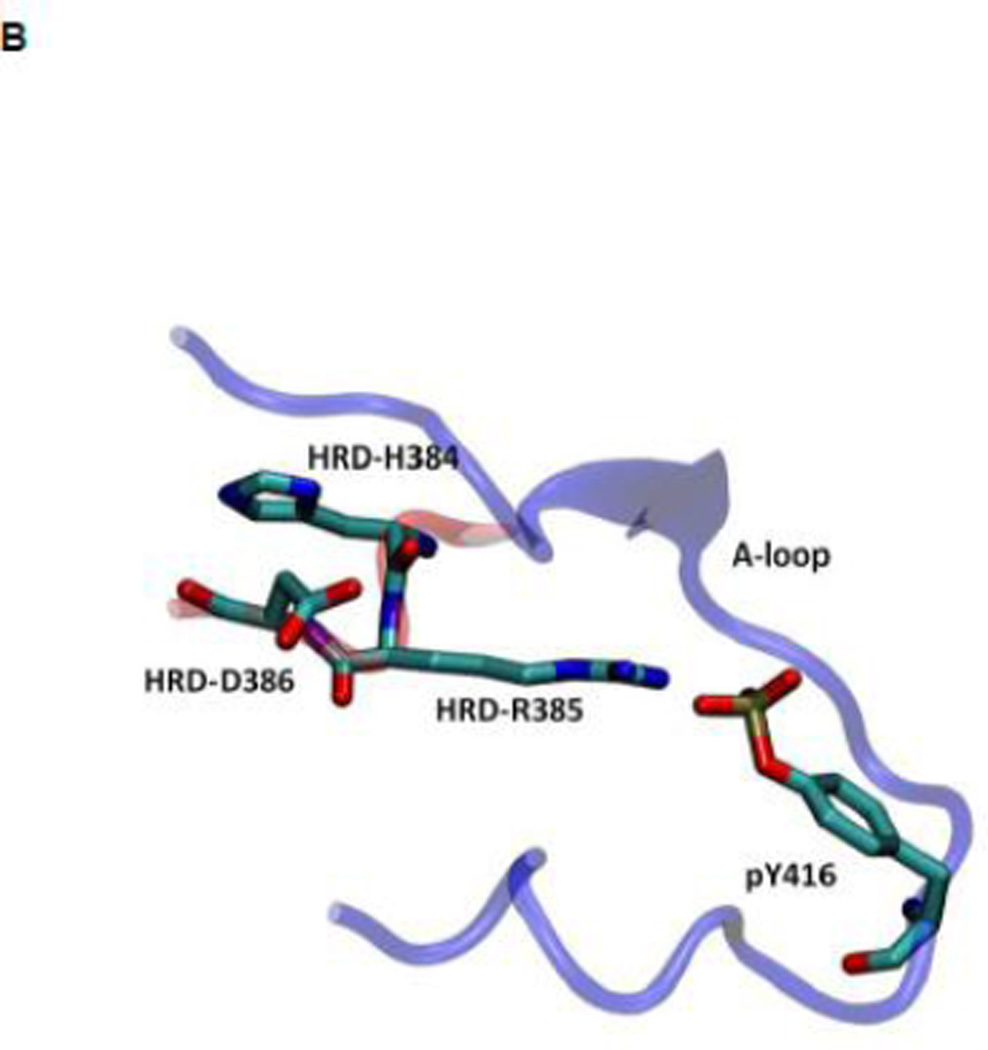
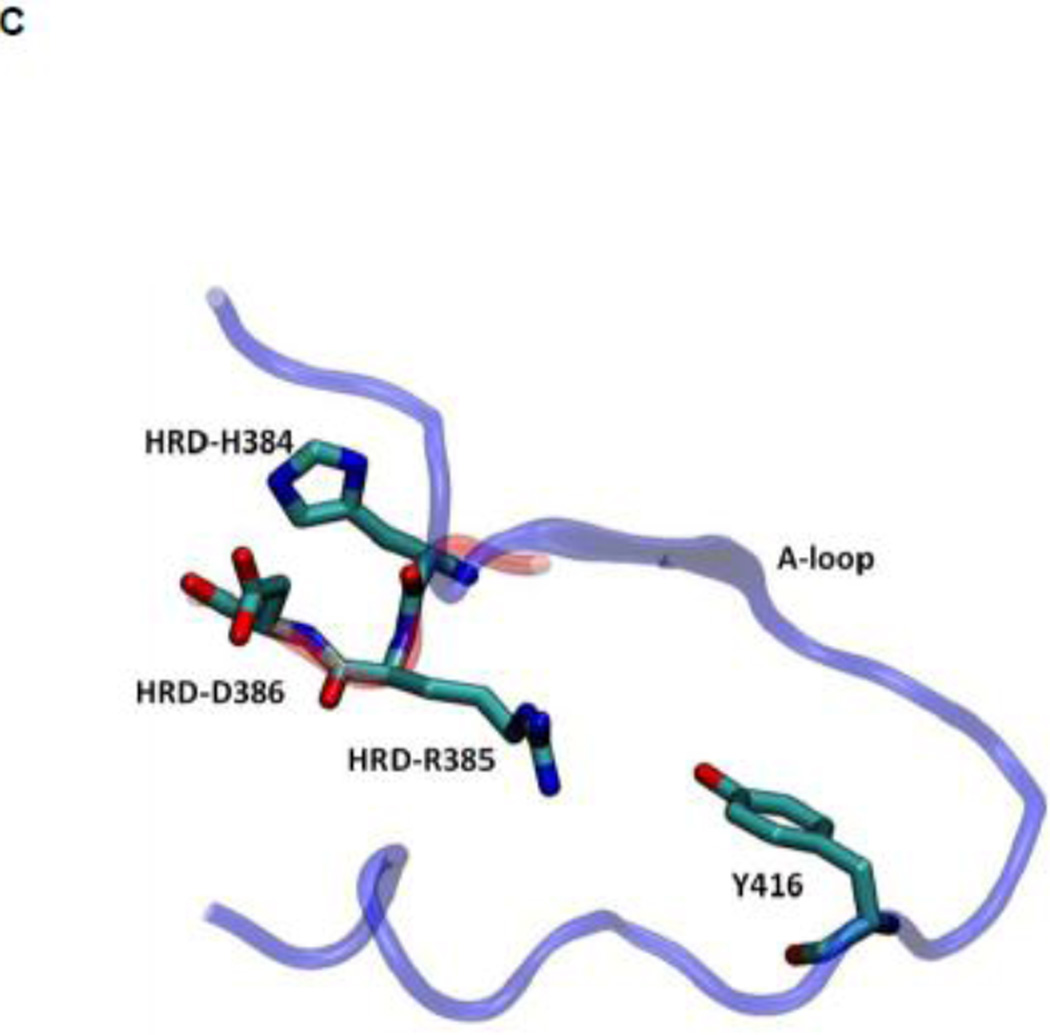
Another structural feature important for catalysis is the so-called HRD motif comprising 3 highly conserved amino acids (His384-Arg385-Asp386) located in the catalytic loop ^{17; 18}. The HRD motif is believed to stabilize the active conformation of the kinase domain and participate in catalysis ^{7; 18}. H384 is also one component of the R-spine. R385 forms a salt-bridge with pY416, which stabilizes phosphorylation in the A-loop and anchors the HRD motif. D386 is the most conserved residue of the HRD motif. It participates in the binding of substrate when the kinase is active, is responsible for the correct orientation of the P-site hydroxyl group in the substrate, and also serves as a Lewis base to accept a proton from the substrate in the phosphorylation reaction ^{7; 50; 51}. Figure 5 demonstrates the free energy profile of the stability of the HRD motif before and after the A-loop is phosphorylated. The 1D PMFs as a function of the RMSD of all heavy atoms of the HRD motif, relative to 1Y57* conformation, are shown in this figure. One should note that those 1D-PMFs are calculated in the same way as those presented in Figure 4B. According to the free energy profiles, the conformation of the HRD motif is stabilized around 2.2 Å of RMSD relative to its active conformation when the A-loop is not phosphorylated, whereas phosphorylation induces a local conformational transition which shifts the HRD motif to the more catalytic competent state and pins it at that state. An inspection of the local conformational change yields that it mainly occurs on the backbone of R385 and D386, as shown in Figure 6. A comparison of the backbone conformations among 1Y57, 1Y57* and wt-3DQW* shows that the conformations of 1Y57* and wt-3DQW* are close to each other and are distinctly separated from 1Y57, for both R385 and D386.

Figure 5.

(A) 1D-PMFs as a function of the RMSD of the HRD motif relative to 1Y57* conformation. All heavy atoms in the HRD motif are used in the calculation of RMSD. (B) A representative structure of the HRD motif in the 1Y57* active state. (C) A representative structure of the HRD motif in the 1Y57 active-like state.

Figure 6.

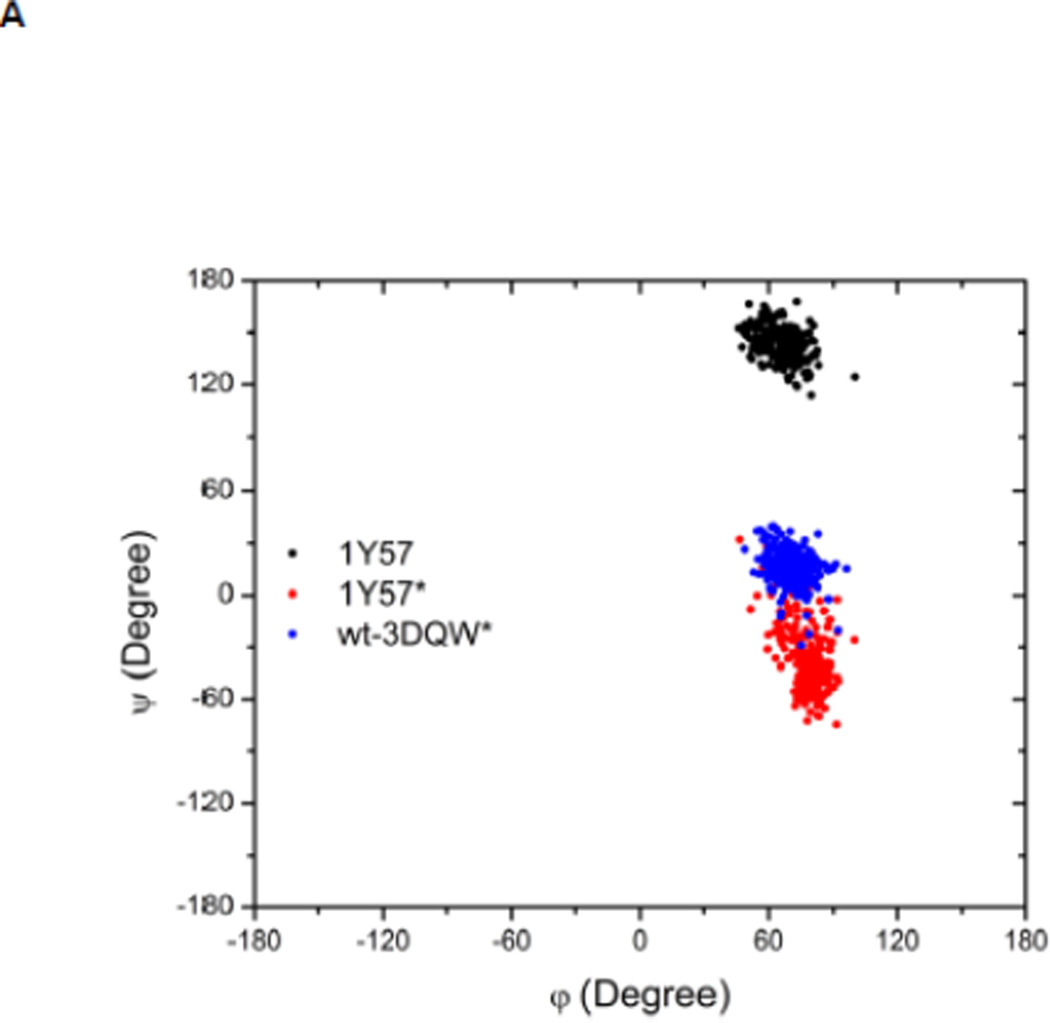
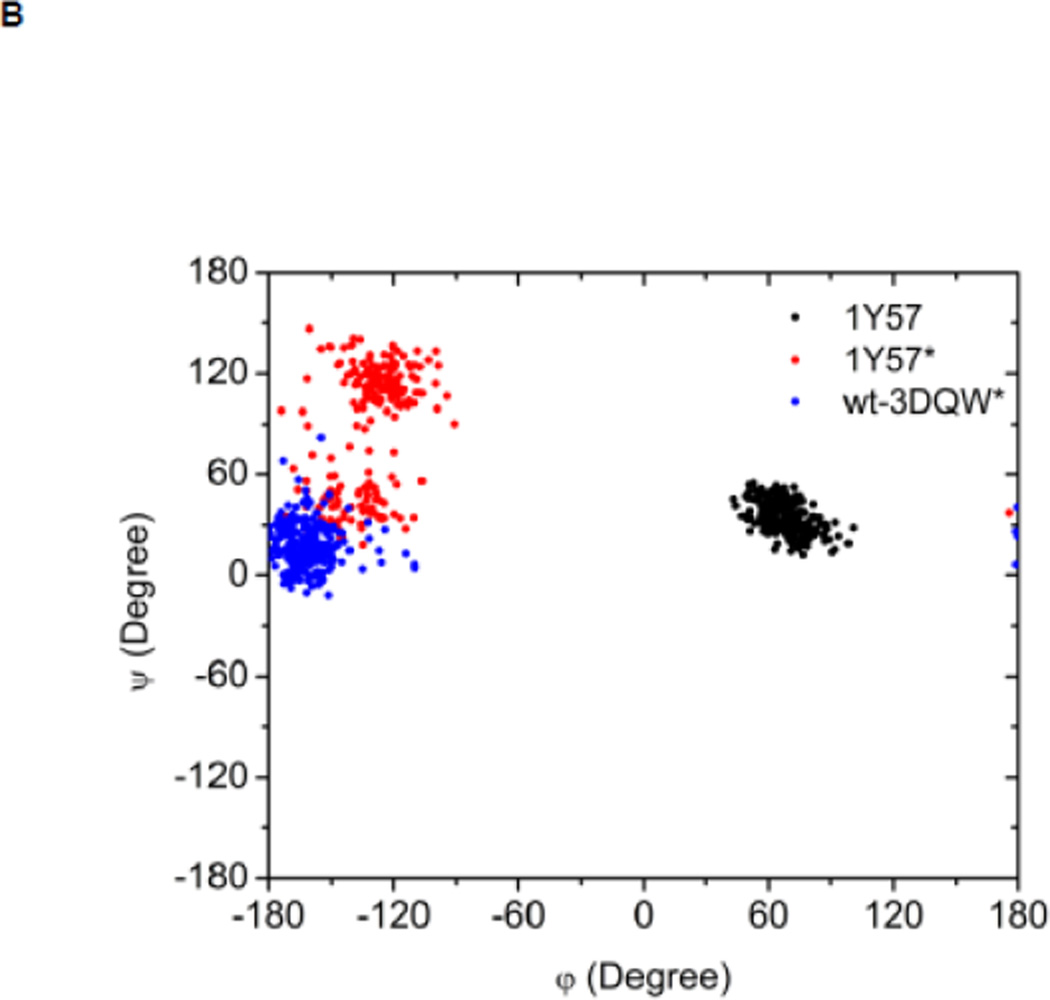
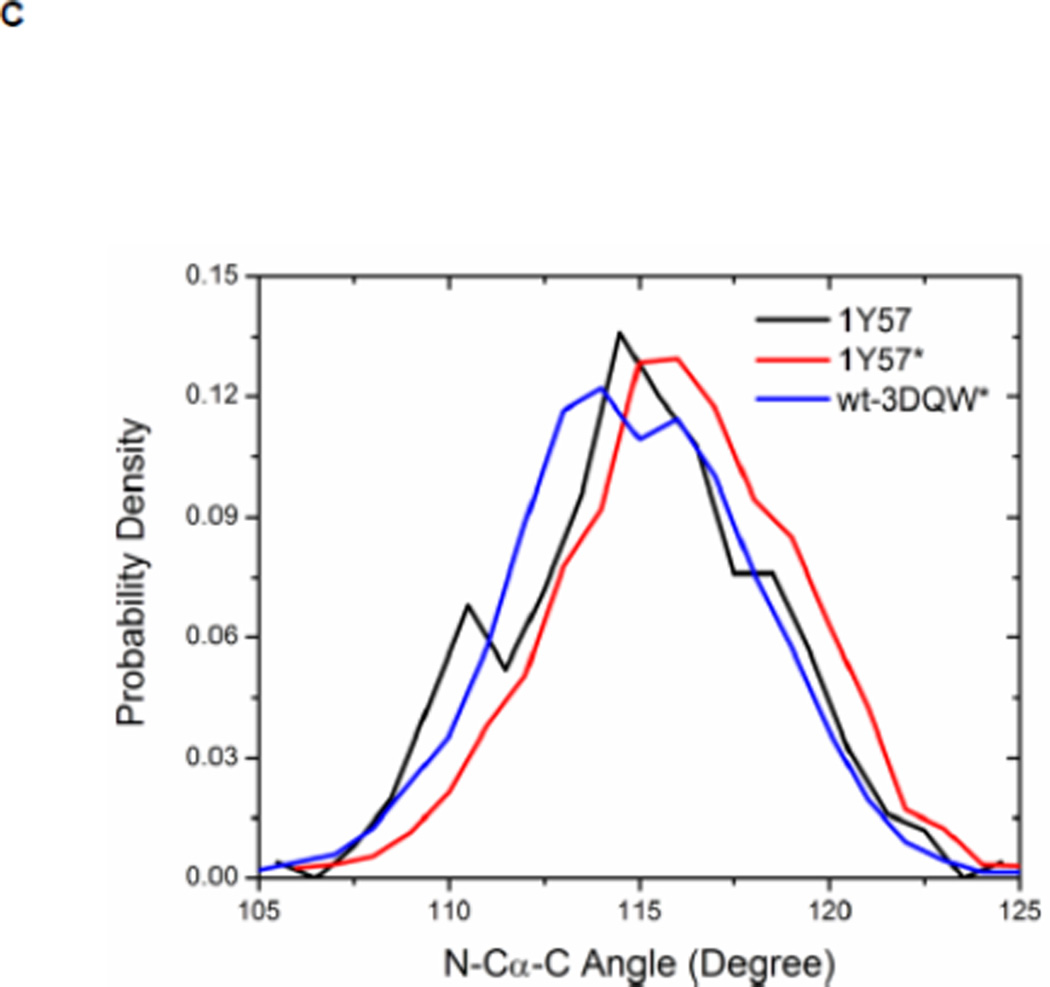
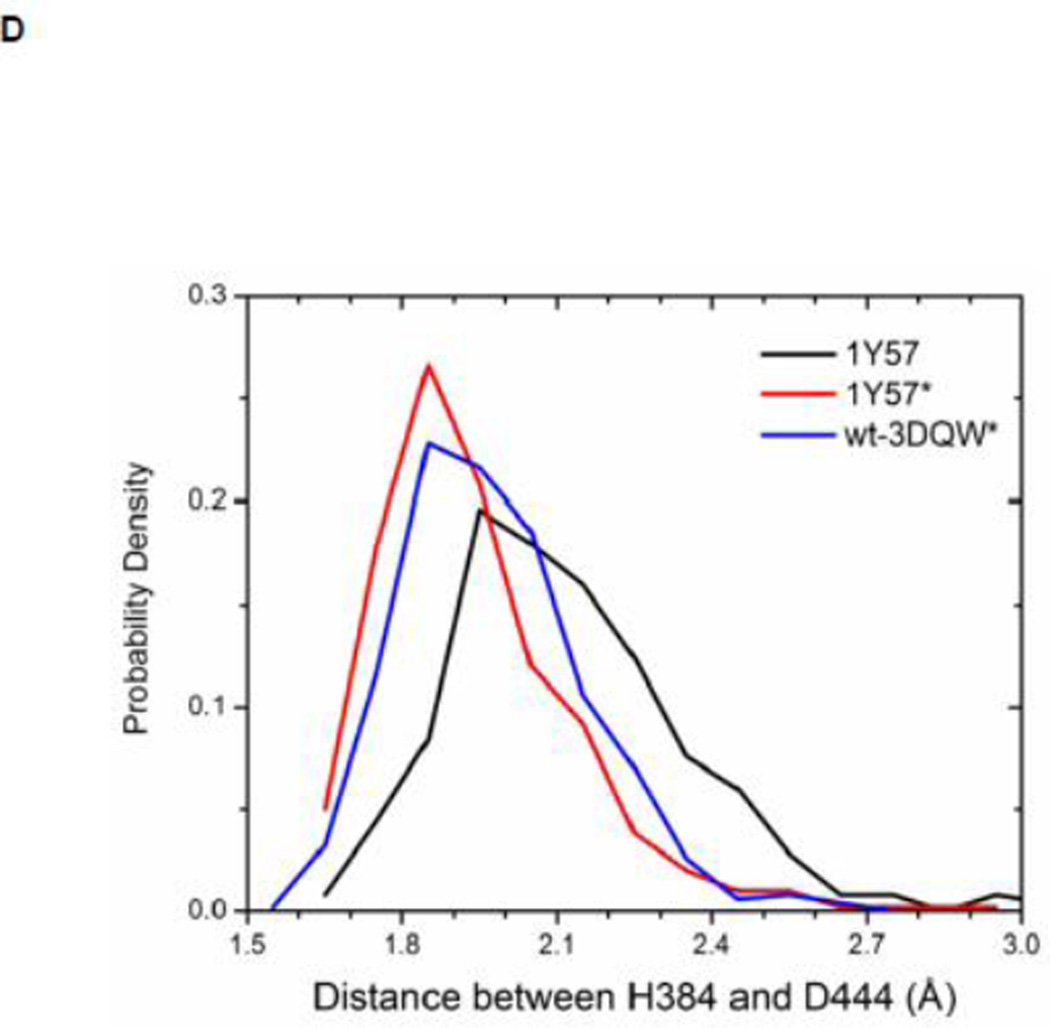
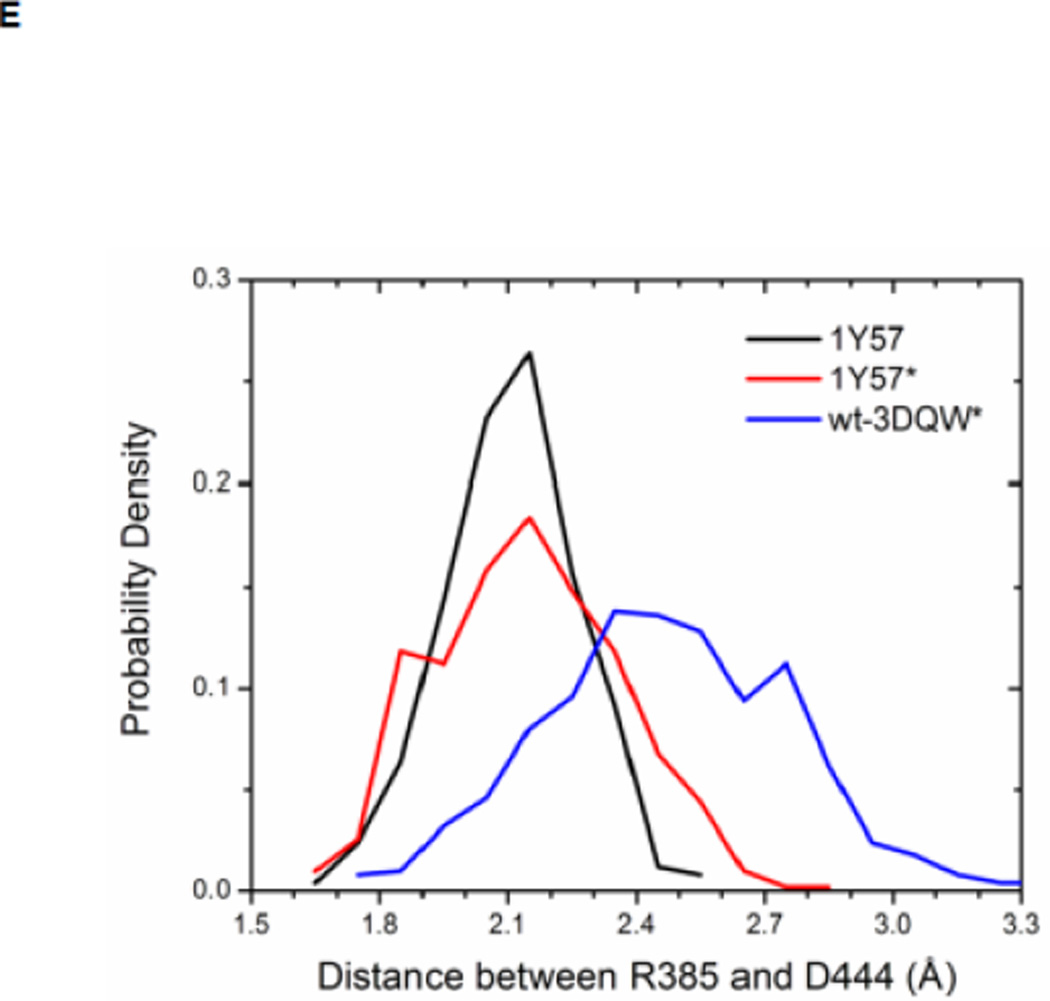
Local conformations of the HRD motif before and after phosphorylation. (A) Scatter plot of backbone φ vs ψ (Ramachandran plot) from R385. (B) Scatter plot of backbone φ vs ψ from D386. (C) Probability density of the backbone bond angle (N-Cα-C) of R385. (D) Probability density of the distance between H384 amide hydrogen atom and D444 side chain oxygen atom. (E) Probability density of the distance between R385 amide hydrogen atom and D444 side chain oxygen atom. Since the two oxygen atoms in the side chain of D444 are equivalent chemically, distances from the hydrogen atom to both oxygen atoms are computed and the smaller one is used to make those probability density plots.

As for the R-spine, an analysis of energy components was also performed for the HRD motif. The ΔE_{unphos → phos} as a function of residue index for R385 and D386 are given in Figure S7. The sum of individual ΔE_{unphos → phos} values for R385 and D386 is −6.6 and 5.0 kcal/mol, respectively. Hence, phosphorylation stabilizes R385 but has the opposite effect on D386. The overall effect of phosphorylation on HRD motif is to stabilize the motif by approximately 10 kcal/mol, taking H384 into consideration. Our energetic analysis confirms that pY416—R385 salt-bridge indeed anchors the HRD motif, but it has to balance many destabilizing factors, especially between R385 and R409 and R419. These destabilizing factors are side effects that are caused by Y416 phosphorylation. pY416 attracts R385, R409, and R419, making the positively-charged side chains closer. Anchoring the HRD motif through the interaction of pY416 with R385 also leads to modification of its side-chain conformation (see Figure S8). For D386, one destabilizing factor upon phosphorylation that is worth noting is from R388. The average distance between D386 C_γ atom and R388 C_ζ atom changes from 3.7 to 4.2 Å, caused by local conformational change upon phosphorylation (see Figure 6). The slightly longer distance between two oppositely charged residues makes D386 less stable. However, the larger separation between D386 and R388 may have important effect in that the separation opens up space for the side chain of substrate tyrosine residue.

Recently, Oruganty et al performed detailed analysis of the HRD motif using the high-resolution crystal structures of protein kinases and found that the backbone conformation of the HRD motif is in a strained geometry in most active conformations, resulting in favorable hydrogen bonds with conserved noncatalytic residues⁵². In particular, they have pointed out that the side chain of D444 in the αF helix is hydrogen-bonded to the backbone amides of H384 and R385 in nearly all the structures where the strained geometry is observed⁵². Point mutations at D444 that altered this hydrogen bonding pattern were shown to impair catalytic activity in Aurora kinase⁵². The average value of backbone (φ, ψ) of R385 is (65°, 145°), (78°, −36°), and (70°, 17°), for 1Y57, 1Y57*, and wt-3DQW* respectively. All three pairs fall in the category of strained geometry that is proposed by Oruganty et al. In addition, the bond angle (N-Cα-C) of R385 is computed for 1Y57, 1Y57*, and wt-3DQW* and its probability density is illustrated in Figure 6C. The average bond angle is 115°, 116°, and 115° for 1Y57, 1Y57*, and wt-3DQW* respectively. Those values of bond angles are in good agreement with that in high-resolution crystal structures and confirm that R385 demonstrates a conformational strain within the HRD motif in both active-like and active states. As proposed by Oruganty et al, one important consequence of this observation is that the backbone in the strained conformation forms hydrogen bonds, with D444 in the αF helix in particular. To inspect the formation of hydrogen bonds between the HRD motif and D444 in the αF helix, the distances between H384 and R385 backbone amide hydrogen atom and D444 side chain oxygen atoms were computed. The probability density as a function of R385−D444 donor hydrogen-acceptor distance is displayed in Figure 6D, while that of H384−D444 interaction is shown in Figure 6E. The average value of the donor hydrogen-acceptor distance is listed in Table 1. Assuming that a hydrogen bond is formed when the distance between donor hydrogen and acceptor is below 2.4 Å, the results in Table 1 suggest that H384 backbone amide group is hydrogen bonded with the side chain of D444 for all three systems. The results in Table 1 also indicate that the R385 amide group forms a hydrogen bond with the side chain of D444 for the 1Y57 active-like and 1Y57* active models. Therefore, analysis of the simulations confirms that the strained backbone conformation of the HRD motif forms hydrogen bonds with the conserved aspartate residue in the αF helix, in support of the model proposed by Oruganty et al.

Table 1. Average donor hydrogen-acceptor distances in the HRD motif (in Å).

The mean value of the distance between donor hydrogen and acceptor. The average value is calculated on the basis of MD equilibration simulation.

	1Y57	1Y57*	Wt-3DQW*
H384(H) ••• D444(OD1)	2.1	1.9	2.0
R385(H) ••• D444(OD2)	2.1	2.1	2.5

The electrostatic switch

One last structural motif that has been proposed to control the activation of the catalytic domain is a network of electrostatic interactions (“electrostatic switch”) involving six charged residues (D386, pY416, R409, E310, K295, and D404) linking the A-loop with the αC helix and active site ^{23; 29}. In the inactive conformation, a three-way network (Figure S9A and S9C) is formed where D386 couples with Y416, E310 interacts with R409, and K295 couples with D404. In the active conformation, the three-way network switches to a two-way network where E310 couples with K295 and R409 couples with Y416, as demonstrated in Figure S9A and S9B. This switch would shift the equilibrium in favor of the active state. Originally discovered in the catalytic domain of Lyn kinase, a similar motion is also found in the simulation of Hck kinase ³⁵. In both the active-like and active conformations, the salt bridge between K295 and E310 is formed. However, our interaction energy calculations show that the two-way network is only partially formed in the unphosphorylated active-like conformation because a strong interaction between Y416 and R409 is lacking. Phosphorylation of the A-loop not only completely turns on the electrostatic network in the active conformation (as the pY416—R409 salt-bridge is formed), it also strenghens the other component of this two-way network. The interaction energy between E310 and K295 changes from −23.94 kcal/mol in the unphosphorylated active-like conformation to −26.28 kcal/mol in the active conformation. Hence, when Y416 is phosphorylated, it also strengthens the two-way electrostatic network more stable.

We characterized the impact of the A-loop phosphorylation by comparing the interaction energy of Y416 and pY416 with other residues. The results as a function of residue number are given in Figure S10A. As expected, the A-loop is the region of the structure that is the most affected by phosphorylation of Y416. This is reflected by the number of residues displaying a non-zero ΔE_{unphos → phos} as well as the scale of ΔE. The impact of phosphorylation of the A-loop is also associated with structutral changes, which are reflected in the RMSD of the A-loop before and after phosphorylation (Figure S10B). The mean RMSD value is 1.6 Å and the maximal value reaches ~2.4 Å. More specifically, phosphorylation of Y416 affects residue R385, R409 and R419. When the A-loop is unphosphorylated, the interaction energy between Y416 and R385, R409, and R419 is −1.94, −3.06, and −0.96 kcal/mol respectively. Once phosphorylated, the negative charge of pY416 strongly attracts the surrounding arginine residues. ΔE value of −37.84, −21.14, and −37.57 is observed for R385, R409, and R419 respectively. Three salt-bridges greatly stabilize pY416 and the A-loop, locking the A-loop in the open conformation and making it ready for binding of a substrate. In turn, the pY416—R385 and pY416—R409 salt-bridges also have important effects on the HRD motif and the electrostatic switch.

METHOD

Atomic models and molecular dynamics simulation

For the sake of simplicity, only the structural stabilization caused by the A-loop phosphorylation inherent to the isolated kinase domain in the absence of the regulatory domains SH2 and SH3 (i.e., residues W260 to T521) was considered in the present simulations. The impact of the SH2 and SH3 domain and of the N-terminal linker region, which is likely to be of significance, shall be the object of future investigation. The simulation of the “active-like” conformation with unphosphorylated A-loop was based on the structure of the catalytic domain from PDB entry 1Y57 ¹⁶. The inhibitor and the sulfate ion were also removed from the system. An ATP molecule and two magnesium ions coordinating the ATP were added based on the high-resolution structure of PKA (PDB 1ATP) ⁴¹. The all-atom system was solvated in a truncated octahedral simulation cell constructed from an equilibrated 80 × 80 × 80 ų box of TIP3P water molecules ⁴²; the system comprises 11216 water molecules in total. The size of the simulation cell was chosen to extend at least 10 Å away from the surface of the protein. In addition, 22 Na⁺ ions and 19 Cl⁻ ions were inserted into the system to neutralize the total charge and to model a salt concentration of approximately 150 mM. The initial system with unphosphorylated A-loop was relaxed and equilibrated for a total of 3.5 ns of MD time (the equilibration time was kept short purposefully to avoid any systematic drift from the crystallographic structure in the absence of the regulatory domains). This system is referred to as the 1Y57 active-like conformation.

The initial structure of the active c-Src kinase domain with phosphorylated of tyrosine 416 (pY416) was also generated from PDB entry 1Y57 as well (the number of counter-ions was adjusted in order to maintain a charge neutral system). The equilibrated model of the unphosphorylated active-like form was used as the starting point to generate the model for the active phosphorylated form. The tyrosine from the equilibrated active-like simulation was phosphorylated. The system was subjected to 500 steps of steepest descent energy minimization, and simulated for 20 ns. The final configuration was used to initiate the self-learning adaptive umbrella sampling (US) for the active conformation with phosphorylated A-loop (see below). This procedure offers the advantage of allowing a direct comparison of the impact of phosphorylation of the A-loop on the flexibility and stability of the kinase domain. This phosphorylated system is referred to as the 1Y57* active conformation. To provide one additional comparison, a simulation of the active conformation with pY416 based on the PDB entry 3DQW ²⁰ was conducted. Since the crystal structure 3DQW contains a point mutation to the wild-type (wt) c-Src kinase, it was mutated back to the WT sequence and is referred as wt-3DQW* hereafter. The wt-3DQW* system was minimized for 500 steps using steepest descent algorithm and was simulated for 20 ns. The resulting MD trajectory was projected onto the two order parameters used to calculate the PMF in order to examine the overlap with the minimum free energy basin. The sequence of the constructs that were used in 1Y57, 1Y57*, and wt-3DQW*simulations was listed in Figure 1C. Specific residues and motifs that were used in US calculations and the following analysis were also included in Figure 1C with a color code.

All energy minimization and MD propagations (including US calculations) were performed using version 2.9 of the molecular simulation package NAMD ⁴³ with the all-atom CHARMM27 force field ⁴⁴. The isobaric-isothermal (NPT) ensemble was employed for all MD calculations. The pressure and temperature were controlled by Langevin piston ⁴⁵ method and Langevin dynamics and kept at 1 atmosphere pressure and 300 K, respectively. Periodic boundary conditions (PBC) were applied and Particle Mesh Ewald (PME) ⁴⁶ was used to treat long-range non-bonded interactions. The short-range non-bonded interactions were truncated at 12 Å, with a switching function turned on from 10 to 12 Å. Covalent bonds involving hydrogen atoms were constrained at their equilibrium distances so that a 2 fs time step was used throughout all simulations.

Self-Learning Adaptive Umbrella Sampling

US simulations were carried out to determine the 2D free energy landscape of conformational transition in c-Src kinase domain. Previous simulations using the string method with swarms of trajectories have been used to determine the minimum free energy pathway (MFEP) connecting the inactive and active-like conformations ³⁹. The MFEP was used to help identifying a small number of particularly meaningful order parameters to monitor the conformational transition. Two order parameters were then chosen to characterize the free energy landscape in the neighborhood of the active-like conformation. Configurations along the MFEP were used to generate the initial windows used to carry out the US calculations. The two order parameters chosen to characterize the conformation of the kinase domain are displayed in Figure 2B and 2C. The difference between the distances of the Glu310–Arg409 salt-bridge (d₁) and Glu310–Lys295 salt-bridge (d₂) is used to characterize the rotation of αC helix during the activation process (Figure 2B), while the average distances between O-Asp413 and N-Thr417, O-Asn414 and N-Ala418, and O-Glu415 and N-Arg419 is used to reflect the opening of the A-loop in the process (Figure 2C). Each umbrella window was simulated for 10 ns. A harmonic biasing potential with a force constant of 20 kcal/(mol · Ų) and a uniform spacing of 0.5 Å are applied on each order parameter.

The self-learning adaptive US method ⁴⁷ was used to compute the 2D PMFs. Briefly, it proceeds according to the following steps: (1) at each cycle the free energy landscape is calculated using currently available windows. (2) Among all possible windows, those with free energy value lower than the threshold W_max relative to the absolute minimum are selected to expand the sampling on the next cycle. (3) Each of the pre-selected windows attempts to create a new window in 3^N-1 neighboring location. Locations already occupied by windows are omitted. (4) In the case when two or more windows want to expand to the same location, the window with the lowest free energy is selected as the source of the system conformation to initiate the new simulation window. (5) This process is repeated until no more windows can be created below the free energy threshold W_max. The self-learning adaptive US calculation can be initiated from all the known states of the system as described above. This includes the possibility to use the configurations along a pathway determined from the string method. In this case, a third parameter Δ₁ is employed to restrict the creation of new windows within a reasonable distance away from the pathway. By employing the self-learning adaptive US methodology ⁴⁷, one could avoid performing extremely long unbiased MD simulations in order to determine the correct relative statistical weight of different regions in the configurational space. Although computational tools are available for such long unbiased MD simulations, the self-learning US method offers a computationally effective strategy to explore the free energy landscape in multiple dimensions.

The self-learning adaptive US of the 1Y57 active-like conformation (with unphosphorylated Y416 in the A-loop) was initiated with equilibrated configurations taken along the pathway determined from the string method. The projection of the pathway onto the two order parameters used for US is displayed in Figure 2D. A free energy threshold of 7.2 kcal/mol was used. The US simulations with the unphosphorylated A-loop were restricted to the region connecting the intermediate and active-like conformations such that a similar region was covered as the simulations with the phosphorylated A-loop. Therefore, the US calculations is effectively restricted to the overall neighborhood of the active-like conformation (as seen in PDB 1Y57) with an open conformation of the A-loop.

The self-learning adaptive US of the 1Y57* active conformation (with pY416 in the A-loop) was initiated from the 1Y57 active-like conformation to avoid corrupting the system with spurious configurations. A total of 28 umbrella windows were initially selected in the first cycle from the 20 ns unrestrained MD simulation such that the Euclidean distance in the order parameter space was minimal between an umbrella window center and the selected structure. A free energy threshold of 15 kcal/mol was used.

At the final stage, there were a total of 614 and 620 umbrella windows for the unphosphorylated and phosphorylated cases, respectively, which were post-processed with the weighted histogram analysis method (WHAM) ^{48; 49} to generate the 2D-PMFs shown in Figure 3A and 3B.

CONCLUSION

In this study, we have used umbrella sampling molecular dynamics simulations to characterize the conformational stability of the active state of the catalytic domain of c-Src kinase when tyrosine 416 in the A-loop is either unphosphorylated or phosphorylated. The computed free energy landscape shows that, while occurrences of an active-like conformation are permitted when the A-loop is unphosphorylated, the kinase domain does not exclusively remain in a catalytically competent state. Considerable flexibility and fluctuations can occur in the overall neighborhood of the active-like conformation of the kinase once the A-loop has been opened but remains unphosphorylated. The A-loop can adopt extended conformations, regardless of the orientation of the αC helix. An extended form of the A-loop can either accommodates substrate or trans-phosphorylates Y416. Therefore, results from our calculations agree with experimental evidence that mixing unphosphorylated kinase with substrate and ATP will demonstrate catalytic activity ^{22; 23}. Phosphorylation of the A-loop considerably reduces those fluctuations, having essentially the effect of locking the kinase in its catalytically competent active state. Phosphorylation of the A-loop has an impact on several catalytically important structural features, including the HRD motif in the catalytic loop, the hydrophobic regulatory spine, and the electrostatic switch network. As a consequence of several interactions, the catalytically competent conformation is thereby stabilized, which is consistent with an increased activity observed experimentally. The local structural features observed in the neighborhood of the active site and A-loop may also have long-range effect in the full length kinase. It is known that locking the kinase domain in the active or inactive state affects the configuration of regulatory domains through the conformation of the N-terminal linker ^{26; 35}. It will be interesting to see how phosphorylation of the A-loop, shown here to lock the kinase domain in the catalytically competent active conformation, will come into play regarding the regulatory modules. Similar computations on the full-length kinase are currently under way to address this issue.

Highlights.

Phosphorylation of the tyrosine 416 in the activation loop of c-Src kinase essentially “locks” the kinase into its catalytically competent conformation.

When the tyrosine 416 is unphosphorylated, there is considerable flexiblity of the kinase. While the active conformation of the kinase is not forbidden and can be visited transiently, it is not the predominant state.

Phosphorylation of the activation loop also contributes to stabilize several structural features that are critical for catalysis such as the hydrophobic regulatory spine.